Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms
Abstract
1. Introduction
2. Study Area
3. Data
3.1. Inventory Data
3.2. Landsat 8 Data
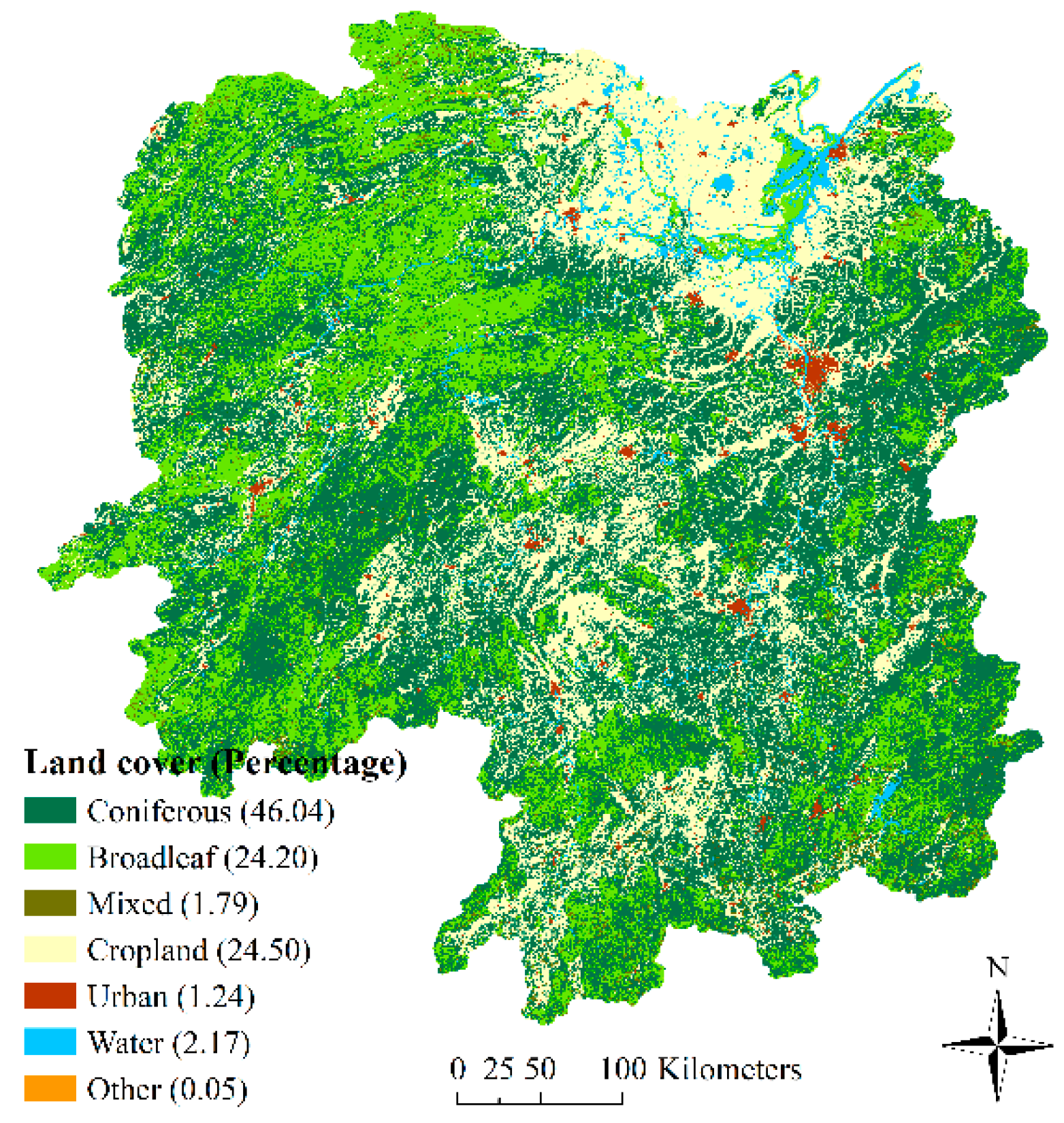
3.3. Land Cover Image
4. Methods
4.1. Algorithms of AGB Estimation
4.1.1. Linear Regression
4.1.2. Random Forest
4.1.3. Extreme Gradient Boosting
- (1)
- Using the second-order Taylor expression for the objective function, making the definition of the objective function more precise, and the optimal solution can be easily found;
- (2)
- The addition of a regularization term into the objective function to control the complexity of the tree to obtain a simple model and to avoid overfitting;
- (3)
- The use of sampling of the column feature to reduce the calculation amount and prevent overfitting; and
- (4)
- The use of an effective cache-aware block structure for out-of-core tree learning to parallel and distributed computing makes learning faster for hundreds of millions of examples.
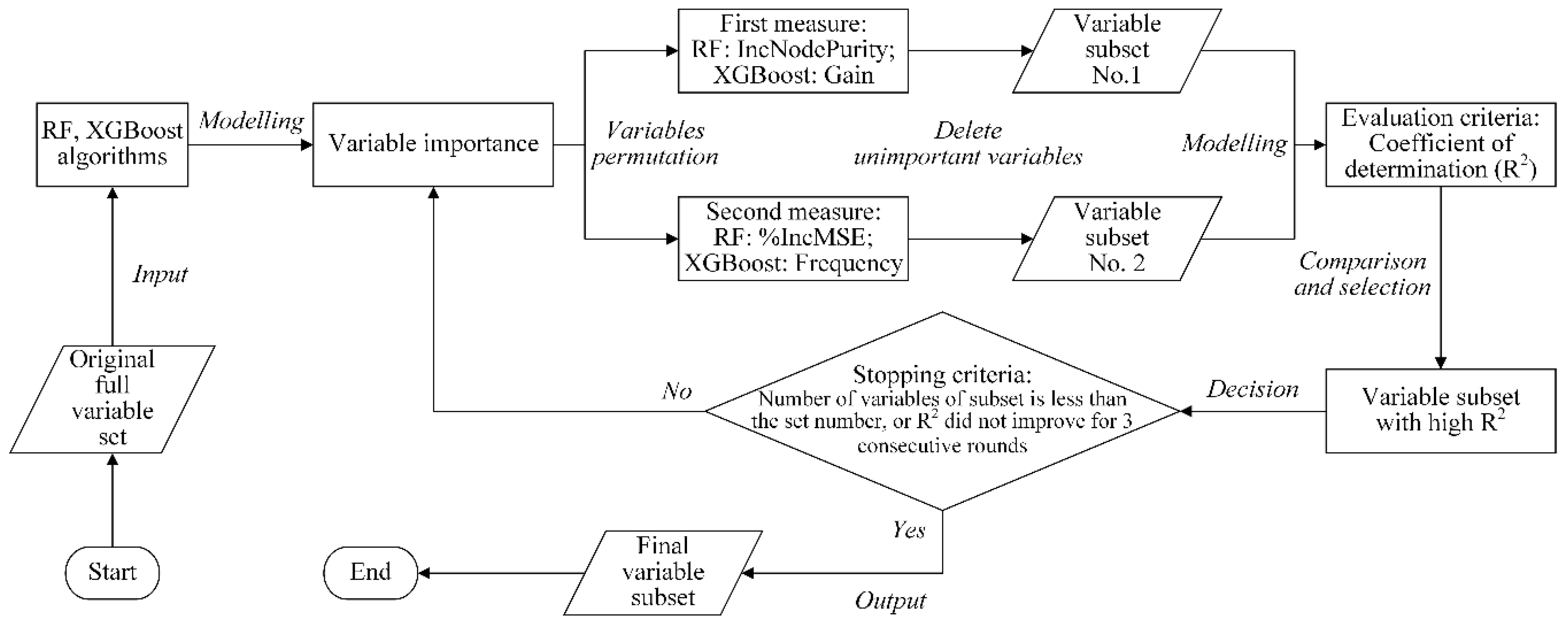
4.2. Methods of Variable Selection
4.2.1. Stepwise Regression Approach
4.2.2. Variable Importance-Based Method
4.3. Variable Interactions
4.4. Evaluation of AGB Models
5. Results
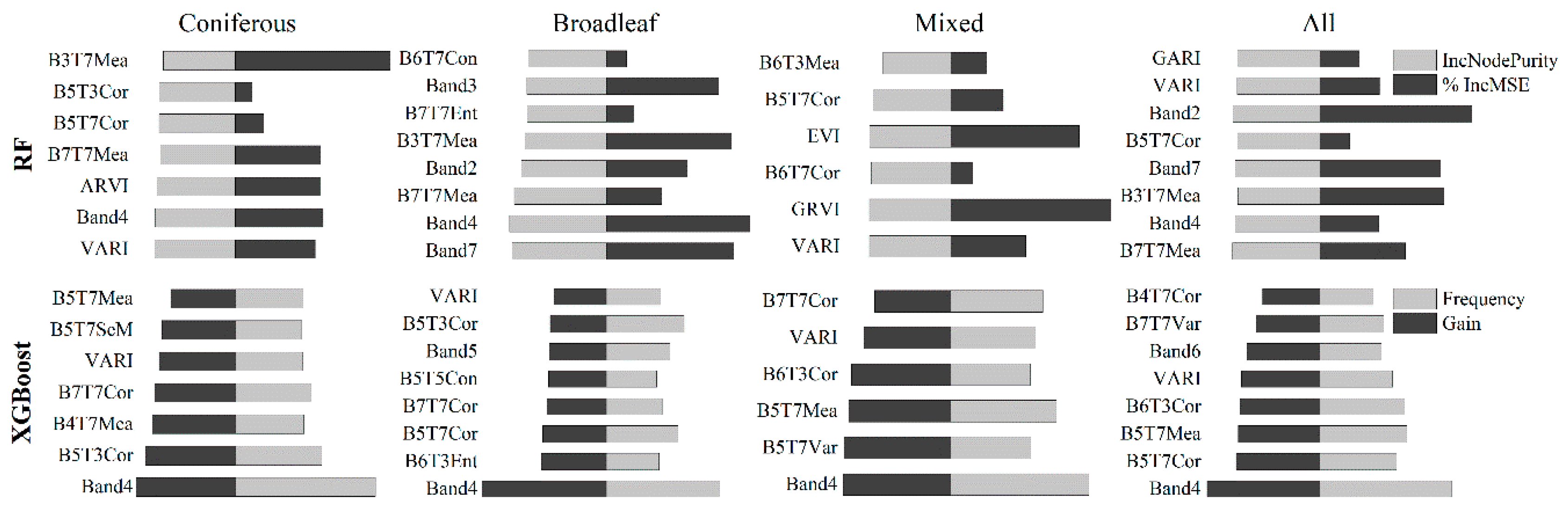
5.1. Role of Predictor Variables
5.1.1. Variable Importance
5.1.2. Variable Interactions
5.1.3. Performance of Variable Selection
5.2. Evaluation of AGB Models
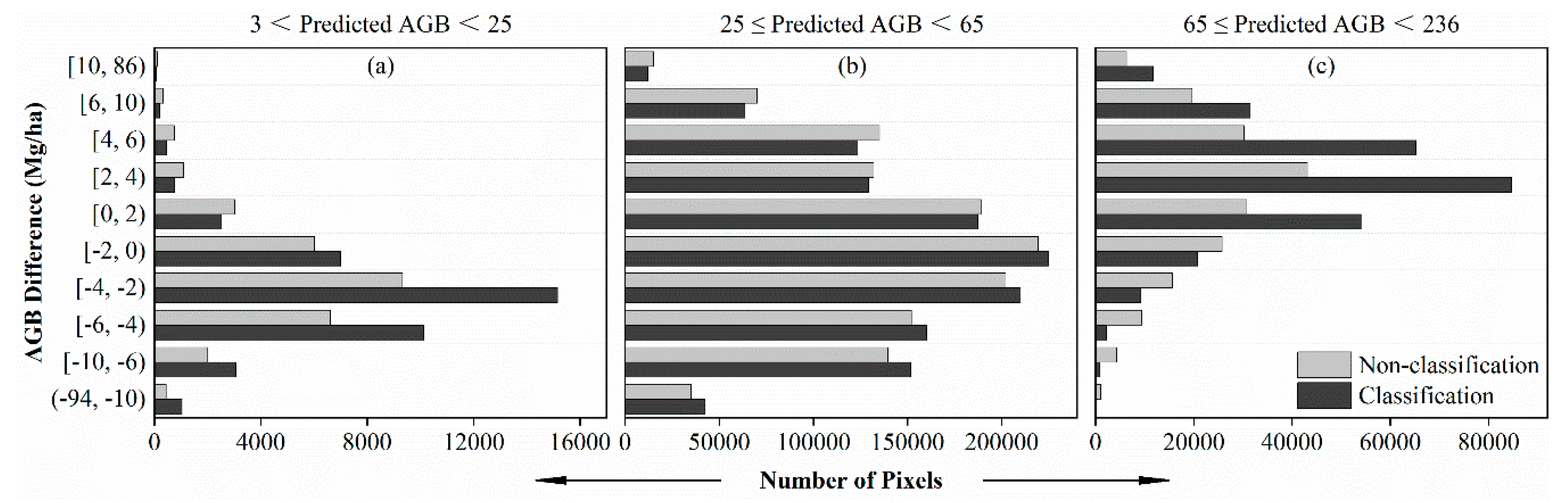
5.3. Mapping AGB
6. Discussion
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| Tree Species/Groups | Wood Density (p) | Tree Species/Groups | Wood Density (p) |
|---|---|---|---|
| Abies | 0.3464 | Pinus massoniana | 0.4476 |
| Betula | 0.4848 | Pinus tabulaeformis | 0.4243 |
| Cinnamomum | 0.4600 | Pinus taiwanensis | 0.4510 |
| Cryptomeria | 0.3493 | Pinus yunnanensis | 0.3499 |
| Cunninghamia lanceolata | 0.3098 | Populus | 0.4177 |
| Cupressus | 0.5970 | Quercus | 0.5762 |
| Eucalyptus | 0.5820 | Robinia pseudoacacia | 0.6740 |
| Fraxinus mandshurica | 0.4640 | Salix | 0.4410 |
| Larix | 0.4059 | Schima superba | 0.5563 |
| Liquidambar formosana | 0.5035 | Tilia | 0.3200 |
| Paulownia | 0.2370 | Ulmus | 0.4580 |
| Picea | 0.3730 | Other conifers | 0.3940 |
| Pinus armandii | 0.3930 | Other pines | 0.4500 |
| Pinus densata | 0.4720 | Other hardwood broadleaves | 0.6250 |
| Pinus elliottii | 0.4118 | Other softwood broadleaves | 0.4430 |
References
- Brown, S. Measuring carbon in forests: Current status and future challenges. Environ. Pollut. 2002, 116, 363–372. [Google Scholar] [CrossRef]
- Gower, S.T. Patterns and mechanisms of the forest carbon cycle. Annu. Rev. Environ. Resour. 2003, 28, 169–204. [Google Scholar] [CrossRef]
- Houghton, R.A. Aboveground forest biomass and the global carbon balance. Glob. Chang. Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
- Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res. Biogeosci. 2009, 114, 1–13. [Google Scholar] [CrossRef]
- Lu, D.; Batistella, M.; Moran, E. Satellite estimation of aboveground biomass and impacts of forest stand structure. Photogramm. Eng. Remote Sens. 2005, 71, 967–974. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, Z.; Sun, H.; Wang, G. Mapping forest ecosystem biomass density for xiangjiang river basin by combining plot and remote sensing data and comparing spatial extrapolation methods. Remote Sens. 2017, 9, 241. [Google Scholar] [CrossRef]
- West, P.W. Tree and Forest Measurement, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 978-3-319-14707-9. [Google Scholar]
- Crosby, M.K.; Matney, T.G.; Schultz, E.B.; Evans, D.L.; Grebner, D.L.; Londo, H.A.; Rodgers, J.C.; Collins, C.A. Consequences of landsat image strata classification errors on bias and variance of inventory estimates: A forest inventory case study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 243–251. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Avitabile, V.; Herold, M.; Heuvelink, G.B.M.; Simon, L.; Phillips, O.L.; Asner, G.P.; Armston, J.; Peter, S.; Banin, L.; Bayol, N.; et al. An integrated pan-tropical biomass map using multiple reference datasets. Glob. Chang. Biol. 2016, 22, 1406–1420. [Google Scholar] [CrossRef]
- Deng, S.; Katoh, M.; Guan, Q.; Yin, N.; Li, M. Estimating forest aboveground biomass by combining ALOS PALSAR and WorldView-2 data: A case study at Purple Mountain National Park, Nanjing, China. Remote Sens. 2014, 6, 7878–7910. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.J.; Fu, L.; Ruan, H.; She, G. Estimation of forest biomass dynamics in subtropical forests using multi-temporal airborne LiDAR data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Loveland, T.R.; Irons, J.R. Landsat 8: The plans, the reality, and the legacy. Remote Sens. Environ. 2016, 185, 1–6. [Google Scholar] [CrossRef]
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of Landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Loveland, T.R.; Dwyer, J.L. Landsat: Building a strong future. Remote Sens. Environ. 2012, 122, 22–29. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderso, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Cranny, M.; Hall, R.J.; Luther, J.E.; Beaudoin, A.; Goodenough, D.G.; Dechka, J.A. Monitoring Canada’s forests. Part 1: Completion of the EOSD land cover project. Can. J. Remote Sens. 2008, 34, 549–562. [Google Scholar] [CrossRef]
- Lehmann, E.A.; Wallace, J.F.; Caccetta, P.A.; Furby, S.L.; Zdunic, K. Forest cover trends from time series Landsat data for the Australian continent. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 453–462. [Google Scholar] [CrossRef]
- Shimabukuro, Y.E.; Batista, G.T.; Mello, E.M.K.; Moreira, J.C.; Duarte, V. Using shade fraction image segmentation to evaluate deforestation in landsat thematic mapper images of the Amazon Region. Int. J. Remote Sens. 1998, 19, 535–541. [Google Scholar] [CrossRef]
- Banskota, A.; Kayastha, N.; Falkowski, M.J.; Wulder, M.A.; Froese, R.E.; White, J.C. Forest monitoring using landsat time series data: A review. Can. J. Remote Sens. 2014, 40, 362–384. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Gitas, I.; Tsakiri-Strati, M. Estimating Mediterranean forest parameters using multi seasonal Landsat 8 OLI imagery and an ensemble learning method. Remote Sens. Environ. 2017, 199, 154–166. [Google Scholar] [CrossRef]
- Lu, D. Aboveground biomass estimation using Landsat TM data in the Brazilian Amazon. Int. J. Remote Sens. 2005, 26, 2509–2525. [Google Scholar] [CrossRef]
- Ouma, Y.O. Optimization of second-order grey-level texture in high-resolution imagery for statistical estimation of above-ground biomass. J. Environ. Inf. 2006, 8, 70–85. [Google Scholar] [CrossRef]
- Lu, D.; Batistella, M. Exploring TM image texture and its relationships with biomass estimation in Rondônia, Brazilian Amazon. Acta Amaz. 2005, 35, 249–257. [Google Scholar] [CrossRef]
- Shen, W.; Li, M.; Huang, C.; Tao, X.; Wei, A. Annual forest aboveground biomass changes mapped using ICESat/GLAS measurements, historical inventory data, and time-series optical and radar imagery for Guangdong province, China. Agric. For. Meteorol. 2018, 259, 23–38. [Google Scholar] [CrossRef]
- Yu, K.; Wu, X.; Ding, W.; Pei, J. Scalable and accurate online feature selection for big data. ACM Trans. Knowl. Discov. Data 2016, 11, 1–39. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, L.; Chen, M. Dictionary of Mathematics, 5th ed.; Science Press: Beijing, China, 2017; ISBN 9787030533364. [Google Scholar]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Sánchez-Maroño, N.; Alonso-Betanzos, A. Feature selection for high-dimensional data. Prog. Artif. Intell. 2016, 5, 65–75. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Li, M. Improving forest aboveground biomass (AGB) estimation by incorporating crown density and using landsat 8 OLI images of a subtropical forest in Western Hunan in Central China. Forests 2019, 10, 104. [Google Scholar] [CrossRef]
- Reese, H.; Nilsson, M.; Sandstro, P. Applications using estimates of forest parameters derived from satellite and forest inventory data. Comput. Electron. Agric. 2002, 37, 37–55. [Google Scholar] [CrossRef]
- Baccini, A.; Laporte, N.; Goetz, S.J.; Sun, M.; Dong, H. A first map of tropical Africa’s above-ground biomass derived from satellite imagery. Environ. Res. Lett. 2008, 3, 1–9. [Google Scholar] [CrossRef]
- Nelson, R.; Montesano, P.; Ranson, K.J.; Kharuk, V.; Sun, G.; Kimes, D.S. Estimating Siberian timber volume using MODIS and ICESat/GLAS. Remote Sens. Environ. 2009, 113, 691–701. [Google Scholar] [CrossRef]
- Monnet, J.-M.; Chanussot, J.; Berger, F. Support vector regression for the estimation of forest stand parameters using airborne laser scanning. IEEE Geosci. Remote Sens. Lett. 2011, 8, 580–584. [Google Scholar] [CrossRef]
- Blackard, J.A.; Finco, M.V.; Helmer, E.H.; Holden, G.R.; Hoppus, M.L.; Jacobs, D.M.; Lister, A.J.; Moisen, G.G.; Nelson, M.D.; Riemann, R.; et al. Mapping U.S. forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Vasconcelos, M.J.; Lucas, R.M. Understanding the relationship between aboveground biomass and ALOS PALSAR data in the forests of Guinea-Bissau (West Africa). Remote Sens. Environ. 2012, 121, 426–442. [Google Scholar] [CrossRef]
- Karlson, M.; Ostwald, M.; Reese, H.; Sanou, J.; Tankoano, B.; Mattsson, E. Mapping tree canopy cover and aboveground biomass in sudano-sahelian woodlands using landsat 8 and random forest. Remote Sens. 2015, 7, 10017–10041. [Google Scholar] [CrossRef]
- Zald, H.S.J.; Wulder, M.A.; White, J.C.; Hilker, T.; Hermosilla, T.; Hobart, G.W.; Coops, N.C. Integrating landsat pixel composites and change metrics with lidar plots to predictively map forest structure and aboveground biomass in Saskatchewan, Canada. Remote Sens. Environ. 2016, 176, 188–201. [Google Scholar] [CrossRef]
- Carmona, P.; Climent, F.; Momparler, A. Predicting failure in the U.S. banking sector: An extreme gradient boosting approach. Int. Rev. Econ. Financ. 2019, 61, 304–323. [Google Scholar] [CrossRef]
- Lei, X.; Tang, M.; Lu, Y.; Hong, L.; Tian, D. Forest inventory in China: Status and challenges. Int. For. Rev. 2009, 11, 52–63. [Google Scholar] [CrossRef]
- Zeng, W.; Tomppo, E.; Healey, S.P.; Gadow, K.V. The national forest inventory in China: History—Results—International context. For. Ecosyst. 2015, 2, 23. [Google Scholar] [CrossRef]
- Xie, X.; Wang, Q.; Dai, L.; Su, D.; Wang, X.; Qi, G.; Ye, Y. Application of China’s National Forest Continuous Inventory Database. Environ. Manage. 2011, 48, 1095–1106. [Google Scholar] [CrossRef]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef]
- Hunan Provincial People’s Government Natural Resources of Hunan Province. Available online: http://www.enghunan.gov.cn/AboutHunan/HunanFacts/NaturalResources/201507/t20150707_1792317.html (accessed on 1 November 2019).
- Zeng, W. Developing one-variable individual tree biomass models based on wood density for 34 tree species in China. For. Res. Open Access 2018, 7, 1–5. [Google Scholar]
- USGS Landsat Surface Reflectance Data. Available online: https://pubs.usgs.gov/fs/2015/3034/pdf/fs20153034.pdf (accessed on 27 March 2019).
- Richter, R. Correction of Atmospheric and Topographic Effects for High Spatial Resolution Satellite Imagery. Int. J. Remote Sens. 1997, 18, 1099–1111. [Google Scholar] [CrossRef]
- Teillet, P.M.; Guindon, B.; Goodenough, D.G. On the slope-aspect correction of multispectral scanner data. Can. J. Remote Sens. 1982, 8, 84–106. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man. Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- ESA Land Cover CCI Product User Guide. Available online: http://maps.elie.ucl.ac.be/CCI/viewer/download/ESACCI-LC-Ph2-PUGv2_2.0.pdf (accessed on 10 April 2017).
- Breiman, L. Random forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Yu, Y.; Li, M.; Fu, Y. Forest type identification by random forest classification combined with SPOT and multitemporal SAR data. J. For. Res. 2018, 29, 1407–1414. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Tantanee, S. How to explain and predict the shape parameter of the generalized extreme value distribution of streamflow extremes using a big dataset. J. Hydrol. 2019, 574, 628–645. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- He, H.; Zhang, W.; Zhang, S. A novel ensemble method for credit scoring: Adaption of different imbalance ratios. Expert Syst. Appl. 2018, 98, 105–117. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Guyon, I.; Andre, E. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Liaw, A.; Wiener, M. RandomForest: Breiman and Cutler’s Random Forests for Classification and Regression. Available online: https://cran.r-project.org/package=randomForest (accessed on 25 March 2018).
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y. xgboost: Extreme Gradient Boosting. Available online: https://cran.r-project.org/package=xgboost (accessed on 1 August 2019).
- Dash, M.; Liu, H. Feature selection for classification. Intell. Data Anal. 1997, 1, 131–156. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Freeman, E.; Frescino, T. ModelMap: Modeling and Map Production Using Random Forest and Related Stochastic Models. Available online: https://cran.r-project.org/web/packages/ModelMap/index.html (accessed on 11 September 2018).
- Suganuma, H.; Abe, Y.; Taniguchi, M.; Tanouchi, H.; Utsugi, H.; Kojima, T.; Yamada, K. Stand biomass estimation method by canopy coverage for application to remote sensing in an arid area of Western Australia. For. Ecol. Manag. 2006, 222, 75–87. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Freeman, E.A.; Moisen, G.G.; Coulston, J.W.; Wilson, B.T. Random forests and stochastic gradient boosting for predicting tree canopy cover: Comparing tuning processes and model performance. Can. J. For. Res. 2016, 46, 323–339. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative analysis of modeling algorithms for forest aboveground biomass estimation in a subtropical region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Kajisa, T.; Murakami, T.; Mizoue, N.; Kitahara, F.; Yoshida, S. Estimation of stand volumes using the k-nearest neighbors method in Kyushu, Japan. J. For. Res. 2008, 13, 249–254. [Google Scholar] [CrossRef]
- Ustin, S.L.; Roberts, D.A.; Gamon, J.A.; Asner, G.P.; Green, R.O. Using imaging spectroscopy to study ecosystem processes and properties. Bioscience 2004, 54, 523. [Google Scholar] [CrossRef]
- USGS Landsat 8 (L8) Data Users Handbook. Available online: https://prd-wret.s3-us-west-2.amazonaws.com/assets/palladium/production/atoms/files/LSDS-1574_L8_Data_Users_Handbook_v4.pdf (accessed on 20 September 2004).
- Barsi, J.; Lee, K.; Kvaran, G.; Markham, B.; Pedelty, J. The spectral response of the Landsat-8 operational land imager. Remote Sens. 2014, 6, 10232–10251. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Stark, R.; Grits, U.; Rundquist, D.; Kaufman, Y.; Derry, D. Vegetation and soil lines in visible spectral space: A concept and technique for remote estimation of vegetation fraction. Int. J. Remote Sens. 2002, 23, 2537–2562. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Kelsey, K.; Neff, J. Estimates of aboveground biomass from texture analysis of landsat imagery. Remote Sens. 2014, 6, 6407–6422. [Google Scholar] [CrossRef]
- Dietterich, T.G. An experimental comparison of three methods for constructing ensembles of decision trees. Mach. Learn. 2000, 40, 139–157. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene selection and classification of microarray data using random forest. BMC Bioinf. 2006, 7, 1–13. [Google Scholar] [CrossRef]
- Sheridan, R.P.; Wang, W.M.; Liaw, A.; Ma, J.; Gifford, E.M. Extreme gradient boosting as a method for quantitative structure—Activity relationships. J. Chem. Inf. Model. 2016, 56, 2353–2360. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Wolff, E. Very high resolution object-based land use–land cover urban classification using extreme gradient boosting. IEEE Geosci. Remote Sens. Lett. 2018, 15, 607–611. [Google Scholar] [CrossRef]
- Dong, J.; Kaufmann, R.K.; Myneni, R.B.; Tucker, C.J.; Kauppi, P.E.; Liski, J.; Buermann, W.; Alexeyev, V.; Hughes, M.K. Remote sensing estimates of boreal and temperate forest woody biomass: Carbon pools, sources, and sinks. Remote Sens. Environ. 2003, 84, 393–410. [Google Scholar] [CrossRef]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of machine learning approaches for biomass and soil moisture retrievals from remote sensing data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef]
- Moghaddam, M.; Dungan, J.L.; Acker, S. Forest variable estimation from fusion of SAR and multispectral optical data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2176–2187. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
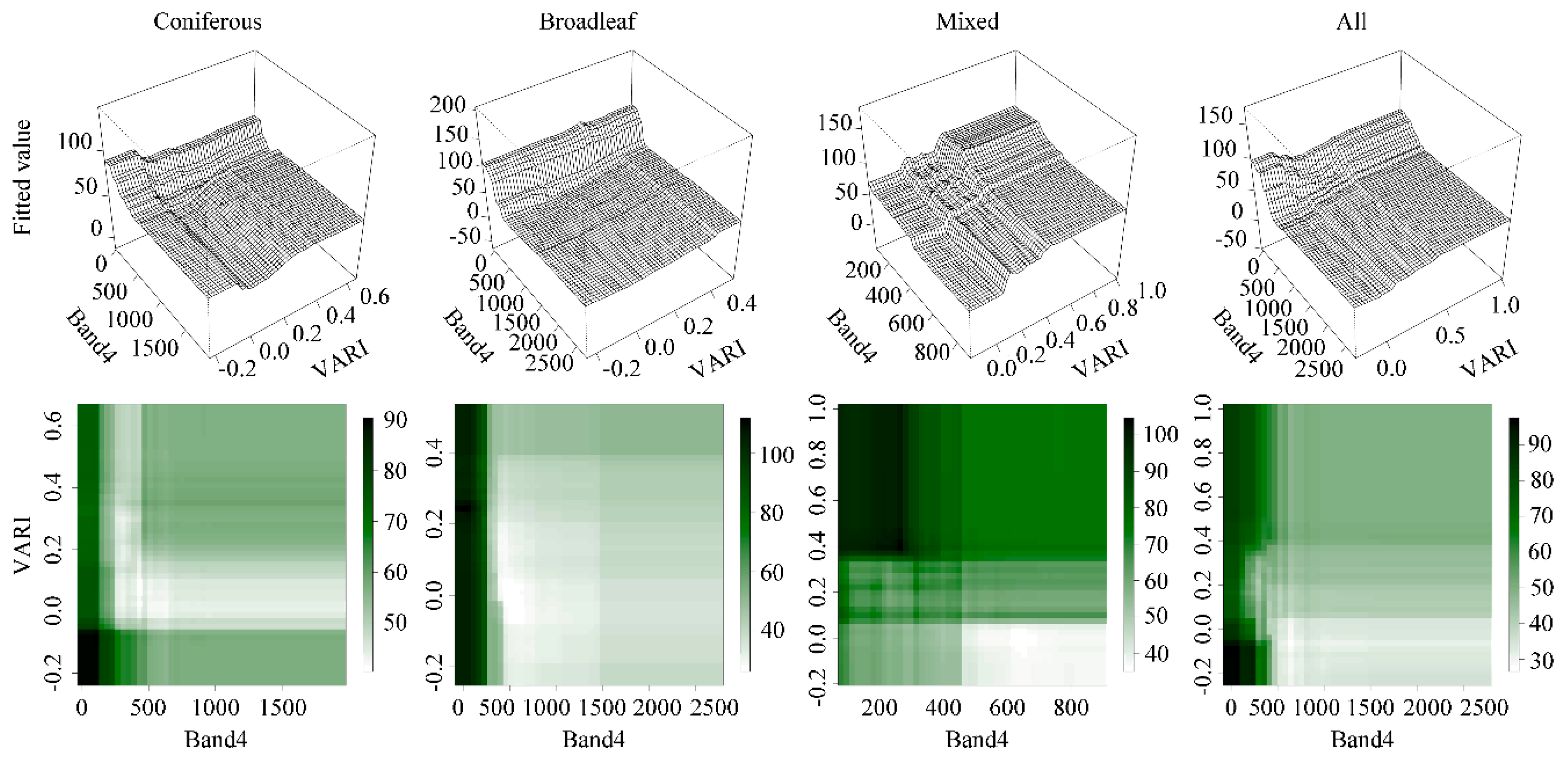
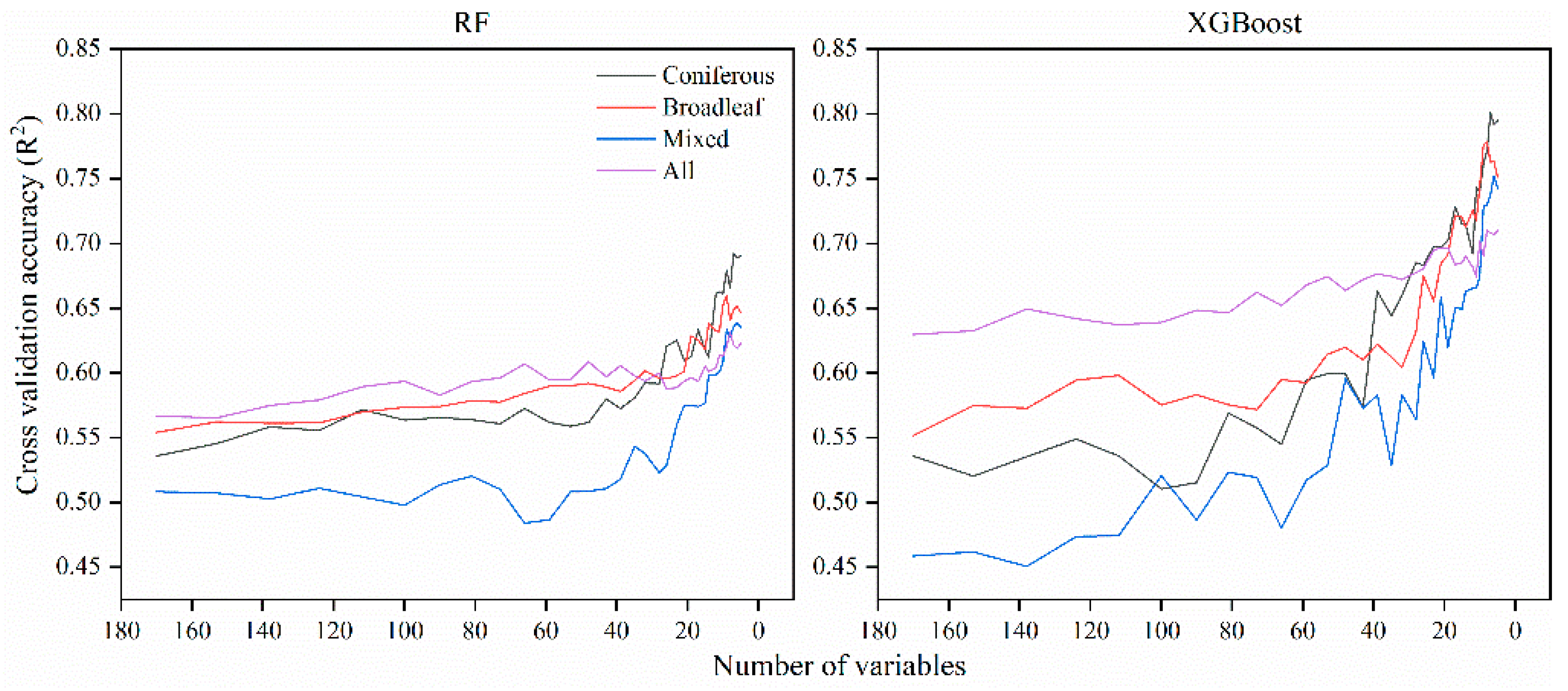
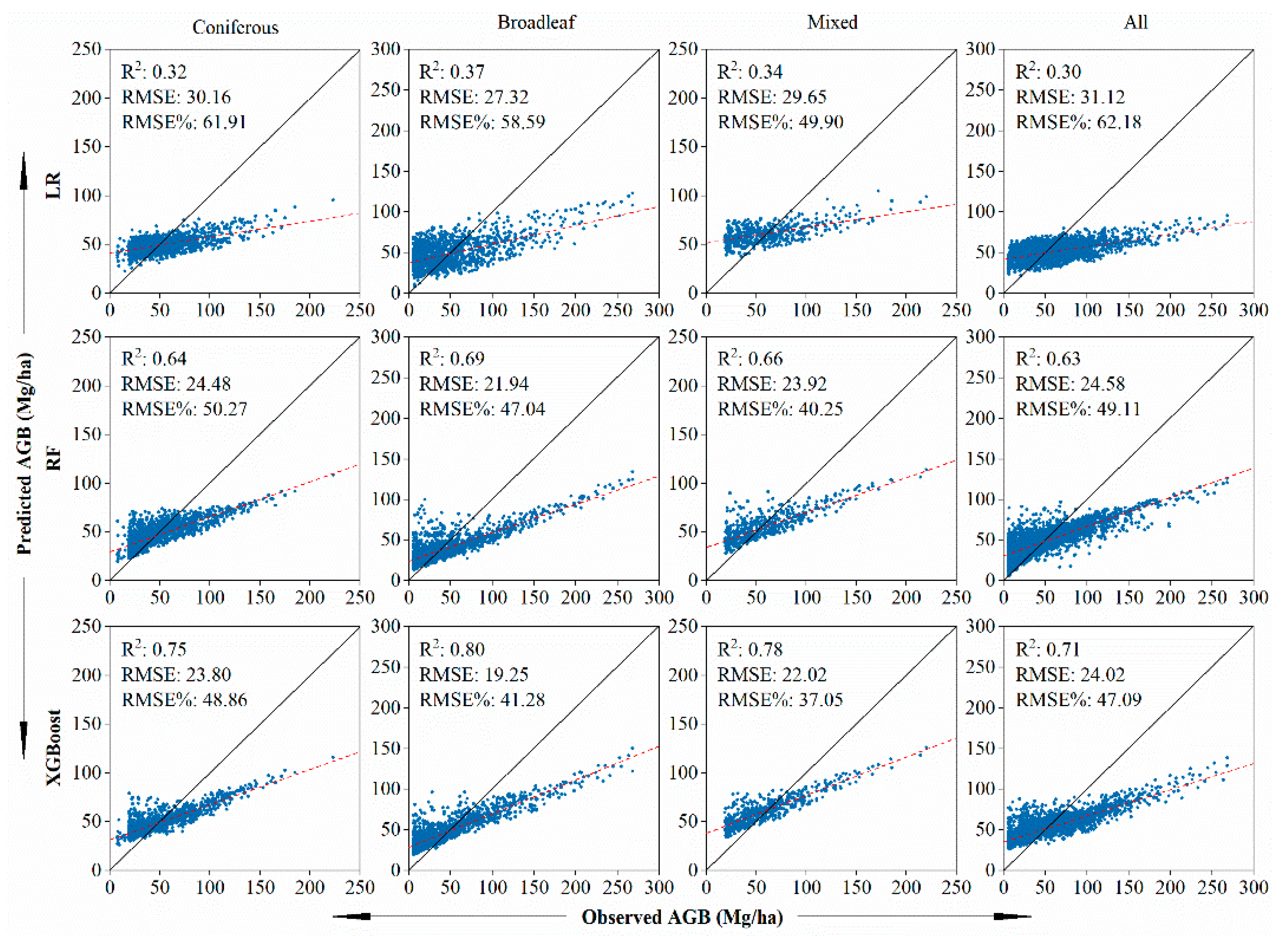

| Forest Type | Standard of Division |
|---|---|
| Coniferous | Pure coniferous forest (single coniferous species stand volume ≥ 65%) |
| Coniferous mixed forest (coniferous species total stand volume ≥ 65%) | |
| Broadleaf | Pure broadleaf forest (single broad-leaved species stand volume ≥ 65%) |
| broadleaf mixed forest (broad-leaved species total stand volume ≥ 65%) | |
| Mixed | Broadleaf-coniferous mixed forest (total stand volume of coniferous or broad-leaved species accounting for 35%–65%) |
| Forest Type | Count | Minimum | Maximum | Mean | Standard Deviation | Percentage of Different AGB Range (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5–30 | 30–60 | 60–90 | 90–120 | 120–270 | ||||||
| Coniferous | 1839 | 7.68 | 223.12 | 48.71 | 26.57 | 27.90 | 45.62 | 19.03 | 5.22 | 2.23 |
| Broadleaf | 1535 | 5.48 | 268.60 | 46.63 | 43.81 | 44.36 | 26.78 | 14.07 | 7.62 | 7.17 |
| Mixed | 512 | 18.60 | 219.95 | 59.43 | 34.21 | 20.31 | 38.87 | 24.61 | 9.38 | 6.84 |
| All | 3886 | 5.48 | 268.60 | 50.06 | 35.34 | 33.40 | 37.29 | 17.81 | 6.72 | 4.79 |
| Variable Type | Variables Number | Variable Name | Description |
|---|---|---|---|
| Band Image | 6 | Band2, Band3, Band4, Band5, Band6, Band7 | Landsat 8 Bands 2–7: Blue, Green, Red, NIR, SWIR1, SWIR2 |
| Vegetation Index | 20 | ARVI | Atmospherically Resistant Vegetation Index |
| DVI | Difference Vegetation Index | ||
| EVI | Enhanced Vegetation Index | ||
| GARI | Green Atmospherically Resistant Index | ||
| GDVI | Green Difference Vegetation Index | ||
| GNDVI | Green Normalized Difference Vegetation Index | ||
| GRVI | Green Ratio Vegetation Index | ||
| GVI | Green Vegetation Index | ||
| IPVI | Infrared Percentage Vegetation Index | ||
| LAI | Leaf Area Index | ||
| MNLVI | Modified Non-Linear Vegetation Index | ||
| MSRVI | Modified Simple Ratio Vegetation Index | ||
| NDVI | Normalized Difference Vegetation Index | ||
| NLVI | Non-Linear Vegetation Index | ||
| OSAVI | Optimized Soil Adjusted Vegetation Index | ||
| RDVI | Renormalized Difference Vegetation Index | ||
| RVI | Ratio Vegetation Index | ||
| SAVI | Soil Adjusted Vegetation Index | ||
| TDVI | Transformed Difference Vegetation Index | ||
| VARI | Visible Atmospherically Resistant Index | ||
| Texture Image | 144 | BiTjCon, BiTjDis, BiTjMea, BiTjHom, BiTjSeM, BiTjEnt, BiTjVar, BiTjCor | Landsat bands 2–7 texture measurement using gray-level co-occurrence matrix |
| Forest Type | Classification of CCI-LC | Producer Accuracy | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Coniferous | Broadleaf | Mixed | Cropland | Urban | Water | Other | |||
| Classification based on NFCI data | Coniferous | 1649 | 76 | 33 | 29 | 7 | 3 | 11 | 0.91 |
| Broadleaf | 62 | 1150 | 20 | 53 | 4 | 6 | 14 | 0.88 | |
| Mixed | 54 | 43 | 627 | 31 | 2 | 5 | 7 | 0.82 | |
| User Accuracy | 0.93 | 0.91 | 0.92 | − | − | − | − | − | |
| Forest Type | Model No. | Count of Variables | R2 | RMSE | RMSE% | Forest Type | Model No. | Count of Variables | R2 | RMSE | RMSE% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Coniferous | 1 | 1 | 0.28 | 34.24 | 70.29 | Mixed | 16 | 1 | 0.23 | 35.42 | 59.6 |
| 2 | 2 | 0.29 | 32.64 | 67.01 | 17 | 2 | 0.28 | 33.09 | 55.68 | ||
| 3 | 3 | 0.3 | 31.1 | 63.85 | 18 | 3 | 0.3 | 30.94 | 52.06 | ||
| 4 | 4 | 0.31 | 30.79 | 63.21 | 19 | 4 | 0.32 | 30.25 | 50.9 | ||
| 5 | 5 | 0.32 | 30.59 | 62.8 | 20 | 5 | 0.33 | 30.01 | 50.5 | ||
| 6 | 6 | 0.32 | 30.26 | 62.12 | 21 | 6 | 0.34 | 29.65 | 49.89 | ||
| 7 | 7 | 0.32 | 30.16 | 61.92 | |||||||
| Broadleaf | 8 | 1 | 0.32 | 30.47 | 65.34 | All | 22 | 1 | 0.26 | 34.57 | 69.06 |
| 9 | 2 | 0.34 | 29.73 | 63.76 | 23 | 2 | 0.27 | 34.33 | 68.58 | ||
| 10 | 3 | 0.34 | 29.87 | 64.06 | 24 | 3 | 0.28 | 34.2 | 68.32 | ||
| 11 | 4 | 0.35 | 28.92 | 62.02 | 25 | 4 | 0.28 | 33.44 | 66.8 | ||
| 12 | 5 | 0.35 | 28.31 | 60.71 | 26 | 5 | 0.29 | 32.61 | 65.14 | ||
| 13 | 6 | 0.36 | 27.97 | 59.98 | 27 | 6 | 0.29 | 31.9 | 63.72 | ||
| 14 | 7 | 0.36 | 27.56 | 59.1 | 28 | 7 | 0.29 | 31.48 | 62.88 | ||
| 15 | 8 | 0.37 | 27.32 | 58.59 | 29 | 8 | 0.3 | 31.12 | 62.17 |
| Forest Type | Predictor Variable | Standardized Coefficients | Estimate (t-Test) | Significance (p-Value) | Collinearity Statistics | Forest Type | Predictor Variable | Standardized Coefficients | Estimate (t-Test) | Significance (p-Value) | Collinearity Statistics |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Coniferous | B4T7Mea | −0.20 | −6.74 | 0 | 1.66 | Mixed | SAVI | 0.22 | 4.24 | 0 | 1.41 |
| B5T7Cor | −0.10 | −4.06 | 0 | 1.11 | B3T7Cor | 0.14 | 3.13 | 0 | 1.08 | ||
| B7T5Cor | 0.07 | 2.8 | 0.01 | 1.15 | B7T3Dis | 0.11 | 2.24 | 0.03 | 1.38 | ||
| B4T3Ent | −0.19 | −3.82 | 0 | 4.69 | B6T3Cor | 0.1 | 2.31 | 0.02 | 1.08 | ||
| B4T5Hom | −0.13 | −2.59 | 0.01 | 4.96 | B5T3Con | 0.16 | 2.54 | 0.01 | 2.18 | ||
| B3T7Cor | 0.05 | 2.1 | 0.04 | 1.06 | B5T7Hom | 0.13 | 1.89 | 0.05 | 2.44 | ||
| GVI | −0.05 | −2.01 | 0.05 | 1.31 | |||||||
| Broadleaf | B5T7Mea | −0.13 | −3.06 | 0 | 3.11 | All | B4T7Mea | −0.14 | −4.25 | 0 | 4.62 |
| LAI | 0.29 | 7.26 | 0 | 2.63 | B3T7Cor | 0.08 | 4.8 | 0 | 1.04 | ||
| B3T7Cor | 0.07 | 2.97 | 0 | 1.02 | B4T7SeM | 0.04 | 2.23 | 0.03 | 1.49 | ||
| B4T7SeM | 0.3 | 2.87 | 0 | 5.14 | B5T7Mea | −0.07 | −2.42 | 0.02 | 3.4 | ||
| B4T5SeM | −0.25 | −2.42 | 0.02 | 3.82 | LAI | 0.18 | 4.82 | 0 | 5.37 | ||
| B7T3Mea | 0.18 | 2.81 | 0 | 4.99 | B7T3Mea | 0.1 | 3.66 | 0 | 3.4 | ||
| B6T7Mea | −0.14 | −2.02 | 0.04 | 2.52 | GDVI | −0.08 | −2.17 | 0.03 | 5.15 | ||
| B6T3Var | −0.05 | −1.83 | 0.05 | 1.09 | B5T7Cor | −0.03 | −1.97 | 0.05 | 1.03 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests 2019, 10, 1073. https://doi.org/10.3390/f10121073
Li Y, Li C, Li M, Liu Z. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests. 2019; 10(12):1073. https://doi.org/10.3390/f10121073
Chicago/Turabian StyleLi, Yingchang, Chao Li, Mingyang Li, and Zhenzhen Liu. 2019. "Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms" Forests 10, no. 12: 1073. https://doi.org/10.3390/f10121073
APA StyleLi, Y., Li, C., Li, M., & Liu, Z. (2019). Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests, 10(12), 1073. https://doi.org/10.3390/f10121073




