Autoregressive Modeling of Forest Dynamics
Abstract
:1. Introduction
1.1. Background
1.2. Forests and Stock Markets
1.3. Understanding and Modeling of Forest Patch Dynamics
1.4. Our Contributions
2. Materials and Methods
2.1. Data Mining of Quebec Provincial Forest Inventories
2.2. Autoregressive Model for Individual Forest Patches
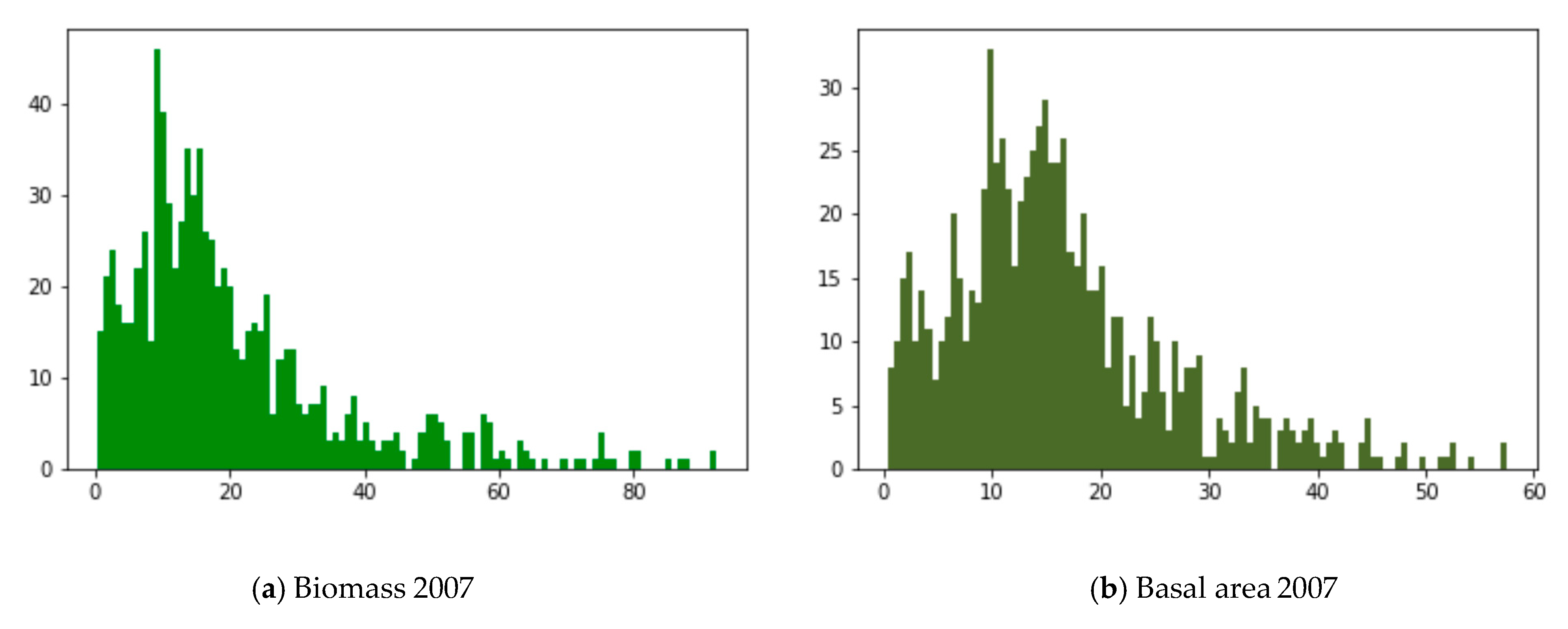
2.3. Annual Averages
3. Results and Discussion
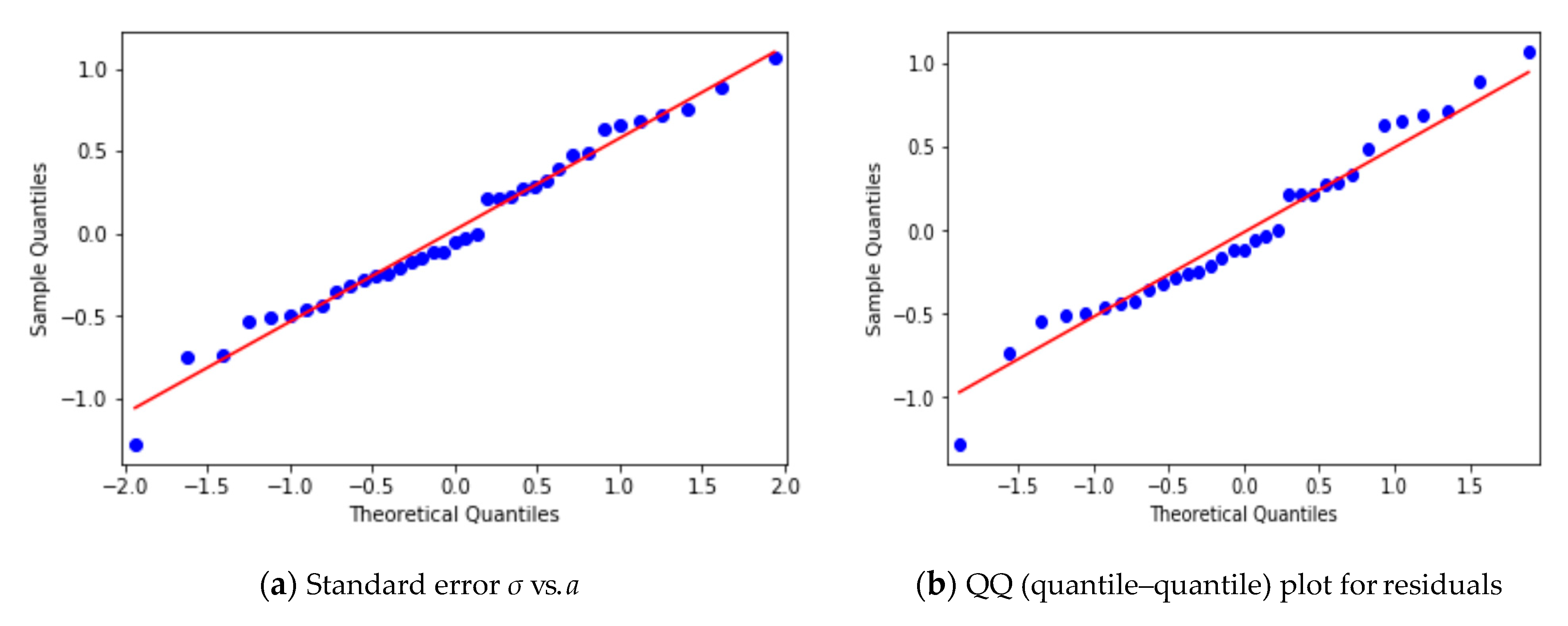
3.1. Autoregressive Model for Individual Patches
C(a, u): = [1 + a2 +…+ a2(u−1)]−1/2
D(a, u): = C(a, u)[1 + a +…+ au−1]
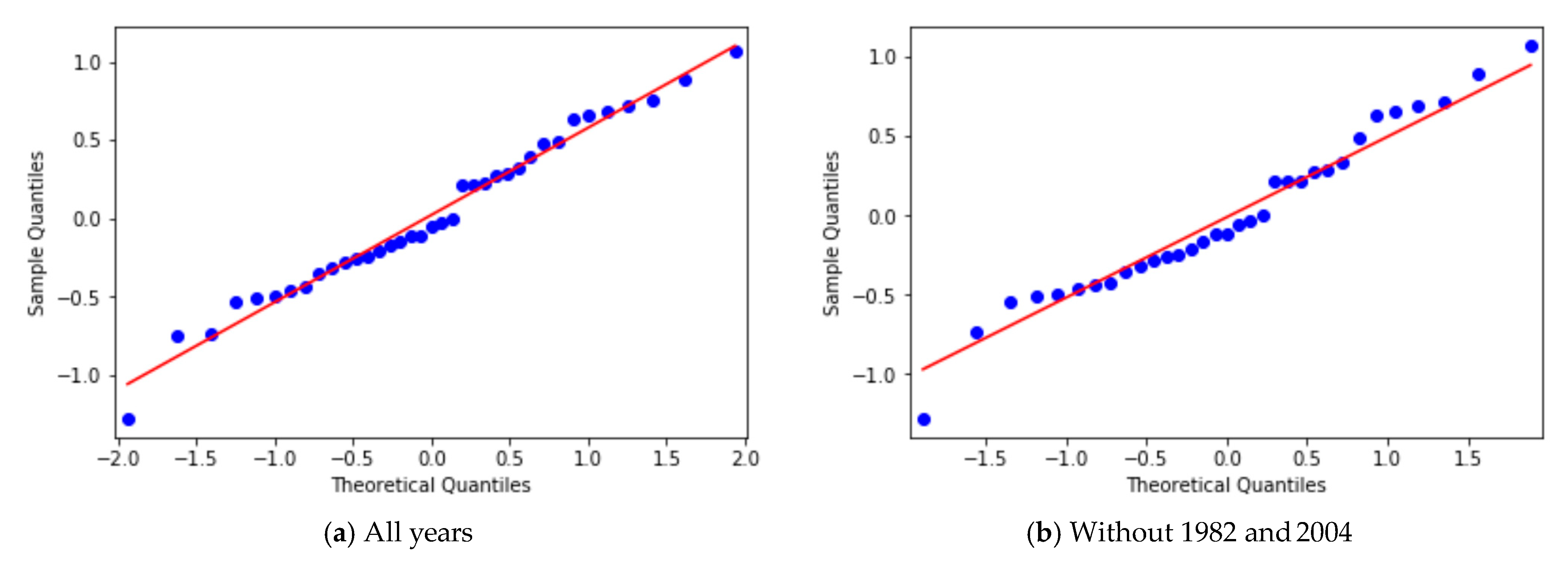
3.2. Yearly Averages, Frequentist Analysis
3.3. Yearly Averages, Bayesian Analysis
4. General Discussion
4.1. Towards Autoregressive Theory of Forest Dynamics
4.2. Future Research
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| quantile-quantile (for a plot) | |
| AR | autoregression |
| FIA | USDA Forest Service Forest Inventory and Analysis Program |
| VARIMA | vector autoregressive integrated moving average model |
| USDA | the United States Department of Agriculture |
| GIS | Geographic Information Systems |
| ARIMA | autoregressive integrated moving average model |
| i.i.d. | independent and identically distributed (random variables) |
Appendix A. Maximal Likelihood and Minimal Standard Error
Appendix B. Background on Autoregressive Models and Random Walk
Appendix C. Background on Bayesian Inference
Appendix D. Empirical Data
| Year Gap | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quantity | 1 | 2 | 65 | 915 | 1381 | 3334 | 1923 | 2214 | 2543 | 2677 | 1972 | 694 |
| Year Gap | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Quantity | 922 | 533 | 391 | 569 | 390 | 123 | 8 | 66 | 8 | 17 | 22 | 22 |
| Year Gap | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |
| Quantity | 4 | 17 | 14 | 9 | 6 | 5 | 12 | 1 | 0 | 5 | 2 | 0 |
| Year | Number of Observations | Yearly Mean of Biomass Logarithm | Yearly Variance of Biomass Logarithm | Yearly Mean of Basal Area Logarithm | Yearly Variance of Basal Area Logarithm |
|---|---|---|---|---|---|
| 1970 | 522 | 1.81 | 0.77 | 1.67 | 0.48 |
| 1971 | 1216 | 2.05 | 0.8 | 1.9 | 0.5 |
| 1972 | 1286 | 1.97 | 0.67 | 1.87 | 0.43 |
| 1973 | 335 | 1.66 | 0.59 | 1.64 | 0.39 |
| 1974 | 304 | 1.68 | 0.55 | 1.66 | 0.36 |
| 1975 | 902 | 1.97 | 0.66 | 1.96 | 0.54 |
| 1976 | 1883 | 2.17 | 0.61 | 2.02 | 0.4 |
| 1977 | 422 | 1.82 | 0.37 | 1.81 | 0.25 |
| 1978 | 1319 | 2.77 | 0.7 | 2.53 | 0.48 |
| 1979 | 1339 | 2.68 | 0.77 | 2.52 | 0.54 |
| 1980 | 1047 | 2.2 | 0.7 | 2.13 | 0.52 |
| 1981 | 396 | 1.86 | 0.7 | 1.8 | 0.51 |
| 1982 | 8 | 1.98 | 0.12 | 1.97 | 0.12 |
| 1983 | 98 | 2.23 | 0.66 | 2.06 | 0.43 |
| 1984 | 358 | 2.65 | 0.57 | 2.32 | 0.36 |
| 1985 | 629 | 2.38 | 0.75 | 2.15 | 0.47 |
| 1986 | 665 | 2.24 | 0.62 | 2.07 | 0.4 |
| 1987 | 732 | 2.22 | 0.62 | 2.05 | 0.42 |
| 1988 | 604 | 1.98 | 0.56 | 1.92 | 0.34 |
| 1989 | 1597 | 2.49 | 0.95 | 2.38 | 0.58 |
| 1990 | 723 | 1.46 | 0.47 | 1.54 | 0.34 |
| 1991 | 581 | 2.02 | 0.61 | 1.92 | 0.38 |
| 1992 | 1782 | 2.67 | 0.68 | 2.54 | 0.46 |
| 1993 | 865 | 2.88 | 0.77 | 2.65 | 0.55 |
| 1994 | 647 | 3.21 | 0.67 | 2.93 | 0.48 |
| 1995 | 625 | 2.85 | 0.77 | 2.66 | 0.52 |
| 1996 | 858 | 2.57 | 0.86 | 2.43 | 0.68 |
| 1997 | 2247 | 3.08 | 0.81 | 2.82 | 0.57 |
| 1998 | 977 | 2.6 | 0.68 | 2.49 | 0.49 |
| 1999 | 905 | 2.11 | 0.67 | 2.13 | 0.54 |
| 2000 | 101 | 2.62 | 1.0 | 2.46 | 0.74 |
| 2001 | 756 | 2.47 | 0.38 | 2.45 | 0.3 |
| 2002 | 309 | 2.32 | 0.47 | 2.32 | 0.39 |
| 2003 | 3414 | 3.08 | 0.85 | 2.83 | 0.61 |
| 2004 | 19 | 2.55 | 0.29 | 2.51 | 0.23 |
| 2005 | 641 | 2.71 | 0.73 | 2.57 | 0.57 |
| 2006 | 599 | 3.42 | 0.81 | 3.08 | 0.53 |
| 2007 | 841 | 2.67 | 0.81 | 2.55 | 0.62 |
References
- Levin, S.A. Fragile Dominion: Complexity and the Commons; Perseus Publishing: Cambridge, MA, USA, 1999. [Google Scholar]
- Levin, S.A. Complex adaptive systems: Exploring the known, the unknown and the unknowable. Am. Math. Soc. 2003, 40, 3–19. [Google Scholar] [CrossRef]
- Strigul, N. Individual-based models and scaling methods for ecological forestry: Implications of tree phenotypic plasticity. In Sustainable Forest Management; Garcia, J., Casero, J., Eds.; InTech: Rijeka, Croatia, 2012; pp. 359–384. [Google Scholar] [CrossRef]
- Botkin, D.B. Forest Dynamics: An Ecological Model; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Shugart, H.H. A Theory of Forest Dynamics: The Ecological Implications of Forest Succession Models; Springer: Berlin, Germany, 1984. [Google Scholar]
- Pacala, S.W.; Canham, C.D.; Silander, J.A., Jr. Forest models defined by field measurements: I. The design of a northeastern forest simulator. Can. J. For. Res. 1993, 23, 1980–1988. [Google Scholar] [CrossRef]
- Pastor, J.; Sharp, A.; Wolter, P. An application of Markov models to the dynamics of Minnesota’s forests. Can. J. For. Res. 2005, 35, 3011–3019. [Google Scholar] [CrossRef]
- Moorcroft, P.; Hurtt, G.; Pacala, S.W. A method for scaling vegetation dynamics: The ecosystem demography model (ED). Ecol. Monogr. 2001, 71, 557–586. [Google Scholar] [CrossRef]
- Strigul, N.; Pristinski, D.; Purves, D.; Dushoff, J.; Pacala, S. Scaling from trees to forests: Tractable macroscopic equations for forest dynamics. Ecol. Monogr. 2008, 78, 523–545. [Google Scholar] [CrossRef]
- Liénard, J.F.; Strigul, N.S. Modelling of hardwood forest in Quebec under dynamic disturbance regimes: A time-inhomogeneous Markov chain approach. J. Ecol. 2016, 104, 806–816. [Google Scholar] [CrossRef]
- Strigul, N.; Florescu, I.; Welden, A.R.; Michalczewski, F. Modelling of forest stand dynamics using Markov chains. Environ. Model. Softw. 2012, 31, 64–75. [Google Scholar] [CrossRef]
- Pacala, S.W.; Canham, C.D.; Saponara, J.; Silander, J.A., Jr.; Kobe, R.K.; Ribbens, E. Forest models defined by field measurements: Estimation, error analysis and dynamics. Ecol. Monogr. 1996, 66, 1–43. [Google Scholar] [CrossRef]
- Liénard, J.; Strigul, N. An individual-based forest model links canopy dynamics and shade tolerances along a soil moisture gradient. R. Soc. Open Sci. 2016, 3, 150589. [Google Scholar] [CrossRef] [PubMed]
- Liénard, J.F.; Gravel, D.; Strigul, N.S. Data-intensive modeling of forest dynamics. Environ. Model. Softw. 2015, 67, 138–148. [Google Scholar] [CrossRef]
- Caswell, H. Matrix Population Models: Construction, Analysis, and Interpretation; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- Wu, J.; Loucks, O.L. From balance of nature to hierarchical patch dynamics: A paradigm shift in ecology. Q. Rev. Biol. 1996, 70, 439–466. [Google Scholar] [CrossRef]
- Watt, A.S. Pattern and process in the plant community. J. Ecol. 1947, 35, 1–22. [Google Scholar] [CrossRef]
- Levin, S.A.; Paine, R.T. Disturbance, patch formation, and community structure. Proc. Natl. Acad. Sci. USA 1974, 71, 2744–2747. [Google Scholar] [CrossRef] [PubMed]
- Scholl, A.E.; Taylor, A.H. Fire regimes, forest change, and self-organization in an old-growth mixed-conifer forest, Yosemite National Park, USA. Ecol. Appl. 2010, 20, 362–380. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, J. Gap dynamics of forest trees: A review with particular attention to boreal forests. Environ. Rev. 2001, 9, 1–59. [Google Scholar] [CrossRef]
- Bugmann, H. A review of forest gap models. Clim. Chang. 2001, 51, 259–305. [Google Scholar] [CrossRef]
- Dubé, P.; Fortin, M.; Canham, C.; Marceau, D. Quantifying gap dynamics at the patch mosaic level using a spatially-explicit model of a northern hardwood forest ecosystem. Ecol. Model. 2001, 142, 39–60. [Google Scholar] [CrossRef]
- Kohyama, T.; Suzuki, E.; Partomihardjo, T.; Yamada, T. Dynamic steady state of patch-mosaic tree size structure of a mixed dipterocarp forest regulated by local crowding. Ecol. Res. 2001, 16, 85–98. [Google Scholar] [CrossRef]
- Hanson, P.J.; Weltzin, J.F. Drought disturbance from climate change: Response of United States forests. Sci. Total Environ. 2000, 262, 205–220. [Google Scholar] [CrossRef]
- Liénard, J.; Florescu, I.; Strigul, N. An Appraisal of the Classic Forest Succession Paradigm with the Shade Tolerance Index. PLoS ONE 2015, 10, e0117138. [Google Scholar] [CrossRef]
- Van Wagner, C.E. Age-class distribution and the forest fire cycle. Can. J. For. Res. 1978, 8, 220–227. [Google Scholar] [CrossRef]
- Liénard, J.; Strigul, N. Linking forest shade tolerance and soil moisture in North America. Ecol. Indic. 2015, 58, 332–334. [Google Scholar] [CrossRef]
- Perron, J.; Morin, P. Normes d’inventaire Forestier: Placettes-échantillons Permanents; Ministry of Forests: Quebec, QC, Canada, 2011. [Google Scholar]
- Jenkins, J.; Chojnacky, D.; Heath, L.; Birdsey, R. National-Scale Biomass Estimators for United States Tree Species. For. Sci. 2003, 49, 12–35. [Google Scholar]
- Woodall, C.W.; Heath, L.S.; Domke, G.M.; Nichols, M.C. Methods and Equations for Estimating Aboveground Volume, Biomass, and Carbon for Trees in the US Forest Inventory; USDA Forest Service: United States Department of Agriculture: Madison, WI, USA, 2010. [Google Scholar]
- Fleming, R.A.; Barclay, H.J.; Candau, J.N. Scaling-up an autoregressive time-series model (of spruce budworm population dynamics) changes its qualitative behavior. Ecol. Model. 2002, 149, 127–142. [Google Scholar] [CrossRef]
- Lichstein, J.W.; Simons, T.R.; Shriner, S.A.; Franzreb, K.E. Spatial autocorrelation and autoregressive models in ecology. Ecol. Monogr. 2002, 72, 445–463. [Google Scholar] [CrossRef]
- Fox, J.C.; Bi, H.; Ades, P.K. Modelling spatial dependence in an irregular natural forest. Silva Fenn. 2008, 42, 35. [Google Scholar] [CrossRef]
- Fama, E.F. Random walks in stock market prices. Financ. Anal. J. 1995, 51, 75–80. [Google Scholar] [CrossRef]
- Barrett, A.; Rappoport, P. Price-Earnings Investing. JP Morgan Asset Manag. Real. Returns 2011, 1, 1–12. [Google Scholar]
- Ioannidis, C.; Peel, D.A.; Peel, M.J. The time series properties of financial ratios: Lev revisited. J. Bus. Financ. Account. 2003, 30, 699–714. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Shiller, R.J. Valuation ratios and the long-run stock market outlook: An update. Tech. Rep. Natl. Bur. Econ. Res. 2001. [Google Scholar] [CrossRef]
- Davis, J.; Aliaga-Díaz, R.; Thomas, C.J. Forecasting Stock Returns: What Signals Matter, and What do They Say Now; The Vanguard Group: Valley Forge, PA, USA, 2012. [Google Scholar]
- Goyal, A.; Welch, I. Predicting the equity premium with dividend ratios. Manag. Sci. 2003, 49, 639–654. [Google Scholar] [CrossRef]
- Ellison, A.M. Bayesian inference in ecology. Ecol. Lett. 2004, 7, 509–520. [Google Scholar] [CrossRef]
- Gurrin, L.C.; Kurinczuk, J.J.; Burton, P.R. Bayesian statistics in medical research: An intuitive alternative to conventional data analysis. J. Eval. Clin. Pract. 2000, 6, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Rachev, S.T.; Hsu, J.S.; Bagasheva, B.S.; Fabozzi, F.J. Bayesian Methods in Finance; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 153. [Google Scholar]
- Craven, B.D.; Islam, S.M. A model for stock market returns: Non-Gaussian fluctuations and financial factors. Rev. Quant. Financ. Account. 2008, 30, 355–370. [Google Scholar] [CrossRef]
- Waggoner, P.E.; Stephens, G.R. Transition probabilities for a forest. Nature 1970, 225, 1160–1161. [Google Scholar] [CrossRef] [PubMed]
- Stephens, G.R.; Waggoner, P.E. A half century of natural transitions in mixed hardwood forests. Bull. Conn. Agric. Exp. Stn. 1980, 783, 44. [Google Scholar]
- Usher, M.B. Markovian approaches to ecological succession. J. Anim. Ecol. 1979, 48, 413–426. [Google Scholar] [CrossRef]
- Logofet, D.; Lesnaya, E. The mathematics of Markov models: What Markov chains can really predict in forest successions. Ecol. Model. 2000, 126, 285–298. [Google Scholar] [CrossRef]
- Liénard, J.; Harrison, J.; Strigul, N. US forest response to projected climate-related stress: A tolerance perspective. Glob. Chang. Biol. 2016, 22, 2875–2886. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rumyantseva, O.; Sarantsev, A.; Strigul, N. Autoregressive Modeling of Forest Dynamics. Forests 2019, 10, 1074. https://doi.org/10.3390/f10121074
Rumyantseva O, Sarantsev A, Strigul N. Autoregressive Modeling of Forest Dynamics. Forests. 2019; 10(12):1074. https://doi.org/10.3390/f10121074
Chicago/Turabian StyleRumyantseva, Olga, Andrey Sarantsev, and Nikolay Strigul. 2019. "Autoregressive Modeling of Forest Dynamics" Forests 10, no. 12: 1074. https://doi.org/10.3390/f10121074
APA StyleRumyantseva, O., Sarantsev, A., & Strigul, N. (2019). Autoregressive Modeling of Forest Dynamics. Forests, 10(12), 1074. https://doi.org/10.3390/f10121074





