1. Introduction
Forest biomass is an important indicator of forest productivity, carbon storage and forest carbon sequestration capacity, and it has been widely investigated by the scientific community [
1,
2,
3]. As a developing country, China has taken measures to increase forest biomass and carbon storage by limiting deforestation and afforestation, and positively supports and implements the mechanism of Reducing emissions from deforestation and forest degradation in developing countries (REDD+). Accurate assessment of forest biomass plays a pivotal role in afforestation management planning, forest resource monitoring, the assessment of the ecological value of forests, climate change impacts and policy formulation for forest harvesting, conservation and management [
4,
5]. The assessment of forest biomass includes the estimation of both above-ground biomass (AGB) and underground biomass. However, the underground biomass is not only difficult to quantify, but it is relatively small to the AGB [
6]. Therefore, the estimation of AGB has always been the main focus in biomass research. AGB calculations rely on tree structure parameters, such as diameter at breast height (DBH), tree height, crown radius, etc., form which the AGB can be calculated using allometric biomass models, which can be very effective when applied to tree species and productivity ranges with reliable calibration data. Conventional methods for AGB measurement, which involve cutting down trees and then drying them for weighing, are destructive, time-consuming, expensive and laborious, and are consequently rarely adopted [
7,
8]. Moreover, the conventional methods can be used only for a small area, as their accuracy could be compromised when used to estimate the AGB of a forest spanning over a larger region [
2,
8,
9,
10,
11].
The use of advanced technologies in forestry, especially remote sensing technology, provides an alternative tool to estimate the AGB with ease and high precision [
10,
12]. Satellite remote sensing technology provides distinct advantages for the assessment and mapping of large-scale and multi-temporal forest biomass and carbon stocks [
13], but it is not applicable or uncertain for forest AGB assessment at the plot and tree level. Recently, the light detection and ranging (LiDAR) technology was developed and advanced rapidly with its special utilization in forest inventory. Primarily, the LiDAR include airborne laser scanning (ALS), terrestrial laser scanning (TLS) and mobile laser scanning (MLS). MLS mounted on vehicles, which is an efficient and effective way to obtain 3D point cloud data in urban forests or forest areas on flat terrain. It relies on GNSS (Global Navigation Satellite System) signals for positioning and the coordinate calculation of points [
14,
15]. This technology has the ability to generate high spatial resolution and accurate three-dimensional (3D) point cloud data. Consequently, it has been widely applied in forestry surveys to acquire basic tree parameters [
16], as well as estimate AGB and carbon storage [
17,
18]. ALS can produce large-scale 3D point cloud data in a short time, from which tree height, DBH, canopy height and density metrics can be obtained, and then the AGB of trees can be evaluated. The accuracy of AGB estimates by this technology is not higher than that of conventional methods [
17], but it is nevertheless higher than that of satellite remote sensing and UAV (unmanned aerial vehicle) aerial photogrammetry [
19,
20]. However, this method of assessing the biomass by ALS is prone to problems, including large estimation uncertainties, large costs, and limited information [
21,
22]. The system’s performance is compromised in forest areas with weak GNSS signals or large variations of topography [
16,
23]. TLS can generate detailed and accurate parameter information of the 3D structure of trees by calculating the time difference between the emission and return of laser pulses and analyzing the energy of the returned laser pulses, which is not affected by GNSS signals and offers opportunities for a consistent and robust framework to support AGB estimates [
3,
24].
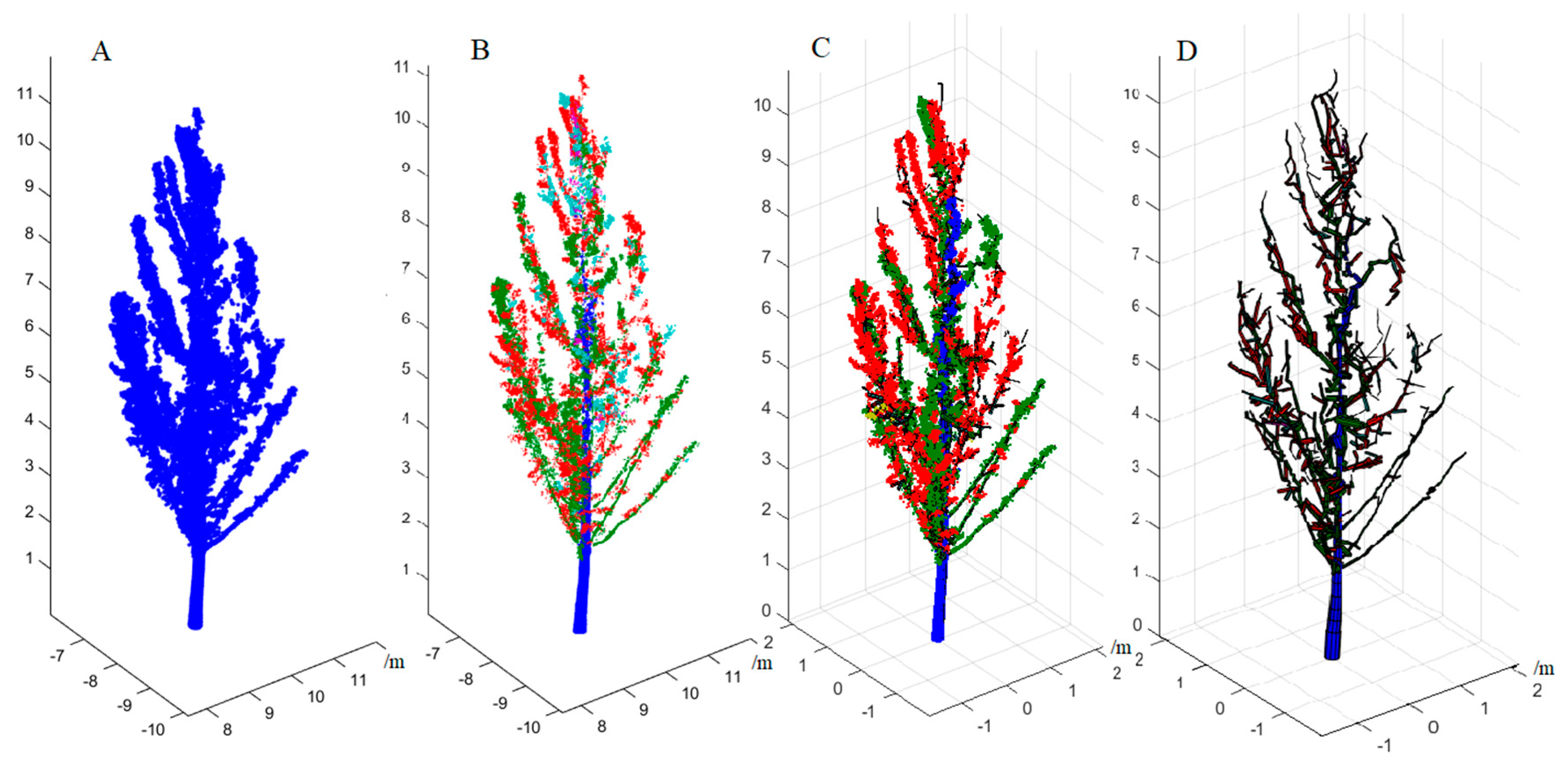
Terrestrial laser scanning (TLS) has shown great potential for accurately assessing forest biomass with greater precision than inferred from the nationwide allometric biomass models [
8,
25]. Yao et al. [
26] used high-precision TLS data to obtain accurate tree structure parameters, and calculated the biomass of New England forest stands using allometric biomass models of specific tree species, demonstrating the accuracy and effectiveness of measuring forest AGB using non-destructive methods. Seidel et al. [
27] measured the DBH of individual trees from the TLS data, and predicted the biomass of trees via a regional allometric biomass model. The mean absolute error and the mean relative error were 12.9 kg and 16.4%, respectively, which significantly reduced fieldwork efforts in dense forests when compared to traditional diameter tallying by calipers or tapes. However, this non-destructive measurement method still relies on an allometric biomass model established by empirical relationships extracted from a sample of trees to evaluate the AGB. Fundamentally, the essence of this method is still to estimate the biomass of trees based on limited structure parameters. A different approach has been developed to reconstruct the complete 3D structure of trees from TLS data rather than several tree structure parameters. The quantitative structure models (QSM) developed by Raumonen et al. [
28] and improved by Raumonen et al. [
25] and Calders et al. [
2] were used to reconstruct the morphological structure of individual trees from TLS data. The volume of the reconstructed model, including the trunk and branches, can be measured from a single tree model constructed by a least squares, cylinder fitting algorithm [
28]. The estimated tree volume is converted into the AGB by multiplying by the basic wood density values of a specific tree species. This method estimates the tree AGB based on a real biological morphological structure model of a specific tree species, which is completely different from the allometric biomass model, which only depends on a limited number of tree structure parameters [
8,
29].
Some study results have shown the feasibility and effectiveness of the QSM method for the estimation of forest AGB. Raumonen et al. [
25] used the QSM algorithm to reconstruct the tree 3D structure models of oak and eucalyptus, and then calculated the AGB of oak and eucalyptus using basic wood density values. Compared with destructively harvested biomass, the calculated biomass of oak was overestimated by 15.3% to 18.8%, and the average relative absolute error of eucalyptus biomass was about 28.5%. Calders et al. [
2] used this algorithm to estimate the biomass of 65 eucalyptus trees in tropical areas, with a coefficient of variation of root mean square error (CV(RMSE)), and concordance correlation coefficient (CCC) of 16.1% and 0.98, respectively, showing a high biomass estimation accuracy. At the same time, Tanago et al. [
8] validated the applicability of the QSM algorithm to the estimation of the biomass of large trees under complex conditions in tropical regions. The CV (RMSE) and CCC of the estimated total AGB of trees were 28.37% and 0.95% respectively. Although these studies all used the QSM algorithm to estimate the AGB of trees, only a few species were involved, and the QSM algorithm had an impact on the reconstruction results of trees with different biophysical and morphological structures, which directly affected the final estimation accuracy of biomass [
25].
In this study, we used a non-destructive method (QSM) to estimate the AGB of trees from TLS point cloud data based on their true morphological structure. We hypothesized that different tree species have different bark roughness and trunk curvature, which could affect the estimation of DBH from point cloud data. To our knowledge, very limited work has been done to investigate the effects of bark roughness and trunk curvature on DBH estimates. Therefore, the main objectives of this study included (1) a quantitative analysis of the influence of TLS data on DBH estimation of tree species with different bark roughness and trunk curvature, and (2) to optimize the QSM algorithm based on 100 trees of 10 different species. (3) We estimated the AGB of 10 tree species with different biophysical and morphological structures using a non-destructive method, and the estimation accuracy of AGB of trees was evaluated by comparing with the results of the regional allometric biomass model of specific tree species from specific areas.
4. Discussion
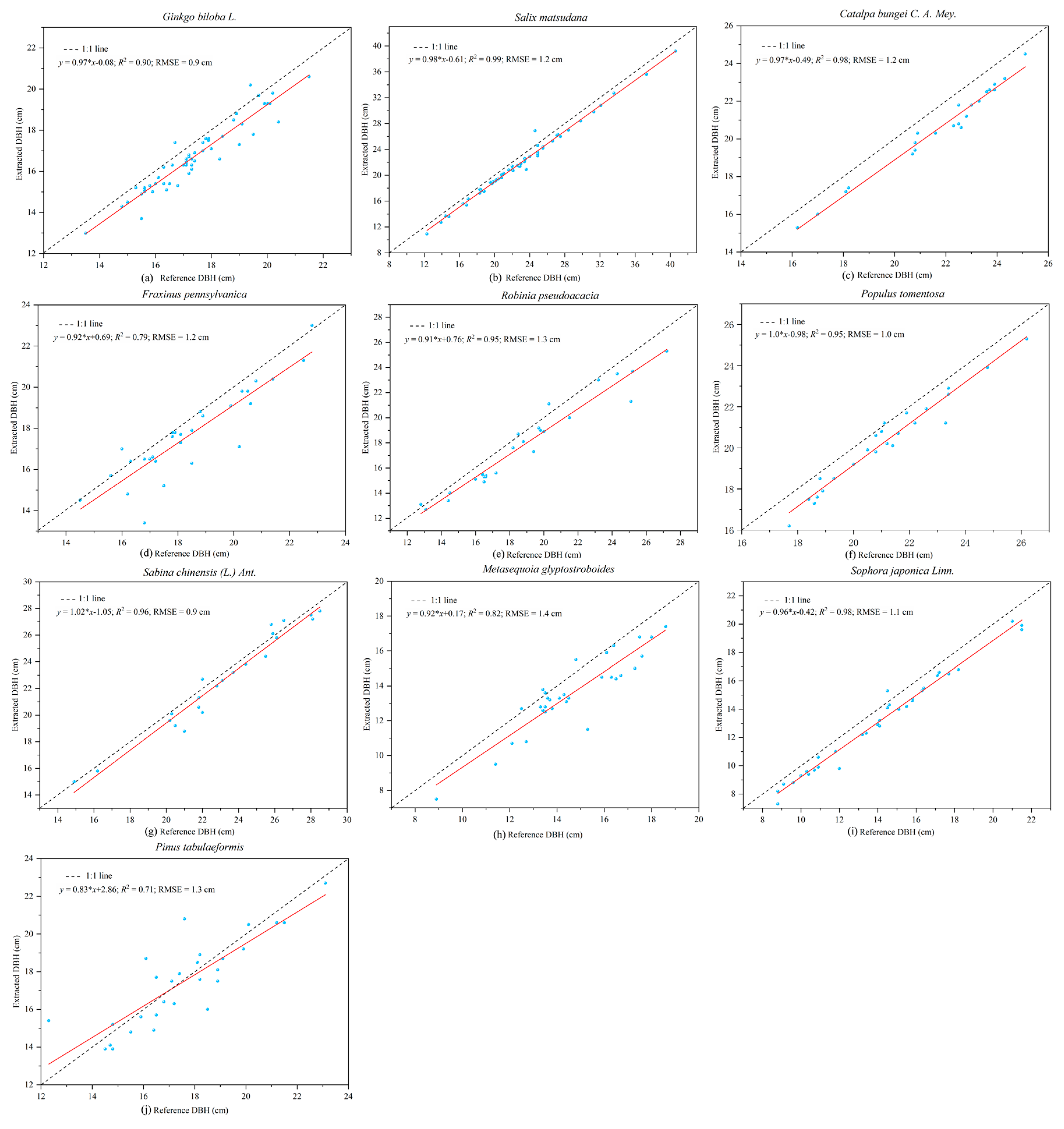
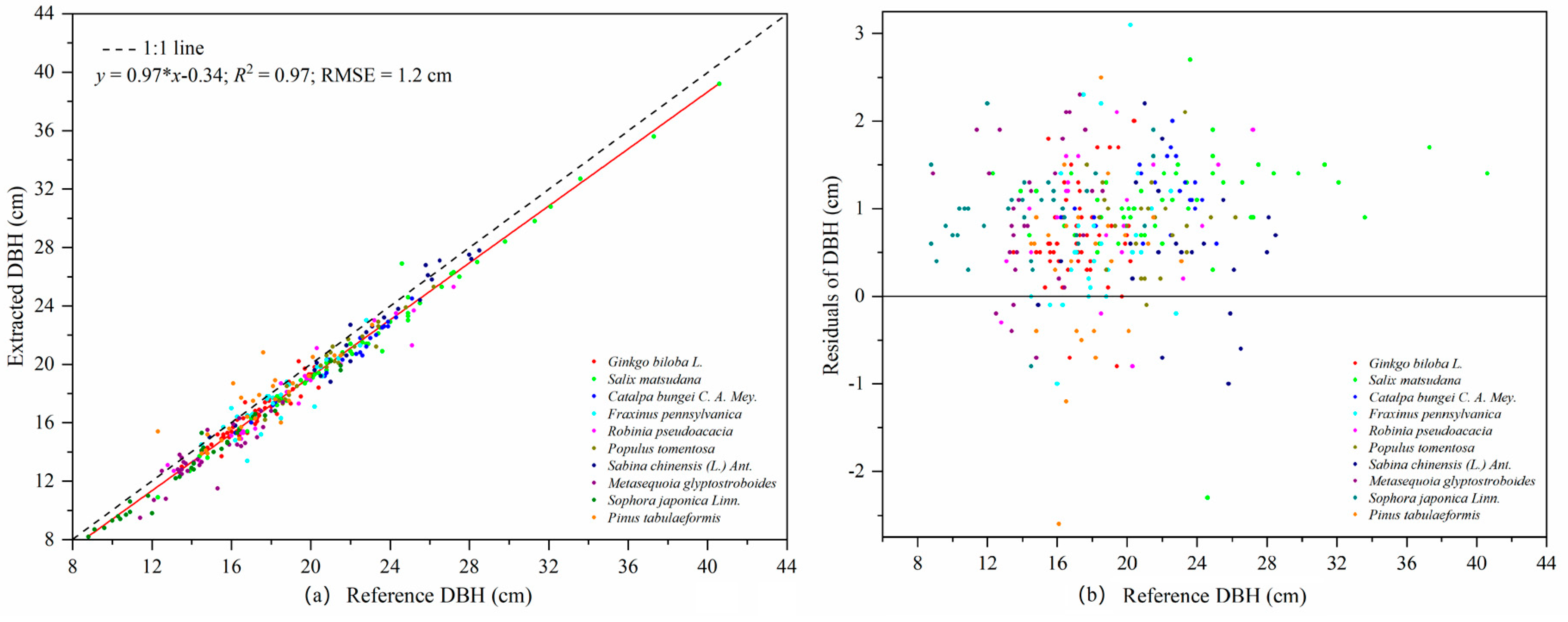
TLS is a powerful and effective tool for obtaining 3D point cloud data of the morphological structures of individual trees, and then extracting a variety of geometric and statistical parameters. The least squares circle fitting algorithm was used to fit point clouds at DBHs of trees with different bark roughness and trunk curvature. The results showed that different bark roughness and trunk curvature had a minor influence on the evaluation of DBH in laser point clouds [
56,
57]. The comparison of DBH from TLS data and field measurements shows a high consistency. The precision of the DBH estimation in our study (RMSE = 1.2 cm) was higher than that reported by Calders et al. [
2] and Cabo et al. [
58]. The slope of the fitting line between the estimated DBH and the measured data was 0.97, which indicated that the DBH of trees was slightly underestimated on the whole. In addition to the influence of bark roughness, the main reasons for the smaller DBH estimation were the shape of the trunk and the low density and uneven distribution of point cloud data [
40,
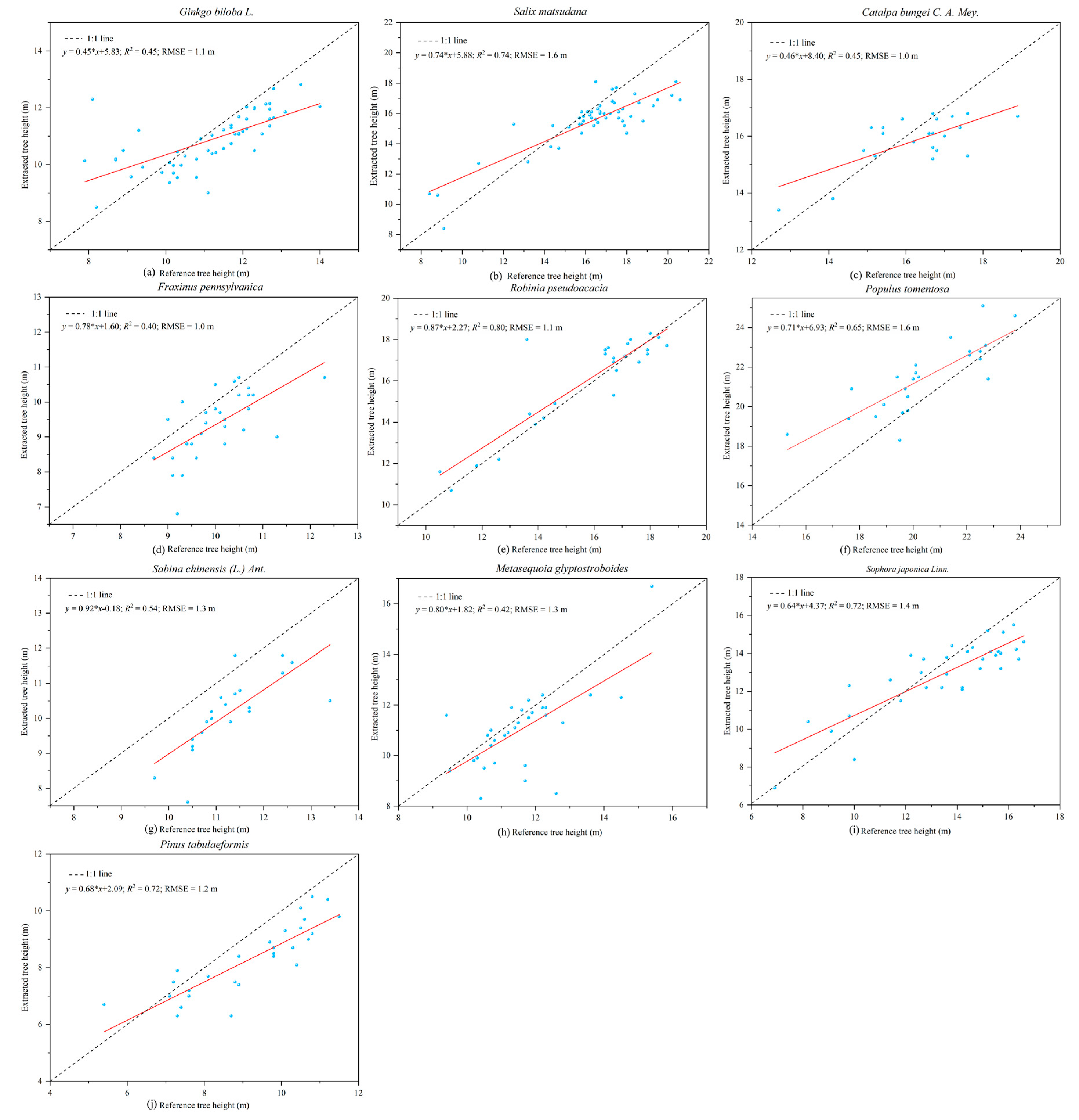
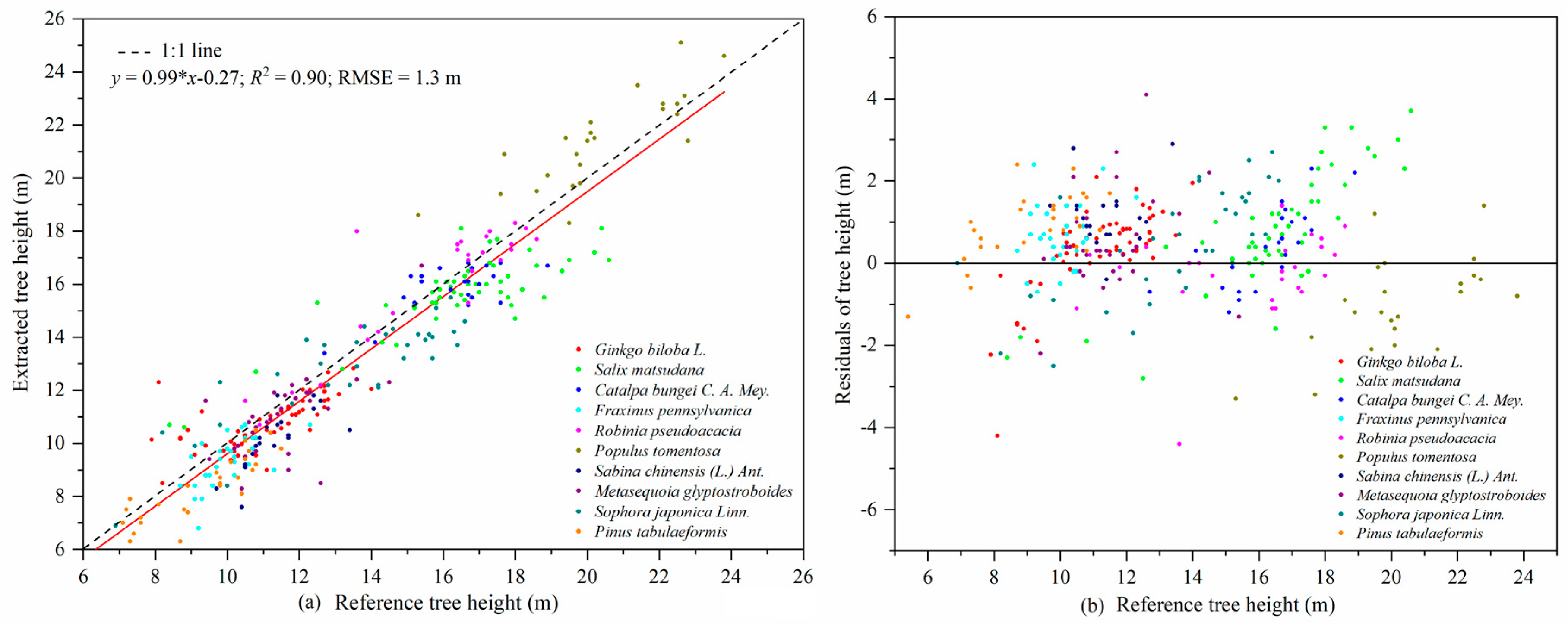
56]. The precision of the tree height estimation (RMSE = 1.3 m) in our study was lower than that reported by Cabo et al. [
58]. That was likely due to the higher trunk density in our plots, which caused occlusion of tree tops, leading to the modelling error of the tree height-DBH model. Obtaining tree height from point cloud data has an obvious advantage over other instruments for measuring tree height since it does not rely on the artificial selection of tree vertices. This method is more advantageous for measuring tree height in dense forests where the tops of trees cannot be seen [
59,
60].
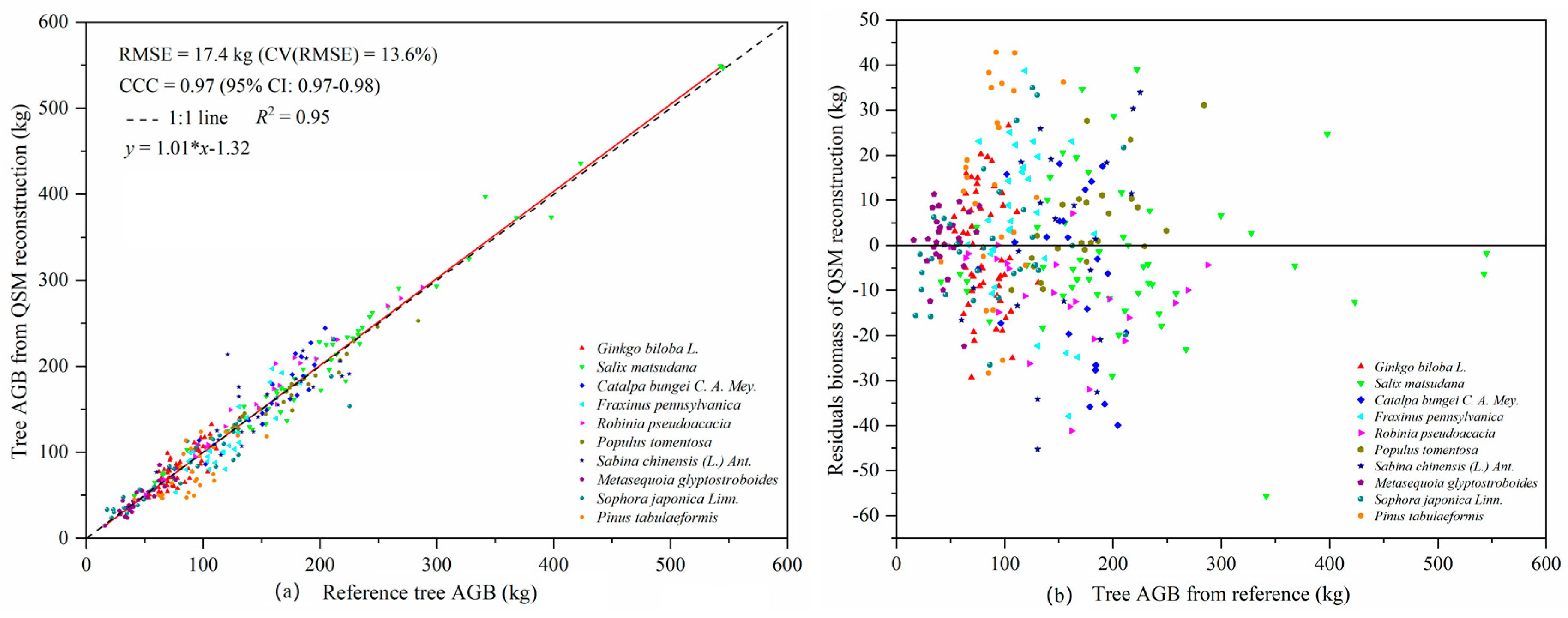
A QSM algorithm optimized for different tree species based on their biophysical characteristics can provide reliable and highly accurate estimates of AGB. The optimal value for the parameter
d was 2 or 3 cm for all investigated tree species except
Salix matsudana, Fraxinus pennsylvanica and
Pinus tabulaeformis, which is consistent with the results of Calders et al. [
2] and Tanago et al. [
8]. The optimal value for the parameter
l for different tree species was always 3, 4 or 5, which was consistent with the results of Raumonen et al. [
28]. The optimum value for the parameters
d and
l for different trees species were obviously different, which was mainly influenced by the different biophysical and morphological structures of the trees. Different parameters of the QSM algorithm have a great impact on the final model reconstruction results. The method we used to reconstruct the model from TLS data does not require prior assumptions about tree structure, nor does it rely on limited tree structure parameters. Calders et al. [
2] used the QSM algorithm to reconstruct the tree structure of
Eucalyptus leucoxylon, E. microcarpa and
E. tricarpa, and then evaluated the tree AGB. The results of the AGBs calculated using their TLS-QSM method were highly consistent with the reference values, with the CV (RMSE) and CCC being 16.1% and 0.98, respectively. The accuracy of the total AGB estimated using the optimized QSM algorithm in our study was higher than that reported by Calders et al. [
2], and our CV (RMSE) and CCC were 13.6% and 0.97 respectively. The accuracy of the AGB estimated in our study was significantly higher than that of an estimate for 29 tropical rainforest trees species during the foliage period (CV(RMSE) = 28.37%,
R2 = 0.90, CCC = 0.95) [
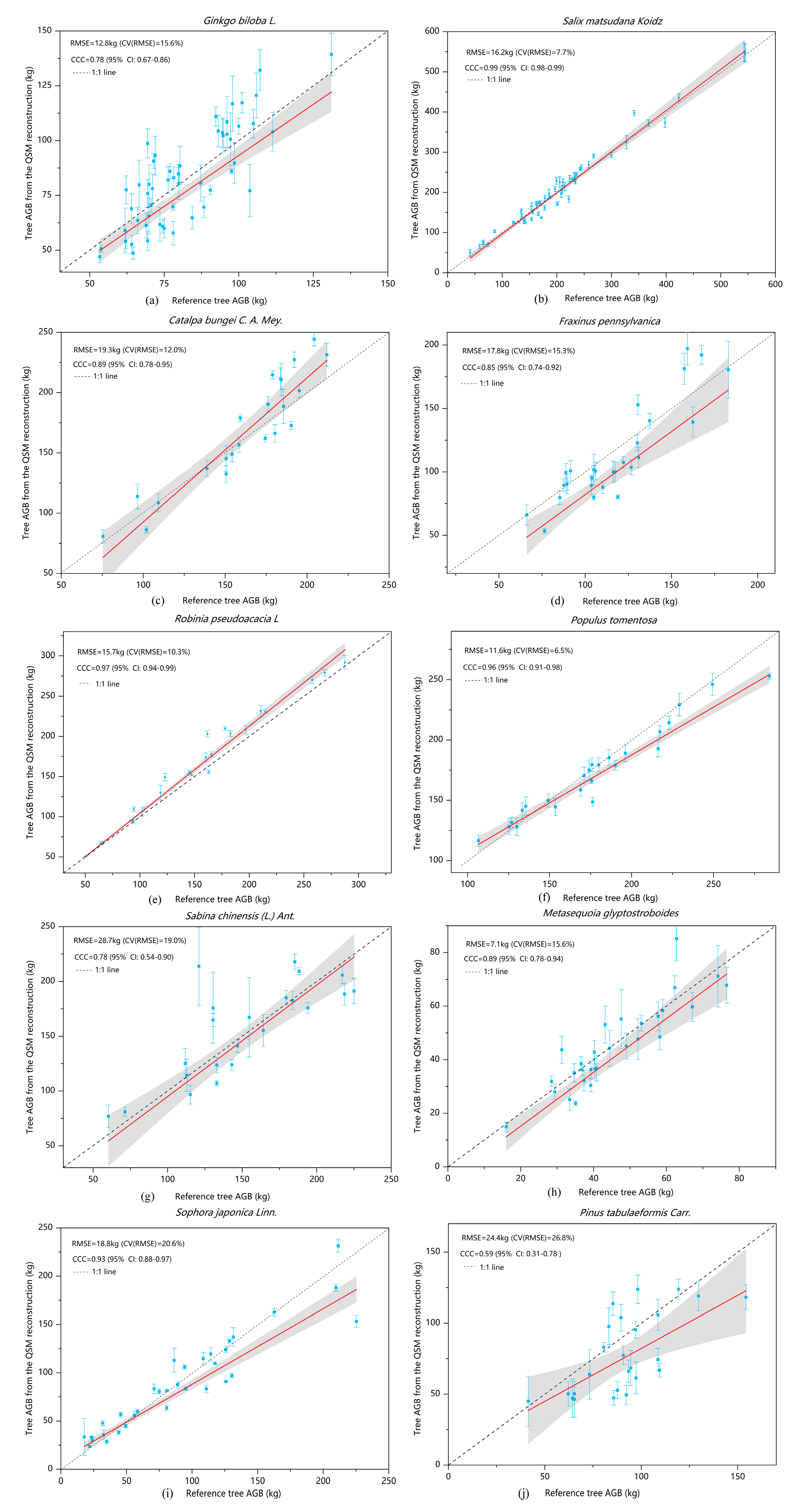
8]. The modelled volumes of different tree species calculated using the QSM algorithm were quite different. In addition to the influence of the biophysical structure of trees, an important reason is the difference in the stem density in the sample plots populated by different species. Among of 322 trees, nine failed to model when performing the 3D reconstruction of tree structure. Possible reasons include a lack of point cloud data in some trees and problems in the algorithm itself. Because different point cloud densities will affect the results of QSM modeling, we used the same scanning resolution and set the same scanning mode and the same point cloud data processing method in ten sample plots to ensure that the single trees used for QSM model reconstruction had similar point cloud densities, which reduces the impact of different point cloud density on the modelling results. The point cloud data of
Ginkgo biloba were acquired in the period of leaf growth, and the acquired data contained the point cloud data of leaves, which led to discrepancies in the cylinders fitted in the modeling of branches, and further. led to a large standard deviation in the biomass of individual modelled trees (
Figure 7a). By contrast, the point cloud data of
Salix matsudana and
Populus tomentosa were less affected by leaves and the biophysical morphologies of the trees were relatively simple, so that the modelled results showed high consistency with the reference biomasses (
Figure 7b,f). When the QSM algorithm was used to repeatedly model the same individual tree a total of 10 times, the modelled volume of the trunk was very similar, whereas the modelled volume of the branches varied greatly, up to several times. An important reason was that the point cloud that newly grows out of the leaves caused the fitted branches to be bulky. This method can not only calculate the volume and biomass of trees, but also monitor the annual natural growth of tree volume, as well as changes of branches and trunks [
28]. Kaasalainen et al. [
61] used this method to monitor the same tree in successive years and quantitatively evaluate its growth of tree volume.
There are many factors influencing the calculated AGBs of trees, including allometric biomass models. The allometric biomass models for a specific area have high accuracy in assessing the biomass of individual trees. Therefore, all allometric biomass models used in this study were specific for the area and tree species under investigation. In this study, the single variable (DBH) AGB prediction model was only adopted for
Juniperus chinensis, and the two variable (DBH and tree height) AGB prediction model, which has higher accuracy of biomass assessment [
62], was used for all the other tree species. There are three main reasons for the inconsistency of the biomass calculated by the QSM algorithm using basic wood density and regional allometric biomass models. First, the model data of the regional allometric biomass equations of different tree species are inconsistent, which lead to differences of model accuracy and inevitable systematic errors of the model itself, all of which had an impact on the final biomass results for specific trees. Secondly, there is sensitivity and instability of the QSM algorithm in the process of volume reconstruction of individual trees and the influence of the differences of basic wood density on the calculation of the AGB of trees. Thirdly, we did not consider the biomass of leaves in this study, because we found that it accounts for only a small part (about 10%) of the total AGB, but it also directly affected the calculated AGBs of trees. In addition, dead branches, lack of branches, incomplete extraction of a tree’s point cloud and other factors also lead to differences between the calculated AGBs of trees reconstructed using the QSM algorithm and the biomasses calculated by the model.
We optimized the reconstruction process of the QSM algorithm based on parameters
d and
l, which have the most influence on the reconstruction results [
2]. The results showed that the optimum values of parameter
d from most of the ten tree species was 2 or 3 cm, which s consistent with the results of Raumonen et al. [
28,
63]. For different tree species, the optimal QSM algorithm had obvious differences. At the same time, the influence of the parameter
l on the modeling results was not very significant. This provides an important reference for researchers who use the QSM algorithm for other research. The QSM algorithm should further implement the automatic determination of the optimal parameters of different tree species in the process of structural reconstruction and the automatic output of the average values of multiple modeling realization as the final result to improve the accuracy of wood volume and biomass assessment.
Future research will focus on more accurate estimation of tree volume and biomass from point cloud data and how to use non-destructive approaches to replace the destructive felling of trees to create and correct new allometric biomass models for specific tree species, especially for large trees.