Modeling Migratory Flight in the Spruce Budworm: Circadian Rhythm
Abstract
1. Introduction
2. Materials and Methods
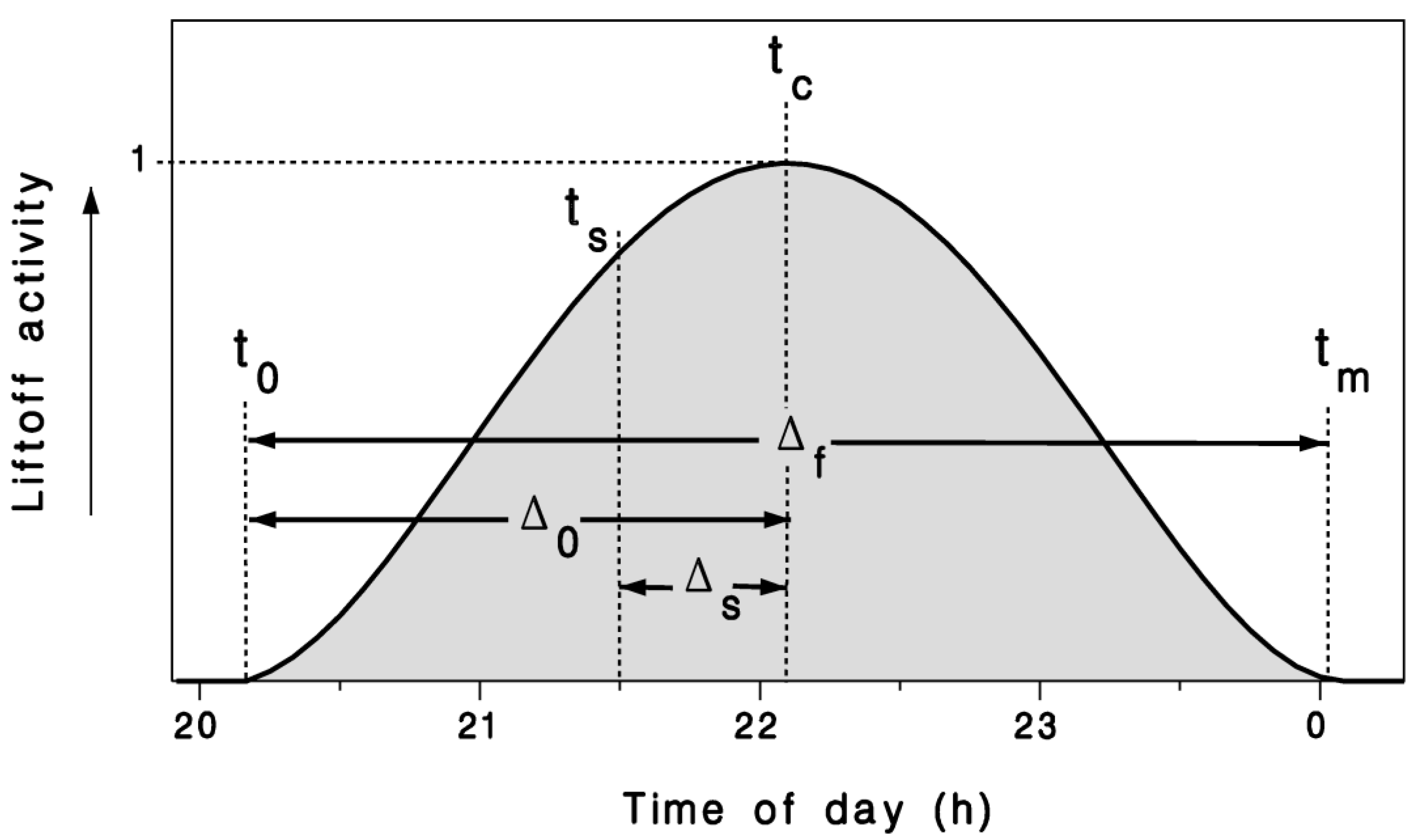
2.1. Mathematical Model
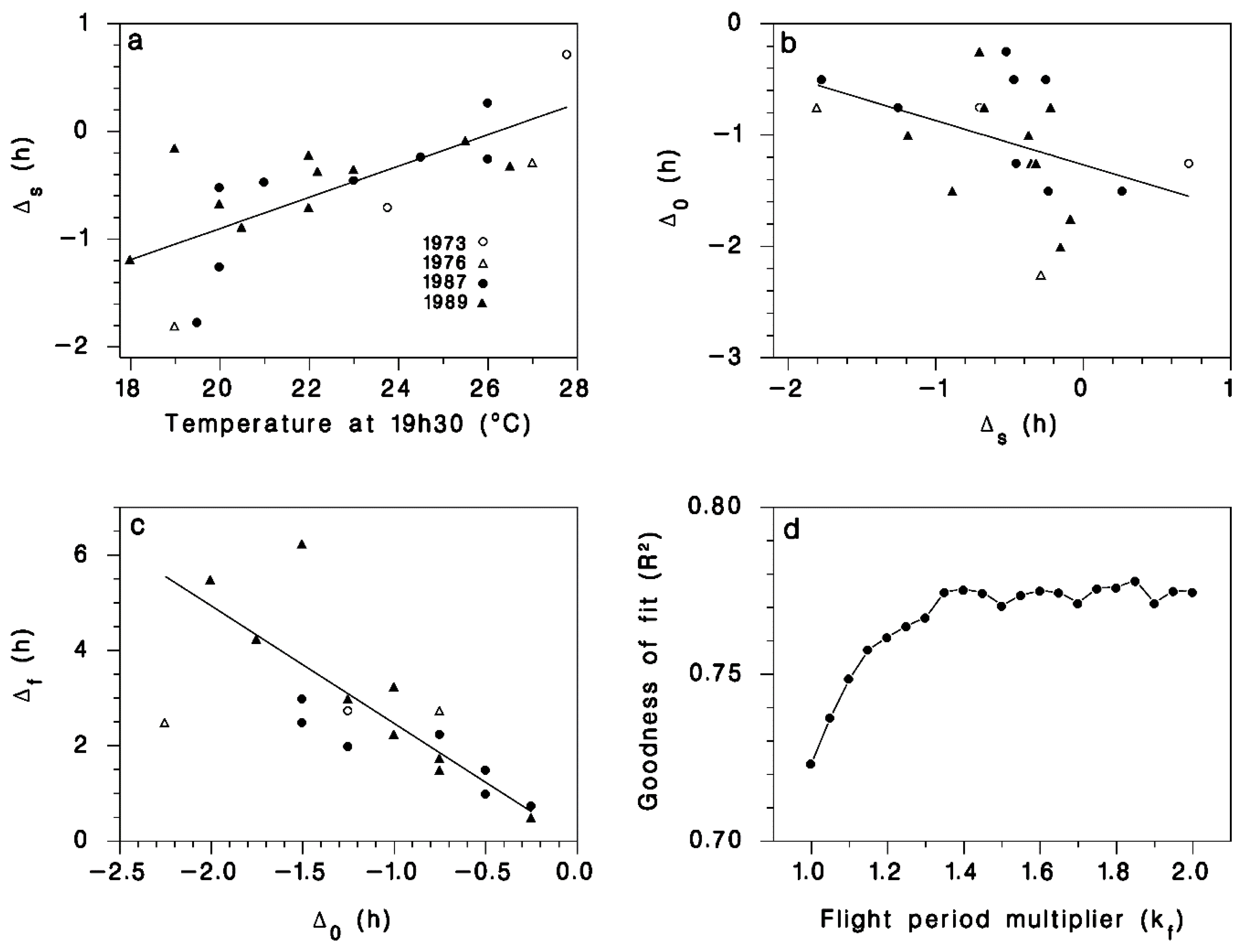
2.2. Observations and Model Calibration
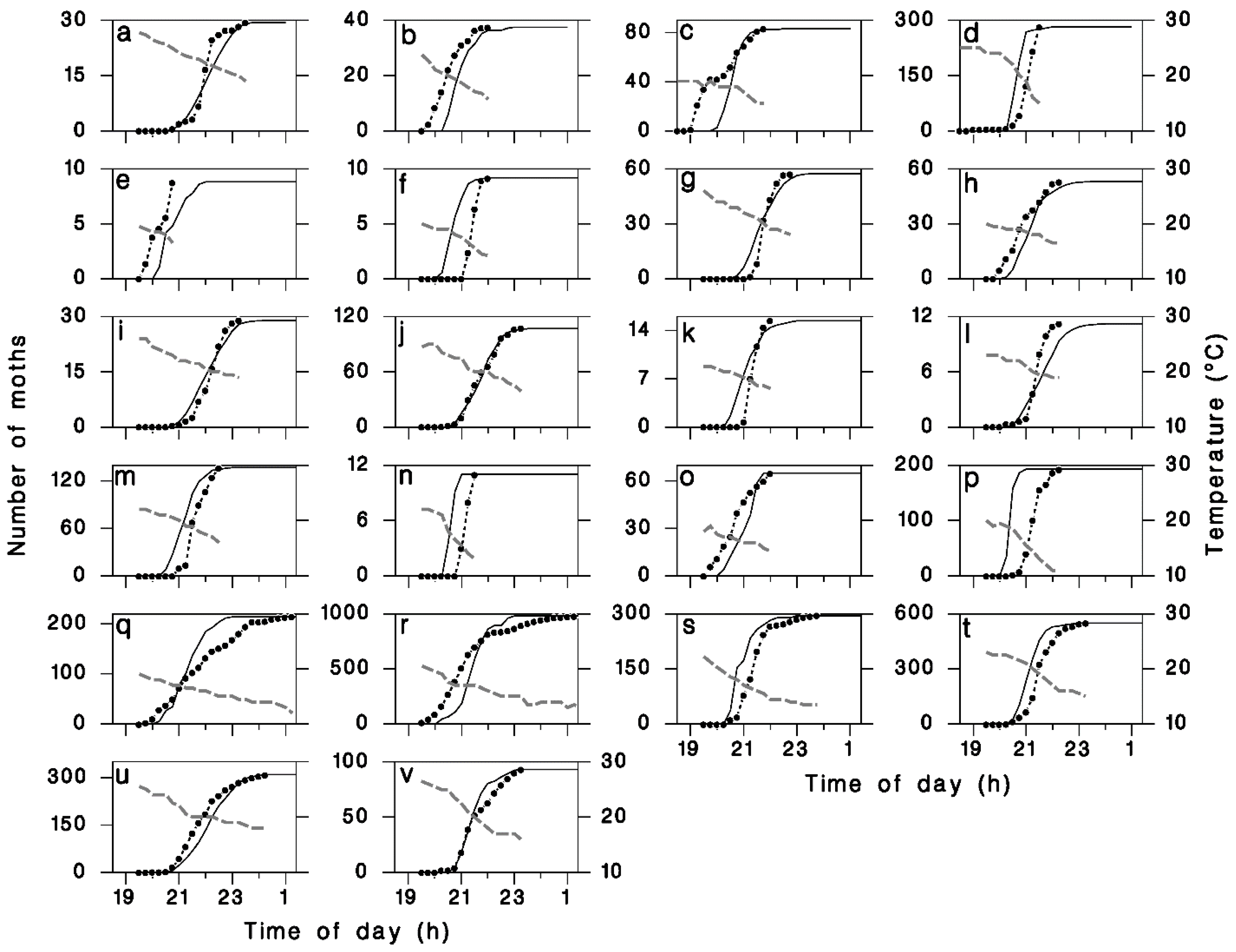
2.3. Simulations
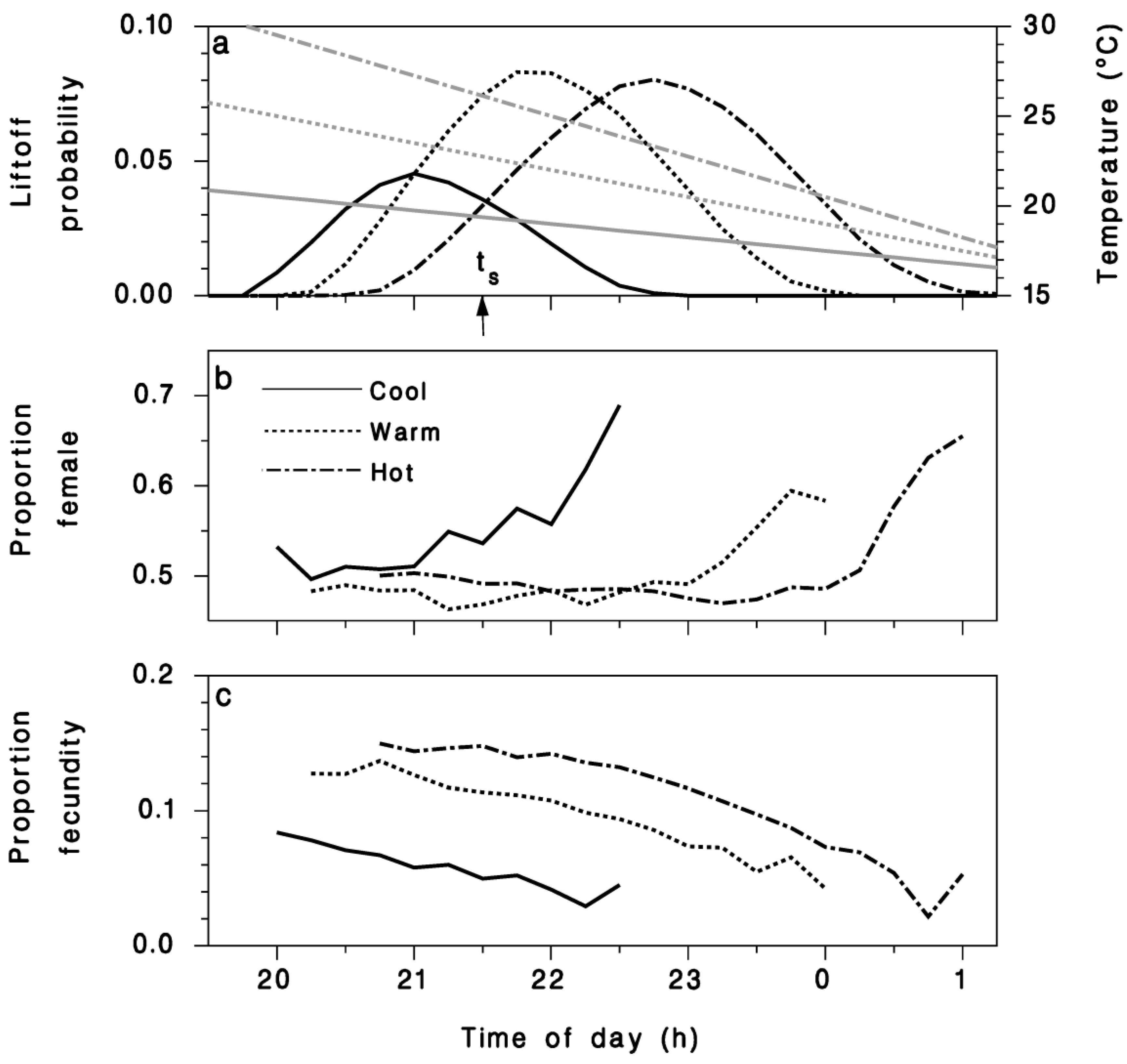
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dingle, H. Migration: The Biology of Life on the Move, 2nd ed.; Oxford University Press: New York, NY, USA, 2014; 326p. [Google Scholar] [CrossRef]
- Régnière, J.; Delisle, J.; Sturtevant, B.R.; Garcia, M.; St-Amant, R. Modeling migratory flight in the spruce budworm: Temperature constraints. Forests 2019, 10, 802. [Google Scholar] [CrossRef]
- Hu, G.; Lim, K.S.; Reynolds, D.R.; Reynolds, A.M.; Chapman, J.W. Wind-related orientation patterns in diurnal, crepuscular and nocturnal high-altitude insect migrants. Front. Behav. Neurosci. 2016, 10, 32. [Google Scholar] [CrossRef] [PubMed]
- Kawahara, A.Y.; Plotkin, D.; Hamilton, C.A.; Gough, H.; St Laurent, R.; Owens, H.L.; Homziak, N.T.; Barber, J.R. Diel behavior in moths and butterflies: A synthesis of data illuminates the evolution of temporal activity. Org. Divers. Evol. 2018, 18, 13–27. [Google Scholar] [CrossRef]
- Rund, S.; O’Donnell, A.; Gentile, J.; Reece, S. Daily rhythms in mosquitoes and their consequences for malaria transmission. Insects 2016, 7, 14. [Google Scholar] [CrossRef]
- Broadhead, G.T.; Basu, T.; von Arx, M.; Raguso, R.A. Diel rhythms and sex differences in the locomotor activity of hawkmoths. J. Exp. Biol. 2017, 220, 1472–1480. [Google Scholar] [CrossRef] [PubMed]
- Wellington, W.G. The light reactions of the spruce budworm, Choristoneura fumiferana Clemens (Lepidoptera: Tortricidae). Can. Entomol. 1948, 80, 56–82. [Google Scholar] [CrossRef]
- Henson, W.R. Mass flights of the spruce budworm. Can. Entomol. 1951, 83, 240. [Google Scholar] [CrossRef]
- Schaefer, G.W. Radar observations of insect flight. Symp. R. Entomol. Soc. Lond. 1976, 7, 157–197. [Google Scholar]
- Greenbank, D.O.; Schaefer, G.W.; Rainey, R.C. Spruce budworm (Lepidoptera: Tortricidae) moth flight and dispersal: New understanding from canopy observations, radar and aircraft. Mem. Entomol. Soc. Can. 1980, 112, 1–49. [Google Scholar] [CrossRef]
- Kipp, L.R.; Lonergan, G.C.; Bell, W.J. Male periodicity and the timing of mating in the spruce budworm (Lepidoptera: Tortricidae): Influence of population density and temperature. Environ. Entomol. 1995, 24, 1150–1159. [Google Scholar] [CrossRef]
- Cardé, R.T.; Roelofs, W.L. Temperature modification of male sex pheromone response and factors affecting female calling in Holomelina immaculata (Lepidoptera: Arctiidae). Can. Entomol. 1973, 105, 1505–1512. [Google Scholar] [CrossRef]
- Cardé, R.T.; Comeau, A.; Baker, T.C.; Roelofs, W.L. Moth mating periodicity: Temperature regulates the circadian gate. Experientia 1975, 31, 46–48. [Google Scholar] [CrossRef] [PubMed]
- Comeau, A.; Cardé, R.T.; Roelofs, W.L. Relationship of ambient temperatures to diel periodicities of sex attraction in six species of Lepidoptera. Can. Entomol. 1976, 108, 415–418. [Google Scholar] [CrossRef]
- Alerstam, T.; Chapman, J.W.; Bäckman, J.; Smith, A.D.; Karlsson, H.; Nilsson, C.; Reynolds, D.R.; Klaassen, H.G.; Hill, J.K. Convergent patterns of long-distance nocturnal migration in noctuid moths and passerine birds. Proc. R. Soc. B Biol. Sci. 2011, 278, 3074–3080. [Google Scholar] [CrossRef]
- Krauel, J.J.; Westbrook, J.K.; McCracken, G.F. Weather-driven dynamics in a dual-migrant system: Moths and bats. J. Anim. Ecol. 2015, 84, 604–614. [Google Scholar] [CrossRef]
- Krauel, J.J.; Brown, V.A.; Westbrook, J.K.; McCracken, G.F. Predator–prey interaction reveals local effects of high-altitude insect migration. Oecologia 2018, 186, 49–58. [Google Scholar] [CrossRef]
- Sanders, C.J. Daily activity patterns and sex pheromone specificity as sexual isolating mechanisms in two species of Choristoneura (Lepidoptera: Tortricidae). Can. Entomol. 1971, 103, 498–502. [Google Scholar] [CrossRef]
- Sanders, C.J.; Lucuik, G.S. Effects of photoperiod and size on flight activity and oviposition in the eastern spruce budworm (Lepidoptera: Tortricidae). Can. Entomol. 1975, 107, 1289–1299. [Google Scholar] [CrossRef]
- Simmons, G.A.; Chen, C.W. Application of harmonic analysis and polynomial regression to study flight activity of Choristoneura fumiferana (Clem.) (Lepidoptera: Tortricidae) in the field. Abstracts, Forty-Seventh Annual Meeting, Eastern Branch Entomological Society of America. J. N. Y. Entomol. Soc. 1975, 83, 266. [Google Scholar]
- Régnière, J.; Powell, J.; Bentz, B.; Nealis, V. Effects of temperature on development, survival and reproduction of insects: Experimental design, data analysis and modeling. J. Insect Physiol. 2012, 58, 634–647. [Google Scholar] [CrossRef]
- Wellington, W.G.; Henson, W.R. Notes on the effects of physical factors on the spruce budworm, Choristoneura fumiferana (Clem.). Can. Entomol. 1947, 79, 168–170. [Google Scholar] [CrossRef]
- Dickison, R.B.B.; Haggis, M.J.; Rainey, R.C. Spruce budworm moth flight and storms: Case study of a cold front system. J. Clim. Appl. Meteorol. 1983, 22, 278–286. [Google Scholar] [CrossRef]
- Dickison, R.B.B.; Haggis, M.J.; Rainey, R.C.; Burns, L.M.D. Spruce budworm moth flight and storms: Further studies using aircraft and radar. J. Clim. Appl. Meteorol. 1986, 25, 1600–1608. [Google Scholar] [CrossRef]
- Pedgley, D.E.; Reynolds, D.R.; Riley, J.R.; Tucker, M.R. Flying insects reveal small-scale wind systems. Weather 1982, 37, 295–306. [Google Scholar] [CrossRef]
- Drake, V.A. The vertical distribution of macro-insects migrating in the nocturnal boundary layer: A radar study. Bound. Layer Meteorol. 1984, 28, 353–374. [Google Scholar] [CrossRef]
- Drake, V.A. Radar observations of moths migrating in a nocturnal low-level jet. Ecol. Entomol. 1985, 10, 259–265. [Google Scholar] [CrossRef]
- Reynolds, D.R.; Chapman, J.W.; Edwards, A.S.; Smith, A.D.; Wood, C.R.; Barlow, J.F.; Woiwod, I.P. Radar studies of the vertical distribution of insects migrating over southern Britain: The influence of temperature inversions on nocturnal layer concentrations. Bull. Entomol. Res. 2005, 95, 259–274. [Google Scholar] [CrossRef]
- Reynolds, D.R.; Smith, A.D.; Chapman, J.W. A radar study of emigratory flight and layer formation by insects at dawn over southern Britain. Bull. Entomol. Res. 2008, 98, 35–52. [Google Scholar] [CrossRef] [PubMed]
- Chapman, J.W.; Drake, V.A.; Reynolds, D.R. Recent insights from radar studies of insect flight. Ann. Rev. Entomol. 2011, 56, 337–356. [Google Scholar] [CrossRef]
- Westbrook, J.K.; Eyster, R.S.; Wolf, W.W. WSR-88D doppler radar detection of corn earworm moth migration. Int. J. Biometeorol. 2014, 58, 931–940. [Google Scholar] [CrossRef]
- Boulanger, Y.; Fabry, F.; Kilambi, A.; Pureswaran, D.S.; Sturtevant, B.R.; Saint-Amant, R. The use of weather surveillance radar and high-resolution three-dimensional weather data to monitor a spruce budworm mass exodus flight. Agric. For. Meteorol. 2017, 234, 127–135. [Google Scholar] [CrossRef]
- Westbrook, J.K.; Eyster, R.S. Doppler weather radar detects emigratory flights of noctuids during a major pest outbreak. Remote Sens. Appl. Soc. Environ. 2017, 8, 64–70. [Google Scholar] [CrossRef]
- Sanders, J.C.; Wallace, D.R.; Luicuik, G.S. Flight activity of female eastern spruce budworm (Lepidoptera: Tortricidae) at constant temperatures in the laboratory. Can. Entomol. 1978, 110, 627–632. [Google Scholar] [CrossRef]
- Régnière, J.; Cooke, B.; Béchard, A.; Dupont, A.; Therrien, P. Dynamics and management of rising outbreak spruce budworm populations. Forests 2019, 10, 748. [Google Scholar] [CrossRef]
- Baklanov, A.A.; Grisogono, B.; Bornstein, R.; Zilitinkevich, S.S.; Taylor, P.; Larsen, S.E.; Rotach, M.W.; Fernando, H.J.S. The nature, theory, and modeling of atmospheric planetary boundary layers. Bull. Am. Meteorol. Soc. 2011, 92, 123–128. [Google Scholar] [CrossRef]
- Angevine, W.M. Transitional, entraining, cloudy, and coastal boundary layers. Acta Geophysica 2008, 56, 2–20. [Google Scholar] [CrossRef]
- Mahrt, L. Stably stratified atmospheric boundary layers. Ann. Rev. Fluid Mech. 2014, 46, 23–45. [Google Scholar] [CrossRef]
- Mahrt, L. The early evening boundary layer transition. Quart. J. R. Meteorol. Soc. 1981, 107, 329–343. [Google Scholar] [CrossRef]
- Mahrt, L. Nocturnal boundary-layer regimes. Bound. Layer Meteorol. 1998, 88, 255–278. [Google Scholar] [CrossRef]
- Mahrt, L. The near-surface evening transition. Quart. J. R. Meteorol. Soc. 2017, 143, 2940–2948. [Google Scholar] [CrossRef]
- Acevedo, O.C.; Fitzjarrald, D.R. The early evening surface-layer transition: Temporal and spatial variability. J. Atmos. Sci. 2001, 58, 2650–2667. [Google Scholar] [CrossRef]
- Sastre, M.; Yagüe, C.; Román-Cascón, C.; Maqueda, G. Atmospheric boundary-layer evening transitions: A comparison between two different experimental sites. Bound. Layer Meteorol. 2015, 157, 375–399. [Google Scholar] [CrossRef]
- Angevine, W.M.; Tjernström, M.; Žagar, M. Modeling of the coastal boundary layer and pollutant transport in New England. J. Appl. Meteorol. Climatol. 2006, 45, 137–154. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M. The turbulent structure of the stable, nocturnal boundary layer. J. Atmos. Sci. 1984, 41, 2202–2216. [Google Scholar] [CrossRef]
- Acevedo, O.C.; Mahrt, L.; Puhales, F.S.; Costa, F.D.; Medeiros, L.E.; Degrazia, G.A. Contrasting structures between the decoupled and coupled states of the stable boundary layer. Quart. J. R. Meteorol. Soc. 2016, 142, 693–702. [Google Scholar] [CrossRef]
- Mahrt, L. Microfronts in the nocturnal boundary layer. Quart. J. R. Meteorol. Soc. 2019, 145, 546–562. [Google Scholar] [CrossRef]
- Reynolds, A.M.; Reynolds, D.R.; Smith, A.D.; Chapman, J.W. Orientation cues for high-flying nocturnal insect migrants: Do turbulence-induced temperature and velocity fluctuations indicate the mean wind flow? PLoS ONE 2010, 5, e15758. [Google Scholar] [CrossRef]
- Riley, J.R.; Reynolds, D.R.; Rainey, R.C. Radar-based studies of the migratory flight of grasshoppers in the middle Niger area of Mali. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1979, 204, 67–82. [Google Scholar] [CrossRef]
- Rennie, S.J. Common orientation and layering of migrating insects in southeastern Australia observed with a Doppler weather radar. Meteorol. Appl. 2014, 21, 218–229. [Google Scholar] [CrossRef]
- Feng, H.; Wu, X.; Wu, B.; Wu, K. Seasonal migration of Helicoverpa armigera (Lepidoptera: Noctuidae) over the Bohai Sea. J. Econ. Entomol. 2009, 102, 95–104. [Google Scholar] [CrossRef]
- Fu, X.; Zhao, X.; Xie, B.; Ali, A.; Wu, K. Seasonal pattern of Spodoptera litura (Lepidoptera: Noctuidae) migration across the Bohai Strait in northern China. J. Econ. Entomol. 2015, 108, 525–538. [Google Scholar] [CrossRef] [PubMed]
- Wood, C.R.; Chapman, J.W.; Reynolds, D.R.; Barlow, J.F.; Smith, A.D.; Woiwod, I.P. The influence of the atmospheric boundary layer on nocturnal layers of noctuids and other moths migrating over southern Britain. Int. J. Biometeorol. 2006, 50, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Wood, C.R.; Reynolds, D.R.; Wells, P.M.; Barlow, J.F.; Woiwod, I.P.; Chapman, J.W. Flight periodicity and the vertical distribution of high-altitude moth migration over southern Britain. Bull. Entomol. Res. 2009, 99, 525–535. [Google Scholar] [CrossRef] [PubMed]
- Wood, C.R.; Clark, S.J.; Barlow, J.F.; Chapman, J.W. Layers of nocturnal insect migrants at high-altitude: The influence of atmospheric conditions on their formation. Agric. For. Entomol. 2010, 12, 113–121. [Google Scholar] [CrossRef]
- Dreyer, D.; El Jundi, B.; Kishkinev, D.; Suchentrunk, C.; Campostrini, L.; Frost, B.J.; Zechmeister, T.; Warrant, E.J. Evidence for a southward autumn migration of nocturnal noctuid moths in central Europe. J. Exp. Biol. 2018, 221, 179218. [Google Scholar] [CrossRef]
- Wang, H.-H.; Grant, W.E.; Elliott, N.C.; Brewer, M.J.; Koralewski, T.E.; Westbrook, J.K.; Alves, T.M.; Sword, G.A. Integrated modelling of the life cycle and aeroecology of wind-borne pests in temporally-variable spatially-heterogeneous environment. Ecol. Model. 2019, 399, 23–38. [Google Scholar] [CrossRef]
- Reynolds, A.M.; Reynolds, D.R.; Smith, A.D.; Chapman, J.W. A single wind-mediated mechanism explains high-altitude “non-goal oriented” headings and layering of nocturnally migrating insects. Proc. R. Soc. Lond. B Biol. Sci. 2010, 277, 765–772. [Google Scholar] [CrossRef]
- Aralimarad, P.; Reynolds, A.M.; Lim, K.S.; Reynolds, D.R.; Chapman, J.W. Flight altitude selection increases orientation performance in high-flying nocturnal insect migrants. Anim. Behav. 2011, 82, 1221–1225. [Google Scholar] [CrossRef]
- Riley, J.R. Collective orientation in night-flying insects. Nature 1975, 253, 113. [Google Scholar] [CrossRef]
- Reynolds, A.M.; Reynolds, D.R.; Riley, J.R. Does a “turbophoretic” effect account for layer concentrations of insects migrating in the stable night-time atmosphere? J. R. Soc. Interface 2009, 6, 87–95. [Google Scholar] [CrossRef][Green Version]
- Holtslag, A.A.M.; Svensson, G.; Baas, P.; Basu, S.; Beare, B.; Beljaars, A.C.M.; Bosveld, F.C.; Cuxart, J.; Lindvall, J.; Steeneveld, G.J.; et al. Stable atmospheric boundary layers and diurnal cycles: Challenges for weather and climate models. Bull. Am. Meteorol. Soc. 2013, 94, 1691–1706. [Google Scholar] [CrossRef]
- Davy, R. The climatology of the atmospheric boundary layer in contemporary global climate models. J. Clim. 2018, 31, 9151–9173. [Google Scholar] [CrossRef]
- McNider, R.T.; Steeneveld, G.J.; Holtslag, A.A.M.; Pielke, R.A.; Mackaro, S.; Pour-Biazar, A.; Walters, J.; Nair, U.; Christy, J. Response and sensitivity of the nocturnal boundary layer over land to added longwave radiative forcing. J. Geophys. Res. Atmos. 2012, 117, D14106. [Google Scholar] [CrossRef]
- Horvath, K.; Koracin, D.; Vellore, R.; Jiang, J.; Belu, R. Sub-kilometer dynamical downscaling of near-surface winds in complex terrain using WRF and MM5 mesoscale models. J. Geophys. Res. Atmos. 2012, 117, D11111. [Google Scholar] [CrossRef]
| Parameter | Calibration Value | Equation | Regression Statistics |
|---|---|---|---|
| p1 | −3.8 ± 0.7 h | (11) | F = 22.5; df = 1,20; R2 = 0.529; p < 0.001 |
| p2 | 0.145 ± 0.031 h/°C | ||
| p3 | −1.267 ± 0.146 h | (12) | F = 4.5; df = 1,20; R2 = 0.183; p < 0.047 |
| p4 | −0.397 ± 0.187 | ||
| p5 | −2.465 ± 0.152 | (13) | |
| kf | 1.35 ± 0.025 | (14) | R2 = 0.775 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Régnière, J.; Garcia, M.; Saint-Amant, R. Modeling Migratory Flight in the Spruce Budworm: Circadian Rhythm. Forests 2019, 10, 877. https://doi.org/10.3390/f10100877
Régnière J, Garcia M, Saint-Amant R. Modeling Migratory Flight in the Spruce Budworm: Circadian Rhythm. Forests. 2019; 10(10):877. https://doi.org/10.3390/f10100877
Chicago/Turabian StyleRégnière, Jacques, Matthew Garcia, and Rémi Saint-Amant. 2019. "Modeling Migratory Flight in the Spruce Budworm: Circadian Rhythm" Forests 10, no. 10: 877. https://doi.org/10.3390/f10100877
APA StyleRégnière, J., Garcia, M., & Saint-Amant, R. (2019). Modeling Migratory Flight in the Spruce Budworm: Circadian Rhythm. Forests, 10(10), 877. https://doi.org/10.3390/f10100877





