Abstract
The Cockroach Swarm Optimization (CSO) algorithm is inspired by cockroach social behavior. It is a simple and efficient meta-heuristic algorithm and has been applied to solve global optimization problems successfully. The original CSO algorithm and its variants operate mainly in continuous search space and cannot solve binary-coded optimization problems directly. Many optimization problems have their decision variables in binary. Binary Cockroach Swarm Optimization (BCSO) is proposed in this paper to tackle such problems and was evaluated on the popular Traveling Salesman Problem (TSP), which is considered to be an NP-hard Combinatorial Optimization Problem (COP). A transfer function was employed to map a continuous search space CSO to binary search space. The performance of the proposed algorithm was tested firstly on benchmark functions through simulation studies and compared with the performance of existing binary particle swarm optimization and continuous space versions of CSO. The proposed BCSO was adapted to TSP and applied to a set of benchmark instances of symmetric TSP from the TSP library. The results of the proposed Binary Cockroach Swarm Optimization (BCSO) algorithm on TSP were compared to other meta-heuristic algorithms.
1. Introduction
Evolutionary Computation (EC) encompasses all population-based algorithms. Algorithms are constructed on a set of multiple solution candidates (which are referred to as a population) and are iteratively refined [1]. EC involves meta-heuristic optimization algorithms whose origins are found in biological systems.
One of the classes of EC is Evolutionary Algorithms (EA), which are generic population-based algorithms that make use of biological evolution mechanisms (such as reproduction, mutation, recombination and selection). Examples of EA algorithms includes Genetic Algorithm (GA), which models genetic evolution; Genetic Programming (GP), which is based on GA, but with individual programs represented as trees; Evolutionary Programming (EP), which is derived from the simulation of adaptive behavior in evolution; Evolutionary Strategies (ES), which are geared towards modeling the strategic parameters that control variation in evolution; and Differential Evolution (DE), which is similar to GA, but differs in the reproduction mechanisms used.
Another class of EC is the Swarm Intelligence (SI) techniques. This class is population-based, where an individual population is initialized randomly, and each individual represents a potential solution. Individuals are simple agents that follow simple rules that mimic social and cognitive insect and animal behavior moving in search patterns to find optimal. Examples include: particle swarm optimization, which mimics the social behavior of birds [2]; ant colony optimization, which mimics the social behavior of ants [3]; Roach Infestation Optimization (RIO) [4] and Cockroach Swarm Optimization (CSO) [5], which mimic the social foraging behavior of cockroaches. Both EA and SI algorithms belong to the EC family, but use different approaches for searching.
Recently, cockroach-based algorithms were introduced into the SI community [4,5]; cockroach swarm algorithms were shown to be inspired by the emergent social behavior of cockroaches. Cockroaches obtain local information via interaction with peers and the immediate environment, on which their decision making is based. Cockroach habits include: swarming, chasing, dispersing, hungering and ruthlessness. The CSO algorithm that was originally introduced by ZhaoHui and HaiYan [5] and its variants have been shown in the literature including [5,6,7,8,9,10,11] as efficient in solving global optimization problems.
According to the literature, the CSO algorithm and variants show competitive results in instances where they were applied to some optimization problems and compared to PSO. The application of CSO reported in the literature include: Solving benchmark functions [5,6]; Cheng et al. applied CSO to the Traveling Salesman Problem (TSP) [7]; and ZhaoHui and HaiYan applied CSO to the Vehicle Routing Problem [8]. Additionally, Obagbuwa et al. enhanced the ability of CSO in solving multi-dimensional space function problems by the introduction of the stochastic constriction factor, and this enables the algorithm to avoid explosion in regions outside of the search space. It also enhances local and global searches of the algorithm, even as a cockroach is able to exploit its local neighborhood and explore the whole search region [9]. Obagbuwa and Adewumi presented an Improved Cockroach Swarm Optimization (ICSO) algorithm by introducing a hunger component, which is described by the Partial Differential Equation (PDE) for the migration method [10]. Wu and Wu proposed a cockroach genetic algorithm for estimating the parameters of the biological system in showing a net interactive effect of systems biology (S-system) where cockroach behavior was imitated and embedded into an advanced genetic algorithm to increase exploration and exploitation abilities [11].
Many optimization problems, such as sensor management, routing and scheduling, have their decision variables in a binary format [12]. Some of the well-known evolutionary algorithms, including the Particle Swarm Optimization (PSO) algorithm [2], the Gravitational Search Algorithm (GSA) [13], the Harmony Search (HS) algorithm [14], the Magnetic Optimization Algorithm (MOA) [15] and the Differential Evolution (DE) algorithm [16], have binary versions that enabled the algorithms to operate in binary spaces. Various techniques have been applied to continuous space searching algorithms to create binary search space versions. The binary versions of PSO, GSA and MOA were designed with the employment of transfer functions and a new position updating procedure [12,17,18]. The binary HS was designed with a set of harmony search and pitch adjustment rules, which causes HS to be converted to a binary version [19]. Furthermore, a probability estimator operator was proposed by Wang et al. to convert DE to a discrete version [20]. Solving various optimization problems such as COP with the techniques mentioned above is determined by the ability to consider specific constraints arising from practical applications, and also from the solution quality.
In this paper, a Binary Cockroach Swarm Optimization (BCSO) algorithm is proposed to solve optimization problems, whose decision variables are in a binary format. A transfer function called a sigmoid function, and a new position updating procedure were used in the design of the BCSO algorithm to map a continuous search space to a binary search space. A set of standard benchmark global optimization function problems as shown in Section 4 were used to evaluate the proposed BCSO algorithm, and the results of the test were compared with the existing Binary PSO (BPSO) and a continuous version of the CSO algorithm results. To validate the performance of the proposed algorithm on the optimization problems with binary decision variables, the TSP, which is probably the most well-known example of such problems, was evaluated. In the TSP case, a salesman wants to visit quite a number of cities, each only once, and then return to the starting point; while minimizing the total distance covered or the trip cost [21,22]. TSP is among the most widely-studied problems in COP included with the NP-hard category of optimization problems. The computational complexity of a TSP increases exponentially with the number of cities [21]. Considering TSP for testing optimization algorithms is of great importance and interest in academic and real-life applications because TSP has potential applications in important areas, including the drilling of printed circuit boards, routing and scheduling, X-ray crystallography, computer wiring and the control of robots [21,22]. Some meta-heuristic algorithms have been applied in the literature to solve TSP, such as the cuckoo search algorithm [21] and PSO [22].
The development of the proposed binary variant of cockroach swarm optimization is important because there is no particular algorithm that has been reported or confirmed to offer solutions to all optimization problems. Likewise, some algorithms provide better solutions in certain problems in comparison to others. The results of the experiments of the proposed algorithm on TSP were compared to other meta-heuristic algorithms. This is shown in Section 4.
EC algorithms are examples of metaheuristics. The term metaheuristic is a combination of the two words “meta” and “heuristic”; meta means beyond high-level, and heuristic means searching. According to Sorensen, a metaheuristic is a high-level problem-independent algorithmic framework that provides a set of guidelines or strategies to develop heuristic optimization algorithms [23]. A metaheuristic is made up of a set of ideas, concepts and operators for constructing heuristic optimization algorithms [23]. A metaheuristic is designed mainly to offer optimum solutions to optimization problems within good computing time, and this makes it free from combinatorial explosion (where the required computing time to locate the optima results of an NP-hard problems increases as an exponential function of the size of the problem). With respect to the solution quality and computing time, which varies across problems and situations, metaheuristic algorithms are designed in a framework that can be adapted to suit the need of real-life optimization problems.
Sorensen [23] criticized how the metaheuristics metaphor is used by some authors of “novel” methods; he argues that metaheuristics research has been flawed with respect some authors. He stated further that the novelty of the original metaphor does not inevitably guarantee the novelty of the resulting framework. However, he pointed out that high quality research in metaheuristics is expected to be framed effectively in the general literature of metaheuristics and optimization, which should involve deconstruction, that is, showing the components it is made up of and the adaptation of the components to a particular problem being solved [23]. In addition, he emphasized that the general optimization terminologies, such as “solution”, should be strictly used to describe any new metaheuristic [23]. The components of cockroach optimization metaheuristics are clearly described in the previous works in the literature, which include [5,6,9,10,24]. These components are constructed based on the inspiration from the social habits of natural cockroaches; each component imitates a cockroach habit; which can be adapted to solve optimization problems. This paper presents the binary version of the existing CSO metaheuristic, where the components were adapted to suit the popular TSP, and was tested on several instances of TSP. The terminologies used in this paper to describe the proposed algorithm are within the context of general optimization, metaheuristics, EC and SI.
The remaining part of the paper is as follows: Section 2 explains CSO and the motivation for the development of its binary version; Section 3 shows the proposed BCSO algorithm models; Section 3 describes the TSP approach; Section 4 presents the set of experiments conducted to evaluate the proposed BCSO algorithm, with the respective results and comparative results; and finally, Section 5 summarises the paper.
2. Cockroach Swarm Optimization
Zhao presented CSO algorithm models that imitate various types of natural cockroach behaviors: chase-swarming, dispersing and ruthlessness [6]. Obagbuwa and Adewumi improved on the efficiency of CSO by the incorporation of a new component called hunger behaviour [10]. See [6,10] for details on CSO models. Two cockroach dispersion models were described in [6,24] in the literature. In this paper, the efficiency of the two models for dispersion operation was investigated through simulation. The dispersion model of [24] was found more efficient and, hence, was used for the proposed binary version of the CSO algorithm.
Table 1 shows the results of the BCSO with the dispersion model [6]. This algorithm was unable to solve the Rosenbrock problem optimally. Table 2 shows the results of the proposed BCSO algorithm, simulated with the dispersion model of [24]. The algorithm was able solve all of the test function problems to optimal, including the Rosenbrock function, which has been reported in the literature being too difficult to solve. The proposed binary version of CSO is described in Section 3.

Table 1.
Simulation results of the Binary Cockroach Swarm Optimization (BCSO) algorithm using the dispersion operation model of [6].

Table 2.
Simulation results of the proposed BCSO algorithm.
The primary motivation in the development of the binary variant of the cockroach swarm optimization is the more sound and comparatively better results obtained from the continuous version when compared to other metaheuristic approaches. Cockroach algorithms have efficient searching capabilities as shown by cockroaches in nature. In their natural habitat, cockroaches display a number of unique social behaviors, that are well adapted to exploitation and exploration. For example, when the presence of a predator is noticed, “vigilance behavior”, displayed by adult cockroaches serving as sentries on the periphery of a group, who then signal the danger to the young ones through body movements and the emission of an alarm pheromone, which results in the rapid dispersion of group members [25]. Cockroaches rapidly disperse to different locations and are able to explore and exploit other areas in the search space to find good solutions. Vigilance behavior, also called dispersion behavior, promotes a high level of diversity as cockroaches disperse rapidly to several locations in the search space, and explore/exploit new sites. This high level of diversity helps in preventing local convergence. Food foraging is another habit of cockroaches that encourages diversity. At any particular point when the cockroach becomes hungry, it leaves the company of other cockroaches and shelter, in search of food. Cockroaches first exploit the immediate neighborhood for food, but when food is depleted or not found, they explores further afield [25]. This is described as hunger behavior in the cockroach swarm algorithm. The ruthlessness of cockroaches is another unique habit that assist in improving the ability to search locally, to escape from the local optimum, and also improve accuracy. Cockroaches can feed on anything, such as soap, paper, clothes, faeces, human food, their cast-off skin and egg capsules. The strong will even eat the weak [25]. This is defined as, when there is a food shortage, the bigger cockroach eats the smaller, and the stronger eats the weaker. It is assumed that when a bigger ones eats the smaller one or a stronger ones eats the weaker one, a good solution emerges.
The performance of the proposed algorithm is supported by the empirical studies shown in Section 4. The algorithm effectively solves instances of the TSP from 30 to as many as 1432 cities. The performance of the algorithm on TSP was compared with other metaheuristic algorithms and was found to have a similar or better performance in respect of these problems.
3. Binary Cockroach Swarm Optimization
Binarization is a method of reducing the number of possible states to feasible solutions [26]. The binarization of continuous space transforms the values of the space into a limited number of possible states [26]. Several binarization techniques are described in the literature, and these include: the sigmoid function, random-key, smallest position value, modified position equation, great value priority and nearest integer [26]. The sigmoid function is a very popular method of transforming continuous space into a binary space. The transformation process converts each element of each dimension to a binary digit [26]. In this paper, the sigmoid function technique of binarization was adopted. We investigated the optimization of a pseudo-Boolean function in cockroach swarm optimization.
Binary Cockroach Swarm Optimization (BCSO) was designed to accommodate some problems that require a binary decision. The cockroach’s probability of decision making, such as, yes or no, true or false, is considered. In the BCSO algorithm, the cockroach position is defined in terms of the probability that a bit will be in the state of either zeros or ones. The positions and personal best are integers of zeros or ones, , , where D is the cockroach population dimension size. The idea of using a sigmoid function in this paper came from the studies on binary versions of some evolutionary algorithms, including [12,17,18]. A logistic transformation was used to actualise the change in cockroach position as described in [12] using a sigmoid function .
The resulting change in position is defined by:
, where N is the swarm size, is a randomly-generated number between zero and one and is the current position of the cockroach.
The BCSO computational steps are given as:
- Initialize a cockroach swarm with uniform distributed random integers of zeros or ones as in , ; and set all parameters with values.
- Perform cockroach operations.
- Use the sigmoid function to transform the position probabilistically using Equation (1). This means the probability that the current position will take on a one or zero value.
- Calculate the fitness value and update the global best position.
- Repeat the loop until the end criteria is reached.
Solving TSP with BCSO
The TSP comprises a salesman and a set of cities. The salesman visits each city beginning with the first city and returning to the same city at the end of his trip. The goal of the salesman problem is to minimize the total cost or length of the trip. TSP can be described as a complete graph , where f is a function , , and G is a graph that contains a traveling salesman tour with a cost that does not exceed t.
The main idea of this work is that BCSO is able to search for an acceptable solution in the space using cockroach operators. The operators enhance local and global searches. The weakness of the chase swarming operation is being trapped in a local optimum. This is strengthened by other operations, such as dispersion and hunger operations. The dispersion operation encourages a high level of diversity, as cockroaches rapidly disperse across the search space and start exploiting and exploring new areas. Likewise, the hunger operation perturbs the search space, as cockroaches travel from one point to another looking for food in the strategic food locations within the search space.
The CSO is extended to solve TSP in order to make use of its advantages in the binary version. The binary version is adapted to TSP based on the re-interpretation of the terminologies of the basic CSO operations.
In the adaptation of BCSO to TSP, the 2-opt and nearest neighbor methods were used for perturbation to change the order of cities visited. 2-opt and the nearest neighbor methods were used respectively for tour construction and improvement. In a combinatorial optimization problem, a solution neighborhood is generated by the smallest perturbation, which causes the minimum number of changes in the solution [21]. 2-opt is a good technique for perturbation, because, for a new solution, two is the minimum number of contiguous edges that can be deleted.
Steps for the 2-opt method:
- Take two pairs of nodes (A, B) and (C, D) respectively from a tour and check if the distance ABCD is longer than ADBC.
- If true, swap A and C, that is, reverse the tour between the two nodes.
- Continue with the improvement process by returning to Step 1; otherwise, stop if no improvement is possible.
Steps of the nearest neighbor method:
- Start on an arbitrary vertex as the current vertex.
- Find out the shortest edge connecting the current vertex and an unvisited vertex V.
- Set the current vertex to V.
- Mark V as visited.
- If all of the vertices in the domain have been visited, then terminate the sequence.
- Go to Step 2.
The result of the algorithm is the sequence of the vertices visited.
The performance of the proposed BCSO algorithm is evaluated in Section 4 against some benchmark function problems, as well as against some instances of TSP.
4. Simulation Studies
This section presents the performance of the proposed BCSO on different optimization problems, and comparisons are made with other meta-heuristic algorithms. The BCSO algorithm was implemented in MATLAB 7.14 (R2012a) and run on a computer with a 2.30-GHz processor with 4.00 GB of RAM.
The performance of BCSO was first investigated on the minimization of benchmarks: Sphere, Rosenbrock, Griewangk and Rastrigin described by Equations (2)–(5), which many researchers have used for evaluating and comparing optimization algorithms. The optimum value for each benchmark is zero (0).
- 1
- Sphere Function
- 2
- Rosenbrock Function
- 3
- Griewank Function
- 4
- Rastrigin Function
The dependence of the results on the parameters was thoroughly studied experimentally, and the selected values are those that give the best results in terms of solution quality and computational time. The stability of the swarm is enhanced by the parameter inertial weight w, which controls the movement of cockroaches and helps the algorithm to avoid swarm explosion. Similarly, parameter manages the step size of the cockroach agent in iterations towards the best solution in the local neighborhood and eventually towards the global best solution in the entire given search space. This enhances exploitation and exploration within the given region.
Experiment parameters are as follows: D is the dimension of the search space for the selected benchmarks; D is set to 3, 5 and 10 with a maximum iteration of 1000; the cockroach range is set to ; population size ; perception distance ; step size ; inertial weight ; time , and dispersion coefficient . The hunger threshold , , is a randomly-generated number in the uniform interval ; speed controller ; and food locations are initialized randomly.
Each experiment was run 10 times, and the Success Ratio (SRT), Success Performance (SP), average and best minimum optimum values are shown in Table 2. The numerical results of BPSO are adopted in [27].
During experiments, we noticed that BCSO was consistent in each iteration. This is proven by the low Standard Deviation (STD) of the minimum optima values of the algorithms shown in Table 2. The SRT of the BCSO algorithm on the selected benchmarks was evaluated during the experiments. A run is considered successful if an algorithm can find the optimal solution for a given problem. The SRT of an algorithm is determined by the number of successful runs out of the total number of runs [28]. SRT was computed using Equation (6).
where denotes the number of successful runs and denotes the number of total runs. The algorithm has a 100% success rate on the benchmarks. The results of SRT for the BCSO algorithm are shown in Table 2. Likewise, the SP of the BCSO was computed during experiments. SP can be used to estimate the number of function evaluations needed for an algorithm to successfully solve a problem [28,29]. SP was computed using Equation (7).
where is the function evaluations of successful runs, denotes the number of total runs and denotes the number of successful runs. The results of SP for the BCSO algorithm are shown in Table 2.
A performance comparison of BCSO with that of BPSO was done on the average minimum optimum values. Table 3 shows the comparison results of BCSO and BPSO [27]. BCSO is shown to have a better performance than BPSO.

Table 3.
Comparison of the mean global best of BCSO and BPSO.
In addition to the basic statistical analysis carried out, the Mann–Whitney U-test was conducted in this paper for comparison of the average performanceob BCSO and BPSO algorithms. The Mann–Whitney U-test null hypothesis is that two groups of data are not different; the U statistics computed from the data determine whether the null hypothesis is accepted or rejected. The calculated p-value is the probability of obtaining either the observed difference or a more extreme value of the difference between the two groups. It is used as a basis for either accepting or rejecting the null hypothesis. If the p-value is less than a threshold value of , we reject the null hypothesis, and the result is considered significant. Otherwise, the null hypothesis is accepted.
Table 4 and Table 5 illustrate the U statistics conducted on the mean optimal performance of BCSO and BPSO [25]. The computed P-values asymptotic significance is less than the threshold value , and the null hypothesis is rejected, which indicates that the performance of the BCSO algorithm is significantly different from the BPSO algorithm for solving the benchmark functions.

Table 4.
Mann–Whitney U-test statistics on the performance of BCSO and BPSO.

Table 5.
Mann–Whitney U-test statistics.
We computed the effect size r of the significant difference of the test, , and is the total number of samples.
Z is negative when the observed data are below the mean and positive when above. Using Cohen’s guideline on effect size r (small: 0.1, medium: 0.3, large: 0.5, very-large: 1.0) [30,31]. The statistic 0.8 is of a very large magnitude effect size, which indicates that the BCSO algorithm performance is significantly different from the BPSO algorithm.
Additionally, in this work, the performances of the original CSO [5] and ICSO [10] were evaluated on the same set of benchmark problems and the same experimental settings as shown in this section and then was compared to the proposed binary version BCSO. Table 6 shows the simulation results of the original CSO, and Table 7 depicts the result of ICSO. The average performance of both the original CSO and its improved version, ICSO, were compared to the proposed BCSO in Table 8. The comparison results clearly show that the proposed binary version BCSO algorithm outperforms the existing continuous versions, CSO and ICSO. BCSO is able to solve optimally all of the tested benchmark problems, including Rosenbrock, which has been shown in the literature to be difficult to solve optimally.

Table 6.
Simulation results of the original CSO.

Table 7.
Simulation results of the improved CSO (ICSO).

Table 8.
Comparison of the mean global best of BCSO, ICSO and original CSO.
In order to validate the effectiveness of the proposed algorithm on the combinatorial optimization problem, its performance was investigated on the TSP instances as shown in Table 9. The experiments were run 10 times for each TSP instance, with a cockroach population size of 20 and a maximum iteration of 20,000. Sixteen instances of TSP with a different number of cities were solved, from 30–1432 cities. Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 show the results of some of the experiments on instances of 30, 431, 535, 1060 and 1432 cities, respectively. Table 9 shows the summary of the results of the experiments; the instances of TSP solved are shown in the first column; the optimum solution length retrieved from the TSP library is shown in the second column; the column “Best” shows the length of the best solution found by the proposed algorithm; the column “Average” shows the average of the solution length for 10 independent runs; the column “Worst” shows the length of the worst solution found by the proposed algorithm; the percentage of deviation of the average solution length over the optimum solution length of 10 runs is shown in column “% error on Average”; the column “% error on Best” shows the percentage of deviation of the best solution over the optimal solution length of 10 runs, and the average time in seconds for 10 runs is depicted in column ”time”.

Table 9.
Simulation results of the BCSO algorithm instances of the Traveling Salesman Problem (TSP) from TSP library.
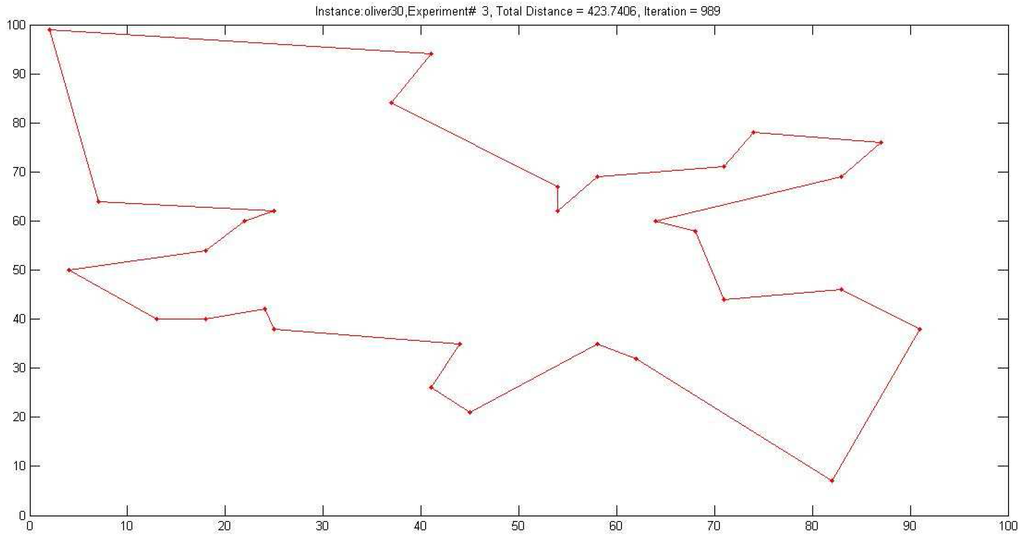
Figure 1.
Graph illustrating one of the experiments on the Oliver 30 instance of TSP (containing 30 cities) solved by the proposed BCSO algorithm.
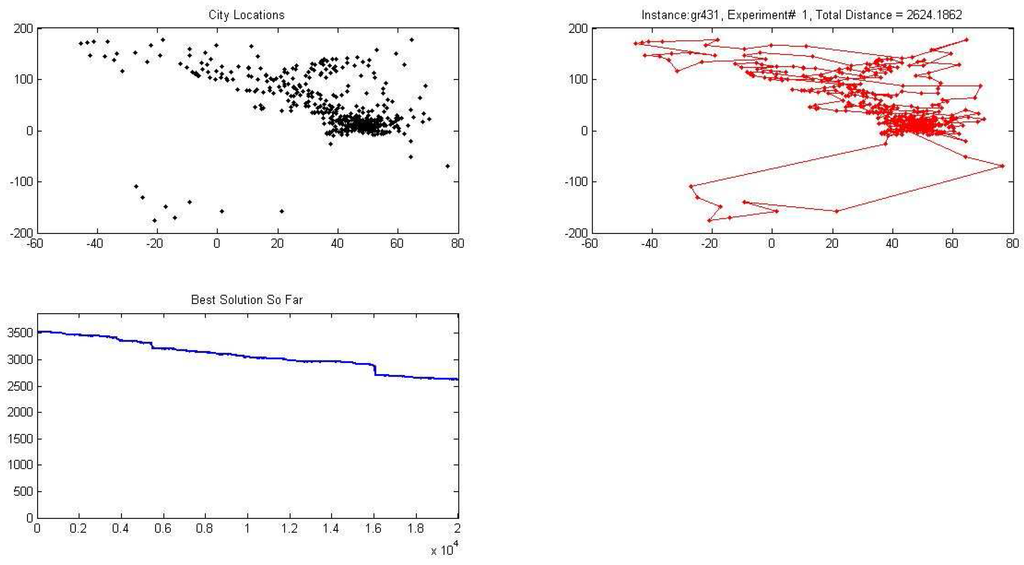
Figure 2.
Graph illustrating one of the experiments on the gr431 instance of TSP (containing 431 cities) solved by the proposed BCSO algorithm. The graph depicts the city location, total distance and best solution found.
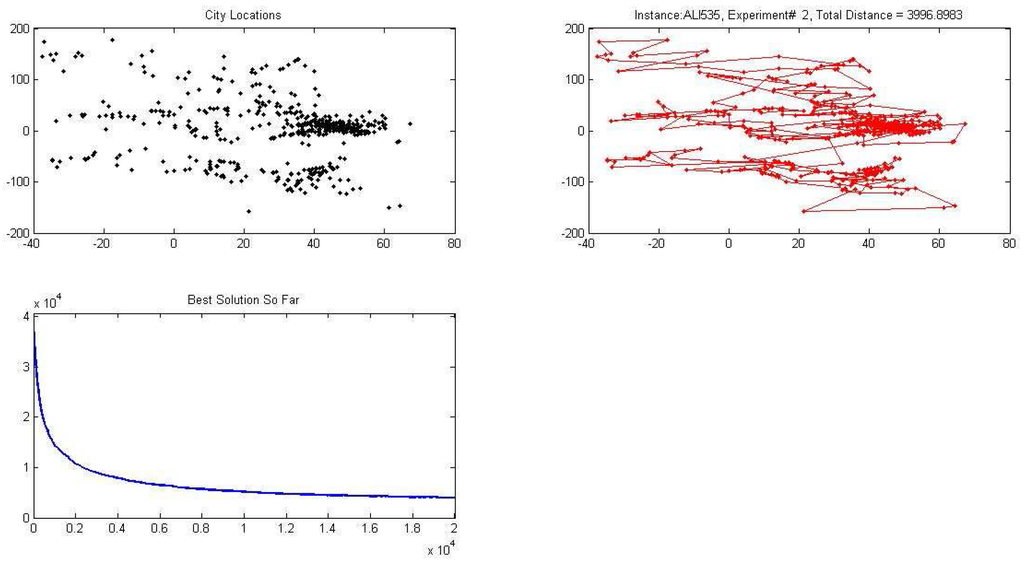
Figure 3.
Graph illustrating one of the experiments on the ali535 instance of TSP (containing 535 cities) solved by the proposed BCSO algorithm. The graph depicts the city location, total distance and best solution found.
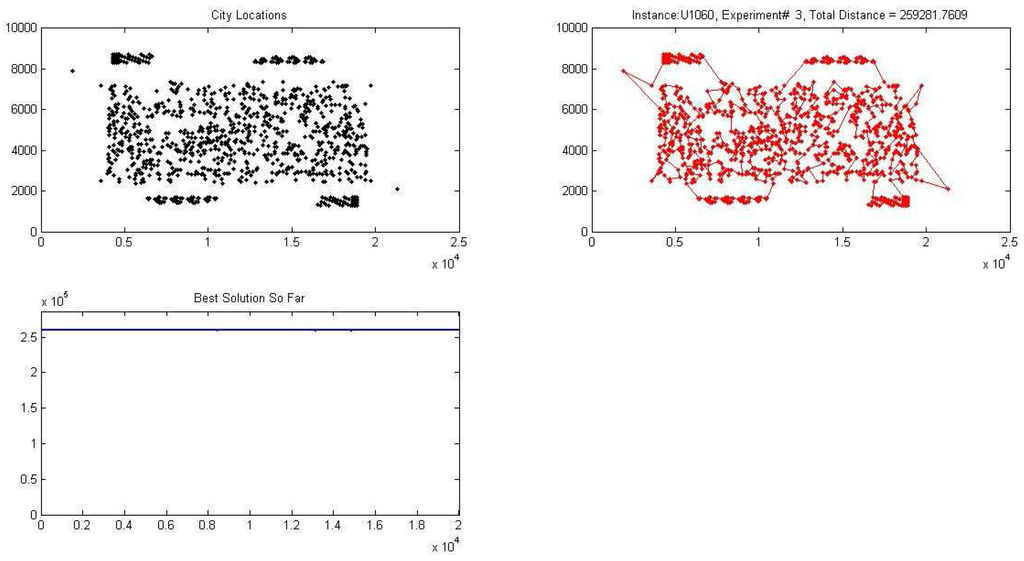
Figure 4.
Graph illustrating one of the experiments on the U1060 instance of TSP (containing 1060 cities) solved by the proposed BCSO algorithm. The graph depicts the city location, total distance and best solution found.
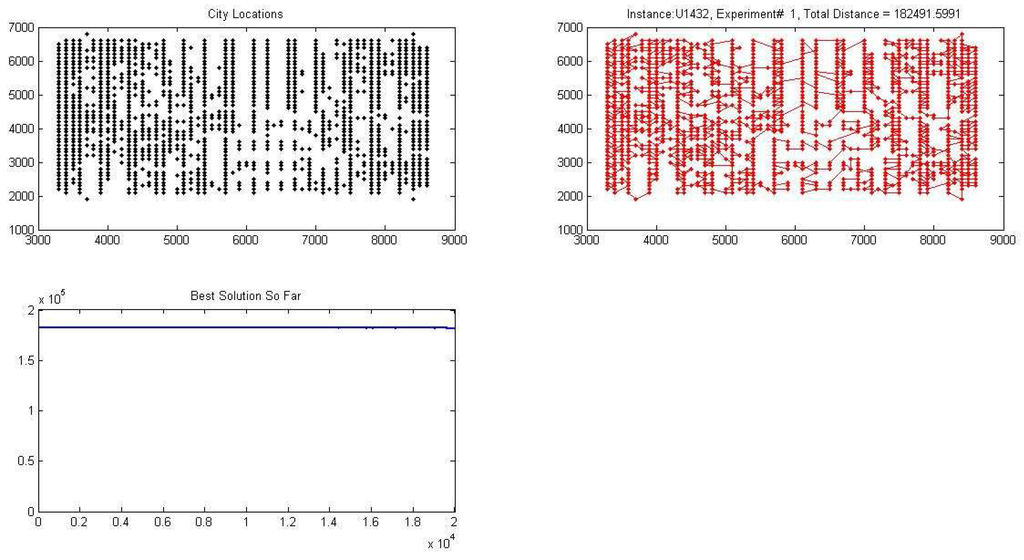
Figure 5.
Graph illustrating one of the experiments on the U1432 instance of TSP (containing 1432 cities) solved by the proposed BCSO algorithm. The graph depicts the city location, total distance and best solution found.
The percentage deviation from the best solution is given as:
where is the best-known tour from TSP library, and is the best tour found.
The percentage deviation from the average solution is given as:
where is the best known tour from TSP library, and is the average tour length for 10 independent runs. The proposed algorithm can solve optimally the instances of TSP evaluated.
Generally, the proposed algorithm performs excellently on the tested instances, especially on large problems. The algorithm is able to find a better solution length for problems gr431 and ali535 than the optimum solution length retrieved from the TSP library.
For comparison with other metaheuristic algorithms, its performance on the berlin52, kroA100, ali535, U1060, and U1432 problems was compared to GA and PSO. The comparison results shown in Table 10 clearly show that the proposed algorithm has a similar performance as GA and PSO on berlin52, kroA100, U1060 and U1432 and is able to solve ali535 better that GA and PSO. The simulation results of GA and PSO were adopted in [32].

Table 10.
Comparison results of the BCSO algorithm with GA and PSO [32] on some instances of TSP from the TSP library.
5. Conclusions
This paper presented the Binary Cockroach Swarm Optimization (BCSO) algorithm. The performance of the proposed algorithm was tested on benchmark test functions and compared with that of the Binary Particle Swarm Optimization (BPSO) algorithm. The statistical comparison results revealed that the BCSO algorithm has a better performance than the BPSO algorithm.
The performance of the proposed binary version BCSO was also compared to the existing continuous versions of CSO on the same set of problems. The comparison results show that BCSO performs better than CSO.
The proposed BCSO algorithm was adapted to the popular TSP and was evaluated on some instances of TSP. It was found to be efficient. The results of the proposed algorithm on TSP were compared with some metaheuristic algorithms on some instances, and BCSO shows similar or better performance to the comparison algorithms.
The focus of further research of this work will be on the investigation and comparison of binarization techniques on the proposed algorithm, and the application of the algorithm to real-life optimization problems.
Acknowledgments
This work was funded by the University of KwaZulu-Natal, South Africa, through a post-doctoral research fellowship grant. The work was motivated by the TSP works presented by Joseph Kirk and Jonas Lundgren in MathWorks.
Author Contributions
Obagbuwa conceived and designed the algorithm; Obagbuwa and Abidoye performed the experiments; Abidoye analysed the data; Obagbuwa wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bergh, F.D. An Analysis of Particle Swarm Optimizer. Ph.D. Thesis, Faculty of Natural and Agricultural Science, University of Pretoria, Pretoria, South Africa, November 2001. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. IEEE Neural Netw. Proc. 1995, 4, 1942–1948. [Google Scholar]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milano, Italy, 1992. [Google Scholar]
- Havens, T.; Spain, C.; Salmon, N.; Keller, J. Roach Infestation Optimization. In Proceedings of the IEEE Swarm Intelligence Symposium, St. Louis, MO, USA, 21–23 September 2008.
- Chen, Z.H.; Tang, H.Y. Notice of Cockroach Swarm Optimization. In Proceedings of the Second International Conference on Computer Engineering and Technology (ICCET), Chengdu, China, 16–18 April 2010.
- Chen, Z. A Modified Cockroach Swarm Optimization. Adv. Eng. Forum 2011, 11, 4–9. [Google Scholar]
- Cheng, L.; Wang, Z.; Song, Y.; Guo, A. Cockroach Swarm Optimization Algorithm for TSP. Adv. Eng. Forum 2011, 1, 226–229. [Google Scholar] [CrossRef]
- Chen, Z.; Tang, H.Y. Cockroach Swarm Optimization for Vehicle Routing Problems. Energy Proced. 2011, 13, 30–35. [Google Scholar]
- Obagbuwa, I.C.; Adewumi, A.O.; Adebiyi, A.A. Stochastic Constriction Cockroach Swarm Optimization for Multidimensional Space Function Problems. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Obagbuwa, I.C.; Adewumi, A.O. An Improved Cockroach Swarm Optimization. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-J.; Wu, C.-T. Computational Optimization for S-type Biology Systems: Cockroach Genetic Algorithm. Math. Biosci. 2013, 245, 299–313. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. A Discrete Binary Version of the Particle Swarm Algorithm. In Proceedings of the IEEE International Conference on System, Man, and Cybernetics, Orlando, FL, USA, 12–15 October 1997.
- Rashedi, E.; Nezamabadi, S.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Geem, Z.; Kim, J.; Loganathan, G. A New Heuristic Optimization Algorithm: Harmony Search. J. Simul. 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Tayarani-N, M.; Akbarzadeh-T, M. Magnetic Optimization Algorithms, A New Synthesis. In Proceedings of the IEEE Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008.
- Storn, R.; Price, K. Differential Evolution: A Simple and Efficient Heuristic for Global Optimization Over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. BGSA: Binary Gravitational Search Algorithm. Nat. Comput. 2009, 9, 727–745. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mohd Hashim, S.Z. BMOA: Binary Magnetic Optimization Algorithm. Int. J. Mach. Learn. Comput. 2012, 2, 204–208. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y.; Mao, Y.; Fei, M. A Discrete Harmony Search Algorithm. In Life System Modelling and Intelligent Computing; Li, K., Li, X., Ma, S., Irwin, G.W., Eds.; Springer: Berlin, Germany, 2010; Volume 98, pp. 37–43. [Google Scholar]
- Wang, L.; Fu, X.; Menhas, M.; Fei, M. A Modified Binary Differential Evolution Algorithm. In Life System Modeling and Intelligent Computing; Li, K., Fei, M., Jia, L., Irwin, G.W., Eds.; Springer: Berlin, Germany, 2010; Volume 6329, pp. 49–57. [Google Scholar]
- Ouaarab, A.; Ahiod, B.; Yang, X.S. Discrete Cuckoo Search Algorithm for the Traveling Salesman Problem. Neural Comput. Appl. 2014, 1, 1659–1669. [Google Scholar] [CrossRef]
- Labed, S.; Gherboudj, A.; Chikhi, S. A Modified Hybrid Particle Swarm Optimization Algorithm for Solving the Traveling Salesman Problem. J. Theor. Appl. Inf. Technol. 2012, 39, 11–16. [Google Scholar]
- Sorensen, K. Metaheuristics—The metaphor exposed. Int. Trans. Oper. Res. 2015, 22, 3–18. [Google Scholar] [CrossRef]
- Obagbuwa, I.C.; Adewumi, A.O. Modified Roach Infestation Optimization. In Proceedings of the IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB 2014), Hilton Hawaiian Village, Honolulu, HI, USA, 21–24 May 2014.
- Williams, J.B.; Louis, M.; Christine, R.; Nalepal, A. Cockroaches Ecology, Behaviour and Natural History; Johns Hopkins University Press: Baltimore, MD, USA, 2007. [Google Scholar]
- Krause, J.; Cordeiro, J.; Parpinelli, R.S.; Lopes, H.S. A Survey of Swarm Algorithms Applied to Discrete Optimization. In Swarm Intelligence and Bio-inspired Computation: Theory and Applications. Elsevier Science & Technology Books; Elsevier Inc.: Amsterdam, The Netherlands, 2013; pp. 169–191. [Google Scholar]
- Khanesar, M.A.; Tavakoli, H.; Teshnehlab, M.; Shoorehdeli, M.A. Novel Binary Particle Swarm Optimization; InTech: Shanghai, China, 2009. [Google Scholar]
- Auger, A.; Hansen, N. Performance Evaluation of an Advanced Local Search Evolutionary Algorithm. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; Volume 2, pp. 1777–1784.
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm with Strategy Adaptation for Global Optimization Numerical Optimization. IEEE Trans. Evol. Comput. 2009, 13, 264–271. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioural Science, 2nd ed.; Routledge: Hillsdale, MI, USA, 1988. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioural Science. Curr. Dir. Psychol. Sci. 1992, 1, 98–101. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, C.; Luo, W.; Li, W.; Chen, W.; Liu, H. Solve Traveling Salesman Problem Using Particle Swarm Optimization Algorithm. Int. J. Comput. Sci. Issues 2012, 9, 264–271. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).