1. Introduction
Broadband signal transmission is considered an indispensable technique in next-generation dependable wireless communication systems [
1,
2,
3]. It is well known that both multipath fading and additive noises are major determinants that impair the system performance. In such circumstances, either coherence detection or demodulation needs to estimate channel state information (CSI) [
1]. In the framework of a Gaussian noise model, some effective channel estimation techniques have been studied [
4,
5,
6,
7,
8,
9,
10]. In the assumptions of the non-Gaussian impulsive noise model, however, existing estimation techniques do not perform robustly due to heavy tailed impulsive interference. Generally speaking, impulsive noise is used to generate natural or man-made electromagnetic waves that are different from the conventional Gaussian noise model [
11]. For example, a second-order statistics-based least mean square error (LMS) algorithm [
4] cannot be directly applied in broadband channel estimation [
12]. To solve this problem, selecting a suitable noise model is necessary to devise a stable channel estimation that can combat the harmful impulsive noises.
The aforementioned non-Gaussian noise can be modeled by the symmetric alpha-stable (SαS) distribution [
13]. Based on the SαS noise model, several adaptive filtering based robust channel estimation techniques have been developed [
14,
15,
16]. These techniques are based on the channel model assumption of dense finite impulse response (FIR), which may not suitable in broadband channel estimation because the channel vector is supported only by a few dominant coefficients [
17,
18].
Considering the sparse structure in a wireless channel, this paper proposes a kind of sparse SLMS algorithm with different sparse norm constraint functions. Specifically, we adopt five sparse constraint functions as follows: zero-attracting (ZA) [
7] and reweighted ZA (RZA) [
7], reweighted
-norm (RL1) [
19],
-norm (LP), and
-norm (L0) [
20], to take advantage of sparsity and to mitigate non-Gaussian noise interference. It is necessary to state that the short versions of the proposed algorithms were initially presented in a conference but we did not give a performance analysis [
21]. In this paper, we first propose five sparse SLMS algorithms for channel estimation. To verify the stability of the proposed SLMS algorithms, convergence analysis is derived with respect to mean and excess mean square error (MSE) performance. Finally, numerical simulations are provided to verify the effectiveness of the proposed algorithms.
The rest of the paper is organized as follows.
Section 2 introduces an alpha-stable impulsive noise based sparse system model and traditional channel estimation technique. Based on the sparse channel model, we propose five sparse SLMS algorithms in
Section 3. To verify the proposed sparse SLMS algorithms, convergence analysis is derived in
Section 4. Later, computer simulations are provided to validate the effectiveness of the propose algorithms in
Section 5. Finally,
Section 6 concludes the paper and proposes future work.
2. Traditional Channel Estimation Technique
An input–output wireless system under the SαS noise environment is considered. The wireless channel vector is described by
N-length FIR sparse vector
at discrete time-index
. The received signal is obtained as
where
is the input signal vector of the
most recent input samples with distribution of
and
denotes a SαS noise variable. To understand the characteristic function of SαS noise, here we define it as
where
In Equation (2),
controls the tail heaviness of SαS noise. Since when
is rare to happen SαS noise in practical systems,
is considered throughout this paper [
11].
denotes the dispersive parameter, which can perform a similar role to Gaussian distribution;
stands for the symmetrical parameter. To have a better understanding of the alpha-stable noise, its probability density function (PDF) curves are depicted in
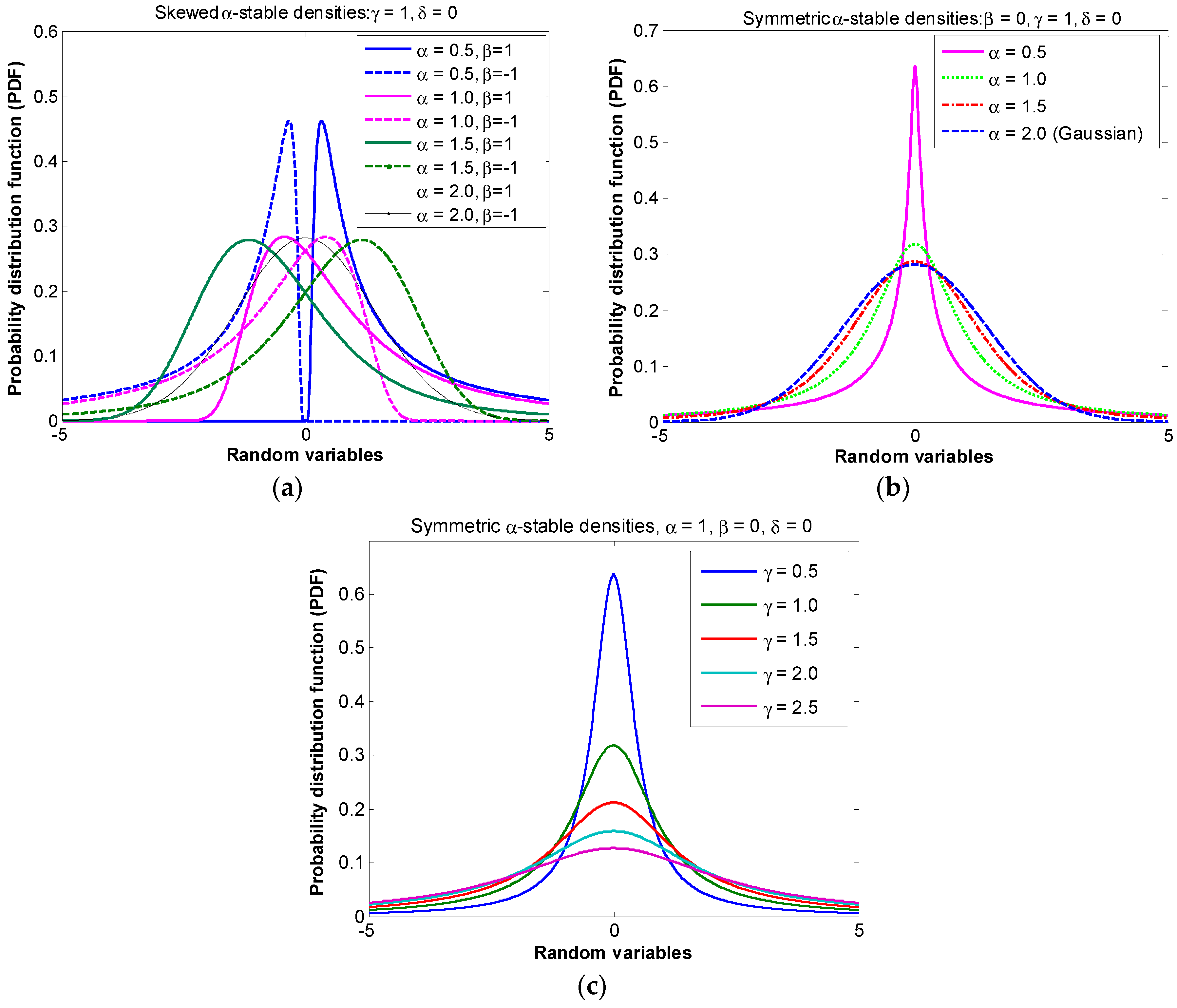
Figure 1 and
Figure 2 as examples.
Figure 1a shows that the PDF curve of symmetric alpha-stable noise changes with the parameter
, i.e., a smaller
produces a larger PDF of the alpha-stable noise model and vice versa. In other words,
controls the strength of the impulsive noise. Similarly,
Figure 1b shows that the PDF curve of skewed α-stable noise model also changes simultaneously with
and
. Since the skewed noise model may not exist in practical wireless communication systems, the symmetrical α-stable noise model is used in this paper; the characteristic function of α-stable process reduces as
For convenience, symmetric α-stable noise variance is defined by
and the generalized received signal noise ratio (GSNR) is defined by
where
denotes the received signal power while
plays the same role as the noise variance.
The objective of adaptive channel estimation is to perform adaptive estimate of
with limited complexity and memory given sequential observation
in the presence of additive noise
. That is to say, the estimate observation signal
is given as
where
denotes channel estimator. By combining (1) and (4), the estimation error
is
where
is the updating error of
at iteration
. The cost function of standard LMS was written as
Using Equation (11), the standard LMS algorithm was derived as
where
denotes a step-size that controls the gradient descend speed of the LMS. Letting
denotes the covariance matrix of input signal
and
as its maximum eigenvalue. The well-known stable convergence condition of the SLMS is
In order to remove SαS noise, the traditional SLMS algorithm [
14] was first proposed as
To ensure the stability of SLMS,
should be chosen as
where
denotes the unconditional variance of estimation error
. For later theoretical analysis, the
is conditioned by
where
denotes the second-order moment matrix of channel estimation error vector
.
3. Proposed Sparse SLMS Algorithms
By incorporating sparsity-aware function into the cost function of the standard SLMS in Equation (6), sparse SLMS algorithms could be developed to take advantage of sparse structure information, to mitigate SαS noise as well as to reconstruct channel FIR. First of all, this section proposes five effective sparse SLMS algorithms with different sparse constraints. These proposed algorithms are SLMS-ZA, SLMS-RZA, SLMS-RL1, SLMS-LP, and SLMS-L0. Later, performance analysis will be given to confirm the effectiveness of the proposed algorithms.
3.1. First Proposed Algorithm: SLMS-ZA
The cost function of the LMS-ZA algorithm [
7] was developed as
where
stands for a positive parameter to trade off instantaneous estimation square error and sparse penalty of
. It is worth noting that the optimal selection of
is very difficult due to the fact that
depends on many variables such as channel sparsity, instantaneous updating error
, SNR, and so on. Throughout this paper, the regularization parameter will be selected empirically via the Monte Carlo method. According to Equation (17), the LMS-ZA algorithm was developed as
where
depends the
and
. To mitigate the SαS noises, by constraining sign function on
, the SLMS-ZA algorithm is developed as
where the first
function is utilized to remove impulsive noise in
while the second one acts as a sparsity-inducing function to exploit channel sparsity in
. Please note that the steady-state mean square error (MSE) performance of the proposed SLMS-ZA depends highly on
.
3.2. Second Proposed Algorithm: SLMS-RZA
A stronger sparse penalty function can obtain more accurate sparse information [
19]. By devising an improved sparse penalty function RZA, we can develop an improved LMS-RZA algorithm. Its cost function can be constructed as
where
is a positive parameter. By deriving Equation (20), the update equation of SLMS-RZA is obtained as
where
. By collecting all of the coefficients as the matrix-vector form, Equation (21) can be expressed as
where
[
7] denotes reweighted factor. By inducing sign function to constraint
in Equation (22), the stable SLMS-RZA algorithm is proposed as
3.3. Third Proposed Algorithm: SLMS-RL1
In addition to the RZA in (23), RL1 function was also considered as an effective sparse constraint in the field of compressive sensing (CS) [
19]. By choosing a suitable reweighted factor,
, RL1 could approach the optimal
-norm (L0) constraint. Hence, the LMS-RL1 algorithm has been considered an attractive application of sparse channel estimation. The LMS-RL1 algorithm [
5] was developed as
where
denotes positive regularization parameter and
is defined as
where
and then
. By taking the derivation of Equation (24), the LMS-RL1 algorithm was updated as
where
. The third step of derivation can be obtained since
and then
. Here the cost function
is convex due to the fact that it does not depend on
. Likewise, sign function is adopted for constraint
and then robust SLMS-RL1 algorithm is obtained as
3.4. Fourth Proposed Algorithm: SLMS-LP
-norm sparse penalty is a nonconvex function to exploit sparse prior information. In [
5], LMS-LP based channel estimation algorithms was developed as
where
is a positive parameter. The update function of LMS-LP is given as
where
is a threshold parameter and
. To remove the SαS noise, SLMS-LP based robust adaptive channel estimation is written as
3.5. Fifth Proposed Algorithm: SLMS-L0
It is well known that the
-norm penalty can exploit the sparse structure information. Hence, the L0-LMS algorithm is constructed as
where
and
stands for optimal
-norm function. However, it is a NP-hard problem to solve the
-norm sparse minimization [
22]. The NP-hard problem in Equation (31) can be solved by an approximate continuous function:
Then, the previous cost function (29) is changed to
The first-order Taylor series expansion of exponential function
can be expressed as
Then, the LMS-L0 based robust adaptive sparse channel estimation algorithm is given as
where
. In Equation (35), the exponential function still exhausts high computational resources. To further reduce it, a simple approximation function
is proposed in [
20]. By introducing sign function into Equation (35), the SLMS-L0 based robust channel estimation algorithm is written as
where
and
are defined as
for
.
4. Convergence Analysis of the Proposed Algorithms
Unlike the standard SLMS algorithm, the proposed sparse SLMS algorithms can further improve estimation accuracy by exploiting channel sparsity. For convenience of theoretical analysis without loss of generality, the above proposed sparse SLMS algorithms are generalized as
where
denotes sparsity constraint function and
denotes the regularization parameter. Throughout this paper, our analysis is based on independent assumptions as below:
Theorem 1. If satisfies (15), the mean coefficient vector approaches Proof. By subtracting
from both sides of (35), the mean estimation error
is derived as
It is worth mentioning that vector
is bounded for all sparse constraints. For example, if
, then the bound is between
and
, where
is an
-length identity vector. For
, Equation (45) can be rewritten as
where
and
are utilized in the above equation. Since
, according to Equation (47), one can easily get Theorem 1.
Theorem 2. Let denotes the index set of nonzero taps, i.e., for .
Assuming is sufficiently small so that for every ,
the excess MSE of sparse SLMS algorithms iswhere , , and are defined as:
Proof. By using the above independent assumptions in Equations (49)–(52), the second moment
of the weight error vector
can be evaluated recursively as
where
,
, and
are further derived as
By substituting Equations (54) and (56) into Equation (53), we obtain
Letting
and using Equation (47), Equation (57) is further rewritten as
Multiplying both sides of Equation (58) by
from right, the following can be derived as
Taking the trace of the two sides of Equation (59), since
, the excess MSE is derived as
The matrix
is symmetric, and its eigenvalue decomposition can be written as
with
being the orthonormal matrix of eigenvectors and
being a diagonal matrix of eigenvalues. Therefore,
. Let
be the largest eigenvalue of the covariance matrix
and
be small enough such that
under certain noise cases. Since
is a diagonal matrix, elements are all non-negative and less than or equal to
, hence,
and
are further derived as
Substituting Equations (62) and (63) into Equation (60), the excess MSE is finally derived as
where
and
. According to Equation (62), one can find that
is bound as
The excess MSE of sparse SLMS in Equation (65) implies that choosing suitable can lead to smaller excess MSE than standard SLMS algorithm.
5. Numerical Simulations and Discussion
To evaluate the proposed robust channel estimation algorithms, we compare these algorithms in terms of channel sparsity and non-Gaussian noise level. A typical broadband wireless communication system is considered in computer simulations [
3]. The baseband bandwidth is assigned as 60 MHz and the carrier frequency is set as 2.1 GHz. Signal multipath transmission causes the
delay spread. According to the Shannon sampling theory, the channel length is equivalent to
n = 128. In addition, average mean square error (MSE) is adopted for evaluate the estimation error. The MSE is defined as
where
and denote actual channel and estimator, respectively.
independent runs are adopted for Monte Carlo simulations. The nonzero channel taps are generated to satisfy random Gaussian distribution as
and all of these positions are randomly allocated within
, which is normalized as
. All of the simulation parameters are listed in
Table 1.
5.1. Experiment 1. MSE Curves of Proposed Algorithms vs. Different Alpha-Stable Noise
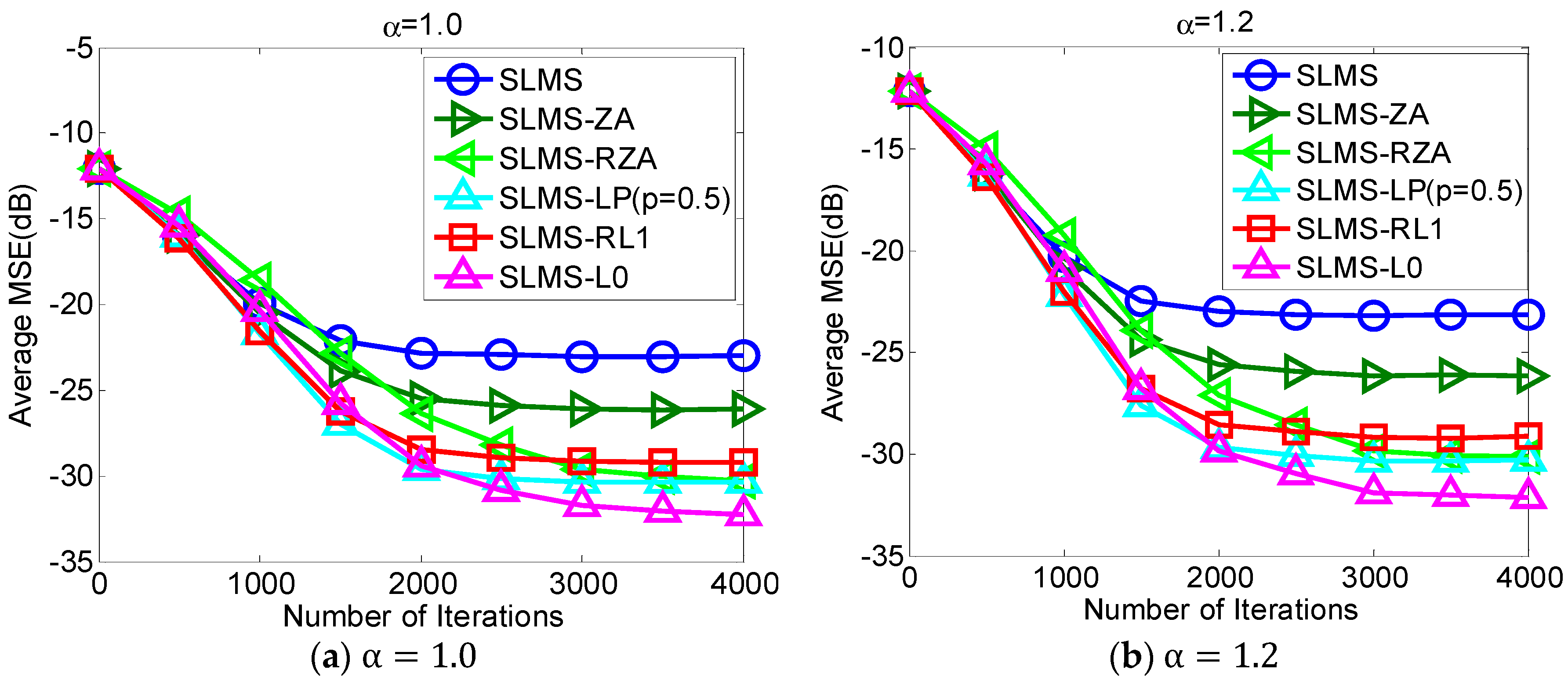
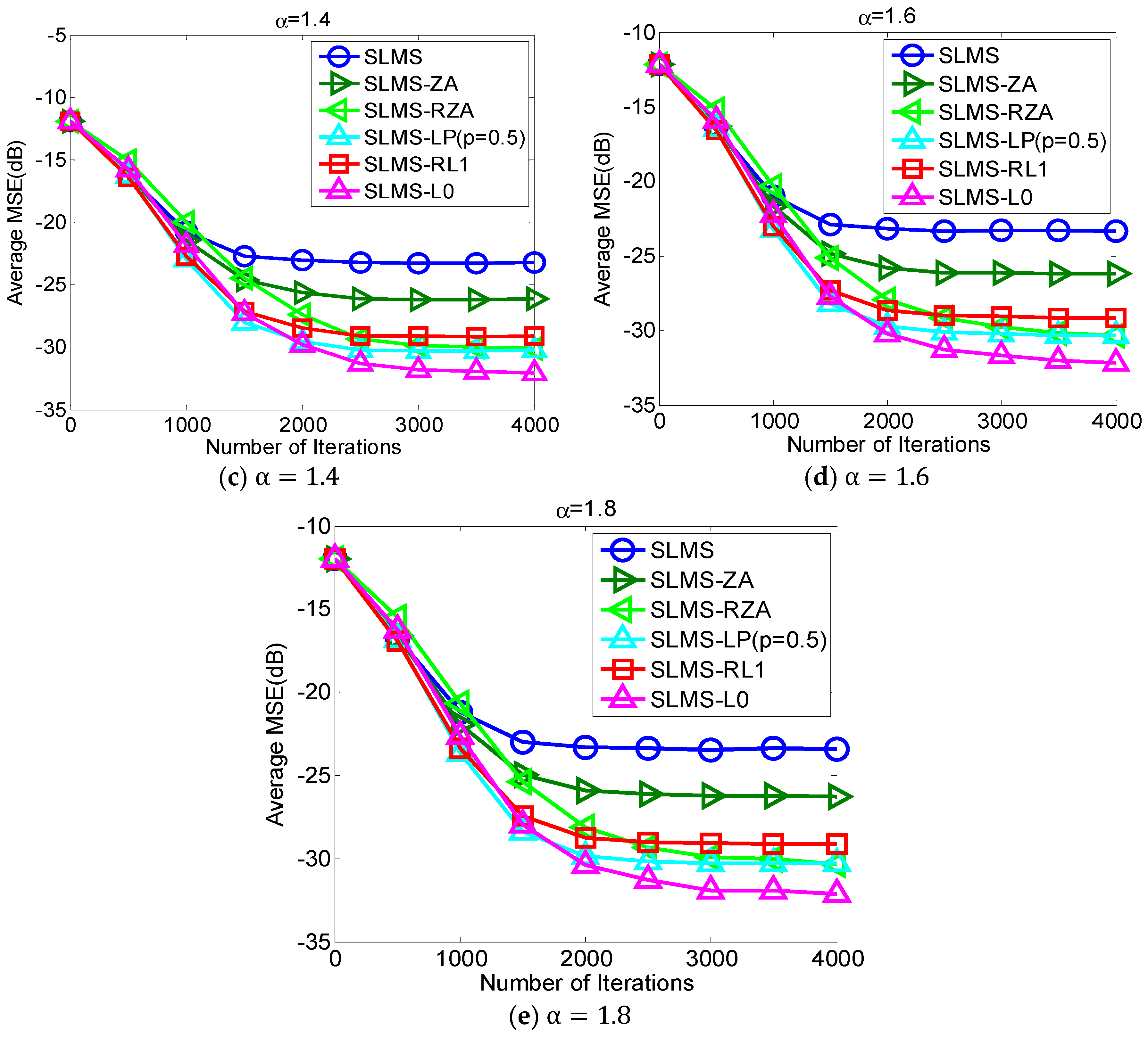
The proposed robust adaptive sparse channel estimation algorithms are evaluated with respect to
in the scenarios of
and SNR = 10 dB, as shown in
Figure 2. Under different alpha-stable noise regimes, i.e.,
, our proposed algorithms can achieve much better MSE performance than standard SLMS. With different sparsity constraint functions, i.e., ZA, RZA, LP, RL1, and L0, different performance gain could be obtained. Since L0-norm constraint exploits channel sparsity most efficiently in these sparse constraint functions,
Figure 2 shows that the lowest MSE of SLMS-L0 results in the lowest MSE. Indeed,
Figure 2 implies that taking more channel sparse structure information can obtain more performance gain. Hence, selecting an efficient sparse constraint function is an important step in devising sparse SLMS algorithms. In addition, it is worth noting that the convergence speed of SLMS-RZA is slightly slower than other sparse SLMS algorithms while its steady-state MSE performance as good as SLMS-LP. According to
Figure 2, proposed SLMS algorithms are confirmed by simulation results in different impulsive noise cases.
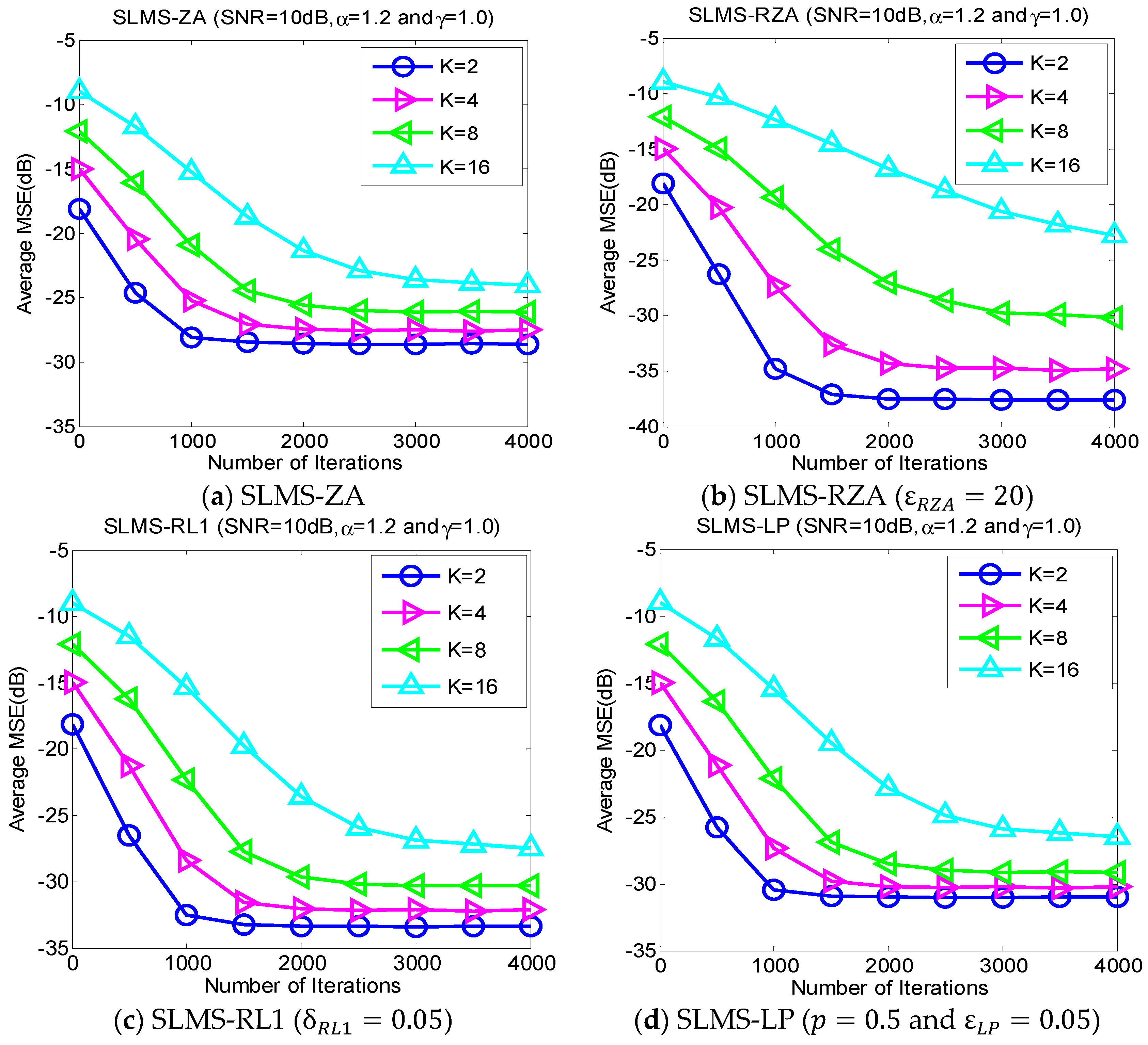
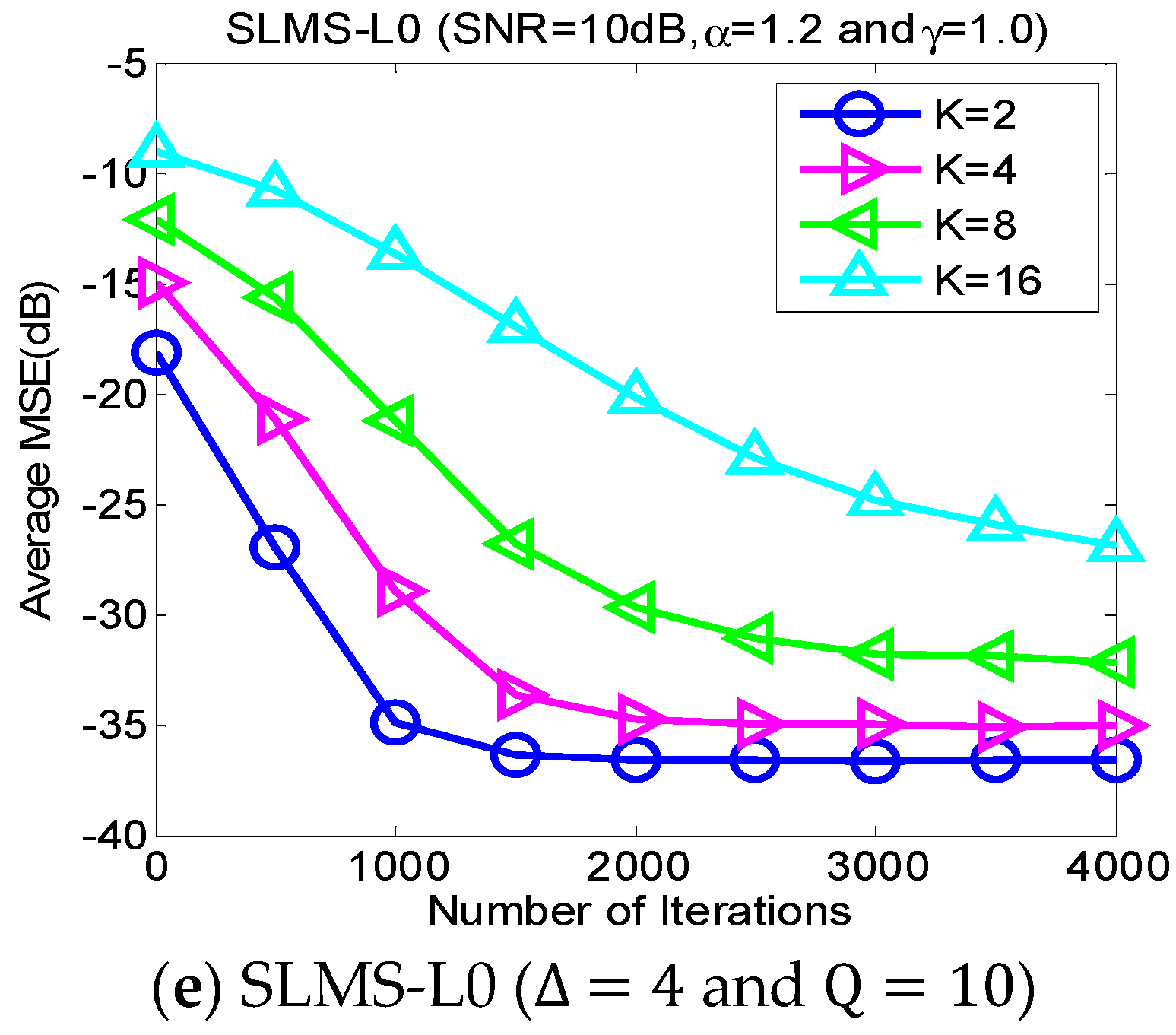
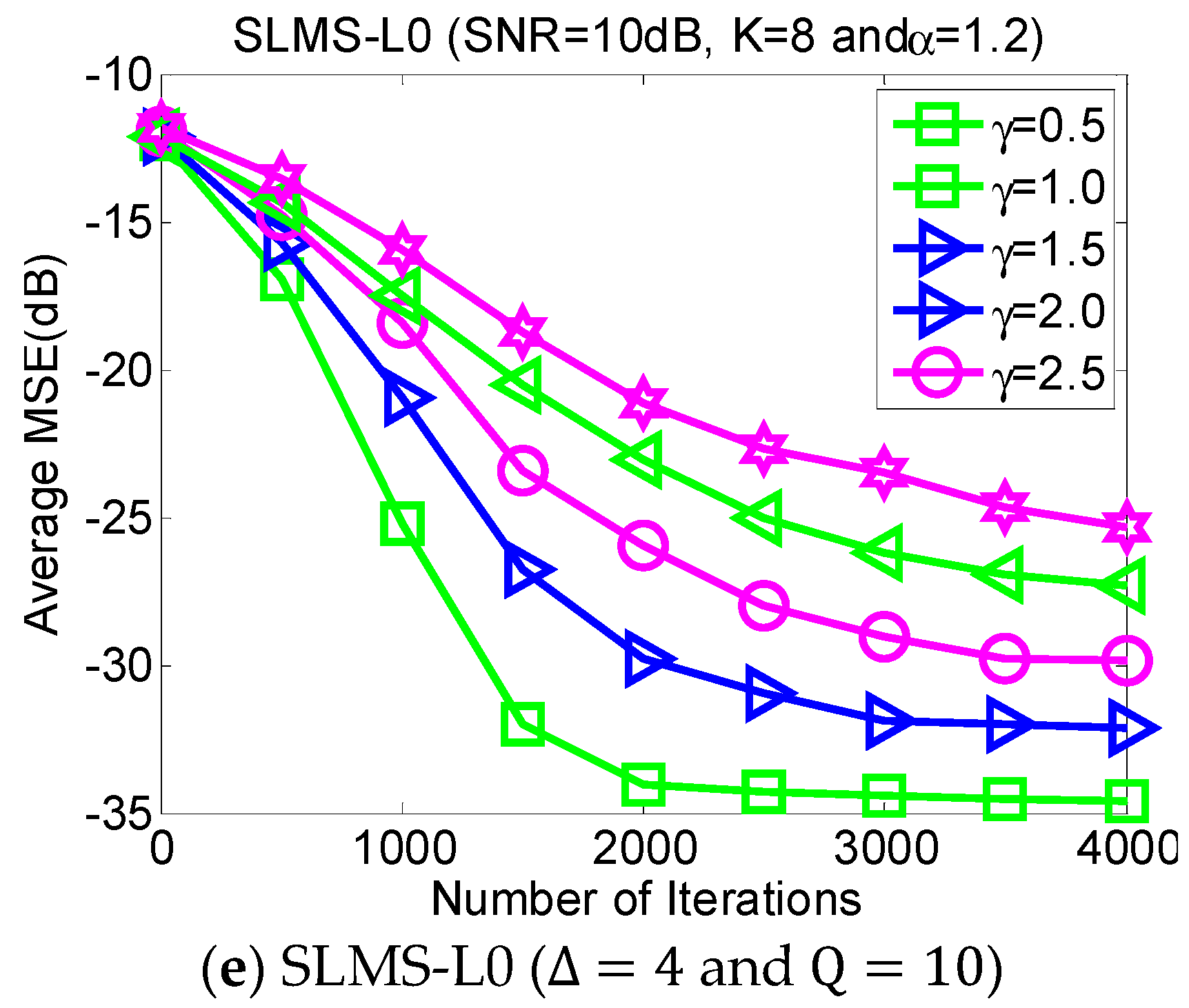
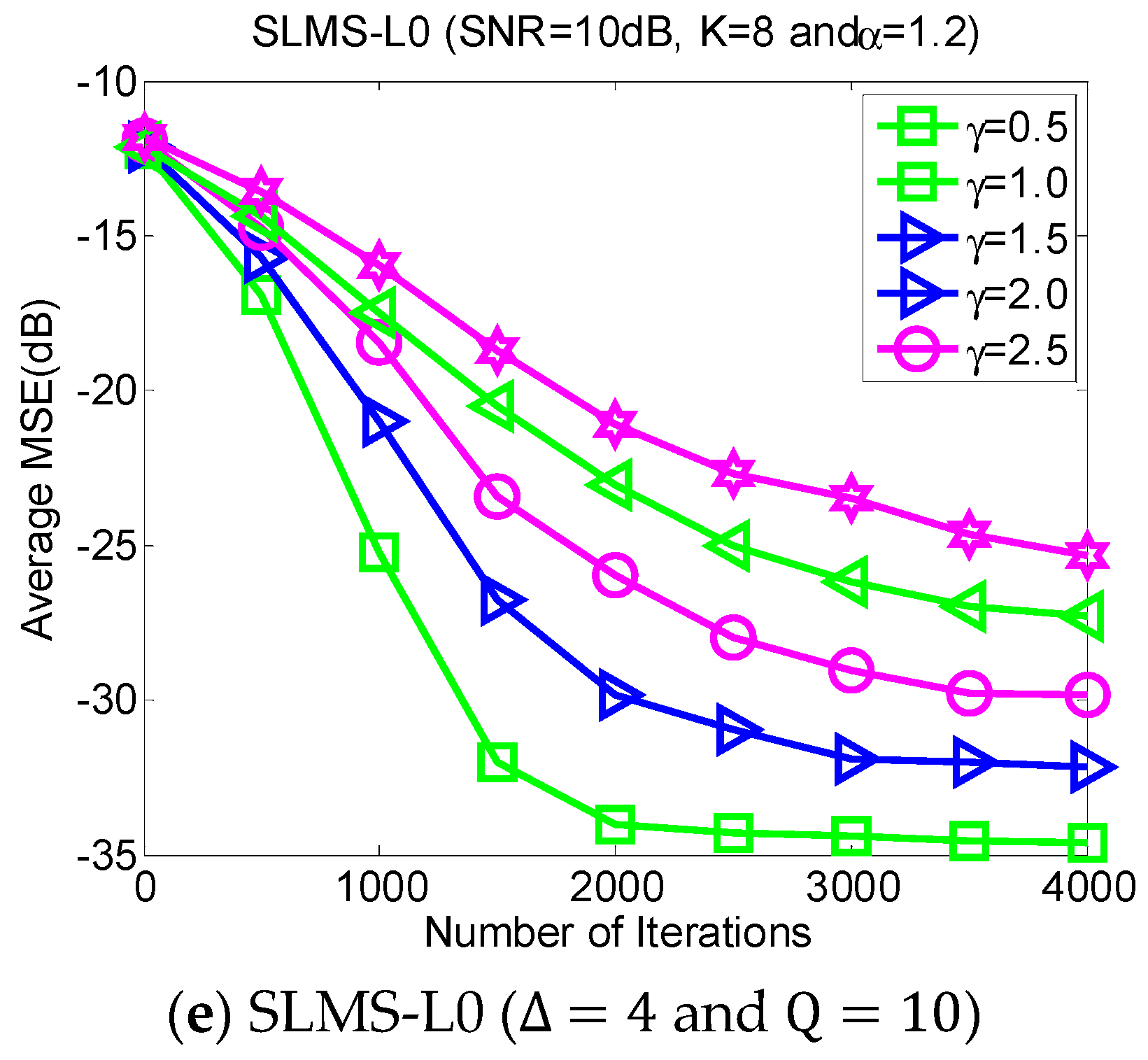
5.2. Experiment 2. MSE Curves of Proposed Algorithms vs. Channel Sparsity
Our proposed channel estimation algorithms are evaluated with channel sparsity
in the scenarios of
,
,
and
, as shown in
Figure 3. We can find that the proposed sparse SLMS algorithms depend on channel sparsity
, i.e., our proposed algorithms obtained correspondingly better MSE performance in a scenario of sparser channels. In other words, exploiting more channel sparsity information could produce more performance gain and vice versa. Hence, the proposed methods are effective to exploit channel sparsity as well as remove non-Gaussian α-stable noise.
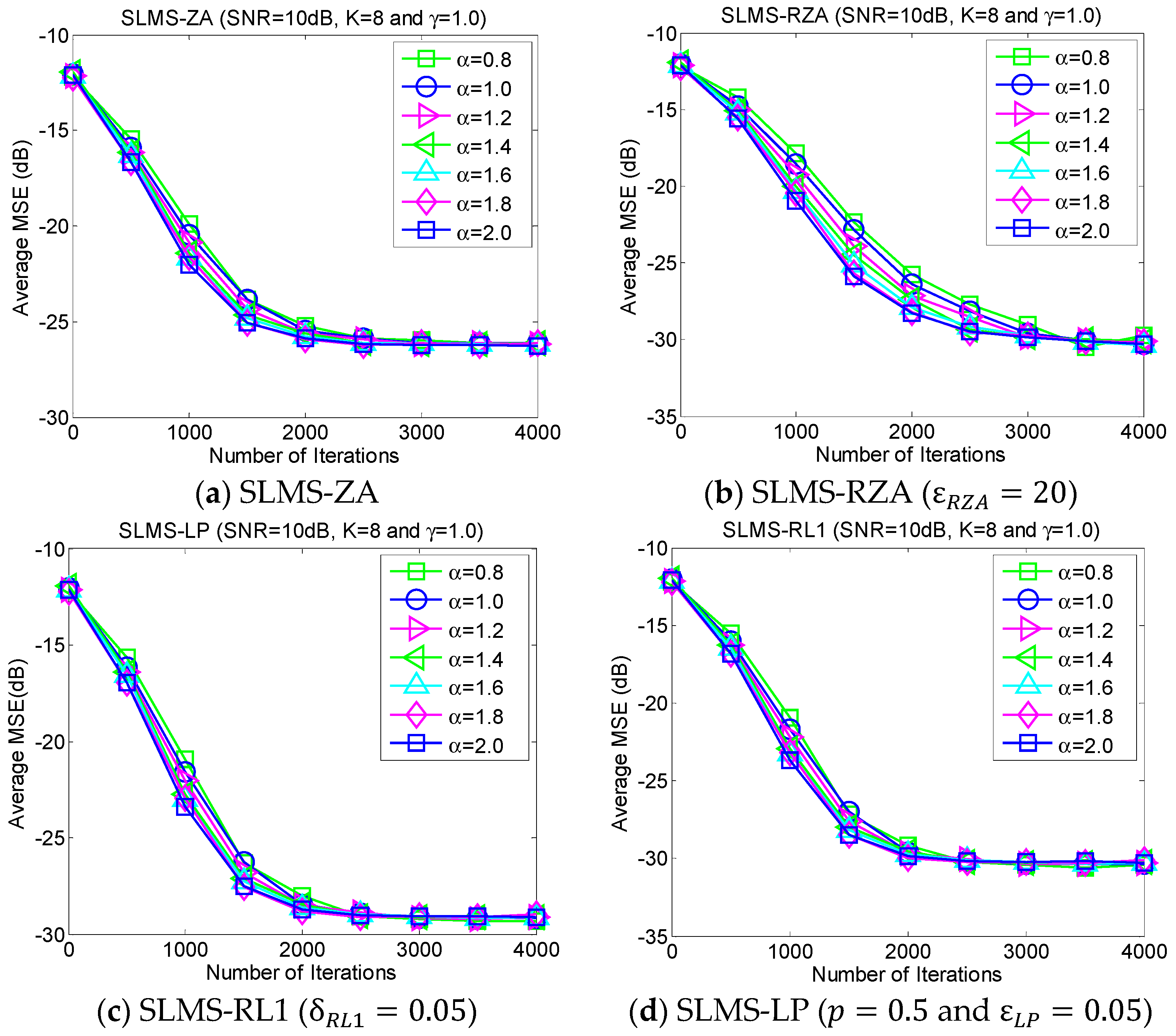
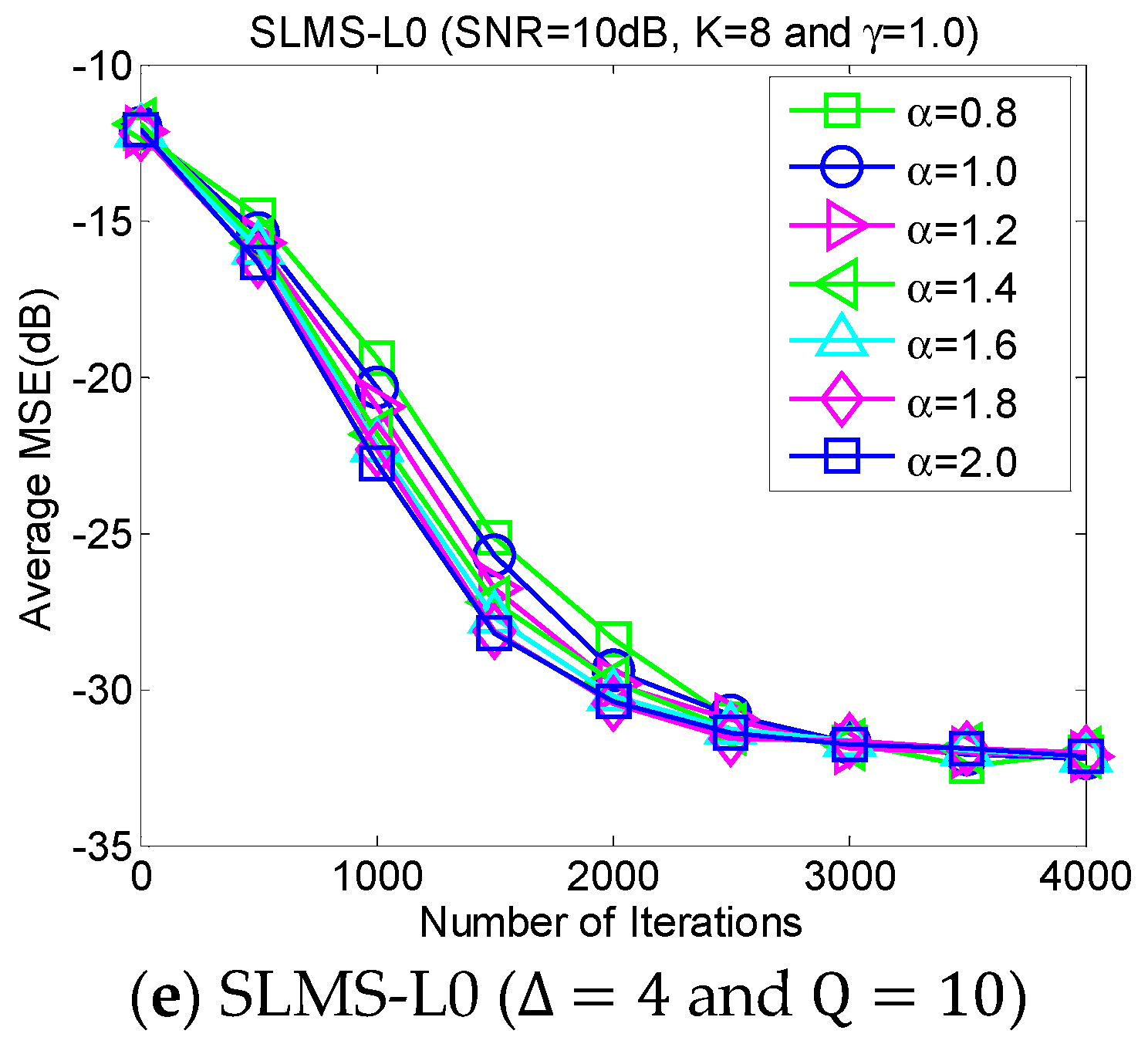
5.3. Experiment 3. MSE Curves of Proposed Algorithms vs. Characteristic Exponent
The average MSE curves of the proposed algorithm with respect to characteristic exponent
in scenarios of dispersion parameter
, channel length
, channel sparsity
and
, are depicted as shown in
Figure 4. The proposed algorithm is very stable for the different strengths of impulsive noises that are controlled by the characteristic exponent
. In addition, it is very interesting that the convergence speed of the proposed SLMS algorithms may be reduced by the relatively small
. The main reason the proposed SLMS algorithm is utilized is that the sign function is stable at different values of
. Hence, the proposed algorithm can mitigate non-Gaussian α-stable noise.
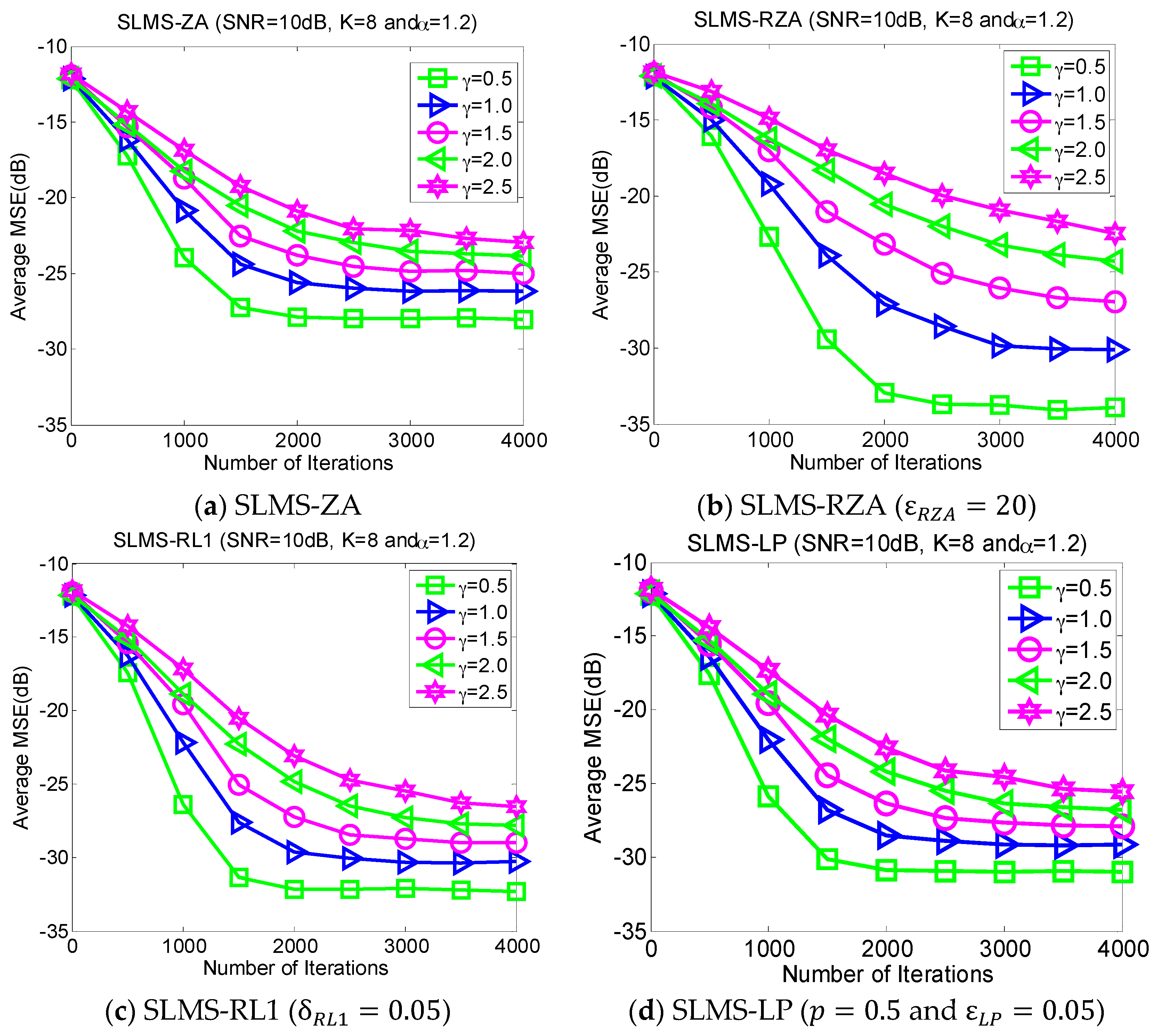
5.4. Experiment 4. MSE Curves of Proposed Algorithms vs. Dispersive Parameter
Dispersive distribution of
-stable noise has harmful effects. This experiment evaluates the MSE performance of proposed SLMS algorithms in different dispersive parameters
in the scenarios of
,
and SNR = 10 dB, as shown in
Figure 5. Larger
means more serious dispersion of α-stable noise and a worse performance for the proposed algorithm and vice versa.
Figure 5 implies that the proposed SLMS algorithms are deteriorated by
rather than
. The main reason is that the proposed SLMS algorithm can mitigate the amplitude effect of the
-stable noise due to the fact that the sign function is utilized in the proposed SLMS algorithms.
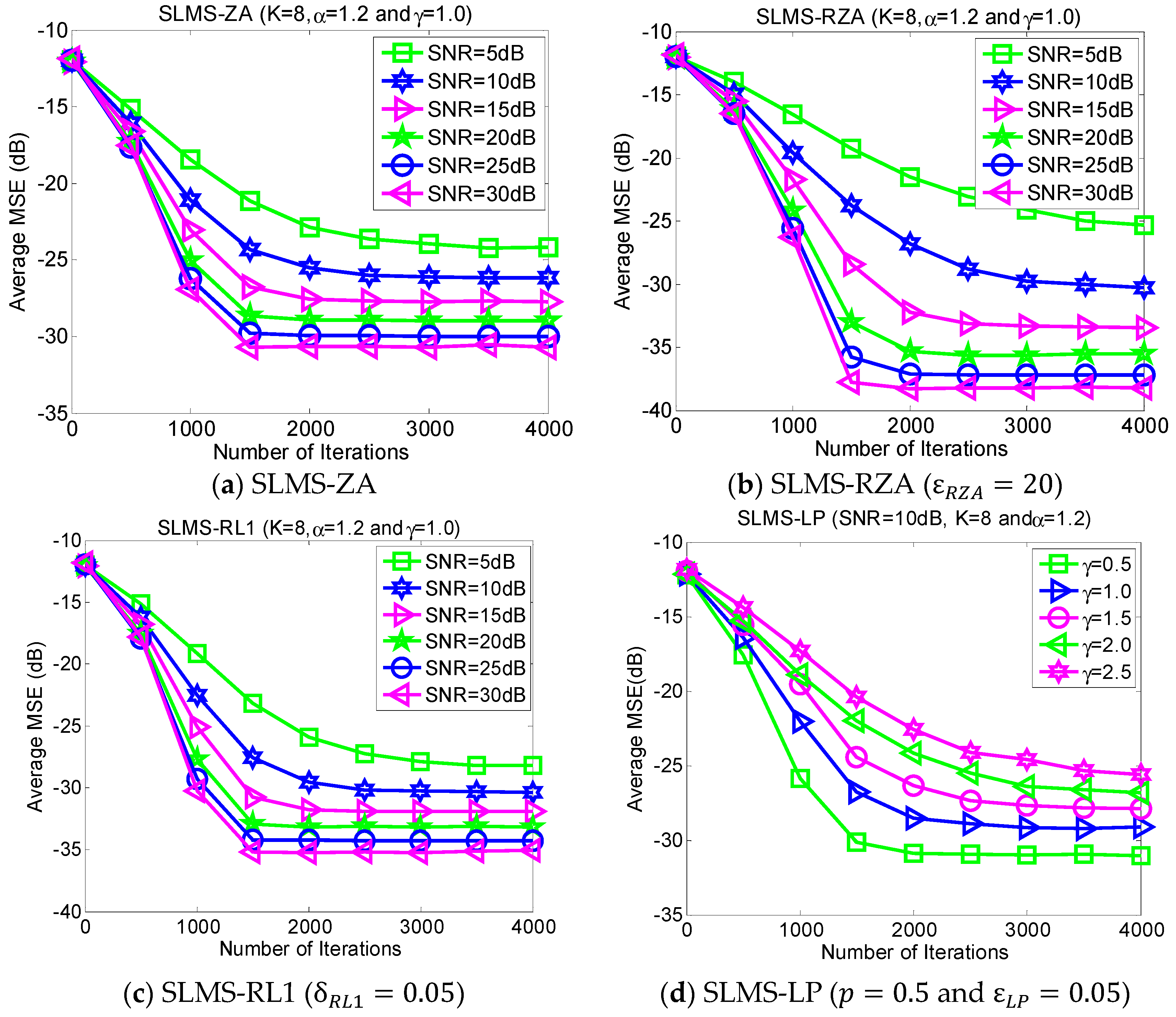
5.5. Experiment 5. MSE Curves of Proposed Algorithms vs. SNR
In the different SNR regimes, the average MSE curves of the proposed algorithms are demonstrated in
Figure 6 in the scenarios of characteristic exponent
, dispersive parameter
, channel length
, and channel sparsity
. The purpose of directing figures in
Figure 6 is to further confirm the effectiveness of the proposed algorithms under different SNR regimes.