1. Introduction
Ship motion control plays an important role in guaranteeing the safety and economy of a ship in navigation. Well-designed control systems allow ships to sail and perform tasks with adequate reliability and economy in severe seas, which are usually due to uncertain environmental forces induced by wind, waves, and current. Since the ship dynamics are nonlinear essentially and often affected by uncertain environmental forces, it is challenging to achieve a robust and accurate control system for ship motion, which refers to course-keeping, roll stabilization, path following, dynamic positioning, vertical motion control, and station-keeping [
1]. Conventional control strategies like PID control can no longer satisfy the requirement of navigation, guidance and control of ships. During recent decades, many advanced control schemes have been developed and successfully applied to ship motion control, including sliding mode variable structure control [
2,
3]; parameter adaptive control [
4,
5]; H-infinity robust control [
6,
7]; neural-network control [
8,
9]; fuzzy control [
10,
11]; neuro-fuzzy control [
12,
13]; line-of-sight based model control [
14,
15], etc.
To obtain a controller for ship motion, knowledge of the ship’s dynamic characteristics is necessary. This knowledge can be obtained through the mathematical model of ship motion. In ship motion control, usually two kinds of mathematical models are available, i.e., control-design models and high-fidelity models [
1]. A precise mathematical model of the plant allows one to design a satisfactory controller by applying some conventional control strategies such as linearization feedback control [
16], PID control [
17], and adaptive control [
18]. However, the ship dynamics is inevitably affected by some uncertainties, which might degrade the controller performance if the uncertainties are not properly compensated for or suppressed in the controller design. Such uncertainties include modeling errors and disturbances. For modeling errors, they refer to parameter errors, ignored high-order modes and unmodelled dynamics of ship motion. Examples of unmodelled dynamics are thrust and torque losses, cross-coupling drag, varying wake, air suction and interaction between the thruster and the hull [
19]. For disturbances, they result from random noises in mechanical and electrical equipments, or the environmental forces induced by wind, waves and current. Usually, neither modeling errors nor disturbances can be described by precise mathematical expressions. Therefore, a robust and accurate control scheme is required. H-infinity control is one of the main choices [
20,
21]. However, there are two difficulties with this method. One is that prior knowledge about the bound of an uncertainty is required, which is challenging sometimes. The other is the difficulty in guaranteeing the control accuracy because of the absence of adaptation to the changing characteristics of uncertainties.
To deal with the uncertainties in a plant, an artificial intelligence (AI)-based controller provides another interesting and effective option. Such an AI-based controller is characterized by nonlinear mapping and on-line learning abilities, which make it possible to identify and compensate for the uncertainties in the plant. Commonly employed AI computing approaches include neural networks (NN), Bayesian probability, fuzzy logic, machine learning, evolutionary computation and genetic algorithms. Combined with AI computation, the controller performance can be greatly improved [
22]. In the field of ship motion control, during last decades there have been many NN applications e.g., [
8,
9,
23,
24]. Comparatively, SVM is a novel technique of Artificial Intelligence. This kind of learning machine aims to achieve structural risk minimization (SRM) [
25] that makes it outperform the algorithms based on empirical risk minimization (ERM) like NN. Better generalization ability can be guaranteed because not only prediction error but also model complexity is considered when performing SRM. Globally optimal solution can also be guaranteed in SVM since convex quadratic programming is performed. Additionally, by applying the kernel trick, the curse of dimensionality can be avoided in SVM, which is usually inevitable in NN. SVM has found wide applications in the field of control engineering and in the past years, there have been some SVM applications to ship motion control. For instance, Liu et al. applied fuzzy SVM to the course-keeping [
26]. Jiang et al. proposed SVM based general predictive control (GPC) for ship course-keeping [
27]. Luo et al. presented a robust SVM controller for the ship course-keeping [
28].
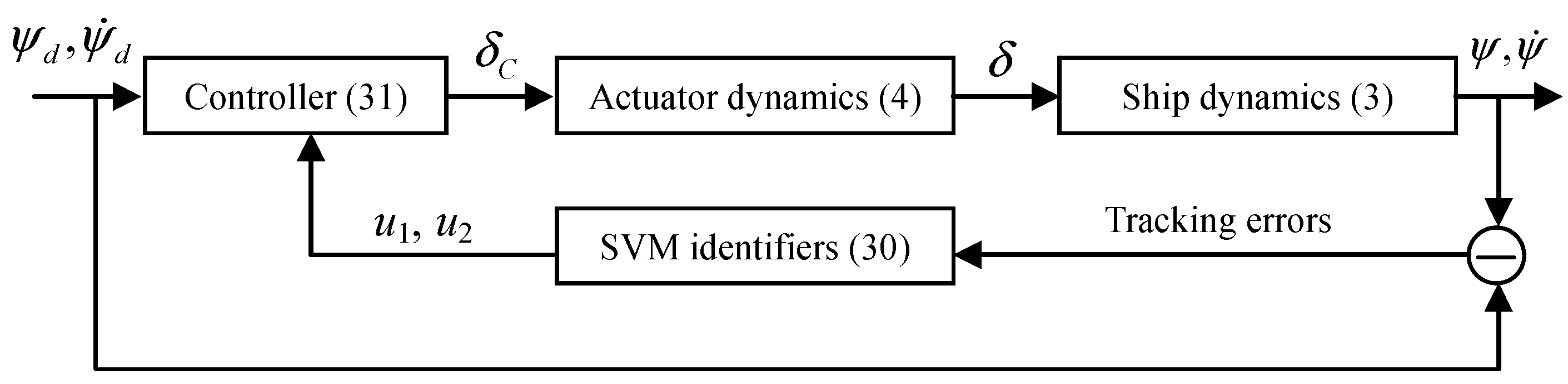
This paper presents a robust controller for the ship course-keeping by using SVM identification and L2-gain design. The investigated plant is composed of the ship dynamics and the dynamics of rudder actuator. Uncertainties are taken account of in the cascaded system, which refer to modeling errors and external disturbance. In the controller design, the modeling errors are identified by SVM while the external disturbance is suppressed by using L2-gain design. To guarantee the robust stability of the controller, a Lyapunov recursive function method is adopted. The main novelty of our approach is the determination of the Lagrangian factors in SVM. Rather than calculate the Lagrangian factors through a matrix equation, one can obtain these factors by solving differential equations proposed. To improve the control accuracy, the parameters in SVM are optimized by incorporating particle swarm optimization (PSO). The rest of the paper is organized as follows. In
Section 2, the mathematical model of ship steering, the methodologies of SVM and PSO are described; in
Section 3, the details of the controller design and the stability analysis are given; in
Section 4, a simulation example is presented to illustrate the validity of the controller designed; and the final section is the concluding remarks.
3. Controller Design and Stability Analysis
Usually, the problem of ship course-keeping control can be viewed as a tracking control issue. Without loss of generality, two general assumptions with respect to the continuous cascaded system described by (5) can be given as [A1]. The desired system output signal is differentiable and the cascaded system is controllable. [A2]. The external disturbance is bounded with
3.1. Controller Design
First of all, feedback control is applied to the certain terms in the System (3). A desired rudder angle can be defined as
where
,
is introduced as an auxiliary controller to deal with the uncertainties in (3).
Three error signals are defined as
Incorporating (11)–(14) into (3), it follows
For the actuator dynamics described by (4), the controller can be designed as
where
is another auxiliary controller. By analogy to (15), it holds
Thus, based on (15) and (17), an error system can be obtained as
As can be seen, the above system is linear with respect to the error vector . Moreover, the convergence of the error system will depend on the design of two auxiliary controllers, i.e., u1 and u2. Lyapunov function method is adopted to obtain proper u1 and u2. This method has been widely used in control engineering since it provides an effective and systematic procedure to obtain a stable controller. For the control of a nonlinear complicated system, this method is usually preferred.
For the System (18), a definitely positive Lyapunov function candidate w.r.t. the error vector
can be defined as
Its derivative w.r.t. time is
As can be seen, to obtain the auxiliary controller
u1, one has to deal with the uncertain terms, i.e.,
and
w. For the disturbance
, L2-gain design is applied. This approach derives from H-infinity control strategy and is considered as an effective way to suppress uncertain disturbance. Using this method, an L2-gain performance index should be defined as
where
are small positive constants,
z is introduced as an evaluation signal.
An identity w.r.t. the evaluation signal
z and the disturbance
w can be obtained as
Let
, the above identity becomes the following inequality
Combining the above inequality with the derivative (20), one has
To obtain
u1, one has to account for another uncertainty, i.e.,
. Different from the way used to deal with the disturbance
w, the modeling error
will be identified and compensated instead of being suppressed by using L2-gain design. This is because although both modeling error and disturbance are uncertainties, the modeling error is usually a continuous signal while the disturbance
w might be instantaneous. In this paper SVM is proposed to approximate such a continuous uncertainty. Besides, the term
in (24) is also dealt with by SVM. As seen from (24), to obtain
u2, it is necessary to calculate the derivative of
δd. According to the Equation (11), one has
The main difficulty is to calculate the derivative of
u1. Therefore, SVM is used to identify this complicated nonlinear function. One can define the two nonlinear functions in (24) and their SVM approximations as
where
is the approximation error and contains the constant
b that is defined in (6). Moreover, it is assumed that
.
and
are Lagrangian factors. If the SVM approximates the nonlinear functions
f1 and
f2 very well, the prediction errors
should be small enough. In that case, the Lagrangian factors,
and
, can be called “ideal” Lagrangian factors. However, these “ideal” factors are actually unable to be obtained in controller design because
and
in (26) and (27) are unknown uncertainties. Suppose
and
are the updated approximations of their “ideal” values with high accuracy, the two nonlinear functions
f1 and
f2 can be approximated by
Thus, the two auxiliary controllers
u1 and
u2 in (24) can be designed as
where
and
are positive control gains.
Combining the auxiliary controllers with (11) and (16), the command rudder angle to the cascaded System (5) can be expressed as
3.2. Stability Analysis
Based on (26), (27) and (30), the inequality (24) becomes
in which
; ;
; ;
To make sure the right hand side of (32) be negative, the estimates
and
are designed by adopting the following on-line tuning algorithms
where
and
are positive constants. In addition, an augmented error signal is defined as
Based on (19), another Lyapunov function candidate that involves the error vector
can be defined as
where
represents the trace of a matrix. Combined with the definition given by (33), the following derivative can be obtained
Let
and
the following inequality w.r.t. (35) holds
Without loss of generality, the Lagrangian factor vectors
H1 and
H2 can be assumed bounded by
where
represents the Frobenius norm with the definition
. Thus, the inequality (37) evolves to
Given a compact set
, if the tracking error
falls within the compact set at any time, the above inequality can be reduced to
Let
, in the case when the disturbance
, the above inequality can be simplified to
The uniformly ultimately bounded (UUB) stability can be proven [
40].
Back to (39), in the case when disturbance exists, i.e.,
, one has
Integrating the above inequality yields
where
is a small positive constant. Compared with the L2-gain performance index given by (21) it can be said that the disturbance
w is suppressed. In other words, the robustness is guaranteed.
If the tracking error
falls outside the compact set, i.e.,
, the following inequality can be obtained
by appropriately selecting parameters so that
holds. By analogy to the analysis of (39), in cases either
or
, the stability and robustness of (43) can be guaranteed.
From the above analysis, it can be concluded that the controller designed by (31) and the SVM algorithms given by (33) can guarantee the stability and robustness of the tracking system. It is noted that although only UUB stability can be guaranteed, the control accuracy can be improved by appropriate selection of the parameters in controller, including the control gains and the parameters in SVM. In the study, PSO is incorporated into SVM to obtain optimal SVM parameters.
4. Example Study
To confirm the validity of the controller designed, a numerical simulation is performed combined with a surface ship. Firstly, the state space equation form of (5) can be obtained as
where
,
,
The model parameters are [
41]
From the point of view of ship manoeuvrability, this ship is unstable because
K is negative. Therefore, an appropriate robust controller is required for the purpose of course-keeping. The controller gains in (31) are selected as
The constant in (14) is selected as
.
For the SVM identification, a Gaussian kernel is adopted as
where
is the kernel width that has an impressive effect on SVM learning ability. The input variable is defined as
For the support vectors
and
, both of them are selected as two successive former input variables which means that
for identifiers in (30). Denote
, the support vectors can be expressed as
where
is the sampling time.
To obtain a optimized SVM, PSO is incorporated to obtain the optimal
in (46). Moreover, the parameters
and
in the tuning algorithms of Lagrangian factors given by (33) are also determined by PSO. The fitness in PSO algorithm adopts the root of mean square error (RSME) as
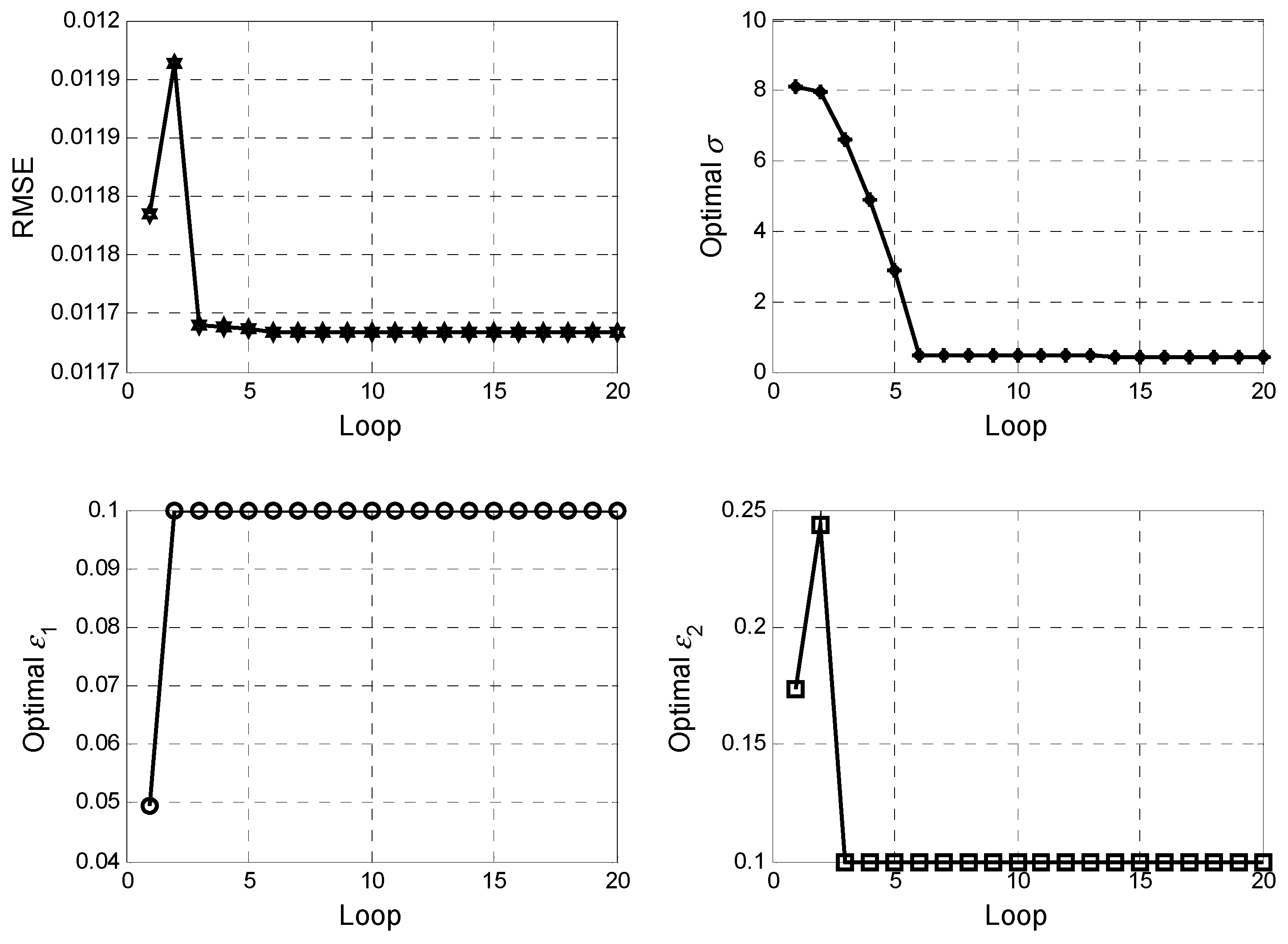
The number of particles in PSO is set to 20, as is the number of iteration. The initial particle’s positions and velocities are assumed randomly distributed within a given range.
Figure 2 presents the results of RMSE,
σ,
ε1 and
ε2. As can be seen from the results, the fitness and the parameters converge to stable values, obtained as
. The three parameters, i.e.,
σ,
ε1 and
ε2, are used in the SVM based controller.
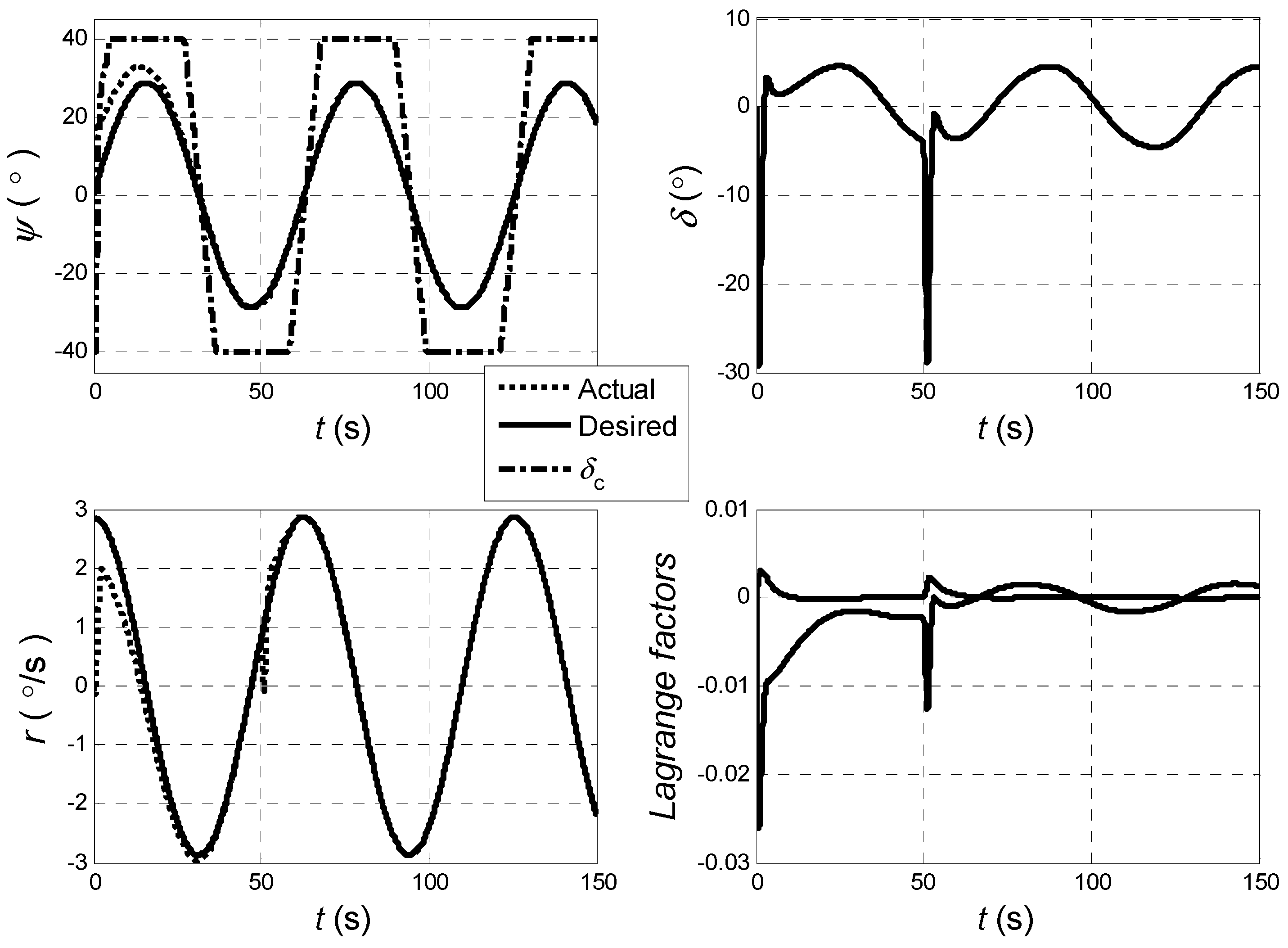
In the study, the control objective is to track a desired heading angle. Without loss of generality, the desired heading angle
is assumed as a harmonic signal. To verify the stability and robustness of the controller designed, deviation of the heading angle is assumed at the start, which indicates that
. For uncertainties, the modeling error is assumed
and the external disturbance is assumed as an instantaneous impulse with the amplitude of 1.5 (°/s) at the time
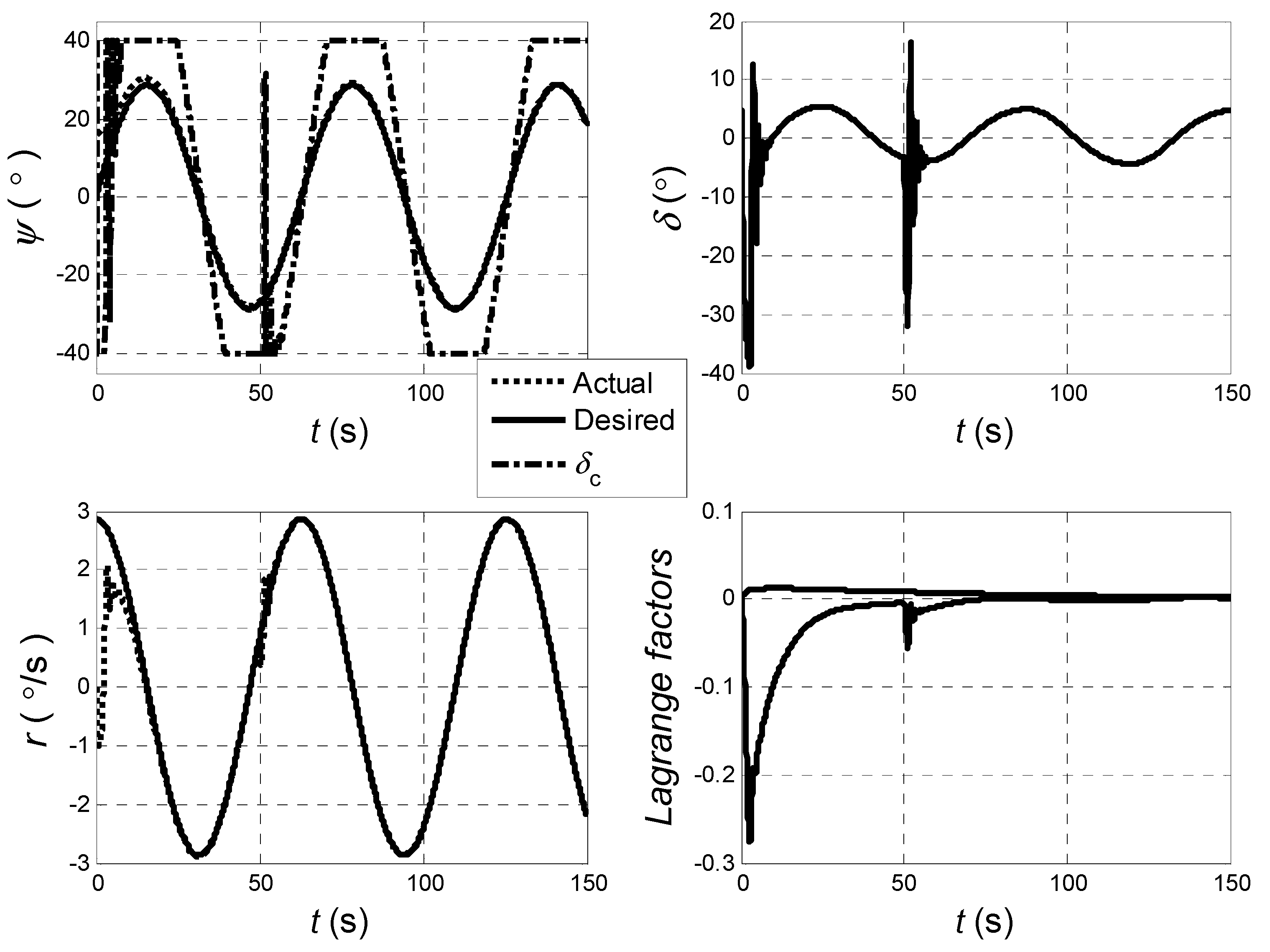
Figure 3 presents the tracking results, including the histories of heading angle
, yaw rate
, demand rudder angle
, actual rudder angle
, and Lagrangian factors
as well.
From the simulation results, it can be seen that both stability and robustness of the tracking system are achieved. The tracking accuracy is satisfactory as well. Moreover, the control inputs are reasonable and applicable from the point of view of operation.
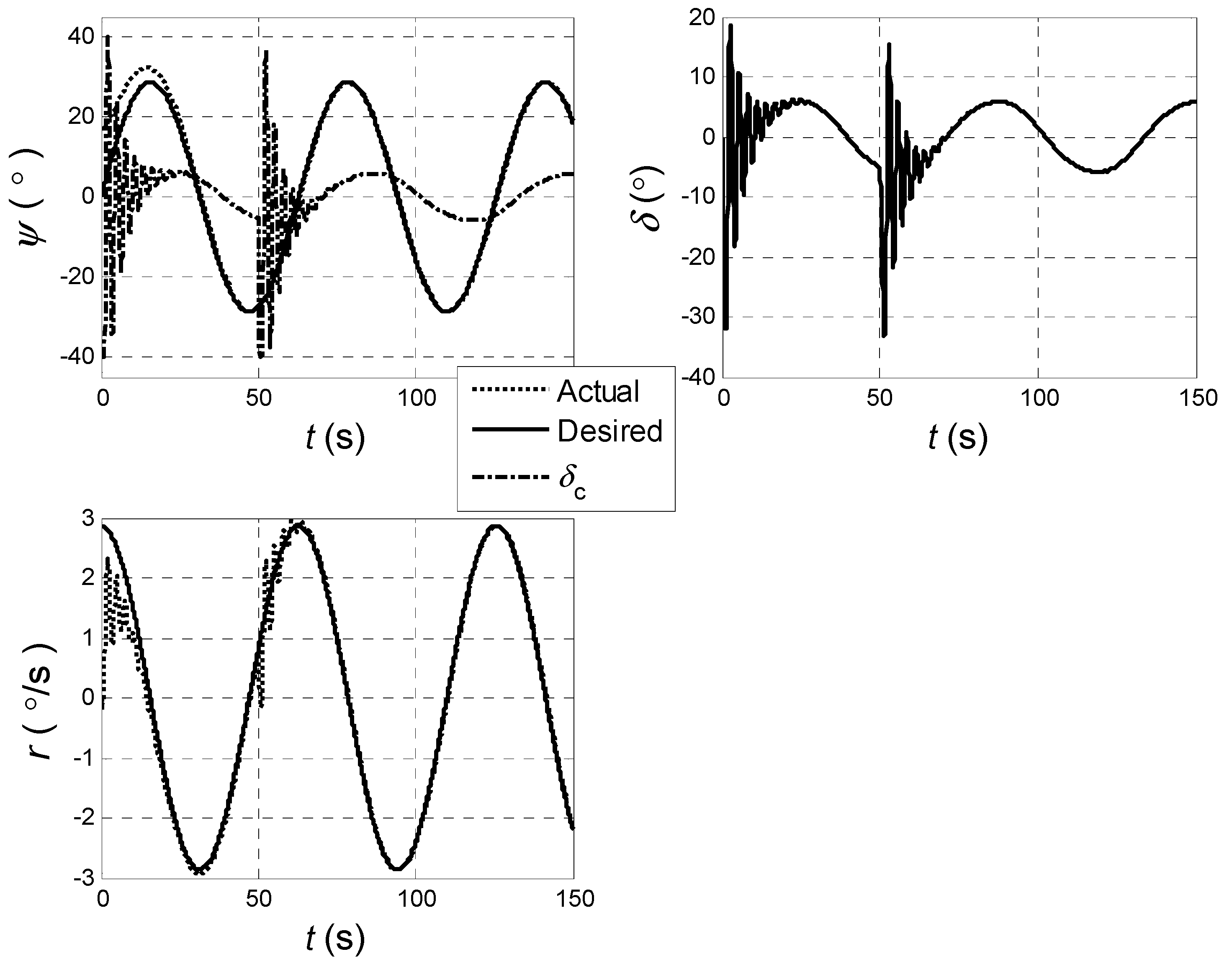
As a comparison, a conventional PD controller is designed as follows,
where
k1,2 are control gains, selected as
k1 = 5,
k2 = 50.
Figure 4 presents the simulation results using the PD controller designed. Compared with the performance of the SVM based controller as shown in
Figure 3, it can be seen that obvious oscillation happens to the command rudder angle for a PD controller, which implies a limitation for the PD controller from an operational point of view despite the simple structure of the PD controller.
Further comparison is carried out by combining the SVM identification and inverse dynamic compensation that is commonly employed to obtain a feedback controller for a certain system (without uncertainties). By observing the inequality (24), the auxiliary controllers
u1 and
u2 can be designed as
which indicates that only the modeling errors
and the derivative of desired rudder angle
in the inequality (20) are approximated by SVM, i.e.,
The terminal control input can be defined as
Comparing controller (54) with (31), one can find that the controller with inverse dynamic compensation in combination with SVM identification (given by (54)) is more complicated than the controller in which the complicated nonlinear function are indentified by SVM (given by (31)).
Figure 5 presents the simulation results using controller (54). The parameters are selected as
. In comparison with the results shown in
Figure 3, it can be seen that oscillation of the command rudder angle happens at the initial stage and at the time of instantaneous external disturbance despite rapid convergence. Further remarks can be made as follows: (
i) no matter whether inverse dynamic compensation is incorporated, the stability and robustness of the control system can be guaranteed due to the use of Lyapunov theory and L2-gain design; (
ii) although the response rate of the controller in the case of inverse dynamic compensation (as described by (54)) is better than the case without compensation (as described by (31)), a moderate helming as shown in
Figure 3, which can be achieved by using the controller (31), is preferable from the practical point of view. Moreover, as can be seen, the structure of the controller (31) is simpler than the controller (54), which makes sense in practice.
5. Conclusions
In this paper, SVM is applied to the control of a cascaded system with uncertainties with regard to ship course-keeping. The dynamics of the rudder actuator are considered in the plant. To guarantee the real-time performance of the controller, the Lagrangian factors in SVM are determined by on-line tuning algorithms. There are two advantages of the on-line SVM proposed in this paper over conventional on-line SVM. First, no supervised signal is required; second, the capacity of the training samples can be small, which improves the efficiency of the learning machine. Nonlinear functions and an uncertainty (modeling error) in the plant can be effectively identified by the proposed SVM, which helps obtain a controller with simple structure. Another method, L2-gain design, is applied to suppress the disturbance to the plant. The validity of the hybrid controller based on SVM and L2-gain design is confirmed by numerical simulation.
PSO is used to obtain the parameters in SVM. It should be noted that the optimal parameters are actually obtained in off-line way instead of on-line way, which limits its practical application to real-time control. In the next work, an on-line approach to the selection of SVM parameters will be studied.