Abstract
This paper is concerned with the application of computational intelligence techniques to the conceptual design and development of a large-scale floating settlement. The settlement in question is a design for the area of Urla, which is a rural touristic region located on the west coast of Turkey, near the metropolis of Izmir. The problem at hand includes both engineering and architectural aspects that need to be addressed in a comprehensive manner. We thus adapt the view as a multi-objective constrained real-parameter optimization problem. Specifically, we consider three objectives, which are conflicting. The first one aims at maximizing accessibility of urban functions such as housing and public spaces, as well as special functions, such as a marina for yachts and a yacht club. The second one aims at ensuring the wind protection of the general areas of the settlement, by adequately placing them in between neighboring land masses. The third one aims at maximizing visibility of the settlement from external observation points, so as to maximize the exposure of the settlement. To address this complex multi-objective optimization problem and identify lucrative alternative design solutions, a multi-objective harmony search algorithm (MOHS) is developed and applied in this paper. When compared to the Differential Evolution algorithm developed for the problem in the literature, we demonstrate that MOHS achieves competitive or slightly better performance in terms of hyper volume calculation, and gives promising results when the Pareto front approximation is examined.
1. Introduction
Floating settlements have become a lucrative alternative for future urban development, given the growing number of environmental concerns, such as disasters and rising sea level. However, their design process is critical and technical and architectural challenges should be considered simultaneously. In this regard, computational intelligence methods may be very useful to handle these complex problems for floating settlement design. This paper aims at the conceptual design and development of a floating neighborhood by using computational intelligence methods. A coastal town, Urla, located on the western coast of Turkey close to the city of Izmir, has been chosen as a site for a floating settlement. We choose to place the proposed settlement in between four small neighboring islands in the proposed region. The reason is that the area between the islands provides protection from strong winds and sea currents otherwise present. The proposed settlement is themed around touristic and yachting activities. In accordance with that, and with respect to conceptual design, we determine four main functions of the floating neighborhood, namely housing, yacht marina, yacht club, and public spaces. We thus come across the design problem of how to locate the abovementioned functions so that a suitable spatial distribution is achieved, in accordance with our objectives.
In particular, we consider the following three objectives: maximization of accessibility, maximization of wind protection for keeping living spaces such as houses and yacht marina protected from wind, as well as maximization of visibility for making commercial places such as houses, a yacht marina, and a yacht club noticeable from outside the settlement. With respect to these objectives, we aim to find the most efficient location for these functions. Since wind protection and visibility objectives, as well as accessibility and visibility, are conflicting objectives, we employ multi-objective algorithms to solve this complex problem. Specifically, we present the results of the application of the multi-objective harmony search (MOHS) algorithm to identify suitable solutions for the problem mentioned above.
To the best of our knowledge, applications of evolutionary computation and swarm intelligence methods on floating neighborhood design do not exist in any previous study. In [1], the author discusses floating architectural design using fuzzy logic and rule-based decision support system. IF...THEN logical statements in the form of a rule base having both controllable and uncontrollable parameters are transformed into simple linguistic variables. The author uses expert knowledge on motion effects due to vibration by framing a rule-based decision support model. The model is formed with seven input variables converted through fuzzy rules into a single output variable. In [2], the author considers urban water management innovations to reduce vulnerability of urban areas and social aspects that are relevant to mainstreaming and application of innovations. The author also reflects on the reasons why the floating structures are more common nowadays, such as land subsidence, increasing sea levels, increasing population, increase in habitation of areas close to the sea, and climate change. Several recommendations have been made for floating structures; however, evolutionary optimization or swarm intelligence methods have not been used in the study. In [3], design considerations for very large floating structures have been discussed.
As seen above, the literature review on floating settlements is very scarce. At the neighborhood scale, there is no floating architectural work making use of evolutionary and swarm algorithms. Evolutionary algorithms are nature-inspired processes mimicking the selection and reproduction processes in living organisms. Evolutionary and Swarm algorithms provide satisfactory good design solutions and handle the complexity of the architectural problems. In this regard, Pareto front approximation is an efficient way to distinguish between inferior and good solutions. Recently, in [4], the authors worked on identifying configurations of functions for a floating neighborhood design proposal by using multi-objective optimization. Two evolutionary algorithms are developed and their results are compared with each other. Differential evolution (DE) algorithm is a stochastic real-parameter optimization algorithm developed by [5]. DE algorithms have three parameters. These are the population size (NP), the crossover rate (CR), and the mutation rate (F). These parameters have a significant impact on the performance of DE algorithms. In [6], a self-adaptive DE algorithm, called JDE, is developed. It is a very simple and effective algorithm that converges much faster than the traditional DE, particularly when the dimensionality of the problem is high or the problem concerned is complicated. In JDE, each individual has its own and values. Initially, they are assigned to and and they are updated at each generation as and , where are uniform random numbers in the range . and denote the probabilities to adjust the and values. They are taken as and and . In [7], the authors investigated sustainable designs of floating settlements by using a multi-objective self-adaptive differential evolution (JDE) algorithm inspired by [6]. The main contribution of the JDE algorithm was to show that many architectural design problems are mainly multi-objective constrained real-parameter optimization problems. This paper is an extension of [7] by developing a multi-objective harmony search (MOHS) algorithm for the same benchmark instance in order to identify a set of design alternatives for decision-makers. The basic harmony search (HS) algorithm is developed in [8,9]. Regarding the multi-objective harmony search algorithms (MOHS), Geem [10,11] proposed two MOHS algorithms for the time–cost trade-off optimization of project management and water distribution network optimization, respectively. These two MOHS algorithms employ a strict domination rule in such a way that a new solution is generated by HS operators and the new solution is replaced by the worst solution in the population if the new solution strictly dominates the worst solution. However, in the MOHS algorithm developed in this paper, a new population of solutions is generated by HS operators. Then, the old and new population are merged. To determine the population in the next generation, the fast non-dominated sorting algorithm in [12] is employed to identify the non-dominated fronts and the constrained-dominance rule in [12] is used to compare the solutions. An excellent survey of the applications of HS algorithm can be found in [13].
2. Problem Definition
As mentioned above, the problem in this study is concerned with the establishment of a floating settlement between four islands in the studied region. We consider four islands (Akça, Yassıca, Incirli, and Pırnarlı), with their locations shown in Figure 1. In establishing such a settlement, our aims include architectural and urban planning related ones, such as accessibility, as well as technical ones, such as location in suitable sea water depths, etc.
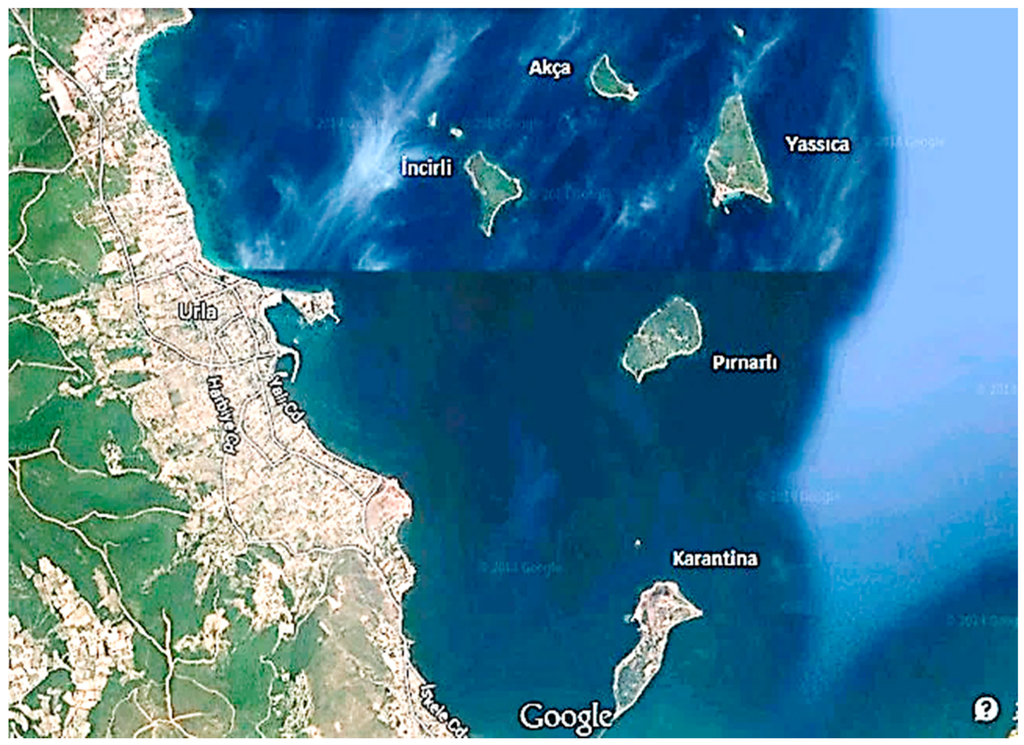
Figure 1.
A top view of the islands of Urla [7].
In particular, we consider three main objectives for our problem definition. The first one concerns the accessibility of our different functions. By accessibility in this study we refer to the walking distance between the functions. We wish to minimize this distance, so that users of the settlement can easily move on foot within the settlement. As such, the need for additional transportation is eliminated. The second objective concerns the protection of our settlement from wind currents present in the area. The third one is maximization of visibility for making commercial places such as houses, a yacht marina, and a yacht club noticeable from outside the settlement.
After the abstract establishment of our functions is complete, we consider how to connect functions, most efficiently with a minimal pedestrian network, which will be realized using pontoons. In other words, this constitutes a form-finding problem. This is a second phase of our problem definition, and takes place after the multi-objective optimization.
The following notations are used in the formulation of the problem:
2.1. Optimization Model
As mentioned before, we have three design goals, accessibility, wind protection, and visibility, subject to the constraints of suitable water depth and intersection resolution. Our decision variables (i.e., chromosome) are given as , which are the coordinates corresponding to one of the following functions: housing, yacht marina, yacht club, and public area.
In our model, we determine the overall accessibility of the public space from all other modules as in Equations (1)–(3) and the proximity between the yacht club and the yacht marina as in Equation (4). These accessibility measures in terms of distances are given as follows:
Minimum and maximum distances are desired to be between 300 m and 1500 m. The following formulas are used to determine the accessibility:
As the second objective, wind protection needs to be maximized for living spaces, such as housing spaces and a yacht marina. Through on-site inspection, we have determined that the area is characterized by a dominant wind coming from the northeast or southeast. For this reason, close offshore islands should protect other islands close to the coastline, and vice versa. Protected regions are determined as secluded areas between each pair of islands. Thus, it is desirable to locate the sensitive functions, namely housing and a yacht marina, near these protected regions. For instance, in Figure 2, housing is close to the protected regions, but the yacht marina is not close enough.
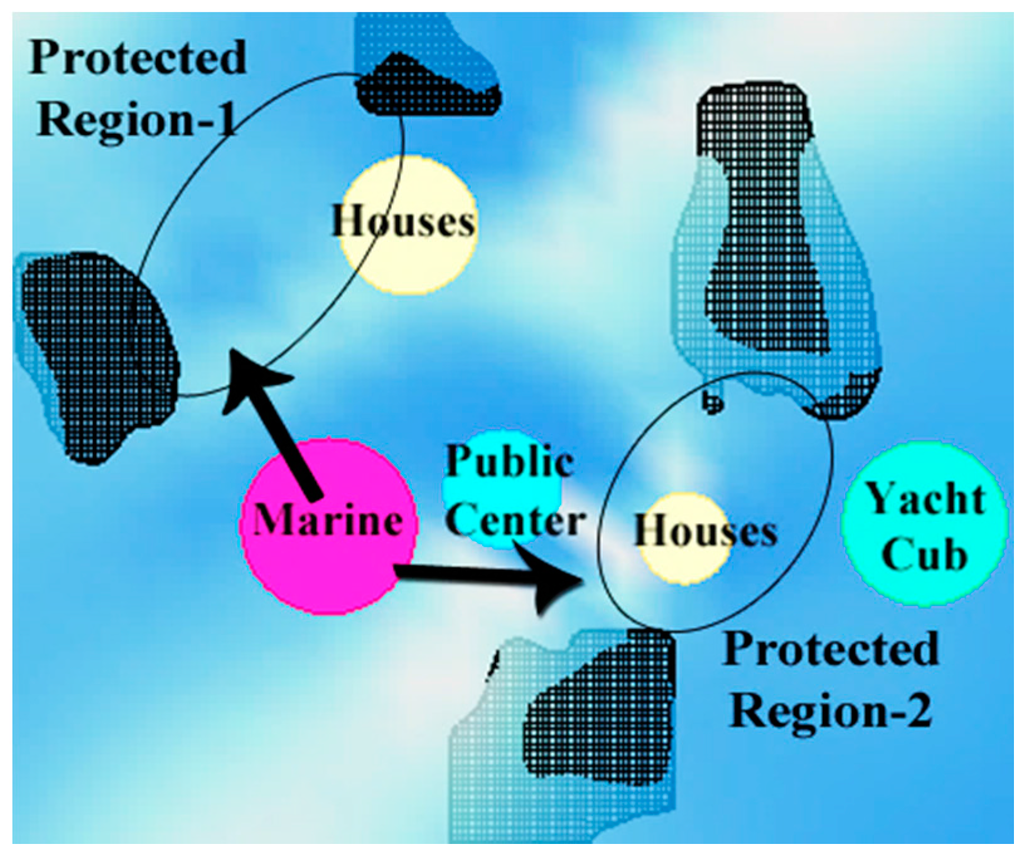
Figure 2.
Top view of the project region to illustrate protected regions [7].
To achieve this objective in the model, the distances between desired functions and the protected regions are first calculated by Equations (11) and (12). Then Equation (13) provides the maximization of wind protection as follows:
The last objective is the maximization of visibility to the functions. Since the yacht club and yacht marina are commercial functions, they should be made noticeable. There is frequent sailing of cruise ships near the location in question, which attracts a lot of tourists to the region.
Objective function calculation begins with establishing visual trajectories between the cruise-ship passing line and the desired functions in the parametric model as illustrated in Figure 3. If the trajectories intersect with the close offshore islands, it is concluded that the function is not visible from the particular point. By tracing multiple visibility trajectories along the cruise ship course, we may obtain a figure of the overall visibility of the settlement functions. We thus focus on maximizing the visibility figure, calculated as described above and shown in Equation (14), for the relevant functions in the settlement. For example, the number of intersected visibility lines with the close offshore islands is six for a housing unit in Figure 4.
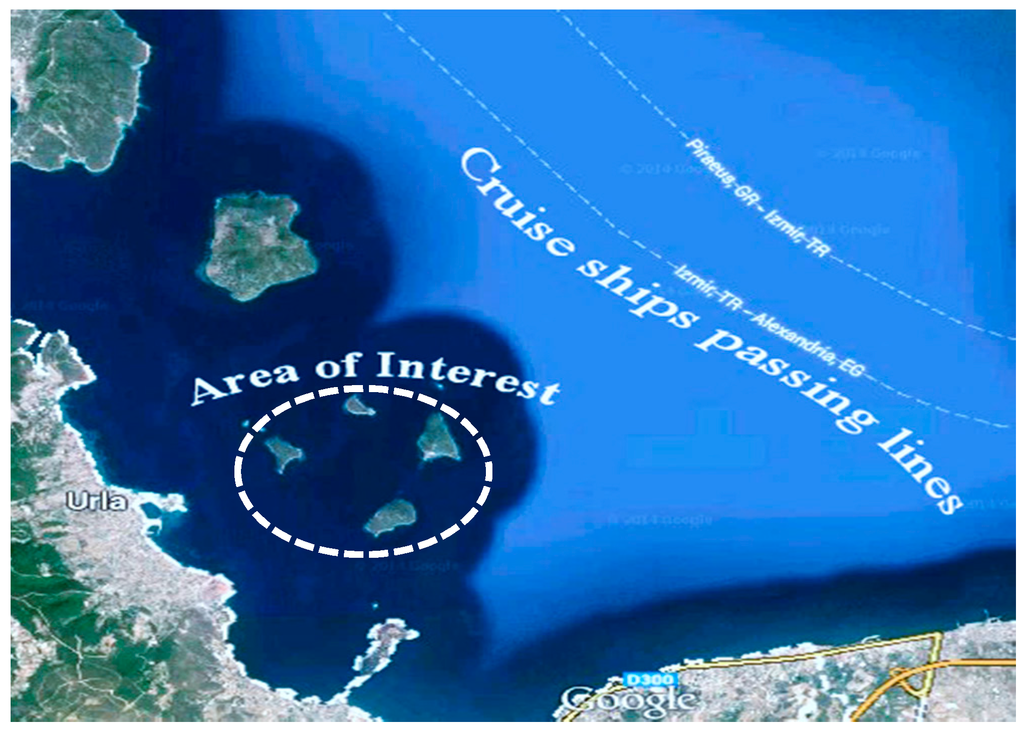
Figure 3.
A view of the project region’s cruise-ship passing lines [7].
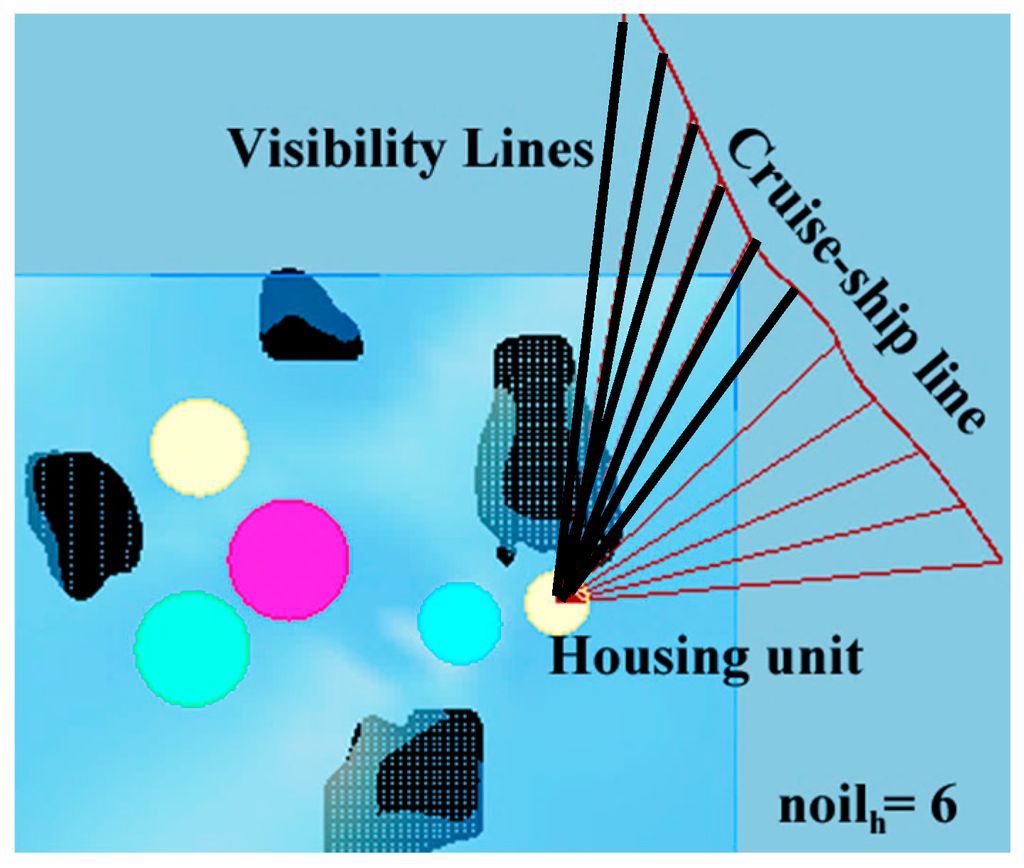
Figure 4.
Example of generating the intersected lines for a housing unit [7].
Decision variables have boundaries, which have been determined so as to describe the water area between the four islands, after on-site observation and expert opinion:
Distances near the wind-protected areas should be restricted to less than 300 m:
Visibility lines should be restricted to less than 5:
The real depth data are taken from NAVIONICS, which is an electronic navigation chart and system for marine and outdoor use. To obtain an approximate sea bottom model, interpolation was used. By doing so, the location of the functions is controlled to be in a specific water depth. The yacht club location is restricted to a water depth greater than 20 m:
This constraint also avoids the surface intersections like functions to functions and islands to functions.
2.2. Form Finding
The second part of the problem is to establish a network of pedestrian pathways among city functions. This step involves connecting each function by establishing meaningful paths between city functions, as seen in Figure 5 and Figure 6. Creating the connections between functions is achieved by the shortest walk algorithm, which obtains the shortest distance between functions, where their locations are already obtained from Pareto front approximated solutions coming from our MOHS algorithm.
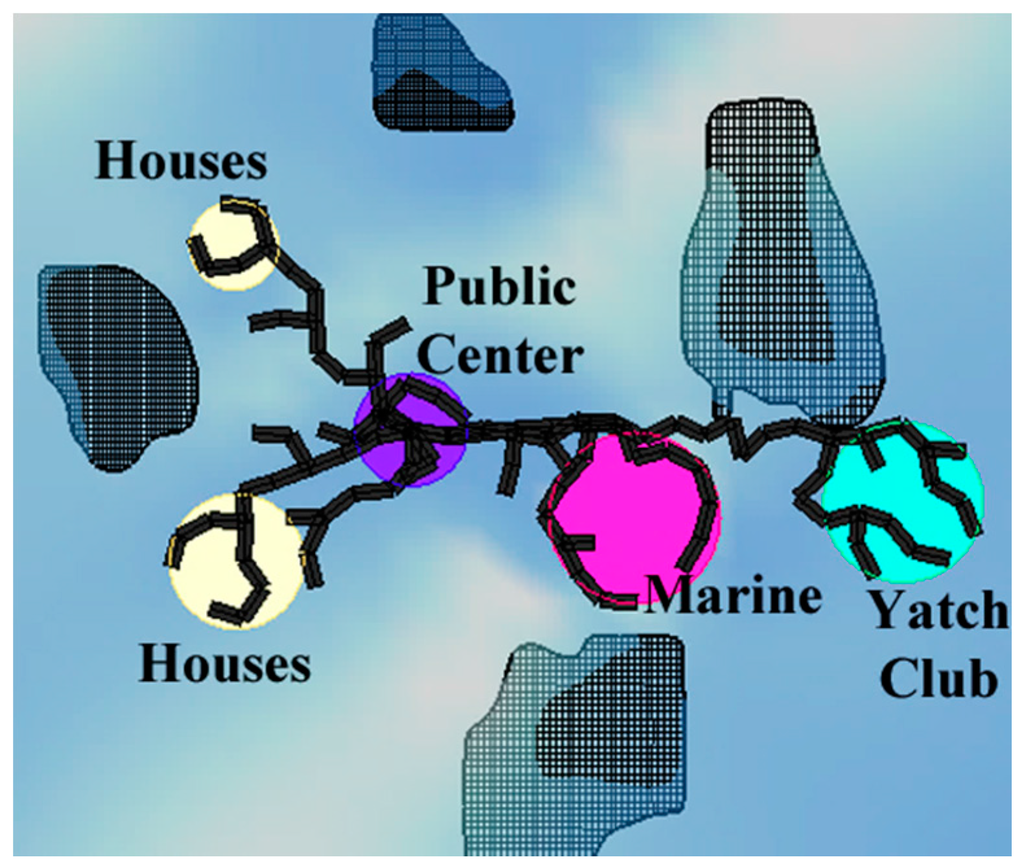
Figure 5.
Generating the roads between functions using the shortest walk algorithm [7].
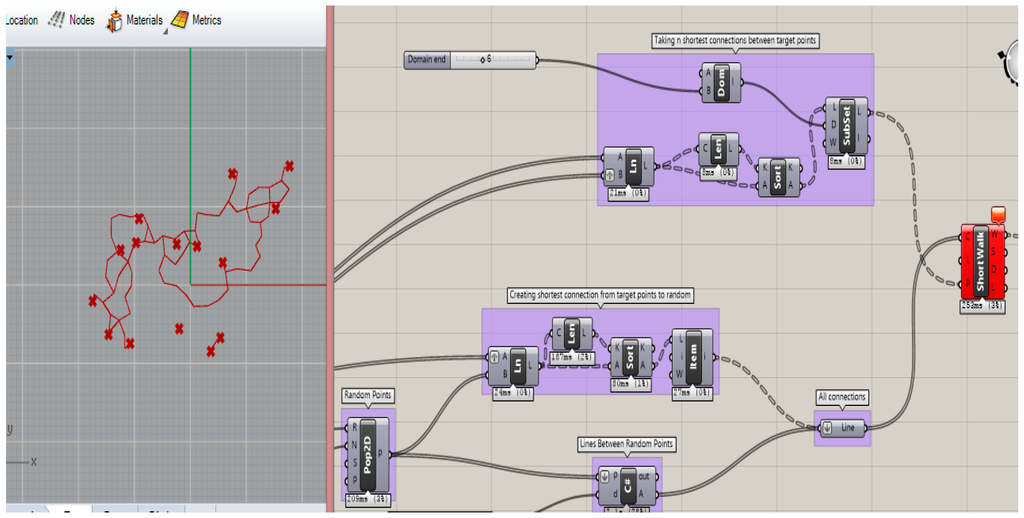
Figure 6.
Shortest walk generation in GH model.
3. Generative Model and MOHS Algorithm
The parametric model has been created in the Grasshopper (GH) [14] platform. GH is a part of Rhinoceros [15], a CAD program; it defines geometric entities and performs calculations on Rhinoceros with great ease through visual programming. The complete GH model can be seen in Figure 7.
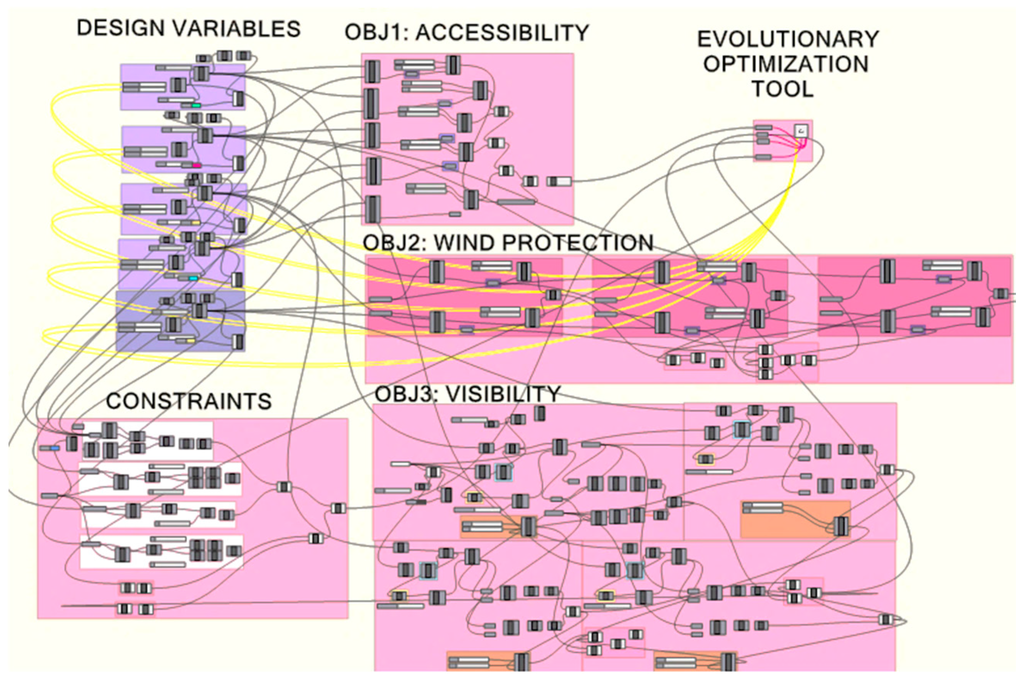
Figure 7.
Overview of the GH model [7].
The MOHS algorithm has been programmed in the C-Sharp programming language. The necessary geometric and measurement operations required for formulating the objectives and constraints in our problem have been implemented in the Grasshopper design tool, which is a part of the Rhinoceros CAD product. This tool has been very useful in offering the necessary building blocks (such as the shortest path algorithm) for computationally implementing our problem. The C-Sharp algorithm makes use of this tool to calculate objective function values and constraint values. The summary of this process is shown in Figure 8.
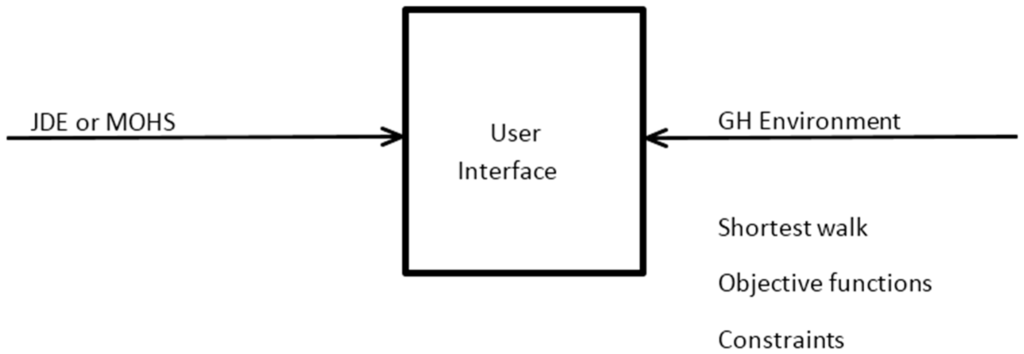
Figure 8.
Grasshopper and algorithm interaction.
In the generative model, the coordinates of the functions are defined first, then the functions are demonstrated with the circles with their specific areas. In the second stage, objective functions are formulized in the GH model. After setting up the constraints, the MOHS algorithm is implemented as a plug-in for the GH environment, as mentioned previously. After choosing a design from the set of design alternatives handled by the optimization, the shortest walk component was used in the GH environment to generate the streets between each function.
As mentioned previously, the basic harmony search (HS) algorithm is developed in [8,9]. It is a populated optimization method. The natural musical performance process is the key to the HS algorithm. This happens when a musician looks for a better state of harmony. In the HS algorithm, solutions are defined as harmonies and each harmony has an n-dimensional real vector. An initial population is randomly constructed as a harmony memory (HM). Then, generation of a new candidate harmony is achieved by all of the harmonies in HM through the use of a memory consideration, a pitch adjustment, and a random selection. Then, HM is updated by comparing the new harmony with the worst harmony vector in HM. This process is repeated until a certain termination criterion is met.
There are five basic parameters in the HS algorithm. These are the harmony memory size (), the harmony memory consideration rate (), the pitch adjusting rate (), the distance bandwidth (), and the termination criterion. Suppose that represent the harmony vector in the harmony memory and where and are the lower and upper bound for each dimension , respectively. The HMS is the total harmonies in the memory as . In other words, the population size is HMS. A harmony vector is randomly and uniformly generated as follows:
where and are lower and upper bounds for each dimension j and is a uniform random number between 0 and 1 for each dimension (decision variables).
Three rules are employed to improvise a new harmony vector, . These rules are a memory consideration, a pitch adjustment, and a random selection. As shown in Algorithm 1, a uniform random number is obtained. If is less than the probability, each dimension is obtained by the memory consideration; otherwise, random selection is used and is obtained by Equation (28). Memory consideration chooses any harmony in the range as . Then, each dimension will be modified by a pitch adjustment rule with a probability if it is updated by the memory consideration. The pitch adjustment rule is given as follows:
where is a uniform random number between 0 and 1 and is the distance bandwidth.
| Algorithm 1 Basic Harmony Search | |
| 1: | for () do |
| 2: | for () do |
| 3: | if () then |
| 4: | where |
| 5: | if then |
| 6: | |
| 7: | else |
| 8: | |
| 9: | endif |
| 10: | endfor |
| 11: | |
| 12: | endfor |
Once a new harmony vector is obtained, it is compared to the worst harmony vector in the HM. The selection is based on the survival of the fittest between and the worst harmony vector in the HM. In other words, if is better than , it will replace the worst harmony vector to become a new member of the HM. In the traditional HS, population size is taken as small and at each iteration only one harmony is generated. However, in this paper, we generate HM number of harmonies as shown in Algorithm 1.
The above HS is designed for single-objective unconstrained/constrained real-parameter optimization problems. In order to extend it to a multi-objective constrained optimization problem as in this paper, we mainly use the non-dominated sorting approach and constrained-domination rule of NSGA-II algorithm of Deb [12]. An excellent review of multi-objective genetic algorithms (GAs) is provided in [16]. In order to ease the understanding of the MOHS algorithm, we briefly summarize the NSGA-II algorithm as follows:
Most GAs employ Pareto-ranking approaches. In the Pareto-ranking approach, the concept of Pareto dominance is used to give a rank to each solution. The population is ranked by using a dominance rule and ranks are determined as . The first rank corresponds to the Pareto front of the population. Goldberg [17] proposed the first Pareto ranking technique with a population with size as follows:
- Step 1:
- Set and .
- Step 2:
- Determine non-dominated solutions in and assign them to rank .
- Step 3:
- Set . If , then go to Step 4, else set and go to Step 2.
- Step 4:
- For every solution at generation , assign a rank .
However, NSGA-II uses the fast non-dominated sorting algorithm to establish non-dominated fronts. Another distinct feature of the NSGA-II algorithm is the crowding distance approach to generate a uniform spread of solutions around the best-known Pareto front. The crowding distance is calculated in NSGA-II as follows:
- Step 1:
- Rank the population and determine non-dominated fronts .
- Step 2:
- For each front , repeat.
- Step 2.1:
- Sort the solutions in for each fitness function in the increasing order. SetSuppose that is the solution in the sorted list with respect to the objective function x. Make sure and . Suppose that the fitness function is denoted as .
- Step 2.2:
- Calculate the crowded distance for as follows:
- Step 3:
- To find a crowding distance of a solution , add up the crowding distances with respective to each fitness function, i.e., .
In NSGA-II, this crowding distance measure is a tiebreaker for the crowded tournament selection operator. Two solutions, and , are randomly selected. Then, if the solutions are in the same non-dominated front, the solution with a higher crowding distance is chosen. Otherwise, the solution with the lowest rank is favored. Since we deal with a constrained problem in this paper, we also employ the constrained-domination concept in NSGA-II [12]. In [12], the constrained-domination concept works as follows: A solution x is said to be constrained-dominated a solution y if one of the following conditions is satisfied:
- Solution x is feasible and solution y is infeasible.
- Solutions x and y are both infeasible; however, solution x has a smaller constraint violation than y.
- Solutions x and y are both feasible, but solution x dominates solution y.
In the constraint tournament method, first, non-constrained-dominance fronts are determined in such a way that the constrained-domination principle is employed instead of the regular domination principle. Note that set is the set of feasible non-dominated solutions in the population. In the constraint tournament selection, two solutions x and y are randomly chosen from the population. Between x and y, the one with a lower front is preferred. If solutions x and y are both in the same front, then the one with a higher crowding distance is the winner. Now, we are ready to give the computational flow of the proposed MOHS algorithm as follows:
Procedure MOHS:
- Step 1:
- Create a random harmony population of size HM and set .
- Step 2:
- Apply harmony search operators to and obtain offspring population of size HM.
- Step 3:
- If the stopping criterion is satisfied, stop and return .
- Step 4:
- Set .
- Step 5:
- Using the fast non-dominated sorting algorithm, identify the non-dominated fronts in .
- Step 6:
- For , do the following steps:
- Step 6.1:
- Calculate crowding distance of the solutions in .
- Step 6.2:
- Create as follows:
- , then set
- , then add the least crowded solutions from to .
- Step 7:
- Use crowded tournament selection to select a harmony from . Apply harmony search operators to and obtain offspring harmony population of size HM.
- Step 8:
- Set and go to Step 3.
4. Computational Results and Discussion
The MOHS algorithm is run on an Intel (R) Core (TM) i5-3210M CPU @2.50GHz computer with 4 GB of RAM. We compare the MOHS algorithm to the JDE algorithm in [6] as mentioned before. The population size is taken as 100 for both algorithms. Both algorithms performed 100 generations for each run. We took five runs for each algorithm with a different seed number. In order to analyze the performance of algorithms, we employ the hypervolume (HV), measuring the volume of the non-dominated portion of the objective space, as a performance metric [18]. Among the five replications with different numbers (S), we report the best, median, worst, and standard deviation values at generation 100 as given in Table 1 for JDE and MOHS algorithms, respectively. In addition, the line plot of HV values for both algorithms is given in Figure 9.

Table 1.
Hypervolume values of JDE and MOHS algorithms at generation 100.
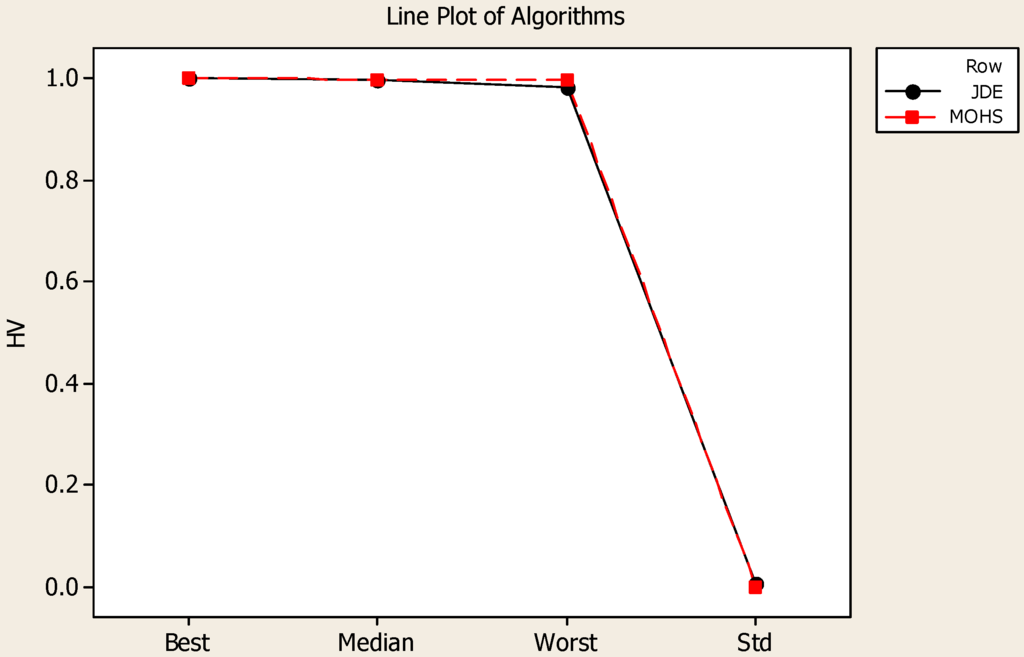
Figure 9.
Line plot of HV volumes for both algorithms.
As seen in Table 1 and Figure 9, both algorithms have a good performance in 100 generations for the best, median, worst, and Std values of HV. In addition, the proportions of non-dominated solutions are similar. The MOHS algorithm was slightly more robust than the JDE algorithm because the standard deviation was slightly smaller. These values are very close to each other because both algorithms employ the non-dominated sorting procedure and constrained-domination principle borrowed and adopted for JDE and MOHS algorithms from NSGA-II.
The chart of the non-dominated solutions () for the JDE algorithm at generation 100 and MOHS at generation 100 can be seen in Figure 10 and Figure 11, respectively. Since we have a feasible set of solutions, the seed number 3 is selected for the JDE algorithm, and seed number 2 is selected for the MOHS algorithm. Additionally, in each figure, we pick three solutions. They represent different design alternatives generated by the algorithms for the decision-maker.
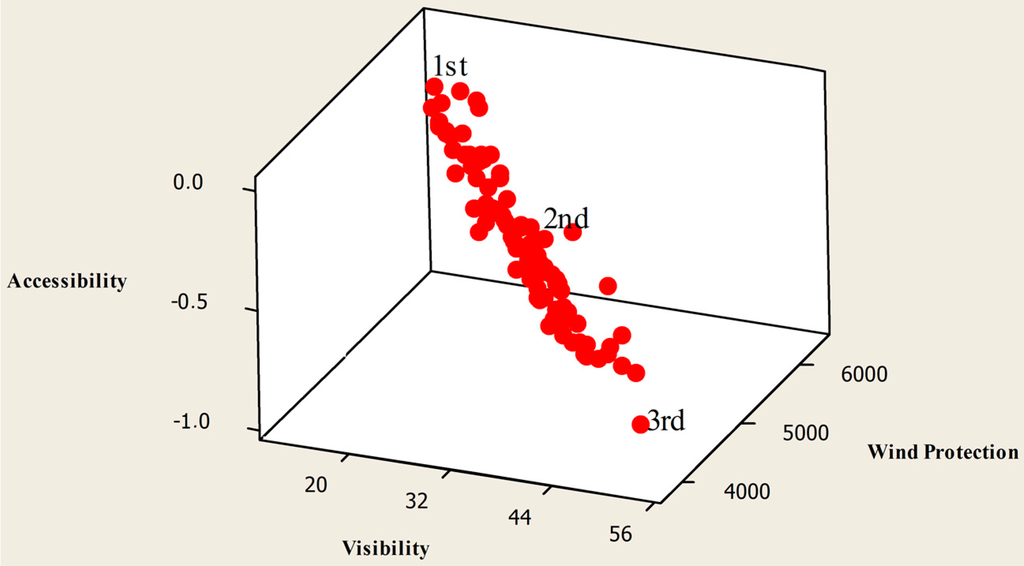
Figure 10.
Scatter plot of the JDE algorithm.
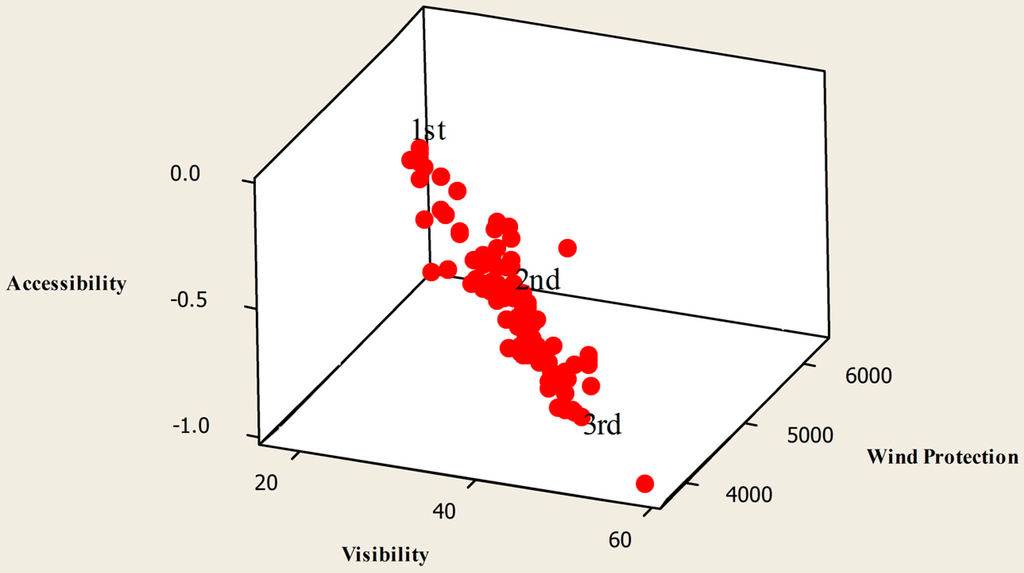
Figure 11.
3D Scatter plot of the MOHS algorithm.
In the first selected solution from the JDE algorithm in Figure 12, wind protection for houses is satisfied but it is not valid for the visibility of the yacht marina. On the other hand, accessibility is very high and the visibility of the yacht club is satisfying. For the second selected solution in Figure 13, privacy is good for both houses and the yacht marina, but there is an interesting placement between houses since different modules of houses are far away from each other. Although the visibility value is higher in this solution, one housing module prevents the visibility of the yacht club. The third selected solution from the JDE algorithm shown in Figure 14 has very poor wind protection. However, the yacht club is very noticeable and accessibility is satisfactory.
Figure 12.
The first selected solution from the JDE algorithm.
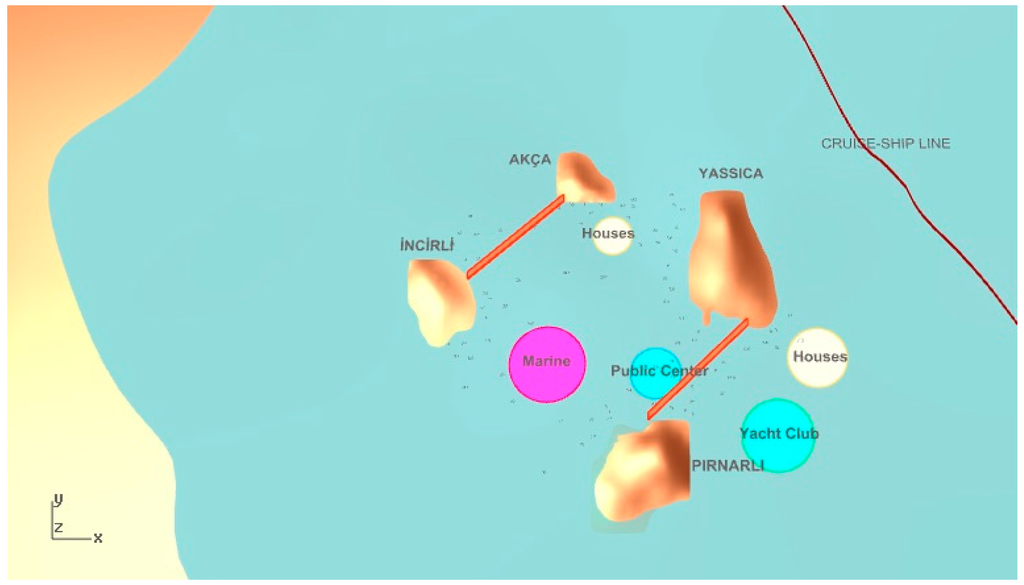
Figure 13.
The second selected solution from the JDE algorithm.
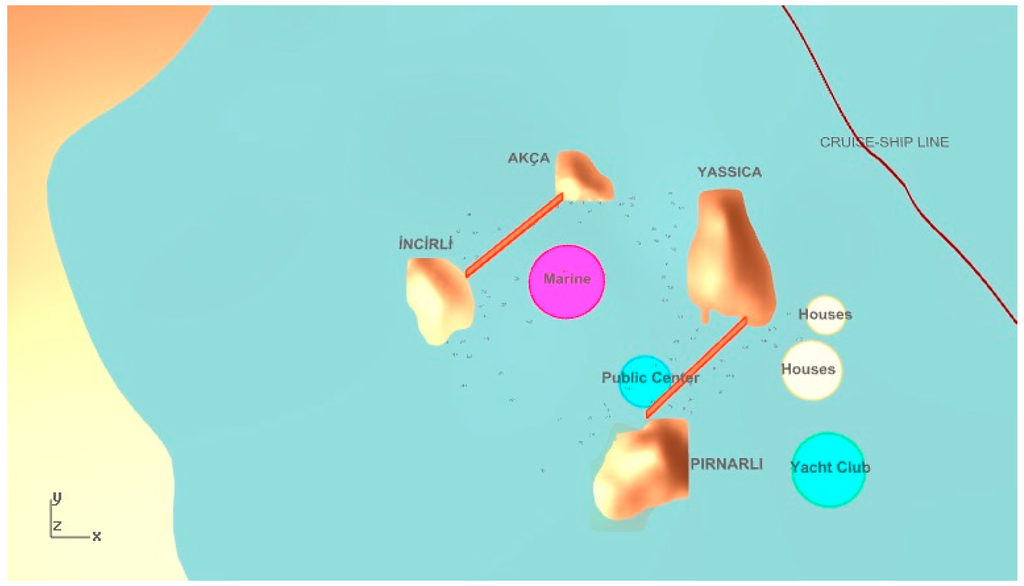
Figure 14.
The third selected solution from the JDE algorithm.
If we consider the selected solutions from the MOHS algorithm, the most accessible solution, which is the first one, represents a different configuration than the one in the JDE algorithm, as seen in Figure 15. This is because, in this design alternative, all functions are coming together. For the second one chosen from the MOHS alternatives (Figure 16), all objectives are highly desirable. However, the third solution chosen from the MOHS algorithm is very similar to the second selected one, with only the location of one house unit seriously changed (Figure 17).
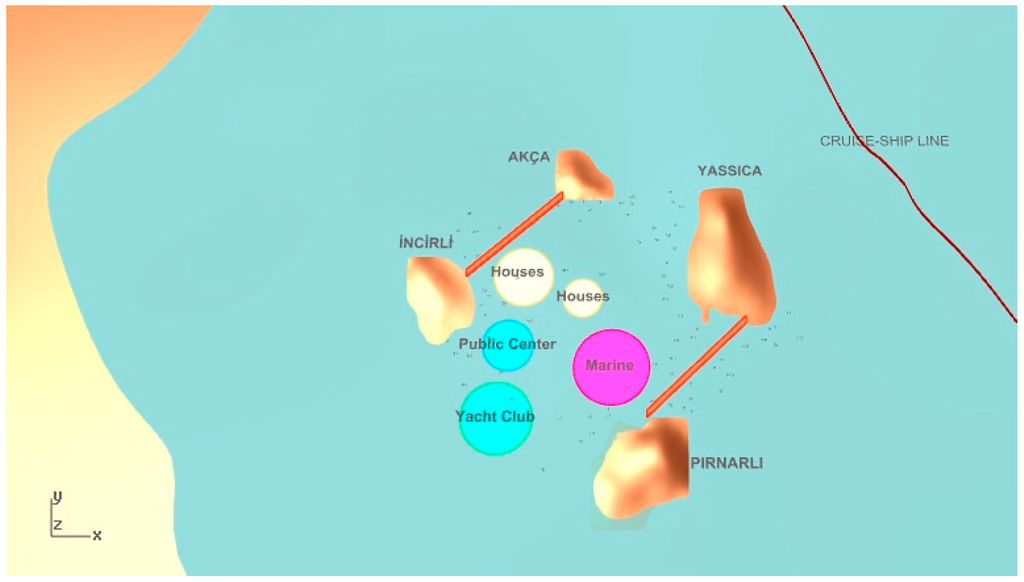
Figure 15.
The first selected solution from the MOHS algorithm.
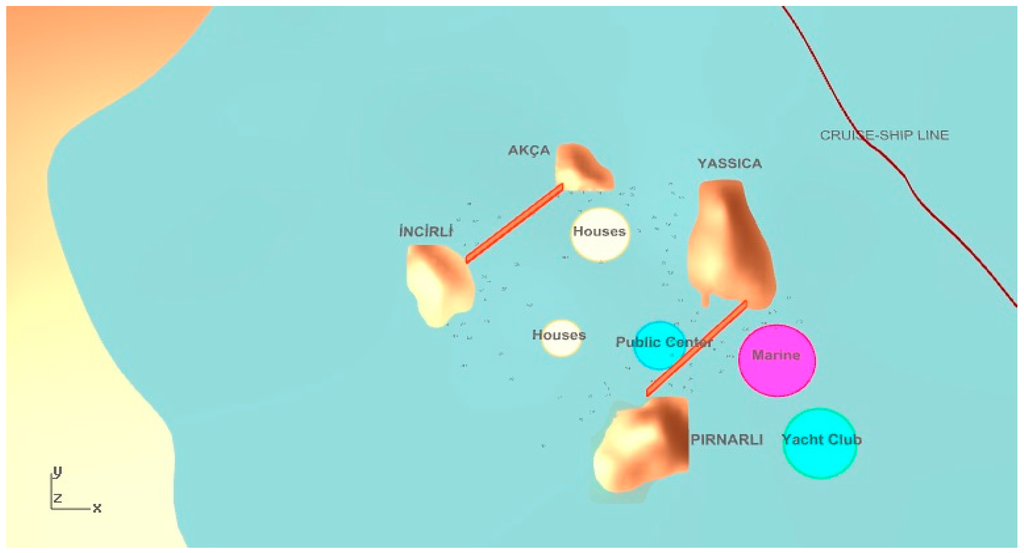
Figure 16.
The second selected solution from the MOHS algorithm.
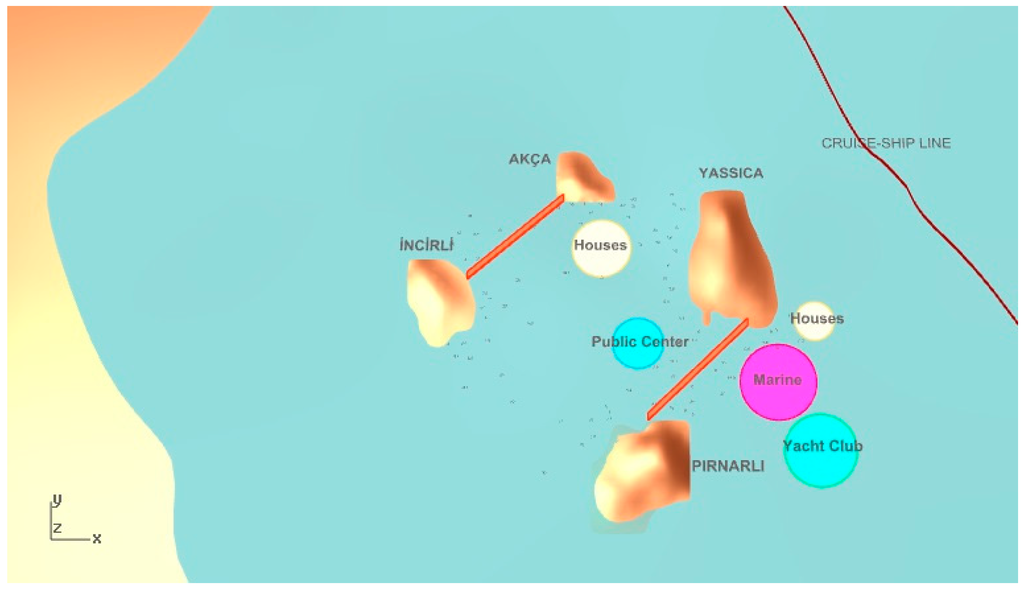
Figure 17.
The third selected solution from the MOHS algorithm.
5. Conclusions
This paper proposed a multi-objective optimization of the conceptual design and development of a floating settlement. The goal was to configure the city functions (i.e., housing and accommodation, yacht marina, yacht club, and public areas) so as to maximize accessibility, wind protection, and visibility subject to both technical and architectural constraints. Then, a suitable form was generated by shortest walk algorithm establishing pathways between functions, where their locations were gathered from solutions through a multi-objective heuristic optimization process.
Because wind protection, accessibility, and visibility objectives can conflict with each other, multi-objective JDE and MOHS algorithms are applied to solve this complex problem and identify alternative design solutions for decision-makers. Through the experimental results, we show that the two proposed algorithms generated satisfactory design solutions. The computer renderings of the proposed floating settlement design can be seen in Figure 18 and Figure 19.

Figure 18.
Computer rendering of the proposed floating settlement.

Figure 19.
Computer rendering of housing units.
Author Contributions
Mehmet Fatih Tasgetiren, Cemre Cubukcuoglu, and Ioannis Chatzikonstantinou wrote the C Sharp Codes for JDE and MOHS algorithms. Quan-Ke Pan provided the C Sharp Codes for the hypervolume calculations. All runs were performed by Cemre Cubukcuoglu. Mehmet Fatih Tasgetiren, Sevil Sariyildiz, and Ioannis Chatzikonstantinou wrote the paper. Final checks were done by Quan-Ke Pan. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tartar, A. Floating Architecture Design Process Modelling Supported by Rule-Based Decision-Making. Ph.D. Thesis, İstanbul Technical University, Istanbul, Turkey, 2012. [Google Scholar]
- De Graaf, R.E. Innovations in Urban Water Management to Reduce the Vulnerability of Cities: Feasibility, Case Studies and Governance. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2009. [Google Scholar]
- Watanabe, E.; Wang, M.; Utsunomiya, T.; Moan, T. Very Large Floating Structures: Application, Analysis and Design; Technical Report No. 2004-02; Available online: http://www.eng.nus.edu.sg/core/Report%20200402.pdf (accessed on 28 July 2016).
- Kirimtat, A.; Chatzikonstantinou, I.; Sariyildiz, S.; Tartar, A. Designing self-sufficient floating neighborhoods using computational decision support. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation, Sendai, Japan, 25–28 May 2015; pp. 2261–2268.
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Ugurlu, C.; Chatzikonstantinou, I.; Sariyildiz, S.; Tasgetiren, M.F. Identification of sustainable designs for floating settlements using computational design techniques. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation, Sendai, Japan, 25–28 May 2015; pp. 2303–2310.
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W. A new meta-heuristic algorithm for continuous engineering optimization: Harmony search theory and practice. Comput. Methods Appl. Mech. Eng. 2005, 194, 3902–3933. [Google Scholar] [CrossRef]
- Geem, Z.W. Multiobjective optimization of time-cost trade-off using harmony search. J. Constr. Eng. Manag. 2010, 136, 711–716. [Google Scholar] [CrossRef]
- Geem, Z.W. Multiobjective optimization of water distribution networks using fuzzy theory and harmony search. Water 2015, 7, 3613–3625. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Manjarres, D.; Landa-Torres, I.; Gil-Lopez, S.; del Ser, J.; Bilbao, M.N.; Salcedo-Sanz, S.; Geem, Z.W. A survey on applications of the harmony search algorithm. Eng. Appl. Artif. Intell. 2013, 26, 1818–1831. [Google Scholar] [CrossRef]
- McNeel, R. Grasshopper 3D. Available online: www.grasshopper3d.com (accessed on 21 September 2015).
- McNeel, R. Rhinoceros 3D. Available online: www.rhino3d.com (accessed on 21 September 2015).
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Bader, J.; Zitzler, E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evolut. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).