Abstract
Type-2 fuzzy logic controllers (T2 FLC) can be viewed as an emerging class of intelligent controllers because of their abilities in handling uncertainties; in many cases, they have been shown to outperform their Type-1 counterparts. This paper presents a literature review on recent applications of T2 FLCs. To follow the developments in this field, we first review general T2 FLCs and the most well-known interval T2 FLS algorithms that have been used for control design. Certain applications of these controllers include robotic control, bandwidth control, industrial systems control, electrical control and aircraft control. The most promising applications are found in the robotics and automotive areas, where T2 FLCs have been demonstrated and proven to perform better than traditional controllers. With the development of enhanced algorithms, along with the advancement in both hardware and software, we shall witness increasing applications of these frontier controllers.
1. Introduction
Fuzzy logic sets were first introduced by Zadeh [1]. Developments in fuzzy logic then stimulated the creation of fuzzy logic systems (FLSs), which emerged in many applications in systems modeling and control. Mamdani and Baaklini are the ones that presented the first fuzzy logic controller (FLC) [2]. Earlier FLS designs were generally categorized as Type-1 fuzzy logic systems (T1 FLSs). T1 FLSs were used by Japanese companies who adopted the FLSs and implemented them in a water treatment plant by Fuji Electric in 1983 and in a subway system by Hitachi in 1987.
One of the main challenges in the design of T1 FLSs is the shape of a membership function (MF) that is used. To incorporate uncertainty in fuzzy systems, Zadeh introduced Type-2 fuzzy sets (T2 FSs). These are an extension of T1 FSs, which adds an extra degree of freedom to entitle an uncertainty factor in the systems [3]. T2 FSs have membership grades, which are also fuzzy [4]. According to Hisdal in [5], “increased fuzziness in a description means increased ability to handle inexact information in a logically correct manner”. This extra uncertainly gives the T2 FLS an extra degree of freedom (DOF) and increases the complexity in most T2 FLS applications [3].
Due to the mathematical complexity of T2 FLSs, a simpler form of them was proposed, called interval Type-2 fuzzy logic systems (IT2 FLS). In an IT2 FLS, the uncertainty is mapped into a third dimension where the value of the MF is also mapped for each point on a two-dimensional domain. This special IT2 FLS is a simpler form of T2 FLS and also relies on the mathematics of T1 FLS [6]. The major difference is that the defuzzifier block of a T1 FLS is replaced by an output processing block in a T2 FLS. This block consists of a type reduction (TR) followed by defuzzification, meaning that the TR is the function that maps a T2 FS to a T1 FS. This enables mapping the uncertainty to an interval between the upper membership function (UMF) and the lower membership function (LMF).
T2 FLSs, including IT2 FLSs, are a more recent approach to solving problems that in many cases a T1 FLS cannot properly accomplish. The robustness of both T1 and IT2 FLSs is investigated in [7]. It was determined that the IT2 FLS outputs have small approximation errors; however, choosing to design a T1 or IT2 FLS is relatively application dependent. Furthermore, in [8], it has been shown that increasing the number of rules and the number of MFs beyond a certain limit is impractical. This increases the complexity of the FLC with almost no effect on the output. Regardless of this, IT2 FLSs are used in many applications, such as robot control, bandwidth control, industrial systems control, electrical control and aircraft control.
In this paper, we present the new applications of T2 FLC and introduce the vital and key areas where they have been successfully implemented and used. While the intent of this paper is not focusing on theory or how to design these systems, we ‘briefly’ review different T2 FLC systems and their structures, so interested readers have a better understanding of them. Consequently, we focus mainly on the applications, present challenges and future directions in this field, which are of interest to engineers, practitioners and researchers who would like to use T2 FLC in their applications.
2. T2 FLS
In this section, we review T2 FLSs. We start with a description of general T2 FLSs in Section 2.1, followed by IT2 FLSs in Section 2.2. Type-1 fuzzy systems are not presented here, as currently, there are many works in this area. The main difference of Type-2 fuzzy systems with respect to Type-1 is the use of membership functions in which the membership is fuzzy instead of crisp. In Type-1, it is assumed that membership can be assigned as a crisp numeric value, which is not necessarily a realistic assumption. On the other hand, in general or interval Type-2 fuzzy sets, it is considered that there is uncertainty in knowing the values of the membership, and therefore, the concept of the footprint of uncertainty is introduced to model uncertainty in real-world problems.
2.1. General T2 FLS
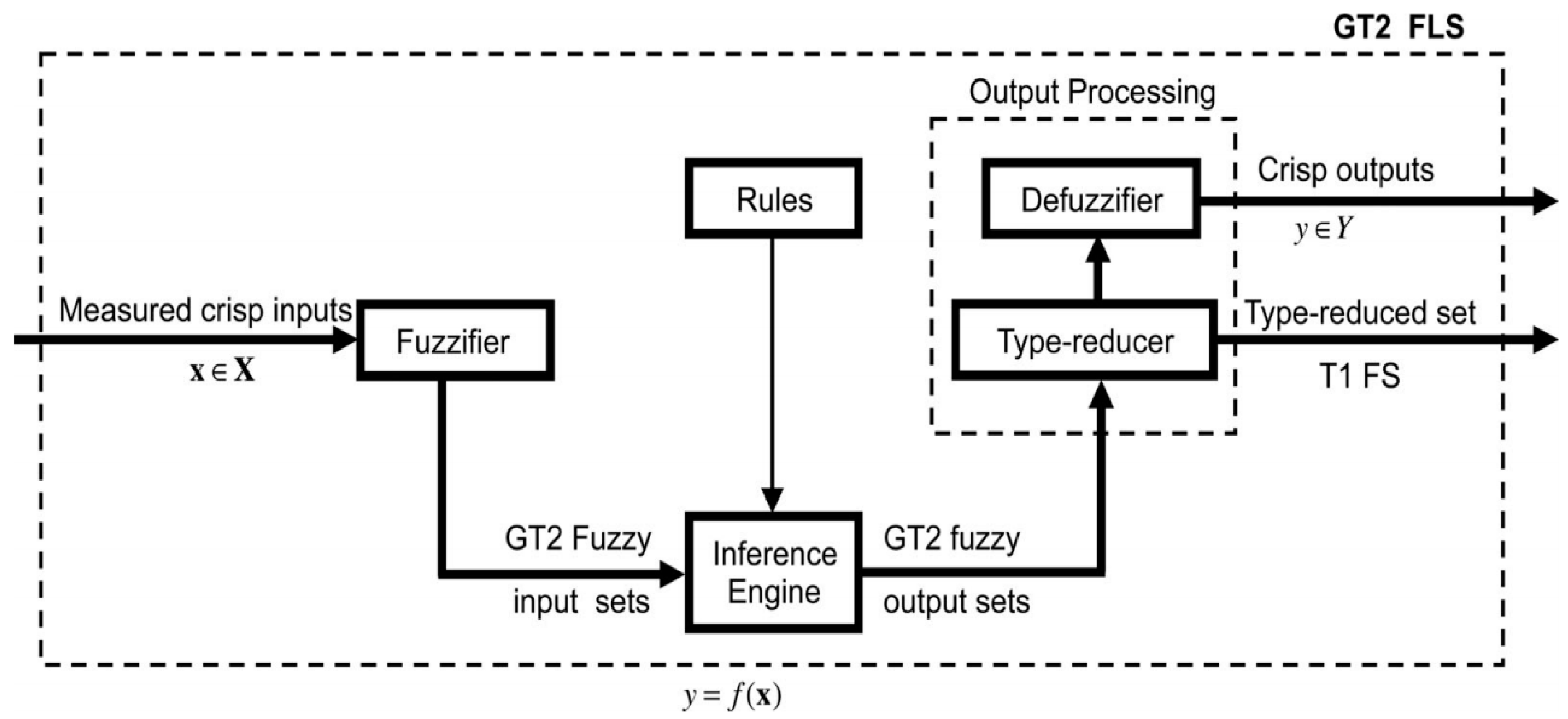
A general T2 FLS (GT2 FLS) accounts for the MF uncertainties, but it weights all of the uncertainties nonuniformly. In an IT2 FLS, however, all of the uncertainty weights are considered to be uniform. The MF of a GT2 FLS is represented in 3D space, where the z-axis resembles the MF value provided by . Both IT2s and GT2 FLSs are parametric models, but GT2 FLSs have more parameters than IT2 FLSs. A GT2 FLS can be represented in four different ways, such as points, wavy slices, horizontal slices and vertical slices [9]. In Figure 1, the structure of a GT2 FLS is shown, which consists of several blocks. The fuzzifier maps a crisp input vector with multiple inputs into other input FSs. These FSs are also known as input T2 FSs. The inference engine combines rules and gives a mapping from input T2 FSs to output T2 FSs. The output of the inference engine is a T2 set, which can give a T1 FS using extended defuzzification methods. This is the TR since it transforms output T2 FSs to T1 FSs, and it obtains a TR set. To get the crisp output from T2 FLS, the TR set is defuzzified by finding the centroid of it or through other methods, such as choosing the highest membership point in the TR set [10].
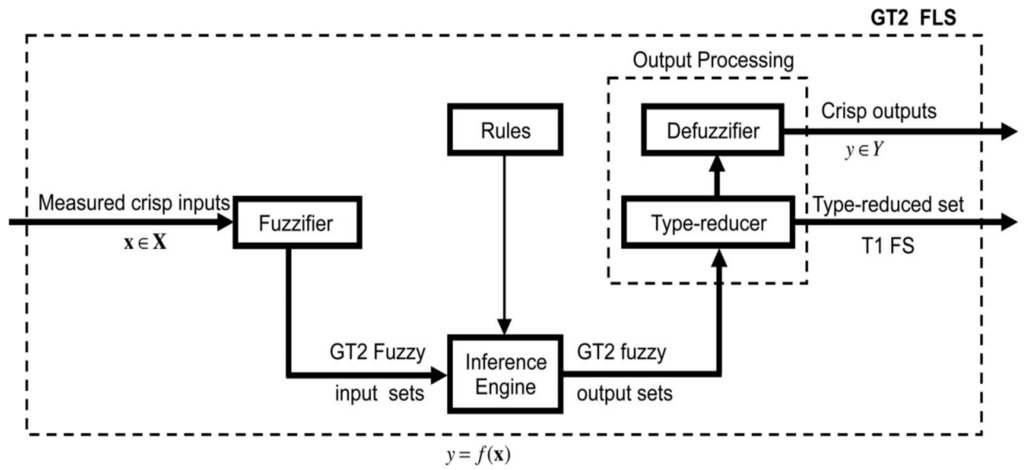
Figure 1.
Structure of a GT2 FLS, with permission from [9].
In Figure 1, the structure of a GT2 FLS is shown which consists of several blocks. The fuzzifier maps a crisp input vector with multiple inputs into other input FSs. These FSs are also known as input T2 FSs. The inference engine combines rules and gives a mapping from input T2 FSs to output T2 FSs. The output of inference engine is a T2 set which can give a T1 FSs using extended defuzzification methods. This is the TR since it transforms output T2 FSs to T1 FSs and it obtains a TR set. To get the crisp output from T2 FLS, the TR set is defuzzified by finding the centroid of it, or through other methods such as choosing the highest membership point in the TR set [10].
The rule structure of a general T2 FLS is given by [9]:
If is and is then y is where .
In the above rule base, is the j-th input to the system (e.g., sensor input), is the j-th input Type-2 fuzzy membership and is the output Type-2 fuzzy membership function.
2.2. IT2 FLS
In this section, we review the most well-known algorithms for computing the output of an IT2 FLS [11]. These algorithms are: Karnik–Mendel (KM), Nie–Tan (NT), Biglarbegian–Melek–Mendel (BMM) and Wu–Mendel (WM) [12]. The KM algorithms contain TR methods, which reduce a T2 set into a T1 set [10]. The other algorithms bypass TR and directly compute the output of a T2 FLS. Alternative methods, such as Coupland–John, Du–Ying, the Tao–Taur–Chang–Chang method, Li–Yi–Zhao and many others are also mentioned.
2.2.1. Karnik–Mendel Method
The KM method was first developed by N.N. Karnik and J.M. Mendel [13,14]. According to [15], this method is the most widely-used method for TR of an IT2 FS. TR is a major road block in computing the output of a T2 FLS.
Many enhanced versions have been proposed that use the KM method; however, they work with a different strategy. Wu and Nie presented the enhanced iterative algorithm with stop Condition (EIASC), where five variations are compared experimentally, and the most efficient one is the optimum algorithm also known as EIASC [16].
Liu and Mendel [17] introduced the α-cut algorithm for solving the fuzzy weighted average (FWA) problem. This algorithm uses the KM algorithm to compute the FWA α-cut endpoints. Another work proposed a boundary function based on the KM TR method of IT2 PID controllers [18]. This KM method generated a boundary function KM, which was proved to be superior and more feasible. Other algorithms were also developed that improve on existing KM algorithms. This is called the enhanced Karnik–Mendel (EKM) originally presented by Wu and Mendel [19]. It was found that on average, the EKM method was able to reduce computational time by 39% compared to KM. In [20], Melgarejo and Duran developed two hardware architectural proposals for the EKM method. The first approach uses a sequential online arithmetic, whereas the second approach includes operators based on the CORDIC (coordinated rotation digital computer) algorithm. The CORDIC algorithm showed better performance in terms of speed and accuracy.
The fundamental KM algorithms converge to exact solutions monotonically and at a super-exponential rate. They can also run in parallel because they are independent [21]. For IT2 FLS, in the above rule base is interval Type-2 sets and is represented by two intervals of . To calculate the IT2 FLS output, we first arrange and in ascending order. The following steps show how to compute left and right intervals for the KM algorithm [11,13]:
- (1)
- Arrange in ascending order.
- (2)
- is calculated as:; let (note that are the firing intervals).
- (3)
- Find , such that .
- (4)
- Find with for and for ; now, let
- (5)
- If , go to Step 6. If set
- (6)
- Let = , and go to Step 3.
The algorithm for computing is similar to that of the algorithm, except that all instances of and are replaced with and , respectively. Finally, the defuzzified output is the average of and as follows:
2.2.2. Wu–Mendel Method
The Wu–Mendel method was presented to speed up the T2 FLC′ by overcoming the TR computational burden. This can be done by reducing the number of iterations before convergence occurs [12]. Wu–Mendel uncertainty bounds method provides mathematical formulas for the inner and outer bound sets, which can be used to approximate the TR set [22]. It has been shown that the WM method produces similar results to those obtained using the KM TR. Furthermore, it can result in much faster responses than the KM algorithms. The bounds derived in the WM method can estimate the uncertainty in IT2 FLS output without performing TR [22]. This algorithm approximates the TR set by using the min-max uncertainty bounds [22]. These uncertainty bounds are defined as and as follows:
The output is then computed as follows:
2.2.3. Biglarbegian–Melek–Mendel Method
The Biglarbegian–Melek–Mendel algorithm computes the output value of an IT2 FLS as a combination of two T1 FS.
This method is similar to the NT method, which replaces TR and is given as follows [23]:
where the parameters m and n are used to tune the system and is the final crisp output of the IT2 FLS.
The structure of this controller embeds two free parameters, m and n, that are used for tuning the controller. This controller has a simpler structure than WM and has been used to determine stability and robust control design [24].
2.2.4. Nie–Tan Method
The Nie–Tan method was developed by Maowen Nie and Woei Wan Tan [25]. It works by calculating the union of a fired rule output set first. It then computes the mean of the LMF and the UMF, respectively. This will result in a T1 FS where the centroid is the defuzzified value. It does not involve embedded sets during processing or derivation, leading to a very conceptually simple method.
The NT algorithm was developed using the vertical slice representation as opposed to the wavy-slice representation, which the KM uses [12]. In the original paper, the NT method and the KM method had minimal differences in the defuzzified output [25]. This is advantageous as the NT method is less computationally expensive. Additionally, the output can be expressed in a closed form thereby providing an efficient tool for the theoretical analysis of IT2 FLSs. Comparatively, the NT method also has a lower computational complexity than the KM and WM algorithms. A disadvantage to this method is that the uncertainty level cannot be provided.
It is also reiterated in [26] that the NT and KM outputs are very close. They simulated various IT2 FS defuzzifiers using various MFs. These MFs were: (1) symmetric Gaussian MFs with uncertain standard deviation; (2) triangular LMF and piecewise Gaussian UMF; (3) piecewise Gaussian MFs; and (4) piecewise linear MFs. Using these MFs, they tested EIASC, enhanced opposite direction searching algorithm (EODS), enhanced KM (EKM), NT and improved NT (INT).
The INT method was proposed in [26], and it was demonstrated that it has less absolute and relative errors than the NT method. The fundamental NT closed-form equation, which replaces the TR, is shown in [25] as:
2.2.5. Other IT2 Algorithms
Alternative methods are also developed to decrease the computational complexity and increase execution speed. Coupland and John (CJ) applied a geometric construction of the centroid to find the crisp output of a T2 FLS [27]. It builds a polygon where the firing strengths lie. If there are “N” fired rules, the polygon then has 2N points on the boundary. The defuzzified output will then lie on the center of the polygon [28]. It was found in [29] that the CJ method provided the best performance. The CJ method also satisfied the left and right end points in a majority of cases.
Similar to the CJ method, Greenfield designed a TR in which each IT2 FS is replaced by a T1 FS with membership grades computed recursively. Once all of the IT2 FSs are replaced by artificial T1 FSs, the entire IT2 FLS is reduced to a T1 FLS. This will then simplify the defuzzification using the collapsing method [30]. This method is identical to the NT method if there is only one input. If there are more inputs, however, the firing level is different.
Another method by Du–Ying (DY) proposes an average defuzzifier [31]. It will compute all of the crisp outputs using all of the possible combinations of upper and lower firing levels to total 2N outputs. The final output is then averaged from all of these values. This method is very computationally expensive as each extra rule will add to the computation exponentially [28].
In the Tao–Taur–Chang–Chang method (TTCCM), a simplified IT2 FLS is generated by a combination of two IT1 FSs [32]. The first IT1 FLS is built from the possible left-most IT1 FS, and the second is built from the possible right-most IT1 FS. From this, an IT2 FS was made by blurring a triangular IT1 FS with both the left and the right. This method has some setbacks, as it does not consider IT2 FSs with irregular FOUs.
The Li–Yi–Zhao (LYZ) method utilizes an inclusion function for each rule. It finds the maximum value of the upper bound for each rule while also finding the minimum value as the lower bound for each rule [33]. These bounds are very loose given that the rule base is low, as well. It does however avoid the iterative procedure of KM methods.
The hierarchical collapsing (HC) method was also developed, which utilizes α-plane decomposition to prepare a direct defuzzification procedure [34]. This proposed method was shown to be fast and robust.
Another method developed by Melgarejo utilized a combination of an exhaustive search with recursive computation in a field-programmable gate array (FPGA) [35]. They proposed a fast recursive TR method, which also finds the left and right centroids. This method avoided using a switch method and had higher computational speed over KM. More in-depth TR methods are discussed in [12]. For the design of IT2 FLSs, please see a recent survey [36].
3. Review of IT2 FLCs
3.1. Robotic Control
In [37], a T2 FLC was designed for navigating a mobile robot in dynamic environments with a hierarchical structure (HFLC). The HFLC reduces the number of rules to increase the speed in real-time applications. Using the T2 FLC resulted in very good real-time control.
In [38], an IT2 Takagi–Sugeno–Kang (TSK) FLC was developed for modular and reconfigurable robots (MRRs). This controller was designed for tracking purposes, which can be implemented in real time. Experiments were done on the IT2 TSK FLC, which shows that it can be applied with guaranteed uniformly ultimately bounded (UUB) stability. It was also determined that the proposed controller can, in some cases, outperform some linear and non-linear controllers in similar configurations.
In [39], Liu et al. proposed a T2 fuzzy control system (FCS) for biped robots based on a switched nonlinear model. This paper also proposes a new fuzzy c-mean variance (FCMV) clustering algorithm to model the T2 FCS. At the time, there were no appropriate mathematical tools to design a control system for the biped robot. Prospects from this work are to develop a switched system theory for industrial applications.
In [40], a mobile robot wall-follower was controlled using a reinforcement ant optimized fuzzy controller (RAOFC). The rules are automatically generated for the robots using an aligned IT2 fuzzy clustering (AIT2FC) technique. Using the AIT2FC reduced the number of FSs for each input dimension. Furthermore, the consequence of each rule is generated using a Q-value-aided ant colony optimization (QACO). It was found that by using T2 FSs, the FC was more robust to uncertainties in the environment and noise.
The Pioneer 3-DX was an experimental platform for which an optimized IT2 fuzzy PID controller was designed [41]. This controller was evaluated for the path tracking problem. It was found that the IT2-FPID controller was superior in the control performance in the presence of disturbances and uncertainties in comparison to PID, T1-PID and T1-FPID self-tuning controllers.
T2 FCs have been implemented in many real-time control applications; however, the main issues of adopting such systems is their complexity in large-scale implementations. T2 FLCs systems have not been “widely” implemented in robotics due to the limitations of mathematical proofs to have closed-loop system stability, although there are some recent works that have been able to overcome this problem, such as the work of Khanesar et al. [42].
In [43], Chaoui and Gueaieb implemented an IT2 FLCs on a flexible-joint manipulator. This work takes into account a trade-off between the link position and the actuators’ internal stability, and it is based on sliding mode control. It was shown that this controller was superior to T1 FLC in simulations.
In [44], an IT2 TSK FLS was developed for tracking control of robot manipulators. The IT2 TSK FLS was able to approximate the uncertainty and the non-linear robot dynamics. This was then incorporated into a controller, which combined the IT2 TSK FLS and a sliding mode control (SMC) with different weights. This controller was designed to minimize the approximation errors and to reduce the amount of uncertainty in the system. An advantage of this design was that the IT2 TSK FLS controller combines the robustness of SMC with the adaptive IT2 TSK FLS. Experiments were done on a robot with two degrees of freedom. It was concluded that the IT2 TSK FLS controller performed better than an adaptive IT1 FLS and provided more flexibility.
In [45], an IT2FLC was used for controlling multiple robots to cooperate and reach certain targets. This controller was optimized using a particle swarm optimization algorithm (PSO). The PSO algorithm can find a solution to an optimization problem by searching space and predict social behavior in the presence of objectives [46]. This method allows the robot to find the best solution by iterations after the particles of the algorithm are randomly distributed. After this, the best values are found, and the particles update their velocity and position. To handle the collision avoidance, a hybrid reciprocal velocity obstacles (HRVO) were used in tandem. It was concluded that the PSO-optimized IT2 FLS was faster the non-optimized IT2 FLS.
Martinez et al. in [47] used a genetic algorithm (GA) for the optimization of a T2 FLC for the dynamic model of a unicycle mobile robot. In [48], a combination of PSO and GA was used and was proved to have the best performance possible. The same combination of algorithms was used later on to minimize the steady state error of linear systems in [49]. Furthermore, in [50], a hybrid PSO-GA optimization method was used for the automatic design of the FLC. The optimal FLC design was tested using benchmark control plants and an autonomous mobile robot for trajectory tracking control. This bio-inspired method was determined to be feasible for these control applications, and it is a feasible method for improving FLC designs.
The ant colony optimization (ACO) is another method used to design optimal T2 FLSs. The ACO technique is inspired by the foraging behavior of real ants. It is a population-based, meta-heuristic technique that takes advantage of past performance memory and mainly depends on values defined for its parameters [51].
ACO was found to be robust and versatile in handling a wide range of combinatorial optimization problems [46]. In [51], a new fuzzy approach was presented for diversity control. This approach was used in controlling the trajectory of a unicycle mobile robot with optimized MFs. For this mobile robot, encouraging results were demonstrated.
Tuning techniques for T2 FLCs are widely used, and they have been applied in two different ways. The first is by tuning the MFs of a given rule set, and the second method is by selecting an optimal subset of rules from all of the possible rules [52]. For tuning FLCs, evolutionary algorithms are the most adopted. However, a simple tuning algorithm (STA) can also be used. The STA was designed to improve the response of T1 FLCs in practical, intuitive and simple ways. In [53], an extension of the STA was presented on the theory of T2 FLCs using a parallel model implementation. This paper also presented a mechanism to calculate the feedback gain, new integral criteria parameters and the effect of the AND/OR operator combinations on the fuzzy rules. All of these mechanisms helped in improving the performance and applicability. Tuning techniques can also be classified as derivative-based, derivative-free and hybrid tuning methods. This classification refers to the information that is used during the tuning process.
Extended discrete action reinforcement learning automata (EDARLA) is a technique that tracks the input reference signal by computing MF parameters. EDARLA was presented in [54], where it is used for adapting parameters and tuning processes. This technique searches for parameters in every cell dimensional space. It updates at discrete sample points, so the chance of obtaining better results is more likely to occur.
Discrete action reinforcement learning automata (DARLA) and continuous action reinforcement learning automata (CARLA) are two other techniques used. The DARLA technique is operated by selecting actions in a stochastic trial and error process in an unknown environment, whereas CARLA is operated on a separate action [54]. The automata set in CARLA runs in a parallel implementation, thus determining multiple parameters. Actions have an associated probability density function, which helps in the selection process for better performance purposes. In [52,54], it was proven that the best results were obtained using T2 FLCs systems using the EDARLA technique compared to CARLA and DARLA.
Robotic excavator controllers were also designed based on IT2 FLC structure. In [55], the servo position control of an electro-hydraulic excavator was demonstrated. The controller utilized fluid flow rates, pump hydraulics and friction forces. The position of the bucket with respect to the boom, arm and bucket axes was controlled.
A Delta Parallel Robot was also studied using a T1 FLC and an IT2 FLC [56]. The performance of the two controllers was evaluated in the presence of sensory noise and other uncertain system parameters. The parameter being evaluated was the position control of the robot. Experiments were done using both controllers and it was determined that the IT2 FLC provided improvements in both performance and robustness. It was also found that increasing the fuzziness also improves the uncertainty robustness to a certain level. Once this level is hit, increasing the fuzziness can lead to massive performance degradations.
3.2. Controller Systems Using IT2 FLC and Neural Networks
In [57], a bilateral teleoperation system was controlled through a T2 fuzzy wavelet neural network (T2FWNN). This teleoperation system allows a human operator to send commands to a local master manipulator where it then drives a slave manipulator in a remote location. This is highly non-linear, as communication delays and corrupt data affect the data link. The main advantage of this controller is that it can handle unknown environmental interactions; it can handle uncertainties associated with information and data in the knowledge base; and it can remove most noise added to data transmitted through the communication channel. This controller was compared to the T1FWNN controller and conventional FC, and it was more efficient.
In [42], the feedback error learning of magnetic satellites was controlled using a T2FWNN with elliptic MFs. The learning is based on the feedback error learning method, and the stability of the learning is proven, but also the stability of the overall system, to ensure robustness. The simulation of the proposed control scheme shows that the adaptive T2FNN when it is used in parallel with a conventional PD controller can control the system effectively, and it outperforms conventional PD controller when it is used alone. It is also shown that the use of T2FNN with elliptic Type-2 MFs added makes it possible to cope with uncertainties in terms of measurement noise more effectively.
3.3. Internet Bandwidth Control
IT2 controllers are not limited to controlling autonomous robots. In a paper by Jammeh et al., an IT2 FLC was used for congestion control across networks [58]. In this specific case, the video streaming quality was measured. This is difficult, as the bit rate must be adjusted in order to account for network traffic volatility. In earlier research, a T1 FLC is capable of reducing packet loss and rate fluctuations; however, to cope with the uncertainty of the network traffic, an IT2 FLC was designed to demonstrate the difference. The two testing methods used were streaming a video during Internet cross-traffic and streaming a video with other videos running at the same time. The proposed IT2 FLC showed a significant performance boost over the IT1 FLC. Furthermore, when subjected to random noise, the IT2 FLC again showed a performance boost. From these results, it can be seen that an IT2 FLC is capable of optimizing congestion control during video streaming during an All-Internet Protocol network.
A similar IT2 FLC controller was developed and implemented for Voice over Internet Protocol (VoIP) [59]. This is due to the real-time delivery requirements of VoIP and the uncertainty of network degradation. The controller infers a network state based on the average delivered perceived quality of service along with the degradation from increased network congestion. From this information, the IT2 FLC updates an adaptive multi-rate codec in real time. The codec is updated to match the network state and the voice quality. This controller was then tested, and it was shown to outperform the existing state-of-the-art scheme implemented.
Broadband wireless Internet Protocol Television (IPTV) applications were also investigated [60]. The IT2 FLC adjusted the bit rate every frame based on the packet delay. This was compared to conventional controllers, such as TCP-friendly rate control (TFRC) and TCP emulation at receivers (TEAR) congestion controllers. This was tested by streaming more video traffic than the network could handle, which in some cases was up to 50 video streams. During an overloaded network, the IT2 FLC improved the quality by approximately 1 dB per client.
In [61], the author used FLCs to adjust prices of bandwidth per one unit based on the demand and availability of bandwidth. It was concluded that the fuzzy logic pricing controller sets the price for the aggregated Obtainable Forwarding (OF) traffic demand at the boundary note of the DiffServ Network.
Improving wireless sensor networks is a challenge in order to provide continuous connectivity in ad hoc networks. To measure the performance of a wireless sensor network, two parameters can be used, which are latency and energy efficiency [62]. In [62], two contributions were proposed; the first was a role-based mobility-aware interference mechanism to determine the main characteristics of a wireless network’s performance, such a, energy, distance, speed, etc.; the second contribution was for the decision making process using T2 FLS. The results showed that an optimal energy balance for the network can be guaranteed for a life time.
3.4. Industrial System Controllers
IT2 FLCs have also been used in industrial operations, as well, e.g., inside a hot strip mill [63]. During the operation of the mill, a steel slab is heated, machined and rolled to a hot rolled coil. Typically, these operations will span more than 500 m, which will affect the temperature of the slab. It is very important to regulate the temperature, as the properties of steel will fluctuate. A T1 and IT2 FLC were implemented to control the coiler entry temperature. This was done by adjusting the cooling water flow to achieve the target entry temperature. In the experiments, the IT2 FLC achieved better performance and stability compared to the T1 FLC. It was concluded that the IT2 FLC controller is feasible in this design.
Finishing strip mills also require the control of the rolling gap positions in order to achieve the desired strip head thickness. To do this, an X-ray gauge sensor was linked to an IT2 FLC [64]. Additional inputs are the transfer bar thickness, the entry width, the entry temperature, the target thickness, the output width, the output temperature, the standing work roll diameter, the work roll speed, the stand entry thickness, the stand exit thickness, the stand rolling force and the percent carbon of the strip. The finishing mill stand screw was adjusted to target the required thickness. The feasibility of the proposed IT2 FLC was also shown, and it was found that this controller equalized the performance of the finishing mill stand screw and achieved the target strip thickness while under high uncertainty.
Precise positioning is required for the fabrication of nano- and micro-components in the semiconductor industry. Since these components are very small, an IT2 FLC was proposed for a linear ultrasonic motor [65]. The simulation results show that the adaptive IT2 did not require prior knowledge of the plant. It was concluded that the IT2 FLC was more effective and robust over the T1 FLC.
IT2 FLCs have been used in AC motors, such as permanent magnet synchronous motors (PMSM) [66] or permanent magnet linear synchronous motor (PMLSM) [67].
PMSM are used in many applications requiring high efficiency and high torque-to-weight ratios. Since they are AC systems, their controllers are typically designed from a PID or PI regulator. These are very efficient; however, they are also subjected to uncertainties, such as varying loads, plant parameter variations and other non-linarites. An IT2 FLC was designed to account for these uncertainties. It was tested in different ways with either extreme parameter variations or external disturbances. It was found that the IT2 FLC was able to maintain the tracking errors within an acceptable interval. PMSMs offer many benefits; however, uncertainties in the drive mechanism can affect their performance, since there are no ball screws or gears. External loads, non-linear friction forces and parameter variations are some examples. In order to account for these, IT2 FLC have been designed and used. First, the self-adaptive IT2 FLC was run in order to learn the inverse kinematics of the system. Then, the inverse self-adaptive IT2 FLC is built with error feedback. From the experimental results, it was shown that the IT2 FLC outperformed the T1 FLC.
An induction motor was also controlled using a T2 FLC [68]. This motor used space vector pulse width modulation (PWM) to control the torque of the motor. Typically, these are run with a proportional-integral (PI) controller; however, a PI controller does not provide efficient performance during sudden changes in the load or speed. It was shown that the IT2 FLC performed better than the PI controller. The flux distortion, starting current, torque pulsation and speed regulation were much lower with the IT2 FLC. This was then tested using a prototype DSPACE DS1104. It was found that the typical PI controller had a current total harmonic distortion of 3.3%, while the T2 FLC reduced that to 2.3%.
A comparative study was done based on the speed control of direct torque and flux control induction motor drives [69]. There were five different speed control techniques, such as PI controllers, sliding-mode speed controllers (SMSC), a T1 FLC, a T1 fuzzy SMSC and a T2 FLC. Each one was tested under parameter uncertainties and load disturbances. The simulations were conducted in MATLAB with a wide variety of different operating conditions. The T1 fuzzy SMSC was shown to have disturbance rejection; however, it was unable to purge the chatter phenomenon during steady state operations. The T2 FLC was the optimal in terms of disturbance rejection and parameter uncertainties.
A permanent magnet DC (PMDC) motor was incorporated into an IT2 FLC [70]. In this study, the control system deals with sector dead-zones and external disturbances. The IT2 model approximates the motor dynamics using fuzzy inference and online update laws. This method improves upon the ordinary model, since this method estimates the non-linear system functions, since the system parameters are unknown. The IT2 configuration parameters can be attenuated to bring the system to an optimal tracking performance. It was found that the IT2 FLC performs better than the ordinary model in the presence of external disturbances and dead zone non-linearity.
An IT2 FLC was designed for a DC motor, but in this case, the variable controlled was the velocity regulation [71]. The IT2 FLC was tested against a T1 FLC and a PID controller to regulate the velocity. Various uncertainties were introduced, and each controller was designed in MATLAB and uploaded into Very High Descriptive Language (VHDL) for an FPGA. It was found that after multiple trials, the IT2 FLC performed better from the results of a t-distribution statistical test.
In a similar paper, the speed control of a DC motor was regulated using an average approximation IT2 FLC (AT2-FLC) [72]. It was used on an FPGA, which provides implementation in real time. It was found that the timing results using 20 bits on the FPGA decreased the error by 62% compared to using eight bits. Using an AT2-FLC decreased the error compared to PID tuning using Ziegler–Nichols tuning. These results show that more T2-MF and fuzzy rules can be utilized for better results with an increase in runtime.
A parallel cable-driven lifting mechanism was also controlled using T2 FSs [73]. This problem was split into six subsystems, where each subsystem had an IT2 fuzzy nonlinear autoregressive exogenous (NARX) model. It controlled all of the actuator tension, while taking in the degrees of inclination as the input. It was found that this control method was able to balance the tensions of the four lifting cables while also keeping the top surface level.
3.5. Power Management and Electrical Control
An energy management system was also controlled using an IT2 FLC [74]. In this application, a hybrid electrical vehicle was tested, which managed three sources of power: batteries, super-capacitors and the fuel cell system. The inputs of the FLC were vehicle speed, reference power, battery power, super-capacitor system power, fuel cell system power, battery voltage, battery state-of-charge and super-capacitor state-of-charge. The system was evaluated using a computer simulation, and it was shown that FL energy management was able to fulfill the energy requirements of the vehicle.
This controller was tested using an actual heavy duty vehicle [75]. The energy management system design was a result of using the knowledge of several experts. During the experimental validation of the IT2 FLCs, it was found that the controller was able to handle the energy management in hybrid electric vehicles. This paper did not cover the optimization of the IT2 FLC; therefore, it was determined that an IT2 FLC was not necessarily better than a T1 FLC.
A T2 FLC was also designed for power systems [76]. For power systems, small magnitude changes and low frequency oscillations could occur. If this persists for long periods of time, this could lead to a loss of synchronization and possibly blackouts. This paper presents a power system stabilizer (PSS) based on a synergetic control approach. A T2 controller was designed that was found to suppress unwanted oscillations rapidly. The results indicated good performance and satisfactory dynamic behavior compared to the T1 controller.
IT2 FLCs have also been used to control numerous electronic components for industrial power systems. In a paper by Tripathy and Mishra, a power system was improved by utilizing a thyristor controlled series capacitor (TCSC) [77]. Often, industrial generators are controlled by a PSS to improve the damping of multi-machine power systems. Unfortunately, there is a frequency range from (0.2 Hz to 1.0 Hz), which is not sufficiently damped using a PSS alone. Using a TCSC can however improve the damping of the power system if the parameters are optimized. Due to the dynamic operation of the power system, the IT2 FLC was proposed. In these conditions the controller was tested and managed to handle the non-linearity of the power system better than a fixed-gain tuned controller. It was also found that since the TCSC worked in parallel with the PSS, it was also able to damp small perturbations within the whole system.
Power systems applications are a popular process to analyze IT2 FLCs. In a paper by Panda et al., an IT2 FLC was designed for a TCSC [78]. This controller was developed to improve the damping of power system oscillations. Simulations were done to compare the effectiveness of particle swarm optimization (PSO), T1 FL and T2 FL. It was determined that the T2 FLC was more effective than the PSO and T1 FL methods. The robustness was tested using different operating conditions, various disturbances and with different parameter variations.
Voltage regulation is also an issue, which can be improved using IT2 FLCs [79]. In this example, the controller was designed to regulate the voltage of a synchronous generator. The uncertainty stems from changing turbine outputs, loads and transmission line parameters. In order to maintain constant power, an exciter was connected to the generator. During the simulations, the IT2 FLC controller surpassed the performance of traditional PID controllers during the step response.
Load frequency control (LFC) applications were also investigated for electrical power systems during their design and operation [80]. The FLC was applied to a two-area interconnected reheat thermal power system. Typically for these applications, a PI controller is used exclusively. When they are tuned, the gain is fixed, which can negatively affect the performance when there is a wide range of operating conditions. In this study, it was found that the T2 FLC is able to guarantee robust stability and robust performance under a large range of uncertainties and loads.
In [81], a recent study presents a new feed water controller under the automatic power regulating system for an advanced boiling water reactor. This controller was designed using a rule-based hierarchical FLC algorithm and was implemented using an FGPA. It was proved that transient response and steady state tracking capabilities showed satisfactory results upon testing of two different trajectories in power and flow maps. It was also proven that FPGA-based hierarchical FLC is a practical and useful method in power operations in advanced nuclear power plant applications.
An IT2 FLC was also utilized to control an active magnetic levitation system [82]. In this levitation system, electromagnets are used to support any component attached within the magnetic field. Due to the non-linearity of levitation systems, it was proposed to use an IT2 FLC instead of a traditional PID controller. This idea was further implemented by reducing the IT2 FLC to a single input IT2 FLC. In this study, it was shown that a less computationally-intensive controller was developed with a better response and speed than both T2 and T1 FLCs.
IT2 FLCs have also been designed for controlling photovoltaic (PV) systems [83]. During the operation of a PV system, the voltage produced by the solar cells cannot be modeled as a constant DC voltage. PV systems are more comparable to a fluctuating current source, which changes according to the temperature, irradiation level, load current and other factors. Due to the nature of PV modules, they are modeled with a current-voltage (I-V) curve, which produces the most power at the maximum power point (MPP) on the curve. To do this, the PV system must be constantly monitored and changed to exploit the MPP. The IT2 FLC changes the duty cycle based on the rate of change of output power and the rate of change on the terminal voltage. Since the IT2 FLC is used, the uncertainty of MPP tracking is accounted for, and the simulation results showed that the MPP tracking was able to rapidly respond to uncertain atmospheric conditions.
Another IT2 FLC was designed for a single-phase grid interactive PV system [84]. In this paper, an MPP tracking boost converter and grid interactive voltage source inverter were used. For the system, the DC source is converted to AC and imported to the electrical grid. Simulations were done in MATLAB, and it was shown that the IT2 FLC had a fast transient response in tracking the MPP.
3.6. Aircraft Control
A T2 fuzzy cerebellar model articulation controller (CMAC) was designed for an automatic aircraft landing system [85]. Conventional automatic aircraft landing systems (ALS) are bounded by certain limits, such as wind shear and turbulence. If these are too high, the ALS cannot be used. It is therefore beneficial to introduce an ALS that can handle higher wind shear and turbulence in order to land the aircraft safely. In this paper, T1 and T2 fuzzy CMACs were added in parallel to the PID to control the pitch autopilot. It was found that the adaptive T2 CMAC was able to guide the aircraft under a turbulence strength of 165 feet per second. This was more robust than the PID-only controller, which can only handle 30 feet per second.
In aircraft control, an IT2 FLC was developed for hypersonic flight, which is defined as speeds faster than Mach 5 [86]. In this study, the generic hypersonic flight vehicle (GHFV) is proposed to cruise at a speed of approximately Mach 15 at an altitude of 33,000 m. This type of flight is highly non-linear, and it includes very large uncertainties. The controller tracks the altitude command signal and was able to maintain the velocity of the vehicle.
IT2 FLCs are also designed for a micro aircraft vehicle (MAV) [87]. This IT2 FLC approximated the function of the altitude angle of the MAV. It was able to account for the non-linearity and the uncertainty of the dynamic model. It used the Lyapunov stability theorem to track the error of the MAV altitude control system. It was found that results from the IT2 gain adaptive sliding mode controller were favorable compared to the T1 sliding mode controller and the conventional-based sliding mode controller.
The same authors created an IT2 FLC for quadrotor micro aircraft vehicles [88]. In this study, two IT2 FLCs and one PD controller were designed. They were designed to account for the system uncertainties, variations and external disturbances of the MAV. The IT2 FLCs were self-organizing (IT2 SO); one IT2 SO was made to learn the inverse model of the MAV, and the other was a secondary copy to account for model errors, uncertainties and disturbances. It was found using real-time experiments that the IT2 SO controllers outperformed the PD controller.
3.7. General Control Problems
IT2 FLCs were designed for other applications than robotics, communication, industrial automation, a few of which were mentioned above. For example, in [89], an IT2 FLC was designed to handle data with uncertainties for nonlinear multiple-input multiple-output (MIMO) systems. Simulations were performed, and it was shown that the IT2 FLC was able to handle unpredicted internal disturbances and data uncertainties very well. It was also shown that a T1 FLC was also capable of handling the errors; however, this controller has more control effort than the IT2 FLC.
In another work [90], an adaptive IT2 fuzzy sliding-based mode controller was designed for a chaotic system. This controller consisted of a fuzzy control design and a hitting control design. An IT2 FLC was designed to imitate the feedback linearization, whereas the hitting controller was designed to control the error between the feedback linearization and the IT2 FLC. From the simulations, it was concluded that the control system was robust while achieving good performance.
An inverted pendulum on a cart system was proposed as a model to be controlled using an IT2 PID system in [91]. This controller was designed using the simplified TR method, which was able to handle the effects of structure uncertainties. The results were compared to a similar controller that used the uncertainty bound method. Results showed improved performance using the TR method. In addition, the proposed controller outperformed a T1F-PID controller.
In [92], a new observer-based indirect adaptive IT2 FLC was developed for a mass-spring-damper system in a tracking application. In the modeling of this system, Coulomb friction, non-linear spring forces, non-linear friction forces and non-linear disturbances were considered. The controller outputs the external forces to control the system position. It was shown in the simulations that the IT2 FLC handles the unpredicted internal disturbance very well. The performance of the IT2 FLC showed better results compared to a T1 FLC. Moreover, the T1 FLC required more control effort.
In [93], an IT2 FS with actuator faults was used to design an IT2 state-feedback sampled data controller. This controller was constructed to guarantee stability and effective performance for possible actuator failures. The IT2 state-feedback sampled data controller was designed such that the closed-loop system is asymptotically stable for all actuator failures using the Lyapunov stability theory. It was then tested using the inverted pendulum model, which was found to be effective. It was found to be reliable because the controller is able to guarantee the asymptotic stability and H∞ performance if the actuator fails. Combining T2 FLC and neural networks can be used in developing controllers with learning capabilities while they handle uncertainties [94].
3.8. Membership Functions Used in T2 FLC Applications
After analyzing all of the papers presented in this section, we consider that is important to mention the types of membership functions that are used in the fuzzy models and what profits did they give. We can observe that in 15 percent of the papers, only triangular MFs are used. On the other hand, 33 percent of the papers make a combination of MFs; using triangular MFs on the center and trapezoidal MFs at the ends. In another case, 40 percent of the papers only use Gaussian MFs in the fuzzy controllers. In two percent of the papers, triangular MFs at the center and Gaussian MFs at the ends are used; also, another two percent uses the elliptic MFs. Finally, in eight percent of the papers, the type of MFs is unknown, as it is not indicated by the authors. In reviewing the developed controllers in the literature, we find that in many cases, triangular membership functions are used when there are software or hardware limitations, e.g., when the fuzzy controller needs to be implemented on a circuit, which is more easily done with triangular functions that do not require a lot of memory resources in hardware. In other cases, when possible, Gaussian functions are used because they provide more continuous performance, but require more memory (space) resources. In applications where the fuzzy controllers could be implemented in software and there is no problem with space and time limitations, Gaussian or combinations with other membership functions can be used.
4. Conclusions
This paper introduced a general overview of T2 FLCs. We briefly reviewed general T2 FLSs, as well as IT2 FLSs algorithms. Next, we presented a comprehensive literature survey of most updated real-world applications of T2 FLCs. The most applied areas of T2 FLCs are seen in robotic control, bandwidth control, industrial systems control, electrical control and aircraft control. The most promising applications are found in robotics and automotive, where improvements over traditional controllers have been achieved. It was shown that IT2 FLCs have many benefits over T1 FLCs, especially in uncertain systems, and in many cases, it was shown that IT2 FLCs outperformed traditional PID controllers, as well [95]. Moving forward, if the computational complexities of T2 FLCs can be compensated using enhanced algorithms or better software/hardware, then using these controllers for systems with uncertainty is promising. As technology develops, it is natural to witness increasing applications of these advanced controllers. It is believed that many other applications can be developed and discovered for generic and industrial applications.
Several algorithms are being developed in the hopes of improving the robustness, performance and speed of existing algorithms. Mostly these approaches seek to calculate the centroid endpoints of IT2 FSs, which is similar to the KM method. Some algorithms that have been discussed are the EKM, INT, CJ, DY, TTCCM, LYZ and HC methods. Some of these methods work better for different applications; however, as of now, there is no conclusive evidence that one is better than the other. It is expected that newer and more advanced techniques will continue to be developed and that improvements to existing algorithms will be discovered.
Other developments in the area of T2 FLCs are the optimization methods that are applied to these controllers. These methods are currently bio-inspired, which include GA, PSO and ACO [96]. There are also optimization methods that involve quantum computing, such as the Type-2 quantum fuzzy logic controller (T2QFLC) [97]. Similar to the T2 algorithms, there is no consensus as to which optimization method is best as of yet. Other optimization methods that have not been used yet are membrane computing, harmony computing and electro-magnetism-based computing.
T2 FLCs have also been increasingly combined with traditional PI, PD or PID controllers. These hybrid methods have shown more robust behavior [94]. It is however unknown whether these hybrid control methods will be implemented in industrial settings due to increased costs and computational time. To increase the speed to near real-time, FPGAs have been increasingly utilized. They are seen as an effective near real-time hardware method, which can tackle the computational time problem. Furthermore, faster FPGAs and improved software will continue to facilitate the implementation of IT2 FLCs for more applications in the future.
An important future direction for work in Type-2 fuzzy control is using general Type-2 fuzzy systems in real control applications, [98]. As shown in our illustrative example of Section 4, general Type-2 fuzzy controllers have the potential to outperform interval Type-2 and Type-1 fuzzy controllers; the only thing limiting right now the use of general Type-2 fuzzy controllers in real-world applications is the extra computational overhead required for processing general Type-2 fuzzy systems. We believe that theoretical advances in Type-2 fuzzy logic and in hardware technology will make the use of general Type-2 fuzzy controllers possible in real-world applications in the near future.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FLS | fuzzy logic systems |
| FLC | fuzzy logic controller |
| T2 | Type-2 |
| IT2 | Type-2 |
| T1 | Type-1 |
| KM | Karnik–Mendel |
| EKM | Enhanced Karnik–Mendel |
| WM | Wu–Mendel |
| BMM | Biglarbegian–Melek–Mendel |
| NT | Nie–Tan |
References
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Baaklini, N. Prescriptive method for deriving control policy in a fuzzy-logic controller. Electron. Lett. 1975, 11, 625–626. [Google Scholar] [CrossRef]
- Zamani, M.; Nejati, H.; Jahromi, A.T.; Partovi, A.R.; Nobari, S.H.; Shirazi, G.N. Toolbox for Interval Type-2 Fuzzy Logic Systems. In Proceedings of the Joint Conference on Information Sciences, Shenzhen, China, 15–20 December 2008.
- Liang, Q.; Mendel, J.M. Interval Type-2 Fuzzy Logic Systems: Theory and Design. IEEE Trans. Fuzzy Syst. 2000, 8, 535–550. [Google Scholar] [CrossRef]
- Hisdal, E. The IF THEN ELSE statement and interval-valued fuzzy sets of higher type. Int. J. Man-Mach. Stud. 1981, 15, 385–455. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.; Liu, F. Interval Type-2 Fuzzy logic Systems Made Simple. IEEE Trans. Fuzzy Syst. 2006, 14, 808–821. [Google Scholar] [CrossRef]
- Biglarbegian, M.; Melek, W.; Mendel, J.M. On the robustness of Type-1 and Interval Type-2 fuzzy logic systems in modeling. Inf. Sci. 2011, 181, 1325–1347. [Google Scholar] [CrossRef]
- Chopra, S.; Mitra, R.; Kumar, V. Fuzzy Controller: Choosing an Appropriate and Smallest Rule Set. Int. J. Comput. Cogn. 2005, 3, 73–79. [Google Scholar]
- Mendel, J.M. General Type-2 fuzzy logic systems made simple: A tutorial. IEEE Trans. Fuzzy Syst. 2014, 22, 1162–1182. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J.M.; Liang, Q. Type-2 Fuzzy Logic Systems. IEEE Trans. Fuzzy Syst. 1999, 7, 643–658. [Google Scholar] [CrossRef]
- Schrieber, M.D.; Biglarbegian, M. Hardware implementation and performance comparison of interval Type-2 fuzzy logic controllers for real-time applications. Appl. Soft Comput. 2015, 32, 175–188. [Google Scholar] [CrossRef]
- Torshizi, A.D.; Zarandi, M.H.F.; Zakeri, H. On type-reduction of Type-2 fuzzy sets: A review. Appl. Soft Comput. 2015, 27, 614–627. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J.M. Centroid of a Type-2 fuzzy set. Inf. Sci. 2001, 132, 195–220. [Google Scholar] [CrossRef]
- Mendel, J.M. Rule-Based Fuzzy Logic Systems: Introduction and New Directions; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Greenfield, S.; Chiclana, F. Accuracy and complexity evaluation of defuzzification strategies for the discretised interval Type-2 fuzzy set. Int. J. Approx. Reason. 2013, 54, 1013–1033. [Google Scholar] [CrossRef]
- Wu, D.; Nie, M. Comparison and Practical Implementation of Type-Reduction Algorithms for Type-2 Fuzzy Sets and Systems. In Proceedings of the IEEE International Conference on Fuzzy Systems, Taipei, Taiwan, 27–30 June 2011.
- Liu, F.; Mendel, J. Aggregation Using the Fuzzy Weighted Average as Computed by the Karnik-Mendel Algorithms. IEEE Trans. Fuzzy Syst. 2008, 16, 1–12. [Google Scholar]
- Dodurka, M.F.; Kumbasar, T.; Sakalli, A.; Yesil, E. Boundary Function based Karnik-Mendel type Reduction Method for Interval Type-2 Fuzzy PID Controllers. In Proceedings of the IEEE International Conference on Fuzzy Systems, Beijing, China, 6–11 July 2014.
- Wu, D.; Mendel, J.M. Enhanced Karnik-Mendel Algorithms. IEEE Trans. Fuzzy Syst. 2009, 17, 923–934. [Google Scholar]
- Melgarejo, M.A.; Duran, L.K. A Hardware Architecture Proposal for the Enhanced Karnik Mendel Algorithm Based on Sequential Arithmetic Operators. In Proceedings of the IEEE International Conference on Fuzzy Systems, Barcelona, Spain, 18–23 July 2010.
- Mendel, J.M. Type-2 Fuzzy Sets and Systems: An Overview. IEEE Comput. Intell. 2007, 2, 20–29. [Google Scholar] [CrossRef]
- Wu, H.; Mendel, J.M. Uncertainity bounds and their use in the design of interval Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 2002, 10, 622–639. [Google Scholar]
- Biglarbegian, M.; Melek, W.; Mendel, J.M. On the Stability of Interval Type-2 TSK Fuzzy Logic Control Systems. IEEE Trans. Syst. Man Cybern. 2010, 40, 798–818. [Google Scholar] [CrossRef] [PubMed]
- Biglarbegian, M. On the design of robust intelligent controllers with application to mobile robot tracking. In Proceedings of the American Control Conference, Montreal, QC, Canada, 27–29 June 2012.
- Nie, M.; Tan, W.W. Toward an efficient type-reduction method for interval Type-2 fuzzy logic systems. In Proceedings of the IEEE International Conference on Fuzzy Systems, Hong Kong, China, 1–6 June 2008.
- Mendel, J.M.; Liu, X. Simplified Interval Type-2 Fuzzy Logic Systems. IEEE Trans. Fuzzy Syst. 2013, 21, 1056–1069. [Google Scholar] [CrossRef]
- Coupland, S.; John, R. Geometric Type-1 and Type-2 Fuzzy Logic Systems. IEEE Trans. Fuzzy Syst. 2007, 15, 3–15. [Google Scholar] [CrossRef]
- Wu, D. Approaches for Reducing the Computational Cost of Interval Type-2 Fuzzy Logic Systems: Overview and Comparisons. IEEE Trans. Fuzzy Syst. 2013, 21, 80–99. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S. Effects of type reduction algorithms on forecasting accuracy of IT2FLS models. Appl. Soft Comput. 2014, 17, 32–38. [Google Scholar] [CrossRef]
- Greenfield, S.; Chiclana, F.; Coupland, S.; John, R. The collapsing method of defuzzification for discretised interval Type-2 fuzzy sets. Inf. Sci. 2009, 179, 2055–2069. [Google Scholar] [CrossRef]
- Du, X.; Ying, H. Derivation and Analysis of the Analytical Structures of the Interval Type-2 Fuzzy-PI and PD Controllers. IEEE Trans. Fuzzy Syst. 2010, 18, 802–814. [Google Scholar]
- Tao, C.W.; Taur, J.S.; Chang, C.-W.; Chang, Y.-H. Simplified Type-2 fuzzy sliding controller for wing rock system. Fuzzy Sets Syst. 2012, 207, 111–129. [Google Scholar] [CrossRef]
- Li, C.; Yi, J.; Zhao, D. A Novel Type-Reduction Method for Interval Type-2 Fuzzy Logic Systems. In Proceedings of the Fifth International Conference on Fuzzy Systems and Knowledge Discovery, Jinan, China, 18–20 October 2008.
- Torshizi, A.D.; Zarandi, M.H.F. Hierarchical collapsing method for direct defuzzification of general Type-2 fuzzy sets. Inf. Sci. 2014, 277, 842–861. [Google Scholar] [CrossRef]
- Melgarejo, M. A Fast Recursive Method to Compute the Generalized Centroid of an Interval Type-2 Fuzzy Set. In Proceedings of the Annual Meeting of the North American Fuzzy Information Processing Society, San Diego, CA, USA, 24–27 June 2007.
- Hassan, S.; Khanesar, M.A.; Kayacan, E.; Jaafar, J.; Khosravi, A. Optimal design of adaptive Type-2 neuro-fuzzy systems: A review. Appl. Soft Comput. 2016, 44, 134–143. [Google Scholar] [CrossRef]
- Hagras, H.A. A Hierarchical Type-2 Fuzzy Logic Control Architecture for Autonomous Mobile Robots. IEEE Trans. Fuzzy Syst. 2004, 12, 524–539. [Google Scholar] [CrossRef]
- Biglarbegian, M.; Melek, W.; Mendel, J.M. Design of Novel Interval Type-2 Fuzzy Controllers for Modular and Reconfigurable Robots: Theory and Experiments. IEEE Trans. Ind. Electron. 2011, 58, 1371–1384. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Wang, Y. A Type-2 Fuzzy Switching Control System for Biped Robots. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2007, 37, 1202–1213. [Google Scholar] [CrossRef]
- Juang, C.-F.; Hsu, C.-H. Reinforcement Ant Optimized Fuzzy Controller for Mobile-Robot Wall-Following Control. IEEE Trans. Ind. Electron. 2009, 56, 3931–3940. [Google Scholar] [CrossRef]
- Kumbasar, T.; Hagras, H. Big Bang—Big Crunch optimization based interval Type-2 fuzzy PID cascade controller design strategy. Inf. Sci. 2014, 282, 277–295. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Kayacan, E. Feedback error learning control of magnetic satellites using Type-2 fuzzy neural networks with elliptic membership functions. IEEE Trans. Cybern. 2015, 45, 858–868. [Google Scholar] [CrossRef] [PubMed]
- Chaoui, H.; Gueaieb, W. Type-2 Fuzzy Logic Control of a Flexible-Joint Manipulator. J. Intell. Robot. Syst. 2008, 51, 159–186. [Google Scholar] [CrossRef]
- Chen, C.-S. Supervisory adaptive tracking control of robot manipulators using interval Type-2 TSK fuzzy logic system. IET Control Theory Appl. 2011, 5, 1796–1807. [Google Scholar] [CrossRef]
- Allawi, Z.T.; Abdalla, T.Y. A PSO-Optimized Type-2 Fuzzy Logic Controller for Navigation of Multiple Mobile Robots. In Proceedings of the IEEE International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 2–5 September 2014.
- Selvi, V.; Umarani, R. Comparative Analysis of Ant Colony and Particle Swarm Optimization Techniques. Int. J. Comput. Appl. 2010, 5, 1–6. [Google Scholar] [CrossRef]
- Astudillo, L.; Castillo, O.; Melin, P.; Alanis, A.; Soria, J.; Aguilar, L.T. Intelligent Control of an Autonomous Mobile Robot using Type-2 Fuzzy Logic. Eng. Lett. 2006, 13, 88–93. [Google Scholar]
- Valdez, F.; Melin, P.; Castillo, O. Fuzzy Control of Parameters to Dynamically Adapt the PSO and GA Algorithms. In Proceedings of the IEEE International Conference on Fuzzy Systems, Barcelona, Spain, 18–23 July 2010.
- Martinez, R.; Rodriguez, A.; Castillo, O.; Aguilar, L.T. Type-2 Fuzzy Logic Controllers Optimization using Genetic Algorithms and Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Granular Computing, San Jose, CA, USA, 14–16 August 2010.
- Martinez-Soto, R.; Castillo, O.; Aguilar, L.T. Type-1 and Type-2 fuzzy logic controller design using a Hybrid PSO-GA optimization method. Inf. Sci. 2014, 285, 35–49. [Google Scholar] [CrossRef]
- Castillo, O.; Neyoy, H.; Soria, J.; Melin, P.; Valdez, F. A new approach for dynamic fuzzy logic parameter tuning in Ant Colony Optimization and its application in fuzzy control of mobile robot. Appl. Soft Comput. 2015, 28, 150–159. [Google Scholar] [CrossRef]
- Mohammadi, S.M.; Gharaveisi, A.A.; Machinchi, M. An Evolutionary Tuning Technique for Type-2 Fuzzy Logic Controller in a Non-linear System Under Uncertainty. In Proceedings of the Electrical Engineering (ICEE), Isfahan, Iran, 11–13 May 2010.
- Cortes-Rios, J.C.; Gomez-Ramirez, E.; Ortiz-de-la-Vega, H.A.; Castillo, O.; Melin, P. Optimal design of interval type 2 fuzzy controllers based on a simple tuning algorithm. Appl. Soft Comput. 2014, 23, 270–285. [Google Scholar] [CrossRef]
- Mohammadi, S.M.; Gharaveisi, A.; Mashinchi, M.; Vaezi-Nejad, S. Development of a novel reinforcement learning automata method for optimum design of proportional integral deviation controller for nonlinear systems. In Proceedings of the World Congress On Engineering, London, UK, 2–4 July 2008.
- Hassan, M.Y.; Kothapalli, G. Interval Type-2 fuzzy position control of electro-hydraulic actuated robotic excavator. Int. J. Min. Sci. Technol. 2012, 22, 437–445. [Google Scholar] [CrossRef]
- Linda, O.; Manic, M. Uncertainty-Robust Design of Interval Type-2 Fuzzy Logic Controller for Delta Parallel Robot. IEEE Trans. Ind. Inf. 2011, 7, 661–670. [Google Scholar] [CrossRef]
- Ganjefar, S.; Solgi, Y. A Lyapunov stable Type-2 fuzzy wavelet network controller design for a bilateral teleoperation system. Inf. Sci. 2015, 311, 1–17. [Google Scholar] [CrossRef]
- Jammeh, E.A.; Fleury, M.; Wagner, C.; Hagras, H.; Ghanbari, M. Interval Type-2 Fuzzy Logic Congestion Control for Video Streaming Across IP Networks. IEEE Trans. Fuzzy Syst. 2009, 17, 1123–1149. [Google Scholar] [CrossRef]
- Jammeh, E.; Mkwawa, I.; Sun, L.; Ifeachor, E. Type-2 fuzzy logic control of PQoS driven adaptive VoIP scheme. Electron. Lett. 2010, 46, 137–138. [Google Scholar] [CrossRef]
- Jammeh, E.A.; Fleury, M.; Ghanbari, M. Fuzzy logic congestion control for broadband wireless IPTV. Electron. Lett. 2008, 44, 1365–1366. [Google Scholar] [CrossRef]
- Kabranov, O.; Yang, T.; Makrakis, D. Fuzzy Control pf Pricing for Bandwidth Demand in Obtainable Forwarding Service for Differentiated Services Architecture. In Proceedings of the IEEE Global Telecommunications Conference, Taipei, Taiwan, 17–21 November 2002.
- Own, C.-M. Predictable Type-2 fuzzy mobile units for energy balancing in wireless sensor networks. Inf. Sci. 2013, 241, 70–84. [Google Scholar] [CrossRef]
- Méndez, G.M.; Leduc-Lezama, L.; Colás, R.; Murillo-Perez, G.; Ramirez-Cuellar, J.; López, J.J. Modelling and control of coiling entry temperature using interval Type-2 fuzzy logic systems. Ironmak. Steelmak. 2010, 37, 126–134. [Google Scholar] [CrossRef]
- Méndez, G.M.; Castillo, O.; Colás, R.; Moreno, H. Finishing mill strip gage setup and control by internal Type-1 non-singleton Type-2 fuzzy logic systems. Appl. Soft Comput. 2014, 24, 900–911. [Google Scholar] [CrossRef]
- Lin, F.-J.; Shieh, P.-H.; Hung, Y.-C. An intelligent control for linear ultrasonic motor using interval Type-2 fuzzy neural network. IET Electr. Power Appl. 2008, 2, 32–41. [Google Scholar] [CrossRef]
- Barkat, S.; Tlemçani, A.; Nouri, H. Noninteracting Adaptive Control of PMSM Using Interval Type-2 Fuzzy Logic Systems. IEEE Trans. Fuzzy Syst. 2011, 19, 925–936. [Google Scholar] [CrossRef]
- Chen, C.-S.; Lin, W.-C. Self-adaptive interval Type-2 neural fuzzy network control for PMLSM drives. Expert Syst. Appl. 2011, 38, 14679–14689. [Google Scholar] [CrossRef]
- Naik, N.V.; Singh, S.P. Improved Torque and Flux Performance of Type-2 Fuzzy-based Direct Torque Control Induction Motor Using Space Vector Pulse-width Modulation. Electr. Power Compon. Syst. 2014, 42, 658–669. [Google Scholar] [CrossRef]
- Ramesh, T.; Panda, A.K.; Kumar, S.S. Type-1 and Type-2 Fuzzy Logic and Sliding-Mode Based Speed Control of Direct Torque and Flux Control Induction Motor Drives—A Comparative Study. Int. J. Emerg. Electr. Power Syst. 2013, 14, 385–400. [Google Scholar] [CrossRef]
- Yu, W.-S.; Chen, H.-S. Interval Type-2 fuzzy adaptive tracking control design for PMDC motor with the sector dead-zones. Inf. Sci. 2014, 288, 108–134. [Google Scholar] [CrossRef]
- Maldonado, Y.; Castillo, O. Genetic Design of an Interval Type-2 Fuzzy Controller for Velocity Regulation in a DC motor. Int. J. Adv. Robot. Syst. 2012, 9. [Google Scholar] [CrossRef]
- Maldonado, Y.; Castillo, O.; Melin, P. A multi-objective optimization of Type-2 fuzzy control speed in FPGAs. Appl. Soft Comput. 2014, 24, 1164–1174. [Google Scholar] [CrossRef]
- Wang, T.; Tong, S. Direct inverse control of cable-driven parallel system based on Type-2 fuzzy systems. Inf. Sci. 2015, 310, 1–15. [Google Scholar] [CrossRef]
- Martínez, J.S.; John, R.I.; Hissel, D.; Péra, M.-C. A survey-based Type-2 fuzzy logic system for energy management in hybrid electrical vehicles. Inf. Sci. 2012, 190, 192–207. [Google Scholar] [CrossRef]
- Martínez, J.S.; Mulot, J.; Harel, F.; Hissel, D.; Péra, M.-C.; John, R.I.; Amiet, M. Experimental validation of a Type-2 fuzzy logic controller for energy management in hybrid electrical vehicles. Eng. Appl. Artif. Intell. 2013, 26, 1772–1779. [Google Scholar] [CrossRef]
- Nechadi, E.; Harmas, M.N.; Hamzaoui, A.; Essounbouli, N. Type-2 fuzzy based adaptive synergetic power system control. Electr. Power Syst. Res. 2012, 88, 9–15. [Google Scholar] [CrossRef]
- Tripathy, M.; Mishra, S. Interval Type-2-based thyristor controlled series capacitor to improve power system stability. IET Gener. Transm. Distrib. 2011, 5, 209–222. [Google Scholar] [CrossRef]
- Panda, M.K.; Pillai, G.; Kumar, V. An interval Type-2 fuzzy logic controller for TCSC to improve the damping of power system oscillations. Front. Energy 2013, 7, 307–316. [Google Scholar] [CrossRef]
- Panda, M.K.; Pillai, G.N.; Kumar, V. Design of an Interval Type-2 Fuzzy Logic Controller for Automatic Voltage Regulator System. Electr. Power Compon. Syst. 2012, 40, 219–235. [Google Scholar] [CrossRef]
- Sudha, K.R.; Santhi, R.V. Robust decentralized load frequency control of interconnected power system with Generation Rate Constraint using Type-2 fuzzy approach. Int. J. Electr. Power Energy Syst. 2011, 33, 699–707. [Google Scholar] [CrossRef]
- Lu, J.-J.; Huang, H.-H.; Chou, H.-P. Evaluation of an FPGA-based fuzzy logic control of feed-water for ABWR under automatic power regulating. Prog. Nucl. Energy 2015, 79, 22–31. [Google Scholar] [CrossRef]
- Kumar, M.; Panda, M.K.; Kundu, S.; Kumar, V. Designing of an Interval Type-2 Fuzzy Logic Controller for Magnetic Levitation System with Reduced Rule base. In Proceedings of the Computing Communication & Networking Technologies (ICCCNT), Coimbatore, India, 26–28 July 2012.
- Altin, N. Interval Type-2 Fuzzy Logic Controller Based Maximum Power Point Tracking in Photovoltaic Systems. Adv. Electr. Comput. Eng. 2013, 13, 65–70. [Google Scholar] [CrossRef]
- Altin, N. Single Phase Grid Interactive PV System With MPPT Capability Based on Type-2 Fuzzy Logic Systems. In Proceedings of the International Conference on Renewable Energy Research and Applications, Nagasaki, Japan, 11–14 November 2012.
- Yang, T.-C.; Juang, J.-G. Application of Adaptive Type-2 Fuzzy CMAC to Automatic Landing System. In Proceedings of the International Symposium on Computational Intelligence and Design, Hangzhou, China, 29–31 October 2010.
- Yang, F.; Yuan, R.; Yi, J.; Fan, G.; Tan, X. Direct adaptive Type-2 fuzzy neural network control for a generic hypersonic flight vehicle. Soft Comput. 2013, 17, 2053–2064. [Google Scholar] [CrossRef]
- Chen, X.; Li, D.; Xu, Z.; Bai, Y. Gain adaptive sliding mode controller based on interval type-II fuzzy neural network designed for attitude control for micro aircraft vehicle. Int. J. Intell. Comput. Cybern. 2008, 7, 209–226. [Google Scholar] [CrossRef]
- Chen, X.; Li, D.; Xu, Z.; Bai, Y. Robust control of quadrotor MAV using self-organizing interval type-II fuzzy neural networks (SOIT-IIFNNs) controller. Int. J. Intell. Comput. Cybern. 2011, 4, 397–412. [Google Scholar] [CrossRef]
- Lin, T.-C.; Liu, H.-L.; Kuo, M.-J. Direct adaptive interval Type-2 fuzzy control of multivariable nonlinear systems. Eng. Appl. Artif. Intell. 2009, 22, 420–430. [Google Scholar] [CrossRef]
- Hwang, J.-H.; Kwak, H.-J.; Park, G.-T. Adaptive interval Type-2 fuzzy sliding mode control for unknown chaotic system. Nonlinear Dyn. 2011, 63, 491–502. [Google Scholar] [CrossRef]
- El-Bardini, M.; El-Nagar, A.M. Interval Type-2 fuzzy PID controller for uncertain nonlinear inverted pendulum system. ISA Trans. 2014, 53, 732–743. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.-C. Observer-based robust adaptive interval Type-2 fuzzy tracking control of multivariable nonlinear systems. Eng. Appl. Artif. Intell. 2010, 23, 386–399. [Google Scholar] [CrossRef]
- Li, H.; Sun, X.; Shi, P.; Lam, H.-K. Control design of interval Type-2 fuzzy systems with actuator fault: Sampled-data control approach. Inf. Sci. 2015, 302, 1–13. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Kayacam, E. Fuzzy Neural Networks for Real Time Control Applications: Concepts, Modeling and Algorithms for Fast Learning; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Wu, D. Interval Type-2 Fuzzy PI Controllers: Why They are More Robust. In Proceedings of the International Conference on Granular Computing, Silicon Valley, CA, USA, 14–16 August 2010.
- Castillo, O.; Melin, P. A review on interval Type-2 fuzzy logic applications in intelligent control. Inf. Sci. 2014, 279, 615–631. [Google Scholar] [CrossRef]
- Shill, P.C.; Amin, M.F.; Akhand, M.A.H.; Murase, K. Optimization of Interval Type-2 Fuzzy Logic Controller Using Quantum Genetic Algorithms. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Brisbane, Australia, 10–15 June 2012.
- Wagner, C.; Hagras, H. zSlices based General Type-2 FLC for the Control of Autonomous Mobile Robots in Real World Environments. In Proceedings of the IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, 20–24 August 2009.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).