Abstract
Inter-cell interference (ICI) is the main factor affecting system capacity and spectral efficiency. Effective spectrum resource management is an important and challenging issue for the design of wireless communication systems. The soft frequency reuse (SFR) is regarded as an interesting approach to significantly eliminate ICI. However, the allocation of resource is fixed prior to system deployment in static SFR. To overcome this drawback, this paper adopts a distributed method and proposes an improved dynamic joint resource allocation algorithm (DJRA). The improved scheme adaptively adjusts resource allocation based on the real-time user distribution. DJRA first detects the edge-user distribution vector to determine the optimal scheme, which guarantees that all the users have available resources and the number of iterations is reduced. Then, the DJRA maximizes the throughput for each cell via optimizing resource and power allocation. Due to further eliminate interference, the sector partition method is used in the center region and in view of fairness among users, the novel approach adds the proportional fair algorithm at the end of DJRA. Simulation results show that the proposed algorithm outperforms previous approaches for improving the system capacity and cell edge user performance.
1. Introduction
With the rapid increasing data rate requirements of mobile users on multimedia applications, the design of spectrum resource allocation methods with high system throughput and spectral efficiency [1] has become one of the hot issues in LTE [2] and LTE-A [3]. In the multi-cell resource allocation environment, ICI is a major problem affecting system throughput, especially for the cell edge users. Fractional frequency reuse (FFR) and soft frequency reuse (SFR) are two common deployments to improve spectral efficiency and reduce ICI. However, FFR eliminates frequency collisions at the cost of spectrum efficiency. The reason for this lies in interior users being forbidden to share the spectrum with cell-edge users in FFR. Soft frequency reuse (SFR) emerged as an alternative resource planning scheme to effectively mitigate ICI in cellular systems. SFR offers cell-center users access to spectrum with a frequency reuse factor equal to one, and cell-edge users with a frequency reuse factor which is greater than one. Reference [4] has proved that SFR outperforms FFR in spectrum efficiency. The original frequency reuse schemes are static frequency reuse. References [5] and [6] described static FFR and SFR, respectively. Although the so-called static frequency reuse scheme demands relatively lower complexity and overhead, it fixes the allocation of power and subcarriers in each cell beforehand, which greatly limits the communication performance. To overcome this drawback, dynamic resource assignment has arisen. The authors of [7,8,9,10] introduced several dynamic FFR schemes. Dynamic SFR approaches were illustrated in [11,12,13,14]. However, there are no works about joint resource allocation for the SFR, except for the method proposed by Qian in [15,16], where [16] is the improvement of [15]. In this paper, we put forward an improved dynamic joint resource allocation algorithm based on SFR, referred to as DJRA. The new algorithm aims at solving several problems in [16]. Qian firstly utilizes joint resource allocation in SFR and proposes an adaptive soft frequency reuse scheme (ASFR). Nevertheless, ASFR can not guarantee that all the users have available resources. Accordingly, we propose two methods to solve this problem. Firstly, DJRA monitors edge-user distribution in the system before using an exhaustive search, which not only guarantees all the users have available resources but also reduces the number of iterations. Secondly, we take the multi-cell resource allocation fairness principle into account by utilizing the proportional fair algorithm (PF). To further mitigate interference, this paper presents the sector partition method in a cell-center.
DJRA obtains the optimal single cell resource allocation scheme by dynamically adjusting resource block (RB) and power allocation according to the real-time distribution of users per cell, and then uses an iteration method to acquire the optimum resource allocation scheme. Compared with previous schemes, it is worth pointing out that the improved dynamic joint resource allocation scheme reduces the influence of ICI, acquires a better cell edge user performance, and guarantees all the users have available resources.
The rest of this paper is structured as follows. Section 2 introduces the system model. The method of dynamic joint resource allocation algorithm based on SFR is described in detail in Section 3. Section 4 provides the results of simulation analysis. Finally, conclusing remarks are presented in Section 5.
2. System Model and Problem Formulation
2.1. System Model
We consider an OFDM-based LTE downlink network where the number of multi-cells is C. Figure 1 illustrates the SFR deployment. Each cell has the same number of users and uniform user distribution is assumed in the whole coverage area. Each cell is divided into two regions, the colored areas are the edge region and the colorless area is the center region. We define a user with the worst channel gain as a virtual user. As seen from the Figure 1, virtual center user and virtual edge user are the users located in their corresponding border area.
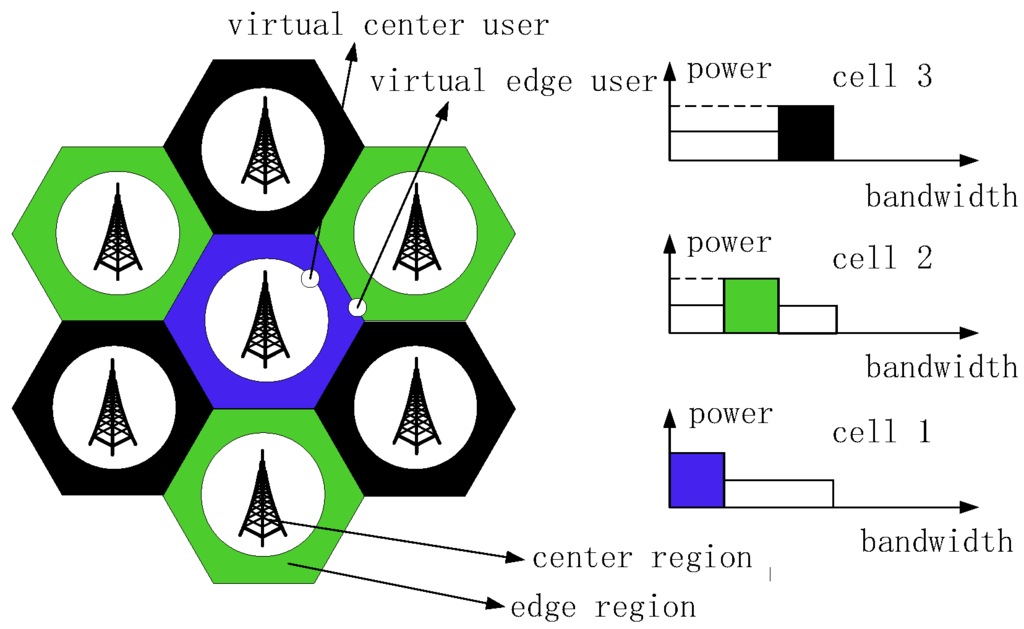
Figure 1.
System networking.
In our system model, denotes the maximum transmission power of the base station (BS). The cell-interior radius and the cell radius are r and R, respectively. The received noise power is . B is the total system bandwidth, which is divided into N blocks, and each RB occupies a bandwidth of . In SFR, RBs are grouped to cell-edge blocks with a bandwidth of and cell-center block with a bandwidth of , where . Other symbols are defined in Table 1.

Table 1.
Symbols definition.
In cellular networks, the signal power received gets weaker with the increasing of the propagation distance. For the convenience of discussion, we only consider the signals tha come from three BSs in terms of 802.16e standard, including a serving BS and two interfering BSs. For a user in cell i, the signal-to-interference-noise ratio on RB j is given as
where is the set of interfering cells which are adjacent to cell i. If j is the edge-block, j is equal to o. If j is the center-block, j is equal to .
In the SFR system, the edge-user interference on RB j comes from the signals on RB j used by center-users in adjacent cells. Thus, we submit Equation (1) into the Shannon capacity formula [17]. The data rate of the edge-user situated in cell i is expressed as [16]
The center-user interference on RB j has two sources: signals reusing the same resource by adjacent cell edge-user or adjacent cell center-user. For simplifying notation, the adjacent cell interference power is unified into the transmit power of cell-edge RBs, i.e., . Therefore, the date rate of center-user in cell i can be approximately given as:
We already know if the data rate requirement of the virtual edge user in each cell is met; the data rate of all users in the same cell can therefore be satisfied. Thus, we take the minimum throughput demands for the virtual users as the minimum throughput requirements for the individual users situated in that cell zone. Thus, the minimum data rate for the edge and center zone in the target cell i is
Let k be the number of users in cell i, and be the set of cell edge users and inter users, respectively. denotes the minimum throughput requirement for the user k.
2.2. Problem Formulation
The major contribution of the adaptive soft frequency reuse scheme is to allocate RBs and transmit powers dynamically, which can not only maximize the system capacity but also guarantee the minimum data rate requirement for each cell zone. Equation (6) is the objective function.
where
In the above formulas, Constraints (7) and (8) denote the cell-interior and cell-edge users need to satisfy their lowest data rate requirements; Constraint (9) ensures that the total power used in each cell can not exceed the maximum power provided by each base station. Constraint (10) states that all RBs can be used in each cell. Constraint (11) indicates that the RBs in any three neighboring cells are non-overlapped, and is the set of three adjacent cells. The total power for cell i is calculated as
3. Proposed Algorithm
3.1. An Improved Dynamic Joint Resource Allocation Algorithm Based on SFR
In this section, we put forward a novel scheme, referred to as the dynamic joint resource allocation algorithm. We aim to find a DJRA solution that maximizes the system data rate and meets the data rate requirements for cell center users and cell edge users at the same time. As objective function (6) is an NP-hard problem and difficult to solve [18]. In this paper, we decompose the multi-cell resource allocation optimization into several single-cell optimization problems. The proposed method is first to find a single cell solution and then extend the solution to optimize multi-cell wireless network performance.
We first propose the single-cell resource allocation solution. For a single cell, we aim to find a RB-power allocation scheme which satisfies the condition that the required transmission power at each BS is lower than the maximum power. The single cell optimization problem is described as follows
where i is the target cell, W denotes the set of DJRA schemes and is one of the DJRA plan. denotes the required transmission power at each BS in cell i when adopting the scheme. Equations (14) to (17) illustrates the constraint conditions.
where and denotes the target data rate for edge user and center user respectively. The condition for equality is that the transmit power is the lowest power in Constraints (14) and (15). Once is determined, we have , ,
where and denotes the power allocated to center RBs and edge RBs in cell m. As and are both integers, there exist () different combinations of RB-power in theory. Before applying the traversing method, DJRA detects edge-user distribution vector . For the sake of guaranteeing that each user has its frequency resource that can be used, there are only combinations of FP (frequency block, power allocation) pairs. Then DJRA selects all the FP pairs that yield the throughput requirements as expressed in Constraints (14) and (15), and submits these FP pairs into Equation (12) to get the power set W.
Once the power set is set up by above steps, we obtain the total power for each allocation plan. Subsequently, we compute in the target cell. The residual power is equally allocated to each edge of RB to enhance the performance of edge users.
In the forth step, DJRA finds the maximum and set and as the new target data rates to recalculate FP pairs, until the cell capacity does not change any more. The single-cell allocation (Algorithm 1) is shown below.
| Algorithm 1. Single-cell Resource Allocation Solution of DJRA |
|
Next, we extend the single-cell solution to find the global joint resource allocation scheme for multi-cell scenarios by using the method illustrated in [16]. After resource allocation is achieved for each cell, DJRA takes the resource allocation in cell i as inputs to its adjacent cells and calculates the multi-cell data rate . It repeats the above steps until the multi-cell data rate does not change any more. Then the algorithm stops iterating and we get the optimal solution.
Finally, DJRA applies the sector partition method in the cell-center to further mitigate interference, and the proportional fair algorithm to guarantee that each user has available resources. Figure 2 shows the sector division in the center region. Each center zone is divided into three sub-regions: A, B and C. Different colors present different resource-using regions. As seen from the figure, increasing the pass loss of interfering signals can eliminate ICI, and thereby improve system performance.
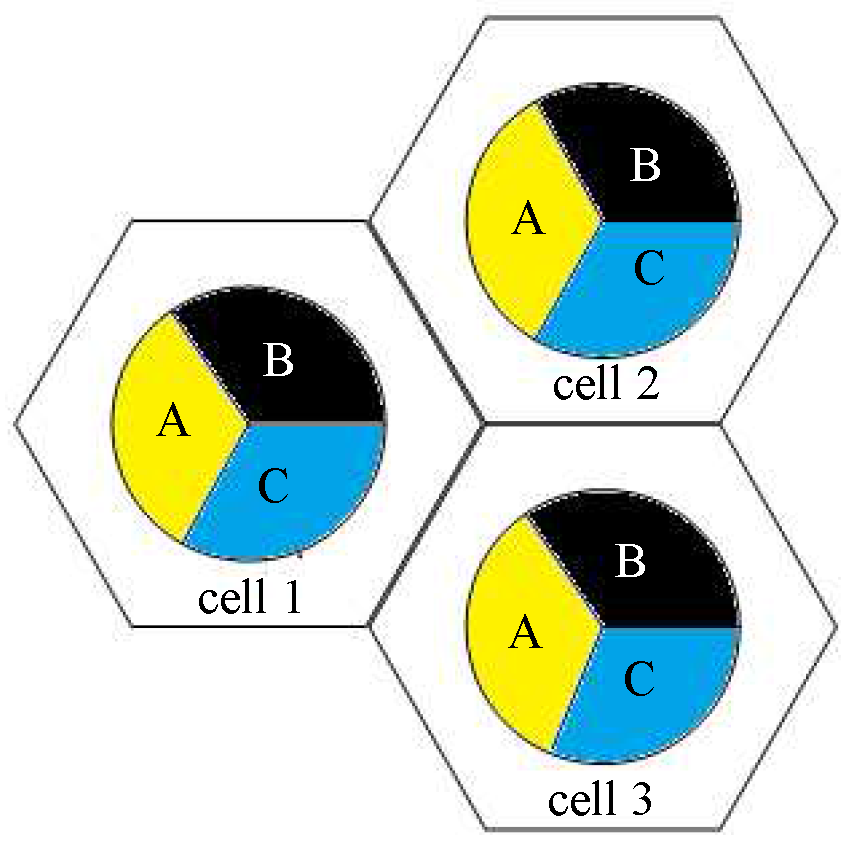
Figure 2.
Interior sector partition.
3.2. Complexity Analysis
Firstly, we analyze the computational complexity of resource allocation for a single cell. Since there are different combinations for (,), DJRA needs traverse to obtain the power set in Step 1. Similarly, Step 2 takes at most operations to assign the remaining powers to edge users. Therefore, the single cell resource allocation process will take operations in one cell per iteration. Step 3 only requires one process, so the complexity for Step 3 is of the order of . So far, we completed the complexity analysis in a single cell.
We define τ as the number of iteration and the computational complexity of interior sector partition is of the order of . Based on the above analysis, the multi-cell computational complexity of DJRA is
In the traditional static resource allocation algorithms, the major/minor subcarrier and power allocations per cell are set prior to network deployment. Therefore, the computational cost for these algorithms is of the order of .
4. Simulation
In this section, we investigate the performance of proposed JPFA algorithm, static FFR, static FFR, and traditional dynamic joint resource allocation algorithm (ASFR) [16]. We consider a 19-cell downlink cellular network where service area consists of all 19 cells, the interior radius and the cell radius is equal to 600 and 750, respectively, each cell owns 50 RBs. There are 20 users in each cell and the lowest throughput requirement is 0.8 Mbps rate per user. A detailed description of simulation parameters is shown in Table 2.

Table 2.
Main simulation parameters.
In static FFR, we divided 50 physical RBs into two groups, Group 1 contains 30 which are shared by edge users with a cell-edge reuse factor of 3, and Group 2 is for the center region with a reuse factor of 1. The transmit power of each RBs is the same. In static SFR, 48 physical RBs are shared by edge users with a reuse factor of 3 and the power ratio factor is 0.5.
Figure 3 shows the user distribution in 19 cells under one simulation. Figure 4 compares the cell-edge RBs distribution of proposed DJRA with the aforementioned static SFR (SSFR) in one Monte Carlo simulation. As seen from Figure 4, a total of 16 sub-resources are available to edge users in SSFR. However, as the users are randomly distributed in each scenario, the resource allocation predetermined scheme can not obtain the best system performance. Compared with the static resource allocation, our dynamic joint resource allocation approach breaks the original fixed patterns via dynamically adjusting the resource allocation ratio of the central and edge regions as the user distribution changes. Each cell has its own resource configuration mode. Though the number of cell-edge RBs changes, the sum of RBs in the three adjacent cells is less than total RBs. In other words, variations in the cell-edge RBs will not influence the orthogonality of the edge zones in the three adjacent cells.
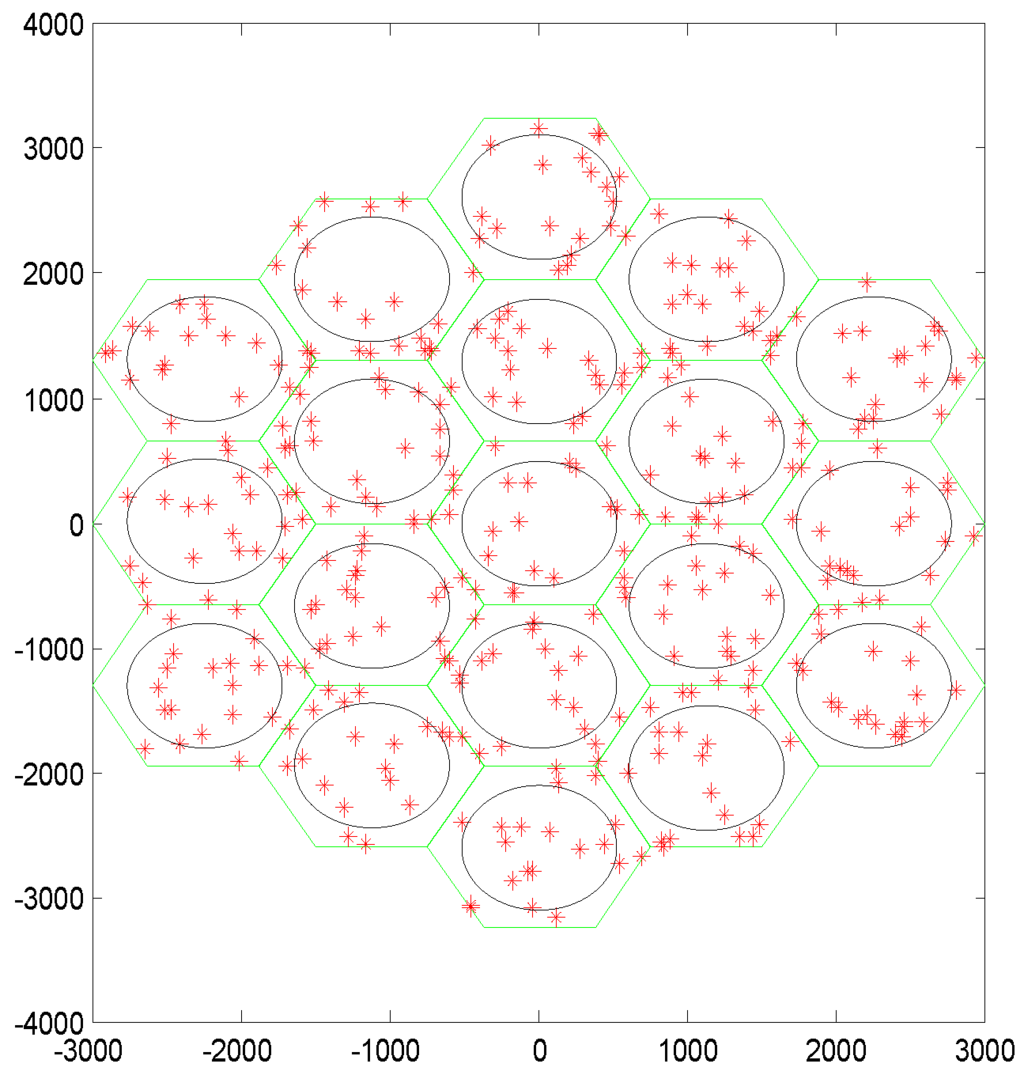
Figure 3.
User distribution in 19 cells.
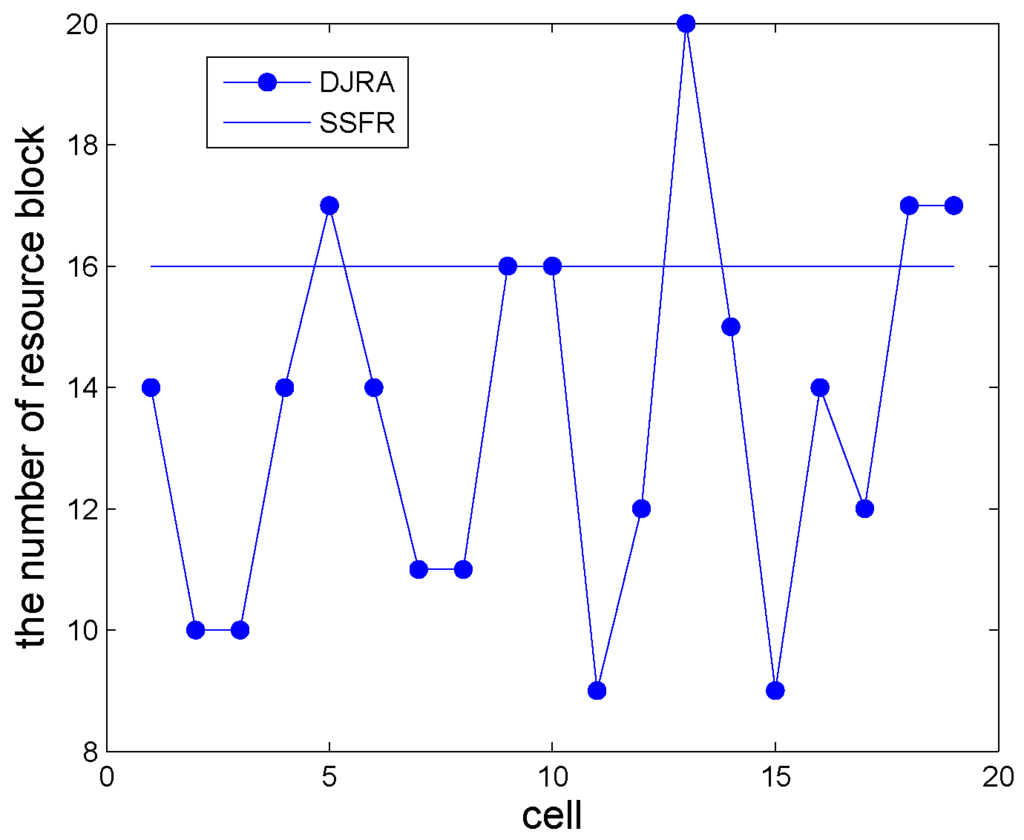
Figure 4.
Cell-edge resource blocks (RBs) distribution of dynamic joint resource allocation algorithm (DJRA) and static soft frequency reuse (SFR).
In Figure 5, we plot the cumulative distribution function (CDF) to show data rate achieved by each user. As seen from the figure, the performance of SFFR is the worst. This is because SFFR sacrifices the spectrum efficiency to suppress ICI. Despite SSFR being superior to SFFR, the fixed resource allocation pattern still limits its performance improvement. ASFR and our scheme achieve a superior rate. As expected, the best results are provided by our scheme and there are significant improvement benefits from adopting the sector partition method in the center region.
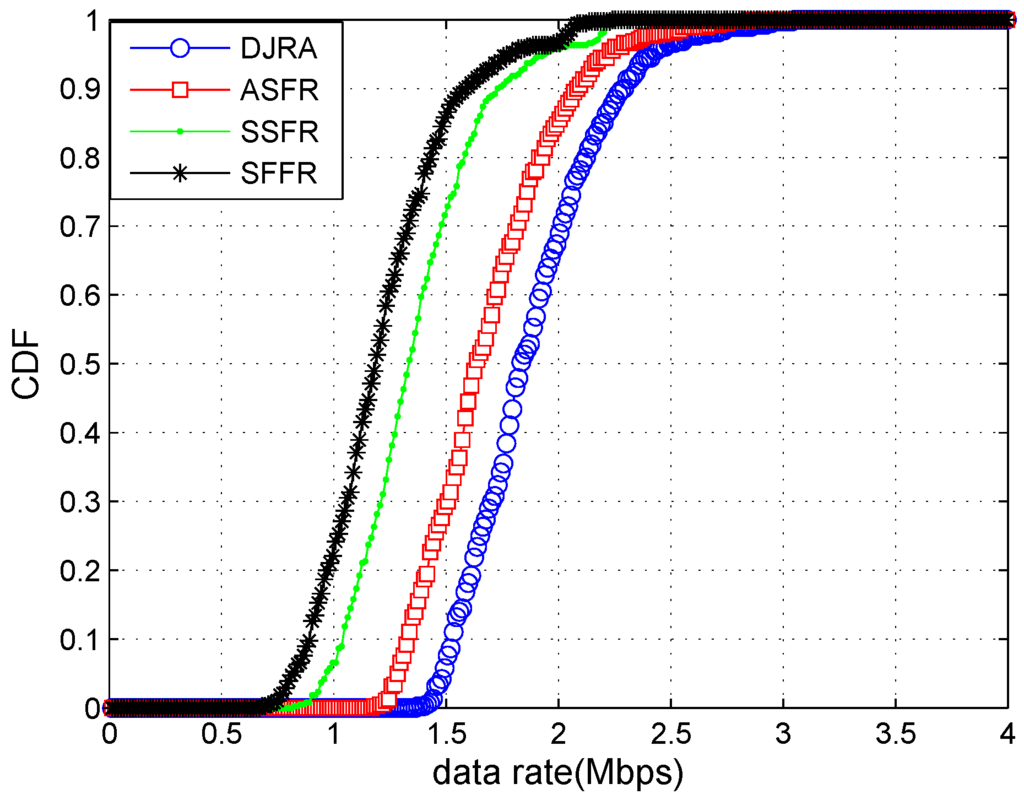
Figure 5.
Data rate achieved by each user under different schemes.
Table 3 is the numerical analysis of Figure 5. It is obvious that our scheme gives a better solution to the cell-edge user interference and the data rate of DJRA is 0.2 Mbps higher than ASFR algorithm.

Table 3.
Numerical analysis (Mbps).
We contrast the average throughput for a single cell and the average data rate achieved by each edge-user in Figure 6. Table 4 and Table 5 are the numerical analysis of Figure 6a,b. Comparing the DJRA algorithm with the ASFR algorithm, we can conclude that applying the sector partition method in the center region is an effective way to improve the system sum rate. This is because the center user interference mainly comes from the edge users in neighboring cells, and the edge user interference mainly comes from the center users in neighboring cells. Thus, eliminating cell-center users ’interference is equal to suppressing the edge users’ interference in its adjacent cells. Thereby, our approach can also achieve a better behavior for cell-edge users.
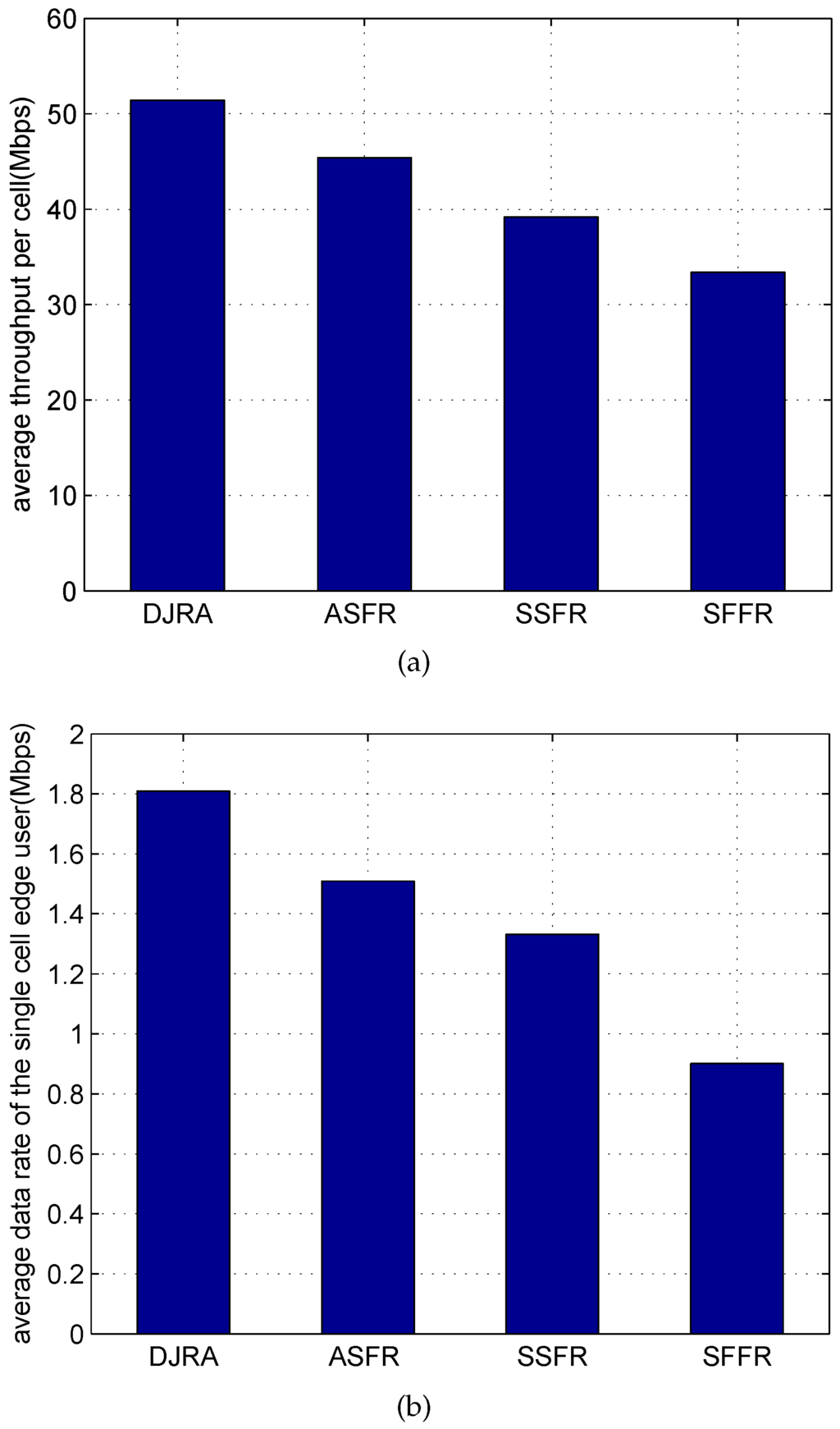
Figure 6.
(a) Average throughput for a single cell (b) Average data rate for a edge-user.

Table 4.
Single cell throughput numerical analysis (Mbps).

Table 5.
Edge-user date rate numerical analysis (Mbps).
5. Conclusions
In this paper, the system model of soft frequency reuse is first analyzed. Then we put forward an improved dynamic joint resource allocation algorithm. The proposed scheme maximizes the system capacity and satisfies the minimum throughput requirements for each center zone and edge zone, simultaneously. DJRA obtains the optimal single cell resource allocation scheme by dynamically adjusting RB-power allocation according to the real-time distribution of users per cell, and then uses an iteration method to acquire the optimum resource allocation scheme. Finally, DJRA utilizes the interior sector partition method and proportional fair algorithm in each cell. Our scheme outperforms previous approaches for system capacity and cell edge user performance. Furthermore, DJRA guarantees that all the users have available resources. Despite the huge potential benefits of DJRA, several challenges must be overcome, for example, decreasing computational complexity. How to solve these problems is our next step along this research path.
Acknowledgments
This paper is partially supported by National Natural Science Foundation of China (No. 61301095, No. 51509049), the Heilongjiang Province Natural Science Foundation(No. F201345) and the Fundamental Research Funds for the Central Universities of China (No. HEUCF160812/160810).
Author Contributions
The idea of this work was proposed by Yibing Li and Xueying Diao. Yibing Li and Xueying Diao performed the experiments and analyzed the simulation results. Fang Ye and Ge Dong assisted in the research work and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ohmori, S.; Yamao, Y.; Nakajima, N. The future generations of mobile communications based on broadband access technologies. IEEE Commun. Mag. 2000, 38, 134–142. [Google Scholar]
- E-UTRA and E-UTRAN Overall Description; Stage 2 (Release 8), 3GPP Technical Specification TS 36.300 V8.12.0. Available online: http://www.3gpp.org (accessed on 21 April 2016).
- Dahlman, E.; Parkvall, S.; Skld, J. Chapter 1-Background of LTE. In 4G: LTE/LTE-Advanced for Mobile Broadband, 2nd ed.; Elsevisr: Portland, OR, USA, 2014; pp. 1–15. [Google Scholar]
- Novlan, T.; Andrews, J.G.; Sohn, I.; Ganti, R.K. Comparison of Fractional Frequency Reuse Approaches in the OFDMA Cellualar Downlink. In Procceings of the IEEE Global Telecommunications Conference (GLOBECOM), Miami, FL, USA, 6–10 December 2010; pp. 1–5.
- Elayoubi, S.E.; BenHaddada, O.; Fourestie, B. Performance evaluation of frequency planning schemes in OFDMA-based networks. IEEE Trans. Wirel. Commun. 2008, 7, 1623–1633. [Google Scholar] [CrossRef]
- R1-050507: Soft Frequency Reuse Scheme for UTRAN LTE. In Huawei 3GPP TSG RAN WG1 Meeting no.41, Athens, Greece, May 2005; Available online: http://www.ljemail.org/reference/ReferencesPapers.aspx?ReferenceID=1192937 (accessed on 22 April 2016).
- Ali, S.H.; Leung, V.C.M. Dynamic Resource Allocation in Fractional Frequency Reused OFDMA Networks. IEEE Trans. Wirel. Commun. 2009, 8, 4286–4295. [Google Scholar] [CrossRef]
- Stolyar, A.L.; Viswanathan, H. Self-organizing Dynamic Fractional Frequency Reuse for Best-Effort Traffic Through Distributed Inter-cell Coordination. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 1287–1295.
- Son, K.; Chong, S.; de Veciana, G. Dynamic Association for Load Balancing and Interference Avoidance in Multi-cell Networks. IEEE Trans. Wirel. Commun. 2009, 8, 3566–3576. [Google Scholar] [CrossRef]
- Ksairi, N.; Bianchi, P.; Ciblat, P.; Hachem, W. Resource Allocation for Downlink Cellular OFDMA Systems-Part II: Practical Algorithms and Optimal Resue Factor. IEEE Trans. Signal Process. 2010, 58, 735–749. [Google Scholar] [CrossRef]
- Zhang, X.; He, C.; Jiang, L.; Xu, J. Inter-cell Interference Coordination Based on Softer Frequency Reuse in OFDMA Cellular Systems. In Proceedings of the IEEE International Conference Neural Networks and Signal Processing, Nanjing, China, 7–11 June 2008; pp. 1–6.
- Chen, L.; Yuan, D. Soft Frequency Reuse in large Networks with Irregular Cell Pattern: How Much Gains To Expect? In Proceedings of the IEEE PIMRC 09, Tokyo, Japan, 13–16 September 2009; pp. 1467–1471.
- Mao, X.; Maaref, A.; Teo, K. Adaptive soft frequency reuse for inter-cell interference coordination in SC-FDMA based 3GPP LTE uplinks. In Proceedings of the IEEE GLOBECOM 2008, New Orleans, LO, USA, 30 November–4 December 2008; pp. 1–6.
- Yu, Y.; Dutkiewicz, E.; Huang, X. Adaptive power allocation for soft frequency reuse in multi-cell LTE networks. In Proceedings of the IEEE ISCIT 2012, Gold Coast, QLD, Australia, 2–5 October 2012; pp. 991–996.
- Qian, M.; Hardjawana, W.; Li, Y.; Vucetic, B.; Shi, J.; Yang, X. Inter-cell Interference Coordination Through Adaptive Soft Frequency Reuse in LTE Networks. In Proceedings of the 2012 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 1–4 April 2012; pp. 1618–1623.
- Qian, M.; Hardjawana, W.; Li, Y.; Vucetic, B.; Yang, X.; Shi, J. Adaptive Soft Frequency Reuse Scheme for Wireless Cellular Networks. IEEE Trans. Veh. Technol. 2015, 64, 118–131. [Google Scholar] [CrossRef]
- Andrea, G. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Tian, L.; Zhou, Y.; Zhang, Y.; Sun, G.; Shi, J. Resource allocation for multicast services in distributed antenna systems with QoS guarantees. IET Commun. 2012, 6, 264–271. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).