Efficient Metaheuristics for the Mixed Team Orienteering Problem with Time Windows

Abstract

Given a graph whose nodes and edges are associated with a profit, a visiting (or traversing) time and an admittance time window, the Mixed Team Orienteering Problem with Time Windows (MTOPTW) seeks for a specific number of walks spanning a subset of nodes and edges of the graph so as to maximize the overall collected profit. The visit of the included nodes and edges should take place within their respective time window and the overall duration of each walk should be below a certain threshold. In this paper we introduce the MTOPTW, which can be used for modeling a realistic variant of the Tourist Trip Design Problem where the objective is the derivation of near-optimal multiple-day itineraries for tourists visiting a destination which features several points of interest (POIs) and scenic routes. Since the MTOPTW is a NP-hard problem, we propose the first metaheuristic approaches to tackle it. The effectiveness of our algorithms is validated through a number of experiments on POI and scenic route sets compiled from the city of Athens (Greece).

1. Introduction

The Tourist Trip Design Problem (TTDP) [1] refers to a route-planning problem for tourists interested in visiting multiple points of interests (POIs) in a destination. TTDP solutions involve daily sightseeing itineraries, i.e., ordered visits to POIs according to tourists’ constraints and POIs’ attributes. Specifically, the main objective of the TTDP is to select POIs that match tourist preferences, thereby maximizing tourist satisfaction (“profit”), while taking into account a multitude of parameters and constraints (e.g., distances among POIs, visiting time required for each POI, POIs visiting days/hours, entrance fees, weather conditions) and without exceeding the time available for sightseeing on a daily basis.

The Orienteering Problem (OP), an NP-hard problem introduced in [2], has been used in the literature as the baseline optimization problem for modeling the TTDP. The OP seeks for a route which starts and ends at fixed locations and maximizes the total collected profit while maintaining the travel cost under a given value. This definition also includes the case of a cyclic route by simply selecting as a start and destination the same location. Clearly, the OP may be used to model the simplest version of the TTDP wherein the POIs are associated with a profit (i.e., a degree of user satisfaction) and the goal is to find a single tourist itinerary that starts and ends at fixed locations and maximizes the profit collected within a given time budget (time allowed for sightseeing in a single day). Extensions of the OP have been successfully applied to model more complex versions of the single itinerary TTDP [1,3]. The OP with Time Windows (OPTW) considers visits at locations within a predefined time window; this allows modeling opening days/hours of POIs. The Time-Dependent OP (TDOP) considers time dependency in the estimation of time required to move from one location to another and therefore, it is suitable for modeling multi-modal transports among POIs. The Team Orienteering Problem (TOP) is the extension of the OP to multiple routes. The TOP with Time Windows (TOPTW) and the Time-Dependent TOPTW (TDTOPTW) have been used to model different versions of the multiple itinerary TTDP.

The Arc Orienteering Problem (AOP), introduced by Souffriau et al. in [4], is the arc routing version of the OP and is applicable to TTDP variants whose modeling involves profits associated with the arcs (rather than the nodes) of the network as some links may be more attractive than others. As an example, consider the problem of deriving personalized bicycle trips. Based on the biker’s personal interests, starting and ending point and the available time budget, a personalized trip can be composed using arcs that better match the cyclist’s profile (for instance, arc values could indicate the scenic value or the gradient of a route segment). The extension of the AOP to multiple routes, introduced by Archetti et al. in [5] and named as Team Orienteering Arc Routing Problem (TOARP), may also find applications to the TTDP.

The combination of the OP and the AOP is proposed in [3] under the name Mixed Orienteering Problem (MOP). In the MOP, profits are associated with the nodes as well as with the arcs of the graph. The problem can be used to formulate TTDP variants wherein, further to typical attractions, certain routes may be of tourist interest. In this paper, we introduce the Mixed Team Orienteering Problem with Time Windows (MTOPTW) which is an extension of the MOP in that multiple tourist itineraries are obtained. These itineraries are walks which can start and finish at different end-points. As mentioned above, the case of cyclic itineraries can easily follow, by using the same location as the start and destination of itineraries. MTOPTW can be used to formulate realistic TTDP variants whose modeling requires multiple tourist itineraries. The profits are associated with both POIs (network nodes) and routes (network edges) as certain routes may be more interesting for traversal than others. Furthermore, both POIs and routes are associated with visiting/traversing time windows. To the best of our knowledge, the MTOPTW has not been studied so far in the literature. Due to its apparent hardness and real-time requirements, we focus on metaheuristic approaches. Specifically, we introduce an Iterated Local Search and a Simulated Annealing metaheuristic algorithm for solving the problem. The proposed algorithms are evaluated and compared using test instances with data related to POIs and scenic routes in the city of Athens, Greece.

The rest of this paper is organized as follows. Section 2 discusses the related work. Section 3 provides the definition of MTOPTW. Section 4 describes the common preprocessing phase of the two metaheuristics. Section 5 and Section 6 present the Iterated Local Search and the Simulated Annealing metaheuristic method, respectively. Section 7 discusses the experimental results and Section 8 concludes the paper.

2. Related Work

Although numerous research works concern the OP as well as many extensions and variants of the OP, only a very limited body of literature concerns the AOP, the MOP and their extensions.

Souffriau et al. in [4] use the AOP to model and solve the problem of planning cycle trips in the province of East Flanders. Their solution approach is based on a Greedy Randomized Adaptive Search Procedure (GRASP), while experimental results are based on instances generated from the East Flanders network. In [6] the cycle trip planning proble (CTPP) is introduced and studied. The CTPP is a variant of AOP considering no fixed starting point for the tour.

Archetti et al. propose a formulation for the Team Orienteering Arc Routing Problem (TOARP) [5], a variant of the extension of AOP to multiple tours where two types of arcs are considered: the arcs that have to be served (compulsory arcs), and the arcs that are associated with profit and may be served if beneficial (profitable arcs). Given a specific number of tours k, the goal is to design k tours including the required arcs and a set of the profitable arcs which maximizes the total profit without exceeding the allowed duration of each tour. Archetti et al. study a relaxation of the polyhedron modelling of the problem and then develop a branch-and-cut algorithm. Archetti et al. in [7] propose a matheuristic approach for the TOARP. Experimental results show that the algorithm gives an average percentage error with respect to the optimal solution which is lower than $1\%$. The Undirected Capacitated Arc Routing Problem with Profits (UCARPP), the arc routing counterpart of the capacitated TOP, is considered in [8]. In this problem a profit and a nonnegative demand is associated with each arc and the objective is to determine a tour for each available vehicle in order to maximize the total collected profit, without violating the capacity and time limit constraints of each vehicle. A potential application of the UCARPP is the creation of personalized bicycle trips. An exact approach for solving the problem along with several heuristics has been proposed in [8]. The problem has also been studied by Zachariadis and Kiranoudis in [9] who investigated a local search procedure.

To the best of our knowledge, the research works mostly relevant to the MOP are the one-period Bus Touring Problem (BTP) introduced by Deitch and Ladany [10], the Outdoor Activity Tour Suggestion Problem (OATSP) introduced by Maervoet et al. [11], and the Most Attractive Cycle Tourist Path Problem (MACTPP) introduced by Cerna et al. [12]. In the BTP, given a constraint on the total touring time, the objective is to select a subset of profitable nodes and arcs which maximize the total profit of the tour. In this problem, the profit of nodes and arcs which are visited multiple times is counted only once. In [10], a heuristic approach is employed to solve the BTP. In [11], an efficient heuristic solution to the OATSP is presented. This problem finds attractive closed paths in a transportation network, tailored to a specific outdoor activity such as hiking and mountain biking. The total path attractiveness is estimated as the sum of the average arc attractiveness and the profits of the nodes along the path. The objective is to find a closed path of maximal attractiveness given a target path’s length and tolerance. Notice that the OATSP requires a target path’s length instead of a maximal travel time required by the BTP; hence, this gives rise to a path length window constraint. In MACTPP [12], the objective is to construct a new bicycle route between two locations with maximum attractiveness, subject to budget and duration constraints. The problem models a real situation in Trebon, Czech Republic where local administrators face the problem of optimally investing scarce resources to set up a network of cycle tracks, exploiting existing trails or by reconstruction works. In this problem, arcs and nodes can be visited more than once, obtaining a decreasing profit after each visit. The authors formulate the problem as a Integer Linear Programming (ILP) problem and then use a commercial ILP solver.

In [13], the first approximation algorithms for both the directed and the undirected versions of the AOP and MOP have been presented. Furthermore, the authors proved that the MOP can be reduced to the AOP and any approximation algorithm for the AOP yields an approximation algorithm for the MOP with the same approximation ratio for both the cases of undirected and directed graphs. As concerns the reduction of the MOP to the OP, although in [10] a transformation of an instance of BTP into an instance of OP is given, this transformation—as admitted by the authors—does not always guarantee a successful re-transformation from a given OP solution to the corresponding BTP solution. It is easy to notice that such a re-transformation is successful for the case of directed graphs. Therefore, the MOP can be reduced to OP for the case of directed graphs while, to the best of our knowledge, there is no reduction in the literature of the MOP to OP for the case of undirected graphs.

In this work, we study the Mixed Team Orienteering Problem with Time Windows (MTOPTW) for the case of windy graphs and we present the first algorithmic approaches for the problem. In windy graphs, like in undirected graphs, each edge $e=\{i,j\}$ can be traversed either from i to j or from j to i. Windy graphs differ from their undirected counterparts in that the cost of the two traversals may differ [14,15,16]. For example, when the costs represent travelling times, such asymmetry in the costs may occur when one direction is downhill and the other is uphill. Windy graphs have been extensively used for modeling arc-orienteering problems. Although, the different edge costs in opposite directions could be modeled with two opposite arcs between the edge end-points, windy graphs can be handy for modeling the above sort of problems, for instance, when trying to impose the constraint that each edge should appear only once in a solution irrespectively of the traversal direction. The windy graphs provide the same convenience also in the modelling of problems where profits are associated with edges and when there is the assumption that the profit of an edge is obtained only once independently of the number of the traversals of this edge in the solution. This is exactly the case we handle in MTOPTW. Finally, since OP (a special case of MTOPTW) is NP-hard [1], MTOPTW is at least that hard. Therefore, we focus on metaheuristic approaches for solving the problem.

3. Problem Definition

The MTOPTW formulates realistic TTDP variants where multiple tourist itineraries should be determined. Also, profits are associated to POIs (nodes of the network) as well as to routes (edges of the network) as certain routes may be more interesting for traversal than others. In addition, the POIs are associated with visiting times and visiting time windows. Similarly, the routes are associated with traversing times and traversing time windows. To formally define the problem we need to employ windy graphs.

We define the MTOPTW on windy multigraphs (A multigraph is a graph where for each pair of nodes there could be more than one edges connecting these nodes.) as follows: Let $G=(V,E)$ be a windy multigraph where $V=\{u_1,u_2,\cdots ,u_N\}$ denotes the node set and E the edge set. Each edge e can be traversed in two directions and let $e^{+}$ and $e^{-}$ be the corresponding directions. The head and the tail of each direction $e^d$ ($d\in \{+,-\}$) will be denoted by $h(e^d)$ and $t(e^d)$, respectively. The edge set E is partitioned into two sets, $E^{\prime }$ and $E^{\prime \prime }$ ($E=E^{\prime }\cup E^{\prime \prime }$), defined as follows:

• The set $E^{\prime }$ contains an edge for any pair of nodes in V representing the shortest path connection between these nodes. Specifically, for each pair of nodes $u_i$ and $u_j$ in V, the set $E^{\prime }$ contains an edge e which connects the two nodes and represents the shortest path route connecting these two nodes in the city road network. The time required for traversing the edge e in the direction from $u_i$ to $u_j$ may be different from the travelling time in the opposite direction; thus, we use the notations $T(e^{+})$ and $T(e^{-})$ for the different travelling times in the two directions (This clearly implies that the shortest path routes may be different between two nodes in the two opposite directions.). Clearly, all these time costs obey the triangle inequality, for instance, it holds that $T(e^d)\le T(e_1^d)+T(e_2^d)$ where $t(e^d)=t(e_1^d)$, $h(e^d)=h(e_2^d)$, $h(e_1^d)=t(e_2^d)$ for $d\in \{+,-\}$. Essentially, each edge e in $E^{\prime }$ is used solely for moving between interesting sites in the city (either POI or scenic route) and thus traversing such an edge does not yield any profit. Therefore, each edge e in $E^{\prime }$ is associated with profit equal to zero ($P_e=0$) .
• The set $E^{\prime \prime }$ contains all the edges modelling the scenic routes. Specifically, if there is a scenic route between nodes $u_i$ and $u_j$ then there is an edge $e\in E^{\prime \prime }$ connecting these nodes. Each edge in $E^{\prime \prime }$ can be traversed in both directions and $T(e^d)$ is again the traversal time in direction d for $d\in \{+,-\}$. Note that the scenic route is not necessarily the shortest one between $u_i$ and $u_j$ and thus the travelling time $T(e^d)$ may not obey the triangle inequality property. Each edge e in $E^{\prime \prime }$ is associated with a profit, $P_e$, which is a measure of the attractiveness of the scenic route.

Overall, between any two nodes in G, there will be at most two edges connecting them, one being the shortest path route and the other being the scenic route (if exists). In case that the scenic route is also the shortest one between two nodes, the two edges are maintained although they actually represent the same route in the road network. This redundancy greatly facilitates the integer programming formulation of the problem which follows. It is also worth mentioning that $G(V,E^{\prime })$ is a complete graph while $G(V,E^{\prime \prime })$ may be not.

For each node $u\in V$, there are two possibilities. First, the node can be visited in a walk with $T_u$ being the visit duration and $P_u$ being a non-negative number denoting the profit gained from that visit. The other possibility is that the walk passes by the node on the way to the next scenic route or POI. In this case, there is no profit from this node and the delay $T_u$ is not incurred.

Also, an integer K is given denoting the number of the walks that will be constructed. Now, each node or edge x is associated with K time windows $[O_x^i,C_x^i]$ ($i=1,\dots ,K$) where $O_x^i$ is the opening time and $C_x^i$ is the closing time of the $i^{th}$ time window of node or edge x. The visit at a node (or the traversal of an edge) can only take place within one its time windows. However, for just passing by a node, this condition does not apply. Also, for each walk $W_i$ ($i=0,\dots ,K-1$) a starting node $s{l}_i$ and an ending node $e{l}_i$ are given ($s{l}_i,e{l}_i\in V$), as well as a starting time $s{t}_i$ and an ending time $e{t}_i$. An implicit assumption here is that for each node or edge x, only one its time windows may be “active” during a walk, namely, for each walk $W_i$, $[O_x^j,C_x^j]\cap [s{t}_i,e{t}_i]=\varnothing$ where $i,j=1,\dots ,K$ with $i\ne j$. This is a reasonable assumption considering the common scenario where each walk $W_i$ takes place on different day and $[O_x^i,C_x^i]$ is the interval in that day during which the route or POI is open.

A feasible solution of the MTOPTW consists of K walks $W_0,W_1,\cdots ,W_{K-1}$ with $W_i=(w_0^i,w_1^i,\cdots ,w_{l_i-1}^i)$ such that $w_0^i=s{l}_i$, $w_{l_i-1}^i=e{l}_i$, the arrival time at $s{l}_i$ equals to $s{t}_i$ and the arrival time at $e{l}_i$ is at most $e{t}_i$. For each edge of the walk $\{w_m^i,w_{m+1}^i\}$, its traversal should take place within its time window. The same holds for all nodes $w_m^i$ which are actually visited and not just passed by. The profit of the solution is equal to the sum of the profits of the visited nodes and the traversed edges. The goal of the MTOPTW is to construct the feasible solution of the highest profit. As has been mentioned above, if an edge appears (i.e., is traversed) more than once in a solution, its profit is counted only once (independently of the direction of the traversal) while the travel cost is charged as many times as it is traversed. The facts that (i) there is no profit gain when revisiting an edge and (ii) there exists a shortest path edge between any two nodes in the graph which obeys the triangle inequality, imply that each edge needs to be traversed at most once in the optimal solution. Likewise, we assume that the no additional profit is gained after the first visit of a node. Thus, it can be easily seen that there is an optimal solution which visits each node at most once due to the aforementioned fact that no additional profit is gained from multiple visits. However, a node may appear more than once in a solution, i.e., as an endpoint of its incident edges which are traversed in the solution. In all these occurrences, the node is only passed by and not visited.

The MTOPTW can be formulated as a mixed integer programming problem. We use the following variables:

• $y^k(e^d)$: a binary variable whose value is 1 if the edge e is traversed in the direction d ($\in \{+,-\}$ ) in the walk $W_k$, and 0, otherwise, for $k=0,\dots ,K-1$.
• $z_u^k$: a binary variable which takes value 1 if the node u is visited in the walk $W_k$, $k=0,\cdots ,K-1$, and 0 otherwise.
• $p^k(e^d)$: a binary variable which is equal to 1 if, the traversal of the edge e along $W_k$ is done in the direction $d\in \{+,-\}$ immediately before the visit at the node $h(e^d)$. Otherwise, $p^k(e^d)=0$. For instance, $p^k(e^d)=0$ in the case that the edge e is traversed in direction d ($y^k(e^d)=1$) but the head of the edge $h(e^d)$ is only passed by.
• $q^k(e^d)$: a binary variable set equal to 1 if, in the walk $W_k$, the node $t(e^d)$ is visited just before the traversal of the edge e in the direction $d\in \{+,-\}$. In all other cases, $q^k(e^d)=0$.
• $r^k(e_1^{d_1},e_2^{d_2})$: a binary variable which is defined only for edges $e_1$, $e_2$ with $h(e_1^{d_1})=t(e_2^{d_2})$. Its value is 1 only if i) the edge $e_1$ is traversed in the direction $d_1$ along the walk $W_k$, just before the traversal of the edge $e_2$ in the direction $d_2$ and ii) the node $h(e_1^{d_1})$ is not visited at that moment, that is, it is only passed by while traversing $e_1$ and $e_2$. In all other cases $r^k(e_1^{d_1},e_2^{d_2})=0$. From the definition of these variables, it is clear that for any two edges $e_1$, $e_2$ and directions $d_1$ and $d_2$, the variable $r^k(e_1^{d_1},e_2^{d_2})$ cannot be equal to 1 when at least one of the variables, $p^k(e_1^{d_1})$ or $q(e_2^{d_2})$, is equal to 1.
• ${\mathrm{start}}_u$: a real variable denoting the starting time of the single visit at the node u.
• ${\mathrm{start}}_e$: a real variable denoting the starting time of the single traversal of the edge e.
• M: a large number (larger enough from the parameters of the problem).
• $[K]$: the set $\{0,1,\dots ,K-1\}$

For avoiding many special cases in the formulation of MTOPTW, we assume that all the endpoints of the walks are different nodes and also none of these nodes are POIs. In case that some of the nodes are the same or POIs, copies of the original nodes are created which are considered as different nodes with no profit. Then, these nodes are used as endpoints of the walks. For instance, if the K walks all start and end at the same node which happens to be a POI, $2K$ copies of this node are created and each of these copies has zero profit and visit time and time window as long as the interval between the starting and ending time of the corresponding walk. Also, all the copies of the node and the node itself are connected with each other through zero-length shortest path edges belonging to $E^{\prime }$. Regarding the remaining nodes of the graph, these copies “inherit” the edge connectivity along with the associated edge costs of the original node. Now, MTOPTW can be formulated as follows:

$$\begin{array}{c}maxP=\sum _{k=0}^{K-1}\sum _{u\in V}{P}_u{z}_u^k+\sum _{k=0}^{K-1}\sum _{e\in E\wedge d\in \{+,-\}}{P}_e{y}^k(e^d)\hfill \\ \mathrm{subject}\mathrm{to}\hfill \end{array}$$

(1)

$$\begin{array}{c}\sum _{e\in E\wedge d\in \{+,-\}\wedge h(e^d)=s{l}_k}{y}^k(e^d)+1=\sum _{e\in E\wedge d\in \{+,-\}\wedge t(e^d)=s{l}_k}{y}^k(e^d),\forall k\in [K]\hfill \end{array}$$

(2)

$$\begin{array}{c}\sum _{e\in E\wedge d\in \{+,-\}\wedge t(e^d)=e{l}_k}{y}^k(e^d)+1=\sum _{e\in E\wedge d\in \{+,-\}\wedge h(e^d)=e{l}_k}{y}^k(e^d),\forall k\in [K]\hfill \end{array}$$

(3)

$$\begin{array}{c}\sum _{e\in E\wedge d\in \{+,-\}\wedge h(e^d)=u}{y}^k(e^d)=\sum _{e\in E\wedge d\in \{+,-\}\wedge t(e^d)=u}{y}^k(e^d),\forall u\in V-\{s{l}_k,e{l}_k\},k\in [K]\hfill \end{array}$$

(4)

$$\begin{array}{c}\sum _{d\in \{+,-\}\wedge k\in [K]}{y}^k(e^d)\le 1,\forall e\in E\hfill \end{array}$$

(5)

$$\begin{array}{c}\sum _{k=0}^{K-1}{z}_u^k\le 1,\forall u\in V\hfill \end{array}$$

(6)

$$\begin{array}{c}{z}_{s{l}_k}^k=z_{e{l}_k}^k=1,\forall k\in [K]\hfill \end{array}$$

(7)

$$\begin{array}{c}{p}^k(e^d)=0,\forall k\in [K],d\in \{+,-\},e\in E\mathrm{with}h(e^d)=s{l}_k\hfill \end{array}$$

(8)

$$\begin{array}{c}{q}^k(e^d)=0,\forall k\in [K],d\in \{+,-\},e\in E\mathrm{with}t(e^d)=e{l}_k\hfill \end{array}$$

(9)

$$\begin{array}{c}{p}^k(e^d)\le y^k(e^d),\forall e\in E,d\in \{+,-\},k\in [K]\hfill \end{array}$$

(10)

$$\begin{array}{c}{q}^k(e^d)\le y^k(e^d),\forall e\in E,d\in \{+,-\},k\in [K]\hfill \end{array}$$

(11)

$$\begin{array}{c}{z}_u^k=\sum _{e\in E\wedge d\in \{+,-\}\wedge h(e^d)=u}{p}^k(e^d),\forall u\in V-\{s{l}_k\},k\in [K]\hfill \end{array}$$

(12)

$$\begin{array}{c}{z}_u^k=\sum _{e\in E\wedge d\in \{+,-\}\wedge t(e^d)=u}{q}^k(e^d),\forall u\in V-\{e{l}_k\},k\in [K]\hfill \end{array}$$

(13)

$$\begin{array}{c}{y}^k(e^d)=\sum _{e^{\prime }\in E\wedge d^{\prime }\in \{+,-\}\wedge h(e^{\prime d^{\prime }})=t(e^d)}{r}^k(e^{\prime d^{\prime }},e^d)+q^k(e^d),\forall e\in E,d\in \{+,-\},k\in [K]\hfill \end{array}$$

(14)

$$\begin{array}{c}{y}^k(e^d)=\sum _{e^{\prime }\in E\wedge d^{\prime }\in \{+,-\}\wedge h(e^d)=t(e^{\prime d^{\prime }})}{r}^k(e^d,e^{\prime d^{\prime }})+p^k(e^d),\forall e\in E,d\in \{+,-\},k\in [K]\hfill \end{array}$$

(15)

$$\begin{array}{c}{\mathrm{start}}_e+T(e^d)-{\mathrm{start}}_{h(e^d)}\le M(1-p^k(e^d)),\forall e\in E,d\in \{+,-\},k\in [K]\hfill \end{array}$$

(16)

$$\begin{array}{c}{\mathrm{start}}_{t(e^d)}+T_{t(e^d)}-{\mathrm{start}}_e\le M(1-q^k(e^d)),\forall e\in E,d\in \{+,-\},k\in [K]\hfill \\ {\mathrm{start}}_e+T(e^d)-{\mathrm{start}}_{e^{\prime }}\le M(1-r^k(e^d,e^{\prime d^{\prime }})),\forall e,e^{\prime }\in E,d,d^{\prime }\in \{+,-\}\mathrm{with}h(e^d)=t(e^{\prime d^{\prime }}),\hfill \end{array}$$

(17)

$$\begin{array}{c}k\in [K]\hfill \end{array}$$

(18)

$$\begin{array}{c}{O}_u^k-M(1-z_u^k)\le {\mathrm{start}}_u,\forall u\in V,k\in [K]\hfill \end{array}$$

(19)

$$\begin{array}{c}{\mathrm{start}}_u+T_u\le C_u^k+M(1-z_u^k),\forall u\in V,k\in [K]\hfill \end{array}$$

(20)

$$\begin{array}{c}{O}_e^k-M(1-y^k(e^d))\le {\mathrm{start}}_e,\forall e\in E,d\in \{+,-\},k\in [K]\hfill \end{array}$$

(21)

$$\begin{array}{c}{\mathrm{start}}_e+T(e^d)\le C_e^k+M(1-y^k(e^d)),\forall e\in E,d\in \{+,-\},k\in [K]\hfill \end{array}$$

(22)

$$\begin{array}{c}{\mathrm{start}}_{s{l}_k}=s{t}_k,\forall k\in [K]\hfill \end{array}$$

(23)

$$\begin{array}{c}{\mathrm{start}}_{e{l}_k}\le e{t}_k,\forall k\in [K]\hfill \\ y^k(e^d),p^k(e^d),q^k(e^d)\in \{0,1\},\forall e\in E,d\in \{+,-\},k\in [K]\hfill \\ z_u^k\in \{0,1\},\forall u\in V,k\in [K]\hfill \\ r^k(e^d,e^{\prime d^{\prime }})\in \{0,1\},\forall e,e^{\prime }\in E,d,d^{\prime }\in \{+,-\},k\in [K]\hfill \\ {\mathrm{start}}_e\in R,\forall e\in E\hfill \\ {\mathrm{start}}_u\in R,\forall u\in V\hfill \\ \hfill \end{array}$$

(24)

The objective Function (1) is to maximize the total profit of the visited nodes and the traversed edges. Constraints (2) and (3) ensure that the walk $W_k$ starts at node $s{l}_k$ and ends at node $e{l}_k$ for $k=0,\cdots K-1$. We also take into account that there may be multiple traversals through $s{l}_k$ and $e{l}_k$ along the same walk. Constraints (4) are flow conservation constraints while Constraints (5) ensure that each edge is traversed at most once in total for both traversal directions. As has been mentioned before, the optimal solution needs to traverse each edge only once and hence these constraints are surely satisfied by such a solution. If those constraints were omitted, then an optimal solution could have been derived with even higher profit. However, this better solution may traverse an edge two times, once in each direction, getting the edge profit twice. Thus, the obtained solution would not be a valid solution in our problem setting.

Regarding Constraints (6), these constraints guarantee that each node is visited at most once, in total. Constraints (7) necessitate the visit at the endpoints $s{l}_k$ and $e{l}_k$. The visit of $s{l}_k$ takes place at the moment of departure from $s{l}_k$ (Constraints (23)). Similarly, the visit of $e{l}_k$ is at the end of the walk $W_k$ and before time $e{t}_k$ (Constraints (24)). Constraints (8)–(15) ensure that the values of variables $p^k(e^d)$, $q^k(e^d)$, $r^k(e^d,e^{\prime d^{\prime }})$ are consistent with those of variables $y^k(e^d)$ and $z_u^k$. Specifically, Constraints (8) combined with the Constraint (7) reflect the fact that the walk $W_k$ starts with the visit of $s{l}_k$. Thus, there cannot be preceding edges in $W_k$ leading to that particular node. A symmetric condition is described in the Constraints (9). Constraints (10) and (11) ensure that the variables $p^k(e^d)$, $q^k(e^d)$ cannot have value 1 if the edge e has not been traversed in the direction d along the walk $W_k$. Constraints (12) ensure that for each visited node u along $W_k$ except the node $s{l}_k$, only one of the edges leading to u has been traversed along $W_k$ and indeed just before the visit of that node. Symmetrically, Constraints (13) guarantee that for each visited node u along $W_k$ except the node $e{l}_k$, only one of the edges starting from u has been traversed along $W_k$, immediately after the visit of that node. Constraints (14) reflect the fact that when an edge e is traversed along the walk $W_k$ ($y^k(e^d)=1$), one of the two mutually exclusive possibilities can occur before this traversal: either the tail node of e has been visited ($q^k(e^d)=1$) and thus all r-variables are zero or that visit did not take place ($q^k(e^d)=0$) and thus only one of the r-variables is 1, that corresponding to the edge $e^{\prime }$ traversed just before e in the walk $W_k$. In case that the edge e is not traversed, ($y^k(e^d)=0$), all variables in these constraints are forced to be 0. Constraints (15) have a similar explanation and determine what is possible after the traversal of an edge. Constraints (16)–(18) ensure that the sequence of starting times of node visits and edge traversals along a walk is feasible. For instance, Constraints (16) ensure that the visit at a node along a walk can start only after the edge which is just before that node on the walk ($p^k(e^d)=1$) has been traversed. Constraints (19) and (20) indicate that the start of a visit at a node can only take place during its time window. Similarly, Constraints (21) and (22) ensure that the edge traversal can only take place during its time window. Finally, Equations (23) and (24) require that the walk $W_k$ should start at time $s{t}_k$ and be completed no later than $e{t}_k$.

As has already been mentioned, the MTOPTW problem is a NP-hard problem which models the core task of suggesting interesting itineraries for tourists. The envisaged tourist application should be on-line and should return suggestions within a few seconds after receiving a user request. Considering these strict time restrictions, solving the MILP directly, either exactly or approximately, is not expected to return the solution in acceptable time. In the following sections, two metaheuristics are presented for the MTOPTW which can be used in practice for deriving approximate solutions to the problem relatively fast.

4. MTOPTW Algorithmic Approaches—Preprocessing Phase

In the sequel, for the sake of simplicity and ease of the presentation of the algorithmic techniques, a different notation of graph edges is followed. Specifically, an edge e between two nodes u and v will be denoted by $\{u,v\}$ hereafter. The same notation will be used for assigning direction of traversal to an edge. For instance, the notation $\{v,u\}$ will denote the traversal of the edge in the direction from v to u. In case of two edges between the nodes u, v (one representing a scenic route and the other the shortest path connection), the notation $\{u,v\}$ will be used for representing either one of the two edges. To distinguish them, we will call an edge $\{u,v\}$ of the input graph with $P_{u,v}>0$ which models a scenic route, as profitable edge. Similarly, we will call a node u of the input graph with $P_u>0$ which models a POI, as profitable node.

With regard to the algorithmic approaches for solving MTOPTW, we propose two metaheuristic approaches, namely an Iterated Local Search approach inspired by the one presented by Vansteenwegen et al. [17] for the TOPTW, and a Simulated Annealing approach. Among other operations, both these approaches repeatedly execute local-search steps. At each of these steps, the neighborhood of the current solution is examined in search of higher profit feasible solutions. Thus, it is important to keep the size of this neighborhood relatively small in order that each local search step can be executed fast. For that reason, the input graph G should satisfy the following requirements:

• for each profitable node u of G there is no profitable edge incident to u, i.e., there is no v such that $P_{u,v}>0$, and
• for each profitable edge $\{u,v\}$ of G there is no other profitable edge incident to u or v, i.e., there is no node w such that $P_{u,w}>0$ or $P_{w,v}>0$.

In the case that G does not satisfy the above requirements then, in a preprocessing phase, G is transformed to a new graph $G^{\prime }$ that satisfies them. This is done in a way that any solution in $G^{\prime }$ can be easily transformed to an equivalent solution of the same profit in G. Specifically, the transformation first separates all profitable nodes from adjacent profitable edges as follows. For each profitable node u of the input graph which is connected to at least one profitable edge, we introduce a dummy node $u^{\prime }$ and a dummy edge $\{u^{\prime },u\}$ with $P_{u^{\prime }}=0$, $T_{u^{\prime }}=0$, $(O_{u^{\prime }}^k,C_{u^{\prime }}^k)=(s{t}_k,e{t}_k)$ ($k\in [K]$) and $P_{u^{\prime },u}=P_{u,u^{\prime }}=0$, $T_{u^{\prime },u}=T_{u,u^{\prime }}=0$, $(O_{u,u^{\prime }}^k,C_{u,u^{\prime }}^k)=(O_{u^{\prime },u}^k,C_{u^{\prime },u}^k)=(s{t}_k,e{t}_k)$ ($k\in [K]$). Then, each profitable edge incident to u in G is connected to the dummy node $u^{\prime }$ in $G^{\prime }$ while each non-profitable edge incident to u in G remains connected to u in $G^{\prime }$. As an example, Figure 1a shows a graph G with a profitable node u with two profitable and two non profitable incident edges, while Figure 1b shows the corresponding new graph $G^{\prime }$. Next, all profitable edges incident to the same node are “separated" by inserting a corresponding number of dummy nodes and edges whose profit and time attributes are set as above. As an example, Figure 1c shows a graph G with three profitable edges incident to the same node u, while Figure 1d shows the corresponding new graph $G^{\prime }$ which includes three dummy nodes and three dummy edges. Admittedly, this preprocessing increases the number of edges and nodes in the graph, however, since the tourist attraction routes (edges) are relatively few in a graph modeling a metropolitan city, this increase will be relatively small and easily offset by the simplification of the solution neighborhoods in the local search steps.

Figure 1. Preprocessing steps. Profitable edges and profitable nodes are colored gray. (a) Profitable edges incident to a profitable node; (b) Elimination of the adjacency among the profitable node and profitable edges; (c) Profitable edges incident to the same node; (d) Elimination of the adjacency among profitable edges.

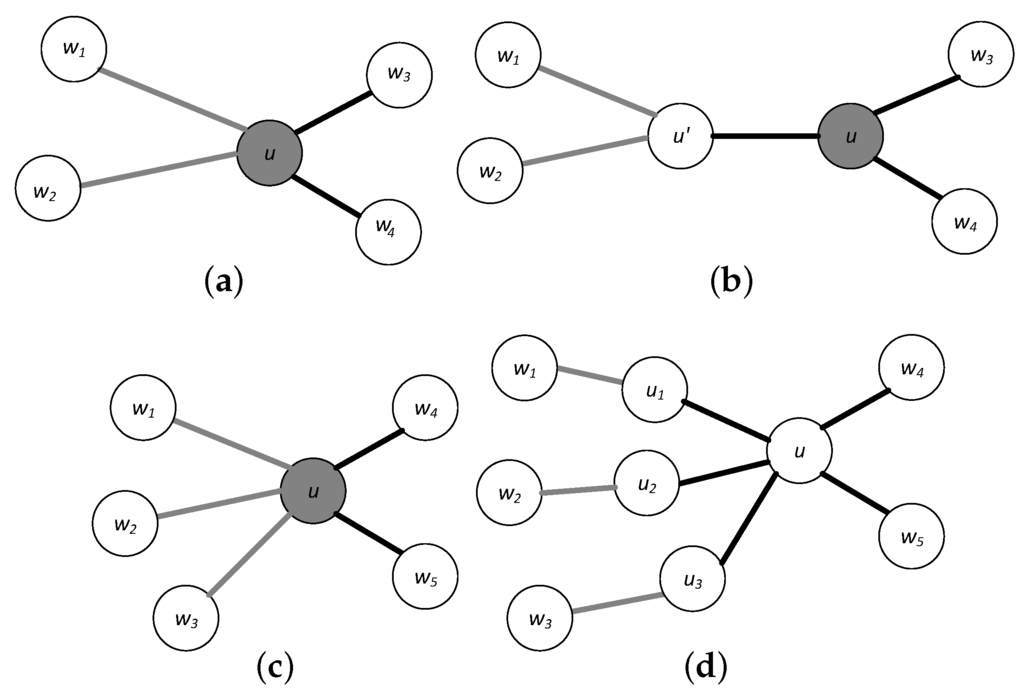
Figure 1. Preprocessing steps. Profitable edges and profitable nodes are colored gray. (a) Profitable edges incident to a profitable node; (b) Elimination of the adjacency among the profitable node and profitable edges; (c) Profitable edges incident to the same node; (d) Elimination of the adjacency among profitable edges.

For convenience, we denote a profitable node or edge as a Tourist Attraction (TA). Then, the TA representation of a walk $W_i$ will be $W_i=(p_0^i,p_1^i,\cdots ,p_{m_i-1}^i)$, with $p_0^i=s{l}_i,p_{m_i-1}^i=e{l}_i$ and $p_j^i,j=1,2,\cdots ,m_{i-2}$ the included TAs in $W_i$. On the other hand, the representation of the walk as a sequence of nodes shall be denoted as the node representation. For example, the walk $W_i$ in Figure 2 consists of the starting/ending locations as well as the nodes $u,v$ and w from which only u has a positive profit. Apart from u, the edge $\{v,w\}$ is also associated with profit, hence the TAs of $W_i$ are the node u and the edge $\{v,w\}$. Therefore, the node representation of the walk is $W_i=(s{l}_i,u,v,w,e{l}_i)$ while its TA representation is $W_i=(p_0^i,p_1^i,p_2^i,p_3^i)$ with $p_1^i=u$ and $p_2^i=\{v,w\}$.

Figure 2. Walk representation.

Figure 2. Walk representation.

5. The Iterated Local Search Metaheuristic

The Iterated Local Search [18,19] is a metaheuristic method widely used in combinatorial optimization problems in order to search the solution space extensively. The intuition of this metaheuristic is to iteratively reach a local optimum solution by applying a local search process and then perturb the solution. Specifically, the local search process explores a neighbourhood by iteratively generating the neighbourhood of the current solution and moving from the current solution to an improving neighbouring solution. This process is repeated until a local optimum is reached. The solution is perturbed in order to escape from the local optimum and reach a different local optimum in the next iteration. By exploring different local optimum solutions, the method is expected to produce better results than a simple local search method.

The neighborhood structure in our MTOPTW metaheuristic approach is obtained as follows. Consider a solution of an instance of the problem and any walk $W_i$ belonging to that solution. A neighboring solution (Insert Neighborhood) can be obtained by inserting a non-included TA between two consecutive nodes of the walk $W_i$ that are not connected with a profitable edge. For example in Figure 3 we consider the neighboring solutions of the single walk solution with node representation $W_i=(s{l}_i,u,v,w,e{l}_i)$ given in Figure 2. We consider that there are only two non-included TAs, the profitable edge $\{y,z\}$ and the profitable node x. Figure 3a–f show the neighboring solutions that are produced by inserting the edge $\{y,z\}$ between two consecutive nodes of the walk. Figure 3a,b depict the two solutions obtained by inserting $\{y,z\}$ between $s{l}_i$ and u, the former with direction from y to z and the latter from z to y. Similarly, Figure 3c,d depict the insertion of $\{y,z\}$ between u and $\{v,w\}$, while Figure 3e,f present the solution obtained by inserting $\{y,z\}$ after $\{v,w\}$. As far as the non-included profitable node x is concerned, the neighboring solutions are depicted in Figure 3g–i, where the insertion after $s{l}_i$, u and $\{v,w\}$ is considered, respectively. Note, that neither $\{y,z\}$ nor x can be inserted between v and w, since $\{v,w\}$ is a profitable edge.

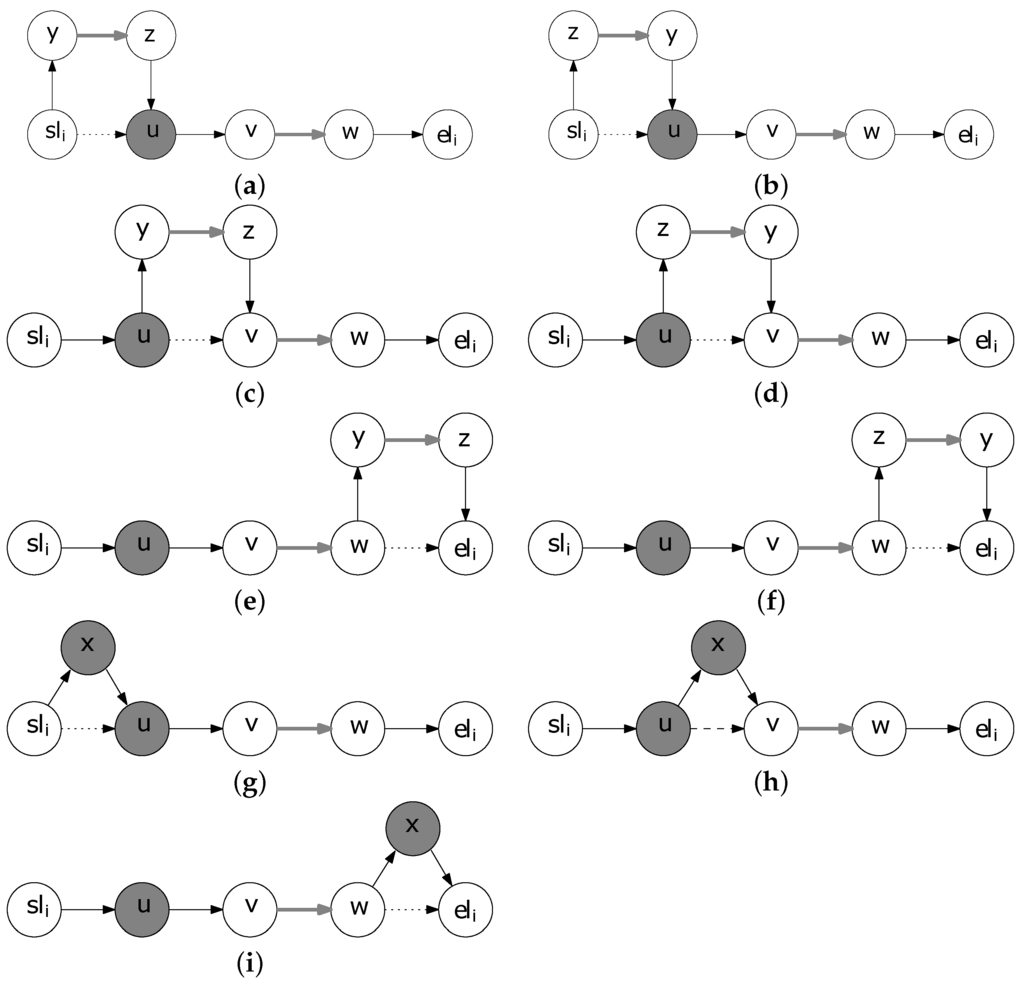
Figure 3. Illustration of the Insert Neighborhood. (a) Insertion of the edge $\{y,z\}$ between $s{l}_i$ and u with direction from y to z; (b) Insertion of the edge $\{y,z\}$ between $s{l}_i$ and u with direction from z to y; (c) Insertion of the edge $\{y,z\}$ between u and $\{v,w\}$ with direction from y to z; (d) Insertion of the edge $\{y,z\}$ between u and $\{v,w\}$ with direction from z to y; (e) Insertion of the edge $\{y,z\}$ after $\{v,w\}$ with direction from y to z; (f) Insertion of the edge $\{y,z\}$ after $\{v,w\}$ with direction from z to y; (g) Insertion of the node x between $s{l}_i$ and u; (h) Insertion of the node x between u and $\{v,w\}$; (i) Insertion of the node x after $\{v,w\}$.

Figure 3. Illustration of the Insert Neighborhood. (a) Insertion of the edge $\{y,z\}$ between $s{l}_i$ and u with direction from y to z; (b) Insertion of the edge $\{y,z\}$ between $s{l}_i$ and u with direction from z to y; (c) Insertion of the edge $\{y,z\}$ between u and $\{v,w\}$ with direction from y to z; (d) Insertion of the edge $\{y,z\}$ between u and $\{v,w\}$ with direction from z to y; (e) Insertion of the edge $\{y,z\}$ after $\{v,w\}$ with direction from y to z; (f) Insertion of the edge $\{y,z\}$ after $\{v,w\}$ with direction from z to y; (g) Insertion of the node x between $s{l}_i$ and u; (h) Insertion of the node x between u and $\{v,w\}$; (i) Insertion of the node x after $\{v,w\}$.

Inspired by [17], each included node in a walk of the solution is associated with its arrival (arrive), starting (start) and leaving (leave) time, as well as the latest time the arrival at the node can take place (maxArrive), such that the walk remains feasible. Considering the walk $W_i=(w_0^i,w_1^i,\cdots ,w_{l_i-1}^i)$ in its node representation, that takes place in day d, the time attributes of each included node are given by the recursive formulas:

• arrive($w_0^i$) = start($w_0^i$) = leave($w_0^i$) = $s{t}_i$ and for each $k=0,1,\cdots ,l_i-2$
• arrive($w_{k+1}^i$) = $max($leave($w_k^i$),$O_{w_k^i,w_{k+1}^i}^i$) + $T_{w_k^i,w_{k+1}^i}$,
• start($w_{k+1}^i$) = $max($arrive($w_{k+1}^i$),$O_{w_{k+1}^i}^i$) and leave($w_{k+1}^i$) = start($w_{k+1}^i$) + $T_{w_{k+1}^i}$.

The maxArrive time of the nodes is calculated recursively from the ending location to the start as follows:

• maxArrive($w_{l_i-1}^i$) = $e{t}_i$ and for each $k=l_i-2,l_i-3,\cdots ,1,0$
• maxArrive($w_k^i$) = $min(C_{w_k^i}^i,C_{w_k^i,w_{k+1}^i}^i-T_{w_k^i},$maxArrive($w_{k+1}^i$) $-T_{w_k^i}-T_{w_k^i,w_{k+1}^i}$).

Using the previously introduced time attributes of the included nodes, checking that the insertion of a non-included TA after an included TA in a walk $W_i$ is feasible requires constant time, i.e., time independent of the size of the walk. To see this, consider that the candidate for insertion TA will be inserted between nodes $w_k^i$ and $w_{k+1}^i$, i.e., after the included TA whose last node is $w_k^i$, (i.e., either the profitable node $w_k^i$ or the profitable edge $(w_{k-1}^i,w_k^i)$) and that the walk takes place at day d. In the case that the candidate for insertion TA is the edge $\{y,z\}$, we have to examine both directions, i.e., from y to z and from z to y. The insertion of $\{y,z\}$ with the direction from y to z after node $w_k^i$ (see Figure 4a) is feasible if and only if the following conditions are satisfied:

• leave($w_k^i$) $\le C_{w_k^i,y}^i$
• the arrival time at y is at most $C_y^i$
• the leaving time from y is at most $C_{y,z}^i$
• the arrival time at z is at most $C_z^i$
• the leaving time from z is at most $C_{z,w_{k+1}^i}^i$
• the new arrival time at $w_{k+1}^i$ is at most maxArrive($w_{k+1}^i$)

If the insertion of the edge $(y,z)$ after the included TA (inclTA) with last node $w_k^i$ is feasible, the difference between the new arrival time at $w_{k+1}^i$ and the former one will be considered as the time shift. Notice that the insertion of a new TA in a walk always results in a positive time shift as this insertion is done over a non profitable edge corresponding to shortest time connection. A negative shift would be possible only if the insertion process allowed insertion over profitable edges. The pseudo code of the method that checks the feasibility of the insertion of the edge $(y,z)$ after an included TA with last node $w_k^i$ follows (Algorithm 1).

In a similar fashion, we may check if the insertion of a non-included profitable node x is feasible after an included TA, just by skipping the time window feasibility of the second node, i.e., the node x can be inserted after $w_k^i$ (see Figure 4b) if and only if the following conditions are satisfied:

• leave($w_k^i$) $\le C_{w_k^i,x}^i$
• the arrival time at x is at most $C_x^i$
• the leaving time from x is at most $C_{x,w_{k+1}^i}^i$
• the new arrival time at $w_{k+1}^i$ is at most maxArrive($w_{k+1}^i$)

Similarly to the Algorithm 1, there is the subroutine check_insertion_feasibilty$(x,w_k^i)$ which implements the logic above.

Figure 4. Illustration of insertion’s feasibility. (a) Insertion of the edge $\{y,z\}$ with the direction from y to z after node $w_k^i$; (b) Insertion of the node x after node $w_k^i$.

Figure 4. Illustration of insertion’s feasibility. (a) Insertion of the edge $\{y,z\}$ with the direction from y to z after node $w_k^i$; (b) Insertion of the node x after node $w_k^i$.

Algorithm 1 Check_insertion_feasibility $((y,z),w_k^i)$

▹ Check if the edge $(y,z)$ can be inserted between $w_k^i$ and $w_{k+1}^i$ shift ← 0 if leave($w_k^i$) >$C_{w_k^i,y}^i$then          ▹ departure when the route ahead is not available     return (FALSE,shift) firstArrive $\leftarrow max($leave($w_k^i$),$O_{w_k^i,y}^i)+T_{w_k^i,y}$ if firstArrive $>C_y^i$then                ▹ arrival at y after its closing time     return (FALSE,shift) firstLeave $\leftarrow max($firstArrive,$O_y^i)+T_y$ if firstLeave $>C_{y,z}^i$then            ▹ departure from y with closed route $(y,z)$     return (FALSE,shift) secondArrive $\leftarrow max($firstLeave,$O_{y,z}^i)+T_{y,z}$ if secondArrive $>C_z^i$then             ▹ arrival at z after its closing time     return (FALSE,shift) secondLeave $\leftarrow max($secondArrive,$O_z^i)+T_z$ if secondLeave $>C_{z,w_{k+1}^i}^i$then       ▹ departure from z with closed route $(z,w_{k+1}^i)$     return (FALSE,shift) newArrive $\leftarrow max($secondLeave,$O_{z,w_{k+1}^i}^i)+T_{z,w_{k+1}^i}$ if newArrive ≤ maxArrive($w_{k+1}^i$) then      ▹ the visits along $W_i$ after $w_{k+1}^i$ still valid     shift ← newArrive − arrive($w_{k+1}^i$)     return (TRUE,shift)

The insertBestTAIn method implements the local search step of the ILS algorithm. The local search step takes as input a walk $W_i$ of the current solution and considers for insertion in $W_i$ all TAs not yet included in any walk. For each such candidate TA every possible insert position is examined, i.e., the insertion between every consecutive pair of included TAs, and the position of the lowest shift is stored. When all candidate TAs and possible insert positions have been examined, the TA achieving the highest ratio of profit over shift is chosen for insertion in $W_i$. The use of the ratio of profit over the shift as a optimization criterion is a common approach in resource-constraint problems where profit should be maximized by properly selecting some items each having a cost and at the same time without exceeding a certain budget. A well-known algorithm which uses this sort of ratios is the optimal greedy algorithm for the fractional knapsack problem, an exemplary problem for all the resource-constrained problems. This particular ratio represents a trade-off between selecting a highly profitable item which at the same time costs a lot. Thus, it will be more beneficial if we first select highly profitable items of low cost for inclusion in the solution, that is, items giving large values in this particular ratio. If we took into account only the profit of a newly inserted TA without seeing the cost, namely the shift caused by the new insertion, we might have ended up choosing a highly profitable TA but associated with large shift value which would consume most of the available time of a walk. This in turn would exclude other subsequent insertions whose total profit could be actually higher than that of the costly TA.

The pseudocode of the insertBestTAIn method is listed below (Algorithm 2). It is also worth mentioning that for each walk, a doubly-linked list is used for storing the TAs in that walk. Specifically, the TAs are stored in this list in the same order that they appear in the walk. This data structure is the most appropriate for Algorithm 2 since for each candidate TA, each possible insertion point is examined along the walk and the linked lists are suitable for this sequential processing, in general. Also, after deciding the best insertion point for each candidate TA, a pointer to the node of the TA preceding that point is kept so that later the insertion of the highest overall ratio can be executed fast. Also, the update of the time attributes of TAs along the just expanded walk also requires a sequential visit of nodes of the corresponding list, which can be implemented fast.

Algorithm 2 InsertBestTAIn ($W_i$)

BestInsertionPoint $\leftarrow \varnothing$ BestTA ←∅ BestRatio $\leftarrow -\infty$ for each candidate TA $cp$ do     TempLowestShift $\leftarrow \infty$     TempBestInsertionPoint $\leftarrow \varnothing$     for each included TA $ip$ in $W_i$ do         (feasible, shift)=check_insertion_feasibility(cp,ip)         if feasible then            if shift < TempLowestShift then                TempLowestShift ← shift                TempBestInsertionPoint ← $ip$     if $\frac{{\mathrm{profit}}_{cp}}{\mathrm{TempLowestShift}}>\mathrm{BestRatio}$ then         BestInsertionPoint ← TempBestInsertionPoint         BestTA ← $cp$         BestRatio $\leftarrow \frac{{\mathrm{profit}}_{cp}}{\mathrm{TempLowestShift}}$ Insert the BestTA after BestInsertionPoint in $W_i$ Update the time attributes of all nodes along $W_i$

The ILS algorithm escapes from the current local optimum by applying the perturb method. In this method a randomly selected chain of consecutive TAs is removed from the TA representation of each walk $W_i$ in the solution. More specifically, for each walk $W_i$, the number of the TAs that will be removed (numberOfRemoved), is chosen randomly. Then, the position (L) in $W_i$ where the removal of the TAs will start, is selected randomly in the range $[1,m_i-1-\mathrm{numberOfRemoved}]$ where $m_i$ denotes the number of TAs in $W_i$. Finally, starting from the position L, (i.e., node $p_L^i$), numberOfRemoved consecutive TAs are removed from $W_i$ and the time attributes associated to each one of the nodes of $W_i$ are recalculated. The pseudocode of the method follows (Algorithm 3).

Algorithm 3 Perturb

for each walk $W_i$ do     $m_i\leftarrow$ the number of TAs in $W_i$     numberOfRemoved ← a random number in $[0,m_i]$     $L\leftarrow$ a random number in $[1,m_i-1-\mathrm{numberOfRemoved}]$     $R\leftarrow$ L + numberOfRemoved $-1$     remove all TAs from L ($p_L^i$) to R ($p_R^i$)     update the time attributes of all the nodes along $W_i$

The ILS algorithm loops for a number of iterations (numberOfIterations) that is given as a parameter. At each iteration, W is a random ordering of the set of the constructed walks $\{W_0,W_1,\dots ,W_{K-1}\}$. Note that at the first iteration each walk $W_i$ in W consists only of the staring and ending nodes, i.e., $W_i=(s{l}_i,e{l}_i),i=0,\cdots ,K-1$. Then, a loop is executed as long as W is not empty. Inside the loop, each walk $W_i$ in W is considered and the best insertion for this walk is applied. If no insertion was feasible, then $W_i$ is removed from W. When the loop is over, the current solution is considered. If its profit is the largest found so far, the current solution becomes the best solution found so far and its profit becomes the best profit (bestProfit). The last step in the loop is the perturb step. When the method ends, the best found solution as well as the best found profit are returned. The pseudocode of the ILS algorithm follows (Algorithm 4).

Algorithm 4 ILS

for numberOfIterations do     $W\leftarrow \{W_{j_0},W_{j_1},\dots ,W_{j_{K-1}}\}$ is a random ordering of the set of walks $\{W_0,W_1,\dots ,W_{K-1}\}$     $\mathrm{DelWalks}\leftarrow \varnothing$     while $W\ne \varnothing$ do         for each $W_i$ in W do            insertBestTAIn($W_i$)            if no insertion was feasible then                $\mathrm{DelWalks}\leftarrow \mathrm{DelWalks}\cup \{W_i\}$         $W\leftarrow W-\mathrm{DelWalks}$     if currentSolutionProfit > bestProfit then         bestProfit ← currentSolutionProfit         bestSolution ← currentSolution     perturb() return bestSolution;bestProfit

6. The Simulated Annealing Metaheuristic

The Simulated Annealing [18,20] is a metaheuristic method that escapes from a local optimum by allowing moves that result in worse solutions. An initial local optimum solution is usually constructed. Then, moves that result in worse solutions are allowed with a probability that is high in the early stages of the algorithm in order to search the solution space in more depth. This probability is reduced along the execution of the method until it becomes negligible in order to allow only improving solutions and find new (possibly better) local optima. In the generic scheme of the Simulated Annealing an auxiliary parameter is used, the temperature (T). The likelihood of worse resulting moves is usually a function inversely proportional to T and proportional to the decrease of the solution’s value, i.e., it may be $exp(\frac{\Delta P}{T})$, where $\Delta P$ is the difference of the value of the resulting solution from the initial. The temperature is initially set to the maximum temperature which is high enough to allow moves to worse solutions with high probability, and is decreased after a number of iterations. The temperature is usually decreased, multiplied by a cooling factor after a number of iterations (coolingIterations). In order to add diversification, we may allow a lot of schemes, i.e., when the temperature becomes too low, we may reinitialize it to the maximum temperature and start a new scheme again.

In our setting the initial solution of the Simulated Annealing procedure will be obtained from the SimultaneousWalkConstruction function. This function produces the same solution with the ILS algorithm executed for a single iteration.

In the Simulated Annealing procedure, apart from the Insert neighborhood we also consider the Replace neighborhood. The Replace neighborhood of a feasible MTOPTW solution consists of all the solutions that can be obtained by replacing an included profitable TA in a walk by a non-included profitable TA. For example, in Figure 5 the neighboring solutions of the walk with node representation $W_i=(s{l}_i,u,v,w,e{l}_i)$ in the Replace neighborhood are presented, considering that the only non-included profitable TAs are the edge $\{y,z\}$ and the node x. Figure 5a,b depict the replacement of u by the edge $\{y,z\}$, considering both directions that the edge can be traversed, i.e., from y to z and from z to y, respectively. Similarly, Figure 5c,d depict the replacement of $\{v,w\}$ by the edge $\{y,z\}$, while Figure 5e,f depict the replacement of u and $\{v,w\}$ by the non-included profitable node x, respectively.

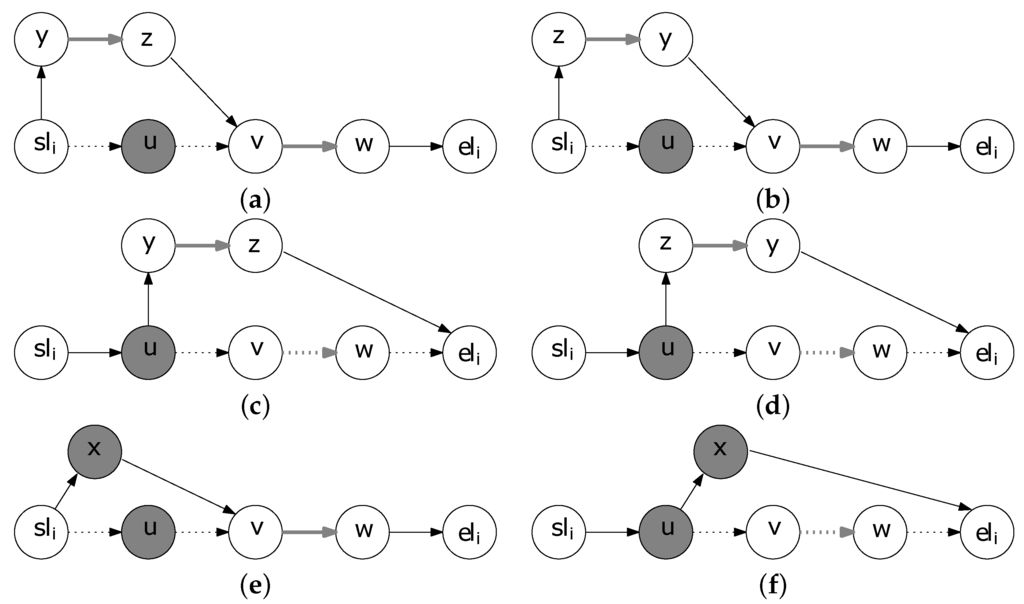
Figure 5. Illustration of Replace Neighborhood. (a) Replacement of the node u by the edge $\{y,z\}$ using the direction from y to z; (b) Replacement of the node u by the edge $\{y,z\}$ using the direction from z to y; (c) Replacement of the edge $\{v,w\}$ by the edge $\{y,z\}$ using the direction from y to z; (d) Replacement of the edge $\{v,w\}$ by the edge $\{y,z\}$ using the direction from z to y; (e) Replacement of the node u by the node x; (f) Replacement of the edge $\{v,w\}$ by the node x.

Figure 5. Illustration of Replace Neighborhood. (a) Replacement of the node u by the edge $\{y,z\}$ using the direction from y to z; (b) Replacement of the node u by the edge $\{y,z\}$ using the direction from z to y; (c) Replacement of the edge $\{v,w\}$ by the edge $\{y,z\}$ using the direction from y to z; (d) Replacement of the edge $\{v,w\}$ by the edge $\{y,z\}$ using the direction from z to y; (e) Replacement of the node u by the node x; (f) Replacement of the edge $\{v,w\}$ by the node x.

Note that the replacement of an included profitable TA $p_k^i$ by a non-included one candTA, is equivalent to the removal of $p_k^i$ followed by the insertion of candTA between $p_{k-1}^i$ and $p_{k+1}^i$.

The Simulated Annealing procedure takes into account five parameters: the number of schemes (numberOfSchemes), the maximum temperature (maxTemperature), the number of iterations executed in each scheme (schemeIterations), the cooling factor (coolingFactor) and the iterations needed in order to update the temperature (coolingIterations). The initial solution of the Simulated Annealing procedure is obtained by the SimultaneousWalkConstruction function. This function derives the same solution with the ILS algorithm executed for a single iteration. Then, the Simulated Annealing method loops for numberOfSchemes schemes. In each scheme, the temperature (T) initially becomes equal to the maxTemperature and an inner loop is executed for schemeIterations iterations. In the inner loop, a non-included profitable piece (candPiece) is randomly selected as well as a walk and an included piece (inclPiece). Then, if candPiece can be inserted after inclPiece without removing any included piece, the insertion takes place. If the insertion is not feasible, then the replacement of the inclPiece by candPiece is examined. If the replacement is feasible, then a randomly computed real number (prob) is obtained in the range $[0,1]$ and if $\mathrm{prob}<exp(\frac{\mathrm{diff}}{T})$, where diff is the difference of profits of candPiece and inclPiece, then candPiece replaces inclPiece. If either the insertion or the replacement results in a solution with the highest profit found, then the solution and its profit are stored as the bestSolution and bestProfit, respectively. Furthermore, if the inner loop has been executed for coolingIterations iterations since the last time the temperature was updated, then the temperature T gets the value $T·\mathrm{coolingFactor}$. When, the first loop is completed, the algorithm returns the best solution and profit found. The pseudocode of the Simulated Annealing algorithm is listed in the sequel (Algorithm 5).

Algorithm 5 The SA Metaheuristic

(bestSol,bestProfit) ← SimultaneousWalkConstruction for numberOfSchemes do     $T\leftarrow$ maxTemperature     counter=1     for schemeIterations do         $candTA$ ← a non-included TA randomly selected         $W_i$ ← a random walk from $\{W_0,W_1,\dots ,W_{K-1}\}$         $inclTA$ ← a randomly selected included TA or the starting location of $W_i$         if the insertion of $candTA$ after $inclTA$ in $W_i$ is feasible then            (Solution,Profit) ← insertion of $candTA$ after $inclTA$ in $W_i$         else if $candTA$ can replace $inclTA$ in $W_i$ then            diff ← profit of $candTA$− profit of $inclTA$            $\mathrm{prob}\leftarrow$ a random real in the range $[0,1]$            if $\mathrm{prob}<exp(\frac{\mathrm{diff}}{T})$ then (Solution,Profit) ← replacement of $inclTA$ from $candTA$         else(Solution,Profit) ← (∅,$-\infty$)         if Profit > bestProfit then            bestProfit ← Profit            bestSolution ← Solution         if counter $mod$ coolingIterations $=0$ then $T\leftarrow T·\mathrm{coolingFactor}$         counter ← counter+1 return (bestSolution,bestProfit)

For an effective algorithm, SA parameters should depend on the particular solution. In our setting, we allow only small changes in the local optimum solutions. Thus, the temperature starts decreasing shortly after the insertion of the first TAs in the walks. If coolIterations was much higher than the size of the solution, a very different solution would be obtained finally, especially with high initial temperature. On the other hand, if coolIterations is relatively small compared to the solution’s size, the solution will not escape from the local optimum. Thus, if #TAs is the number of TAs in the initial solution of SimultaneousWalkConstruction, the coolingIterations is set equal to #TAs · coolItFactor where coolItFactor is a constant much smaller than 1. By the same token, schemeIterations is given by the product coolingIterations · schemeItFactor.

7. Experimental Results

7.1. Test Instances

To evaluate and compare the proposed algorithms, we have created test instances containing data related to the city of Athens, Greece (http://dgavalas.ct.aegean.gr/public/aop_instances/ instance.zip). Our topology contains 18 scenic routes and 113 points of interest (POIs) that have been compiled from various tourist portals (http://www.tripadvisor.com/, http://index.pois.gr/) and web services offering open APIs (https://developers.google.com/places/documentation/). We have also included 100 hotels in our topology. The hotels are used as starting and ending locations of daily tourist walks. Therefore, the graph consists of 249 nodes, i.e., the endpoints of the scenic routes (36 nodes) plus the 113 POIs and the 100 hotels. The travel costs between the locations of the topology were calculated using the OpenTripPlanner project (http://www.opentripplanner.org/).

The attributes of the POIs (time windows, visiting times and profits) are chosen as follows (see also Table 1):

• 20% of POIs are open all day long in both weekdays and weekends, i.e., their time window is 0–1439, while they have profit and visiting time between 15–30.
• 20% of the POIs have time windows 540–960 for weekdays and are closed in weekends, while their profit and visiting time is between 30–60.
• 20% of POIs have time windows 540–960 for weekdays and weekends, while their profit is between 70–100 and the visiting time is between 60–120.
• 20% of POIs have time windows 840–1140 for weekdays and weekends, while their profit and visiting time is between 30–60.
• 20% of POIs have time windows 480–780 for weekdays and are closed in weekends, while their profit is between 30–60.

The attributes of the scenic routes (time windows and profits) are chosen as follows:

• 25% of them are open all day long (their time windows is between 0–1439) for each day of the week.
• 25% of them have time windows 540–960 for weekdays and weekends.
• 25% of scenic routes have time windows 480–840 for weekdays and weekends.
• 25% of the scenic routes have time windows 540–960 for weekdays and are closed in weekends.
• All scenic routes have profit between 10 and 50.

Table 1. Points of interest (POI) and scenic route parameters.

	Percent	Time Window (Min)		Visiting Time (Min)	Profit
		Weekdays	Weekends
POIs	20%	all day	all day	15–30	15–30
	20%	540–960	closed	30–60	30–60
	20%	540–960	540–960	60–120	70–100
	20%	840–1140	840–1140	30–60	30–60
	20%	480–780	closed	30–60	30–60
Scenic routes	25%	all day	all day	N/A	10–50
	25%	540–960	540–960		10–50
	25%	480–840	480–840		10–50
	25%	540–960	closed		10–50

Table 1. Points of interest (POI) and scenic route parameters.

	Percent	Time Window (Min)		Visiting Time (Min)	Profit
		Weekdays	Weekends
POIs	20%	all day	all day	15–30	15–30
	20%	540–960	closed	30–60	30–60
	20%	540–960	540–960	60–120	70–100
	20%	840–1140	840–1140	30–60	30–60
	20%	480–780	closed	30–60	30–60
Scenic routes	25%	all day	all day	N/A	10–50
	25%	540–960	540–960		10–50
	25%	480–840	480–840		10–50
	25%	540–960	closed		10–50

Solutions of 1, 2, 3 and 4 walks are required. For each case, 100 test instances are considered, each with starting/ending location one of the hotels. In particular, pref100–pref199 preferences ask for solutions of 1 walk, while pref2*(pref200–pref299), pref3*(pref300–pref399) and pref4*(pref400–pref499) ask for $2,3$ and 4 walks, respectively. Considering the starting/ending time of each walk in an instance, we assign the starting time to a randomly chosen time between 480–600, while we assign a randomly chosen number between 840–1080 to the ending time. Note, that for instances requiring more than 1 walk, different walks have the same starting/ending location, however they usually have different starting/ending times.

7.2. Results

All computations have been executed on a personal computer Intel Core i3 with 2.30 GHz processor and 4 GB RAM. Our tests aim at comparing the presented ILS and SA algorithm. The algorithms are compared with respect to the obtained profit and the execution time. Mostly prefered solutions are those associated with high profit values (higher profit values denote higher quality solutions) and reduced execution time (as this denotes improved suitability for real-time applications). Both algorithms have been coded in C++.

The numberOfIterations parameter in ILS takes the values 100, 200, 400 and 800 and the corresponding results are reported as ILS_100, ILS_200, ILS_400 and ILS_800. We use the same parameter numberOfIterations(=numSchemes · schemeIt) for denoting the total number of iterations in SA. The parameters maxTemperature and coolingFactor are always set equal to 10 and $0.5$, respectively. These values have been chosen due to providing marginally better results, as demonstrated experimentally. Also, they guarantee that a large part of the search space is searched. The other parameters of SA are set to the following values: numberOfIterations = 0.5 and 1 million, coolItFactor = $0.8,0.5$ and $0.25$, and the schemeItFactor = 8 and 10. We use the notation SA_numberOfIterations_coolItFactor_schemeItFactor for denoting the results for the SA for specific values of the SA parameters; for example, for numberOfIterations equal to $0.5$ million, coolItFactor equal to $0.8$ and schemeItFactor equal to 8, the results obtained are indicated with SA_0.5M_0.8_8.

Each one of the proposed algorithms is executed 5 times for each instance. Table 2 illustrates the experimental results compiled from the executed algorithms for each value of the parameters. The results obtained are averaged with respect to the number of requested walks. In more detail, each algorithm with its associated parameter values is shown in the first column. The next four pairs of columns present the experimental results obtained for instances requesting 1, 2, 3 and 4 walks, respectively. Each pair of columns shows the average profit obtained and the average execution time of each algorithm for the 5 executions of each instance asking for a specific number of walks. So, the average profit and execution time (in ms) for instances requesting 1 walk (pref100-pref199) are given in the first pair of columns of Table 2, while the average results obtained for 2 (pref200-pref299), 3 (pref300-pref399) and 4 (pref400-pref499) walks are given in the second, third and fourth pair of columns of Table 2, respectively.

Table 2. Experimental Results–Same number of Iterations.

Algorithm	1 Walk		2 Walks		3 Walks		4 Walks
	Profit	Time (ms)	Profit	Time (ms)	Profit	Time (ms)	Profit	Time (ms)
ILS_100	816.698	295.728	1359.972	340.59	1865.546	387.194	2286.534	402.608
ILS_200	821.578	590.264	1365.354	678.658	1872.24	771.248	2291.818	803.022
ILS_400	823.754	1179.93	1368.992	1354.696	1876.248	1542.638	2296.038	1604.118
ILS_800	826.342	2353.616	1375.468	2708.656	1880.298	3080.624	2299.984	3203.474
SA_0.5M_0.8_8	818.59	271.05	1333.24	275.958	1815.88	278.432	2233.714	279.096
SA_0.5M_0.5_8	818.16	271.778	1332.56	276.204	1816.134	278.806	2233.43	279.62
SA_0.5M_0.25_8	819.644	272.708	1333.426	277.302	1816.378	279.238	2233.71	279.954
SA_0.5M_0.8_10	820.736	268.846	1335.488	274.206	1818.05	276.85	2236.38	277.52
SA_0.5M_0.5_10	820.58	269.698	1334.888	274.414	1819.804	276.796	2235.72	277.838
SA_0.5M_0.25_10	818.574	271.284	1334.864	275.728	1819.41	277.968	2235.454	278.124
SA_1M_0.8_8	821.072	525.35	1333.036	534.368	1815.194	537.652	2234.246	538.258
SA_1M_0.5_8	820.6	526.03	1334.716	535.174	1815.97	538.54	2234.072	538.6
SA_1M_0.25_8	820.324	530.034	1334.178	536.93	1815.918	539.41	2233.732	539.794
SA_1M_0.8_10	820.066	522.626	1336.474	531.182	1818.038	534.66	2235.464	535.366
SA_1M_0.5_10	820.944	523.026	1336.128	531.81	1819.59	534.704	2237.192	535.798
SA_1M_0.25_10	820.3	527.324	1335.462	533.492	1820.054	536.534	2236.73	537.258

Table 2. Experimental Results–Same number of Iterations.

Algorithm	1 Walk		2 Walks		3 Walks		4 Walks
	Profit	Time (ms)	Profit	Time (ms)	Profit	Time (ms)	Profit	Time (ms)
ILS_100	816.698	295.728	1359.972	340.59	1865.546	387.194	2286.534	402.608
ILS_200	821.578	590.264	1365.354	678.658	1872.24	771.248	2291.818	803.022
ILS_400	823.754	1179.93	1368.992	1354.696	1876.248	1542.638	2296.038	1604.118
ILS_800	826.342	2353.616	1375.468	2708.656	1880.298	3080.624	2299.984	3203.474
SA_0.5M_0.8_8	818.59	271.05	1333.24	275.958	1815.88	278.432	2233.714	279.096
SA_0.5M_0.5_8	818.16	271.778	1332.56	276.204	1816.134	278.806	2233.43	279.62
SA_0.5M_0.25_8	819.644	272.708	1333.426	277.302	1816.378	279.238	2233.71	279.954
SA_0.5M_0.8_10	820.736	268.846	1335.488	274.206	1818.05	276.85	2236.38	277.52
SA_0.5M_0.5_10	820.58	269.698	1334.888	274.414	1819.804	276.796	2235.72	277.838
SA_0.5M_0.25_10	818.574	271.284	1334.864	275.728	1819.41	277.968	2235.454	278.124
SA_1M_0.8_8	821.072	525.35	1333.036	534.368	1815.194	537.652	2234.246	538.258
SA_1M_0.5_8	820.6	526.03	1334.716	535.174	1815.97	538.54	2234.072	538.6
SA_1M_0.25_8	820.324	530.034	1334.178	536.93	1815.918	539.41	2233.732	539.794
SA_1M_0.8_10	820.066	522.626	1336.474	531.182	1818.038	534.66	2235.464	535.366
SA_1M_0.5_10	820.944	523.026	1336.128	531.81	1819.59	534.704	2237.192	535.798
SA_1M_0.25_10	820.3	527.324	1335.462	533.492	1820.054	536.534	2236.73	537.258

Based on the experimental results, we can easily conclude that increasing the algorithms’ execution time, i.e., increasing the allowed number of iterations, improves the solutions’ quality marginally. To see this, consider first the ILS algorithm. The average profit for 200 iterations is higher than that for 100 iterations by less than $0.7\%$ for all number of walks. The same holds when comparing the results for 400 and 200 iterations as well as for 800 and 400 iterations. With regard to the SA algorithm, the profit for one million iterations is higher than that of half a million iterations by at most $0.5\%$ for any number of walks.

As for the parameters coolItFactor and schemeItFactor, the results indicate that the parameter coolItFactor does not significantly influence the output of SA algorithm. For example, for half a million iterations and schemeItFactor equal to 10, the difference of SA_0.5M_0.8_10’s profit and SA_0.5M_0.25_10’s profit is less than $0.27\%$ and this is the largest difference, given that the other parameters are the same. The parameter schemeItFactor seems to influence the results slightly more, however, the difference in profit is always less than $0.5\%$.

The experimental results demonstrate that ILS outperforms SA with respect to solution quality, yet, at the expense of longer execution time. For one walk, the solutions obtained by both ILS and SA are of similar profit, i.e., the ILS_100 produces slightly inferior solutions than those of SA overall, while ILS_200, ILS_400, ILS_800 produce marginally better solutions, however, with higher running time. For more than one walks, ILS prevails over SA even with 100 iterations. For example, ILS_100’s profit for two walks is higher than that of SA by at least $1.7\%$, regardless of the particular parameters of SA. For three or four walks, the profit is at least $2.47\%$ and $2.19\%$ respectively, higher than the profit obtained from any execution of SA. However, ILS requires more execution time than SA. For constant number of iterations, the running time of ILS increases with the number of walks, since in the perturbation step, ILS removes a chain of included TAs from each walk. This increases the running time when the number of walks is large, since reaching a local optimum requires inserting TAs to all the walks. On the other hand, the execution time of the SA algorithm does not depend on the number of the constructed walks, but only on the number of iterations. This is because at each step of SA, only one walk is modified, hence, the execution time is independent of the number of walks.

In the sequel we examine the behavior of ILS and SA in the case that the same running time is allowed to both algorithms, whatever the number of iterations. Table 3, Table 4 and Table 5 present the results obtained when the running time is fixed to one second, five and ten seconds respectively. Again, the experimental results show that ILS outperforms SA in solution quality. For one walk, the solutions obtained by both ILS and SA are of similar profit while the difference in solution quality increases as the number of walks increases. A reasonable explanation for the observed differences is that in the case of multiple walks, SA does not explicitly allow an exchange between walks, so it may move around less efficiently within the feasible region.

Table 3. Experimental Results—Same Execution Time (1 s).

Algorithm	1 Walk	2 Walks	3 Walks	4 Walks
	Profit	Profit	Profit	Profit
ILS	824.54	1367.09	1872.44	2292.89
SA_0.8_8	822.47	1332.41	1816.25	2234.34
SA_0.5_8	821.95	1332.52	1815.94	2234.58
SA_0.25_8	822.08	1332.13	1816.58	2234.47
SA_0.8_10	822.84	1335.05	1819.53	2236.54
SA_0.5_10	821.79	1333.94	1819.09	2235.98
SA_0.25_10	822.92	1336.21	1818.63	2236.30

Table 3. Experimental Results—Same Execution Time (1 s).

Algorithm	1 Walk	2 Walks	3 Walks	4 Walks
	Profit	Profit	Profit	Profit
ILS	824.54	1367.09	1872.44	2292.89
SA_0.8_8	822.47	1332.41	1816.25	2234.34
SA_0.5_8	821.95	1332.52	1815.94	2234.58
SA_0.25_8	822.08	1332.13	1816.58	2234.47
SA_0.8_10	822.84	1335.05	1819.53	2236.54
SA_0.5_10	821.79	1333.94	1819.09	2235.98
SA_0.25_10	822.92	1336.21	1818.63	2236.30

Table 4. Experimental Results—Same Execution Time (5 s).

Algorithm	1 Walk	2 Walks	3 Walks	4 Walks
	Profit	Profit	Profit	Profit
ILS	832.48	1381.05	1886.10	2303.01
SA_0.8_8	823.34	1332.36	1816.23	2233.94
SA_0.5_8	824.15	1332.59	1815.91	2234.28
SA_0.25_8	824.05	1333.06	1816.29	2234.76
SA_0.8_10	824.70	1335.58	1819.55	2236.04
SA_0.5_10	824.80	1336.19	1818.93	2236.74
SA_0.25_10	825.53	1335.78	1819.42	2235.84

Table 4. Experimental Results—Same Execution Time (5 s).

Algorithm	1 Walk	2 Walks	3 Walks	4 Walks
	Profit	Profit	Profit	Profit
ILS	832.48	1381.05	1886.10	2303.01
SA_0.8_8	823.34	1332.36	1816.23	2233.94
SA_0.5_8	824.15	1332.59	1815.91	2234.28
SA_0.25_8	824.05	1333.06	1816.29	2234.76
SA_0.8_10	824.70	1335.58	1819.55	2236.04
SA_0.5_10	824.80	1336.19	1818.93	2236.74
SA_0.25_10	825.53	1335.78	1819.42	2235.84

Table 5. Experimental Results—Same Execution Time (10 s).

Algorithm	1 Walk	2 Walks	3 Walks	4 Walks
	Profit	Profit	Profit	Profit
ILS	834.46	1386.06	1889.16	2306.26
SA_0.8_8	824.85	1333.96	1816.68	2234.28
SA_0.5_8	825.01	1333.66	1815.88	2234.76
SA_0.25_8	823.98	1333.85	1815.84	2234.60
SA_0.8_10	824.54	1336.20	1819.04	2236.72
SA_0.5_10	824.85	1336.39	1818.31	2237.52
SA_0.25_10	825.62	1336.11	1818.51	2237.23

Table 5. Experimental Results—Same Execution Time (10 s).

Algorithm	1 Walk	2 Walks	3 Walks	4 Walks
	Profit	Profit	Profit	Profit
ILS	834.46	1386.06	1889.16	2306.26
SA_0.8_8	824.85	1333.96	1816.68	2234.28
SA_0.5_8	825.01	1333.66	1815.88	2234.76
SA_0.25_8	823.98	1333.85	1815.84	2234.60
SA_0.8_10	824.54	1336.20	1819.04	2236.72
SA_0.5_10	824.85	1336.39	1818.31	2237.52
SA_0.25_10	825.62	1336.11	1818.51	2237.23

8. Conclusions

In this work, we introduced the Mixed Team Orienteering Problem with Time Windows, i.e., the extension of the MOP to multiple tours which can be used for modeling a realistic variant of the Tourist Trip Design Problem where the objective is the derivation of near-optimal multiple-day tours for tourists visiting a destination which features several points of interest (POIs) and scenic routes. We presented the first two algorithmic (metaheuristic) approaches to tackle it. We employed a preprocessing phase for speeding-up the local search operations heavily used by both heuristics. The main conclusion from the experimental evaluation of the two proposed heuristics is that the ILS approach derives solutions of higher quality than those of the SA approach.