A Novel Complex-Valued Encoding Grey Wolf Optimization Algorithm
Abstract
:1. Introduction
2. Grey Wolf Optimization (GWO)
| Algorithm 1. GWO algorithm |
| 1. Initialize the grey wolf population |
| 2. Initialize , , and |
| 3. For all do |
| 4. Calculate fitness |
| 5. End for |
| 6. Get the first three best wolves as , , and |
| 7. While () |
| 8. For each search agent |
| 9. Update the position of the current search agent by Equation (5) |
| 10. End for |
| 11. Update , , and |
| 12. For all do |
| 13. Calculate fitness |
| 14. End for |
| 15. Update , , and |
| 16. |
| 17. End while |
| 18. Return |
3. Complex-Valued Encoding Grey Wolf Optimization Algorithm (CGWO)
3.1. The Complex-Valued Encoding Method
| … |
3.1.1. Initializing the Complex-Valued Encoding Population
3.1.2. The Updating Method of CGWO
3.1.3. The Calculation Method of Fitness Value
3.2. CGWO Algorithm
| Algorithm 2. CGWO algorithm |
| 1. Initialize the grey wolf population: Let |
| 2. Get the real and imaginary part of the complex number by Equation (8) |
| 3. Convert to real variables by Equations (15) and (16) |
| 4. For all do |
| 5. Calculate fitness |
| 6. End for |
| 7. Get the first three best wolves as , , and |
| 8. While () |
| 9. For each search agent |
| 10. Update the real part of the current search agent by Equations (9–11) |
| 11. Update the imaginary part of the current search agent by Equations (12–14) |
| 12. End for |
| 13. Modify the real and imaginary part by “DE/best/2” |
| 14. Select randomly |
| 15. |
| 16. Update , , and |
| 17. Convert to real variables by Equations (15) and (16) |
| 18. For all do |
| 19. Calculate fitness |
| 20. End for |
| 21. Update , , and |
| 22. |
| 23. End while |
| 24. Return |
4. Experimental Results and Discussion
4.1. Simulation Platform
4.2. Benchmark Functions
| Benchmark Functions | Range | Dim | |
|---|---|---|---|
| Unimodal functions | 0 | ||
| : Sphere function | [−100,100] | 10,30,50,100,200,300,400 | 0 |
| : Schwefel’s problem 2.22 | [−10,10] | 10,30,50,100,200,300,400 | 0 |
| : Schwefel’s problem 2.21 | [−100,100] | 10,30,50,100,200,300,400 | 0 |
| : Generalized Rosenbrock’s function | [−30,30] | 10,30,50,100,200,300,400 | 0 |
| : Quartic function i.e., Niose | [−1.28,1.28] | 10,30,50,100,200,300,400 | 0 |
| : Shifted sphere function | [−100,100] | 10,30,50,100,200,300,400 | −450 |
| : Shifted Schwefel’s | [−100,100] | 10,30,50,100,200,300,400 | −450 |
| : Generalized Rosenbrock’s function | [−100,100] | 10,30,50,100,200,300,400 | −450 |
| Multimodal functions | |||
| : Generalized Rastrigin’s function | [−5.12,5.12] | 10,30,50,100,200,300,400 | 0 |
| : Ackley’s function | [−32,32] | 10,30,50,100,200,300,400 | 0 |
| : Generalized Griewank function | [−600,600] | 10,30,50,100,200,300,400 | 0 |
| : Generalized Penalized 1 function | [−50,50] | 10,30,50,100,200,300,400 | 0 |
| : Alpine function | [−10,10] | 10,30,50,100,200,300,400 | 0 |
| : Shifted Rosenbrock’s function | [−100,100] | 10,30,50,100,200,300,400 | 390 |
| : Shifted Rastrigin’s function | [−5,5] | 10,30,50,100,200,300,400 | −330 |
| : Expanded extended Griewank’s plus Rosenbrock’s function | [−3,1] | 10,30,50,100,200,300,400 | −130 |
| Algorithm | Parameter | Value |
|---|---|---|
| CGWO | Number of grey wolves | 50 (dim = 10, 30, 50, 100, 200, 300, 400) |
| Linearly decreased from 2 to 0 | ||
| Scaling factor | 0.1 | |
| Max iteration | 500 | |
| Stopping criteria | Max iteration | |
| DGWO | Number of grey wolves | 50 (dim = 10, 30, 50, 100, 200, 300, 400) |
| Linearly decreased from 2 to 0 | ||
| Scaling factor | 0.1 | |
| Max iteration | 500 | |
| Stopping criteria | Max iteration | |
| GWO | Number of grey wolves | 50 (dim = 10, 30, 50, 100, 200, 300, 400) |
| Linearly decreased from 2 to 0 | ||
| Max iteration | 500 | |
| Stopping criteria | Max iteration | |
| GGSA | Number of particles | 50 (dim = 10, 30, 50, 100, 200, 300, 400) |
| 1 | ||
| 20 | ||
| Max iteration | 500 | |
| Stopping criteria | Max iteration | |
| ABC | Number of bees | 50 (dim = 10, 30, 50, 100, 200, 300, 400) |
| Limit | dim | |
| Max iteration | 500 | |
| Stopping criteria | Max iteration |
| Dim | ||||||||
|---|---|---|---|---|---|---|---|---|
| CGWO | ||||||||
| 10 | 8.0777E −20 ± 0.0000E+00 | 0.0000E+00 ± 0.0000E+00 | 8.4729E − 43 ± 3.2969E−42 | 5.5016E−04 ± 3.5231E−04 | 2.9091E−04 ± 4.3211E−04 | −4.4889E+02 ± 1.0776E+00 | −1.9339E+02 ± 4.0809E+02 | −3.0527E+01 ± 8.6684E+02 |
| 30 | 1.4398E−71 ± 4.8237E−71 | 1.2998E−39 ± 2.5518E−39 | 4.1033E−15 ± 1.0312E−14 | 1.8100E−02 ± 1.0057E−02 | 7.2160E−04 ± 5.1996E−04 | −4.4915E+02 ± 5.8509E−01 | 1.1352E+04 ± 3.3158E+03 | 1.7787E+04 ± 5.0959E+03 |
| 50 | 3.7431E−50 ± 1.1867E−49 | 4.4998E−27 ± 8.4186E−27 | 1.9027E−09 ± 3.3531E−09 | 4.7794E+01 ± 1.2119E+00 | 9.3468E−04 ± 6.6121E−04 | −1.2732E+02 ± 1.9633E+02 | 3.4063E+04 ± 5.9884E+03 | 3.9004E+04 ± 5.1989E+03 |
| 100 | 7.3423E−30 ± 3.1587E−29 | 1.6124E−16 ± 3.5312E−16 | 3.9660E−01 ± 1.7639E+00 | 9.7484E+01 ± 7.2242E−01 | 1.5909E−03 ± 1.0240E−03 | 2.1759E+04 ± 7.5580E+03 | 1.2869E+05 ± 2.1842E+04 | 1.8549E+05 ± 2.6968E+04 |
| 200 | 1.4070E−19 ± 3.6121E−19 | 1.5064E−10 ± 2.5796E−10 | 1.2359E+00 ± 1.0011E+00 | 1.9738E+02 ± 5.6856E−01 | 4.2014E−03 ± 2.7884E−03 | 5.0140E+05 ± 1.7003E+04 | 1.9216E+06 ± 1.9621E+05 | 3.3979E+06 ± 3.5774E+05 |
| 300 | 2.8113E−15 ± 5.6022E−15 | 7.0321E−08 ± 6.7782E−08 | 3.6366E+00 ± 1.0280E+00 | 2.9626E+02 ± 1.5730E−01 | 4.7128E−02 ± 1.4278E−01 | 8.0008E+05 ± 1.5269E+04 | 4.1571E+06 ± 5.1269E+05 | 4.9800E+06 ± 6.5065E+05 |
| 400 | 3.4737E−12 ± 7.1267E−12 | 3.0327E−06 ± 2.5241E−06 | 2.1025E+01 ± 5.6457E+00 | 3.9548E+02 ± 4.4863E−01 | 4.2727E−02 ± 7.0163E−02 | 1.1130E+06 ± 1.7554E+04 | 7.5565E+06 ± 1.0621E+06 | 1.2198E+07 ± 2.2352E+06 |
| DGWO | ||||||||
| 10 | 1.1360E−06 ± 4.7184E−07 | 1.9937E−04 ± 4.2277E−05 | 2.1312E−01 ± 9.2890E−02 | 8.3090E+00 ± 1.0305E+00 | 3.4367E−02 ± 1.0888E−02 | 2.3163E+03 ± 2.5481E+03 | 4.7482E+03 ± 2.8687E+03 | 7.5883E+03 ± 4.1176E+03 |
| 30 | 7.3667E−02 ± 1.8195E−02 | 1.1711E−01 ± 2.9090E−02 | 2.4785E+01 ± 5.9882E+00 | 4.3406E+01 ± 3.4415E+01 | 1.2390E−01 ± 2.3564E−02 | 2.6585E+04 ± 8.6640E+03 | 2.1542E+04 ± 6.2293E+03 | 4.3638E+04 ± 1.0900E+04 |
| 50 | 2.4476E+00 ± 6.0988E−01 | 9.9901E−01 ± 1.5113E−01 | 4.4000E+01 ± 5.2551E+00 | 1.4580E+02 ± 6.4864E+01 | 2.7228E−01 ± 4.7428E−02 | 4.7804E+04 ± 1.1059E+04 | 4.3616E+04 ± 1.1237E+04 | 1.2208E+05 ± 3.4060E+04 |
| 100 | 1.0877E+02 ± 1.6232E+01 | 1.0042E+01 ± 1.1552E+00 | 6.2858E+01 ± 6.3695E+00 | 2.3664E+03 ± 4.5620E+02 | 7.9759E−01 ± 9.3228E−02 | 1.1471E+05 ± 1.3791E+04 | 1.6432E+05 ± 2.4980E+04 | 5.1550E+05 ± 8.8341E+04 |
| 200 | 1.9645E+03 ± 1.9254E+02 | 5.2295E+01 ± 5.2466E+00 | 7.8652E+01 ± 3.6098E+00 | 1.0148E+05 ± 1.9510E+04 | 3.5616E+00 ± 4.4507E−01 | 8.4322E+05 ± 6.2948E+04 | 3.6436E+06 ± 4.5426E+05 | 4.4553E+06 ± 8.5486E+05 |
| 300 | 7.6823E+03 ± 5.6428E+02 | 1.2337E+02 ± 6.7399E+00 | 8.3316E+01 ± 4.7333E+00 | 9.1603E+05 ± 2.4689E+05 | 1.0789E+01 ± 1.3892E+00 | 1.3864E+06 ± 6.5113E+04 | 8.7852E+06 ± 1.4109E+06 | 9.9956E+06 ± 2.2905E+06 |
| 400 | 1.9250E+04 ± 1.5647E+03 | 2.1533E+02 ± 8.3003E+00 | 8.5761E+01 ± 4.7751E+00 | 3.8053E+06 ± 7.6087E+05 | 2.9632E+01 ± 2.5582E+00 | 1.9203E+06 ± 9.4239E+04 | 1.5215E+07 ± 3.6273E+06 | 1.7677E+07 ± 2.6455E+06 |
| GWO | ||||||||
| 10 | 2.5805E −69 ± 7.6450E −69 | 2.7692E−40 ± 6.3910E−40 | 2.7524E−22 ± 3.4511E−22 | 6.4337E+00 ± 6.8791E−01 | 4.9730E−04 ± 4.5395E−04 | −4.0937E+02 ± 1.3607E+02 | 8.9662E+02 ± 1.1030E+03 | 1.7674E+03 ± 1.6258E+03 |
| 30 | 2.1070E−33 ± 4.4964E−33 | 8.1447E−20 ± 6.4357E−20 | 1.4089E−08 ± 1.2034E−08 | 2.6904E+01 ± 9.2161E−01 | 1.1748E−03 ± 5.2271E−04 | 9.2889E+02 ± 1.6474E+03 | 2.0771E+04 ± 4.9830E+03 | 2.8285E+04 ± 6.7382E+03 |
| 50 | 6.2067E−24 ± 7.8311E−24 | 1.3044E−14 ± 6.4281E−15 | 3.0825E−05 ± 3.2791E−05 | 4.6971E+01 ± 9.0888E−01 | 2.2703E−03 ± 1.1187E−03 | 4.8602E+03 ± 2.9308E+03 | 5.4895E+04 ± 1.1910E+04 | 7.7969E+04 ± 2.8450E+04 |
| 100 | 5.7949E−15 ± 4.8422E−15 | 1.5493E−09 ± 7.8417E−10 | 1.9884E−01 ± 2.4874E−01 | 9.7657E+01 ± 7.4917E−01 | 4.2428E−03 ± 1.5897E−03 | 2.9473E+04 ± 5.9709E+03 | 3.4850E+05 ± 8.0002E+04 | 4.7813E+05 ± 1.4313E+05 |
| 200 | 2.2316E−09 ± 1.2787E−09 | 3.1753E−06 ± 6.9032E−07 | 1.6292E+01 ± 6.3378E+00 | 1.9754E+02 ± 6.5867E−01 | 9.3098E−03 ± 2.8591E−03 | 5.9583E+05 ± 3.0287E+04 | 2.7874E+06 ± 3.3331E+05 | 3.4073E+06 ± 4.9504E+05 |
| 300 | 6.3147E−07 ± 2.7324E−07 | 1.0829E−04 ± 1.8965E−05 | 3.7255E+01 ± 8.5676E+00 | 2.9764E+02 ± 3.1645E−01 | 1.4354E−02 ± 4.0319E−03 | 9.4557E+05 ± 5.1007E+04 | 6.8111E+06 ± 8.6399E+05 | 7.9226E+06 ± 1.2337E+06 |
| 400 | 1.7267E−05 ± 4.6512E−06 | 7.4353E−04 ± 1.3332E−04 | 5.2035E+01 ± 7.0599E+00 | 3.9747E+02 ± 4.8978E−01 | 2.0391E−02 ± 7.0124E−03 | 1.3036E+06 ± 3.3161E+04 | 1.2296E+07 ± 1.7584E+06 | 1.3510E+07 ± 1.6044E+06 |
| GGSA | ||||||||
| 10 | 9.2519E−21 ± 4.2801E−21 | 3.1151E−10 ± 9.2607E−11 | 8.9514E−11 ± 2.7214E−11 | 6.7009E+00 ± 1.2573E−01 | 3.2674E−03 ± 2.4999E−03 | −4.5000E+02 ± 0.0000E+00 | 2.6272E+03 ± 6.2941E+02 | 1.4392E+04 ± 2.6931E+03 |
| 30 | 2.6712E−18 ± 1.2549E−18 | 9.3694E−09 ± 4.4274E−09 | 2.9579E+00 ± 1.6414E+00 | 5.8188E+01 ± 6.3740E+01 | 1.0137E−01 ± 1.9933E−01 | 2.3067E+04 ± 3.3726E+03 | 3.3267E+04 ± 4.3653E+03 | 1.1119E+05 ± 3.3148E+04 |
| 50 | 1.5507E+01 ± 2.1611E+01 | 5.1348E−02 ± 1.5918E−01 | 8.6753E+00 ± 1.6597E+00 | 2.7657E+02 ± 1.2526E+02 | 3.0945E−01 ± 2.1183E−01 | 7.4669E+04 ± 4.5502E+03 | 1.3785E+05 ± 3.2422E+04 | 4.1812E+05 ± 9.6508E+04 |
| 100 | 1.6676E+03 ± 4.9714E+02 | 6.1052E+00 ± 1.8933E+00 | 1.2955E+01 ± 1.0841E+00 | 1.7308E+04 ± 8.9446E+03 | 5.3262E+00 ± 2.3408E+00 | 2.1907E+05 ± 1.0291E+04 | 7.8679E+05 ± 1.5218E+05 | 1.3530E+06 ± 3.0243E+05 |
| 200 | 8.4275E+03 ± 1.2512E+03 | 3.6763E+01 ± 3.8134E+00 | 1.6661E+01 ± 1.4115E+00 | 3.1464E+05 ± 8.8699E+04 | 8.1100E+01 ± 2.5622E+01 | 5.8479E+05 ± 5.1987E+04 | 2.7680E+06 ± 4.0291E+05 | 2.2675E+06 ± 3.1986E+05 |
| 300 | 1.5914E+04 ± 1.3725E+03 | 8.2638E+01 ± 5.8110E+00 | 1.9064E+01 ± 1.3577E+00 | 9.6178E+05 ± 1.7308E+05 | 2.7728E+02 ± 5.9165E+01 | 9.2981E+05 ± 4.1542E+04 | 6.2326E+06 ± 5.7420E+05 | 7.0990E+06 ± 1.0544E+06 |
| 400 | 2.3949E+04 ± 2.1892E+03 | 1.4341E+02 ± 8.2441E+00 | 1.9783E+01 ± 1.0119E+00 | 1.5492E+06 ± 2.2445E+05 | 6.0587E+02 ± 1.2483E+02 | 1.2460E+06 ± 5.7645E+04 | 1.0610E+07 ± 1.3024E+06 | 9.0430E+06 ± 8.0266E+05 |
| ABC | ||||||||
| 10 | 6.0129E−01 ± 6.1553E−01 | 1.5859E−01 ± 8.4510E−02 | 2.1272E+01 ± 4.3992E+00 | 2.6585E+02 ± 1.6000E+02 | 1.2359E−01 ± 4.6076E−02 | −1.4954E+02 ± 4.9579E+02 | 3.4097E+03 ± 1.2049E+03 | 5.0882E+03 ± 1.8545E+03 |
| 30 | 3.2478E−01 ± 4.5597E−01 | 1.2980E−01 ± 4.3760E−02 | 7.0218E+01 ± 2.3338E+00 | 8.5263E+02 ± 7.9645E+02 | 8.2804E−01 ± 2.1601E−01 | 1.4170E+04 ± 7.2822E+03 | 3.5650E+04 ± 8.3039E+03 | 7.4794E+04 ± 9.2037E+03 |
| 50 | 1.2333E+02 ± 8.4279E+01 | 4.3301E+00 ± 9.9440E−01 | 8.2147E+01 ± 3.8170E+00 | 4.6490E+04 ± 6.1813E+04 | 1.5872E+00 ± 3.3977E−01 | 4.0359E+04 ± 9.7105E+03 | 9.5767E+04 ± 1.0755E+04 | 2.0713E+05 ± 4.4398E+04 |
| 100 | 1.0303E+04 ± 2.3400E+03 | 6.9117E+01 ± 1.0120E+01 | 9.1392E+01 ± 1.3538E+00 | 1.4325E+07 ± 7.5061E+06 | 2.3301E+01 ± 1.3000E+01 | 1.4927E+05 ± 1.5295E+04 | 4.2471E+05 ± 4.8962E+04 | 8.3245E+05 ± 1.3602E+05 |
| 200 | 1.2821E+05 ± 1.4533E+04 | 3.6342E+02 ± 2.7770E+01 | 9.6506E+01 ± 4.9955E−01 | 9.6506E+01 ± 4.9955E−01 | 1.1262E+03 ± 1.7396E+02 | 9.1173E+05 ± 2.9096E+04 | 3.7621E+06 ± 4.2790E+05 | 4.3386E+06 ± 6.2251E+05 |
| 300 | 3.3265E+05 ± 2.2887E+04 | 1.1978E+47 ± 4.2891E+47 | 9.7796E+01 ± 3.1432E−01 | 1.1327E+09 ± 1.1732E+08 | 1.1327E+09 ± 1.1732E+08 | 1.4685E+06 ± 2.9655E+04 | 7.8441E+06 ± 9.3926E+05 | 9.5687E+06 ± 1.7075E+06 |
| 400 | 5.9389E+05 ± 1.8295E+04 | 4.2575E+88 ± 1.7165E+89 | 9.8452E+01 ± 4.2393E−01 | 2.2510E+09 ± 1.1498E+08 | 1.4309E+04 ± 1.1349E+03 | 2.0582E+06 ± 4.8368E+04 | 1.5176E+07 ± 1.8401E+06 | 1.8247E+07 ± 2.5257E+06 |
| Dim | ||||||||
|---|---|---|---|---|---|---|---|---|
| CGWO | ||||||||
| 10 | 0.0000E+00 ± 0.0000E+00 | 1.5987E−15 ± 1.4580E−15 | 4.0602E−03 ± 1.3531E−02 | 1.3706E−07 ± 1.2330E−07 | 0.0000E+00 ± 0.0000E+00 | 1.4299E+03 ± 1.4439E+03 | −3.2642E+02 ± 2.0518E+00 | −1.2860E+02 ± 6.7363E−01 |
| 30 | 4.2633E−14 ± 1.7773E−13 | 1.1191E−14 ± 3.4387E−15 | 6.2267E−04 ± 2.7847E−03 | 1.3788E−06 ± 2.0390E−06 | 5.8309E−37 ± 2.5356E−36 | 1.8721E+04 ± 2.3273E+04 | −3.1258E+02 ± 4.7012E+00 | −1.2340E+02 ± 1.0595E+00 |
| 50 | 2.8422E−15 ± 1.2711E−14 | 2.5580E−14 ± 7.1497E−15 | 6.3696E−04 ± 2.8486E−03 | 1.2605E−03 ± 1.7930E−03 | 4.9439E−26 ± 9.7835E−26 | 1.3906E+07 ± 1.8383E+07 | −2.9335E+02 ± 7.2684E+00 | −1.2123E+02 ± 2.2688E+00 |
| 100 | 2.6767E−09 ± 1.1970E−08 | 9.1305E−14 ± 1.5656E−14 | 0.0000E+00 ± 0.0000E+00 | 1.2196E−03 ± 2.0664E−03 | 5.9151E−16 ± 2.0987E−15 | 4.9142E+10 ± 6.6649E+09 | −1.3387E+02 ± 2.6121E+01 | −2.6579E+01 ± 2.0246E+01 |
| 200 | 2.6565E+01 ± 1.1300E+02 | 2.7021E−11 ± 2.7854E−11 | 5.4207E−04 ± 2.4242E−03 | 7.0711E−02 ± 4.2341E−02 | 2.0131E−09 ± 8.0141E−09 | 1.7580E+11 ± 5.4392E+09 | 2.8640E+03 ± 5.8923E+01 | 7.4045E+01 ± 2.7698E+01 |
| 300 | 2.1291E+02 ± 5.9239E+02 | 8.4466E−09 ± 1.1293E−08 | 1.1102E−16 ± 0.0000E+00 | 8.6895E−02 ± 3.6233E−02 | 9.2315E−08 ± 1.5863E−07 | 2.8611E+11 ± 1.4562E+10 | 4.6189E+03 ± 5.9492E+01 | 1.8003E+02 ± 1.7963E+01 |
| 400 | 5.1274E+02 ± 1.0278E+03 | 1.4933E−07 ± 2.1924E−07 | 6.6570E−04 ± 2.9771E−03 | 1.0286E−01 ± 3.9337E−02 | 3.4892E−06 ± 6.7040E−06 | 4.5924E+11 ± 2.7140E+10 | 6.3501E+03 ± 4.8900E+01 | 3.2995E+02 ± 7.8903E+01 |
| DGWO | ||||||||
| 10 | 4.5352E+01 ± 1.5435E+01 | 1.6427E+01 ± 2.2320E+00 | 1.6030E+00 ± 1.1451E+00 | 2.6231E+01 ± 1.3377E+01 | 3.4938E+00 ± 1.8937E+00 | 6.8943E+08 ± 1.6356E+09 | −2.7396E+02 ± 1.4121E+01 | −1.2400E+02 ± 4.8791E+00 |
| 30 | 1.8919E+02 ± 3.1312E+01 | 1.8618E+01 ± 7.9104E−01 | 1.3173E−01 ± 3.4766E−02 | 2.5088E+01 ± 8.3795E+00 | 1.9820E+01 ± 6.5702E+00 | 1.2290E+10 ± 4.1999E+09 | −2.3561E+01 ± 5.4322E+01 | −6.6789E+01 ± 3.0823E+01 |
| 50 | 3.5037E+02 ± 4.5994E+01 | 1.9096E+01 ± 3.5597E−01 | 9.8671E−01 ± 4.7635E−02 | 2.5352E+01 ± 6.0001E+00 | 3.5632E+01 ± 7.5088E+00 | 2.1232E+10 ± 5.9364E+09 | 2.2694E+02 ± 5.3681E+01 | 5.2913E+01 ± 1.0449E+02 |
| 100 | 7.8978E+02 ± 9.6092E+01 | 1.9541E+01 ± 1.7359E−01 | 1.9791E+00 ± 1.7258E−01 | 3.5454E+01 ± 6.0199E+00 | 8.9551E+01 ± 1.0858E+01 | 4.3486E+10 ± 8.2896E+09 | 9.5214E+02 ± 9.5931E+01 | 3.9850E+02 ± 1.8512E+02 |
| 200 | 1.7170E+03 ± 1.4305E+02 | 1.9806E+01 ± 1.3330E−01 | 1.8272E+01 ± 2.1260E+00 | 5.2363E+01 ± 5.6970E+00 | 2.1950E+02 ± 1.9719E+01 | 7.7228E+11 ± 1.1214E+11 | 3.7987E+03 ± 1.6113E+02 | 1.5229E+04 ± 4.3600E+03 |
| 300 | 2.7346E+03 ± 1.3286E+02 | 2.0016E+01 ± 1.1159E−01 | 6.9860E+01 ± 7.1631E+00 | 7.2126E+01 ± 4.9733E+00 | 3.7320E+02 ± 3.0975E+01 | 1.2386E+12 ± 1.3913E+11 | 5.9785E+03 ± 1.9659E+02 | 2.7460E+04 ± 8.9549E+03 |
| 400 | 3.7757E+03 ± 2.0535E+02 | 2.0131E+01 ± 1.0322E−01 | 1.6753E+02 ± 1.0906E+01 | 2.2940E+02 ± 2.8030E+02 | 5.3048E+02 ± 4.0597E+01 | 1.7939E+12 ± 1.7536E+11 | 8.2816E+03 ± 2.9714E+02 | 3.8426E+04 ± 7.0501E+03 |
| GWO | ||||||||
| 10 | 3.1745E−01 ± 1.4197E+00 | 6.3949E−15 ± 1.8134E−15 | 2.2698E−02 ± 2.3047E−02 | 9.8002E−04 ± 4.3798E−03 | 9.9794E−05 ± 2.3508E−04 | 1.0356E+05 ± 2.2061E+05 | −3.1551E+02 ± 7.9110E+00 | −1.2816E+02 ± 7.4021E−01 |
| 30 | 1.0576E+00 ± 2.5877E+00 | 4.4231E−14 ± 4.8356E−15 | 5.7637E−03 ± 8.7308E−03 | 3.0060E−02 ± 1.1083E−02 | 2.1473E−04 ± 3.4751E−04 | 6.4158E+07 ± 1.2761E+08 | −2.1396E+02 ± 3.6415E+01 | −1.2312E+02 ± 3.5263E+00 |
| 50 | 4.6654E+00 ± 6.3566E+00 | 5.5849E−13 ± 2.8125E−13 | 3.5817E−03 ± 8.8102E−03 | 6.6260E−02 ± 2.0916E−02 | 6.4731E−04 ± 8.0489E−04 | 5.1876E+08 ± 4.1005E+08 | −7.7278E+01 ± 7.6566E+01 | −1.0549E+02 ± 1.0994E+01 |
| 100 | 8.8310E+00 ± 1.5376E+01 | 8.1183E−09 ± 3.8031E−09 | 2.5595E−03 ± 6.3188E−03 | 2.2714E−01 ± 5.6793E−02 | 2.7201E−03 ± 1.7511E−03 | 5.3591E+09 ± 2.0717E+09 | 3.2458E+02 ± 6.6970E+01 | −8.0325E+00 ± 3.3479E+01 |
| 200 | 1.5325E+01 ± 6.5521E+00 | 3.8682E−06 ± 1.1846E−06 | 3.3148E−03 ± 8.8221E−03 | 4.5483E−01 ± 4.7011E−02 | 8.4679E−03 ± 3.7215E−03 | 2.6151E+11 ± 5.1126E+10 | 3.0724E+03 ± 1.1861E+02 | 2.1298E+03 ± 2.2768E+02 |
| 300 | 3.1528E+01 ± 7.6771E+00 | 4.7213E−05 ± 1.0407E−05 | 4.5271E−03 ± 1.4858E−02 | 5.7484E−01 ± 3.6978E−02 | 2.0768E−02 ± 4.5727E−03 | 4.5381E+11 ± 1.1393E+11 | 4.9000E+03 ± 1.1343E+02 | 4.0573E+03 ± 4.8996E+02 |
| 400 | 3.7025E+01 ± 1.0455E+01 | 2.1345E−04 ± 5.2073E−05 | 7.0955E−03 ± 1.7393E−02 | 6.4186E−01 ± 4.2966E−02 | 3.4143E−02 ± 8.6240E−03 | 5.6113E+11 ± 6.2542E+10 | 6.7909E+03 ± 1.5308E+02 | 6.4142E+03 ± 1.0602E+03 |
| GGSA | ||||||||
| 10 | 3.3331E+00 ± 1.4172E+00 | 1.3906E−10 ± 3.2542E−11 | 1.9795E+00 ± 1.2491E+00 | 1.8251E−22 ± 1.0118E−22 | 2.8670E−11 ± 9.2788E−12 | 3.6879E+03 ± 2.4434E+03 | −3.2050E+02 ± 2.1413E+00 | −1.2858E+02 ± 4.3780E−01 |
| 30 | 1.8456E+01 ± 5.1898E+00 | 1.1140E−09 ± 2.9021E−10 | 1.0267E+01 ± 3.2103E+00 | 5.5544E−01 ± 6.3755E−01 | 2.5030E−04 ± 7.6750E−04 | 4.8066E+09 ± 1.1258E+09 | 6.0902E+01 ± 2.3871E+01 | −1.1323E+02 ± 5.6022E+00 |
| 50 | 4.3579E+01 ± 8.0998E+00 | 1.7715E−01 ± 3.6017E−01 | 1.8261E+01 ± 4.7142E+00 | 1.6202E+00 ± 5.5207E−01 | 1.3236E−02 ± 1.0920E−02 | 1.7675E+10 ± 2.7512E+09 | −2.4984E+02 ± 1.6804E+01 | −1.1488E+02 ± 2.4858E+00 |
| 100 | 1.1579E+02 ± 1.8440E+01 | 2.5164E+00 ± 6.0464E−01 | 4.3977E+01 ± 8.3030E+00 | 4.2369E+00 ± 1.0887E+00 | 2.2041E+00 ± 1.2578E+00 | 6.3146E+10 ± 5.3312E+09 | 7.8922E+01 ± 3.1585E+01 | −9.6724E+01 ± 8.2722E+00 |
| 200 | 4.4349E+02 ± 4.4235E+01 | 5.7483E+00 ± 3.1385E−01 | 1.0432E+02 ± 1.2268E+01 | 9.1683E+00 ± 1.5203E+00 | 2.0142E+01 ± 3.3920E+00 | 2.2668E+11 ± 4.3978E+10 | 4.8773E+03 ± 2.1568E+02 | 2.1701E+02 ± 2.9341E+01 |
| 300 | 9.6926E+02 ± 8.5582E+01 | 7.0468E+00 ± 2.1066E−01 | 1.6476E+02 ± 1.9402E+01 | 1.3009E+01 ± 2.3856E+00 | 4.9205E+01 ± 7.1350E+00 | 3.7441E+11 ± 4.7771E+10 | 4.8773E+03 ± 2.1568E+02 | 4.8710E+02 ± 7.8587E+01 |
| 400 | 1.5894E+03 ± 1.2892E+02 | 7.7598E+00 ± 3.2412E−01 | 2.2403E+02 ± 1.7685E+01 | 1.6699E+01 ± 3.0792E+00 | 9.0176E+01 ± 6.1805E+00 | 5.2723E+11 ± 6.8051E+10 | 6.7839E+03 ± 2.1081E+02 | 8.3395E+02 ± 1.4858E+02 |
| ABC | ||||||||
| 10 | 9.1750E+00 ± 2.3732E+00 | 2.8183E+00 ± 7.0818E−01 | 8.5511E−01 ± 1.6535E−01 | 1.2647E−01 ± 7.7671E−02 | 2.8306E−01 ± 1.2643E−01 | 7.6133E+06 ± 1.9969E+07 | −3.0848E+02 ± 9.7380E+00 | −1.2813E+02 ± 4.5518E−01 |
| 30 | 1.3199E+01 ± 3.3583E+00 | 9.9923E−01 ± 3.1808E−01 | 3.0353E−01 ± 1.6465E−01 | 4.6248E−02 ± 4.8526E−02 | 2.1445E−01 ± 1.2395E−01 | 3.3062E+09 ± 2.3993E+09 | −1.4954E+02 ± 3.3221E+01 | −1.1151E+02 ± 4.9187E+00 |
| 50 | 4.9709E+01 ± 8.6579E+00 | 4.1506E+00 ± 4.3372E−01 | 1.7922E+00 ± 4.8016E−01 | 1.5856E+00 ± 9.4589E−01 | 2.2899E+00 ± 5.0491E−01 | 1.1100E+10 ± 5.8365E+09 | 1.0383E+02 ± 4.4515E+01 | −9.0741E+01 ± 4.5782E+00 |
| 100 | 2.9863E+02 ± 1.8723E+01 | 1.2376E+01 ± 8.6558E−01 | 9.2611E+01 ± 2.5847E+01 | 1.5095E+07 ± 1.2545E+07 | 2.4913E+01 ± 2.8451E+00 | 7.3054E+09 ± 4.5816E+09 | 8.2247E+02 ± 7.2309E+01 | 7.7688E+00 ± 6.1501E+01 |
| 200 | 1.2958E+03 ± 3.2622E+01 | 1.8047E+01 ± 2.4832E−01 | 1.1472E+03 ± 8.9146E+01 | 7.2551E+08 ± 1.6454E+08 | 1.3825E+02 ± 9.8552E+00 | 8.8023E+11 ± 5.0733E+10 | 3.8667E+03 ± 7.0574E+01 | 2.6009E+04 ± 3.4016E+03 |
| 300 | 2.6343E+03 ± 7.7325E+01 | 1.9385E+01 ± 8.0440E−02 | 2.9939E+03 ± 1.2926E+02 | 2.4355E+09 ± 2.7651E+08 | 3.1744E+02 ± 1.4506E+01 | 1.5472E+12 ± 6.5726E+10 | 6.2579E+03 ± 7.7842E+01 | 4.8368E+04 ± 4.1046E+03 |
| 400 | 4.0672E+03 ± 8.2970E+01 | 1.9842E+01 ± 6.6639E−02 | 5.3203E+03 ± 1.9270E+02 | 5.0604E+09 ± 3.3310E+08 | 5.2991E+02 ± 1.3637E+01 | 2.2105E+12 ± 8.2257E+10 | 8.7173E+03 ± 1.0780E+02 | 7.6065E+04 ± 6.0210E+03 |
| Dim = 10 | ||||||||
| CGWO vs. DGWO | 2.4426E−08 | 8.0065E−09 | 6.2771E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 1.2346E−07 | 1.6571E−07 |
| CGWO vs. GWO | 2.4426E−08 | 8.0065E−09 | 6.2771E−08 | 6.7956E−08 | 2.1393E−03 | 3.5070E−01 | 4.1658E−05 | 1.1045E−05 |
| CGWO vs. GGSA | 2.4426E−08 | 8.0065E−09 | 6.2771E−08 | 6.7956E−08 | 7.9479E−07 | 8.0065E−09 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. ABC | 2.4426E−08 | 8.0065E−09 | 6.2771E−08 | 6.7956E−08 | 6.7956E−08 | 9.1728E−08 | 6.7956E−08 | 9.1728E−08 |
| Dim = 10 | ||||||||
| CGWO vs. DGWO | 8.0065E−09 | 2.4037E−08 | 1.5149E−08 | 6.7956E−08 | 8.0065E−09 | 2.5629E−07 | 6.3761E−08 | 1.0646E−07 |
| CGWO vs. GWO | 1.6259E−01 | 1.7005E−07 | 8.2529E−04 | 6.9166E−07 | 8.0065E−09 | 7.5774E−06 | 1.1613E−07 | 4.9864E−02 |
| CGWO vs. GGSA | 7.3831E−09 | 2.4037E−08 | 1.5149E−08 | 6.7956E−08 | 8.0065E−09 | 3.7499E−04 | 1.5605E−07 | 3.2348E−01 |
| CGWO vs. ABC | 8.0065E−09 | 2.4037E−08 | 1.5149E−08 | 6.7956E−08 | 8.0065E−09 | 1.9177E−07 | 7.4151E−08 | 7.1135E−03 |
| Dim = 30 | ||||||||
| CGWO vs. DGWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 2.0616E−06 | 7.8980E−08 |
| CGWO vs. GWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 5.1153E−03 | 6.7956E−08 | 2.5629E−07 | 2.3025E−05 |
| CGWO vs. GGSA | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. ABC | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| Dim = 30 | ||||||||
| CGWO vs. DGWO | 1.5149E−08 | 4.7371E−08 | 1.1267E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. GWO | 3.6853E−05 | 3.8179E−08 | 1.8196E−02 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 4.7348E−01 |
| CGWO vs. GGSA | 1.4970E−08 | 4.7371E−08 | 1.1267E−08 | 1.8074E−05 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. ABC | 1.5149E−08 | 4.7371E−08 | 1.1267E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 7.8980E−08 |
| Dim = 50 | ||||||||
| CGWO vs. DGWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 1.3486E−03 | 6.7956E−08 |
| CGWO vs. GWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 3.0566E−03 | 3.7051E−05 | 6.7956E−08 | 7.9479E−07 | 3.9388E−07 |
| CGWO vs. GGSA | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. ABC | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| Dim = 50 | ||||||||
| CGWO vs. DGWO | 1.1267E−08 | 5.6939E−08 | 1.1267E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. GWO | 1.1168E−08 | 5.6775E−08 | 1.6493E−01 | 6.7956E−08 | 6.7956E−08 | 1.0646E−07 | 6.7956E−08 | 1.0646E−07 |
| CGWO vs. GGSA | 1.1267E−08 | 5.6611E−08 | 1.1267E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 1.6571E−07 | 5.2269E−07 |
| CGWO vs. ABC | 1.1267E−08 | 5.6939E−08 | 1.1267E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| Dim = 100 | ||||||||
| CGWO vs. DGWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 1.0373E−04 | 6.7956E−08 |
| CGWO vs. GWO | 6.7956E−08 | 6.7956E−08 | 2.0616E−06 | 2.7329E−01 | 5.1658E−06 | 5.6290E−04 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. GGSA | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. ABC | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| Dim = 100 | ||||||||
| CGWO vs. DGWO | 5.6042E−08 | 6.5041E−08 | 8.0065E−09 | 6.7956E−08 | 6.7956E−08 | 4.6792E−02 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. GWO | 1.1910E−07 | 6.5041E−08 | 7.9480E−09 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 9.2780E−05 |
| CGWO vs. GGSA | 5.6042E−08 | 6.5041E−08 | 8.0065E−09 | 6.7956E−08 | 6.7956E−08 | 9.1266E−07 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. ABC | 5.6042E−08 | 6.5041E−08 | 8.0065E−09 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 1.1355E−01 |
| Dim = 200 | ||||||||
| CGWO vs. DGWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 1.1045E−05 |
| CGWO vs. GWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 4.0936E−01 | 1.4149E−05 | 6.7956E−08 | 7.8980E−08 | 9.8921E−01 |
| CGWO vs. GGSA | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 7.8980E−08 | 2.9598E−07 | 6.7956E−08 |
| CGWO vs. ABC | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 5.8736E−06 |
| Dim = 200 | ||||||||
| CGWO vs. DGWO | 6.6532E−08 | 6.7956E−08 | 1.9544E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. GWO | 1.3953E−05 | 6.7956E−08 | 2.7851E−07 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 3.9874E−06 | 6.7956E−08 |
| CGWO vs. GGSA | 1.0292E−06 | 6.7956E−08 | 1.9544E−08 | 6.7956E−08 | 6.7956E−08 | 6.6737E−06 | 5.1153E−03 | 7.8980E−08 |
| CGWO vs. ABC | 6.6532E−08 | 6.7956E−08 | 1.9544E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| Dim = 300 | ||||||||
| CGWO vs. DGWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 1.0646E−07 |
| CGWO vs. GWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 8.3923E−01 | 6.7956E−08 | 6.7956E−08 | 7.8980E−08 |
| CGWO vs. GGSA | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 7.8980E−08 | 5.2269E−07 |
| CGWO vs. ABC | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 9.1728E−08 |
| Dim = 300 | ||||||||
| CGWO vs. DGWO | 6.7956E−08 | 6.7956E−08 | 8.0065E−09 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. GWO | 1.6098E−04 | 6.7956E−08 | 8.0065E−09 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 9.1728E−08 | 6.7956E−08 |
| CGWO vs. GGSA | 1.5997E−05 | 6.7956E−08 | 8.0065E−09 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 9.7480E−06 | 6.7956E−08 |
| CGWO vs. ABC | 6.7956E−08 | 6.7956E−08 | 8.0065E−09 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| Dim = 400 | ||||||||
| CGWO vs. DGWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 9.1266E−07 |
| CGWO vs. GWO | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 1.2346E−07 | 7.3527E−01 | 6.7956E−08 | 9.1728E−08 | 7.2045E−02 |
| CGWO vs. GGSA | 6.7956E−08 | 6.7956E−08 | 7.3527E−01 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 1.9177E−07 | 2.3025E−05 |
| CGWO vs. ABC | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 3.9388E−07 |
| Dim = 400 | ||||||||
| CGWO vs. DGWO | 1.4309E−07 | 6.7956E−08 | 3.3727E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. GWO | 7.1135E−03 | 6.7956E−08 | 4.4078E−07 | 6.7956E−08 | 6.7956E−08 | 6.9166E−07 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. GGSA | 1.6098E−04 | 6.7956E−08 | 3.3727E−08 | 6.7956E−08 | 6.7956E−08 | 7.5788E−04 | 6.7956E−08 | 6.7956E−08 |
| CGWO vs. ABC | 6.7956E−08 | 6.7956E−08 | 3.3727E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 | 6.7956E−08 |
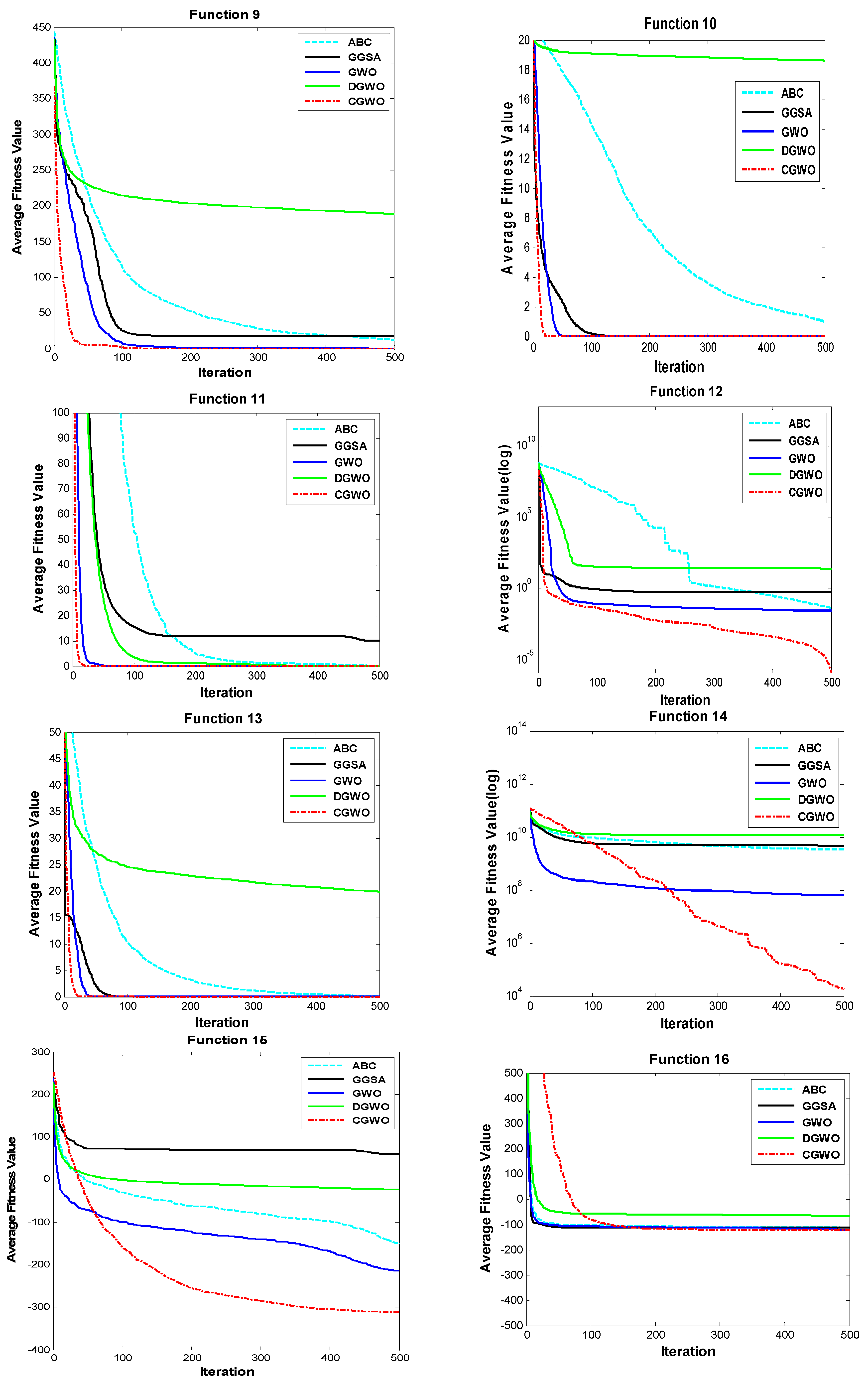
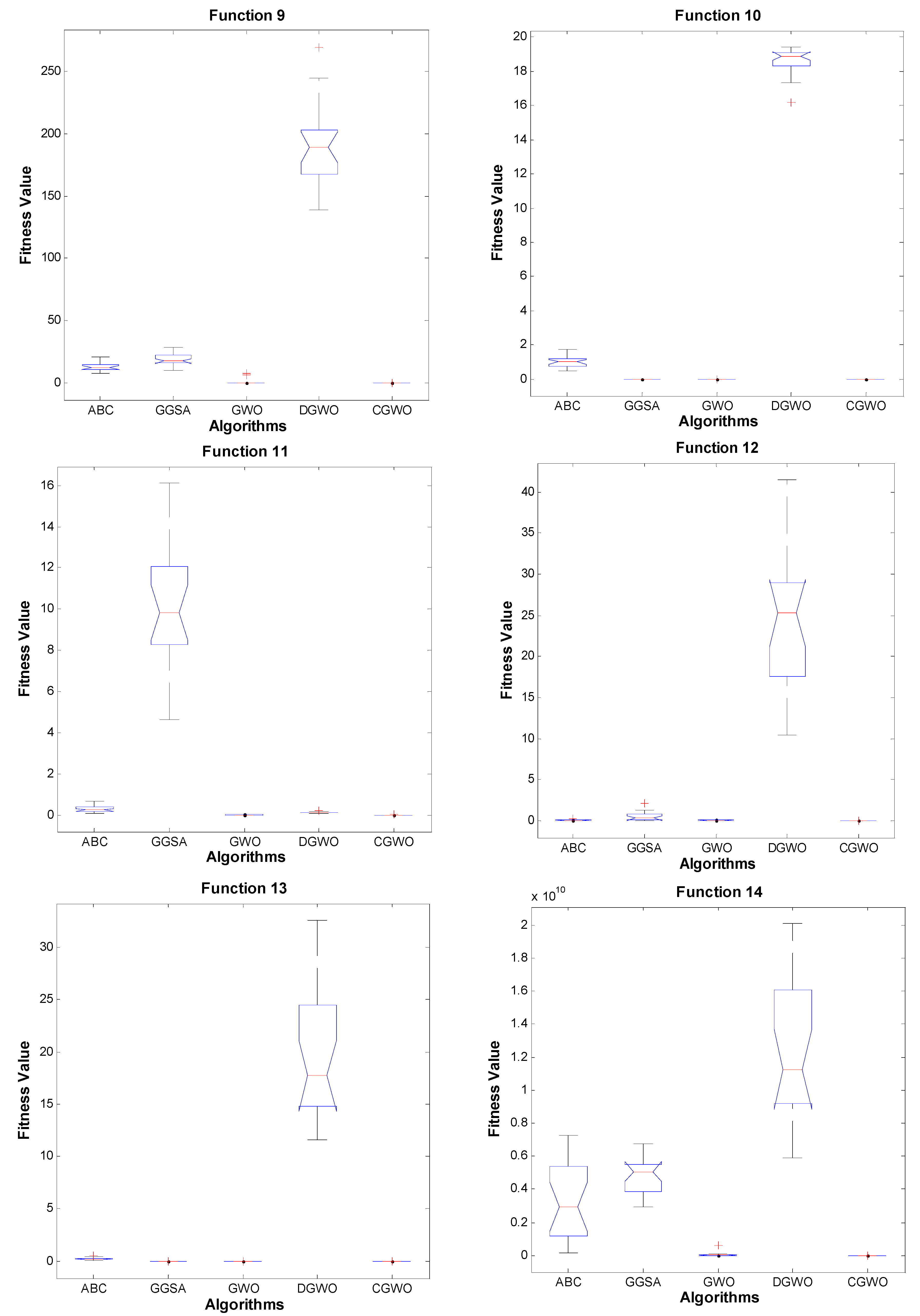
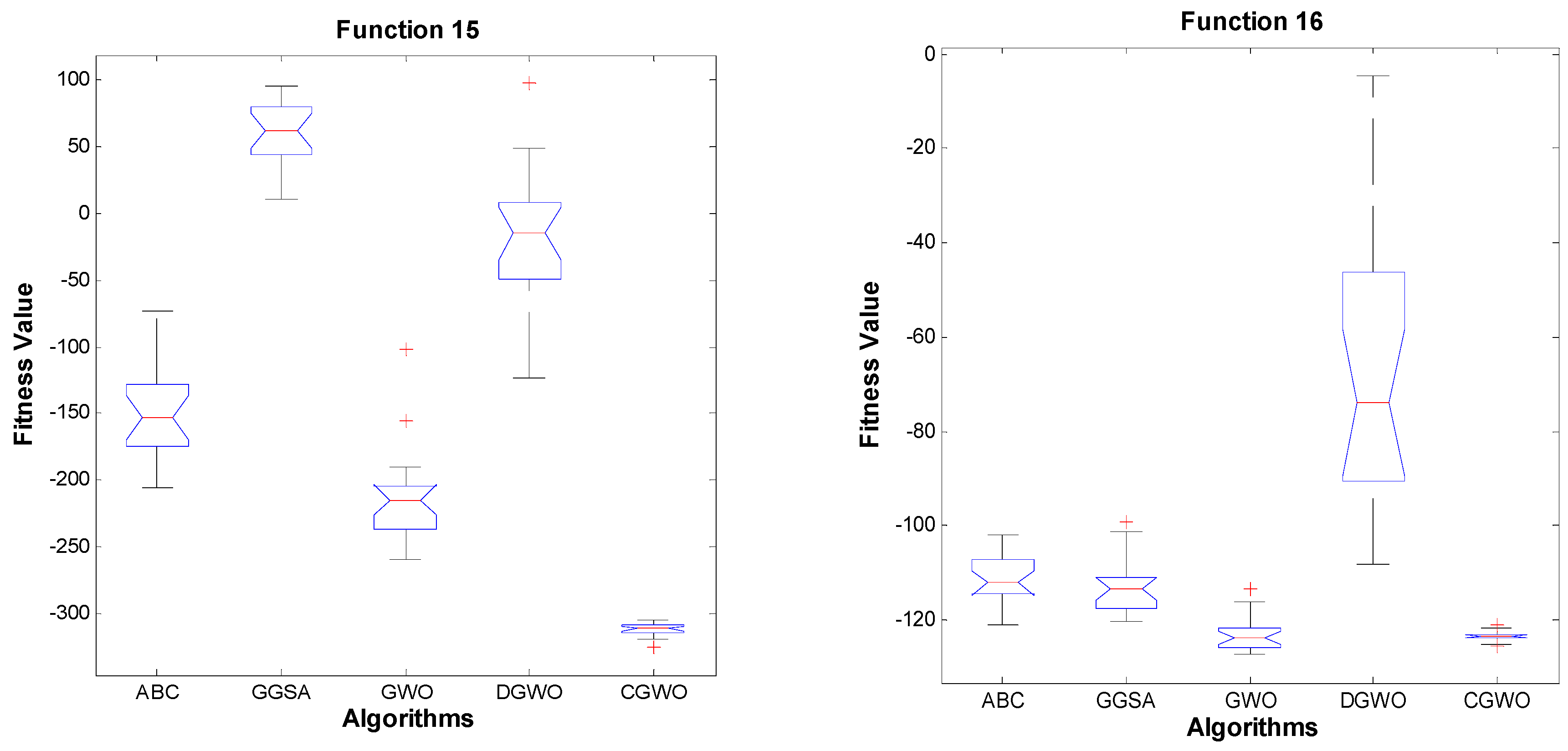
4.3. Unimodal Benchmark Functions
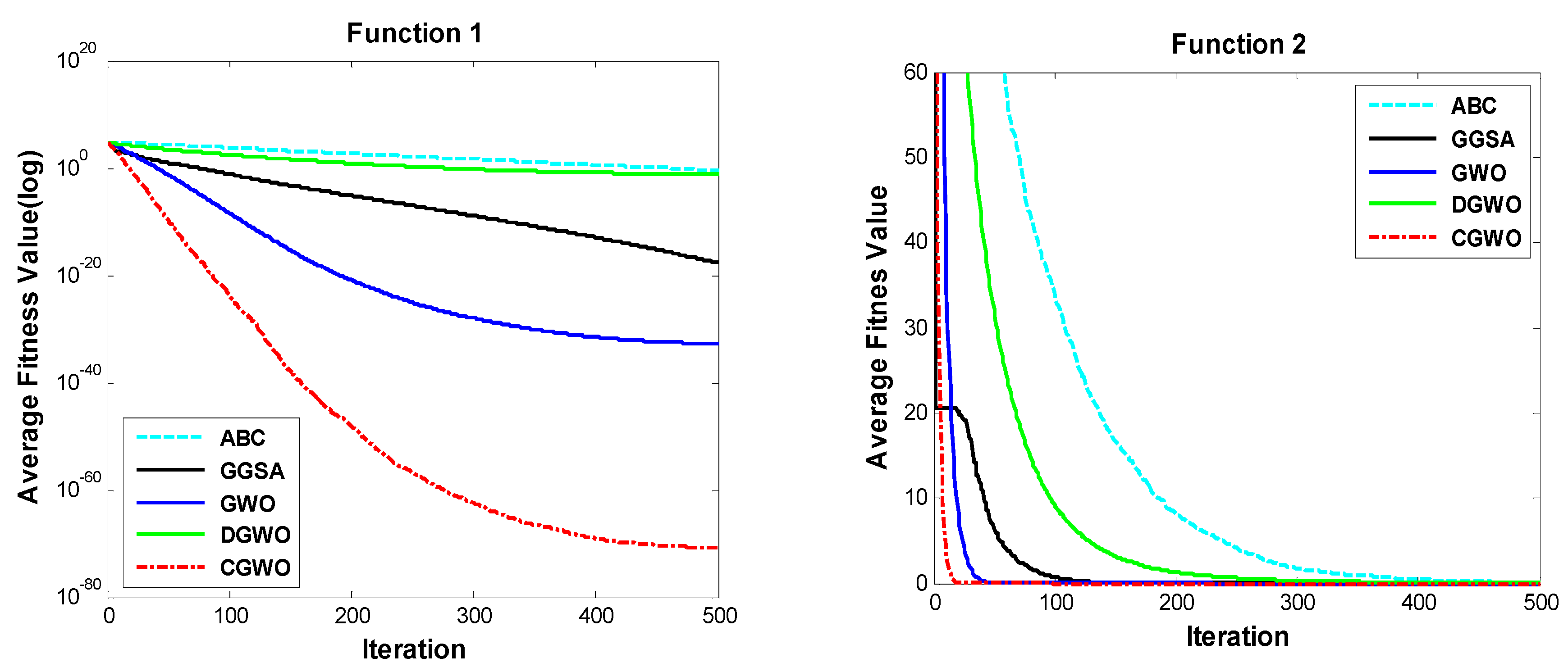
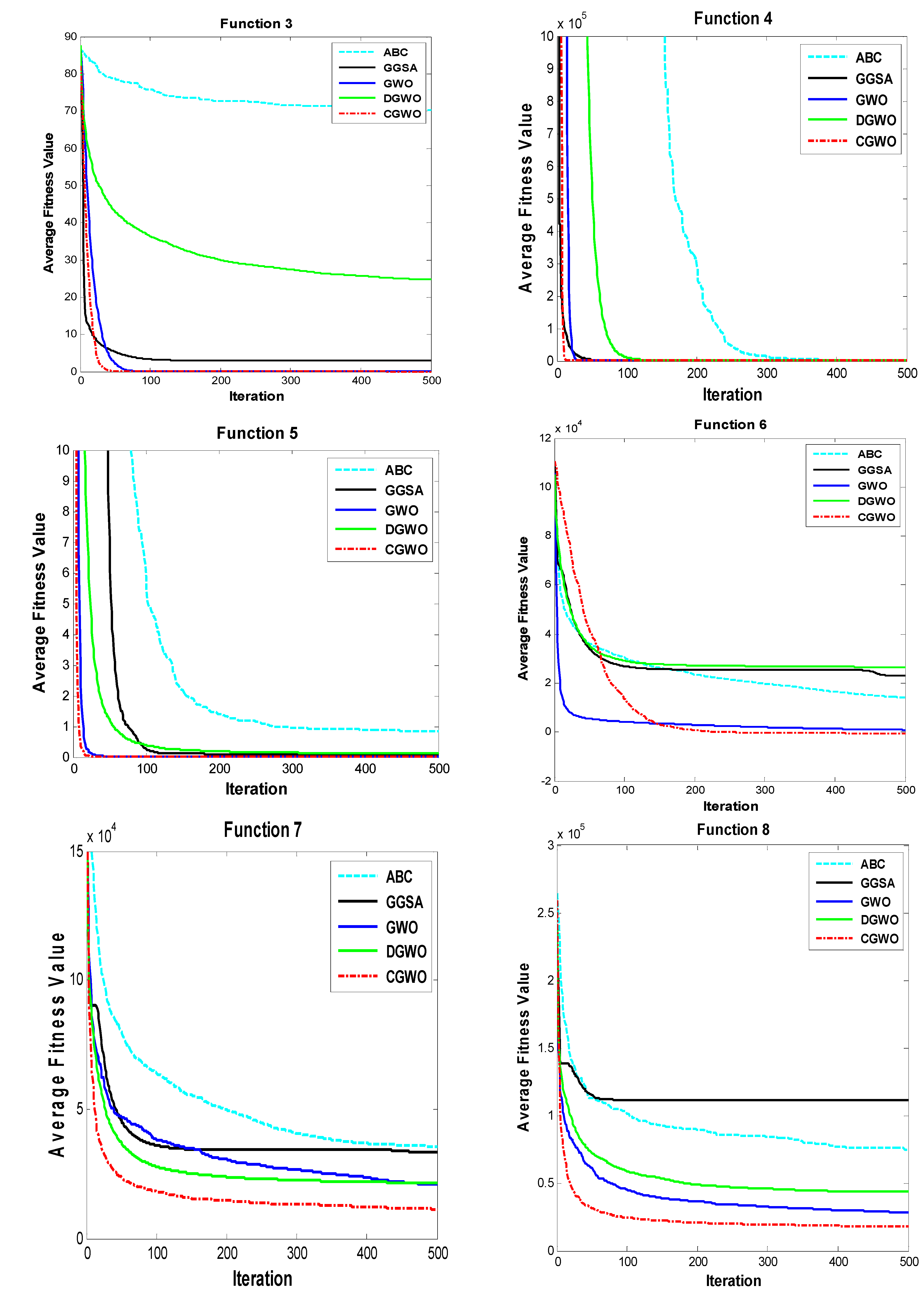
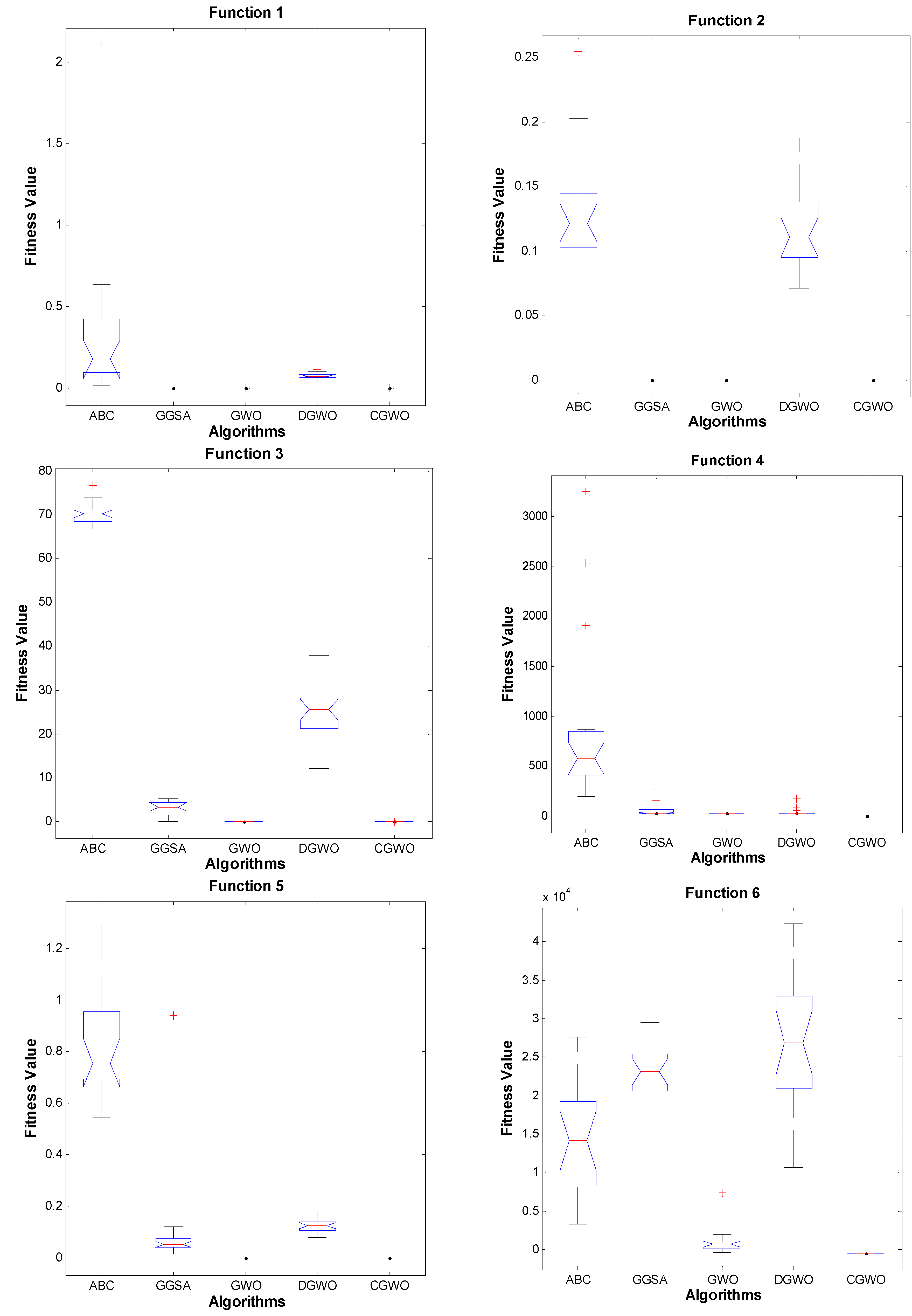
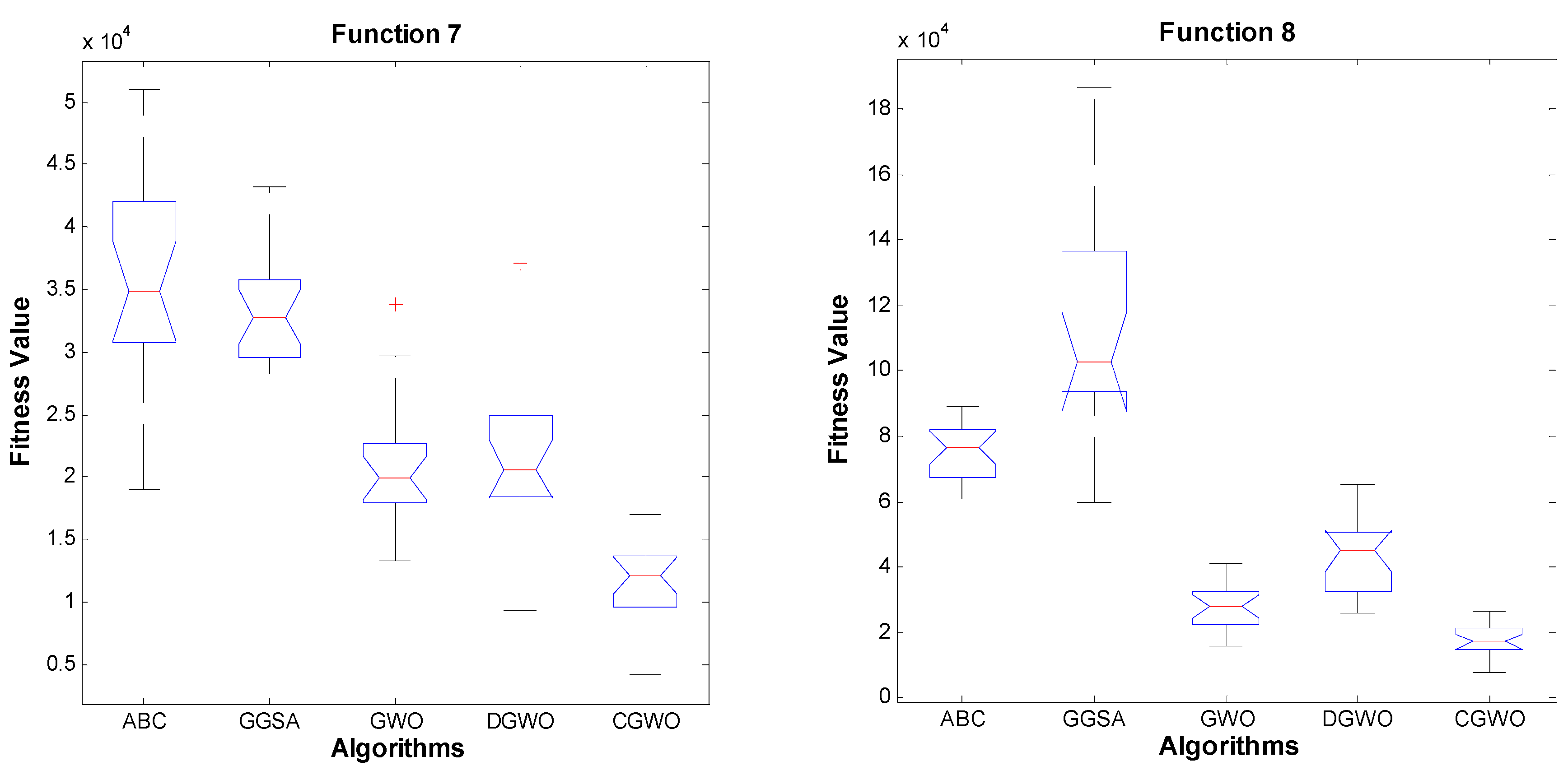
4.4. Multimodal Benchmark Functions
5. IIR Model Identification
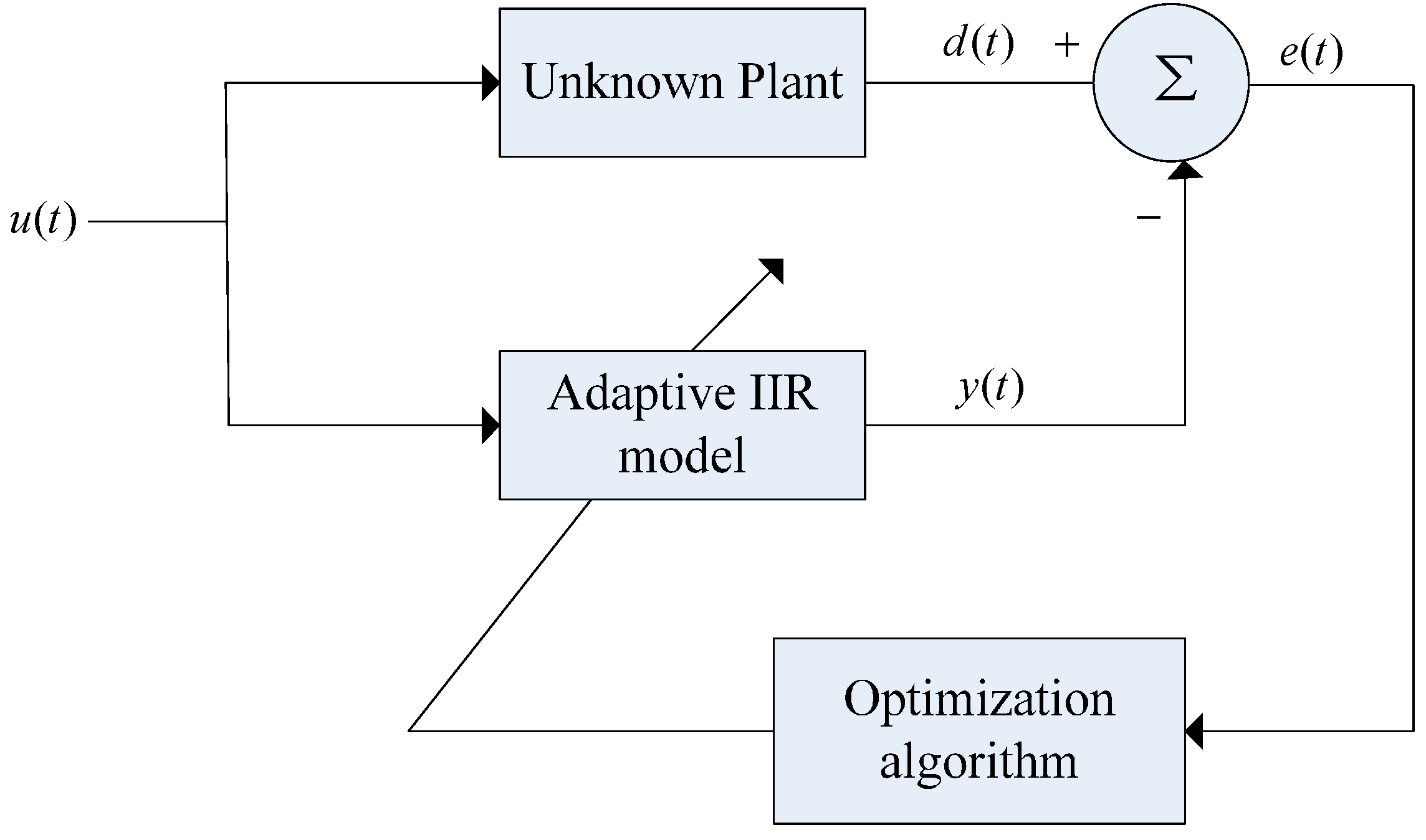
IIR Model Identification Result
| Algorithms | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| CGWO | 1.1093E−02 | −4.9144E−01 | −2.9101E−03 | −3.3551E−01 | 9.8932E−01 | 1.3089E−02 | −1.2463E−01 | −1.5870E−02 | −7.3745E−02 |
| DGWO | 1.2382E−01 | 5.5593E−02 | −4.9268E−04 | 1.0155E−01 | 2.1844E−01 | −1.6315E−01 | −8.9793E−02 | −1.1818E−01 | 6.1028E−02 |
| GWO | −2.8883E−02 | −2.6764E−01 | −2.3851E−02 | −2.4399E−01 | 9.1861E−01 | −2.9241E−03 | 4.8354E−02 | −2.7404E−02 | 4.9129E−02 |
| GGSA | 4.6698E−01 | −1.1299E−01 | 5.7827E−02 | 1.8673E−01 | −3.6432E−02 | 1.0900E−01 | −8.4527E−02 | −8.4070E−02 | 3.0088E−01 |
| ABC | 9.9479E−03 | 4.4119E−02 | 5.9096E−02 | −2.2442E−01 | 8.3829E−01 | −1.1020E−01 | 2.8357E−01 | −4.1144E−02 | 1.1184E−01 |
| Algorithms | AVE | STD |
|---|---|---|
| CGWO | 3.4013E−03 | 2.1644E−03 |
| DGWO | 1.2513E−01 | 7.1059E−02 |
| GWO | 5.5317E−03 | 4.9962E−03 |
| GGSA | 1.2537E−02 | 2.4702E−03 |
| ABC | 4.7898E−02 | 1.2004E−02 |

6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, USA, 27 November–1 December 1995; pp. 1942–1948.
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Price, K.; Storn, R. Differential evolution. Dr. Dobb’s J. 1997, 22, 18–20. [Google Scholar]
- Price, K.V.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: New York, NY, USA, 2005. [Google Scholar]
- Kirkpatrick, S.; Gelati, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Maniezzo, V.; Colorni, A. The ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. Adaptive gbest-guided gravitational search algorithm. Neural Comput. Appl. 2014, 25, 1569–1584. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Tayarani, N.M.H.; Akbarzadeh, T.M.R. Magnetic optimization algorithms a new synthesis. In Proceedings of the IEEE Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008; pp. 2659–2664.
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Let a biogeographybased optimizer train your multi-layer perceptron. Inf. Sci. 2014, 269, 188–209. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novelmethod for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. 2015, 32, 286–292. [Google Scholar] [CrossRef]
- Song, X.H.; Tang, L.; Zhao, S.T.; Zhang, X.Q.; Li, L.; Huang, J.Q.; Cai, W. Grey Wolf Optimizer for parameter estimation in surface waves. Soil Dyn. Earthq. Eng. 2015, 75, 147–157. [Google Scholar] [CrossRef]
- Komaki, G.M.; Kayvanfar, V. Grey Wolf Optimizer algorithm for the two-stage assembly flow shop scheduling problem with release time. J. Comput. Sci. 2015, 8, 109–120. [Google Scholar] [CrossRef]
- Casasent, D.; Natarajan, S. A classifier neural network with complex-valued weights and square-law nonlinearities. Neural Netw. 1995, 8, 989–998. [Google Scholar] [CrossRef]
- Chen, D.-B.; Li, H.-J.; Li, Z. Particle swarm optimization based on complex-valued encoding and application in function optimization. Comput. Eng. Appl. 2009, 45, 59–61. [Google Scholar]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Yang, X.S. Appendix a: Test problems in optimization. In Engineering Optimization; Yang, X.S., Ed.; John: Hoboken, NJ, USA, 2010; pp. 261–266. [Google Scholar]
- Tang, K.; Yao, X.; Suganthan, P.N.; MacNish, C.; Chen, Y.P.; Chen, C.M.; Yang, Z. Benchmark Functions for the CEC’2008 Special Session and Competition on Large Scale Global Optimization; Technical Report; Nature Inspired Computation and Applications Laboratory, University of Science and Technology of China: Hefei, China, 2007; pp. 153–177. [Google Scholar]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization; Technical Report; Nanyang Technological University: Singapore, 2005; Volume 2005005. [Google Scholar]
- The Matlab Code of the GGSA Algorithm. Available online: http://www.alimirjalili.com/Projects.html (accessed on 10 October 2014).
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- White, M.S.; Flockton, S.J. Adaptive recursive filtering using evolutionary algorithms. In Evolutionary Algorithms in Engineering Applications; Dasgupta, D., Michalewicz, Z., Eds.; Springer: Berlin, Germany, 1997; pp. 361–376. [Google Scholar]
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: A case study on the CEC’2005 special session on real parameter optimization. J. Heuristics 2009, 15, 617–644. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods; Biometrics Bulletin; International Biometric Society: Washington, DC, USA, 1945; pp. 80–83. [Google Scholar]
- Alcalá-Fdez, J.; Sánchez, L.; García, S.; del Jesus, M.J.; Ventura, S.; Garrell, J.M.; Otero, J.; Romero, C.; Bacardit, J.; Rivas, V.M.; et al. KEEL: A Software Tool to Assess Evolutionary Algorithms to Data Mining Problems. Soft Comput. 2009, 13, 307–318. [Google Scholar] [CrossRef]
- Kukrer, O. Analysis of the dynamics of a memoryless nonlinear gradient IIR adaptive notch filter. Signal Process. 2011, 91, 2379–2394. [Google Scholar] [CrossRef]
- Cuevas, E.; Gálvez, J.; Hinojosa, S.; Avalos, O.; Zaldívar, D.; Pérez-Cisneros, M. A Comparison of Evolutionary Computation Techniques for IIR Model Identification. J. Appl. Math. 2014, 2014, 768516. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Q.; Zhang, S.; Li, Z.; Zhou, Y. A Novel Complex-Valued Encoding Grey Wolf Optimization Algorithm. Algorithms 2016, 9, 4. https://doi.org/10.3390/a9010004
Luo Q, Zhang S, Li Z, Zhou Y. A Novel Complex-Valued Encoding Grey Wolf Optimization Algorithm. Algorithms. 2016; 9(1):4. https://doi.org/10.3390/a9010004
Chicago/Turabian StyleLuo, Qifang, Sen Zhang, Zhiming Li, and Yongquan Zhou. 2016. "A Novel Complex-Valued Encoding Grey Wolf Optimization Algorithm" Algorithms 9, no. 1: 4. https://doi.org/10.3390/a9010004
APA StyleLuo, Q., Zhang, S., Li, Z., & Zhou, Y. (2016). A Novel Complex-Valued Encoding Grey Wolf Optimization Algorithm. Algorithms, 9(1), 4. https://doi.org/10.3390/a9010004





