Gradient-Based Iterative Identification for Wiener Nonlinear Dynamic Systems with Moving Average Noises
Abstract
:1. Introduction
- To establish the identification model of the Wiener nonlinear OEMA system from input to output.
- To present a gradient-based iterative identification algorithm for the Wiener nonlinear OEMA model.
- To analyze the performances of the proposed algorithm using a numerical simulation, including the convergence rates and the estimation errors of this algorithm.
2. The Derivation of the Wiener OEMA Model
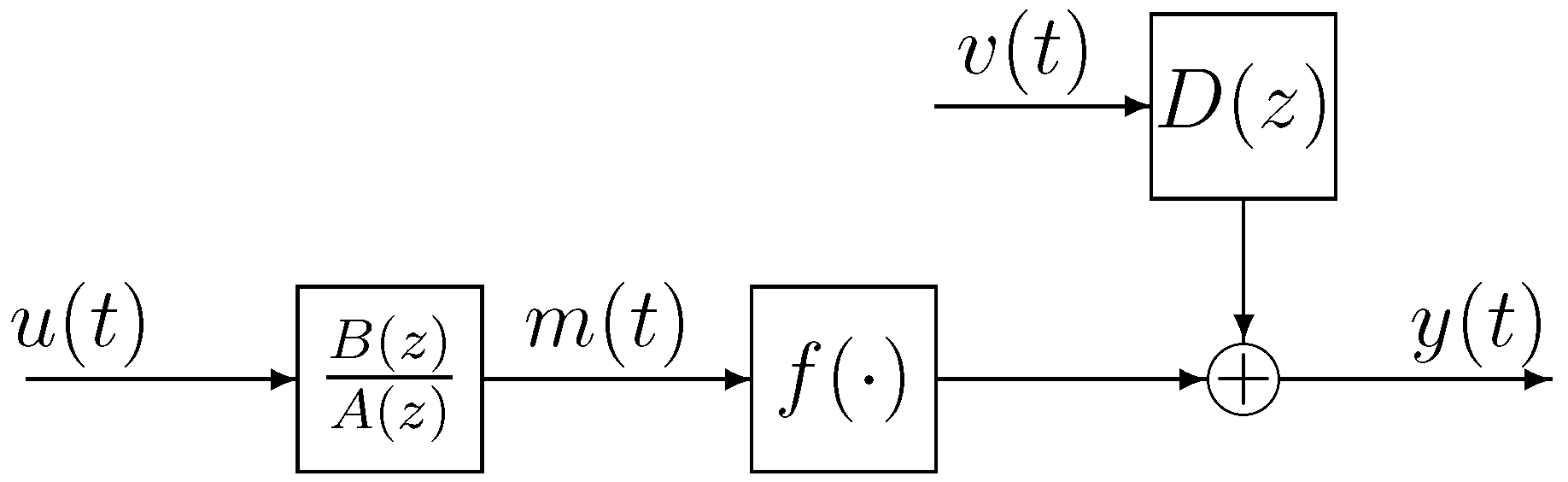
3. The Gradient-Based Iterative Algorithm
- Collect the input-output data and form by Equation (25).
- Compare with : if , then terminate the procedure and obtain the iterative times k and estimate ; otherwise, increment k by 1 and go to step 3.
4. Example
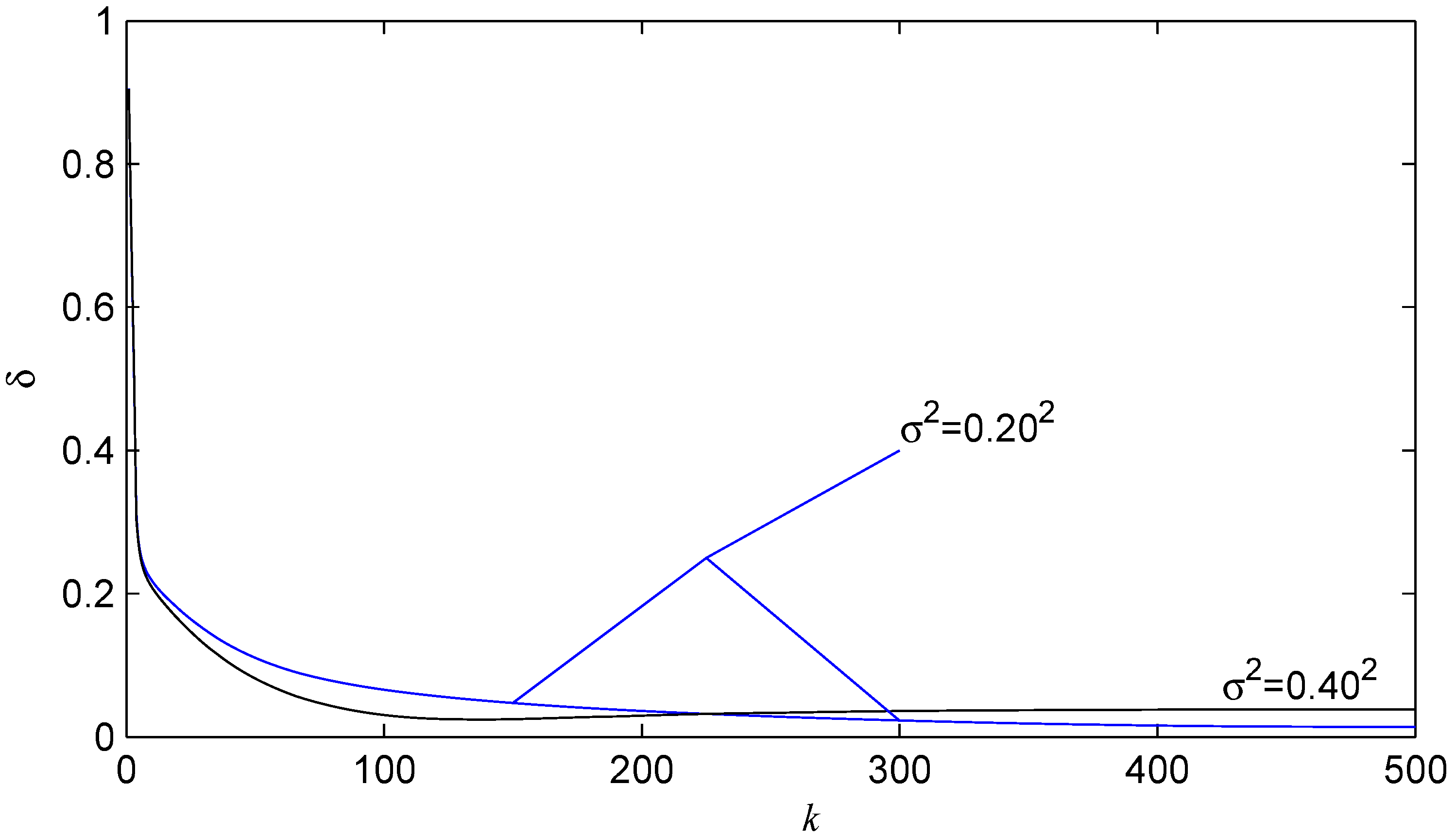
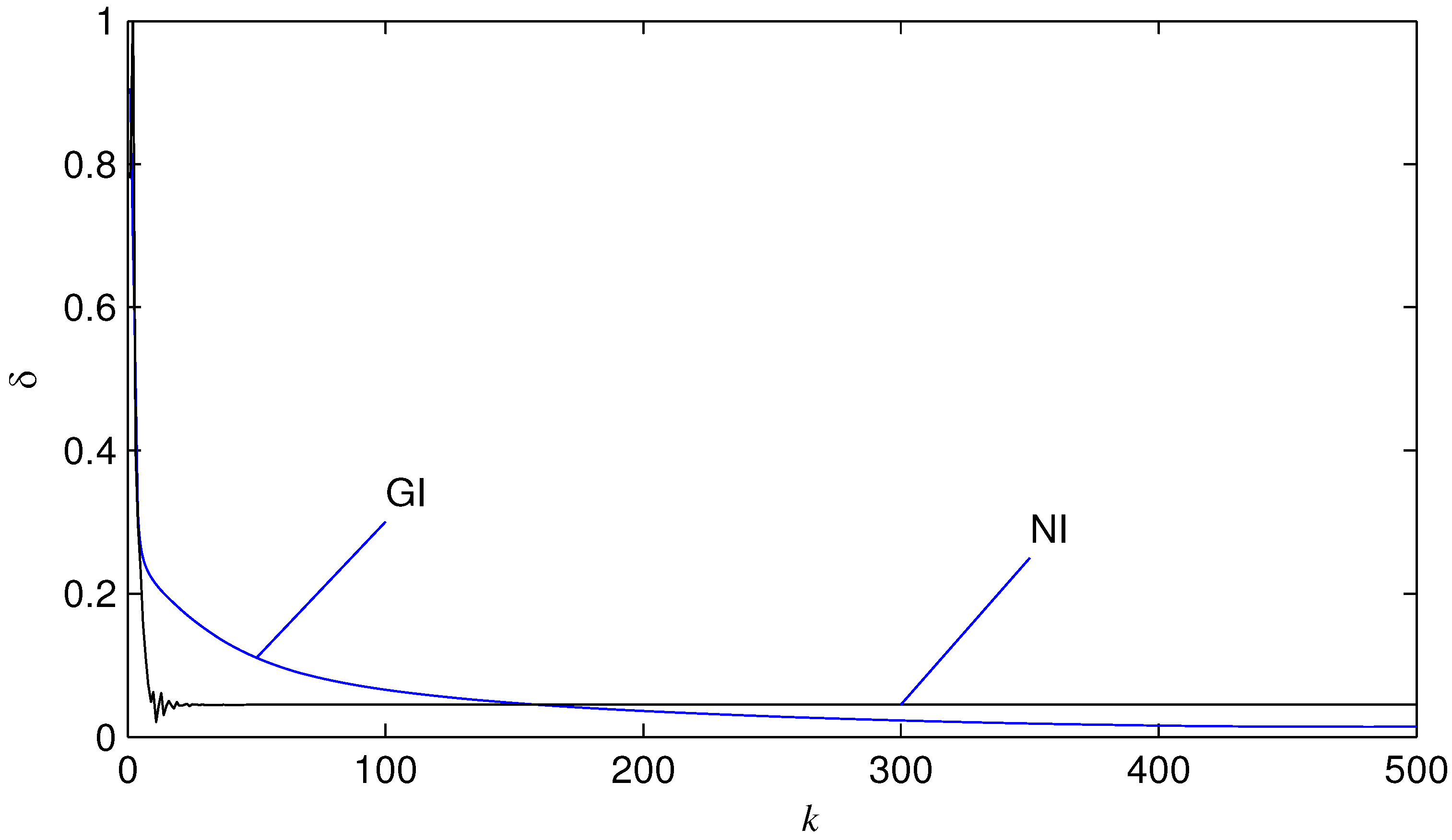
- The NI algorithm has a faster convergence rate than the GI algorithm, but the GI algorithm can generate more accurate parameter estimates than the NI algorithm: see the error curves in Figure 3.
| k | a1 | a2 | b1 | b2 | γ2 | γ3 | d1 | δ(%) |
|---|---|---|---|---|---|---|---|---|
| 10 | 0.02215 | 0.40793 | 1.00446 | 0.11168 | 0.49314 | 0.27343 | 0.15400 | 20.88476 |
| 50 | 0.14113 | 0.43950 | 0.97319 | 0.23592 | 0.53438 | 0.27736 | 0.17933 | 8.15348 |
| 100 | 0.19382 | 0.44038 | 0.97556 | 0.29595 | 0.52870 | 0.26852 | 0.21157 | 3.04925 |
| 200 | 0.21402 | 0.44122 | 0.99065 | 0.32470 | 0.50913 | 0.24897 | 0.23549 | 2.97170 |
| 300 | 0.21692 | 0.44127 | 0.99601 | 0.33017 | 0.50279 | 0.24304 | 0.24145 | 3.59966 |
| 400 | 0.21757 | 0.44127 | 0.99744 | 0.33149 | 0.50114 | 0.24152 | 0.24314 | 3.79156 |
| 500 | 0.21773 | 0.44127 | 0.99780 | 0.33182 | 0.50071 | 0.24112 | 0.24364 | 3.84560 |
| True values | 0.20000 | 0.44000 | 0.99000 | 0.30000 | 0.50000 | 0.25000 | 0.21000 |
| k | a1 | a2 | b1 | b2 | γ2 | γ3 | d1 | δ (%) |
|---|---|---|---|---|---|---|---|---|
| 10 | 0.02115 | 0.40802 | 1.02095 | 0.10735 | 0.47432 | 0.25670 | 0.12715 | 21.79777 |
| 50 | 0.13019 | 0.43964 | 0.98093 | 0.22118 | 0.52043 | 0.27002 | 0.12067 | 11.04226 |
| 100 | 0.18373 | 0.43985 | 0.97722 | 0.28055 | 0.52339 | 0.26897 | 0.13687 | 6.58059 |
| 200 | 0.20564 | 0.44044 | 0.98854 | 0.30949 | 0.50892 | 0.25355 | 0.16558 | 3.61544 |
| 300 | 0.20865 | 0.44051 | 0.99326 | 0.31470 | 0.50328 | 0.24815 | 0.18529 | 2.28582 |
| 400 | 0.20927 | 0.44054 | 0.99454 | 0.31591 | 0.50170 | 0.24670 | 0.19970 | 1.57463 |
| 500 | 0.20943 | 0.44057 | 0.99489 | 0.31622 | 0.50122 | 0.24628 | 0.21044 | 1.39000 |
| True values | 0.20000 | 0.44000 | 0.99000 | 0.30000 | 0.50000 | 0.25000 | 0.21000 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ding, F.; Liu, X.P.; Liu, G. Identification methods for Hammerstein nonlinear systems. Digit. Signal Proc. 2011, 21, 215–238. [Google Scholar] [CrossRef]
- Li, J.H. Parameter estimation for Hammerstein CARARMA systems based on the Newton iteration. Appl. Math. Lett. 2013, 26, 91–96. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.P.; Ding, R.F. Gradient based estimation algorithm for Hammerstein systems with saturation and dead-zone nonlinearities. Appl. Math. Model. 2012, 36, 238–243. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, J.B.; Liao, Y.; Ding, J. Parameter estimation error bounds for Hammerstein finite impulsive response models. Appl. Math. Comput. 2008, 202, 472–480. [Google Scholar] [CrossRef]
- Li, X.L.; Ding, R.F.; Zhou, L.C. Least-squares-based iterative identification algorithm for Hammerstein nonlinear systems with non-uniform sampling. Int. J. Comput. Math. 2013, 90, 1524–1534. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Wang, X.D.; Wang, D.Q. Identification of Dual-Rate Sampled Hammerstein Systems with a Piecewise-Linear Nonlinearity Using the Key Variable Separation Technique. Algorithms 2015, 8, 366–379. [Google Scholar] [CrossRef]
- Vörös, J. Parameter identification of Wiener systems with multisegment piecewise-linear nonlinearities. Syst. Control Lett. 2007, 56, 99–105. [Google Scholar] [CrossRef]
- Zhou, L.C.; Li, X.L.; Pan, F. Gradient based iterative parameter identification for Wiener nonlinear systems. Appl. Math. Model. 2013, 37, 8203–8209. [Google Scholar] [CrossRef]
- Zhou, L.C.; Li, X.L.; Pan, F. Gradient-based iterative identification for Wiener nonlinear systems with non-uniform sampling. Nonlinear Dyn. 2014, 76, 627–634. [Google Scholar] [CrossRef]
- Chen, J. Gradient based iterative algorithm for wiener systems with piece-wise nonlinearities using analytic parameterization methods. Comput. Appl. Chem. 2011, 28, 855–857. [Google Scholar]
- Zhou, L.C.; Li, X.L.; Pan, F. Gradient-based iterative identification for MISO Wiener nonlinear systems: Application to a glutamate fermentation process. Appl. Math. Model. 2013, 26, 886–892. [Google Scholar] [CrossRef]
- Pelckmans, K. MINLIP for the identification of monotone Wiener systems. Automatica 2011, 47, 2298–2305. [Google Scholar] [CrossRef]
- Wang, D.Q.; Ding, F. Least squares based and gradient based iterative identification for Wiener nonlinear systems. Signal Process. 2011, 91, 1182–1189. [Google Scholar] [CrossRef]
- Hagenblad, A.; Ljung, L.; Wills, A. Maximum likelihood identification of Wiener models. Automatica 2008, 44, 2697–2705. [Google Scholar] [CrossRef]
- Liu, Y.J.; Ding, F.; Shi, Y. Least squares estimation for a class of non–uniformly sampled systems based on the hierarchical identification principle. Circuits Syst. Signal Process. 2012, 31, 1985–2000. [Google Scholar] [CrossRef]
- Liu, Y.J.; Wang, D.Q.; Ding, F. Least squares based iterative algorithms for identifying Box-Jenkins models with finite measurement data. Digit. Signal Process. 2010, 20, 1458–1467. [Google Scholar] [CrossRef]
- Chen, H.; Lv, X.; Qiao, Y. Application of gradient descent method to the sedimentary grain-size distribution fitting. J. Comput. Appl. Math. 2009, 233, 1128–1138. [Google Scholar] [CrossRef]
- Chen, J.; Ding, F. Modified stochastic gradient algorithms with fast convergence rates. J. Vib. Control 2011, 17, 1281–1286. [Google Scholar] [CrossRef]
- Jiang, H.; Wilford, P. A stochastic conjugate gradient method for the approximation of functions. J. Comput. Appl. Math. 2012, 236, 2529–2544. [Google Scholar] [CrossRef]
- Calo, V.M.; Collier, N.; Gehre, M.; Jin, B.; Radwan, H.; Santillana, M. Gradient-based estimation of Manning’s friction coefficient from noisy data. J. Comput. Appl. Math. 2013, 238, 1–13. [Google Scholar] [CrossRef]
- Ding, J.; Shi, Y.; Wang, F.; Ding, H. A modified stochastic gradient based parameter estimation algorithm for dual-rate sampled-data systems. Digit. Signal Process. 2010, 20, 1238–1249. [Google Scholar] [CrossRef]
- Liu, Y.J.; Yu, L.; Ding, F. Multi-innovation extended stochastic gradient algorithm and its performance analysis. Circuits Syst. Signal Process. 2010, 29, 649–667. [Google Scholar] [CrossRef]
- Ding, F.; Liu, X.P.; Liu, G. Gradient based and least-squares based iterative identification methods for OE and OEMA systems. Digit. Signal Process. 2010, 20, 664–677. [Google Scholar] [CrossRef]
- Xie, L.; Yang, H.Z. Gradient based iterative identification for non-uniform sampling output error systems. J. Vib. Control 2011, 17, 471–478. [Google Scholar] [CrossRef]
- Xiong, W.L.; Ma, J.X.; Ding, R.F. An iterative numerical algorithm for modeling a class of Wiener nonlinear systems. Appl. Math. Lett. 2013, 26, 487–493. [Google Scholar] [CrossRef]
- Wang, D.Q.; Yang, G.W.; Ding, R.F. Gradient-based iterative parameter estimation for Box-Jenkins systems. Comput. Math. Appl. 2010, 60, 1200–1208. [Google Scholar] [CrossRef]
- Li, J.H.; Ding, R.F.; Yang, Y. Iterative parameter identification methods for nonlinear functions. Appl. Math. Model. 2012, 36, 2739–2750. [Google Scholar] [CrossRef]
- Zhang, Z.N.; Ding, F.; Liu, X.G. Hierarchical gradient based iterative parameter estimation algorithm for multivariable output error moving average systems. Comput. Math. Appl. 2011, 61, 672–682. [Google Scholar] [CrossRef]
- Wang, D.Q.; Chu, Y.Y.; Ding, F. Auxiliary model-based RELS and MI-ELS algorithms for Hammerstein OEMA systems. Comput. Math. Appl. 2010, 59, 3092–3098. [Google Scholar] [CrossRef]
- Liu, M.M.; Xiao, Y.S.; Ding, R.F. Iterative identification algorithm for Wiener nonlinear systems using the Newton method. Appl. Math. Model. 2013, 37, 6584–6591. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Li, X.; Xu, H.; Zhu, P. Gradient-Based Iterative Identification for Wiener Nonlinear Dynamic Systems with Moving Average Noises. Algorithms 2015, 8, 712-722. https://doi.org/10.3390/a8030712
Zhou L, Li X, Xu H, Zhu P. Gradient-Based Iterative Identification for Wiener Nonlinear Dynamic Systems with Moving Average Noises. Algorithms. 2015; 8(3):712-722. https://doi.org/10.3390/a8030712
Chicago/Turabian StyleZhou, Lincheng, Xiangli Li, Huigang Xu, and Peiyi Zhu. 2015. "Gradient-Based Iterative Identification for Wiener Nonlinear Dynamic Systems with Moving Average Noises" Algorithms 8, no. 3: 712-722. https://doi.org/10.3390/a8030712
APA StyleZhou, L., Li, X., Xu, H., & Zhu, P. (2015). Gradient-Based Iterative Identification for Wiener Nonlinear Dynamic Systems with Moving Average Noises. Algorithms, 8(3), 712-722. https://doi.org/10.3390/a8030712





