3.1. Description of the Proposed PSO Algorithm
The population of the proposed PSO algorithm consists of 15 particles, each one comprising a two-dimensional array. Although the population size is different from the one used in [
20], the particle encoding is the same. The number of rows of each particle equals the number of different classes of each school, while the number of columns is 35, since the timeslots of a weekly Greek school timetable are 35 at the most [
20]. Each particle’s cell contains a number ranging from 1 to the number of different teachers of each school or a “−1” value. For example, if cell [
i,
j] equals “4”, that means that the 4th teacher teaches one of his/her lessons at the
i-th class at the
j-th timeslot. If cell [
i,
j] equals “−1”, that means that the
i-th class has the
j-th timeslot empty. The interested reader can find more details about the particle encoding used in [
20].
In Algorithm 1, the pseudo code of the proposed PSO based algorithm is presented. The algorithm is a hybrid one consisting of two basic components:
the main algorithm, which has four basic differences compared to the algorithm presented in [
20].
a local search procedure, which is the same as the one used in [
20] and aims improving the quality of the resulted timetable after the execution of the main algorithm.
In this contribution we limit our description on the main algorithm, since all differences between the proposed PSO algorithm and the one presented in [
20] lie there. The interested reader can find more details about the local search procedure in [
20]. The differences of the proposed PSO algorithm compared to the algorithm presented in [
20] are the following:
Line 3: The number of particles P (
i.e., the population size) is set to 15, while in [
20] equals 50.
Lines 22–23: Procedure
SwapWithProbability() is applied to two randomly selected timeslots, while in [
20] one of the two timeslots selected should have a hard clash (if such a timeslot exists).
Line 22: Procedure
SwapWithProbability() accepts swaps causing a hard clash with probability equal to 50%, while in [
20] this probability equals 2.2%.
Line 22: Procedure
SwapWithProbability() accepts swaps which cause a raise in the individual’s fitness with probability equal to 0.5%, while in [
20] this probability equals 2.2%.
Lines 29–34: The probability of exiting the
While Loop Structure is set to 1.08%, while in [
20] equals 1.1%.
| Algorithm 1: The pseudo code of the main PSO algorithm. |
| In what follows, P is the number of particles (i.e., the population size), particle(p) is the p-th particle of the population, Personal_best(p) is the personal best achieved by particle p till current generation and Global_best is the globally best particle among all particles till current generation, i.e. the particle with smallest fitness. In addition, F() stands for the fitness function, F stands for the fitness function value, while auxiliary_particle is a structure identical to any particle’s structure that serves for temporal storage of a particle. |
| 1. Start of hybrid PSO algorithm |
| 2. Start of main algorithm |
| 3. Read input Data; // i.e. teachers, classes, hours, co teachings etc. |
| 4. Initialize P particles with random structure; |
| 5. For each particle(p) { |
| 6. Personal_best(p) ← particle(p); |
| 7. F(Personal_best(p)) ← F(particle(p)); |
| 8. } // end For |
| 9. Global_best ← the particle with smallest fitness; |
| 10. F(Global_best) ← the smallest fitness among all particles; |
| 11. While generation < numOfGenerations { // numOfGenerations is set to 10,000 |
| 12. For each particle(p) { |
| 13. F(particle(p)) ← compute fitness of particle(p); |
| 14. If (F(particle(p)) <= F(Personal_best(p)) then { |
| 15. F(Personal_best(p)) ← F(particle(p)); |
| 16. Personal_best(p) ← particle(p); |
| 17. If F(particle(p) <= F(Global_best) then { |
| 18. F(Global_best) ← F(particle(p)); |
| 19. Global_best ← particle(p); |
| 20. } // end If |
| 21. } // end If |
| 22. Select two different timeslots t1, t2 at random; |
| 23. Execute procedure SwapWithProbability(particle(p), t1, t2); |
| 24. Select a timeslot t at random; |
| 25. Execute procedure InsertColumn(Personal_best(p), particle(p), t); |
| 26. Select a timeslot t at random; |
| 27. Execute procedure InsertColumn(Global_best, particle(p), t); |
| 28. F_before_entering_While_Loop_Structure ← F(particle(p)); |
| 29. auxiliary_particle ← particle(p); |
| 30. While F(particle(p)) > F(Global_best) { // this is the While Loop Structure |
| 31. Every 10 loop-cycles break the while-loop with a fixed probability; |
| 32. Select a timeslot t at random; |
| 33. Execute procedure InsertColumn(Global_best, particle(p), t); |
| 34. F(particle(p)) ← compute fitness of particle(p); |
| 35. } // end While (While Loop Structure) |
| 36. If F(particle(p)) > F_before_entering_While_Loop_Structure then { |
| 37. particle(p) ← auxiliary_particle; |
| 38. F(particle(p)) ← F_before_entering_While_Loop_Structure; |
| 39. } // end If |
| 40. } // end For each particle(p) |
| 41. ++generation; |
| 42. } // end While termination criterion is not met |
| 43. End of main algorithm //Here is where the main algorithm ends and the refinement phase starts |
| 44. Execute Local Search Procedure |
| 45. output ← Global_best; |
| 46. End of hybrid PSO algorithm |
As seen in Algorithm 1, the main algorithm involves three major components, namely, procedure
SwapWithProbability(), procedure
InsertColumn() and a
While Loop Structure. These three parts are described in short in the next paragraphs. The interested reader can find more details about these parts in [
20].
The parameters of procedure SwapWithProbability() are the current particle (particle(p)) and two different timeslots t1 and t2. Procedure SwapWithProbability() investigates all swaps between the cells of timeslots (columns) t1 and t2 for all classes of particle(p). Swaps that cause no hard clash and result in a smaller or equal fitness value are always accepted and executed. Swaps that cause hard constraint violations are accepted with probability equal to 50%. Swaps that do not cause hard constraint violations but lead to larger (worse) fitness function values are accepted with probability equal to 0.5%. Note that the acceptance of invalid swaps permits the algorithm to escape from local optima in most cases.
Procedure InsertColumn() is used in order to substitute timeslots of current particle (particle(p)) with timeslots either from the personal best of current particle (Personal_best(p)) or the global best (Global best) found until that point. Procedure InsertColumn() takes as first parameter either Personal_best(p) or Global_best, as second parameter particle(p) and as third parameter a random selected timeslot t, which is the timeslot to be replaced in particle(p) either from Personal_best(p) or Global_best.
The While Loop Structure tries to discover, for each particle(p), a particle with the best or equal fitness value to the fitness value of Global_best, by applying procedure InsertColumn() between Global_best and particle(p). In order to avoid being trapped into an infinite loop, the algorithm can exit the While Loop Structure with a probability set to 1.08%, no matter what the achieved fitness value is, every time 10 more loops are executed.
3.2. Description of the Proposed AFS Algorithm
The population of the proposed AFS algorithm consists of 24 fish, each of which is a two-dimensional array. The fish encoding is the same as the one used by the proposed PSO algorithm and the algorithm presented in [
20]. In Algorithm 2, the pseudo code of the proposed AFS based algorithm is presented. The algorithm is a hybrid one consisting of two basic components:
As seen in Algorithm 2, the main algorithm includes seven basic procedures, namely, procedure Prey(), procedure InnerPrey(), procedure SwarmNChace(), procedure CreateNeighborhood(), procedure CalculateLocalCentre(), procedure Leap(), and procedure Turbulence(). A detailed description of these procedures is given in the following paragraphs.
We define Distance d between two fish f1 and f2 as the number of cells of the timetable, in which the two fish differ. The distance of two fish takes values in the interval [0, number of classes × 35]. As the algorithm progresses, the fish tend to approach each other and the population loses the desired diversity that allows fish to seek in wider solutions area. To prevent this phenomenon, a shaker process of the space of solutions is used, called procedure Turbulence() (Algorithm 2, Line 10). This procedure is activated when the current maximum distance between all fish becomes less than MIN_DISTANCE_COEF × number of classes × 35, wherein MIN_DISTANCE_COEF is a user defined “proximity factor”, constant throughout the execution of the algorithm. During the execution of procedure Turbulence(), a random fish, a random row (class) in this fish and two random periods are selected. Then, utilizing procedure Swap() teachers assigned to classes during these periods are swapped. Procedure Swap() is repeated a specified number of times, which in all experiments conducted was equal to TURBULENCE_ITERATIONS × NUMBER_OF_FISH, wherein TURBULENE_ITERATIONS is user defined, constant throughout the execution of the algorithm. The parameters of procedure Swap(), as used in procedure Turbulence(), are four: a randomly selected fish, a randomly selected row in this fish and two randomly selected columns in this fish. It swaps the values of two cells in the same row of the timetable of fish f, i.e., teachers who are assigned to the two periods of the timetable of the class.
Procedure
Leap() (Algorithm 2, Line 12) is activated when the improvement of the obtained best fitness (
i.e., the fitness of minGlobalFish) during the last LEAP_NUMBER generations is less than MIN_IMR, where LEAP_NUMBER and MIN_IMR are user defined and constant. Parameter MIN_IMR is the threshold of desired fitness’ rate improvement in order to start the
Leap() procedure (see also
Table 1). Procedure
Leap() is triggered repeatedly until the desired rate of improvement has been achieved or 10 executions without desired rate of improvement have been completed. In order to achieve the desired rate of improvement, procedure
Leap() applies procedure
Approach(), which forces current fish f to approach minGlobalFish. Procedure
Approach() is repeated, inside the body of procedure
Leap(), a specified number of times, which in all experiments conducted was equal to NUMBER_OF_FISH.
The
Approach() procedure is one of the two procedures (the second one is
RandomApproach() presented below) aimed to make fish f
1 approach fish f
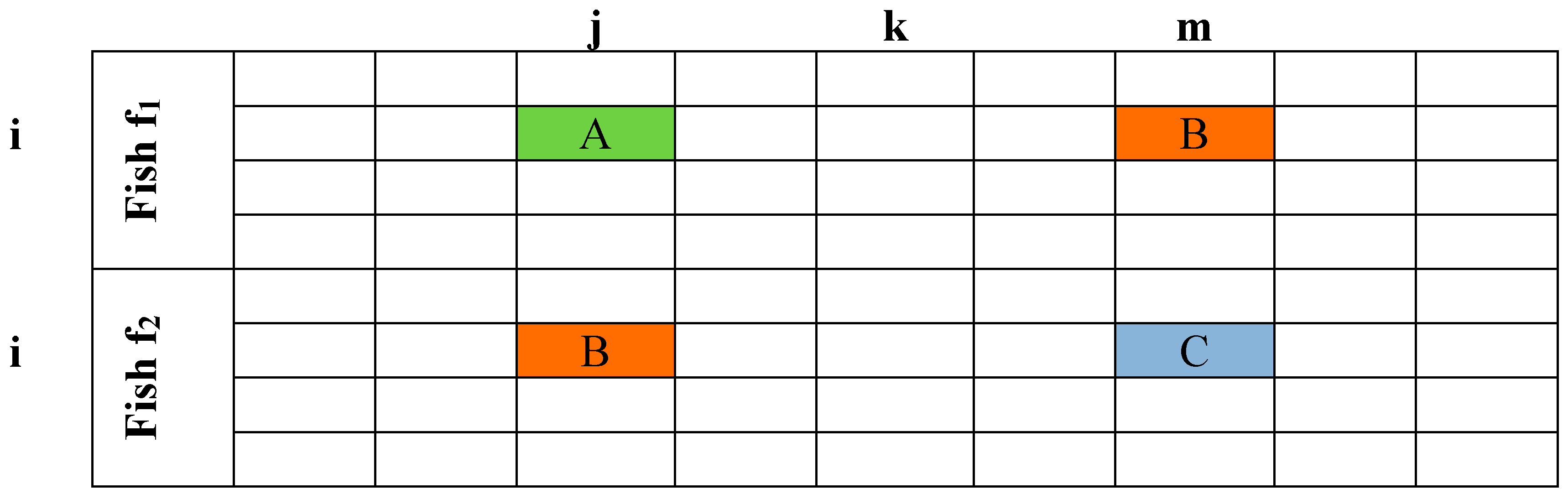
2. To achieve this, it initially identifies the cells in which the teachers in the timetables of the two fish are different. So, if the values of fish f
1 and f
2 in cell (
i,
j) are different, say, “Professor A” and “Professor B”, then it is certain that there will be another cell (
i,
m), having “Professor B” as a value (this is assured by the initialization procedure) (
Figure 1). Procedure
Approach() is executed as follows: It randomly selects two cells of f
1 among cells in which timetables of f
1 and f
2 are different. Then, utilizing procedure
Swap(), the algorithm switches the values of cells (
i,
j) and (
i,
m) of f
1 (
Figure 2). In this way, the distance of the two fish is decreased by at least one unit (perhaps two if A = C). By choosing to make alternations per class (horizontal) we ensure that the number of hours that each teacher is assigned to each class is not violated (this has been ensured by the initialization procedure). The process ends when the percentage of the initial distance between the two fish becomes less than (1.0-STEP_RATIO), where STEP_RATIO is a user defined variable, constant throughout the execution of the algorithm.
| Algorithm 2: The pseudo code of the main AFS algorithm. |
| In what follows, minGlobalFish is the fish with best fitness in population, personalBest is the current personal best structure of each fish, localBest is the fish with the best fitness in a neighborhood, localCentre is the centre of a fish neighborhood and leapNumber is the number of generations every which the algorithm checks whether an improvement over threshold MIN_IMPR in the fitness of minGlobalFish has occurred. |
| 1. Start of hybrid AFS algorithm |
| 2. Start of main algorithm |
| 3. Read input Data; //i.e., teachers, classes, hours, co teachings etc. |
| 4. Create initial population of fish, each fish having random structure; //The size of initial population is set to NUMBER_OF_FISH=24 |
| 5. minGlobalFish ← The fish with best fitness in population; |
| 6. Make every fish best position equal to current (i.e., initial) position; |
| 7. generation ← 0; |
| 8. While generation < NUM_OF_GENERATIONS { // NUM_OF_GENERATIONS is set to 10,000 |
| 9. If maximum distance between all fish is less than a minimum threshold then |
| // Threshold is equal to MIN_DISTANCE_COEF × number of classes × 35 |
| 10. Execute procedure Turbulence(); // perturb the population of fish |
| 11. If the % improvement of minGlobalFish fitness for the last LEAP_NUMBER generations is not bigger than MIN_IMPR then |
| // MIN_IMPR is a threshold in the improvement of minGlobalFish |
| 12. Execute procedure Leap(); // make fish approach minGlobalFish |
| 13. For each fish f { |
| 14. If fitness of fish f has been improved then |
| 15. update fish f personalBest; |
| 16. Execute procedure CreateNeighborhood(f); // recreate the neighborhood of fish f |
| 17. Execute procedure CalculateLocalCentre(f); // calculate the localCentre of the neighborhood of fish f and the localBest of fish f |
| 18. If the neighborhood of fish f is sparse then // if it contains less than SPARSE_COEF × NUMBER_OF_FISH members |
| 19. Execute procedure Prey(f); // try to find for fish f, in the whole population, a structure having better fitness |
| 20. Else |
| 21. If the neighborhood of fish f is dense then // if it contains more than DENSE_COEF × NUMBER_OF_FISH members |
| 22. Execute procedure InnerPrey(f); // try to find for fish f, in its neighborhood, a structure having better fitness |
| 23. Else |
| 24. Execute procedure SwarmNChase(f); // try to find for fish f a structure having better fitness in case its neighborhood is neither dense nor sparse |
| 25. If fitness of fish f < = fitness of minGlobalFish then |
| 26. minGlobalFish ← f; |
| 27. } // end For each fish f |
| 28. ++generation; |
| 29. } // end While generation < numOfGenerations |
| 30. End of main algorithm //Here is where the main algorithm ends and the refinement phase starts |
| 31. Execute Local Search Procedure |
| 32. output ← minGlobalFish; |
| 33. End of hybrid AFS algorithm |
Figure 1.
Two fish timetables which differ in cell (i, j).
Figure 1.
Two fish timetables which differ in cell (i, j).
Figure 2.
The fish f1 after switching cells (i, j) and (i, m).
Figure 2.
The fish f1 after switching cells (i, j) and (i, m).
Procedure CreateNeighborhood() (Algorithm 2, Line 16) plays a major role in the operation of the algorithm. Its aim is to create in every generation, the current neighborhood for each fish. As the fish move, their mutual distances change and they are getting far or near to each other. Thus, neighborhoods of fish evolve dynamically during execution of the algorithm. This means that in every generation, the neighborhood of each fish is recalculated. We define that a fish f1 is assumed to lie in the neighborhood of a fish f, if its distance from f is less than minDist + (maxDist – minDist) × VISUAL_SCOPE_COEF, where minDist and maxDist are respectively the minimum and maximum distance among all fish of current population and VISUAL_SCOPE_COEF is a user defined parameter, constant throughout the execution of the algorithm. As stated before, the distance d between two fish f1 and f2 is the number of cells of the timetable, in which the two fish differ. Procedure CreateNeighborhood() sets the fish in the neighborhood of f in increasing fitness order. So, the first fish in the neighborhood of f, is the one with the best fitness among all its neighbors. A neighborhood is considered “sparse” (Algorithm 2, Line 18), when containing less than SPARSE_COEF × NUMBER_OF_FISH members, where NUMBER_OF_FISH is the population size and SPARSE_COEF is a user defined parameter, constant throughout the execution of the algorithm. A neighborhood is considered “dense” (Algorithm 2, Line 21), when containing more than DENSE_COEF × NUMBER_OF_FISH members, where DENSE_COEF is a user defined parameter, constant throughout the execution of the algorithm.
One of the key behaviors simulated in AFS algorithms is the tendency of fish to gather in flocks to maximize food-finding and survival chances [
17]. The concentration of fish in flocks (swarming) is simulated by moving the fish to a “notional” fish located in the “center” of their neighborhood (localCentre fish). This “notional” fish, is created by procedure
CalculateLocalCentre() (Algorithm 2, Line 17). At first, the localCentre fish is set equal to the first fish in the neighborhood of f, which is the fish with the best fitness among all fish in the neighborhood, since procedure
CreateNeighborhood() sets the fish in the neighborhood of f in increasing fitness order (see above). Then, for an arbitrary number of times (without, of course, exceeding the size of the neighborhood), the localCentre approaches the
i-th fish of the neighborhood, utilizing procedure
Approach(), with a diminishing step given by the expression
. For example, the localCentre approaches the second fish of the neighborhood with step equal to
, the third fish of the neighborhood with step equal to
and so on. As a result, the participation of the most robust fish of the neighborhood to the creation of the localCentre is greater than that of the less robust.
A fish f performs Prey() (Algorithm 2, Line 19) procedure when its neighborhood is not rich enough in fish, towards which it could make a move. A fish f1, different from f, is selected randomly from fish population and if it has better fitness than f then fish f moves towards f1 using procedure RandomApproach() and procedure Prey() is completed. If the fitness of f1 is not better than the fitness of f then f can also move towards f1 using procedure RandomApproach() with probability equal to (dc is the difference in fitness between fish f1 and fish f and gen is the current generation) and procedure Prey() is completed, too. This is repeated PREY_TRY_NUMBER times at most, where PREY_TRY_NUMBER is a user defined parameter, constant throughout the execution of the algorithm. In case none of the above situations take place, fish f moves towards its personalBest using procedure RandomApproach(). The pseudo code of procedure Prey() is presented in Algorithm 3.
| Algorithm 3: The pseudo code of procedure Prey(). |
| 0. For try ← 1 to PREY_TRY_NUMBER { |
| 1. accept ← random number between 0 and 1; |
| 2. pick a random fish f1 among the population; |
| 3. dc ← fitness of f1 – fitness of f; |
| 4. If fitness of f1 <= fitness of f then { |
| 5. Execute procedure RandomApproach(); // move randomly fish f towards fish f1; |
| 6. return; |
| 7. } // end If |
| 8. If (fitness of f1 > fitness of f) and ( > = accept) then { |
| 9. Execute procedure RandomApproach(); // move randomly fish f towards fish f1; |
| 10. return; |
| 11. } // end If |
| 12. } // end For |
| 13. Execute procedure RandomApproach(); // move randomly fish f towards its personalBest |
| 14. return; |
Procedure RandomApproach() works the same way as procedure Approach(), with the difference that it completes its operation if f1 achieves better fitness than its initial one during the execution of the procedure. It chooses, just like in procedure Approach(), a random location at which both fish differ and then tests all the swaps (in same way as described in procedure Approach()). From all these swaps, procedure RandomApproach() finally chooses to carry out the one that leads to better fitness among all available swaps. The process ends either when a better fitness to f1 is achieved or when—as in procedure Approach()—the percentage of the initial distance between the two fish becomes less than (1.0-STEP_RATIO).
A fish f performs InnerPrey() (Algorithm 2, Line 22) procedure when its neighborhood is quite rich in fish, towards which it could make a move. A fish f1, different from f, is selected randomly from the neighbors of f and if it has better fitness than f then fish f moves towards f1 using procedure RandomApproach() and procedure InnerPrey() is completed. If the fitness of f1 is not better than the fitness of f then f can also move towards f1 using procedure RandomApproach() with probability equal to (dc is the difference in fitness between fish f1 and fish f and gen is the current generation) and procedure InnerPrey() is completed, too. This is repeated PREY_TRY_NUMBER times at most. In case none of the above situations take place, procedure Prey() is executed. The pseudo code of procedure InnerPrey() is presented in Algorithm 4.
| Algorithm 4: The pseudo code of procedure InnerPrey(). |
| 0. For try ← 1 to PREY_TRY_NUMBER { |
| 1. accept ← random number between 0 and 1; |
| 2. pick a random fish f1 among its neighbors; |
| 3. dc ← fitness of f1 – fitness of f; |
| 4. If fitness of f1 <= fitness of f then { |
| 5. Execute procedure RandomApproach(); // move randomly fish f towards fish f1; |
| 6. return; |
| 7. } // end If |
| 8. If (fitness of f1 > fitness of f) and ( > = accept) then { |
| 9. Execute procedure RandomApproach(); // move randomly fish f towards fish f1; |
| 10. return; |
| 11. } end If |
| 12. } end For |
| 13. Execute procedure Prey(); // See Algorithm 3 |
| 14. return; |
A fish f performs procedure
SwarmNChase() (Algorithm 2, Line 24) when its neighborhood is neither “dense” nor “sparse” in fish. Fish f, using procedure
RandomApproach(), moves separately and independently to the localCentre fish of its neighborhood (swarm behavior) and to the localBest fish of its neighborhood (chase behavior) [
17,
24]. The fish f finally takes the move which gives better fitness. If neither of the two moves lead to better fitness, the fish executes procedure
InnerPrey(). The pseudo code of procedure
SwarmNChase() is presented in Algorithm 5.
| Algorithm 5: The pseudo code of procedure SwarmNChase(). |
| 0. tempFish1 ← f; |
| 1. tempFish2 ← f; |
| 2. move randomly fish tempFish1 towards the localBest of neighborhood of f; |
| 3. move randomly fish tempFish2 towards the localCentre of neighborhood of f; |
| 4. tempFish ← fish with the minimum fitness among tempFish1 and tempFish2; |
| 5. If fitness of tempFish <= fitness of f then |
| 6. f ← tempFish; |
| 7. Else |
| 8. InnerPrey(f); // See Algorithm 4 |
| 9. Return; |
As seen in the previous paragraphs, the proposed AFS algorithm uses many user-defined parameters that affect the algorithm’s convergence and efficiency. In
Table 1 all user defined parameters are summarized and explained. Moreover, their values used in all experiments are listed. Although the adjustment of user-defined parameter values remains an open issue, as there is no obvious way to tune them, after having conducted exhaustive experiments we decided to use the values presented in
Table 1, since this combination of values resulted in the best performance of the proposed AFS algorithm.
Table 1.
The user defined parameters used by the proposed AFS algorithm.
Table 1.
The user defined parameters used by the proposed AFS algorithm.
| Parameter | Value | Comments |
|---|
| NUMBER_OF_GENERATIONS | 10,000 | The number of generations the algorithm is executed |
| NUMBER_OF_FISH | 24 | The size of the population of fish. We decided to use 24 fish since, after exhaustive experiments we came to the conclusion, that this is the minimum number of fish which guarantees that the AFS algorithm will always reach feasible solutions. |
| VISUAL_SCOPE_COEF | 0.7 | A fish f1 is located in the neighborhood of a fish f, if its distance from f is less than minDist + (maxDist – minDist) × VISUAL_SCOPE_COEF, where minDist and maxDist are respectively the minimum and maximum distance among all fish of current population |
| SPARSE_COEF | 0.1 | A neighborhood is considered “sparse”, when containing less than SPARSE_COEF × NUMBER_OF_FISH individuals |
| DENSE_COEF | 0.8 | A neighborhood is considered “dense”, when containing more than DENSE_COEF × NUMBER_OF_FISH individuals |
| STEP_RATIO | 0.047 | Fish approaching factor. Procedures Approach() and RandomApproach() are completed when the percentage of the initial distance between two fish becomes less than (1.0 - STEP_RATIO) |
| PREY_TRY_NUMBER | 3 | Number of iterations for procedures Prey() and InnerPrey() |
| MIN_DIST_COEF | 0.01 | The turbulence activating factor. Procedure Turbulence() is activated when the current maximum distance between all fish becomes less than MIN_DISTANCE_COEF × number of classes × 35 |
| LEAP_NUMBER | 100 | Procedure Leap() is activated when the improvement of the obtained best fitness (i.e. the fitness of minGlobalFish) during the last LEAP_NUMBER generations is less than MIN_IMR |
| TURBULENCE_ITERATIONS | 5 | Number of repetitions of procedure Swap() inside procedure Turbulence() equals to TURBULENCE_ITERATIONS × NUMBER_OF_FISH |
| MIN_IMPR | 0.01 | Threshold of desired fitness’ rate improvement in order to start the Leap() procedure |