Abstract
Gain tuning is very important in order to obtain good performances for a given controller. Contour tracking performance is mainly determined by the selected control gains of a position domain PID controller. In this paper, three popular evolutionary algorithms are utilized to optimize the gains of a position domain PID controller for performance improvement of contour tracking of robotic manipulators. Differential Evolution (DE), Genetic Algorithm (GA), and Particle Swarm Optimization (PSO) are used to determine the optimal gains of the position domain PID controller, and three distinct fitness functions are also used to quantify the contour tracking performance of each solution set. Simulation results show that DE features the highest performance indexes for both linear and nonlinear contour tracking, while PSO is quite efficient for linear contour tracking. Both algorithms performed consistently better than GA that featured premature convergence in all cases.
1. Introduction
Since the introduction of PID controllers, a great number of methods such as trial-and-error, D-partitioning, Ziegler-Nichols, and pole placement have been developed for the gain tuning of PID controlled systems [1]. Nonetheless, most of these direct methods have been developed for linear, time invariant systems and require extensive knowledge of the system and its frequency response in order to be employed efficiently. Due to these facts, various meta-heuristic optimization methods have been used for the gain tuning of PID controllers for nonlinear systems such as robotic systems. More specifically, evolutionary algorithms such as genetic algorithm (GA), differential evolution (DE), and particle swarm optimization (PSO) have been very popular for PID tuning of various systems [2].
Recent research suggests that meta-heuristic algorithms such GA, DE, and PSO produce consistently better results than conventional tuning techniques with DE outperforming the other algorithms in results and computational cost [3].Furthermore, Kachitvichyanukul [2], in a comparison of the three algorithms, concluded that GA falls into local minima with greater tendency than the other algorithms, while PSO tends to result in higher density of solutions within the solution space with DE being closely comparable to PSO.
Comparing PSO with GA, controllers tuned by the PSO method were found to be more efficient, with the PSO exhibiting better performance and a higher convergence rate than GA [4]. This can be attributed to PSO’s ability to avoid premature convergence to local minima and therefore provides higher quality solutions [5]. Similarly, in [6] DE was found to produce better tuning results than the GA with the authors, however noting that for high order systems, the results of both optimization techniques were quite similar. Furthermore, controllers optimized by DE performed better than the PSO tuned equivalents, leading to the conclusion that DE can be more robust than PSO [7]. However, it should be noted that the performance of each optimization algorithm is also subject to the optimization problem itself as demonstrated in [8].
In our previous research, the concept of position domain (PDC) was introduced in the form of PD and PID control types [9,10,11], with its main feature being its good contour tracking efficiency when compared to pre-existing control schemes in time domain. The main idea behind PDC is the discretization of the system into master and slave motions, with the use of the master motion as reference for the slave motions instead of time [9,10,11].
In this paper, the performance of GA, DE and PSO are studied for the gain tuning of a position domain PID controller (PDC-PID). The controller is tasked with contour tracking of a 3R planar serial robotic manipulator on the end-effector level. The robotic manipulator is used to track two different contours, one is linear and the one is nonlinear, for which different optimized control gains are generated. Furthermore, the optimizations are executed under various fitness functions for a large variation in performance criteria.
The rest of this paper is organized as follows: Section 2 summarizes the concept of position domain control and the PDC-PID controller. Section 3 synopsizes optimization algorithms to be compared. Section 4 describes the details of optimization, and Section 5 exhibits some optimized results for contour tracking of the end-effector of a robotic manipulator. Finally, Section 6 provides some conclusions.
2. Position Domain Control for Contour Tracking
The dynamic model of an n-DOF robotic manipulator can be expressed as:
where
is the inertial matrix,
is the matrix of coriolis and centrifugal forces,
is the vector of gravitational terms,
is the vector of friction forces,
is the vector of joint torques, and
and
are the joint position, velocity, and acceleration vectors, respectively [12,13,14].
In the position domain control approach, the robotic manipulator is viewed as a combination of a master motion and a number of slave motions [9,10,11], and the dynamic model in Equation (1) can be discretized in a master motion and slave motions by taking the following form:
with subscripts m and s indicating the master and the slave motions, respectively.
The position of the master motion replaces time as the main reference for the slave motions, something that requires the reinterpretation of the slave section of Equation (2) as functions of the master motion. This reinterpretation takes the form of a one-to-one mapping from time domain to position domain as described in the following subsection.
2.1. Relative Derivatives and Position Domain Mapping
To transform the dynamics of slave motions from time domain to position domain, a relationship has to be developed that relates time domain to position domain for master motion and slave motions. This relationship can be introduced by the relative derivative of the ith slave motion () with regard to the master motion ():
Equation (3) indicates that
, also called the relative position velocity, is the ratio of the slave motion speed over the master motion speed, and it describes the synchronized relationship of motions between the master and the slave motions.
Similarly, the relative position acceleration of the slave motions can be expressed as the second relative derivative of Equation (3):
According to Equations (3) and (4), a one-to-one transformation from time domain to position domain can be defined as:
Equation (5) shows the relationship between the absolute motions and the relative motions, and relate the absolute velocities and accelerations in time domain to the relative velocities and accelerations in position domain. These two equations are used to transform a dynamic system from time domain to position domain [9,10,11].
2.2. Dynamic Model in Position Domain
Substituting Equation (5) in the slave section of Equation (2), the position domain slave motion dynamics [10,11] is derived as functions of the master motion as follows:
2.3. PDC-PID Control Law
Similar to a time domain PID controller, a PDC-PID controller can be expressed as:
where
,
, and
are the control gains for the ith slave motion, respectively. The tracking errors of the slave motions are defined as follows:
It should be noticed that the errors of the system, and consequently the control input, are functions of the master axis motion. Furthermore, the master motion is still being controlled in time domain by a conventional PID controller [10]. The tracking performance mainly depends on the selection of PID control gains. DE, PSO, and GA are compared and used to determine the optimal gains of the PDC-PID controller to obtain better contour tracking performances.
3. Optimization Algorithms
3.1. Differential Evolution
The DE optimization algorithm was first introduced by Storn and Price [15] as a simple, robust alternative to pre-existing heuristic optimizations approaches. The DE optimization procedure starts with a randomly generated population of
individuals, each characterized by D parameters which represent a candidate solution to the optimization problem. A mutation is introduced to the population at each generation, creating a new mutated population. The mutation for each individual of the population is defined as the sum of the weighted difference of two individuals added to a third individual, all of which are randomly selected from the existing non-mutated population. Mathematically, the mutation equation can be expressed as:
where is the ith mutated individual of the (k + 1)th generation,
are randomly selected members of the kth generation with
and
is a constant mutation factor.
To introduce greater diversity for the population of the optimization, a crossover procedure is introduced that compares the current generation with the mutated population by passing the values of both in a test population
as follows:
where,
is randomly generated,
is a user determined crossover constant and
is a randomly chosen index which ensures that at least one characteristic is part from the mutated population to the test population.
The new generation is selected based on the performance of the test population
compared to the performance of the existing generation . If the ith individual of the test population performs better than the ith individual of the current generation, it takes its place in the new generation and the procedure is repeated until the end of the optimization [16].
3.2. Genetic Algorithm
One of the older evolutionary optimization algorithms, GA, is inspired by the change in inherited characteristics of living organisms over successive generations, and similar to DE, it features selection, crossover, and mutations as its main mechanisms. In GA, each individual of the optimization population features a set of “chromosomes” that constitutes a set of possible solutions for a given optimization problem. As in real life evolution, the most successful members of the generation are selected as the most likely to reproduce and create the successful offspring for the next generation. Each offspring is created by usually two individuals of the previous generation and its chromosomes are a combination of its parents’ chromosomes. Mutation is also introduced in order to avoid population stagnation. This usually takes the form of randomly generated changes in the chromosomes of a part of the population which may be bounded or unbound depending on whether the optimization is constrained or unconstrained [17].
Although a number of different methods have been developed for the crossover of the individuals (Single-point, Two-point, Heuristic, Arithmetic, etc.), for the purposes of this paper, the Intermediate Crossover method is used. This method produces the offspring as a weighted average of the parents, and it can be expressed as:
where rand is a randomly generated variable and
[18].
3.3. Particle Swarm Optimization
PSO is a heuristic search method inspired by social interaction of animals living in groups. PSO begins with a group (swarm) of randomly generated particles, each of which represents a possible solution for the optimization problem. Each particle is characterized by two main properties: position and velocity. The position of a particle is the evaluation of the optimization’s fitness function, which represents the particles distance from the ideal optimum solution (i.e., zero). Similarly, each particle’s velocity dictates the motion of the particle in the solution space.
The social behaviour of the swarm is represented by two important variables, pbest and gbest. pbest represents the personal best position that a particle can achieve through the iterations of the optimization, while the best position achieved by the whole swarm is represented by gbest. Both variables do not change in every iteration, but only gain new values if the swarm or the particles have achieved better positions in the current iteration that the stored gbest and pbest. In a sense, gbest represents the goal position for the particles of the swarm while pbest represents the memory of each particle [19].
In each operation, the position and velocity of each particle are calculated as follows:
where
and
are the position and velocity of the ith particle in the kth iteration,
and
are uniformly distributed parameters of the ith particle, and
,
are acceleration constants.
The acceleration parameters
, and
of Equation (19) have a great impact on the convergence of the optimization.
represents the swarm’s cognitive acceleration parameter, which determines the “confidence” of each particle in itself, while
represents the influence of the gbest position on every particle of the swam and is named social acceleration parameter.
Additionally, parameter
represents the particle inertia that produces a certain momentum for the swarm and is defined as:
where K is the maximum number of iterations and
are inertia constants defined as [20]:
4. Optimization Process
4.1. Dynamic Model
For the purposes of the simulation, a 3-DOF planar robotic manipulator shown in Figure 1 is used, set on a vertical plane. The robotic manipulator consists of three revolute joints and structural properties of the robot are listed in Table 1 [11].
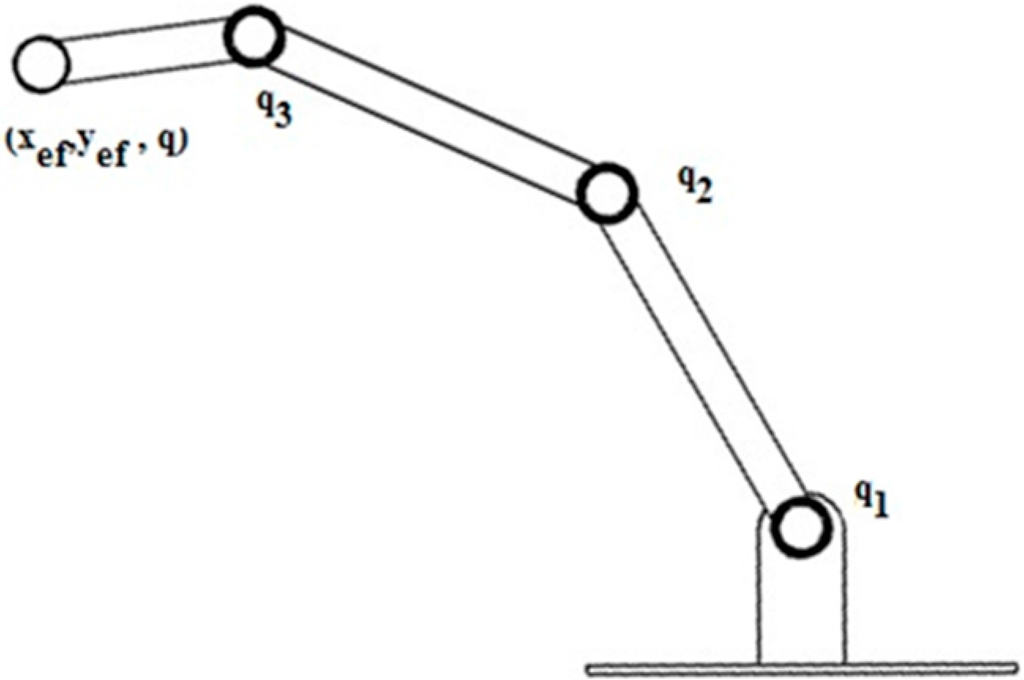
Figure 1.
Scheme of 3-DOF serial robotic manipulator.

Table 1.
Structural properties of a serial robotic manipulator.
| Link | Mass | Length | Centre of Mass | Inertia |
|---|---|---|---|---|
| 1 | 1.00 | 0.50 | 0.25 | 0.10 |
| 2 | 1.00 | 0.50 | 0.25 | 0.10 |
| 3 | 0.50 | 0.30 | 0.25 | 0.05 |
Furthermore, the following friction model [21] is used to provide a more realistic model for the optimization:
with the following properties:
- act as an approximation of the static coeffient of friction
- is the equivalent of the Stribeck friction effect
- is the term representing Coulomb friction
- is the viscous dissipation term [21].
The friction parameters
to
are chosen as described in Table 2.

Table 2.
Friction parameters.
| Parameter | Value |
|---|---|
| 3 | |
| 100 | |
| 10 | |
| 0.1 | |
| 100 | |
| 0.01 |
Finally, three actuators of the robotic manipulator are assumed to produce finite torque with the maximum allowable torque being
.
4.2. Contours
To demonstrate the efficiency of the optimization procedure, the controller is tuned for two different types of contours: linear and nonlinear. Specifically, a straight line and a circular contour are traced by the end-effector of the manipulator. The linear contour is a fast and short type of motion while the circular contour is longer in duration, slower in speed and covers a greater distance. The characteristics of the two contours can be found in Table 3.

Table 3.
Simulation contours.
| Contour Type | Linear | Circular |
|---|---|---|
| Starting Point | ||
| Ending Point | ||
| Maximum Joint Speed | ||
| Duration | 8 |
4.3. Fitness Functions
A fitness function is needed in the optimization in order to convert the contour error from a vector into a singular arithmetic value that can be used for optimization purposes. In this paper, three different fitness functions are used. Two of them, ISE and IAE, are existing and widely used fitness functions in controller tuning via optimization. The third one, MSMAE, was introduced by the authors in order to investigate its practicality as an alternative to the existing fitness functions.
where
is the contour error,
,
, and
are the mean, standard derivation, and maximum value of the absolute contour error that will be defined in the next section. The rationale to propose MSMAE is to consider the statistics of the contour error distributions.
4.4. Optimization Parameters
Table 4 summarizes the values of parameters affecting the optimization. It should be noted that the sampling frequency of the system is kept low in order for the optimization to maintain logical completion times. Furthermore, Table 5 displays the optimization parameters for each optimization method used in this paper.

Table 4.
Optimization parameters.
| Master Motion Sampling Frequency | 100 [Hz] |
| Population Size | 30 |
| Maximum Allowed Iterations | 30 |
| Feasible Bounds of gain | 0– |

Table 5.
Optimization methods parameters.
| Optimization Method | Optimization Parameter | Value/Method |
|---|---|---|
| Differential Evolution | 0.7 | |
| 0.8 | ||
| Genetic Algorithm | Selection | Stochastic Universal Sampling * |
| R | 1 | |
| Mutation | Gaussian * | |
| Particle Swarm Optimization | 0.5 | |
| 1.0 |
* More information on Stochastic Universal Sampling and Gaussian Mutation can be found in [17].
5. Results
In the optimization process for the 3-dof robotic manipulator, the first joint connecting to the ground is used as the master motion and controlled by the time domain PID controller, and the other two joints are viewed as he slave motions and controlled by the PDC-PID controller. There are nine control gains that need to be optimized for the control of the 3-dof robotic manipulator for contour tracking. The optimized control gains for linear and nonlinear contours under three different fitness functions can be seen in Table 6 and Table 7, respectively. All optimization procedures are successful, producing gains inside the specified bounds and providing valid solutions for each case.
Figure 2 shows the best values of each fitness function per iteration for every optimization algorithm in the linear contour. One can see that, in all cases, GA converged faster (locally minima) than DE and PSO, something that was expected mostly due to literature. DE and PSO took a similar number of iterations to converge with convergence values of PSO however being closer to GA than DE. Also, Figure 3 shows that, for the nonlinear case, GA converged once again faster than the other two algorithms which featured similar convergence trends. However, this time DE led to lower fitness values than PSO for all three fitness functions.

Table 6.
Resulting gains for linear contour.
| Optimization Algorithm | Fitness Function | |||
|---|---|---|---|---|
| DE | ISE | |||
| IAE | ||||
| MSMAE | ||||
| GA | ISE | |||
| IAE | ||||
| MSMAE | ||||
| PSO | ISE | |||
| IAE | ||||
| MSMAE |

Table 7.
Resulting gains for nonlinear contour.
| Algorithm | Fitness Function | |||
|---|---|---|---|---|
| DE | ISE | |||
| IAE | ||||
| MSMAE | ||||
| GA | ISE | |||
| IAE | ||||
| MSMAE | ||||
| PSO | ISE | |||
| IAE | ||||
| MSMAE |
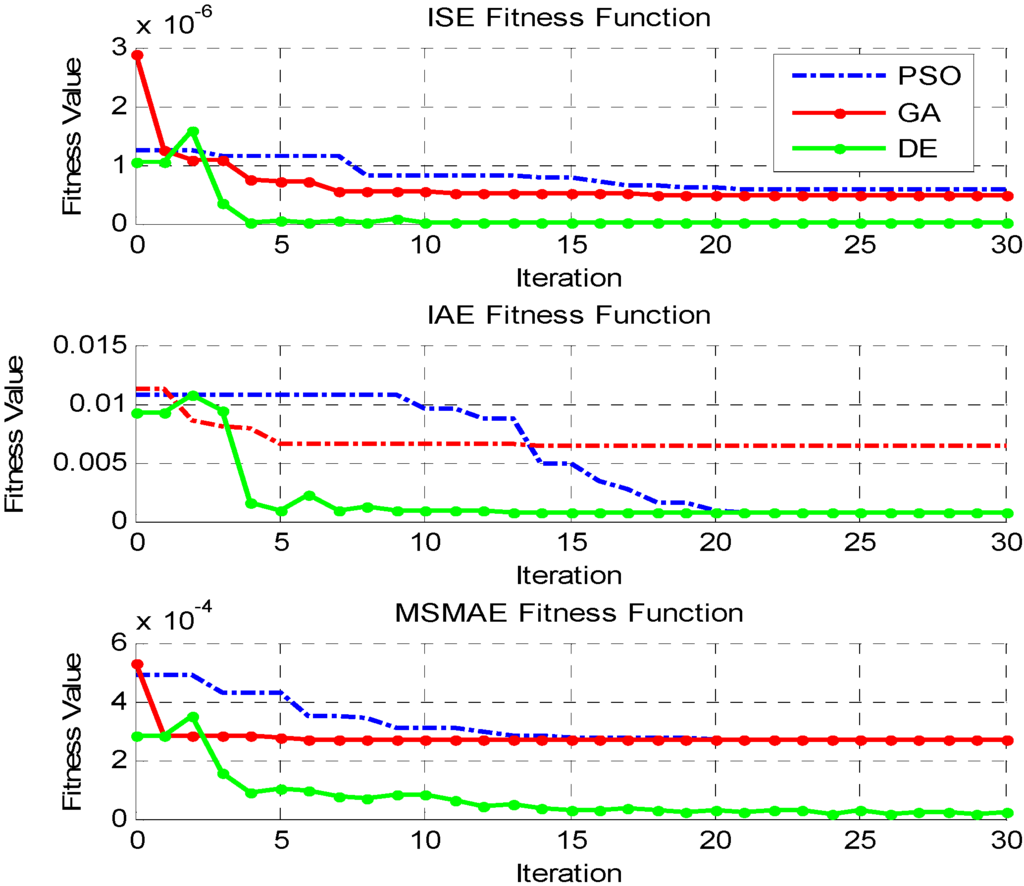
Figure 2.
Fitness function best values for linear contour.
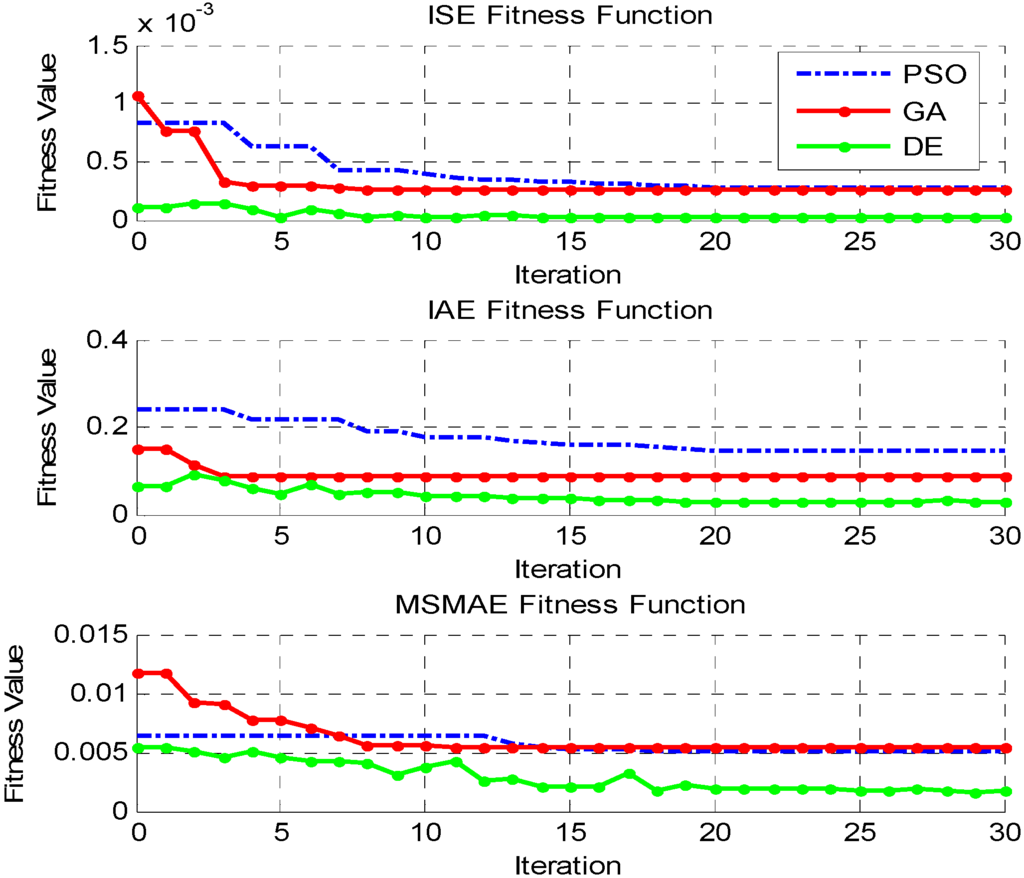
Figure 3.
Fitness function best values for nonlinear contour.
For the linear contour, it can be deduced from Figure 4 that the DE-ISE case was the one to produce the lowest contour error from all the cases, with DE-MSMAE coming a close second. In fact, DE produced the best optimization results for all fitness function cases. GA and PSO, on the other hand, produced contour errors an order of magnitude greater than DE, with the exception of PSO-IAE that was numerically closer to DE-IAE. GA produced the worst results, something that was expected due to the convergence rates as shown in Figure 2.
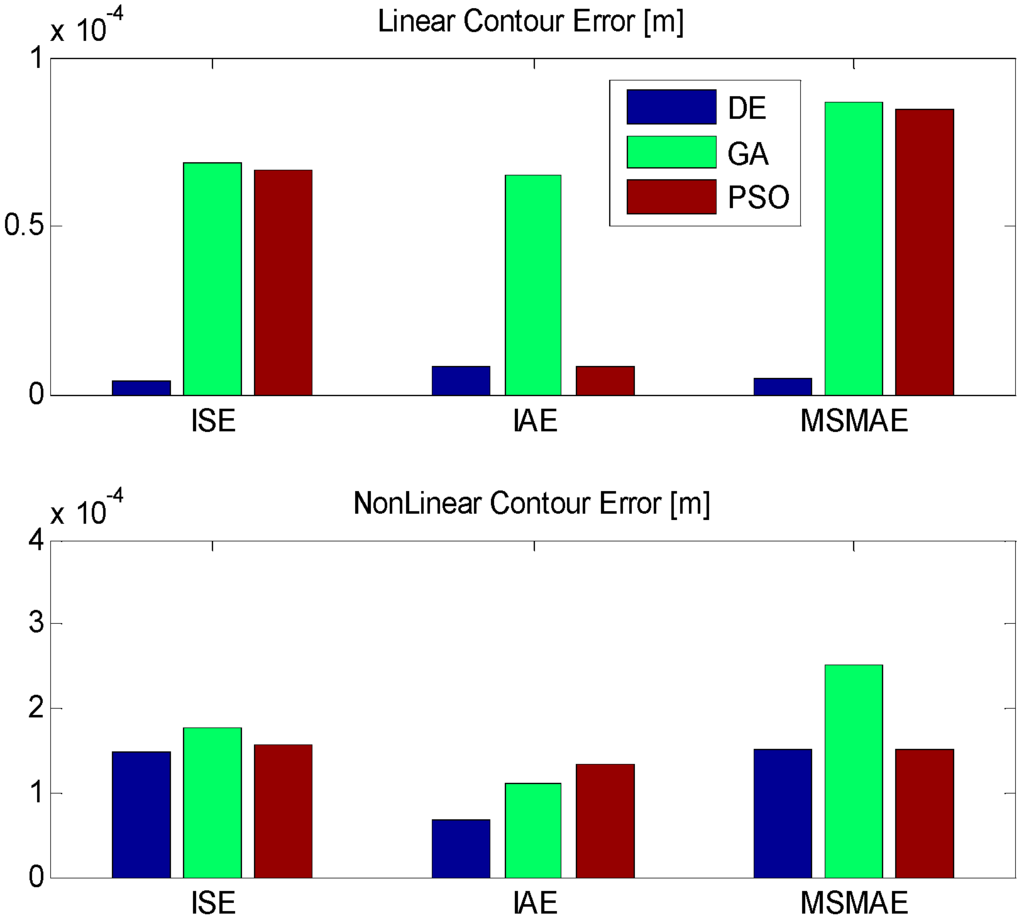
Figure 4.
Contour errors produced by the optimized gains.
For the nonlinear contour case, the contour errors were numerically close for all three optimization methods. For nonlinear contour tracking, DE-IAE produced the lowest contour error. GA was once again the worst algorithm with the exception of GA-IAE that actually produced the second lowest contour error. The PSO algorithm produced contour errors relatively close to DE for ISE and MSMAE but featured the worst performance for IAE. The contour performances of each algorithm for both linear and nonlinear contour cases are catalogued in Table 8 and also can be seen in Figure 5 and Figure 6.

Table 8.
Resulting contour errors and mean torques.
| Algorithm | Linear Contour | Nonlinear Contour | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (Mean) | (Mean) | (Mean) | (Mean) | (Mean) | (Mean) | ||||
| DE | ISE | ||||||||
| IAE | |||||||||
| MSMAE | |||||||||
| GA | ISE | ||||||||
| IAE | |||||||||
| MSMAE | |||||||||
| PSO | ISE | ||||||||
| IAE | |||||||||
| MSMAE | |||||||||
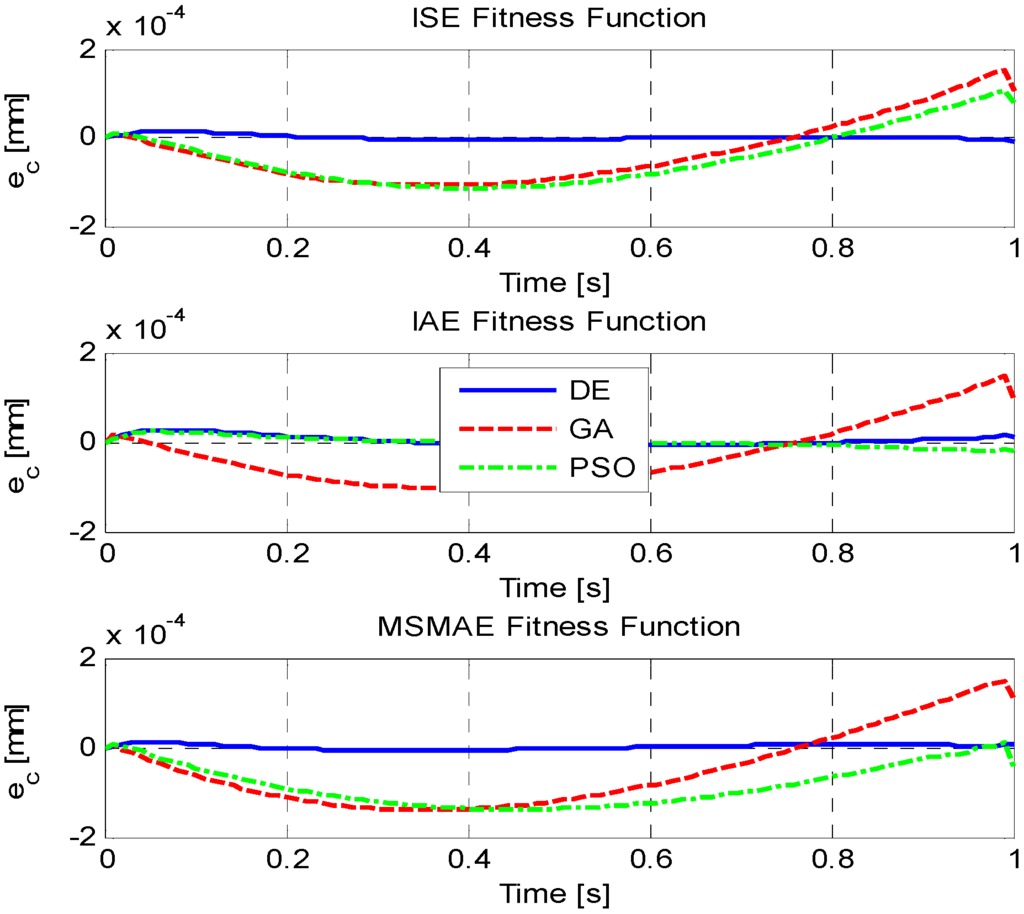
Figure 5.
Contour performance for linear contour.
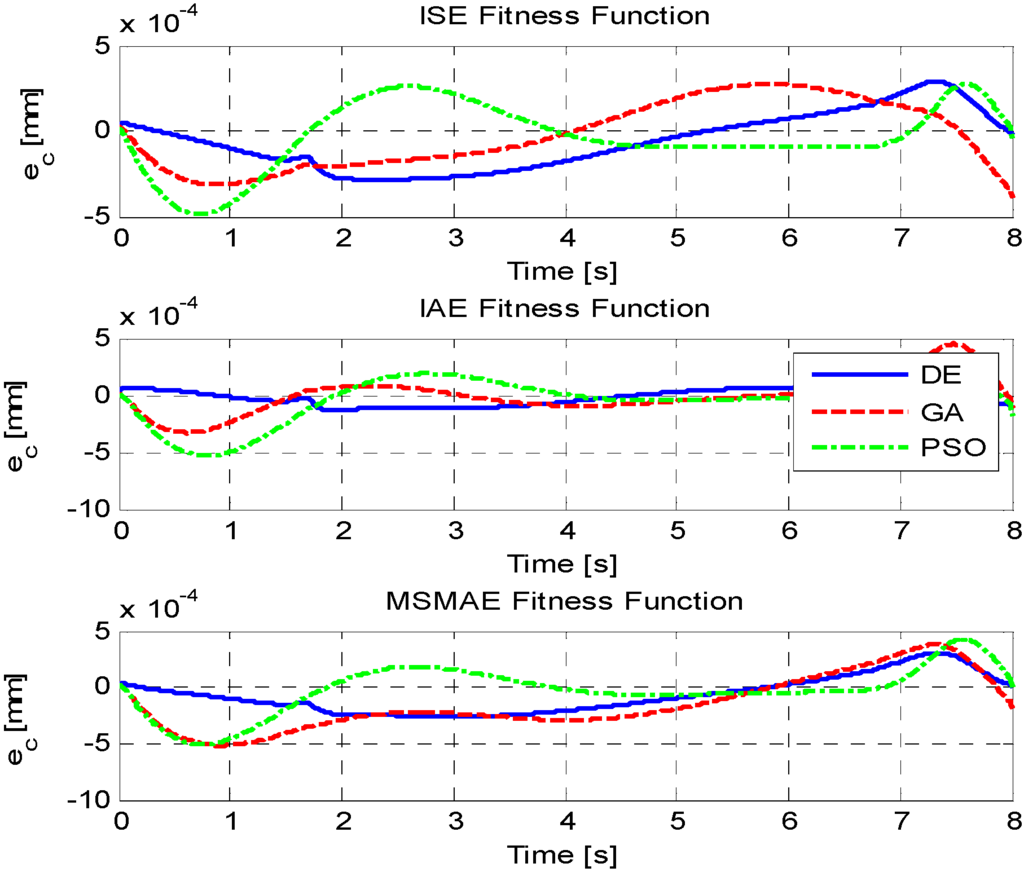
Figure 6.
Contour performance for nonlinear contour.
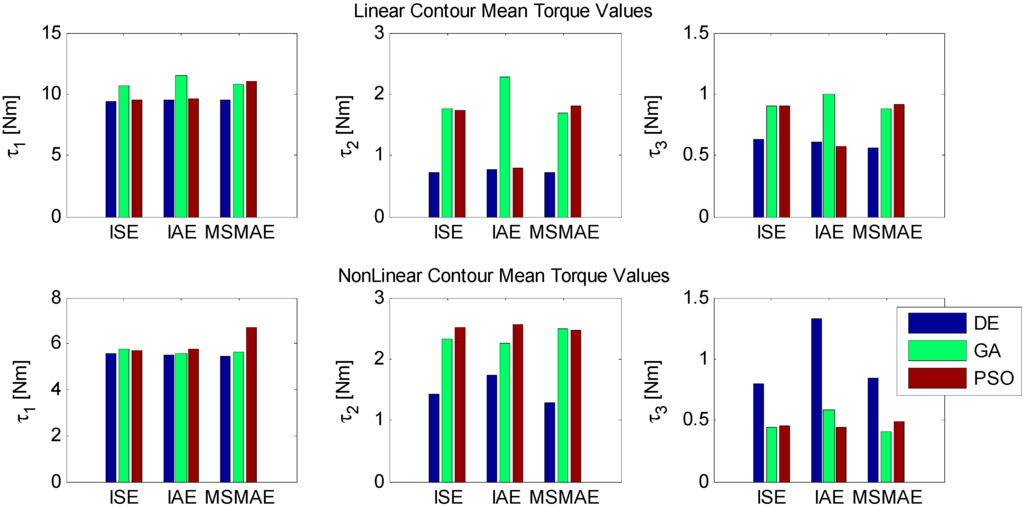
Figure 7.
Mean required torques for both contours.
Taking a close look at the required torque produced by each gain solution set in Figure 7, one can see that all optimization algorithms produced similar mean torques values for the first actuator while the torque from the other two actuators varied greatly. In the linear contour, DE, which produced the lowest contour errors, produced the lowest mean required torques. Similarly, the best performing algorithm for the nonlinear contour, DE, produced the lowest required mean torques, with the exception of the third actuator where all DE cases produced the highest mean torque.
6. Conclusion
In this paper, a position domain PID controller for a robotic manipulator was tuned using three distinct meta-heuristic optimization algorithms. The gains of the controller were determined based on the algorithms of differential evolution, genetic algorithm, and particle swarm optimization, with the main goal being the minimum of the contour error on the end-effector level. Three different fitness functions were used to measure the efficiency of each optimization, and two different contours, a linear and a nonlinear, were used in order to assess the validity of the optimization process.
From the comparative study results, it is shown that the DE-ISE case produced the least contour error for the linear contour tracking, while the DE-IAE case was proven to be the most efficient for the nonlinear contour tracking. More specifically, the DE algorithm performed consistently better than the other two algorithms for both linear and nonlinear contours. This can be attributed to DE’s more efficient population diversification due to Equation (9) that makes DE more flexible in avoiding local minima. The PSO and DE algorithms performed generally better than GA that was always the first to converge without producing the best fitness values or results. However, it should be noted that all the optimizations resulted in relatively close results for the nonlinear contour.
It should be mentioned that the gain tuning optimization methods can be extended to other controller designs of the contour tracking problems of robotic manipulators, as the principle and parameter selection methods are the same for all the controller designs.
Acknowledgements
This research is supported by Hunan Province innovation platform and talent plan (Applied Fundamental Research) No. 2015JC3109, and the Natural Sciences and Engineering Research Council of Canada (NSERC) through a Discovery Grant.
Author Contributions
The contributions of both authors are similar. All of them have worked together to develop this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cominos, P.; Munro, N. PID Controllers: Recent Tuning Methods and Design to Specification Control Theory and Applications. IEE Proc. Control Theory Appl. 2002, 149, 46–53. [Google Scholar] [CrossRef]
- Kachitvichyanukul, V. Comparison of Three Evolutionary Algorithms: GA, PSO and DE. Ind. Eng. Manag. Syst. 2012, 11, 215–223. [Google Scholar] [CrossRef]
- Chandrasekar, K.; Ramana, N.V. Performance Comparison of GA, DE, PSO and SA Approaches in Enhancements of Total Transfer Capability Using FACTS Devices. J. Electr. Eng. Technol. 2012, 7, 493–500. [Google Scholar] [CrossRef]
- Kumar, A.; Gupta Rajeev, R. Compare the Results of Tuning of PID Controller by Using PSO and GA Technique for AVR System. Intern. J. Adv. Res. Comput. Engin. Technol. 2013, 2, 2131–2138. [Google Scholar]
- Ou, C.; Lin, W. Comparison Between PSO and GA for Parameter Optimization of PID Controller. IEEE Intern. Conf. Mechatron. Autom. 2006. [Google Scholar] [CrossRef]
- Saad, M.S.; Jamaluddin, H.; Darus, I.Z. Implementation of PID Controller Tuning Using Differential Evolution and Genetic Algorithm. Intern. J. Innov. Comput. Inf. Control. 2012, 8, 7761–7779. [Google Scholar]
- Dong, R. Differential Evolution versus Particle Swarm Optimization for PID Controller Design. Intern. Conf. Nat. Computat. 2009, 3, 236–240. [Google Scholar]
- Hassan, R.; Cohanim, B.; de Weck, O. A Comparison of Particle Swarm Optimization and Genetic Algorithm. In Proceedings of the 1st AIAA Multidisciplinary Design Optimziation Specialist Conference, Austin, TX, USA, 18–21 April 2005; pp. 18–21.
- Ouyang, P.R.; Huang, J.; Zhang, W.J.; Dam, T. Contour Tracking Control in Position Domain. Mechatronics 2012, 22, 934–944. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Pano, V.; Dam, T. PID Position Domain Control for Contour Tracking. Intern. J. Syst. Sci. 2015, 46, 111–124. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Pano, V. Position Domain Synchronization Control of Multi-Degrees of Freedom Robotic Manipulator. ASME J. Dyn. Syst. Measurem. Control. 2014, 136, 021017. [Google Scholar] [CrossRef]
- Koren, Y. Cross-Coupled Biaxial Computer Control of Manufacturing Systems. ASME J. Dyn. Syst. Measurem. Control. 1980, 102, 265–272. [Google Scholar] [CrossRef]
- Yeh, S.; Hsu, P.L. A New Approach to Biaxial Cross-Coupled Control. In Proceedings of the IEEE International Conference on Control Applications, Anchorage, AK, USA, 25–27 September 2000; pp. 168–173.
- Koren, Y.; Lo, C.C. Variable Gain Cross-Coupling Controller for Contouring. Ann. CIRP 1991, 40, 371–374. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Panda, S. Robust Coordinated Design of Multiple and Multi-Type Damping Controller Using Differential Evolution Algorithm. Electr. Power Energy Syst. 2011, 33, 1018–1030. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Massachusetts, UK, 1998. [Google Scholar]
- Ladkany, G.S.; Trabia, M.B. A Novel Crossover Operator for Genetic Algorithms: Ring Crossover. Appl. Mathem. 2012, 3, 1220–1235. [Google Scholar] [CrossRef]
- Nagaraj, B.; Vijayakumar, P. A Comparative Study of PID Controller Tuning Using GA, EP, PSO and ACO. J. Autom. Mob. Robot. Intell. Syst. 2011, 5, 42–48. [Google Scholar]
- Ebbesen, S.; Kiwitz, P; Guzzella, L. A Generic Particle Swarm Optimization Matlab Function. In Proceedings of the IEEE American Control Conference, Montreal, QC, Canada, 27–29 June 2012; pp. 1519–1524.
- Makkar, C.; Dixon, W.E.; Sawyer, W.G.; Hu, G. A New Continuously Differentiable Friction Model for Control Systems Design. Advanced Intelligent Mechatronics. In Proceedings of the IEEE/ASME International Conference, Monterey, CA, USA, 24–28 July 2005; pp. 600–605.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).