Numerical Solution of Turbulence Problems by Solving Burgers’ Equation

Abstract

In this work we generate the numerical solutions of Burgers’ equation by applying the Crank-Nicholson method and different schemes for solving nonlinear systems, instead of using Hopf-Cole transformation to reduce Burgers’ equation into the linear heat equation. The method is analyzed on two test problems in order to check its efficiency on different kinds of initial conditions. Numerical solutions as well as exact solutions for different values of viscosity are calculated, concluding that the numerical results are very close to the exact solution.

1. Introduction

The numerical solution of nonlinear equations and systems is widely used in different branches of Science and Technology, as in the analysis of diffusion phenomena (see, for example, [1,2]), the study of dynamical models of chemical reactors [3], the numerical computing of the dominant eigenvalue of the neutron transport criticality problem (see [4]), the study of radioactive transfer [5], or in the orbit determination of artificial satellites (see [6]), among others.

Burgers’ equation arises in the theory of shock waves, in turbulence problems and in continuous stochastic processes. It has a large variety of applications: modeling of water in unsaturated oil, gas dynamics, heat conduction, elasticity, statics of flow problems, mixing and turbulent diffusion, cosmology, seismology, etc. (see [7] and the references therein).

We consider the one-dimensional Burgers’ equation

$$\frac{\partial u}{\partial t}-\frac{1}{Re}\frac{{\partial }^{2}u}{\partial x^2}+u\frac{\partial u}{\partial x}=0,a<x<b,t>0$$

(1)

with initial condition $u(x,0)=f\left(x\right)$, $a<x<b$, and boundary conditions $u(a,t)=g_1\left(t\right)$, $u(b,t)=g_2\left(t\right)$, $t\ge 0$; where $Re$ is the Reynolds number of the viscous fluid flow problem and $f\left(x\right)$, $g_1\left(t\right)$ and $g_2\left(t\right)$ are given functions. Usually ε instead of $\frac{1}{Re}$ is used, for simplicity. Numerical difficulties have been experienced in getting the solution of Burgers’ equation for big values of ε.

This problem shows a roughly similar structure to that of Navier-Stokes equations due to the form of the nonlinear convection term and the occurrence of the viscosity term. So, this can be considered as a simplified form of the Navier-Stokes equation. In recent years, many researchers have used different numerical methods specially based on finite difference, finite element boundary techniques and direct variational methods to solve this problem (see, for example, [7,8,9] and the references therein). It has been shown by Hopf and Cole that Burgers’ equation can be solved exactly for an arbitrary initial function $f\left(x\right)$. The transformation

$$u=-\frac{2\text{ε}}{\text{ϕ}}\frac{\partial \text{ϕ}}{\partial x}$$

(2)

relates $u=u(x,t)$ and $\text{ϕ}=\text{ϕ}(x,t)$, and if ϕ is a solution of the linear diffusion equation

$$\frac{\partial \text{ϕ}}{\partial t}=\text{ε}\frac{{\partial }^2\text{ϕ}}{\partial x^2}$$

(3)

then u is a solution of the quasilinear Burgers’ Equation (1). This transformation let us obtain the exact values of $u(x,t)$ because Equation (3) has a Fourier series solution, however its computational cost is very high and we only use it for comparing the precision of our results (as we will see in the Numerical Section, the integrals of the Fourier coefficients must be calculated). As we can see in [7], some researchers have taken advantage of this transformation and have applied the Crank-Nicolson scheme to the linear Equation (3) in order to obtain the values of $\text{ϕ}(x,t)$ and after it the values of $u(x,t)$. Other authors have used the implicit scheme, where $\frac{\partial u}{\partial t}$ is approximated by backward differences, however, due to its truncation error has order one, the precision of the results decreases.

In this paper, we apply a particular difference scheme called Crank-Nicolson type method, obtained by applying divided differences directly on the nonlinear Equation (1), needing to solve a nonlinear system of equations for obtaining the solution in each value of t. These nonlinear systems are solved by using fixed point iterative methods. In particular, we are going to use the classical Newton’s method of order two,

$$\begin{array}{c}\hfill x^{(k+1)}=x^{\left(k\right)}-{\left[F^{\text{'}}\left(x^{\left(k\right)}\right)\right]}^{-1}F\left(x^{\left(k\right)}\right)\end{array}$$

(4)

Traub’s method of order three (see [10])

$$\begin{array}{c}\hfill y^{\left(k\right)}=x^{\left(k\right)}-{\left[F^{\text{'}}\left(x^{\left(k\right)}\right)\right]}^{-1}F\left(x^{\left(k\right)}\right),\end{array}$$

(5)

$$\begin{array}{c}\hfill x^{(k+1)}=y^{\left(k\right)}-{\left[F^{\text{'}}\left(x^{\left(k\right)}\right)\right]}^{-1}F\left(y^{\left(k\right)}\right)\end{array}$$

and the method denoted by M5 (see [11]) of fifth order of convergence, whose expression is reminded in the following

$$\begin{array}{ccc}\hfill y^{\left(k\right)}& =& x^{\left(k\right)}-{\left[F^{\text{'}}\left(x^{\left(k\right)}\right)\right]}^{-1}F\left(x^{\left(k\right)}\right),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill z^{\left(k\right)}& =& y^{\left(k\right)}-5{\left[F^{\text{'}}\left(x^{\left(k\right)}\right)\right]}^{-1}F\left(y^{\left(k\right)}\right),\hfill \\ \hfill x^{(k+1)}& =& z^{\left(k\right)}-\frac{1}{5}{\left[F^{\text{'}}\left(x^{\left(k\right)}\right)\right]}^{-1}[-16F\left(y^{\left(k\right)}\right)+F\left(z^{\left(k\right)}\right)]\hfill \end{array}$$

In these iterative expressions, $F\left(x\right)$ denotes the vectorial real function that describes the nonlinear system and $F^{\text{'}}\left(x\right)$ is the associated Jacobian matrix.

The stability of the method is numerically analyzed and found to be unconditionally stable. The presented method has the accuracy of second order in space and time. We test our method by using several values of ε and different initial conditions in order to analyze its stability and consistence, and for doing this it is compared with other known methods and with the exact solution. From these numerical results several interesting conclusions are obtained.

2. Development of the Procedure

The easiest way to discretize a partial differential equation problem (like we have on Equation (1)) consist on reducing the continuous domain into an equispaced finite number of points $(x_i,t_j)$ located on the nodes of a uniform rectangular mesh. The partial derivatives of u can be estimated now by the following difference quotients

$$\frac{\partial u(x_i,t_j)}{\partial x}\approx \frac{u_{i+1,j}-u_{i,j}}{h},\frac{\partial u(x_i,t_j)}{\partial t}\approx \frac{u_{i,j+1}-u_{i,j}}{k}$$

(7)

which are called forward differences and have a truncation error of order 1. The partial derivatives of u can also be obtained by

$$\frac{\partial u(x_i,t_j)}{\partial x}\approx \frac{u_{i,j}-u_{i-1,j}}{h},\frac{\partial u(x_i,t_j)}{\partial t}\approx \frac{u_{i,j}-u_{i,j-1}}{k}$$

(8)

which are backward differences and have also a truncation error of order 1. Finally the partial derivatives of u can also be obtained by the following

$$\frac{\partial u(x_i,t_j)}{\partial x}\approx \frac{u_{i+1,j}-u_{i-1,j}}{2h},\frac{\partial u(x_i,t_j)}{\partial t}\approx \frac{u_{i,j+1}-u_{i,j-1}}{2k}$$

(9)

$$\frac{{\partial }^{2}u(x_i,t_j)}{\partial x^2}\approx \frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{h^2},\frac{{\partial }^{2}u(x_i,t_j)}{\partial t^2}\approx \frac{u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{k^2}$$

(10)

which are called central differences and have a truncation error of order 2. In these expressions, $u_{i,j}$ denotes the approximated value of the unknown u function on $(x_i,t_j)$, $h=\frac{b-a}{n}$ and $k=\frac{t_{max}-t_{min}}{m}$ are respectively the space and time step on the mesh and n and m are respectively the space and time amount of subintervals to be considered. Then, we consider $x_{i+1}=x_i+h$ and $t_{j+1}=t_j+k$, where $i=0,1,...,n-1$ and $j=0,1,...,m-1$.

Let us apply Crank-Nicolson difference scheme, which consists of discretizing Equation (1) in two consecutive time instants of j and average them. In the first instant $t_j$ we approximate $\frac{\partial u}{\partial t}$ by the forward difference described on Equation (7) and in the second instant $t_{j+1}$ we do it by the backward one. At both instants we approximate $\frac{\partial u}{\partial x}$ and $\frac{{\partial }^{2}u}{\partial x^2}$ by using the central differences (described by Equations (9) and (10) respectively). By means of this procedure we get, for the first instant,

$$\frac{u_{i,j+1}-u_{i,j}}{k}-\text{ε}\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{h^2}+u_{i,j}\frac{u_{i+1,j}-u_{i-1,j}}{2h}=0$$

(11)

and for the second one,

$$\frac{u_{i,j+1}-u_{i,j}}{k}-\text{ε}\frac{u_{i+1,j+1}-2u_{i,j+1}+u_{i-1,j+1}}{h^2}+u_{i,j+1}\frac{u_{i+1,j+1}-u_{i-1,j+1}}{2h}=0$$

(12)

After averaging both expressions, it results

$$\begin{array}{c}\hfill B{u}_{i,j+1}{u}_{i+1,j+1}-B{u}_{i,j+1}{u}_{i-1,j+1}-C{u}_{i+1,j+1}+2C{u}_{i,j+1}-C{u}_{i-1,j+1}+A{u}_{i,j+1}=\\ \hfill C{u}_{i+1,j}+(A-2C)u_{i,j}+C{u}_{i-1,j}+B{u}_{i,j}{u}_{i+1,j}-B{u}_{i,j}{u}_{i-1,j}\end{array}$$

(13)

where $A=\frac{1}{k}$, $B=\frac{1}{4h}$, $C=\frac{\text{ε}}{2h^2}$ and the range of indices is $i=1,...,n-1$ and $j=0,1,...,m-1$. This expression (which has a truncation error of order 2) results on a m nonlinear systems of $n-1$ unknowns and $n-1$ equations. Each one of these systems comes after considering that we already know the value of $u_{0,j}$ and $u_{n,j}$, $\forall j$ (from the boundary conditions) and $u_{i,0}$, $\forall i$ from the initial condition. Let us notice that the values corresponding to the j subindex have been calculated on the previous systems and the only unknowns will be those with the $j+1$ subindex.

3. Numerical Results

We are comparing our results with the exact solution, which can be obtained by the Hopf-Cole transformation mentioned on Equations (2) and (3). For doing this, we first calculate

$$\text{ϕ}(x,t)=A_0+\sum _{p=1}^{\infty }{A}_p{e}^{-p^2\text{ε}{\pi }^{2}t}cos\left(p\pi x\right)$$

and after it, by Equation (2), we obtain

$$u(x,t)=2\pi \text{ε}\frac{{\sum }_{p=1}^{\infty }{A}_p{e}^{-p^2\text{ε}{\pi }^{2}t}psin\left(p\pi x\right)}{A_0+{\sum }_{p=1}^{\infty }{A}_p{e}^{-p^2\text{ε}{\pi }^{2}t}cos\left(p\pi x\right)}$$

(14)

where

$$A_0={\int }_a^b{e}^{-\frac{1}{2\text{ε}}{\int }_a^{x}u(\xi ,0)d\xi }dx,$$

$$A_p=2{\int }_a^b{e}^{-\frac{1}{2\text{ε}}{\int }_a^{x}u(\xi ,0)d\xi }cos\left(p\pi x\right)dx,p=1,2,...$$

Our goal is to obtain at least five exact decimals from the exact solution in order to prove the precision of our results, and for that we have seen that it is enough with two summands of the Fourier series, thereby only $A_0$, $A_1$ and $A_2$ will have to be calculated.

In the following examples we consider that the boundary conditions are zero, so we have that $g_1\left(t\right)=0$ and $g_2\left(t\right)=0$, what means that $u_{0,j}=0$ and $u_{n,j}=0$, $\forall j$. We can compare our results with the exact solution in this case, however our method has been found numerically to be unconditionally stable whatever the boundary conditions are. We use the R2013a version of Matlab with double precision for obtaining both approximated and exact solutions. The stopping criterion used is

$$\parallel u^{(k+1)}(x,t_j)-u^{\left(k\right)}(x,t_j)\parallel +\parallel F(u^{(k+1)}(x,t_j))|<{10}^{-15}$$

Example 1. The initial and boundary conditions of Burgers’ equation for this example are

$$u(x,0)=\frac{2\text{εβ}\pi sin\left(\pi x\right)}{\text{α}+\text{β}cos\left(\pi x\right)},0\le x\le 2$$

and $u(0,t)=u(2,t)=0,t\ge 0$ where $\text{α}=5$ and $\text{β}=4$.

In the following tables we show, for different values of n, m and ε, the average number of iterations by using Newton’, Traub’s and M5 methods. We also show the greatest error, GE, that we obtain for every value of $x_i$ and $t_j$, where $i=0,1,...,n-1$ and $j=0,1,...,m-1$. The initial approximation of each nonlinear system to be solved is the solution of the previous one (and for the first system the initial approximation is the exact value of the initial condition). After that, we obtain the matrix of errors as the absolute difference between the approximated solution and the exact solution on each node, finally we call the greatest error as the greatest element from that matrix. While other authors prefer to only compare and give the value of the error in some points of the mesh we have preferred a more rigorous criterium, it consists on comparing all the error values from the matrix of errors and giving the value of GE, in this way we get a better idea about how bad is the worst possible situation and we know for sure that the error of the rest of the points will always be below this GE, the other way we can not know if there is some point that has a greater one.

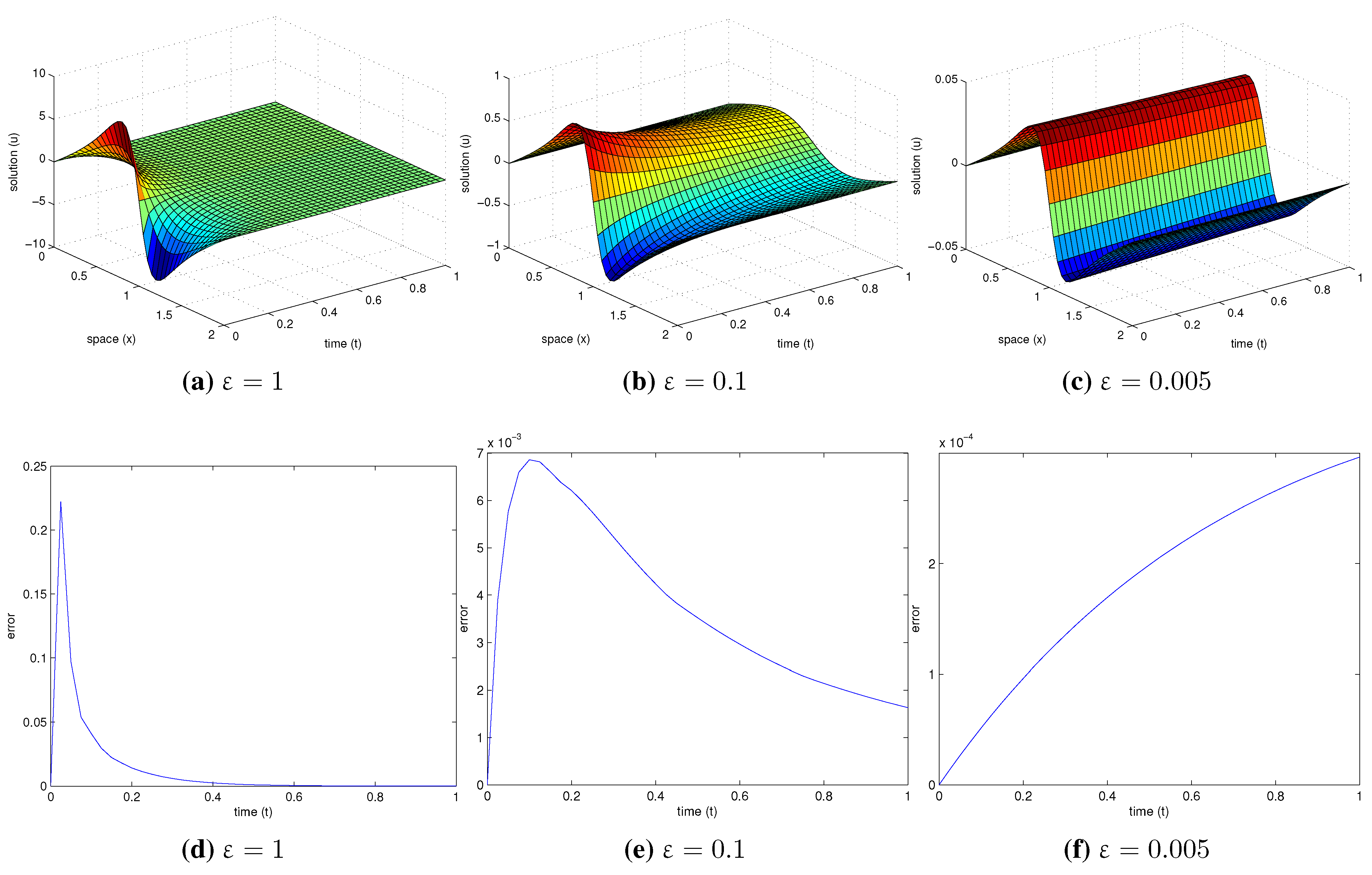
An interesting result emerges from that error matrix if we consider a sufficiently high upper bound of the studied time. If we obtain the GE between all values of x on each time we observe that the GE increase really fast at first but after the peak is reached it starts to decrease. This result can be seen on the Figure 1.

In Table 1 we set the maximum time of the study, the number of time nodes and the Reynolds constant as $t_{max}=1$, $m=100$ and $\text{ε}=\frac{1}{Re}=0.1$ and we try different amount of space nodes. In each case we obtain the already mentioned GE and the average number of iterations (Avg. iter.) needed to solve each nonlinear system by using Newton’, Traub’s and M5 methods.

From these results we observe that, in general, the more space subintervals we take (smaller space step), the less is GE.

In Table 2, we repeat the same process but in this case we set the number of space nodes and try different amount of time nodes. So $t_{max}=1$, $n=100$ and $\text{ε}=\frac{1}{Re}=0.1$.

As we can observe, at first it seems that the more time subintervals we take, the less is GE (similarly as it happened with the previous table, where we tried different amount of space subintervals) however there is a limit for this which if we exceed the error starts to increase again. In this case, the minimum error is obtained for $m=20$.

Figure 1. Solution (a–c) and error progression curve (d–f) for different times and ε values, with $n=m=40$ and $t_{max}=1$.

Figure 1. Solution (a–c) and error progression curve (d–f) for different times and ε values, with $n=m=40$ and $t_{max}=1$.

Table 1. Comparison of the GE (greatest error) and methods iterations for different amount of space subintervals.

	$n=10$	$n=20$	$n=40$	$n=80$	$n=160$
Greatest error	0.09033	0.029932	0.0070658	0.0017149	0.00039376
Avg. iter. Newton	4	4	4	4	4
Avg. iter. Traub	3	3	3	3	3
Avg. iter. M5	3	3	3	3	3

Table 1. Comparison of the GE (greatest error) and methods iterations for different amount of space subintervals.

	$n=10$	$n=20$	$n=40$	$n=80$	$n=160$
Greatest error	0.09033	0.029932	0.0070658	0.0017149	0.00039376
Avg. iter. Newton	4	4	4	4	4
Avg. iter. Traub	3	3	3	3	3
Avg. iter. M5	3	3	3	3	3

Table 2. Comparison of the GE and methods iterations for different amount of time subintervals.

	$m=10$	$m=20$	$m=40$	$m=80$	$m=160$
Greatest error	0.0043069	0.00015291	0.00083542	0.0010565	0.0011128
Avg. iter. Newton	4.4	4.15	4	4	4
Avg. iter. Traub	3.4	3.1	3	3	3
Avg. iter. M5	3	3	3	3	3

Table 2. Comparison of the GE and methods iterations for different amount of time subintervals.

	$m=10$	$m=20$	$m=40$	$m=80$	$m=160$
Greatest error	0.0043069	0.00015291	0.00083542	0.0010565	0.0011128
Avg. iter. Newton	4.4	4.15	4	4	4
Avg. iter. Traub	3.4	3.1	3	3	3
Avg. iter. M5	3	3	3	3	3

In Table 3, we repeat the process again, however now we study the effect of choosing a small, regular or big value of the Reynolds constant ($Re$), although we actually use $\text{ε}=\frac{1}{Re}$ for simplicity. For doing this, we set the number of space and time nodes and the maximum time of study, so $t_{max}=1$, $n=40$ and $m=40$.

Table 3. Comparison of the GE and methods iterations for different values of ε.

	$\text{ε}=1$	$\text{ε}=0.1$	$\text{ε}=0.05$	$\text{ε}=0.03$	$\text{ε}=0.02$	$\text{ε}=0.01$	$\text{ε}=0.005$
Greatest error	0.22216	0.0068572	0.0035207	0.0021242	0.0014188	0.000708	0.000296
Avg. iter. Newton	3.9	4	4	4	4	3.85	3
Avg. iter. Traub	3.15	3	3	3	3	3	3
Avg. iter. M5	2.8	3	3	3	3	3	2

Table 3. Comparison of the GE and methods iterations for different values of ε.

	$\text{ε}=1$	$\text{ε}=0.1$	$\text{ε}=0.05$	$\text{ε}=0.03$	$\text{ε}=0.02$	$\text{ε}=0.01$	$\text{ε}=0.005$
Greatest error	0.22216	0.0068572	0.0035207	0.0021242	0.0014188	0.000708	0.000296
Avg. iter. Newton	3.9	4	4	4	4	3.85	3
Avg. iter. Traub	3.15	3	3	3	3	3	3
Avg. iter. M5	2.8	3	3	3	3	3	2

First of all, it has to be said that the maximum value of ε that can be used to keep the method working properly will depend of the amount of time subintervals we take, it happens because the bigger is the attenuation, more abrupt are the curves on the time axis. For keeping the error low, a finer mesh will be needed, what can be obtained by increasing the amount of time subintervals. From Table 3 we can numerically see this phenomenon, for a fast attenuation ($\text{ε}=1$) the error is quite big due to the curve is very abrupt (as we said we could decrease the error of this case by taking more time subintervals), however the slower is the attenuation (lower values of ε), lower is GE. If we keep on taking lower values of attenuation (lower ε), the peak of the GE characteristic curve will not be reached and consequently the GE will be even lower (for this example it happens for $\text{ε}=0.01$ and even more for $\text{ε}=0.005$). See Figure 1 for a better understanding of these different situations.

Some conclusions can be obtained from Table 1, Table 2 and Table 3: to use a higher order method (like M5) does not represent a bigger advantage compared with a typical third order method (like Traub), however there is a significant difference between using a third order method compared to a typical second order method (like Newton). The more space subintervals we take, lower is GE; however, it does not happen with the amount of time subintervals, it means that there is an optimum amount of time subintervals that reduces the GE to its minimum but after it the error starts to increase again and the computational cost of having to solve so many systems does not make any sense (due to the increasing number of floating points operations, execution time,...). As we have seen from Table 3, if we want to study a situation with a big attenuation (low $Re$), we will need a higher amount of time subintervals compared to those situations where the attenuation is lower (it means that the computational cost for having to solve more nonlinear systems will be higher), however taking more space subintervals does not seem to help.

Example 2. Let us consider now the following initial and boundary conditions for Burgers’ equation

$$\begin{array}{c}\hfill u(x,0)=\left\{\begin{array}{cc}sin\left(\pi x\right),\hfill & 0<x\le 1\hfill \\ -\frac{1}{2}sin\left(\pi x\right),\hfill & 1<x\le 2\hfill \\ 0\hfill & 2<x\le 5\hfill \end{array}\right.\end{array}$$

(15)

and $u(0,t)=u(5,t)=0,t\ge 0$.

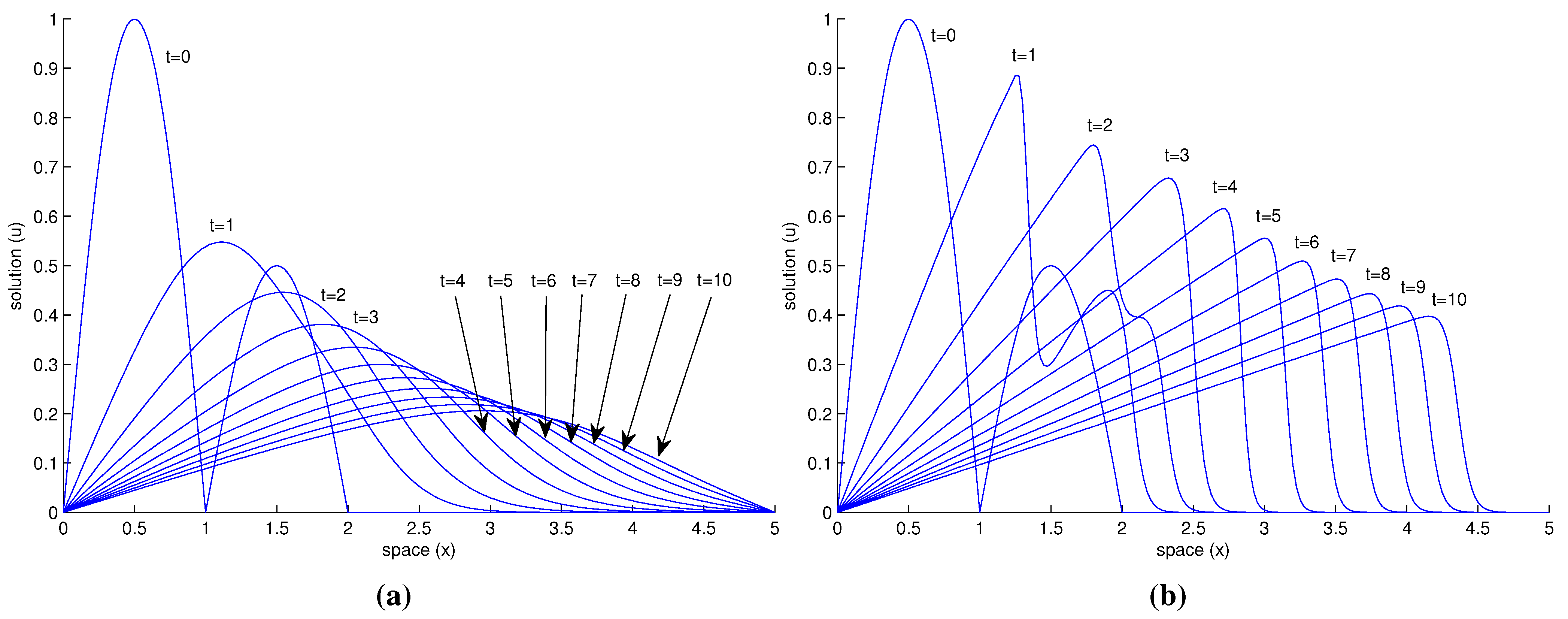
In Figure 2 we see a plot of the approximated solution by our method at different times for $0\le x\le 5$ and for two different values of ε, and in Table 4 we show the numerical results of this solution for some values of $x,t$ and ε.

Figure 2. Solution for different times and ε values, both of them with $n=m=200$ and $t_{max}=10$. (a) $\text{ε}=0.1$; (b) $\text{ε}=0.01$.

Figure 2. Solution for different times and ε values, both of them with $n=m=200$ and $t_{max}=10$. (a) $\text{ε}=0.1$; (b) $\text{ε}=0.01$.

Table 4. Numerical results of the approximated solution for different values of $x,t$ and ε.

x	t	$\text{ε}=0.1$	$\text{ε}=0.01$
1.5	2	0.44533	0.63548
	4	0.28961	0.34573
	6	0.20701	0.23678
	8	0.16020	0.17999
	10	0.13041	0.14516
3	2	0.02972	0.00000
	4	0.14900	0.00470
	6	0.22312	0.47269
	8	0.22501	0.35971
	10	0.20562	0.29021
4.5	2	0.00001	0.00000
	4	0.00145	0.00000
	6	0.01171	0.00000
	8	0.03557	0.00000
	10	0.06242	0.02066

Table 4. Numerical results of the approximated solution for different values of $x,t$ and ε.

x	t	$\text{ε}=0.1$	$\text{ε}=0.01$
1.5	2	0.44533	0.63548
	4	0.28961	0.34573
	6	0.20701	0.23678
	8	0.16020	0.17999
	10	0.13041	0.14516
3	2	0.02972	0.00000
	4	0.14900	0.00470
	6	0.22312	0.47269
	8	0.22501	0.35971
	10	0.20562	0.29021
4.5	2	0.00001	0.00000
	4	0.00145	0.00000
	6	0.01171	0.00000
	8	0.03557	0.00000
	10	0.06242	0.02066

This results are very similar to those obtained for Mittal and Singhal on their paper (see [12]), where they transform Burgers’ equation into a system of nonlinear ordinary differential equations and solve it by Runge-Kutta-Chebyshev second order method. Although the techniques used to solve the problem are different, the results obtained by Mittal-Singhal and ours, showed in Table 4 and Figure 2 have the same order of magnitude. As we can see in Figure 2 it happens indeed that the lower is ε, slower is the attenuation. Although in this example we have used a piecewise initial condition, and it usually brings more problems, we still have obtained satisfactory results. Since we have considered a quite high upper bound of the studied time ($t=10$) we have had to take a bigger value of m in order to keep a fine mesh size. The results obtained in both Figure 2 and Table 4 are the same regardless if we use Newton’, Traub’s or M5 method.

4. Conclusions

As we have seen from Example 1 and Example 2 our method has the same precision than those methods which apply Hopf-Cole transformation, after it obtain the solution of the linearized equation and finally apply the inverse transformation for obtaining the solution of nonlinear Burgers’ equation. Our method is more straightforward due to it does not need to apply the mentioned transformation.

We also have taken advantage of the numerical results for obtaining some conclusions about the importance of the quantity of space and time subintervals for obtaining the solution mesh as well as the dependency between the error and the value of Reynolds number: if we want to decrease the error, we can take more space subintervals, although the computational cost will raise due to then there will be more unknowns per system to be solved. Another way to decrease the error is by taking more time subintervals, however we have seen that there is a limit from where if we keep on taking bigger values of m, the error increases again. At the same time, taking more time subintervals also means to raise the computational cost since then there will be more systems to be solved. We also have seen that choosing bigger values of attenuation (ε) involve bigger errors due to the faster is the attenuation, more abrupt is the curve and worse is the approximation; for solving this, more time subintervals should be taken but there is no need to take more space subintervals.