From Enumerating to Generating: A Linear Time Algorithm for Generating 2D Lattice Paths with a Given Number of Turns

Abstract

We propose a linear time algorithm, called G2DLP, for generating 2D lattice L(n₁, n₂) paths, equivalent to two-item {A^n₁, B^n₂} multiset permutations, with a given number of turns. The usage of turn has three meanings: in the context of multiset permutations, it means that two consecutive elements of a permutation belong to two different items; in lattice path enumerations, it means that the path changes its direction, either from eastward to northward or from northward to eastward; in open shop scheduling, it means that we transfer a job from one type of machine to another. The strategy of G2DLP is divide-and-combine; the division is based on the enumeration results of a previous study and is achieved by aid of an integer partition algorithm and a multiset permutation algorithm; the combination is accomplished by a concatenation algorithm that constructs the paths we require. The advantage of G2DLP is twofold. First, it is optimal in the sense that it directly generates all feasible paths without visiting an infeasible one. Second, it can generate all paths in any specified order of turns, for example, a decreasing order or an increasing order. In practice, two applications, scheduling and cryptography, are discussed.

1. Introduction

It is common to find ourselves confronted with problems in which an exhaustive examination of all solutions is necessary or desirable [1]. However, we do not want to use brute force to go through all possible solutions. Therefore, there is a clear need to design an efficient algorithm that can eliminate certain cases from consideration. More than this, our goal is to design an optimal algorithm, whereby all infeasible solutions can be ignored. That is, it directly generates all feasible solutions without visiting any infeasible solutions. For example, we have proposed an algorithm for generating all permutations of {1, 2, … , n} with a given number of inversions, while never visiting any of the unqualified permutations [2]. In most applications of permutation generation we are interested in minimizing the total running time, not the maximum time between successive visits [1].

In this study, by utilizing the enumeration results of a previous study [3] and the method of integer partition, we propose an optimal algorithm for generating 2D lattice L(n₁, n₂) paths according to a given number of turns. It identically generates two-item ${\text{{A}}^{n_1},{\text{B}}^{n_2}\}$ multiset permutations according to a given number of turns. Herein, 2D lattice L(n₁, n₂) denotes an integer rectangular lattice that has a horizontal x-axis and a vertical y-axis. A path is a route that starts at point (0, 0) then moves through a succession of steps, usually under the step set {<1, 0>, <0, 1>}, and finally ends at the target point (n₁, n₂). In other words, after leaving the starting point (0, 0), the path can apply unit steps only eastward or northward, but can change direction at any point (x, y) until it reaches the target point (n₁, n₂). Some studies deal with an under-diagonal path that only contains points (x, y) with $x\ge y$, for example [4]. Some studies deal with a higher dimensional lattice, for example [5]. For a comprehensive survey on the topic of lattice paths, please see [6].

The word “multiset” (often shortened to mset) which abbreviates the term “multiple-membership set”, is now the commonly accepted name for replacing “bag”, “bunch”, “weighted set”, “occurrence set”, “heap”, “sample”, and “fireset” [7]. A multiset is a set such that each item in the set has a multiplicity that specifies how many times the item repeats, and the cardinality of a multiset is the sum of the multiplicities of its all items. In short, a multiset is a set with repeated items. Obviously, a set is a special case of multiset in which each item occurs only once. Multisets are of interest in mathematics, physics, philosophy, logic, linguistics and computer science [7]. Many studies have been devoted to multiset permutations [8,9,10,11,12,13,14,15]. However, we know of no published algorithms for generating multiset permutations with a given number of turns.

There are various motivations behind the interest in the turn enumeration of lattice paths. Krattenthaler described three motivations from probability, statistics, and commutative algebra, respectively [16]. He also showed the wide diversity of connections and applications in other domains like combinatorics, representation theory, and q-series. The motivation of our studies on the topic of lattice path was inspired by trying to solve a kind of open shop scheduling problem that is concerned with setup time among different types of machines [17]. Here, setup time means the delay time that occurs when we arrange the processing route (or path) of a job from one type of machine to another. This kind of open shop scheduling problem is, intrinsically, a multiset permutation problem, while the latter is, essentially, a lattice path enumeration problem.

Therefore, in this study, turn has three meanings. In open shop scheduling problems, it means that we transfer a job from one type of machine to another type of machine; in multiset permutation problems, it refers to two consecutive elements of a permutation that belong to two different items (In fact, the number of turns of a multiset permutation is equal to the number of blocks of a multiset permutation minus one, if we call a block as a maximal sequence of consecutive elements that are belonging to same item. Note that, in a permutation of a set of n integers, a maximal sequence of consecutive integers that appear in consecutive positions is called a block. For example, the permutation π = (456723189) contains four blocks namely 4567, 23, 1, and 89.); in lattice path enumeration problems, it means that the path changes its direction either from eastward to northward (called an EN-turn) or from northward to eastward (called an NE-turn). Viewed in this light, the number of turns of paths in a 2D lattice L(n₁, n₂) can be regarded in the same way as in a permutation statistics, referring to turns of a two-item {e^n₁, n^n₂} multiset permutation. Here, notation “e” denotes eastward, and notation “n” denotes northward. Since we have studied the enumeration of a 2D lattice path with a given number of turns, it is natural to a step further: from enumerating to generating.

The remainder of this paper is organized as follows. In Section 2, the proposed algorithm is described. In Section 3, analyses of algorithms are discussed. In Section 4, some experimental results are presented. In Section 5, two applications, scheduling and cryptography, are discussed. Finally, conclusions are summarized and a concomitant problem is proposed for future research.

2. Algorithms

In this Section, we propose an optimal algorithm for generating 2D lattice L(n₁, n₂) paths according to a given number of turns. For completeness, the following results are introduced without proof [3]. Note that, throughout the paper, all variables are positive integers.

Definition 1. Let t denote the number of turns of a path that has a EN-turns and b NE-turns, that is, $t=a+b$.

Lemma 1. |a − b| = 0 or |a − b| = 1.

Lemma 2. If t is even (2k), then a = b = k. If t is odd (2k − 1), then $a=k$ and $b=k-1$ when first step is eastward, or $a=k-1$ and $b=k$ when first step is northward.

Lemma 3. For a 2D integer rectangular lattice L(n₁, n₂), $n_1>0$ and $n_2>0$, assume that n₁ ≤ n₂ the minimum number of turns of a path is one and the maximum number of turns of a path is 2n₁ − 1 if $n_1=n_2$ or $2n_1$ if n₁ < n₂.

Theorem 1. Let $P(n_1,n_2,t)$ denote the number of paths with a given number of turns t, then:

$$P(n_1,n_2,2k)=\left(\begin{array}{c}{n}_1-1\\ k\end{array}\right)\left(\begin{array}{c}{n}_2-1\\ k-1\end{array}\right)+\left(\begin{array}{c}{n}_2-1\\ k\end{array}\right)\left(\begin{array}{c}{n}_1-1\\ k-1\end{array}\right)$$

(1)

and

$$P(n_1,n_2,2k-1)=2\left(\begin{array}{c}{n}_1-1\\ k-1\end{array}\right)\left(\begin{array}{c}{n}_2-1\\ k-1\end{array}\right)$$

(2)

In the identity (1), the term of $\left(\begin{array}{c}{n}_1-1\\ k\end{array}\right)\left(\begin{array}{c}{n}_2-1\\ k-1\end{array}\right)$ stands for the number of paths that their first step is eastward, and the term of $\left(\begin{array}{c}{n}_2-1\\ k\end{array}\right)\left(\begin{array}{c}{n}_1-1\\ k-1\end{array}\right)$ stands for the number of paths that their first step is northward. The reason is explained as follows. For a path with even (2k) turns, by Definition 1 and Lemma 2, we know that it must be composed of k EN-turns and k NE-turns. Thus, when the first step is eastward, what we need to do in the whole route is choose k points from n₁ − 1 points and choose $k-1$ points from n₂ − 1 points; when the first step is northward, what we need to do in the whole route is choose k points from $n_2-1$ points and choose $k-1$ points from $n_1-1$ points. Since the first step is either eastward or northward, we have the identity (1).

Similarly, for a path with odd ($2k-1$) turns, by Definition 1 and Lemma 2, we know that it must be composed of k NE-turns and k − 1 EN-turns when first step is northward, or that it must be composed of k EN-turns and $k-1$ NE-turns when first step is eastward. Thus, when the first step is northward, what we need to do in the whole route are choose $k-1$ points from $n_2-1$ points and choose $k-1$ points from $n_1-1$ points; when the first step is eastward, what we need to do in the whole path are choose k − 1 points from $n_1-1$ points and choose k − 1 points from n₂ − 1 points. Since the first step is either northward or eastward, we have the identity (2).

Based on Theorem 1, we propose the Algorithm G2DLP where two Algorithms H and L, borrowed from others with some amendments and additions to meet the purpose of this study, are embedded respectively in Algorithms Partition and Permute. (The Algorithm G2DLP is put in Appendix) Algorithm Partition is based on an Algorithm H that generates all partitions of an integer [18] (p. 38). Since Algorithm H treats, for example partitioning integer 11 into 4 parts, a partition of 8111 as same as another partition of 1811, we need to call Algorithm Permute to permute the partitions produced by Algorithm H. On the other hand, Algorithm Permute is based on an Algorithm L that generates all permutations of a multiset in lexicographic order [1] (pp. 39–40). Since Algorithm L assumes that the initial elements are in a non-decreasing order but Algorithm H produces partitions of an integer in a colex order (That is, lexicographic order of the reflected sequence.), we have to reverse the elements of a partition, provided by Algorithm H, in accordance with Algorithm L.

The strategy of G2DLP is divide-and-combine. According to a given number of turns t, we first delicately divide n₁ and n₂, the x-axis and vertical y-axis of a 2D lattice L(n₁, n₂), to several small parts respectively, totally t + 1 parts. The division is based on the identities (1) and (2) and achieved by aid of an integer partition algorithm (Partition) and a multiset permutation algorithm (Permute). Then combine these small parts, by Algorithm Concatenate, to a path that is we require.

Note that, in 2D lattice L(n₁, n₂), from the starting point (0, 0), if the first step is eastward then totally there are n₁ − 1 points the path can choose that will not arrive directly to the target point (n₁, n₂); if the first step is northward then totally there are n₂ − 1 points the path can choose that will not arrive directly to the target point (n₁, n₂). It is also worth noting that the upper indexes n₁ − 1 and n₂ − 1 in Theorem 1 stands for how many choices of point we can choose to change a path’s direction, and the parameters $n\_1$ and $n\_2$ in Algorithm G2DLP stand for what integer we want to partition. The relations between parameters ($n\_1$ and $n\_2$) and upper indexes (n₁ and n₂) are n_1 = n₁ and n_2 = n₂ respectively. Similarly, the lower indexes k − 1 and k in Theorem 1 stand for how many decisions of point we have to make to change a path’s direction, and that the parameters k and k+1 in Algorithm G2DLP stand for how many parts we want to partition an integer. The relation between parameters (k and k+1) and lower indexes (k − 1 and k) is k = k.

Why are n₁ − 1 and n₂ − 1 in the upper index of Theorem 1 but we use n_1 and n_2 in Algorithm G2DLP? Why are k − 1 and k in the lower index of Theorem 1 but we use k and k+1 in Algorithm G2DLP? The reasoning is that when we choose k − 1 (or k) points from n₁ − 1 (or n₂ − 1) points it means we partition an integer n₁ (or n₂) into k (or k + 1) parts.

We will present the experimental results, in Section 4, on some cases of 2D lattice L(n₁, n₂) in Table 1.

For a 2D lattice L(3, 4), if we set t = 2, then after two callings of Algorithm Partition and those concomitant callings of Algorithm Permute, the contents of arrays perm1 and perm2 are {(1, 2), (2, 1)} and {(4)} respectively. Now, when calling Concatenate (parts, “e”, “n”), we alternatively access these two array through three pickups. The first parameter of algorithm Concatenate, parts, means we have decomposed a path to parts parts. Here, since t = 2 we have parts = 3. Therefore, we need three pickups to construct a path. First, we pick up the first element of (1, 2), here is 1, then pick up the first element of (4) and finally pick up the second element of (1, 2), here is 2, thus we have one “e”, four “n”, and two “e”, that is “ennnnee.” Next, we pick up the first element of (2, 1), here is 2, then pick up the first element of (4) and finally pick up the second element of (2, 1), here is 1, thus we have two “e”, four “n”, and one “e”, that is “eennnne.” The two paths, numbered 3 and 4, can be found in Table 2, which is presented in Section 4.

3. Analyses

Obviously, the problem of generating 2D lattice L(n₁, n₂) paths according to a given number of turns is more challenging than a simple multiset permutation problem. This is because, for a simple multiset permutation algorithm, to generate permutations with a given number of turns, it requires both a time to generate all permutations and a time to perform additional comparisons and calculations to pick out those permutations with a given number of turns. Furthermore, if we want generate all paths in a specified order of turns, for example a decreasing or an increasing, we must spend additional time to sort them according to the number of turns they have. Not surprisingly, we can easily prove the following theorem.

Theorem 2. The time complexity of a simple multiset permutation algorithm for generating two-item {A^n₁, B^n₂} multiset permutations according to a given number of turns is $O(\frac{n^{n+1.5}}{n_1^{n_1+0.5}\times n_2^{n_2+0.5}})$, here n = n₁ + n₂; and in case of n₁ = n₂ the time complexity is $O(n^{0.5}{2}^{n+1}).$

Proof. For a two-item multiset permutation, there are totally $\frac{n!}{n_1!n_2!}$ permutations, and each one needs $n-1$ comparisons to calculate how many turns it has. It is well known that the factorial function is exponential growth. By using the Stirling approximation, $n!=\sqrt{2\pi n}{\left(\frac{n}{e}\right)}^n$, we have:

$$\frac{n!}{n_1!n_2!}=\frac{\sqrt{2\pi n}{\left(\frac{n}{e}\right)}^n}{\sqrt{2\pi n_1}{\left(\frac{n_1}{e}\right)}^{n_1}\sqrt{2\pi n_2}{\left(\frac{n_2}{e}\right)}^{n_2}}=\sqrt{\frac{1}{2\pi }}\frac{n^{n+0.5}}{n_1^{n_1+0.5}\times n_2^{n_2+0.5}},$$

then after multiplying the term by n = 1 we have $O(\frac{n^{n+1.5}}{n_1^{n_1+0.5}\times n_2^{n_2+0.5}})$. Moreover, in the case of n₁ = n₂ the time complexity is $O(n^{0.5}{2}^{n+1}).$ In other words, the running time is exponential growth on the problem size n. □

Fortunately, the proposed Algorithm G2DLP significantly reduces this time complexity to a linear order. Now, let us analyze the complexity of three components of Algorithm G2DLP individually. Since the amendments and additions to Algorithms H and L have little influence in time complexity, we can directly use the time complexity of Algorithms H and L, respectively, to stand for the time complexity of Algorithms Partition and Permute. First, if we let $\left|\begin{array}{c}n\\ m\end{array}\right|$ denote the number of partitions of n that have exactly m parts, then the running time per partition of Algorithm Partition is $3+m/\left|\begin{array}{c}n\\ m\end{array}\right|$. By Knuth [18] (p. 39), we know that the total running time of Algorithm H is at most a small constant multiplied by the number of partitions visited, plus O(m). The key quantity is the value of j, in H4, the smallest subscript for which $a_j<a_1-1$. Let $c_m(n)$ be the accumulated total value of $j-1$ summed over all of the $\left|\begin{array}{c}n\\ m\end{array}\right|$ partitions generated by Algorithm H. Knuth [18] (p. 50) has proved that the cost measure $c_m(n)$ for Algorithm H is at most $3\left|\begin{array}{c}n\\ m\end{array}\right|+m$. Regard $c_m(n)/\left|\begin{array}{c}n\\ m\end{array}\right|$ as a good indicator of the running time per partition, therefore, the running time per partition of Algorithm H is $3+m/\left|\begin{array}{c}n\\ m\end{array}\right|$.

Second, with regard to the Algorithm Permute, the running time is reasonably efficient [1] (p. 40). When the partition produced by Algorithm H is simply a set containing distinct elements, for example 5321 as a partition of partitioning integer 11 into 4 parts, the means of the number of comparisons by step L2 and step L3 are about 1.718 and 1.359, respectively [1] (pp. 101–102); and the average number of interchanges in step L4 is about 0.543 [1] (p. 102). On the other hand, when the partition produced by Algorithm H is a multiset, for example 7211 as a partition of partitioning integer 11 into 4 parts, the means of the number of comparisons by step L2 and step L3 are a little more complicated; even so, it is reasonably efficient. For details, see [1] (p. 102).

Finally, as to the Algorithm Concatenate, for generating a path, it only performs n_1 + n_2 concatenations (either “e” or “n”). These concatenations are accomplished by parts pickups that access the two arrays, perms1 and perms2, alternatively. Moreover, since Algorithm G2DLP generates all feasible paths without visiting any infeasible ones, we claim that Algorithm G2DLP is a linear time, or CAT algorithm. An algorithm runs in constant amortized time (CAT) if the amount of computation, after a small amount of preprocessing, is proportional to the number of objects that are generated [19]. What they call CAT has been called linear by Reingold, Nievergelt, and Deo [20], and in several papers [21]. The experimental results, in next Section, Table 3 and Table 4 and Figure 1 will support this assertion, Table 5 and Figure 2 will support the Theorem 2.

4. Experimental Results

In the following, we present path distributions with respect to their number of turns on some cases of two-item {e^n₁, n^n₂} multiset in Table 1. Among then, all paths of the 2D lattice L(3, 4) generated by G2DLP are presented, according to the number of turns, in Table 2.

Table 1. The path distributions with respect to their number of turns.

Turns	n1	3	4	4	4	4	4	5	5	5	5	5	5
	n2	4	6	7	8	9	10	6	7	8	9	10	11
1		2	2	2	2	2	2	2	2	2	2	2	2
2		5	8	9	10	11	12	9	10	11	12	13	14
3		12	30	36	42	48	54	40	48	56	64	72	80
4		9	45	63	84	108	135	70	96	126	160	198	240
5		6	60	90	126	168	216	120	180	252	336	432	540
6		1	40	75	126	196	288	100	180	294	448	648	900
7		0	20	40	70	112	168	80	160	280	448	672	960
8		0	5	15	35	70	126	30	80	175	336	588	960
9		0	0	0	0	0	0	10	30	70	140	252	420
10		0	0	0	0	0	0	1	6	21	56	126	252
Total Paths		35	210	330	495	715	1001	462	792	1287	2002	3003	4368

Table 1. The path distributions with respect to their number of turns.

Turns	n1	3	4	4	4	4	4	5	5	5	5	5	5
	n2	4	6	7	8	9	10	6	7	8	9	10	11
1		2	2	2	2	2	2	2	2	2	2	2	2
2		5	8	9	10	11	12	9	10	11	12	13	14
3		12	30	36	42	48	54	40	48	56	64	72	80
4		9	45	63	84	108	135	70	96	126	160	198	240
5		6	60	90	126	168	216	120	180	252	336	432	540
6		1	40	75	126	196	288	100	180	294	448	648	900
7		0	20	40	70	112	168	80	160	280	448	672	960
8		0	5	15	35	70	126	30	80	175	336	588	960
9		0	0	0	0	0	0	10	30	70	140	252	420
10		0	0	0	0	0	0	1	6	21	56	126	252
Total Paths		35	210	330	495	715	1001	462	792	1287	2002	3003	4368

Table 2. All paths of the 2D lattice L(3, 4).

Path Number	Step 1	Step 2	Step 3	Step 4	Step 5	Step 6	Step 7	Number of Turns
1	e	e	e	n	n	n	n	1
2	n	n	n	n	e	e	e	1
3	e	n	n	n	n	e	e	2
4	e	e	n	n	n	n	e	2
5	n	e	e	e	n	n	n	2
6	n	n	n	e	e	e	n	2
7	n	n	e	e	e	n	n	2
8	e	n	e	e	n	n	n	3
9	e	n	n	n	e	e	n	3
10	e	n	n	e	e	n	n	3
11	e	e	n	e	n	n	n	3
12	e	e	n	n	n	e	n	3
13	e	e	n	n	e	n	n	3
14	n	e	n	n	n	e	e	3
15	n	e	e	n	n	n	e	3
16	n	n	n	e	n	e	e	3
17	n	n	n	e	e	n	e	3
18	n	n	e	n	n	e	e	3
19	n	n	e	e	n	n	e	3
20	e	n	e	n	n	n	e	4
21	e	n	n	n	e	n	e	4
22	e	n	n	e	n	n	e	4
23	n	e	n	e	e	n	n	4
24	n	e	e	n	e	n	n	4
25	n	e	n	n	e	e	n	4
26	n	e	e	n	n	e	n	4
27	n	n	e	n	e	e	n	4
28	n	n	e	e	n	e	n	4
29	e	n	e	n	e	n	n	5
30	e	n	e	n	n	e	n	5
31	e	n	n	e	n	e	n	5
32	n	e	n	e	n	n	e	5
33	n	e	n	n	e	n	e	5
34	n	n	e	n	e	n	e	5
35	n	e	n	e	n	e	n	6

Table 2. All paths of the 2D lattice L(3, 4).

Path Number	Step 1	Step 2	Step 3	Step 4	Step 5	Step 6	Step 7	Number of Turns
1	e	e	e	n	n	n	n	1
2	n	n	n	n	e	e	e	1
3	e	n	n	n	n	e	e	2
4	e	e	n	n	n	n	e	2
5	n	e	e	e	n	n	n	2
6	n	n	n	e	e	e	n	2
7	n	n	e	e	e	n	n	2
8	e	n	e	e	n	n	n	3
9	e	n	n	n	e	e	n	3
10	e	n	n	e	e	n	n	3
11	e	e	n	e	n	n	n	3
12	e	e	n	n	n	e	n	3
13	e	e	n	n	e	n	n	3
14	n	e	n	n	n	e	e	3
15	n	e	e	n	n	n	e	3
16	n	n	n	e	n	e	e	3
17	n	n	n	e	e	n	e	3
18	n	n	e	n	n	e	e	3
19	n	n	e	e	n	n	e	3
20	e	n	e	n	n	n	e	4
21	e	n	n	n	e	n	e	4
22	e	n	n	e	n	n	e	4
23	n	e	n	e	e	n	n	4
24	n	e	e	n	e	n	n	4
25	n	e	n	n	e	e	n	4
26	n	e	e	n	n	e	n	4
27	n	n	e	n	e	e	n	4
28	n	n	e	e	n	e	n	4
29	e	n	e	n	e	n	n	5
30	e	n	e	n	n	e	n	5
31	e	n	n	e	n	e	n	5
32	n	e	n	e	n	n	e	5
33	n	e	n	n	e	n	e	5
34	n	n	e	n	e	n	e	5
35	n	e	n	e	n	e	n	6

To confirm the claim that the Algorithm G2DLP is a linear time algorithm, we perform a series of experiments and present the results in Table 3 and Figure 1. The running time (h: m: s) is for generating only but without printing out the paths, by using an Acer ® notebook with an Intel® Core™ i5-4200U CPU @ 1.6 GHz and a VBA program executed under the Microsoft Excel environment. Based on the experimental results in Table 3 and Figure 1, we confirm that Algorithm G2DLP is a linear time algorithm.

Table 3. Running Time of G2DLP vs. Total Paths.

n1	n2	Total Paths	Running Time (h:m:s)	n1	n2	Total Paths	Running Time (h:m:s)
7	13	77520	0:00:01	9	15	1307504	0:00:13
9	10	92378	0:00:01	11	12	1352078	0:00:12
7	14	116280	0:00:01	10	14	1961256	0:00:18
8	12	125970	0:00:01	11	13	2496144	0:00:23
9	11	167960	0:00:01	12	12	2704156	0:00:25
7	15	170544	0:00:01	10	15	3268760	0:00:31
10	10	184756	0:00:02	11	14	4457400	0:00:43
8	13	203490	0:00:02	12	13	5200300	0:00:51
9	12	293930	0:00:03	11	15	7726160	0:01:17
8	14	319770	0:00:02	12	14	9657700	0:01:38
10	11	352716	0:00:04	13	13	10400600	0:01:46
8	15	490314	0:00:05	12	15	17383860	0:03:09
9	13	497420	0:00:04	13	14	20058300	0:03:31
10	12	646646	0:00:07	13	15	37442160	0:06:43
11	11	705432	0:00:06	14	14	40116600	0:07:11
9	14	817190	0:00:07	14	15	77558760	0:14:31
10	13	1144066	0:00:13	15	15	155117520	0:29:36

Table 3. Running Time of G2DLP vs. Total Paths.

n1	n2	Total Paths	Running Time (h:m:s)	n1	n2	Total Paths	Running Time (h:m:s)
7	13	77520	0:00:01	9	15	1307504	0:00:13
9	10	92378	0:00:01	11	12	1352078	0:00:12
7	14	116280	0:00:01	10	14	1961256	0:00:18
8	12	125970	0:00:01	11	13	2496144	0:00:23
9	11	167960	0:00:01	12	12	2704156	0:00:25
7	15	170544	0:00:01	10	15	3268760	0:00:31
10	10	184756	0:00:02	11	14	4457400	0:00:43
8	13	203490	0:00:02	12	13	5200300	0:00:51
9	12	293930	0:00:03	11	15	7726160	0:01:17
8	14	319770	0:00:02	12	14	9657700	0:01:38
10	11	352716	0:00:04	13	13	10400600	0:01:46
8	15	490314	0:00:05	12	15	17383860	0:03:09
9	13	497420	0:00:04	13	14	20058300	0:03:31
10	12	646646	0:00:07	13	15	37442160	0:06:43
11	11	705432	0:00:06	14	14	40116600	0:07:11
9	14	817190	0:00:07	14	15	77558760	0:14:31
10	13	1144066	0:00:13	15	15	155117520	0:29:36

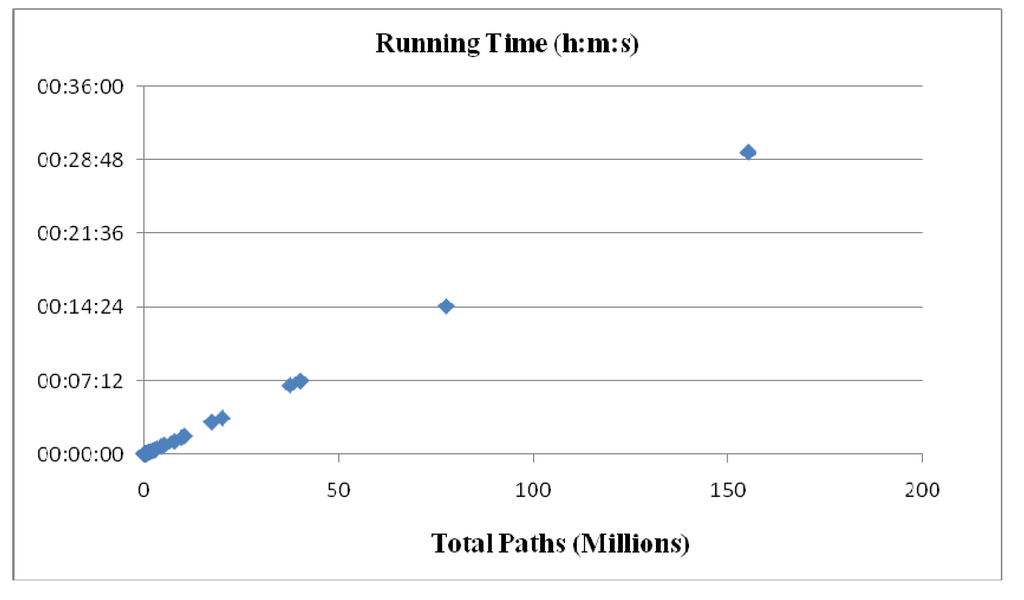
Figure 1. Running Time of G2DLP vs. Total Paths.

Figure 1. Running Time of G2DLP vs. Total Paths.

In order to highlight the superiority of Algorithm G2DLP, we perform a series of experiments and present the running times for generating 2D lattice L(15, 15) paths, according to the number of turns, in the following Table 4. Note that we skip the two trivial paths that with number of turns 1. From the results of Table 4, it is easy to know that, on average, the running time of Algorithm G2DLP for generating a path is almost a constant (mean: $9\times {10}^{-6}$ seconds, standard deviation: 7.8 × 10⁻⁶ seconds). This result confirms again that Algorithm G2DLP is a linear time algorithm.

Table 4. Running Time of G2DLP for 2D lattice L(15, 15).

Number of Turns	Number of Paths	Running Time (h:m:s)	Number of Turns	Number of Paths	Running Time (h:m:s)
2	28	≈0:00:00	16	20612592	0:04:36
3	392	≈0:00:00	17	18036018	0:04:03
4	2548	≈0:00:00	18	12024012	0:02:50
5	16562	≈0:00:00	19	8016008	0:01:56
6	66248	≈0:00:00	20	4008004	0:01:01
7	264992	0:00:03	21	2004002	0:00:32
8	728728	0:00:08	22	728728	0:00:12
9	2004002	0:00:21	23	264992	0:00:04
10	4008004	0:00:44	24	66248	0:00:01
11	8016008	0:01:43	25	16562	≈0:00:00
12	12024012	0:02:19	26	2548	≈0:00:00
13	18036018	0:03:32	27	392	≈0:00:00
14	20612592	0:04:11	28	28	≈0:00:00
15	23557248	0:04:59*	29	2	≈0:00:00

* Please refer to the running time listed at the bottom row of Table 5.

Table 4. Running Time of G2DLP for 2D lattice L(15, 15).

Number of Turns	Number of Paths	Running Time (h:m:s)	Number of Turns	Number of Paths	Running Time (h:m:s)
2	28	≈0:00:00	16	20612592	0:04:36
3	392	≈0:00:00	17	18036018	0:04:03
4	2548	≈0:00:00	18	12024012	0:02:50
5	16562	≈0:00:00	19	8016008	0:01:56
6	66248	≈0:00:00	20	4008004	0:01:01
7	264992	0:00:03	21	2004002	0:00:32
8	728728	0:00:08	22	728728	0:00:12
9	2004002	0:00:21	23	264992	0:00:04
10	4008004	0:00:44	24	66248	0:00:01
11	8016008	0:01:43	25	16562	≈0:00:00
12	12024012	0:02:19	26	2548	≈0:00:00
13	18036018	0:03:32	27	392	≈0:00:00
14	20612592	0:04:11	28	28	≈0:00:00
15	23557248	0:04:59*	29	2	≈0:00:00

* Please refer to the running time listed at the bottom row of Table 5.

To confirm the assertion of Theorem 2, we perform a series of experiments, by using a simple multiset permutation algorithm Permute⁺. Here, we only include the L2, L3, L4 parts of Algorithm Permute, and substitute L1 part with a loop of statements to perform comparisons and calculations to pick out those permutations according to a given number of turns. The running times for generating 2D lattice L(n₁, n₂) paths, with n₁ = n₂ according to a given number of turns are presented in the following Table 5 and Figure 2. Based on the experimental results in Table 5 and Figure 2, we have supported the assertion of Theorem 2.

Table 5. Running Time of Permute⁺.

n = n1 + n2	Number of Turns	Number of Paths	Total Paths	Running Time (h:m:s)
4	2	2	6	0:00:00
6	3	8	20	0:00:00
8	4	18	70	0:00:00
10	5	72	252	0:00:00
12	6	200	924	0:00:00
14	7	800	3432	0:00:00
16	8	2450	12870	0:00:00
18	9	9800	48620	0:00:00
20	10	31752	184756	0:00:01
22	11	127008	705432	0:00:04
24	12	426888	2704156	0:00:16
26	13	1707552	10400600	0:01:07
28	14	5889312	40116600	0:04:29
30	15	23557248	155117520	0:17:52**

**Note that, although there are some differences in the running time for generating the paths with a different number of turns, but the difference is very small. For example, in the case of $n=30$ even for generating the paths with a given number of turns 2, only 28 paths, its running time is 0:17:54. Therefore, for each case of n, we only run Permute⁺ for generating the paths with a given number of turns $n_1$ that will have the maximum number of paths; for example, in the case of n = 30 please refer to the data in Table 4 where the number 23557248 is the maximum.

Table 5. Running Time of Permute⁺.

n = n1 + n2	Number of Turns	Number of Paths	Total Paths	Running Time (h:m:s)
4	2	2	6	0:00:00
6	3	8	20	0:00:00
8	4	18	70	0:00:00
10	5	72	252	0:00:00
12	6	200	924	0:00:00
14	7	800	3432	0:00:00
16	8	2450	12870	0:00:00
18	9	9800	48620	0:00:00
20	10	31752	184756	0:00:01
22	11	127008	705432	0:00:04
24	12	426888	2704156	0:00:16
26	13	1707552	10400600	0:01:07
28	14	5889312	40116600	0:04:29
30	15	23557248	155117520	0:17:52**

**Note that, although there are some differences in the running time for generating the paths with a different number of turns, but the difference is very small. For example, in the case of $n=30$ even for generating the paths with a given number of turns 2, only 28 paths, its running time is 0:17:54. Therefore, for each case of n, we only run Permute⁺ for generating the paths with a given number of turns $n_1$ that will have the maximum number of paths; for example, in the case of n = 30 please refer to the data in Table 4 where the number 23557248 is the maximum.

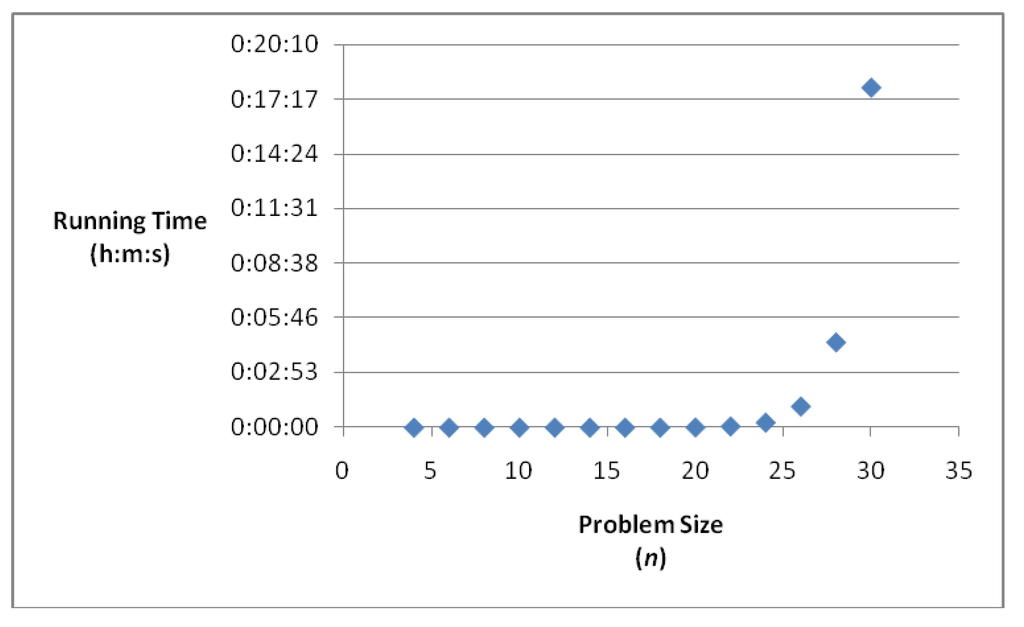
Figure 2. Running Time of Permute⁺ vs. Problem Size.

Figure 2. Running Time of Permute⁺ vs. Problem Size.

5. Applications

Lattice paths have been applied in several areas, for example to solve interesting and nontrivial problems in the theory of queues [22]. In addition, scholars engaged in cryptography have long been aware of the importance of lattices and lattice reduction in cryptography, both for cryptographic construction and cryptographic analysis [23]. Kaparthi [5] points out that, it has been shown, by [24], that lattice path enumeration problems are equivalent to the partial orders enumeration problems that have applications in the area of computer science in deciding the efficiency of sorting algorithms [25], and in social choice theory in studying various kinds of discrete ranking structures, and preference orders among decision makers [26]. Here, we propose two potential applications as follows.

5.1. Scheduling

As mentioned in Introduction, the motivation of this study was inspired by trying to solve a kind of open shop scheduling problem that is concerned with setup time among different types of machines [17]. Here, setup time means delay time that occurs when we arrange the processing route (or path) of a job from one type of machine to another type of machine. In scheduling problems, if the paths of jobs are fixed beforehand, and are the same for all jobs, it is called a flow-shop [27]; on the other hand, if the paths of jobs are not given in advance, but chosen by the scheduler, it is called an open-shop [28]. What we are trying to solve is an open shop scheduling problem that comprised a set of J jobs, {1, 2, …, J}, and n machines with two types of A and B. That is, every job must pass through all n machines for each machine once.

Assume that n₁ and n₂ be the number of machines of type A and B respectively, and that n = n₁ + n₂. Now, let ${\text{π}}_j={\text{π}}_{j1}{\text{π}}_{j2}\cdots {\text{π}}_{jn}$ be a path of job j where ${\text{π}}_{jk}$, for all $k\in \{1,2,\cdots ,n\},$ can be a symbol of “A” or “B” that stands for the k^th operation of job j is processed by a machine of type A or B, respectively. To be a valid path, obviously, in a path ${\text{π}}_j$ of a job j there must have n₁ A’s, and n₂ B’s. For example, if $n_1=4$ and $n_1=6$ then ${\text{π}}_j=\text{AAABBABBBB}$ and ${\text{π}}_j^{\prime }=\text{AABBBABBBA}$ can be two feasible paths of a job j. It is trivial that there are totally $\frac{n!}{n_1!n_2!}$ different feasible paths for a job. If we assume that there are no two jobs with the same path, there are totally $\left(\begin{array}{c}\frac{n!}{n_1!n_2!}\\ \text{J}\end{array}\right)$ different feasible schedules can be chosen by the scheduler. How to choose a schedule depends on what objective the scheduler aims at. One widely used objective is to minimize the make span, the time needed to complete all jobs.

Traditionally, it is common to assume that, when its previous operation has been completed by a machine, a job is immediately available to be processed by another machine. However, in practice, there is often a significant time delay between the completion of an operation and the start of the next operation of the same job. Furthermore, in some cases, the processing times might be negligible compare to the delay times. Therefore, they have a small influence on the make span [29]. Several real world applications can be found in [30]. The open shop scheduling problem with time delays was first introduced in [31], and shown to be NP-hard even for two machines and identical time delays.

Let d stand for the delay times needed to transfer a job from a machine of type A (or B) to a machine of type B (or A), and D_j stand for the total delay times needed for a job j to complete its path. Here, we assume that transfer a job between two machines of the same type does not cause any delay time. Without loss of generality, we can set delay times $d=1.$ Therefore, for two paths such as ${\text{π}}_1=\text{AAABBABBBB}$ and ${\text{π}}_2=\text{AABBBABBBA,}$ we have $D_1=3$ and $D_2=4.$ Our objective is to minimize the total delay times of all jobs, that is, to minimize ${\displaystyle {\sum }_{j=1}^{j=\text{J}}{D}_j}.$

Since a path of a job can be viewed as a permutation of a two-item ${\text{{A}}^{n_1},{\text{B}}^{n_2}\}$ multiset, the feasible paths of a job can be obtained by an algorithm that can generate all feasible permutations of this multiset. The question is how to choose J permutations, from the $\frac{n!}{n_1!n_2!}$ feasible permutations, for these J jobs such that ${\displaystyle {\sum }_{j=1}^{j=\text{J}}{D}_j}$ is minimized. Note that in the multiset permutation, we call there is a turn if two consecutive elements are belonging to two different items. That is, a turn occurs if we transfer a job from a machine of type A (or B) to a machine of type B (or A). This means that the delay time of a job that goes through a path with t turns is t.

Being a scheduler, a reasonable strategy for us is to choose, as soon as possible, those feasible and available paths that possess minimum turns. To do that, we are confronted with two issues. The first one is to answer the question of what is the number of permutations that possess a given number of turns, the second one is to design an algorithm that can generate the paths in a non-decreasingly order of turns. The first question has been resolved in [3], and now we have answered the second question. Therefore, the result of this study can provide for a scheduler as a good start to plan his scheduling.

5.2. Cryptography

The proposed algorithm can be used in cryptography. For example, we can combine the G2DLP with a substitution cipher system to become a product cipher system [32], [33] (p. 67). Since there are in total $29!=8.8417619937397\times {10}^{30}\approx 2^{102}$ possible permutations of 29 characters (include 26 letters of the English alphabet plus comma, period and space), we can use any integer κ, $1\le \text{κ}\le 29!$, as a secret key to choose a permutation of {A, B, …, Z, “,”, “.”, “”} as a substitution Σ. This can be accomplished by an unranking algorithm that we proposed in a previous study [34]. For example, if we select $\text{κ}=7.13164755752291E+30$ as a secret key, then by using the unranking algorithm, we can obtain a substitution Σ as the following Table 6.

Table 6. A substitution Σ of 29 characters.

A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
x	k	.	q	v	h	n	j	f	w	c	z	,	a	s
24	11	28	17	22	8	14	10	6	23	3	26	27	1	19
P	Q	R	S	T	U	V	W	X	Y	Z	,	.	-	Not Available
o	t	e	b	p	l	m		u	i	d	g	r	y	Not Available
15	20	5	2	16	12	13	29	21	9	4	7	18	25	Not Available

Table 6. A substitution Σ of 29 characters.

A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
x	k	.	q	v	h	n	j	f	w	c	z	,	a	s
24	11	28	17	22	8	14	10	6	23	3	26	27	1	19
P	Q	R	S	T	U	V	W	X	Y	Z	,	.	-	Not Available
o	t	e	b	p	l	m		u	i	d	g	r	y	Not Available
15	20	5	2	16	12	13	29	21	9	4	7	18	25	Not Available

By using the substitution Σ, we can encrypt a plaintext Ψ of l characters into a cipher text Ω₁ of l numbers that each one is an integer between 1 and 29. Then, by using the G2DLP, we can choose two integers, for example $n_1\ge 15$ and $n_2\ge 15$, as a pair of secret keys to encrypt the cipher text Ω₁ into a new cipher text Ω₂ of strings of $(n_1+n_2)$ bits. On the other hand, we can use a decoder to compute the number of turns of each string to obtain the cipher text Ω₁ of l numbers. Finally, by using the substitution Σ^-1, we can transfer the cipher text Ω₁ into the plaintext Ψ of l characters. The cryptosystem mentioned above is presented as following Figure 3.

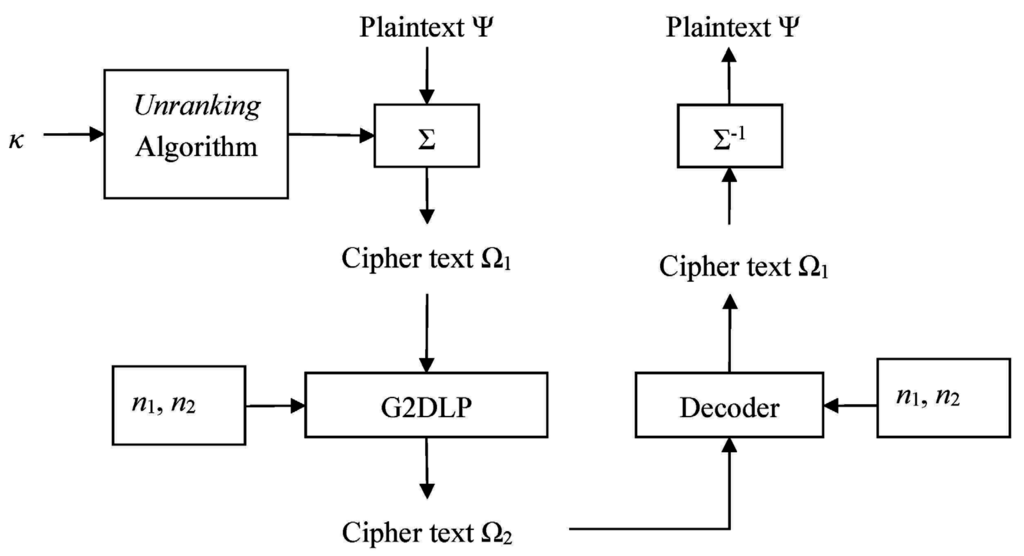
Figure 3. Encryption-Decryption Scheme.

Figure 3. Encryption-Decryption Scheme.

The characteristic of the proposed cryptosystem is threefold. First, to be a polyalphabetic cryptosystem [33] (p. 13), we can run the unranking algorithm several times, each time use the same secret key κ and the latest generated substitution Σ that is initialized as {A, B, …, Z, “,”, “.”, “”} at first. Therefore, as being a polyalphabetic cryptosystem, it can exempt from the cryptanalysis that is based on the statistical properties of usage frequencies of English alphabet [33] (p. 27). Second, the proposed cryptosystem can encrypt a character into one of different numbers of strings. For example, if we use n₁ = 15 and n₂ = 15 as a pair of secret keys to encrypt the cipher text Ω₁ into a new cipher text Ω₂, then we can encrypt the character “P” into one of 20612592 different strings of 30 bits, and encrypt the character “M” into one of 18036018 different strings of 30 bits. This is because, see Table 6, the letter “P” represents the number 16, and the character “M” represents the number 13; and in a 2D lattice L(15, 15), see Table 4, there are totally 20612592 different paths possess 16 turns, and 18036018 different paths possess 13 turns. If someone tries to break the cryptosystem but he does not know the decryption scheme, this will make his attack very difficult. Third, it is easy to implement the proposed cryptosystem to become a non-synchronous stream cipher [33] (p. 24). That is, we can use the unranking algorithm as a key stream generator that depends not only on the secret key κ but also on the plaintext itself. This strategy can greatly increase the complexity of breaking the proposed cryptosystem. Based on the characteristics mentioned above, we can say that the proposed cryptosystem can be an applicable and safe system.

6. Conclusions

Basically, the problem of generating 2D lattice L(n₁, n₂) paths, equivalent to two-item multiset {A^n₁, B^n₂} permutations, according to a given number of turns is more challenging than a simple multiset permutation problem. The time complexity of a simple multiset permutation algorithm for generating two-item ${\text{{A}}^{n_1},{\text{B}}^{n_2}\}$ multiset permutations according to a given number of turns is $O(\frac{n^{n+1.5}}{n_1^{n_1+0.5}\times n_2^{n_2+0.5}})$, here $n=n_1+n_2$ ; and in case of $n_1=n_2$ the time complexity is $O(n^{0.5}{2}^{n+1}).$ We propose an efficient Algorithm G2DLP that significantly reduces this time complexity to a linear order.

The principle behind Algorithm G2DLP is divide-and-combine. According to a given number of turns t, we first delicately divide n_1 and n_2, the horizontal x-axis and vertical y-axis of a 2D lattice L(n₁, n₂), to several small parts respectively, totally t + 1 parts. The division is based on the enumeration results of a previous study and is achieved by aid of an integer partition algorithm (Partition) and a multiset permutation algorithm (Permute). Then combine these small parts, by a concatenate algorithm (Concatenate), to the paths we require. The experimental results confirm that Algorithm G2DLP is a linear time, or CAT (constant amortized time), algorithm. That is, its amount of computation, after a small amount of preprocessing, is proportional to the number of paths it generates.

The advantage of G2DLP is twofold. First, it is optimal in the sense that it directly generates all feasible paths without visiting any infeasible path. Second, it can generate all paths in any specified order of turns, for example, a decreasing order or an increasing order. In practice, the result of this study can provide a good starting point for a scheduler attempting to deal with an open shop scheduling problem, and can be used as an encryption scheme of a cryptosystem. Finally, a concomitant problem, how to design an algorithm that can generate 3D lattice L(n₁, n₂, n₃) paths according to a given number of turns, is proposed for future research.