A Hybrid Metaheuristic Approach for Minimizing the Total Flow Time in A Flow Shop Sequence Dependent Group Scheduling Problem

Abstract

Production processes in Cellular Manufacturing Systems (CMS) often involve groups of parts sharing the same technological requirements in terms of tooling and setup. The issue of scheduling such parts through a flow-shop production layout is known as the Flow-Shop Group Scheduling (FSGS) problem or, whether setup times are sequence-dependent, the Flow-Shop Sequence-Dependent Group Scheduling (FSDGS) problem. This paper addresses the FSDGS issue, proposing a hybrid metaheuristic procedure integrating features from Genetic Algorithms (GAs) and Biased Random Sampling (BRS) search techniques with the aim of minimizing the total flow time, i.e., the sum of completion times of all jobs. A well-known benchmark of test cases, entailing problems with two, three, and six machines, is employed for both tuning the relevant parameters of the developed procedure and assessing its performances against two metaheuristic algorithms recently presented by literature. The obtained results and a properly arranged ANOVA analysis highlight the superiority of the proposed approach in tackling the scheduling problem under investigation.

1. Introduction

During the last few decades, the Cellular Manufacturing (CM) production philosophy has been implemented with favorable results in many manufacturing firms. According to CM principles, parts requiring similar production processes are grouped in distinct manufacturing cells, made by dedicated clusters of machines. The main advantages connected to the use of CM production strategies usually include reduction of setup and throughput times, simplified material handling, centralization of responsibilities, better quality, and production control [1,2,3]. Furthermore, the CM approach also facilitates the adoption of advanced manufacturing technologies, such as computer integrated manufacturing, Just In Time JIT production and flexible manufacturing systems [4].

The design of a Cellular Manufacturing System (CMS) usually starts with the cell formation phase, in which parts are clustered in families and groups of machines are identified; the second step consists in defining the machine layout within each cell and the arrangement of cells with regards to each other; then, a proper schedule concerning part families to be processed at each cell has to be determined; finally, the issue of allocating tools, materials, and human resources to each cell has to be addressed [5].

Due to similarities among their process requirements, parts belonging to the same family generally visit machines in a cell according to the same sequence. Therefore, manufacturing operations within cells often follow a flow-shop scheme [6]. An important benefit of the CM approach actually lies in the fact that even traditional batch or job-shop manufacturing operations may be easily converted in simpler flow-lines [7]. Furthermore, there often exist minor differences in terms of setup requirements among parts belonging to the same family. Notably, each family may be divided into smaller groups made by jobs sharing the same setup operations to be performed on the machines composing the cell [8]. The problem of scheduling jobs in such a manufacturing system is usually referred to as the Flow-Shop Group Scheduling (FSGS) problem.

In a classical FSGS problem, a measurable setup is required when switching from one group of parts to another, whereas the setup time between jobs belonging to the same group either is assumed to be negligible or it can be included along with the run time. Therefore, there exists a clear advantage in processing together jobs belonging to the same group, arranging the whole production schedule through subsequent groups. The decision issue to be addressed when facing a FSGS problem is, thus, twofold: the optimal sequence of groups and the optimal sequence of jobs within each group have to be determined with reference to a given performance measure. However, since each feasible solution for a FSGS problem may be described by a simple sequence of jobs passing through each machine belonging to the manufacturing cell, such a problem still remains a permutation scheduling issue, as in classical flow-shops.

A pioneer research on the FSGS problem was carried out by Ham, Hitomi, and Yoshida [9], who proposed an optimizing algorithm for minimizing the total completion time in a two-machine group-scheduling problem. A similar issue was addressed by Logendran and Sriskanadarajah [10] under the makespan minimization viewpoint. The authors investigated the NP-hardness of such a problem, taking into account blocking effects and anticipatory setups. Two years later, Logendran, Mai and Talkington [11] compared the performances reported by several single-pass and multi-pass heuristic algorithms for minimizing the makespan in FSGS problems with up to 10 machines.

The recent research addressing group scheduling issues in flow-shop manufacturing environments has been mainly focused on the Flow-Shop Sequence-Dependent Group Scheduling (FSDGS) problem, in which the time required for performing setup operations of each group of jobs depends on the technological features of the previously processed group. The interest towards the FSDGS problem has been basically motivated by the implications of such a scheduling issue in the real industrial practice. Examples of FSDGS problems have been observed in Printed Circuit Boards (PCBs) manufacturing [12], in furniture production [13], in paint and press shops of automobile manufacturers [14].

The reviews proposed by Allahverdi, Gupta, and Aldowaisan [15], Cheng, Gupta, and Wang [16], and Zhu and Whilelm [17], respectively, have discussed the basic aspects of the FSDGS issue, together with other cases of flow-shop problems involving setup considerations. Schaller, Gupta, and Vakharia [18] provided lower bounds and efficient heuristic algorithms for minimizing makespan in a flow-line manufacturing cell with sequence dependent family setup times. One year later, a similar topic was addressed by Schaller [6], who developed a heuristic method combining a branch and bound approach with an interchange procedure specifically designed to search for better job sequences within each group. França, Gupta, Mendes, Moscato, and Veltink [19] evaluated the performances of two evolutionary algorithms—a Genetic Algorithm (GA) and a Memetic Algorithm (MA) equipped with a local search—in terms of makespan minimization in a flow-shop manufacturing cell with sequence dependent family setups. After an extensive comparison conducted against the best metaheuristic available in literature and a properly developed multi-start algorithm, the authors demonstrated the superiority of both the proposed metaheuristics, with a slight outperformance of the memetic procedure. Logendran, Salmasi, and Sriskandarajah [20] proposed three different search algorithms based on Tabu Search (TS) for minimizing the total completion time in industry-size two-machine group scheduling problems with sequence dependent setups. The authors performed an extensive comparison among the developed procedures making use of mathematical programming-based lower bounds. A few years later, Hendizadeh, Faramarzi, Mansouri, Gupta, and ElMekkawy [21] presented various TS-based metaheuristics integrating features from Simulated Annealing (SA) for minimizing makespan in FSDGS problems up to 10 machines. A TS-based approach for the same scheduling issue was concurrently investigated by Salmasi and Logendran [22], who assessed the proposed procedure by means of the lower bounding technique proposed by Salmasi [23]. Celano, Costa, and Fichera [24] analyzed a flow shop sequence-dependent group scheduling problem with limited inter-operational buffer capacity truly observed in the inspection department of a company producing electronic devices. The authors proposed a matrix-encoding GA, validating its performances against a TS and the heuristic proposed by Nawaz, Enscore, and Ham [25] for the classical flow-shop problem. Salmasi, Logendran, and Skandari [14] developed a mathematical programming model in order to minimize the total flow time on the FSDGS problem, together with a TS and a Hybrid Ant Colony Optimization (HACO) algorithm for solving large-size issues. After having defined a wide benchmark of test cases arisen from real world manufacturing environments, the authors fulfilled an extensive comparison among the proposed metaheuristics, from which the outperforming results of the ant colony approach clearly emerged. One year later, Salmasi, Logendran, and Skandari [26] investigated the use of the HACO method for minimizing the makespan in a FSDGS problem, confirming the superiority of such metaheuristic compared to a memetic algorithm. With reference to the total flow time minimization objective, Hajinejad, Salmasi, and Mokthari [27] succeeded in outperforming the ant colony approach by means of a properly developed hybrid Particle Swarm Optimization (PSO) algorithm. As far as the total completion time minimization is concerned, Naderi and Salmasi [28] improved the performances of the HACO method through a metaheuristic procedure, called GSA, hybridizing genetic and simulated annealing algorithms.

Recently, Costa, Fichera, and Cappadonna [29] investigated the use of genetic algorithms for effectively addressing the makespan minimization issue in a FSDGS problem entailing skill differences among workers assigned to machines for executing setup tasks between groups. With reference to the same topic, Costa, Cappadonna, and Fichera [30] also demonstrated how a genetic algorithm-based approach outperforms the latest metaheuristic procedures available in literature.

The aim of the present paper is to propose a GA-based algorithm for minimizing the total flow time in the classical FSDGS problem, able to improve the alternative optimization procedures recently presented in such field of research, namely the PSO by Hajinejad, Salmasi, and Mokthari [27] and the GSA by Naderi and Salmasi [28]. To this end, a hybrid genetic algorithm, hereinafter called GARS (Genetic Algorithm with Random Sampling), integrating features from the Random Sampling (RS) search technique, was specifically developed and assessed on the basis of a well-established problem benchmark. The proposed GARS is powered by two distinct crossover operators and two mutation methods. A specific diversity operator embedded in the algorithm allows to avoid premature convergence towards local optima, enhancing solution space exploration. On the other hand, the main contribution to the exploitation phase arises from the RS algorithm that cyclically investigates the space of solutions around the current best solutions.

The remainder of the paper is organized as follows: Section 2 provides a description of the FSDGS problem. Section 3 illustrates the structure and the operators of the proposed metaheuristic procedure. Section 4 describes test problem specifications and reports results of the calibration campaign performed. In Section 5 an extensive comparison between the proposed algorithm and two alternative metaheuristic procedures arising from the latest literature is reported. Finally, Section 6 concludes the paper.

2. Problem Description

The proposed flow-shop group-scheduling problem can be stated as follows. A set of G groups of jobs has to be processed in a manufacturing cell with M machines arranged in a flow-shop layout. Each group g = 1, 2, ..., G holds n_g jobs; the total amount of jobs to be processed along the system is equal to ${\displaystyle \sum _{g=1}^G{n}_g}=N$. The setup time of each j-th job pertaining to group g (j = 1, 2, ..., n_g) on machine i (i = 1, 2, ..., M) is included in its runtime t_igj and does not depend on the preceding job. On the other hand, a sequence-dependent setup time S_ihg is necessary when switching from a group h to group g on a given machine i. All jobs and groups are processed in the same sequence through each workstation. Group setup operations are assumed to be anticipatory, as they can be performed even if the first job belonging to the group is still unavailable. Pre-emption is not allowed, i.e., when a job starts to be processed, it must be completed before leaving the machine. All jobs are ready to be worked at the beginning of the scheduling period, being their release time equal to zero. Machines are continuously available during the whole production session. No precedence relationship exists either among groups or among jobs belonging to the same group. The objective function to be minimized is the total flow time, i.e., the sum of completion times of all jobs.

For sake of clarity, Table 1 and Table 2 reports setup and processing times for an example problem in which M = 2, G = 2, n₁ = 3, n₂ = 2. It is worth noting that symbol S_i0g denotes the time required to setup a group of jobs g whether it is the first group to be processed in machine i. An illustrative example is reported in the following paragraph to clarify what stated before. It refers to Table 1 where two groups with two and three jobs have been recognized, respectively. Let suppose to process a sequence of groups 2-1, while the corresponding job schedules for each group are: 1-2 for group two and 2-3-1 for group one. The related Gantt is shown in Figure 1, the total flow time value associated to such a schedule is F₁₁ + F₁₂ + F₁₃ + F₂₁ + F₂₂ = 25 + 17 + 20 + 9 + 11 = 82.

Table 1. Setup times for a Flow-Shop Sequence-Dependent Group Scheduling (FSDGS) example with M = 2, G = 2, n₁ = 3, n₂ = 2.

Machine (i)	Preceding Group (h)	Group (g)	Setup time (Sihg)
1	0	1	1
1	0	2	3
1	1	2	1
1	2	1	2
1	0	1	2
1	0	2	3
1	1	2	5
1	2	1	3

Table 1. Setup times for a Flow-Shop Sequence-Dependent Group Scheduling (FSDGS) example with M = 2, G = 2, n₁ = 3, n₂ = 2.

Machine (i)	Preceding Group (h)	Group (g)	Setup time (Sihg)
1	0	1	1
1	0	2	3
1	1	2	1
1	2	1	2
1	0	1	2
1	0	2	3
1	1	2	5
1	2	1	3

Table 2. Processing times for a Flow-Shop Sequence-Dependent Group Scheduling (FSDGS) example with M = 2, G = 2, n₁ = 3, n₂ = 2.

Machine (i)	Group (g)	Job (j)	Processing time (Sihg)
1	1	1	7
1	1	2	2
1	1	3	4
1	2	1	1
1	2	2	2
2	1	1	4
2	1	2	3
2	1	3	3
2	2	1	2
2	2	2	2

Table 2. Processing times for a Flow-Shop Sequence-Dependent Group Scheduling (FSDGS) example with M = 2, G = 2, n₁ = 3, n₂ = 2.

Machine (i)	Group (g)	Job (j)	Processing time (Sihg)
1	1	1	7
1	1	2	2
1	1	3	4
1	2	1	1
1	2	2	2
2	1	1	4
2	1	2	3
2	1	3	3
2	2	1	2
2	2	2	2

Figure 1. Gantt chart for a FSDGS example with M = 2, G = 2, n₁ = 3, n₂ = 2.

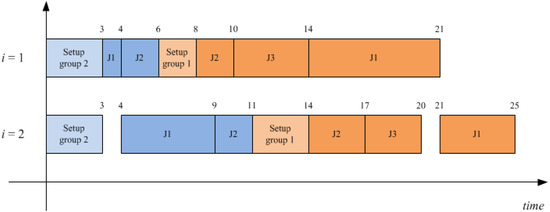
Figure 1. Gantt chart for a FSDGS example with M = 2, G = 2, n₁ = 3, n₂ = 2.

3. The Proposed Optimization Procedure

According to Salmasi, Logendran, and Skandari [14], the total flow time minimization in a FSDGS problem is NP-hard. Therefore, a metaheuristic procedure is required to obtain valid solutions within a polynomial time. Since Costa, Cappadonna, and Fichera [30] recently proved both the efficacy and the efficiency of the genetic algorithm approach for solving the FSDGS problem, a GA-based optimization procedure embedding a random sampling search technique has been proposed for tackling the problem under investigation.

Generally, a GA works with a set of problem solutions called population. At every iteration, a new population is generated from the previous one by means of two operators, crossover and mutation, applied to solutions (chromosomes) selected on the basis of their fitness, i.e., the objective function value; thus, best solutions have greater chances of being selected. Crossover operator generates new solutions (offspring) by coalescing the structures of a couple of existing ones (parents), while mutation operator brings a change into the scheme of selected chromosomes, with the aim to avoid the procedure to remain trapped into local optima. The algorithm proceeds by evolving the population through successive generations, until a given stopping criterion is reached.

Whenever a real problem should be addressed through an evolutionary algorithm, the choice of a proper encoding scheme (i.e., the way a solution is represented by a string of genes) plays a key role under both the quality of solutions and the computational burden viewpoints [31]. In addition, a valid decoding procedure able to transform a given string into a feasible solution should be provided.

The following subsections hold a detailed description of the proposed GA-based optimization procedure, along with the encoding/decoding strategies and the adopted genetic operators. A proper random sampling local search technique to be embedded in the proposed algorithm for enhancing its search performance will be dealt with in the next paragraphs.

3.1. Problem Encoding

For the proposed GARS procedure, a matrix-encoding scheme has been selected in order to simultaneously describe the sequence of groups and the sequence of jobs to be processed within each group. Making use of the notation introduced in the nomenclature Section, each chromosome is coded by an array of G + 1 row vectors. The first G vectors are the permutations π^g indicating the sequence of jobs pertaining to each group g. The last vector is the permutation Ω representing the sequence of groups:

(1)

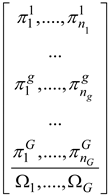
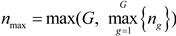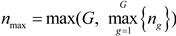It is worth pointing out that the number of elements in each vector is generally unequal. Therefore, indicating with n_max the maximum length of all vectors, i.e., , all rows having a number of elements lower than n_max are completed with a string of zero digits. In such a way, a (G + 1) × n_max matrix is created, and the chromosome may be easily handled for executing all genetic operators. However, all the digits equal to zero do not take part either to the solution decoding or to the genetic evolutionary process.

Each row of the partitioned matrix adopted in the proposed encoding scheme will be denoted as a sub-chromosome. Figure 2 depicts a feasible chromosome solution, named C, for a problem in which G = 3, n₁ = 2, n₂ = 5, n₃ = 4. Sub-chromosomes from 1 to 3 hold the schedules of jobs within each group (i.e., schedule 2-1 for group 1, schedule 1-4-3-5-2 for group 2, schedule 2-1-4-3 for group 3. Sub-chromosome 4 fixes the sequence of groups Ω = 3-2-1. Once the problem encoding is defined, the fitness function of each chromosome pertaining to the genetic population may be computed as the reciprocal of the total flow time, i.e., $1/{\displaystyle \sum _{g=1}^G{\displaystyle \sum _{j=1}^{n_g}{F}_{gj}}}$.

Figure 2. GARS matrix-encoding scheme.

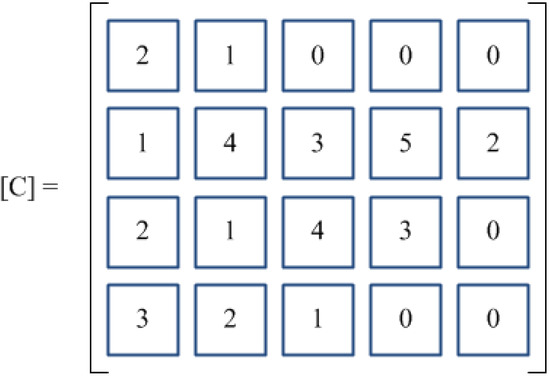
Figure 2. GARS matrix-encoding scheme.

3.2. Crossover Operator

The genetic material of two properly selected parent chromosomes is recombined through the crossover operator in order to generate offspring. The selection mechanism employed by the proposed GARS procedure is the well-known roulette wheel scheme [32], according to which individuals with a better fitness have a higher chance to be selected. Once two parent chromosomes have been chosen from the current population, each couple of homogenous sub-chromosomes belonging to the parent solutions may be subject to crossover according to a certain probability p_cr. Two methods of crossover operators have been adopted to recombine alleles within each couple of sub-chromosomes: they are denoted as Position Based Crossover (PBC) and Two Point Crossover (TPC), respectively.

PBC method [33] works by randomly selecting two or more positions in a couple of parent sub-chromosomes (P1) and (P2). The genes of (P1) located in such positions are re-arranged in the same order as they appear in (P2), thus, keeping unchanged the other genes. The same procedure is then executed for parent (P2). Figure 3 provides an example of the PBC method for a couple of parents where positions {2}, {3}, and {5} have been selected. TPC crossover is a variant of the classical order crossover [34], specifically developed for the problem at hand. According to such method, two positions are randomly selected for each parent sub-chromosome, and the block of adjacent jobs located within such positions is re-arranged conforming to the order in which jobs appear in the other parent (see Figure 4). Whether a couple of sub-chromosomes is selected for crossover, the choice between PBC and TPC methods is performed according to a “fair coin toss” probability equal to 0.5.

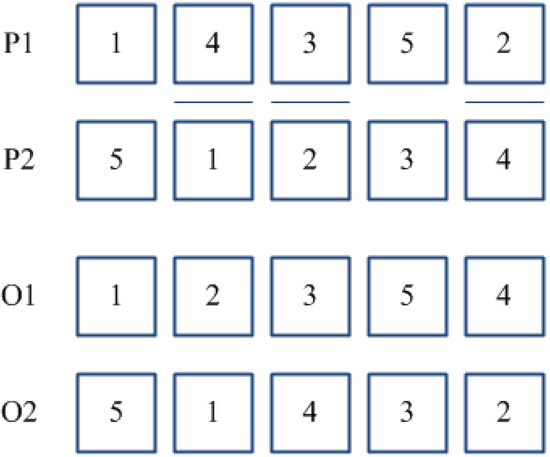
Figure 3. Position Based Crossover (PBC).

Figure 3. Position Based Crossover (PBC).

Figure 4. Two Point Crossover (TPC).

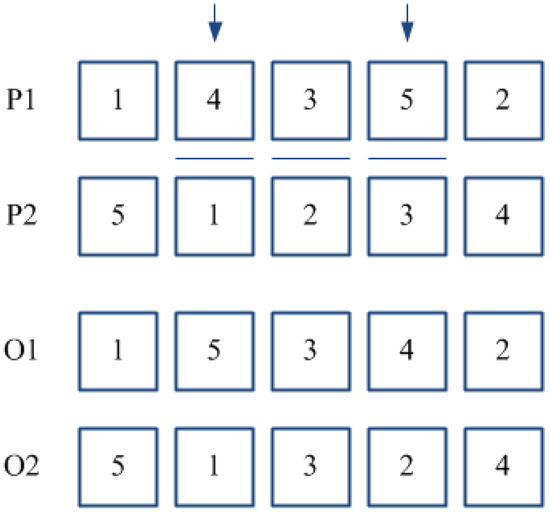
Figure 4. Two Point Crossover (TPC).

3.3. Mutation Operator

After a new population has been generated from the previous one by means of crossover, mutation operator is applied according to an a-priori fixed probability p_m. Whether mutation occurs, a chromosome is randomly chosen from the population and then, a single sub-chromosome is randomly selected for mutation. The proposed GARS procedure makes use of two different operators, selected on the basis of a “fair coin toss” probability equal to 0.5: an Allele Swapping Operator (ASO), which performs an exchange of two randomly selected alleles; and a Block Swapping Operator (BSO) which exchanges two blocks of adjacent genes (see Figure 5).

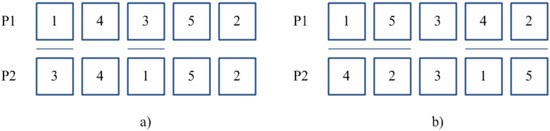
Figure 5. (a) Allele Swapping (ASO); and (b) Block Swapping (BSO) mutation Operators.

Figure 5. (a) Allele Swapping (ASO); and (b) Block Swapping (BSO) mutation Operators.

3.4. Random Sampling Local Search

Once a new population has been generated through crossover and mutation operators, a Biased Random Sampling (BRS) search procedure [35] is applied in order to search for better solutions in the neighbourhood of the best-performing chromosomes created so far. To this end, a sub-population having size N_best ≤ N_pop made by the best individuals obtained after each generation, is selected. For each chromosome C_r (r = 1, 2, ..., N_best) belonging to the sub-population, a sample of N_BRS neighbour solutions is generated by modifying the sequence Ω of groups, i.e., the last sub-chromosome. In the present research N_BRS has been set equal to 4. For each neighbour chromosome NC^k_r (k = 1, 2, ..., N_BRS) of C_r, the sequence of groups ${\overline{\Omega }}^k$ is obtained as follows.

The first group ${\overline{\Omega }}_1^k$ of ${\overline{\Omega }}^k$ is drawn from the elements of Ω according to the following distribution of probabilities:

$$p_{q,g}={\alpha }^g\times \frac{1}{{\displaystyle \sum _g{\alpha }^g}} g=1,2\dots ,G$$

(2)

where p_1,g is the probability to select Ωg, i.e., the g-th group of Ω, as first element of ${\overline{\Omega }}^k$. Such probability is “biased” in the sense that it favours the first group of Ω to the second, the second to the third, and so on. The parameter α is used to control how the probability decreases when moving from a group of Ω to the next. Conforming to Baker and Trietsch [35], a value of α = 0.8 has been selected. Thus, supposing to have G = 3, the first element of the new sub-chromosome ${\overline{\Omega }}^k$ will be drawn from Ω according to probabilities 0.410, 0.328, and 0.262 for the first, the second, and the third group of Ω, respectively.

Once ${\overline{\Omega }}_1^k$ has been drawn, the second group of ${\overline{\Omega }}^k$, i.e., ${\overline{\Omega }}_2^k$, will be extracted from the remaining ones. More in general, the q-th group of ${\overline{\Omega }}^k$ will be drawn from the remaining elements of Ω according to the following distribution of probabilities:

$$p_{q,g}={\alpha }^g\times \frac{1}{{\displaystyle \sum _g{\alpha }^g}} g=1,2,\mathrm{...},G+1-q$$

(3)

After a total amount of N_BRS neighbor solutions are originated from chromosome C_r, the best one is used for replacing C_r in the current population, just in case it leads to a lower total flow time value. Then, the same procedure is executed for the next chromosome of the selected sub-population.

3.5. Diversity Operator

In order to avoid any premature convergence towards the final solution, the proposed algorithm makes full use of a population diversitycontrol technique, which identifies the number of duplicate solutions in the population generated after crossover, mutation and BRS search procedure. Then, a mutation operator is applied to those identical chromosomes exceeding a pre-selected value D_max. As a consequence, each newly-generated population cannot hold more than D_max copies of the same solution.

It is worth noting that the lower is D_max, the higher is the pressure towards population heterogeneity. Nevertheless, the computational burden of the whole metaheuristic algorithm tends to increase as D_max decreases, since a higher number of mutation operations have to be performed after each generation. In the present research, a D_max = 2 value has been selected, thus avoiding to have more than two identical solutions within the population created at each generation.

3.6. Elitist Strategy and Stopping Criterion

In order to avoid any loss of the current best genetic information, an elitist strategy has been adopted at each generation to avoid any loss of the two best individuals. The termination rule of the proposed procedure consists in N∙M seconds of CPU time, similarly being done by Naderi and Salmasi [28]. The convergence of the algorithm within such time limit has been verified through a preliminary experimental campaign.

3.7. Procedure of GARS Algorithm

To sum up, the whole optimization strategy followed by the proposed GARS can be illustrated through the following steps:

Step 1:

Initialization of parameters N_pop, p_cr, p_m, D_max, N_best, N_BRS, α;

Step 2:

Generation of initial random population of chromosomes;

Step 3:

Application of crossover operator, chosen between Position Based and Two Point Crossover, to a couple of chromosomes chosen through roulette-wheel selection;

Step 4:

Generation of the new population after crossover operator through the insertion of the two best chromosomes individuated between parents and offspring: the two individuals with best values of fitness are introduced in the population;

Step 5:

Evaluation of p_m. If it is verified go to Step 6, else go to Step 7;

Step 6:

Application of mutation operator, chosen among two different operators: Allele Swapping and Block Swapping. The operator is applied randomly to a chromosome of the population;

Step 7:

Application of BRS procedure to the N_best best individuals of the population;

Step 8:

Population control: a mutation operator is applied on duplicates exceeding D_max.;

Step 9:

Updating of the current population, then return to Step 3.

4. Experimental Calibration and Test Cases

Before comparing the proposed GARS against alternative optimization procedures emerging from the recent literature in the field of the FSDGS problems, a comprehensive calibration phase has been fulfilled in order to properly set all the relevant parameters of the developed metaheuristic. To this end, the experimental benchmark proposed by Salmasi, Logendran, and Skandari [26] has been employed. Therefore, three-distinct sub-benchmarks, entailing problems with 2, 3, and 6 machines, respectively, have been considered. Within each sub-benchmark, test cases have been generated combining three factors, namely number of groups, number of jobs within groups and setup times of groups on each machine, in a full-factorial experimental design, as shown in Table 3, Table 4 and Table 5. On the whole, a total of 27 + 81 + 27 = 135 separate instances, describing a consistent dataset for the presented problem have been generated. All instances have been created by extracting job processing times according to a uniform distribution in the range [1,20].

Table 3. Sub-benchmark of instances for the 2-machine FDSGS problem.

Factor	Level	Value
Number of groups	1	U [1,5]
	2	U [6,10]
	3	U [11,16]
Number of jobs in a group	1	U [2,4]
	2	U [5,7]
	3	U [8,10]
Setup times of machine Mi	1	M1 $\to$ U [1,50]	M2 $\to$ U [17,67]
	2	M1 $\to$ U [1,50]	M2 $\to$ U [1,50]
	3	M1 $\to$ U [17,67]	M2 $\to$ U [1,50]

Table 3. Sub-benchmark of instances for the 2-machine FDSGS problem.

Factor	Level	Value
Number of groups	1	U [1,5]
	2	U [6,10]
	3	U [11,16]
Number of jobs in a group	1	U [2,4]
	2	U [5,7]
	3	U [8,10]
Setup times of machine Mi	1	M1 $\to$ U [1,50]	M2 $\to$ U [17,67]
	2	M1 $\to$ U [1,50]	M2 $\to$ U [1,50]
	3	M1 $\to$ U [17,67]	M2 $\to$ U [1,50]

Table 4. Sub-benchmark of instances for the 3-machine FDSGS problem.

Factor	Level	Value
Number of groups	1	U [1,5]
	2	U [6,10]
	3	U [11,16]
Number of jobs in a group	1	U [2,4]
	2	U [5,7]
	3	U [8,10]
Setup times of machine Mi	1	M1 $\to$ U [1,50]	M2 $\to$ U [17,67]	M3 $\to$ U [45,95]
	2	M1 $\to$ U [17,67]	M2 $\to$ U [17,67]	M3 $\to$ U [17,67]
	3	M1 $\to$ U [45,95]	M2 $\to$ U [17,67]	M3 $\to$ U [1,50]
	4	M1 $\to$ U [1,50]	M2 $\to$ U [17,67]	M3 $\to$ U [17,67]
	5	M1 $\to$ U [1,50]	M2 $\to$ U [17,67]	M3 $\to$ U [1,50]
	6	M1 $\to$ U [17,67]	M2 $\to$ U [17,67]	M3 $\to$ U [45,95]
	7	M1 $\to$ U [17,67]	M2 $\to$ U [17,67]	M3 $\to$ U [1,50]
	8	M1 $\to$ U [45,95]	M2 $\to$ U [17,67]	M3 $\to$ U [45,95]
	9	M1 $\to$ U [45,95]	M2 $\to$ U [17,67]	M3 $\to$ U [17,67]

Table 4. Sub-benchmark of instances for the 3-machine FDSGS problem.

Factor	Level	Value
Number of groups	1	U [1,5]
	2	U [6,10]
	3	U [11,16]
Number of jobs in a group	1	U [2,4]
	2	U [5,7]
	3	U [8,10]
Setup times of machine Mi	1	M1 $\to$ U [1,50]	M2 $\to$ U [17,67]	M3 $\to$ U [45,95]
	2	M1 $\to$ U [17,67]	M2 $\to$ U [17,67]	M3 $\to$ U [17,67]
	3	M1 $\to$ U [45,95]	M2 $\to$ U [17,67]	M3 $\to$ U [1,50]
	4	M1 $\to$ U [1,50]	M2 $\to$ U [17,67]	M3 $\to$ U [17,67]
	5	M1 $\to$ U [1,50]	M2 $\to$ U [17,67]	M3 $\to$ U [1,50]
	6	M1 $\to$ U [17,67]	M2 $\to$ U [17,67]	M3 $\to$ U [45,95]
	7	M1 $\to$ U [17,67]	M2 $\to$ U [17,67]	M3 $\to$ U [1,50]
	8	M1 $\to$ U [45,95]	M2 $\to$ U [17,67]	M3 $\to$ U [45,95]
	9	M1 $\to$ U [45,95]	M2 $\to$ U [17,67]	M3 $\to$ U [17,67]

Table 5. Sub-benchmark of instances for the 6-machine FDSGS problem.

Factor	Level	Value
Number of groups	1	U [1,5]
	2	U [6,10]
	3	U [11,16]
Number of jobs in a group	1	U [2,4]
	2	U [5,7]
	3	U [8,10]
Setup times of machine Mi	1	M1 $\to$ U [1,50]	M2 $\to$ U [17,67]	M3 $\to$ U [45,95]	M4 $\to$ U [92,142]	M5 $\to$ U [170,220]	M6 $\to$ U [300,350]
	2	M1 $\to$ U [1,50]	M2 $\to$ U [1,50]	M3 $\to$ U [1,50]	M4 $\to$ U [1,50]	M5 $\to$ U [1,50]	M6 $\to$ U [1,50]
	3	M1 $\to$ U [300,350]	M2 $\to$ U [170,220]	M3 $\to$ U [92,142]	M4 $\to$ U [45,95]	M5 $\to$ U [17,67]	M6 $\to$ U [1,50]

Table 5. Sub-benchmark of instances for the 6-machine FDSGS problem.

Factor	Level	Value
Number of groups	1	U [1,5]
	2	U [6,10]
	3	U [11,16]
Number of jobs in a group	1	U [2,4]
	2	U [5,7]
	3	U [8,10]
Setup times of machine Mi	1	M1 $\to$ U [1,50]	M2 $\to$ U [17,67]	M3 $\to$ U [45,95]	M4 $\to$ U [92,142]	M5 $\to$ U [170,220]	M6 $\to$ U [300,350]
	2	M1 $\to$ U [1,50]	M2 $\to$ U [1,50]	M3 $\to$ U [1,50]	M4 $\to$ U [1,50]	M5 $\to$ U [1,50]	M6 $\to$ U [1,50]
	3	M1 $\to$ U [300,350]	M2 $\to$ U [170,220]	M3 $\to$ U [92,142]	M4 $\to$ U [45,95]	M5 $\to$ U [17,67]	M6 $\to$ U [1,50]

Table 6 illustrates the tested parameters, and denotes in bold the best combination of values, chosen after an ANOVA analysis [36] performed by means of Stat-Ease^® Design-Expert^® 7.0.0 commercial tool. As it can be noticed, four experimental factors have been tested at three different levels. Therefore, 3⁴ = 81 distinct configurations of GARS procedure have been considered, gaining a total of 135 × 81 = 10,935 experimental runs. GARS procedure has been coded in MATLAB^® language and executed on a 2 GB RAM virtual machine embedded on a workstation powered by two quad-core 2.39 GHz processors.

The response variable chosen for the calibration phase was the Relative Percentage Deviation (RPD) from the best heuristic solution available, calculated according to the following formula:

$$RPD=100\times \frac{GAR{S}_{sol}-Bes{t}_{sol}}{Bes{t}_{sol}} g=1,2\dots ,G$$

(4)

where GARS_sol is the solution provided by the heuristic procedure running with a certain combination of parameters, and Best_sol is the best solution among those provided by all configurations of GARS launched with reference to a given test problem.

Table 6. Genetic Algorithm with Random Sampling GARS experimental calibration.

Parameter	Notation	Values
Population size	Npop	(30, 50, 70)
Crossover probability	pcr	(0.5, 0.7, 0.9)
Mutation probability	pm	(0.05, 0.1, 0.2)
Size of the sub-population to be modified through BRS procedure	Nbest	($0.3\cdot N_{pop}$, $0.5\cdot N_{pop}$,$N_{pop}$)

Table 6. Genetic Algorithm with Random Sampling GARS experimental calibration.

Parameter	Notation	Values
Population size	Npop	(30, 50, 70)
Crossover probability	pcr	(0.5, 0.7, 0.9)
Mutation probability	pm	(0.05, 0.1, 0.2)
Size of the sub-population to be modified through BRS procedure	Nbest	($0.3\cdot N_{pop}$, $0.5\cdot N_{pop}$,$N_{pop}$)

5. Numerical Results

Once the calibration phase has been completed, an extensive comparison campaign has been performed in order to assess the performances of the proposed GARS against the latest alternative metaheuristic procedures proposed by the relevant literature in the field of FSDGS. To this end, the hybrid Particle Swarm Optimization (PSO) algorithm developed by Hajinejad, Salmasi and Mokhtari [27] and the hybridizing metaheuristic procedure combining genetic algorithm and simulated annealing (GSA) devised by Naderi and Salmasi [28] have been considered. The same experimental benchmark employed for the calibration phase has been adopted. This time, two distinct replicates have been randomly generated for each combination of experimental factors. Therefore, a total amount of 54 + 162 + 54 = 270 separate test cases have been created. Each instance has been solved by the three optimization procedures, running with a stopping criterion of N × M seconds of CPU time. On the whole, a number of 270 × 3= 810 experimental runs have been executed. In order to perform a fair comparison among the procedures considered, the Relative Percentage Deviation from the best heuristic solution has been computed for each algorithm and for each experimental instance as follows:

$$RPD=100\times \frac{AL{G}_{sol}-Bes{t}_{sol}}{Bes{t}_{sol}} g=1,2\dots ,G$$

(5)

where ALG_sol is the solution provided by a given algorithm with reference to a certain test problem and Best_sol is the best heuristic solution available for the same problem, i.e., the lowest total flow time value among those provided by the three aforementioned algorithms. The average random percentage deviations RPDs obtained by GARS, PSO, and GSA are reported in Table 7, Table 8 and Table 9. Each table refers to a given sub-benchmark of the proposed experimental design, at varying number of machines. Boldfaced values put in evidence the best average RPD the combination experimental factors changes.

Table 7. Average Random Percentage Deviation RPD values for two-machine problems.

Level of Factors			Average RPD
Number of groups	Number of jobs in a group	Setup times of machine Mi	GARS	PSO	GSA
1	1	1	0.000	0.000	0.000
1	1	2	0.000	1.033	0.061
1	1	3	0.000	2.337	11.527
1	2	1	0.000	0.599	0.158
1	2	2	0.245	1.044	1.430
1	2	3	0.000	1.644	9.532
1	3	1	0.000	0.976	0.406
1	3	2	0.000	0.653	2.378
1	3	3	0.053	0.956	2.774
2	1	1	0.000	0.049	0.000
2	1	2	0.000	0.051	0.013
2	1	3	0.000	2.265	13.402
2	2	1	0.000	0.016	0.064
2	2	2	0.000	0.505	0.460
2	2	3	0.000	3.979	10.625
2	3	1	0.000	0.246	0.294
2	3	2	0.000	0.576	0.497
2	3	3	0.000	1.243	5.488
3	1	1	0.000	0.021	0.000
3	1	2	0.034	0.153	3.093
3	1	3	1.624	0.000	6.121
3	2	1	0.000	0.000	0.000
3	2	2	0.000	1.027	2.141
3	2	3	0.816	0.210	1.678
3	3	1	0.000	0.156	0.254
3	3	2	0.000	1.156	1.444
3	3	3	0.000	1.948	5.737
average	-	-	0.103	0.846	2.947

Table 7. Average Random Percentage Deviation RPD values for two-machine problems.

Level of Factors			Average RPD
Number of groups	Number of jobs in a group	Setup times of machine Mi	GARS	PSO	GSA
1	1	1	0.000	0.000	0.000
1	1	2	0.000	1.033	0.061
1	1	3	0.000	2.337	11.527
1	2	1	0.000	0.599	0.158
1	2	2	0.245	1.044	1.430
1	2	3	0.000	1.644	9.532
1	3	1	0.000	0.976	0.406
1	3	2	0.000	0.653	2.378
1	3	3	0.053	0.956	2.774
2	1	1	0.000	0.049	0.000
2	1	2	0.000	0.051	0.013
2	1	3	0.000	2.265	13.402
2	2	1	0.000	0.016	0.064
2	2	2	0.000	0.505	0.460
2	2	3	0.000	3.979	10.625
2	3	1	0.000	0.246	0.294
2	3	2	0.000	0.576	0.497
2	3	3	0.000	1.243	5.488
3	1	1	0.000	0.021	0.000
3	1	2	0.034	0.153	3.093
3	1	3	1.624	0.000	6.121
3	2	1	0.000	0.000	0.000
3	2	2	0.000	1.027	2.141
3	2	3	0.816	0.210	1.678
3	3	1	0.000	0.156	0.254
3	3	2	0.000	1.156	1.444
3	3	3	0.000	1.948	5.737
average	-	-	0.103	0.846	2.947

Table 8. Average RPD values for three-machine problems.

Level of Factors			Average RPD
Number of groups	Number of jobs in a group	Setup times of machine Mi	GARS	PSO	GSA
1	1	1	0.000	0.000	0.000
1	1	2	0.000	0.388	1.841
1	1	3	1.297	0.000	6.550
1	1	4	0.000	0.215	0.051
1	1	5	0.000	0.392	1.745
1	1	6	0.317	1.495	4.575
1	1	7	0.000	0.389	0.288
1	1	8	0.662	0.282	0.167
1	1	9	0.199	0.000	2.637
1	2	1	0.000	0.946	0.000
1	2	2	0.000	0.000	0.092
1	2	3	0.438	1.575	7.851
1	2	4	0.000	0.000	0.000
1	2	5	0.000	1.065	0.138
1	2	6	0.000	1.287	6.672
1	2	7	0.000	1.025	0.210
1	2	8	0.000	1.153	1.147
1	2	9	0.000	2.348	2.968
1	3	1	0.000	0.000	0.000
1	3	2	0.000	0.621	1.084
1	3	3	0.000	1.112	6.562
1	3	4	0.000	0.282	0.165
1	3	5	0.000	0.518	1.233
1	3	6	0.000	1.096	2.454
1	3	7	0.000	0.597	0.147
1	3	8	0.000	1.091	0.445
1	3	9	0.000	2.039	5.476
2	1	1	0.000	0.415	0.000
2	1	2	0.326	0.000	1.145
2	1	3	0.000	0.408	6.590
2	1	4	0.000	0.260	0.032
2	1	5	0.017	0.349	1.089
2	1	6	0.318	0.578	4.110
2	1	7	0.442	1.356	0.064
2	1	8	0.000	0.984	1.734
2	1	9	0.000	1.732	3.991
2	2	1	0.000	0.091	0.000
2	2	2	0.000	0.294	0.624
2	2	3	0.000	0.723	10.149
2	2	4	0.000	0.030	0.114
2	2	5	0.000	0.599	1.343
2	2	6	0.550	0.376	3.401
2	2	7	0.000	0.535	0.336
2	2	8	0.132	0.409	0.415
2	2	9	0.000	1.768	2.571
2	3	1	0.000	0.000	0.000
2	3	2	0.000	0.436	0.527
2	3	3	0.212	0.189	2.433
2	3	4	0.000	0.007	0.136
2	3	5	0.000	0.334	0.696
2	3	6	0.000	0.987	5.687
2	3	7	0.052	1.019	0.061
2	3	8	0.000	1.412	0.998
2	3	9	0.000	1.023	3.635
3	1	1	0.000	0.000	0.000
3	1	2	0.000	0.231	0.035
3	1	3	1.955	0.005	5.798
3	1	4	0.000	1.477	0.289
3	1	5	0.000	0.604	0.361
3	1	6	0.000	1.599	6.493
3	1	7	0.000	1.001	0.221
3	1	8	0.000	1.263	0.596
3	1	9	0.000	1.622	3.721
3	2	1	0.000	0.000	0.000
3	2	2	0.000	0.164	2.327
3	2	3	1.146	1.220	5.157
3	2	4	0.000	0.155	0.000
3	2	5	0.000	0.681	0.918
3	2	6	0.000	2.853	7.268
3	2	7	0.000	0.424	0.226
3	2	8	0.006	1.103	0.188
3	2	9	0.225	0.190	3.545
3	3	1	0.000	0.000	0.000
3	3	2	0.000	0.276	0.023
3	3	3	0.000	0.484	5.681
3	3	4	0.000	0.000	0.054
3	3	5	0.035	0.194	0.431
3	3	6	0.000	1.781	5.212
3	3	7	0.000	0.774	0.106
3	3	8	0.000	0.312	0.328
3	3	9	0.000	1.325	3.354
average	-	-	0.103	0.691	1.959

Table 8. Average RPD values for three-machine problems.

Level of Factors			Average RPD
Number of groups	Number of jobs in a group	Setup times of machine Mi	GARS	PSO	GSA
1	1	1	0.000	0.000	0.000
1	1	2	0.000	0.388	1.841
1	1	3	1.297	0.000	6.550
1	1	4	0.000	0.215	0.051
1	1	5	0.000	0.392	1.745
1	1	6	0.317	1.495	4.575
1	1	7	0.000	0.389	0.288
1	1	8	0.662	0.282	0.167
1	1	9	0.199	0.000	2.637
1	2	1	0.000	0.946	0.000
1	2	2	0.000	0.000	0.092
1	2	3	0.438	1.575	7.851
1	2	4	0.000	0.000	0.000
1	2	5	0.000	1.065	0.138
1	2	6	0.000	1.287	6.672
1	2	7	0.000	1.025	0.210
1	2	8	0.000	1.153	1.147
1	2	9	0.000	2.348	2.968
1	3	1	0.000	0.000	0.000
1	3	2	0.000	0.621	1.084
1	3	3	0.000	1.112	6.562
1	3	4	0.000	0.282	0.165
1	3	5	0.000	0.518	1.233
1	3	6	0.000	1.096	2.454
1	3	7	0.000	0.597	0.147
1	3	8	0.000	1.091	0.445
1	3	9	0.000	2.039	5.476
2	1	1	0.000	0.415	0.000
2	1	2	0.326	0.000	1.145
2	1	3	0.000	0.408	6.590
2	1	4	0.000	0.260	0.032
2	1	5	0.017	0.349	1.089
2	1	6	0.318	0.578	4.110
2	1	7	0.442	1.356	0.064
2	1	8	0.000	0.984	1.734
2	1	9	0.000	1.732	3.991
2	2	1	0.000	0.091	0.000
2	2	2	0.000	0.294	0.624
2	2	3	0.000	0.723	10.149
2	2	4	0.000	0.030	0.114
2	2	5	0.000	0.599	1.343
2	2	6	0.550	0.376	3.401
2	2	7	0.000	0.535	0.336
2	2	8	0.132	0.409	0.415
2	2	9	0.000	1.768	2.571
2	3	1	0.000	0.000	0.000
2	3	2	0.000	0.436	0.527
2	3	3	0.212	0.189	2.433
2	3	4	0.000	0.007	0.136
2	3	5	0.000	0.334	0.696
2	3	6	0.000	0.987	5.687
2	3	7	0.052	1.019	0.061
2	3	8	0.000	1.412	0.998
2	3	9	0.000	1.023	3.635
3	1	1	0.000	0.000	0.000
3	1	2	0.000	0.231	0.035
3	1	3	1.955	0.005	5.798
3	1	4	0.000	1.477	0.289
3	1	5	0.000	0.604	0.361
3	1	6	0.000	1.599	6.493
3	1	7	0.000	1.001	0.221
3	1	8	0.000	1.263	0.596
3	1	9	0.000	1.622	3.721
3	2	1	0.000	0.000	0.000
3	2	2	0.000	0.164	2.327
3	2	3	1.146	1.220	5.157
3	2	4	0.000	0.155	0.000
3	2	5	0.000	0.681	0.918
3	2	6	0.000	2.853	7.268
3	2	7	0.000	0.424	0.226
3	2	8	0.006	1.103	0.188
3	2	9	0.225	0.190	3.545
3	3	1	0.000	0.000	0.000
3	3	2	0.000	0.276	0.023
3	3	3	0.000	0.484	5.681
3	3	4	0.000	0.000	0.054
3	3	5	0.035	0.194	0.431
3	3	6	0.000	1.781	5.212
3	3	7	0.000	0.774	0.106
3	3	8	0.000	0.312	0.328
3	3	9	0.000	1.325	3.354
average	-	-	0.103	0.691	1.959

Table 9. Average RPD values for six-machine problems.

Level of Factors			Average RPD
Number of groups	Number of jobs in a group	Setup times of machine Mi	GARS	PSO	GSA
1	1	1	0.000	0.000	0.000
1	1	2	0.000	0.024	0.015
1	1	3	0.000	0.120	3.982
1	2	1	0.000	0.031	0.015
1	2	2	0.000	0.160	0.418
1	2	3	0.314	0.075	2.316
1	3	1	0.000	0.126	0.108
1	3	2	0.000	0.146	0.944
1	3	3	0.132	0.171	1.769
2	1	1	0.012	0.145	0.000
2	1	2	0.000	0.677	0.000
2	1	3	1.092	0.057	5.610
2	2	1	0.000	0.630	0.083
2	2	2	0.526	1.359	0.802
2	2	3	0.000	3.110	3.778
2	3	1	0.027	0.682	0.184
2	3	2	0.000	2.838	0.722
2	3	3	0.000	2.050	4.169
3	1	1	0.000	0.000	0.000
3	1	2	0.000	0.048	0.018
3	1	3	0.000	0.154	0.818
3	2	1	0.000	0.000	0.000
3	2	2	0.000	0.169	0.309
3	2	3	0.000	0.265	0.608
3	3	1	0.000	0.349	0.071
3	3	2	0.000	0.506	0.418
3	3	3	0.000	0.395	1.748
average	-	-	0.078	0.529	1.071

Table 9. Average RPD values for six-machine problems.

Level of Factors			Average RPD
Number of groups	Number of jobs in a group	Setup times of machine Mi	GARS	PSO	GSA
1	1	1	0.000	0.000	0.000
1	1	2	0.000	0.024	0.015
1	1	3	0.000	0.120	3.982
1	2	1	0.000	0.031	0.015
1	2	2	0.000	0.160	0.418
1	2	3	0.314	0.075	2.316
1	3	1	0.000	0.126	0.108
1	3	2	0.000	0.146	0.944
1	3	3	0.132	0.171	1.769
2	1	1	0.012	0.145	0.000
2	1	2	0.000	0.677	0.000
2	1	3	1.092	0.057	5.610
2	2	1	0.000	0.630	0.083
2	2	2	0.526	1.359	0.802
2	2	3	0.000	3.110	3.778
2	3	1	0.027	0.682	0.184
2	3	2	0.000	2.838	0.722
2	3	3	0.000	2.050	4.169
3	1	1	0.000	0.000	0.000
3	1	2	0.000	0.048	0.018
3	1	3	0.000	0.154	0.818
3	2	1	0.000	0.000	0.000
3	2	2	0.000	0.169	0.309
3	2	3	0.000	0.265	0.608
3	3	1	0.000	0.349	0.071
3	3	2	0.000	0.506	0.418
3	3	3	0.000	0.395	1.748
average	-	-	0.078	0.529	1.071

The obtained results confirm the effectiveness of GARS in solving the FSDGS problem at hand. With reference to two-machine problems (See Table 7), the proposed algorithm achieves the best average RPD 25 times out of 27. Its performance is strengthen by the lowest grand average RPD value equal to 0.103, against PSO and GSA that gain 0.846 and 2.947, respectively. The same trend in terms of grand average RPD values may be observed for problems with three-machines (See Table 8), according to which GARS assures the best average RPD 72 times out of 81, while PSO and GSA gather with 16 and 13 wins, respectively. As far as six-machine problems are concerned, GARS still reports the best performances, providing the lowest average RPD 24 times out of 27 and a grand average RPD significantly lower than PSO and GSA.

In order to infer some statistical conclusion over the difference observed among the tested algorithms, an ANOVA analysis has been performed by means of Stat-Ease^® Design-Expert^® 7.0.0 version commercial tool, calculating Least Significant Difference (LSD) intervals at 95% confidence level for the RPDs connected to each optimization procedure. The corresponding chart (see Figure 6) clearly shows how GARS outperforms PSO and GSA in a statistically significant manner, as no any overlap among the LSD bars connected to the tested algorithms exists.

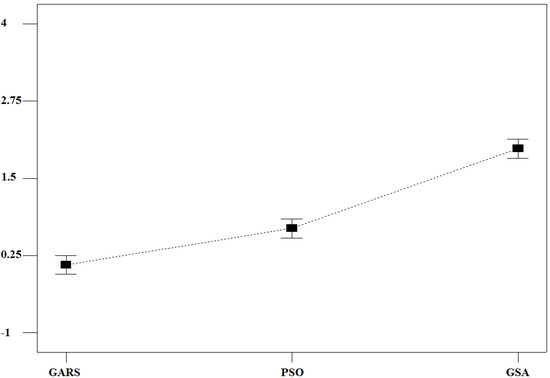
Figure 6. LSD bar chart at 95% confidence level.

Figure 6. LSD bar chart at 95% confidence level.

6. Conclusions

In this paper, a hybrid metaheuristic procedure integrating features from genetic algorithms and biased random sampling local search has been proposed with the aim of minimizing the total flow time in a classical scheduling issue emerging from cellular manufacturing environments, i.e., the flow-shop sequence-dependent group-scheduling problem. Thanks to the matrix-encoding scheme employed, the proposed metaheuristic procedure can simultaneously manage a twofold combinatorial problem: sequencing of groups and sequencing of jobs within each group to be processed. Stochastic selection mechanisms among two distinct crossover operators and two mutation techniques have been considered. Furthermore, a random sampling local search scheme has been embedded for enhancing the exploitation phase of the genetic framework.

The proposed procedure has been validated against two recent metaheuristic techniques emerging from the relevant literature in the field of FSDGS problem. To this end, a well-known benchmark of test cases has been employed. An extensive comparison campaign, supported by a properly developed ANOVA analysis, demonstrated the superiority of the proposed approach.

Future research could include the application of the proposed GARS algorithm to other scheduling problems in the field of group scheduling issues, e.g., single machine or flow shop with multi-processors. Considering pre-emptions, i.e., interruptions of job processing operations due to the arrival of higher-priority jobs or groups at the system, could be an interesting direction for further analysis, as well. In alternative, other metaheuristic techniques like ant-colony and immune systems algorithm may be compared with the proposed GARS as to further validate its effectiveness in solving FSDGS problems.