Pareto Optimization or Cascaded Weighted Sum: A Comparison of Concepts
Abstract
:1. Introduction
2. Short Introduction to Pareto Optimization and Two Aggregation Methods
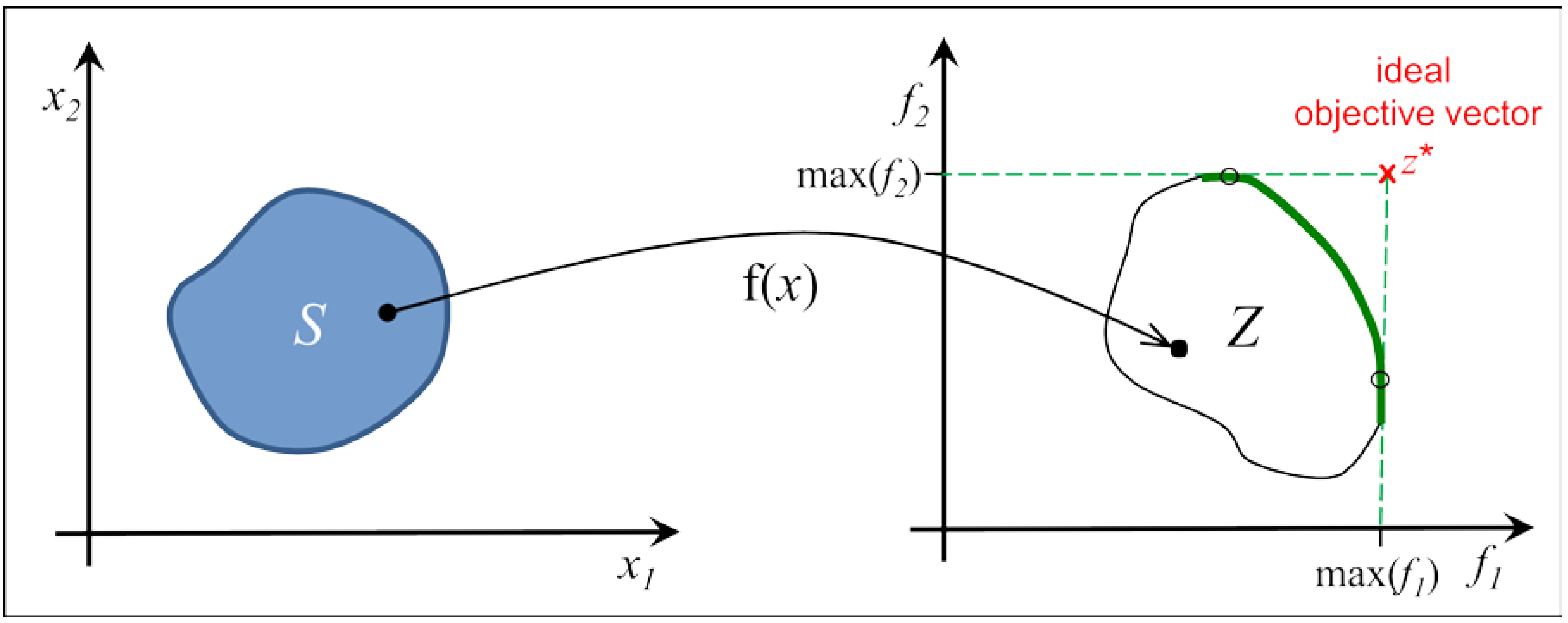
2.1. Pareto Optimization
- Solution x is feasible and y is not.
- Both solutions are feasible and x dominates y.
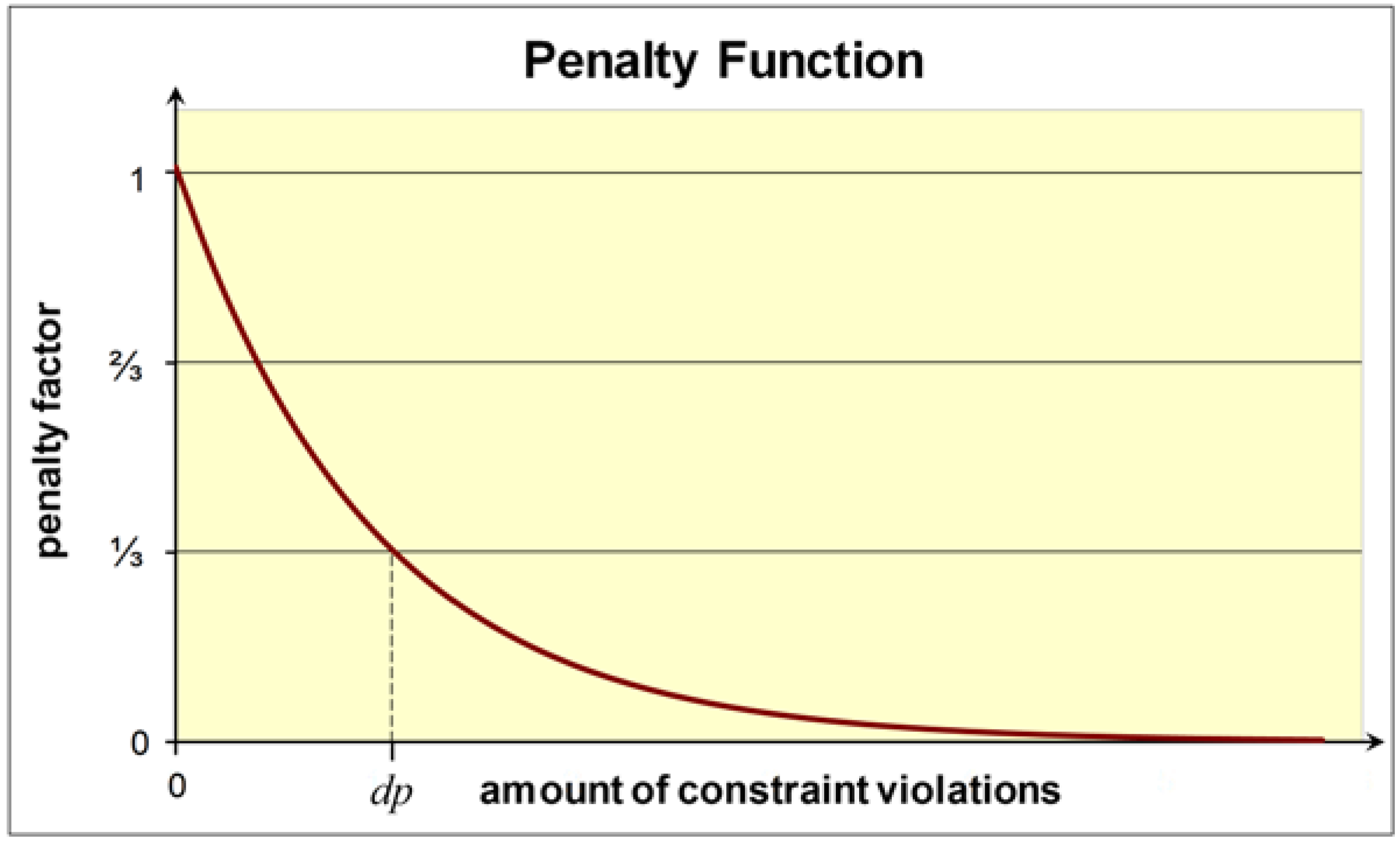
- Both solutions are infeasible, but x has a smaller constrained violation than y. If more than one constraint is violated, the violations are normalized, summed up, and compared.
2.2. Weighted Sum
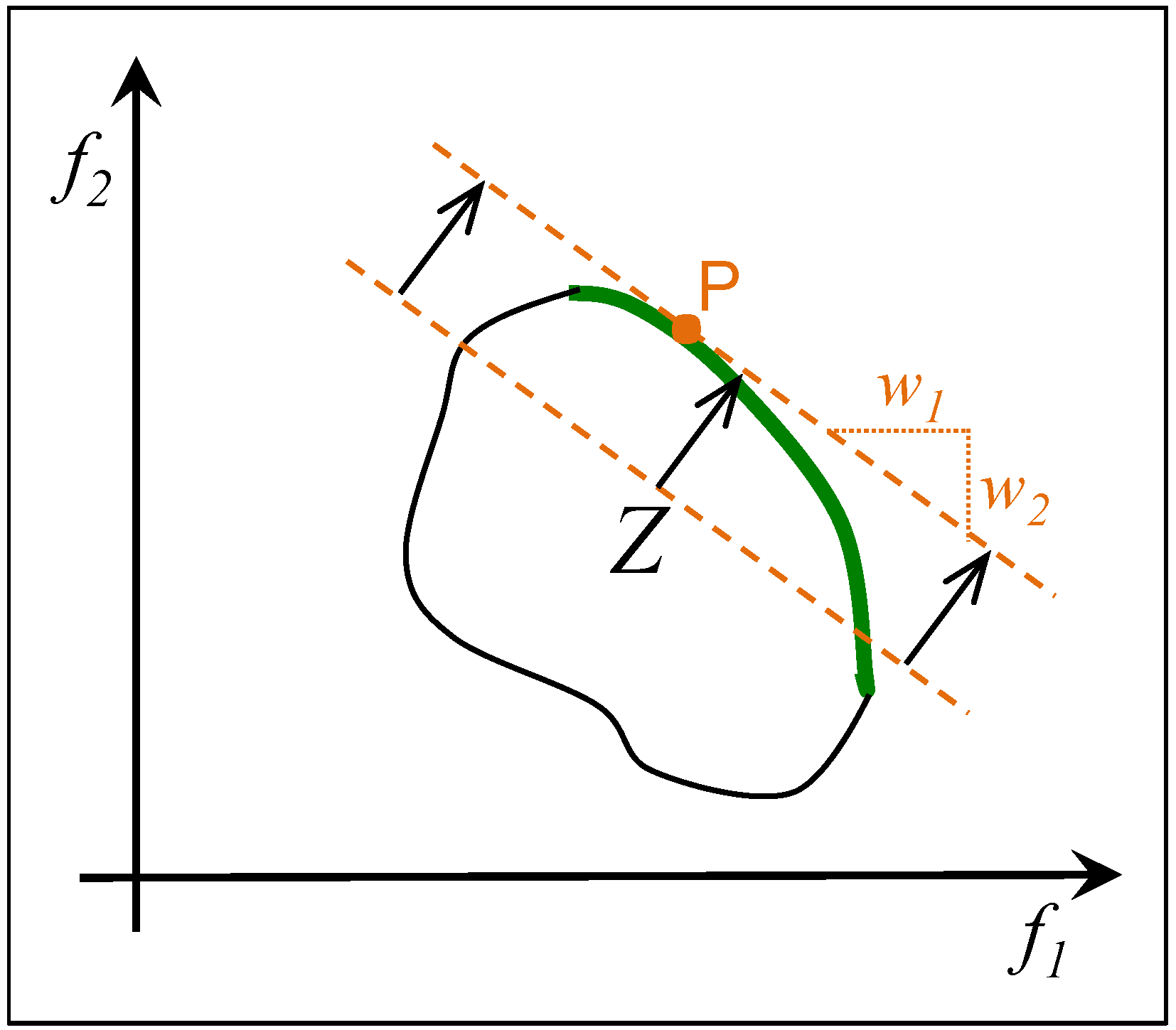
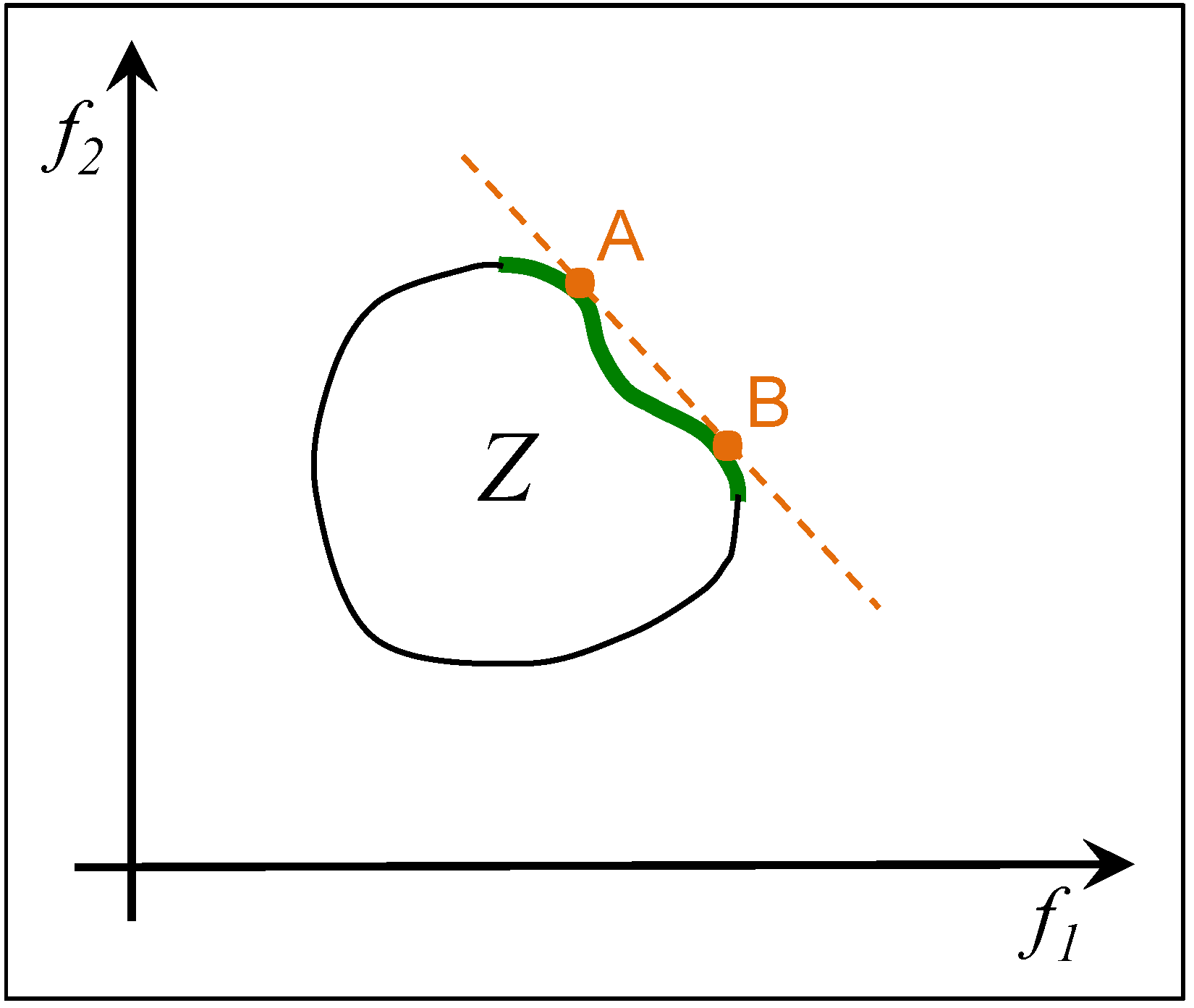
2.3. ε-Constrained Method
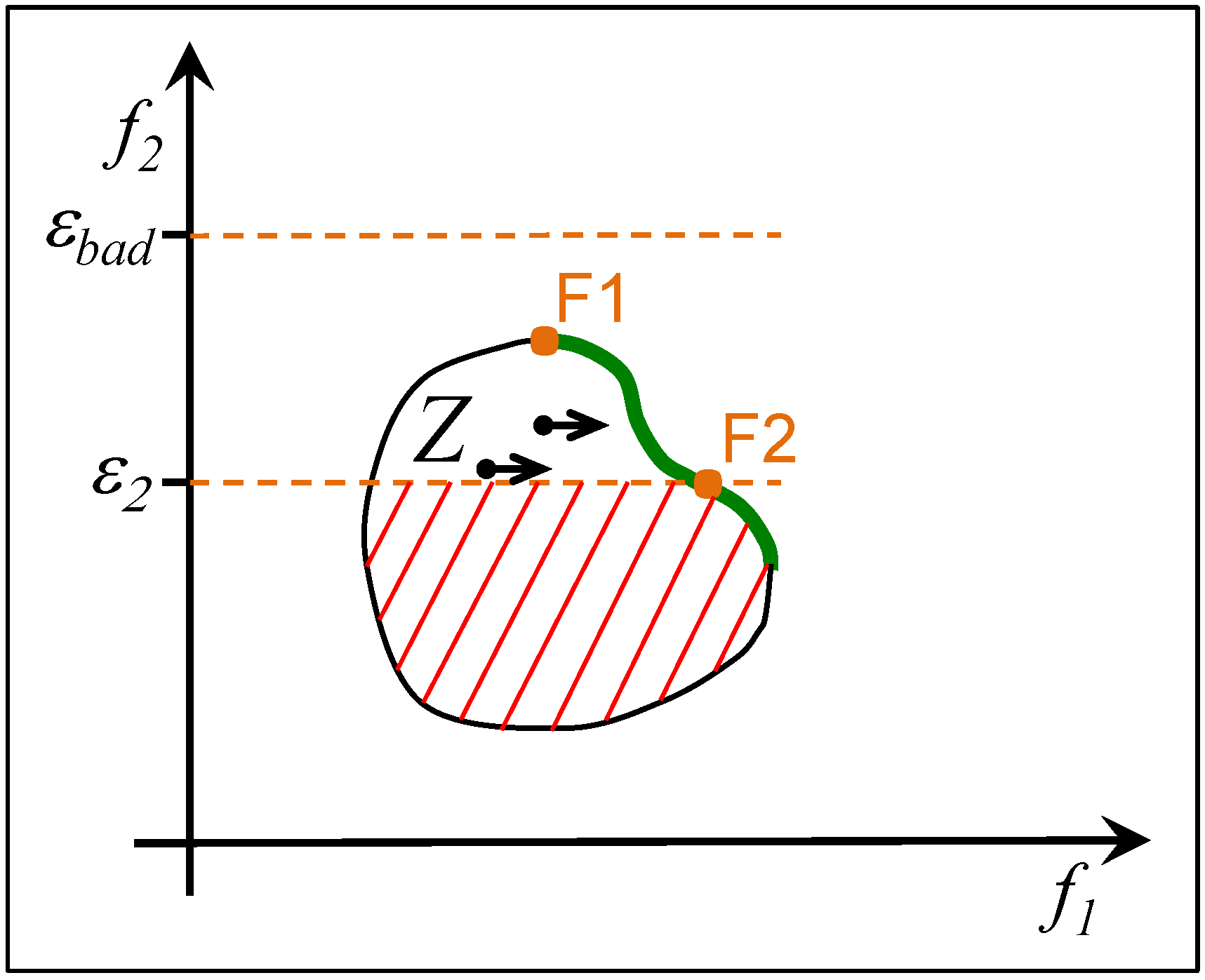
2.4. Summary
3. Cascaded Weighted Sum
3.1. Short Introduction to Evolutionary Algorithms and GLEAM
3.2. Definition of the Cascaded Weighted Sum

3.3. Example of the CWS
| Priority | Objective | Weight [%] | Threshold εi |
|---|---|---|---|
| 1 | job time | 30 | 0.4 |
| 1 | job costs | 40 | 0.25 |
| 2 | makespan | 20 | - |
| 2 | utilization rate | 10 | - |
3.4. The Effect of the CWS on the Search
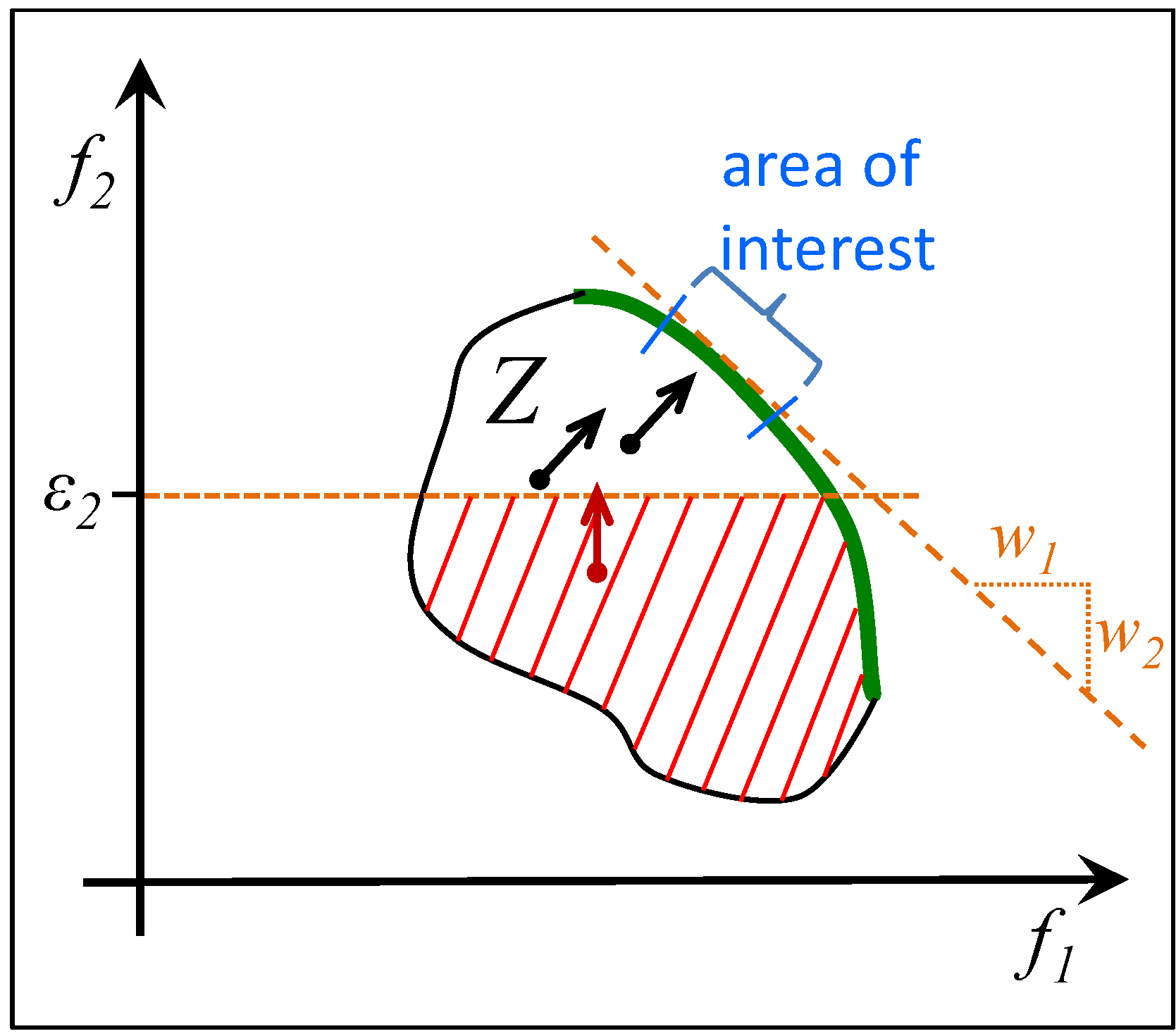
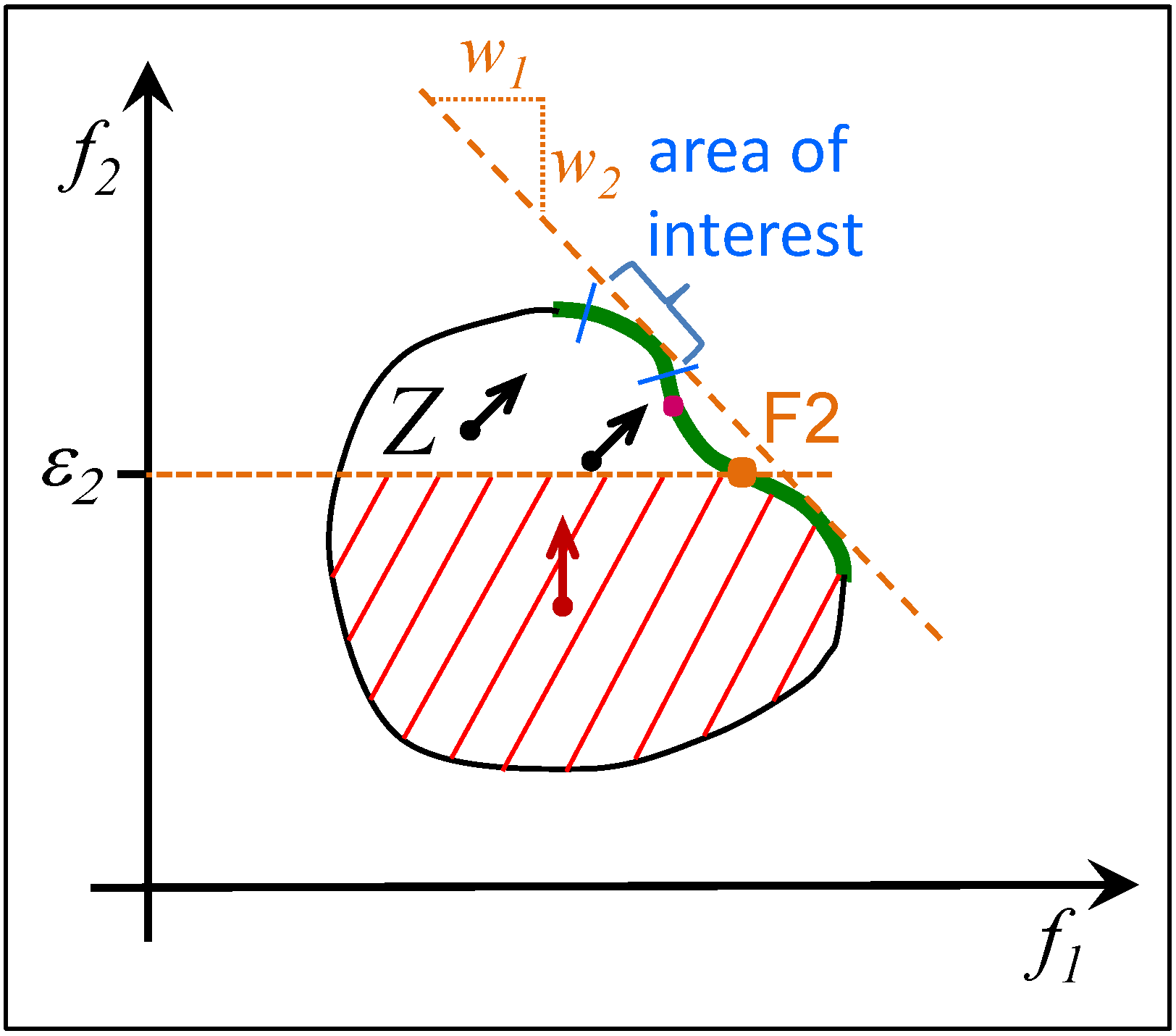

3.5. Summary
4. Cascaded Weighted Sum and Its Field of Application
4.1. Number of Objectives

4.2. Classification of Application Scenarios and Examples
- The nonrecurring type, which is performed once with little or no prior knowledge of e.g., the impact and relevance of decision variables or the behavior of objectives. This type requires many decisions regarding e.g., the number and ranges of decision variables, the number and kind of objectives, of restrictions, and more.
- The extended nonrecurring project, where some variants of the first optimization task are handled as well. Frequently, the modifications of the original project are motivated by the experience gained in the first optimization runs. As in the first type, decisions are usually made by humans.
- The recurring type, usually based on experience gained from a predecessor project and frequently part of an automated process without or with minor human interaction only.
4.3. Comparison of Pareto Optimization and CWS in Different Application Scenarios
4.3.1. Individual Optimization Project
4.3.2. Optimization Project with Some Task Variants
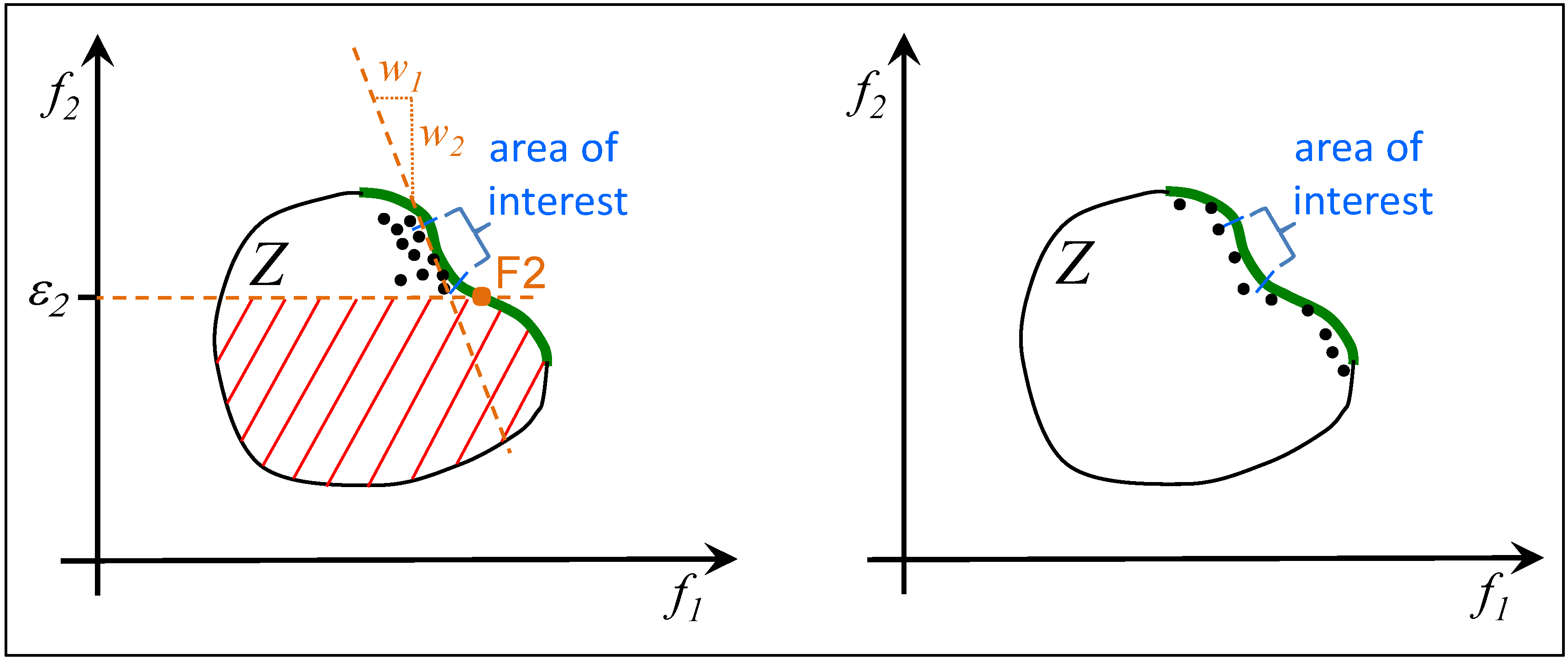
4.3.3. Repeated Optimization, also as Part of an Automated Process
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Pareto, V. Cours d’Économie Politique; (in French). F. Rouge: Lausanne, Switzerland, 1896. [Google Scholar]
- Hoffmeister, F.; Bäck, T. Genetic Algorithms and Evolution Strategies: Similarities and Differences; Technical Report SYS-1/92; FB Informatik, University of Dortmund: Dortmund, Germany, 1992. [Google Scholar]
- Multiobjective Optimization: Interactive and Evolutionary Approaches; Lecture notes in computer science 5252; Branke, J.; Deb, K.; Miettinen, K.; Słowiński, R. (Eds.) Springer: Berlin, Germany, 2008.
- Deb, K. Introduction to evolutionary multiobjective optimization. In Multiobjective Optimization: Interactive and Evolutionary Approaches; Branke, J., Deb, K., Miettinen, K., Słowiński, R., Eds.; Lecture notes in computer science 5252; Springer: Berlin, Germany, 2008; pp. 58–96. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; International series in operations research & management science 12; Kluwer Academic Publishers: Boston, MA, USA, 1999. [Google Scholar]
- Jakob, W.; Strack, S.; Quinte, A.; Bengel, G.; Stucky, K.-U.; Süß, W. Fast rescheduling of multiple workflows to constrained heterogeneous resources using multi-criteria memetic computing. Algorithms 2013, 2, 245–277. [Google Scholar] [CrossRef]
- Haimes, Y.Y.; Lasdon, L.S.; Wismer, D.A. On a bicriterion formulation of the problems of integrated system identification and system optimization. IEEE Trans. Syst. Man Cybern. 1971, 3, 296–297. [Google Scholar]
- Osyczka, A. Multicriterion Optimization in Engineering with FORTRAN Programs; Ellis Horwood series in mechanical engineering; E. Horwood: London, UK, 1984. [Google Scholar]
- Miettinen, K. Introduction to multiobjective optimization: Noninteractive approaches. In Multiobjective Optimization: Interactive and Evolutionary Approaches; Branke, J., Deb, K., Miettinen, K., Słowiński, R., Eds.; Lecture notes in computer science 5252; Springer: Berlin, Germany, 2008; pp. 1–26. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 2, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength pareto evolutionary algorithm for multiobjective optimization. In Evolutionary Methods for Design Optimization and Control with Applications to Industrial Problems, Proceedings of the EUROGEN’2001 Conference, Athens, Greece, 19–21 September 2001; Giannakoglou, K.C., Tsahalis, D.T., Périaux, J., Papailiou, K.D., Fogarty, T., Eds.; International Center for Numerical Methods in Engineering: Athens, Greece, 2001; pp. 95–100. [Google Scholar]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 3, 1653–1669. [Google Scholar] [CrossRef]
- Blume, C. GLEAM—A system for simulated “intuitive learning”. In Parallel Problem Solving from Nature: Proceedings of the 1st Workshop, Dortmund, Germany, 1–3 October 1990; Schwefel, H.-P., Männer, R., Eds.; Lecture notes in computer science 496. Springer: Berlin, Germany, 1991; pp. 48–54. [Google Scholar]
- Blume, C.; Jakob, W.; Krisch, S. Robot trajectory planning with collision avoidance using genetic algorithms and simulation. In Proceedings of the 25th International Symposium on Industrial Robots (ISIR), Hanover, Germany, 25–27 April, 1994; pp. 169–175.
- Blume, C.; Jakob, W. GLEAM—General Learning Evolutionary Algorithm and Method. Ein evolutionärer Algorithmus und seine Anwendungen; (in German); Schriftenreihe des Instituts für Angewandte Informatik, Automatisierungstechnik am Karlsruher Institut für Technologie 32. KIT Scientific Publishing: Karlsruhe, Germany, 2009. [Google Scholar]
- Gorges-Schleuter, M. Explicit parallelism of genetic algorithms through population structures. In Proceedings of the 1st Workshop on Parallel Problem Solving from Nature (PPSN I), Dortmund, Germany, 1–3 October 1990; Schwefel, H.-P., Männer, R., Eds.; LNCS 496, Springer: Berlin, Germany, 1991; pp. 150–159. [Google Scholar]
- Sarma, K.; de Jong, K. An analysis of the effects of neighborhood size and shape on local selection algorithms. In Proceedings of the 4th International Conference on Parallel Problem Solving from Nature (PPSN IV), LNCS 1141, Berlin, Germany, 22–26 September 1996; Voigt, H.-M., Ebeling, W., Rechenberg, I., Schwefel, H.-P., Eds.; Springer: Berlin, Germany, 1996; pp. 236–244. [Google Scholar]
- Nguyen, Q.H.; Ong, Y.-S.; Lim, M.H.; Krasnogor, N. Adaptive cellular memetic algorithms. Evol. Comput. 2009, 17, 231–256. [Google Scholar]
- Jakob, W. A general cost-benefit-based adaptation framework for multimeme algorithms. Memet. Comput. 2010, 3, 201–218. [Google Scholar] [CrossRef]
- Lotov, A.V.; Miettinen, K. Visualizing the Pareto Frontier. In Multiobjective Optimization: Interactive and Evolutionary Approaches; Branke, J., Deb, K., Miettinen, K., Słowiński, R., Eds.; Lecture notes in computer science 5252; Springer: Berlin, Germany, 2008; pp. 213–243. [Google Scholar]
- Klamroth, K.; Tind, J.; Wiecek, M.M. Unbiased approximation in multicriteria optimization. Math. Method Oper. Res. 2003, 3, 413–437. [Google Scholar] [CrossRef]
- Jakob, W.; Gorges-Schleuter, M.; Sieber, I.; Süß, W.; Eggert, H. Solving a highly multi-modal design optimization problem using the extended genetic algorithm GLEAM. In Computer Aided Optimum Design of Structures VI: Conf. Proc. OPTI 99; Hernandez, S., Kassab, A.J., Brebbia, C.A., Eds.; WIT Press: Southampton, UK, 1999; pp. 205–214. [Google Scholar]
- Stewart, T.; Bandte, O.; Braun, H.; Chakraborti, N.; Ehrgott, M.; Göbelt, M.; Jin, Y.; Nakayama, H.; Poles, S.; di Stefano, D. Real-world applications of multiobjective optimization. In Multiobjective Optimization: Interactive and Evolutionary Approaches; Branke, J., Deb, K., Miettinen, K., Słowiński, R., Eds.; Lecture notes in computer science 5252; Springer-Verlag: Berlin, Germany, 2008; pp. 285–327. [Google Scholar]
- Blume, C. Automatic Generation of Collision Free Moves for the ABB Industrial Robot Control. In Proceedings of the 1997 First International Conference on Knowledge-Based Intelligent Electronic Systems (KES ’97), Adelaide, SA, Australia, 21–23 May 1997; Volume 2, pp. 672–683.
- Blume, C. Optimized Collision Free Robot Move Statement Generation by the Evolutionary Software GLEAM. In Real World Applications of Evolutionary Computing: Proceedings; Cagnoni, S., Ed.; Lecture notes in computer science 1803; Springer: Berlin, Germany, 2000; pp. 327–338. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jakob, W.; Blume, C. Pareto Optimization or Cascaded Weighted Sum: A Comparison of Concepts. Algorithms 2014, 7, 166-185. https://doi.org/10.3390/a7010166
Jakob W, Blume C. Pareto Optimization or Cascaded Weighted Sum: A Comparison of Concepts. Algorithms. 2014; 7(1):166-185. https://doi.org/10.3390/a7010166
Chicago/Turabian StyleJakob, Wilfried, and Christian Blume. 2014. "Pareto Optimization or Cascaded Weighted Sum: A Comparison of Concepts" Algorithms 7, no. 1: 166-185. https://doi.org/10.3390/a7010166
APA StyleJakob, W., & Blume, C. (2014). Pareto Optimization or Cascaded Weighted Sum: A Comparison of Concepts. Algorithms, 7(1), 166-185. https://doi.org/10.3390/a7010166




