1. Introduction
In the stable marriage problem of Gale and Shapley [
1], there are
n men and
n women, and each person ranks the members of the opposite gender arbitrarily according to an individual strict preference order. A
marriage scheme in this model is a set of marriages between different men and women. Such a scheme is
unstable if there exists a
blocking pair, that is, a man
m and a woman
w, such that
m is either unmarried or
m prefers
w to his wife, and at the same time,
w is either unmarried or prefers
m to her partner. A marriage scheme is
stable if it is not unstable, that is, not blocked by any pair. It is a natural problem to find a stable marriage scheme if it exists at all. Nowadays, it is already folklore that for any preference rankings of the
n men and
n women, a stable marriage scheme does exist. This theorem was proved first by Gale and Shapley in [
1]. They constructed a special stable marriage scheme with the help of a finite procedure, the so-called deferred acceptance algorithm. It also turned out that for the existence of a stable scheme, it is not necessary that the number of men is the same as the number of women or that for each person, all members of the opposite group are acceptable: the deferred acceptance algorithm is so robust, that it works properly under these more general conditions.
Several interesting properties of the structure of stable marriage schemes are known. Donald Knuth [
2] attributes to John Conway the observation that stable marriages have a lattice structure: if each man picks the better assignment out of two stable marriage schemes, then another stable marriage scheme is created in which each woman receives the worst partner out of the two.
There are further known extensions of the stable marriage problem. Baïou and Balinski proved in [
3] that if each edge of the underlying bipartite graph has a nonnegative capacity and each vertex has a nonnegative quota, then the accordingly modified deferred acceptance algorithm always finds a so-called stable allocation. An allocation is an assignment of nonnegative values to the edges that do not exceed the corresponding capacities, such that the total allocation of no vertex exceeds its quota. In other words, an allocation is a marriage scheme where a bipartite marriage can be formed with an “intensity” different from zero and one, and each participant has an individual upper bound on his/her total “marriage intensity”. An allocation is stable if any unsaturated edge,
e, has a saturated end vertex,
v, such that each edge,
, incident with
v has an assigned value of zero whenever
v prefers
e to
. That is, if the intensity of a marriage is not maximum, then one of the spouses has maximum total marriage intensity, and none of his/her marriages is worse than the particular marriage. Beyond proving the existence of stable assignments, Baïou and Balinski used flow-type arguments to speed up the deferred acceptance algorithm in [
3]. Later, Dean and Munshi came up with an even faster network flow based algorithm for the same problem [
4].
It is fairly well-known that the bipartite matching problem can be formulated in the more general network flow model, and the alternating path algorithm for maximum bipartite matchings is a special case of the augmenting path algorithm of Ford and Fulkerson for maximum flows. However, it seems that the question of whether there exists a flow generalization of the stable marriage theorem has not been addressed so far. This very problem is the focus of our present work. It turned out that our model is closely related to so-called “supply chains” well known in the economics literature. Prior to our work, Ostrovsky published a related result in [
5]. The main difference between Ostrovsky’s and our model is that Ostrovsky’s one is acyclic and discrete, whereas ours allows cycles and has a fractional formulation, as well. There is however a feature of Ostrovsky’s model in which it is far more general than ours: instead of the Kirchhoff’s law, it only requires a less restrictive property called “same-side substitutability” and “cross-side complementarity”. Ostrovsky proved the existence of a “chain stable network” and justified that “chain stable networks” form a lattice under a natural partial order. These results are very close to ours and cry for a common generalization that is the subject of ongoing research. Later on, Hatfield and Kominers proved a generalization of Ostrovsky’s result in [
6], where the generalized model is still discrete and acyclic. The authors prove that a stable allocation always exists in their model and that acyclicity is necessary for stability. Our result is that there always exists a stable flow in any network, so also in non-acyclic ones. The reason for this difference is that our stability concept differs from that of Hatfield and Kominers: theirs corresponds to our complete stability notion. In this present work, we show that this latter result of Hatfield and Kominers also holds in our more restricted setting by exhibiting an instance in which no completely stable flow exists.
After the original versions of our present work ([
7,
8]), Hatfield
et al. generalized the Hatfield-Kominers result [
6] in [
9] to a “half-discrete” model (prices are arbitrary, but trading is done with integral amounts of goods) that allows cycles. The authors claim that under full substitutable preferences, there always exists a competitive equilibrium that corresponds to a stable outcome.
Note that Westerkamp has also proved some related results. In [
10], he studied the relation between the existence of solutions satisfying different stability criteria and the acyclicity and so-called bundling property of the particular market structures.
This present work is organized as follows. In
Section 2, we formulate the stable flow problem and give an alternative fixed point proof of the result of [
3] by Baïou and Balinski on stable allocations.
Section 3 contains the stable flow theorem, a generalization of the Gale–Shapley theorem to flows. Our reduction of the stable flow problem to the stable allocation problem resembles the reduction of the maximum flow problem to the maximum
b-matching problem. Actually, our construction has to do also with the one that Cechlárová and Fleiner used in [
11] to extend the stable roommates model to a multiple partner model.
Section 4 is devoted to certain structural results on stable flows; in particular, we show the consequences of the lattice structure of stable marriages. To achieve this, we lean on the construction we used for the reduction. We conclude in the last section by describing some generalizations of stable flows that can be handled with our method and by asking some open problems. In particular, we indicate that our results can easily be extended from the flow model to one where instead of two terminals, we have several.
2. Preliminaries
Recall that by a network, we mean a quadruple , where is a digraph, s and t are different nodes of D, and is a function that determines the capacity, , of each arc, a, of A. (Sometimes it is assumed that no arc enters vertex s and no arc leaves vertex t. We do not require this assumption for the reason that this way, we prove a more general result. Still, if the reader finds it difficult to follow the argument, it might be convenient to consider the source-sink case and skip the irrelevant parts.) Vertices s and t are called terminals; other vertices of G are nonterminals. A flow of the network is a function , such that the capacity condition holds for each arc, a, of A and each nonterminal vertex, v, of D satisfies the Kirchhoff law: , that is, the amount of the incoming flow equals the amount of the outgoing flow for v. Note that there is no conceptual difference between terminals s and t: both are ordinary vertices that are exempt from Kirchhoff’s law. (It seems that this fact is not completely clear for many. Perhaps, the reason is that when network flows are taught, it is usually emphasized that the role of s and t are different: the former is “the source”, and the latter one is “the sink”. To convince the skeptic, it is illuminative to find a formula for the minimum value of an -flow in a network. Surprisingly to some, this minimum is not zero in general.)
A network with preferences is a network along with a preference order, , for each vertex, v, such that is a linear order on the arcs that are incident to v, and we say that v prefers a to if holds. (Note that preference orders and of the terminals do not play a role in the notion of stability, as we shall never compare an incoming and an outgoing arc of the same vertex. Therefore, we may think that for each nonterminal vertex, v, there are two independent preference orders: one is on the incoming arcs and the other one on the outgoing ones.) For a given network with preferences, it is convenient to think that vertices of D are “players” that trade with a certain good. An arc of D from player u to player v with capacity represents the possibility that player u can supply at most units of goods to player v. A “trading scheme” is described by a flow, f, of the network, as for any two players, u and v, flow determines the amount of goods that u sells to v. Everybody in the market would like to trade as much as possible, that is, each player v strives to maximize the amount of flow through v. In particular, if flow f allows player v to receive some more flow (that is, there are goods on the market offered to v and v is happy to buy them) and v can also send some more flow (i.e., some other player would be happy to buy more goods from v), then flow f does not correspond to a stable market situation.
Another instability occurs when (player v prefers to sell to w rather than to u), and flow f is such that w would be happy to buy more goods from v (that is , and w has some extra selling opportunity); moreover, (v sells a positive amount of goods to u). In this situation, v would send flow rather to w than to u; hence, this cannot occur in a stable market situation. A similar instability can be described if we talk about entering arcs instead of outgoing ones, that is, if we exchange the roles of buying and selling.
To formalize our concept of stability, we need a few definitions. For a network
and flow
f, we say that arc
a is
f-unsaturated if
, that is, if it is possible to send some extra flow through
a. A
blocking walk of flow f is a directed walk
, such that
and
(
) and the following properties hold.
Therefore, directed walk
P is blocking if each player that corresponds to an inner vertex of
P is happy and capable of increasing the flow along
P. Moreover,
can send extra flow, either because
is a terminal node or because
may decrease the flow toward some vertex,
u, that
prefers less than
, and at last,
can receive some extra flow, either because either
is a terminal node or
can refuse flow from
w, which
ranks below
. We say that a walk,
P, is
f-unsaturated if property Equation (
3) holds for each arc,
, of
P. An
f-unsaturated walk
is
f-dominated at if Equation (
4) does not hold, and
P is
f-dominated at if Equation (
5) does not hold. A flow,
f, of a network with preferences is
stable if no blocking walk of
f exists. In the
stable flow problem, we have given a network with preferences, and our task is to find a stable flow if it exists.
A special case of the stable flow problem is the stable allocation problem of Baïou and Balinski [
3]. The
stable allocation problem is defined by finite disjoint sets
W and
F of workers and firms, a map,
, a set,
E, of edges between
W and
F, along with a map,
, and for each worker or firm,
, a linear order,
, on those pairs of
E that contain
v. We shall refer to pairs of
E as “edges”, and hopefully, it will not cause ambiguity. Quota
denotes the maximum of total assignment that worker or firm
v can accept, and capacity
of edge
means the maximum allocation that worker
w can be assigned to firm
f along
e. An
allocation is a nonnegative map,
, such that
holds for each
, and for any
, we have:
that is, the total assignment,
, of player
v cannot exceed quota
of
v. If Equation (
6) holds with equality, then we say that player
v is
g-saturated. An allocation is
stable if for any edge,
, of
E, at least one of the following properties hold:
Note that Equations (
8) and (
9) imply that if
g is a stable allocation, then for each firm,
f, and each worker,
w:
If
and
are allocations and
is a worker, then we say that
allocation dominates allocation for worker w (in notation,
) if one of the following properties is true:
That is, if
w can freely choose his allocation from
, then
w would choose
, either because
and
are identical for
w or because
w is saturated in both allocations and
represents
w’s choice out of
. By exchanging the roles of workers and firms, one can define domination relation
for any firm,
f, as well.
For any stable allocation problem, one can design a network
, such that
,
, and
,
and
for any worker
w and firm
f. That is, we consider the underlying bipartite graph, orient its edges from
W to
F, add new vertices,
s and
t, with an arc from
s to each worker-node and an arc from each firm-node to
t, and capacities are given by the original edge-capacities and the corresponding quotas. Preference orders
on the arcs incident to
v are induced by the preference order on the corresponding edges incident to
v, or, if there is no such edge, then it is a trivial linear order. It is straightforward to see from the definitions that
g is a stable allocation if and only if there exists a stable flow
f, such that
holds for each edge,
, where
is the arc that corresponds to edge
e. The stable allocation problem was introduced by Baïou and Balinski as a certain “continuous” version of the stable marriage problem in [
3]. It turned out that a natural extension of the deferred acceptance algorithm of Gale and Shapley [
1] works for the stable allocation problem, and the structure of stable allocations is similar to that of stable marriages. Below, we state the results of Baïou-Balinski.
Theorem 1 (See Baïou and Balinski [
3]).
1. In any stable allocation problem instance described by and q, there exists a stable allocation, g. Moreover, if p and q are integral, then there exists an integral stable allocation, g. 2. If and are stable allocations and , then or holds.
3. Stable allocations have a natural lattice structure. Namely, if and are stable allocations, then and are stable allocations, where:In other words, if workers choose from two stable allocations, then we get another stable allocation, and this is also true for the firms’ choices. Moreover, it is true that:That is, in stable allocation , where each worker picks his better assignment, each firm receives the worst out of the two. Similarly, in , the choice of the firms means the less preferred situation for the workers. The interested reader may find an alternative proof of Theorem 1 in [
7] that illustrates the use of two powerful tools: the fixed-point approach and the application of graph theory.
3. Stable Flows
Our goal in this section is to prove a generalization of Theorem 1. The “natural” approach to achieve this would be an appropriate generalization of the deferred acceptance algorithm of Gale and Shapley. The difficulty is that though the Gale–Shapley algorithm can handle quota function q, somehow, it has problems with ensuring Kirchhoff’s law.
Theorem 2. If network and preference orders describe a stable flow problem, then there always exists a stable flow, f. If capacity function c is integral, then there exists an integral stable flow.
Note that it is possible to prove Theorem 2 by a mixture of the deferred acceptance algorithm and the augmenting path algorithm. That is, starting from some terminal vertex, we follow a “first choice walk” until they arrive to some terminal vertex. We augment along this walk while observing the capacity constraints and iterate. If a vertex has no more outgoing capacity, then some amount of flow is refused by the receiving vertex, and we try to reroute the flow excess from the starting point of the refused arc (that might be different from the last arc of the current path). We have a stable flow as soon as we cannot find an augmenting path between terminals.
Our proof of Theorem 2 follows a different approach for two reasons. On the one hand, it seems that in the area of stable matchings, neither the reduction of one problem to another nor the use of graph terminology is routine. We demonstrate here that these methods may be fruitful. On the other hand, the “deferred augmentation” algorithm we sketched above does not give much information about the rich structure of stable flows that easily follows from the lattice property of stable allocations.
With the help of the given instance of the stable flow problem, we shall define a particular instance of the stable allocation problem. For each vertex,
v, of
D, calculate:
that is,
is the maximum total capacity of those arcs of
D that enter and leave
v. Therefore,
is an upper bound on the amount of flow that can flow through vertex
v. Choose
. Construct graph
as follows. Split each vertex,
v, of
D into two distinct vertices,
and
, and for each arc,
, of
D, add edge
to
.
Figure 1.
Node splitting to create .
Figure 1.
Node splitting to create .
For each nonterminal vertex, v, of D, add two parallel edges between and ; to distinguish between them, we will refer to them as and . Let , and . To finish the construction of the stable allocation problem, we need to fix a linear preference order for each vertex of . For vertex , let be the most preferred and be the least preferred edge (if these edges are present, that is, if v is nonterminal), and the order of the other edges incident to are coming from the preference order of v on the corresponding arcs. For vertex , the most preferred edge is and the least preferred one is (if these edges are present), and the other preferences are coming from .
The proof of Theorem 2 is a consequence of Theorem 1 and the following Lemma that describes a close relationship between stable flows and stable allocations.
Lemma 3. If network and preference orders describe a stable flow problem, then is a stable flow if and only if there is a stable allocation, g, of , such that holds for each arc, , of D.
Proof. Assume first that g is a stable allocation in . This means that none of the edges are blocking, so either or must be g-dominated at ; hence, is assigned to a amount of allocation. As is more than the total capacity of arcs leaving v, or must hold. Therefore, must have exactly a amount of allocation whenever is present. An exchange of “” and “” shows that the presence of implies that has exactly allocation. These observations directly imply that Kirchhoff’s law holds for f at each node different from s and t. The capacity condition is also trivial for f; hence, f is indeed a flow of D. Observe that by the choice of q, neither s nor t is g-saturated; hence, no edge is g-dominated at s or at t.
Assume that walk blocks flow f. As P is f-unsaturated, each edge of must be g-dominated at or at . Walk P is blocking; hence, either is terminal, and hence, cannot be dominated at or there is a arc with a positive flow value, such that . In both cases, edge has to be g-dominated at . This means that . As arc is f-unsaturated, it follows that edge must be g-dominated at . This yields that . Again, arc is f-unsaturated; hence, edge has to be g-dominated at , and so on. At the end, we get that is g-dominated at . As terminal vertices s and t are g-unsaturated, cannot be a terminal vertex. Therefore, by the blocking property of P, there is an arc, , with a positive flow and ; hence, again, cannot be g-dominated at . The contradiction shows that no walk, P, can block f.
Assume now that f is a stable flow of D. We have to exhibit a stable allocation, g, of , such that f is the “restriction” of g. Define , so we only need to determine the and values for all nonterminal vertices, v. Actually, the stable allocation that we look for might not be unique. In what follows, we shall construct a particular one, the so-called canonical representation, , of f.
Let
S be the set of those vertices,
u, of
D, such that there exists an
f-unsaturated directed walk
that is not
f-dominated at
. As no walk can block
f,
S is disjoint from terminal vertices
. To determine
, for each nonterminal vertex,
v, allocate the remaining quota of
v to
or to
, depending on whether
or
holds. More precisely, define:
By the definition of
q, both
and
are nonnegative. If
, then the amount of total allocation of
is
by Equation (
18), and for
, the amount of total allocation of
is
by Equation (
19). Therefore, if
, then the total allocation of
and
is
by Kirchhoff’s law. The total allocations of
and
is less than
and
, respectively, by the choice of
q. That is,
is an allocation on
.
To justify the stability of , we have to show that no blocking edge exists. To see that neither nor is blocking, observe that both and are saturated in . Therefore, is dominated at , and is dominated at . Assume now that holds. Our goal is to prove that is not blocking.
If there is an f-unsaturated walk, P, ending with arc that is not f-dominated at its starting node, then by the definition of S; hence, . Moreover, if some edge, , with would have a positive allocation, then walk P would block f, a contradiction. As has a amount of total allocation, edge is -dominated at .
The last case is when any f-unsaturated walk that ends with arc is f-dominated at its starting vertex. In particular, ; so, . Moreover, f-unsaturated walk must be f-dominated at v; hence, , and is -dominated at as has a amount of allocation. The conclusion is that is a stable allocation, just as we claimed. ☐
At this point, we are ready to prove our main result.
Proof of Theorem 2. There is a stable allocation for by Theorem 1; hence there is a stable flow for D, due to the first part of Lemma 3. If c is integral, then is an integer for each vertex, v, of D; hence, p is integral for . The integrality property of stable allocations in the first part of Theorem 1 shows that there is an integral stable allocation, g, of that describes an integral stable flow, f, of D. ☐
At the end of this section, let us point out a weakness of our stability concept. The motivation behind the notion is that we look for a flow that corresponds to an equilibrium situation, where the players represented by the vertices of the network act in a selfish way. This equilibrium situation occurs if no coalition of the players can block the underlying flow,
f, and this blocking is defined by an
f-unsaturated walk with a certain property. Along such a walk, the players are capable and prefer to increase the flow. However, any closed
f-unsaturated walk,
C, per se causes some kind of instability, because the players along
C mutually agree to send some extra flow along
C, even if properties Equations (
4) and (
5) do not hold for vertex
of
C. This motivates us to define flow
f of network
with preferences to be
completely stable if
f is stable and there exists no
f-unsaturated cycle in
D whatsoever. If
f is a stable flow, then we can “augment” along
f-unsaturated cycles, and hence, we can construct a flow,
, such that there no longer exists an
-unsaturated cycle. However, unfortunately, flow
might not be stable any more, because we might have created a blocking walk by the cycle augmentations.
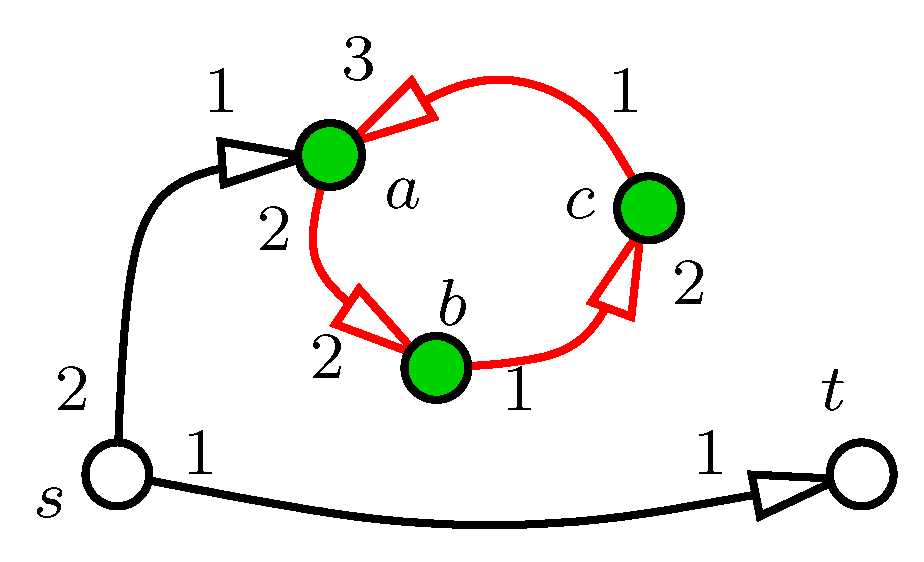
In fact, there exist networks with preferences that do not have a completely stable flow. One example is in the figure: each arc has a unit capacity; preferences are indicated around the vertices (a lower rank is preferred to the higher).
As no arc leaves subset of the vertices, no flow can leave U; hence, no flow enters U. In particular, arc has zero flow. If we assume indirectly that f is a completely stable flow, then cycle cannot block; hence, there must be a unit flow along it. However, then, walk is blocking, a contradiction.
Figure 2.
Stable flows have a blocking cycle.
Figure 2.
Stable flows have a blocking cycle.
4. The Structure of Stable Flows
For the stable marriage problem, it is well known about the stable marriage problem that in each stable marriage scheme, the same set of participants get married. That is, if someone does not get a marriage partner in some stable scheme, then this very person remains single in all stable marriage schemes. A generalization of this property is the rural hospital theorem by Roth [
12] (see also Theorem 5.13 in [
13]). It is about the college model, where instead of men, we work with colleges, women correspond to students and each college has a quota on the maximum number of admissible students. In the college admission problem, it is true that if a certain college,
c, cannot fill up its quota in a stable admission scheme, then
c receives the same set of students in any stable admission scheme (the phenomenon is named after the assignment problem of medical interns to hospitals).
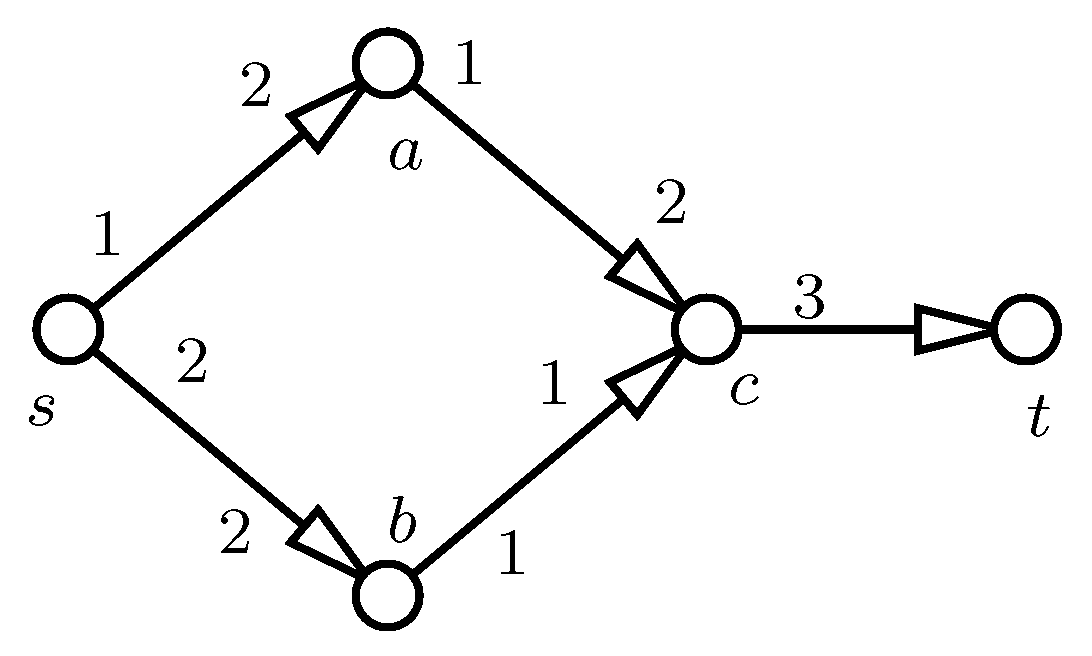
It seems that the rural hospital theorem cannot be generalized to the stable flow problem. It may happen in a network that a certain vertex transmits different amounts of flow in two stable flows. An example is shown in the figure, where each arc has a unit capacity. There are two stable flows: one is along path , and the other follows path . Therefore, in one stable flow, vertex a transmits one unit of flow, and no flow passes through a in the other one.
Figure 3.
Network for a stable flow.
Figure 3.
Network for a stable flow.
There is, however, a consequence of the rural hospital theorem that can be generalized; namely, that the size of a stable matching is always the same. More generally, it can also be proven that in any instance of the stable allocation problem, the size of any two stable allocations is the same. (The size of an allocation is the total amount of assignments in it). If we consider a stable allocation instance as a stable flow, then the size of the allocation corresponds to the value of the flow.
Theorem 4. If network and preference orders describe a stable flow problem and and are stable flows, then the value of and are the same. Moreover, for any arc of D that is incident to terminal vertex s or t.
Proof. As the value of a flow is the net amount that leaves s, one can calculate it in as the difference of the total allocation of and . This means that the second part of the theorem directly implies the first one. Therefore, below, we prove only the second part of Theorem 4.
Let
and
be the canonical representations of flows
and
defined in Lemma 3. As there is no edge between
and
, the definition of
implies that both
and
are
-unsaturated. Hence, property Equation (
13) can hold neither for
nor for
. However, Theorem 1 implies that
and
are
and
-comparable. Therefore, property Equation (
12) must be true for flows
and
for both vertices
and
. In particular,
holds for each arc,
a, incident to
s. This shows the second part of the Theorem for
s. The argument for
t is analogous to the above one. ☐
As we have seen in Theorem 1, stable allocations have a lattice structure. Based on the connection of stable allocations and stable flows described in Lemma 3, we can prove that stable flows of a network with preferences also form a natural lattice. Therefore, assume that f is a stable flow in network with preferences, and let stable allocation of be the canonical representation of f, as in the proof of Lemma 3.
Observe that any nonterminal vertex, v, of D, exactly one of and is positive by the choice of q and . For stable flow f, we can classify the vertices of D different from s and t as follows: v is an f-vendor if , and v is an f-customer if . If v is an f-vendor, then no edge can be -dominated at (as ); hence, player v sends as much flow to other vertices as they accept. Similarly, if v is an f-customer, then no edge can be -dominated at ; that is, player v receives as much flow as the others can supply her.
To explore the promised lattice structure of stable flows, let and be two stable flows with canonical representations and , respectively. From Theorem 1, we know that stable allocations form a lattice; so, and are also stable allocations of , and by Theorem 2, these stable allocations define stable flows and , respectively. How can we determine these latter flows directly, without the canonical representations? To answer this, we translate the lattice property of stable allocations on to stable flows of D.
Theorem 4 shows that stable flows cannot differ on arcs incident to terminal vertex
s or
t, so on these arcs,
and
are determined. However, vertices different from
s and
t may have completely different situations in stable flows
and
. The two color classes of graph
are formed by the
- and
-type vertices, respectively. Therefore, by Theorem 1,
can be determined, such that (say) each vertex,
, selects the better allocation and each vertex,
, receives the worst allocation out of the ones that
and
provide them. Similarly, for stable allocation
, the “in”-type vertices choose according to their preferences, and the “out”-type ones are left with the less preferred allocations. This means the following in the language of flows. If we want to construct
and
v is a vertex different from
s and
t, then either all arcs entering
v will have the same flow in
as in
or for all arcs
a entering
v, equation
holds. A similar statement is true for the arcs leaving
v. To determine which of the two alternatives is the right one, the following rules apply:
If v is an -vendor and an -customer, then v chooses . If v is an -vendor and an -customer, then v chooses . That is, each vertex strives to be a customer.
If v is an -vendor and an -vendor and v transmits more flow in than in (i.e., ) then v chooses . That is, vendors prefer to sell more.
If v is an -customer and an -customer and v transmits more flow in than in (i.e., ), then v chooses . That is, customers prefer to buy less.
Otherwise, v is a customer in both and or v is a vendor in both flows, and v transmits the same amount in both flows (i.e., and ). In this situation, v chooses the better “selling position” and gets the worse “buying position” out of stable flows and .
Clearly, for the construction of , one always has to choose the “other” options rather than the one that the above rules describe.
5. Conclusions
There are some well-known generalizations of network flows where stability is an interesting property. Luckily, some of these can be handled with the help of the construction we used to prove Theorem 2. If our “network” has unoriented edges, then the usual trick helps: one substitutes each edge by two oppositely oriented arcs, each having the capacity of the corresponding edge. If some vertex, v, of the network has a certain throughput capacity, , then we can handle this by reducing the capacity of both vertices, and , from to . The third usual generalization is where the network has several source and sink nodes. The usual trick with a supersource and supersink works in this case, as well, but there is an alternative approach. Namely, the problem with several terminals can be regarded as a problem where there exist more than two vertices that do not obey Kirchhoff’s law. As we have seen in the proof of Theorem 2, such vertices, v, can be modeled in such a way that in the graph, , edges and are not present. Any stable allocation of this sparser, , determines a stable flow with more terminals. However, with this approach, it is possible that we have a flow from some “source” node to another “source” node. This weirdness can actually happen in our basic flow model, as well: a stable flow might go from t to s and have a negative value. Can we avoid this? The answer is yes (up to some extent): one has to introduce an edge, , for each “source” node, s, and an edge, , for each “sink” node, t. By this, we can make sure that each source node sends more (or an equal amount of) flow as the amount it receives and no target node receives less flow than the amount it sends.
Summarizing the last observations, we can say that if both edges, and , are present, then vertex v obeys Kirchoff’s law; if no edge is present, then Kirchoff’s law is not required for v. If there is exactly one of these edges belonging to , then depending on which edge is the one, v becomes a net sender or a net receiver of flow.
Circulation is a well-known notion closely related to flows. Roughly speaking, it is a flow without terminals; that is, beyond the capacity constraint, Kirchhoff’s law has to hold for each vertex. Obviously, our approach can handle the stable circulation problem, if we have both parallel edges between and for each vertex, v, of D. However, it turns out that zero is a stable circulation, and this is somehow disturbing. It makes more sense to look for a completely stable circulation that has no blocking walk and no blocking cycle. However, just like for flows, a completely stable circulation might not exist. A natural problem is to find an efficient algorithm for constructing a completely stable circulation (or flow) in a network.
Another direction of possible generalizations of stable flows is that we allow more complex preferences, e.g., ties in the preference lists. As the stable flow model is a genuine generalization of stable allocations that generalize stable matchings, each negative complexity result is valid for flows, as well. However, it is interesting to observe that the special exchange economy of housing markets can be formulated in our flow model by allowing indifferences. If each vertex of D represents a player, each arc and each vertex has unit capacity, and arc means that player u prefers the house of player v to her own one. Then, we have preferences only on the arcs leaving v, and v is indifferent to the arcs entering v. With these settings, core allocations of the housing market correspond bijectively to completely stable circulations. This indicates that the top trading cycles algorithm of Gale might be useful to handle some stable flow problems where indifferences are present.