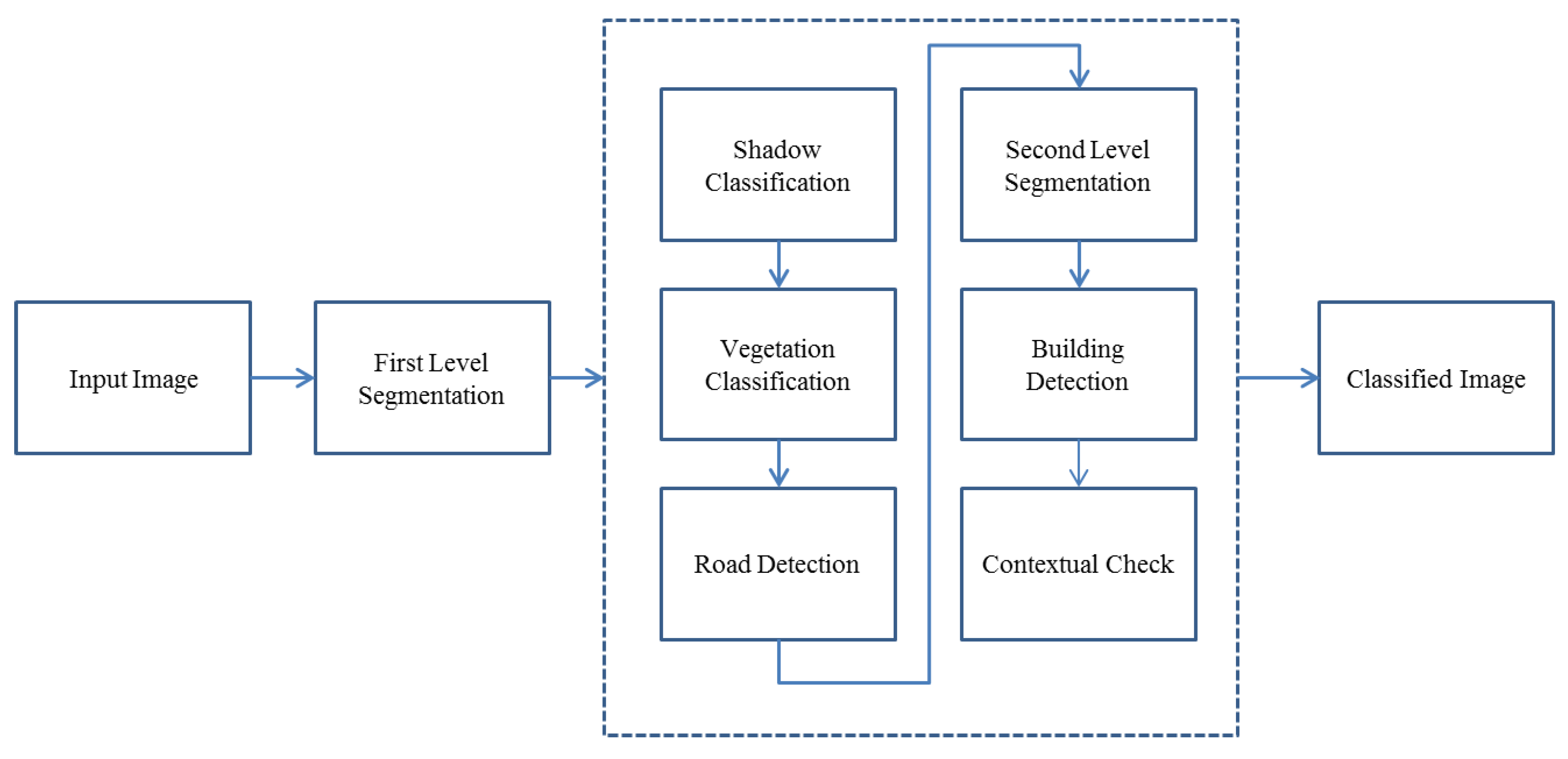
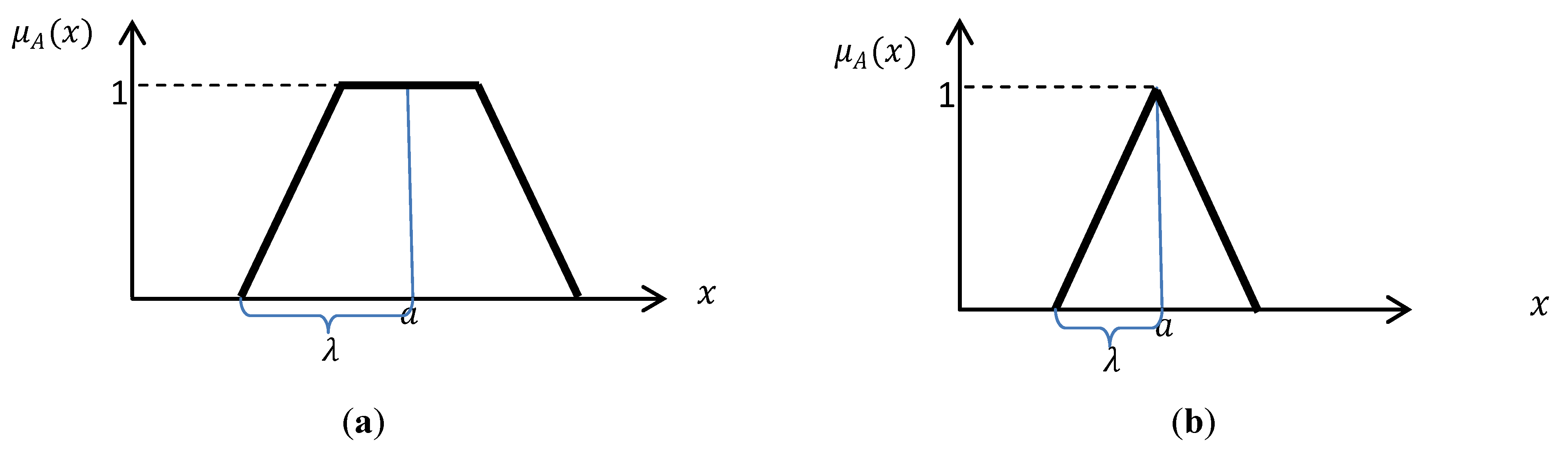In this project the image is classified into 5 major classes: Shadow, Vegetation, Road, Building, and Bare land. In the hierarchy of the classification, first shadow is extracted. Then, from shadow and unclassified segments, vegetation is extracted. This means that shadow is not excluded from the classification process in this step. The logic behind it is that some parts of vegetation are covered by the shadow of the others, while still demonstrating similarities to vegetation and we do not want to exclude them from vegetation class. After, vegetation extraction, road classification, building detection and contextual analysis are done, respectively. Finally, the remaining unclassified features are assigned to bare land.
Figure 1 shows the flow chart of the presented method.
Figure 1.
Flow chart of the presented method.
In this study, in order to classify a VHRSI, first the image is segmented, and then using the related fuzzy rules, segments are assigned to specific classes; this process is explained in the rest of this article.
3.2. Fuzzy Image Classification
In traditional classification methods such as minimum distance method, each pixel or each segment in the image will have an attribute equal to 1 or 0 expressing whether the pixel or segment belongs to a certain class or not, respectively. In fuzzy classification, instead of a binary decision-making, the possibility of each pixel/segment belonging to a specific class is considered, which is defined using membership functions. A membership function offers membership degree values ranging from 0 to 1, where 1 means fully belonging to the class and 0 means not belonging to the class [
24].
Implementing fuzzy logic ensures that the borders are not crisp thresholds any more, but membership functions within which each parameter value will have a specific probability to be assigned to a specific class are used. Appending more parameters to this classification, for example, using NIR ratio and NDVI for vegetation classification, better results will be achieved. Using fuzzy logic, classification accuracy is less sensitive to the thresholds.
is a fuzzy membership function over domain
X.
is called membership degree, which ranges from 0 to 1 over domain
X [
23,
24].
can be a Gaussian, Triangular, Trapezoidal, or other standard functions depending on the application. In this research, trapezoidal and triangular functions are used (
Figure 2). The associated formulas are given in Equations (1) and (2) [
25,
26].
Figure 2.
Typical (a) Trapezoidal. (b) Triangular fuzzy functions which are used in this study.
Figure 2.
Typical (a) Trapezoidal. (b) Triangular fuzzy functions which are used in this study.
Trapezoidal function:
where,
a is the
x coordinate of the middle point of the trapezoidal function or the x coordinate of the peak of the triangular function and λ equals half of base of triangle or half of the long base of the trapezoidal. All the parameters of the functions are specified based on human expertise [
25].
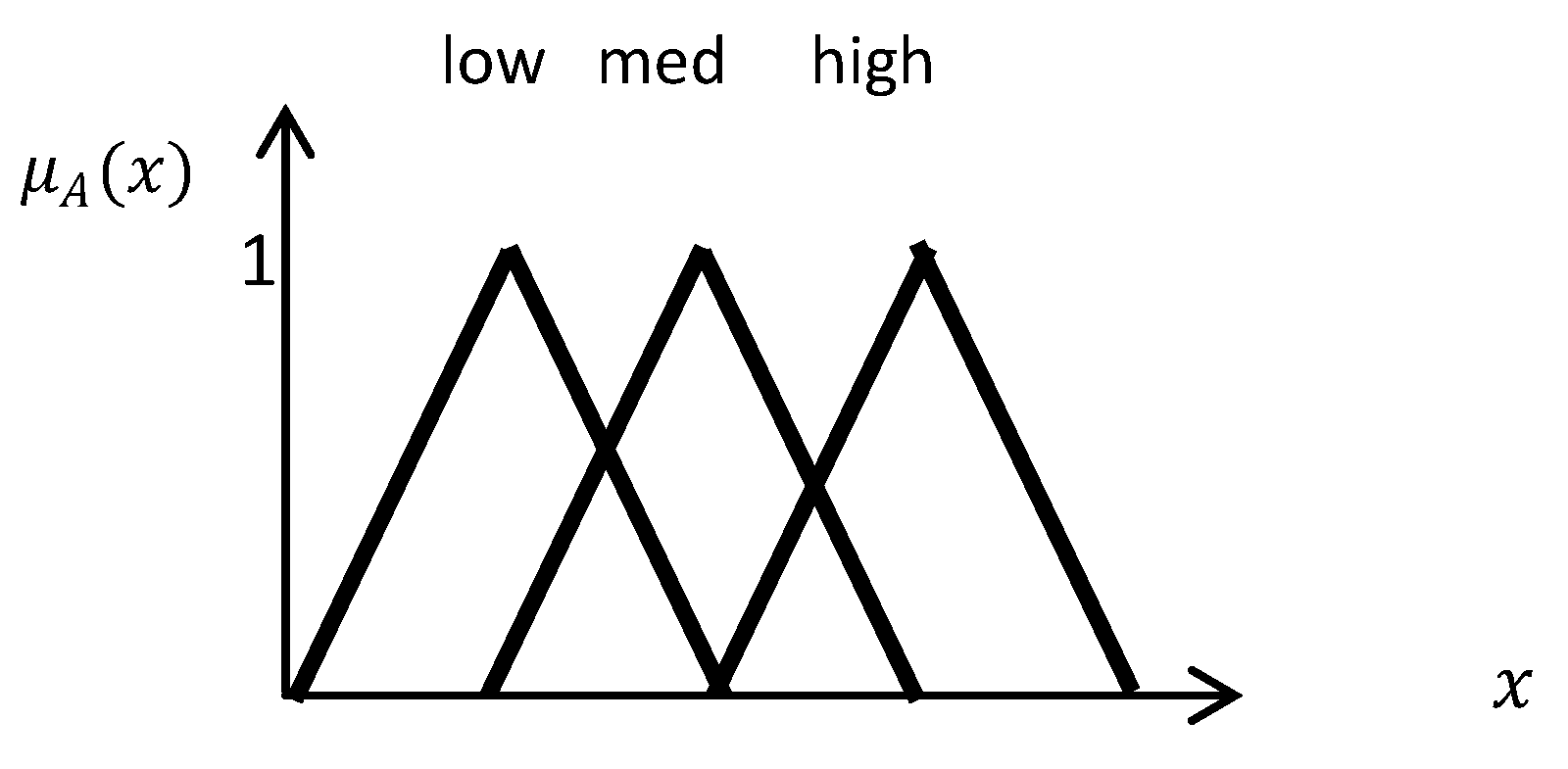
Figure 3.
Lingual variable example.
Figure 3.
Lingual variable example.
In fuzzy rule-based systems, lingual variables are introduced, which replace the crisp thresholds. For example, instead of defining vegetation with a threshold for NDVI, a lingual value, such as high, medium, or low, with a specific fuzzy function is identified which assigns a membership degree to specific ranges of NDVI.
Figure 3 shows an example of lingual variables [
25,
26,
27]. In this research, the only lingual variables which are useful for this study are defined.
The other important specification for a fuzzy rule-based system is a fuzzy inference system, which uses Fuzzy rules for decision making. In this project the inference system of eCognition software is used. More details of fuzzy classification in eCognition software are given in [
28].
In the presented method, the specifications of each object are tested using the fuzzy rules defined for each class based on the hierarchy mentioned in
Section 3. Each segment receives a degree specifying the similarity of the segment to each class. The segments which have high similarity degrees will be assigned to the associated class after deffuzification of the results. This step is also done in eCognition software.
In the following, the details of the parameters used for different object classification are presented.
3.2.1. Shadow
In satellite images, it is very likely that shadows will be mistaken for roads, since they both are narrow elongated objects. Hence, it is necessary to label shadow segments in advance. In addition, shadows can help in defining elevated objects [
9]. In this research, 2 parameters are used for shadow detection: Brightness and Density, which are explained in this section.
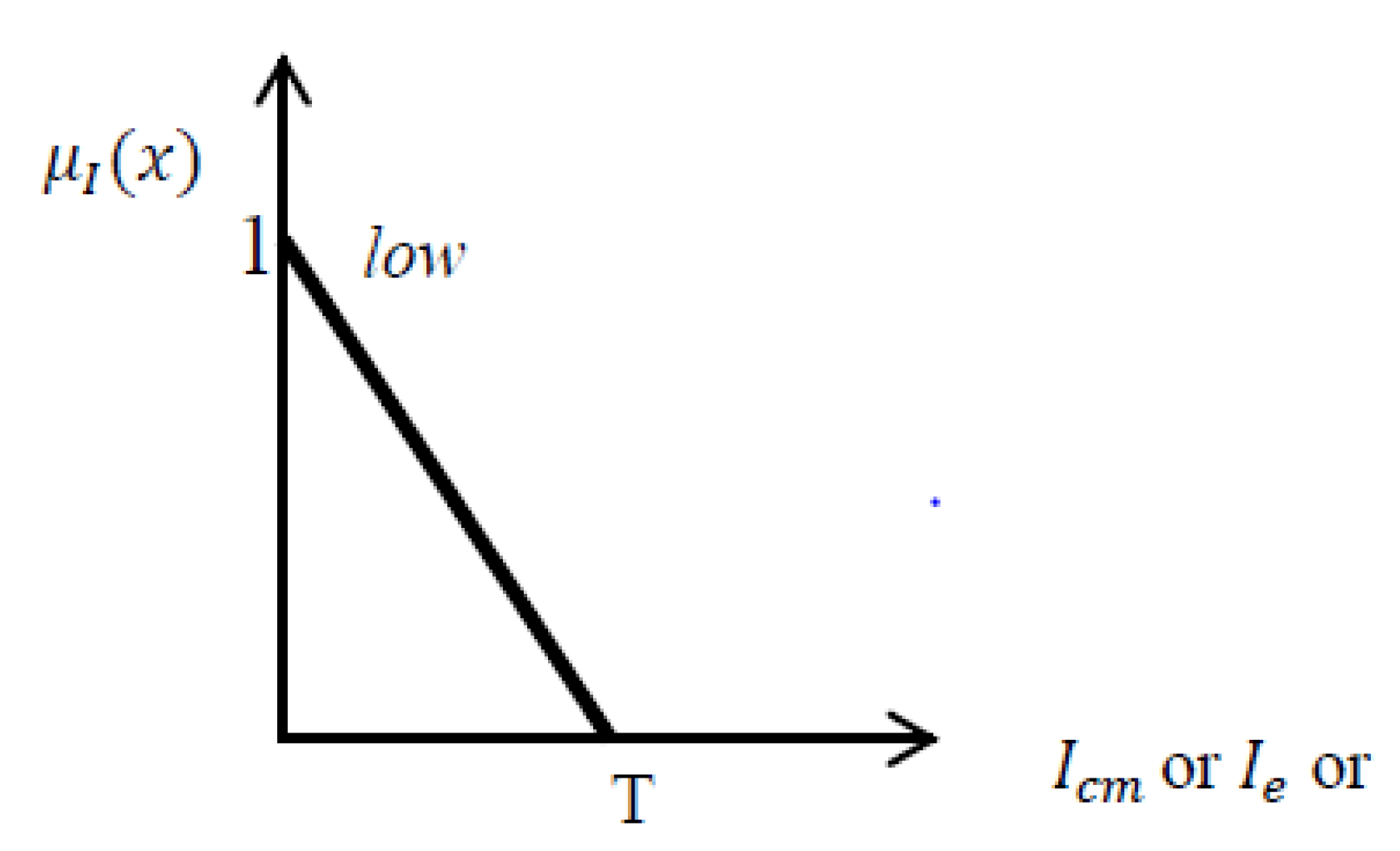
Brightness: Brightness is the mean of gray values of all bands for each pixel/segment given in Equation (3).
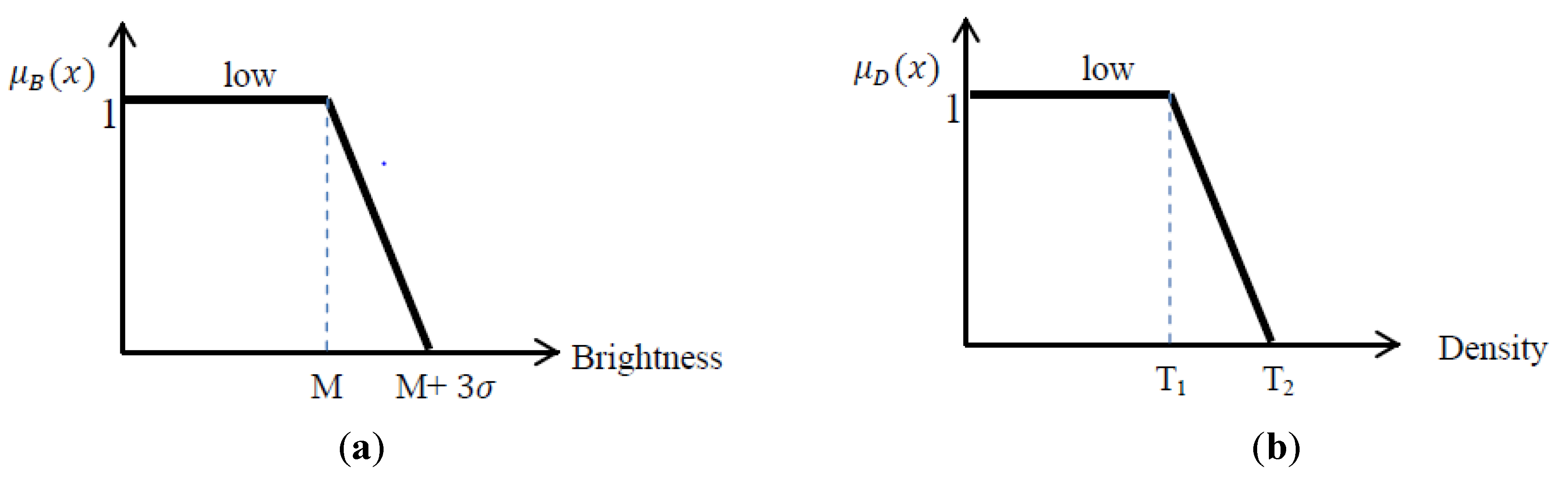
Since shadows tend to have low brightness values, here, in order to specify the parameters of the fuzzy function associated with
low brightness in the image, an unsupervised image classification method called the fuzzy k-means method is used to find the darkest cluster. The fuzzy k-means clustering method is applied on the image to generate 15 clusters. (Generally, the number of the clusters in the unsupervised classification methods should be between 3 and 5 times of the number of actual classes in the image [
29]). Then, the mean and standard deviation of the darkest cluster, amongst all clusters, are used to define the fuzzy function for Shadow brightness. The fuzzy function used in this process is presented in
Figure 4a.
Figure 4.
(a) fuzzy function for Brightness: M is the mean of the darkest cluster and sigma is the associated standard deviation; (b) fuzzy function for Density.
Figure 4.
(a) fuzzy function for Brightness: M is the mean of the darkest cluster and sigma is the associated standard deviation; (b) fuzzy function for Density.
The upper threshold is considered to be mean of the darkest cluster plus three times the associated standard deviation; statistically speaking, in normal distribution, the probability of 99% is given by M + 3σ and that is why in this study the upper threshold equals M + 3. It is aimed to cover 99% of the shadows, but the membership probability is the least value in this threshold.
Density: Density is a feature presented in eCognition software, which describes the distribution of the pixels of an image object in space [
28].
where,
is the diameter of a square object with
pixels and
is the diameter of the fitted ellipse to the segment.
The more the object is like a square, the higher the value of density. Consequently, filament shaped objects have low values of density, which is consistent with the shape of shadows looked for in this study. Here, we look for shadows to help in finding buildings. In this project the majority of shadows had a density less than 1. There are also shadows as well as some other objects with density between 1 and 1.2, which means this range is the fuzzy range of shadow classification. Thus, the membership degree for those segments with the density less than 1 is 100% (the membership degree equals one) and those in between 1 and 1.2 are in the fuzzy range with membership degree ranging from 1 to 0 (
Figure 4b). Equations (5) and (6) show the formula for
low brightness and density that are associated with
Figure 4. In other projects, density of shadows might be slightly different than the mentioned numbers.
The fuzzy rule used for shadow detection is:
3.2.2. Vegetation
As mentioned earlier in this article, vegetation extraction is one of the most straightforward methods in image classification. In this research, 2 parameters are used for vegetation detection: NDVI and NIR ratio, which are explained in this section.
NDVI: Normalized Difference Vegetation Index (NDVI) is a proper tool for vegetation extraction [
30].
NIR Ratio: Because of high reflectivity of vegetation in the NIR region of the electromagnetic wave spectrum, the value of the NIR ratio, which is given by Equation (7), is higher in vegetated areas compared to other parts of the image [
28].
The value of the NDVI and the NIR ratio in vegetated areas slightly differ from one image to another. Generally, the NDVI value for vegetation is around 0.2 and the NIR ratio is around 0.3, depending on the density of vegetation. However, if a crisp threshold is selected to classify the image into vegetated and non-vegetated areas, there might be some vegetation segments in the image with the NDVI and the NIR ratio values slightly less than thresholds which will be miss-classified as non-vegetation. In order to improve error of omission, the presented fuzzy rule-based system offers a wider margin to include uncertain segments and provides them a second chance to be examined for classification qualification.
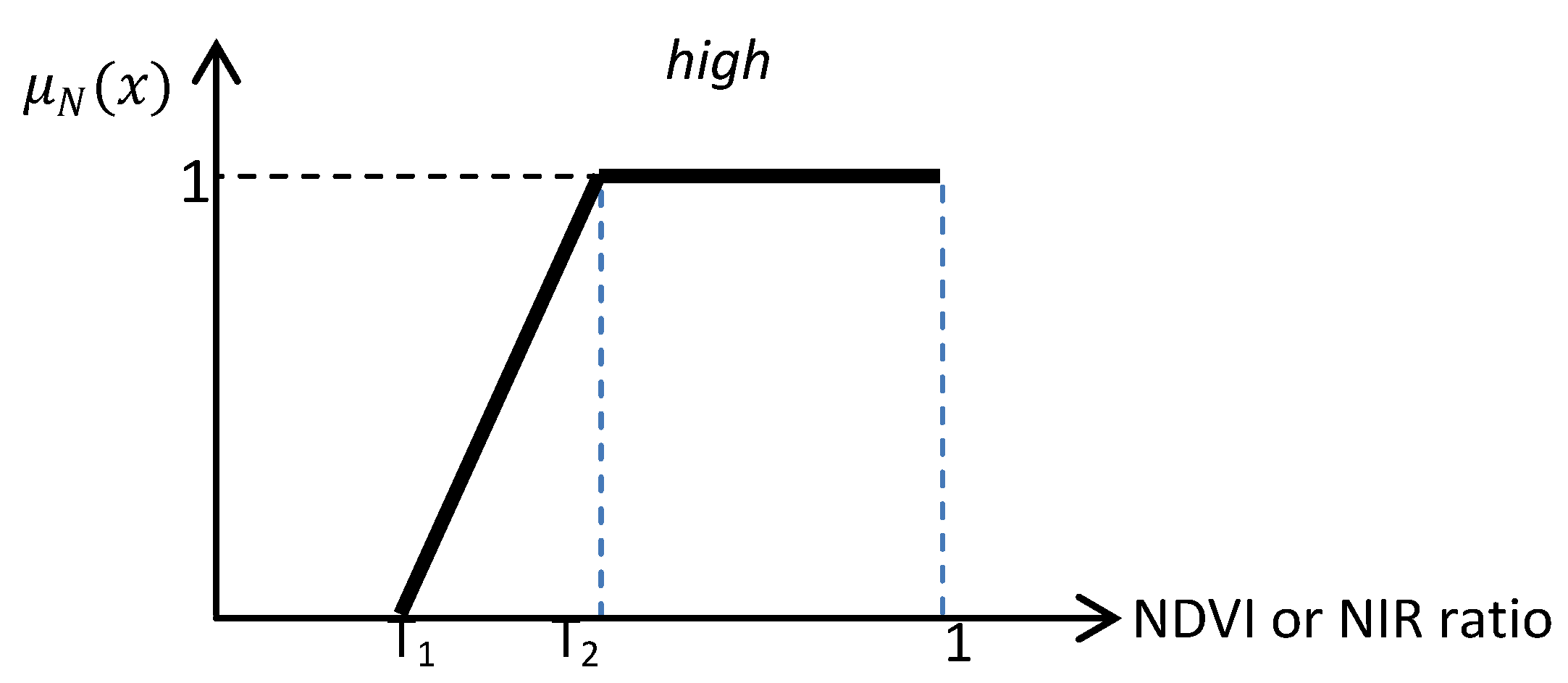
Figure 5.
NDVI or NIR Ratio fuzzy function. In this study for NDVI, T1 = 0.05, T2 =0.25, For NIR Ratio: T1 = 0.15, T2 = 0.4.
Figure 5.
NDVI or NIR Ratio fuzzy function. In this study for NDVI, T1 = 0.05, T2 =0.25, For NIR Ratio: T1 = 0.15, T2 = 0.4.
The used membership function is presented in
Figure 5 and the associated formula is given in Equation (8).
The related fuzzy rule is:
3.2.3. Road
Roads are elongated objects with smooth surfaces having low variations in the gray values. Therefore, criteria which show lengthened objects and gray value variances can be used for defining roads. Classifying road segments without any ancillary data is a challenging issue. In this project, first strict limitations are used for road detection. Therefore, the real road segments will be classified as Road class. Then, using spectral similarity with neighbor objects, other parts of the road can also be correctly classified. In this study, 3 parameters called , , and standard deviation are used for road detection which are explained in this section.
and : Equation (9) and (10) are used for defining elongated objects [
6].
Having compared different class segments, one comes to the understanding that road segments have low value for
and
, while buildings have high values of them. The exact range for
and
associated with road segments depends on the image spatial resolution, road width,
etc., However, a rough estimation for the used GeoEye image is that
for road segments is less than 0.5 and
is less than 0.1 (These numbers are slightly different in the used QuickBird imagery). Although there are some other segments belonging to roads which have higher values of
and
, this tight limitation decreases the risk of error of commission, which means it prevents non-road elongated segments to be miss-classified in road class. Later, as explained above, using contextual information, those unclassified road segments will be properly classified to road class (see
Section 3.2.5). The fuzzy function defined for
and
is presented in
Figure 6.
Standard deviation (Std): Std shows variation of pixel values in a specific segment [
28]. Since the surfaces of the roads are smooth with low variations in gray levels, the lower the standard deviation of segments, the higher the possibility to be assigned to the road class. The upper limit of standard deviation for roads depends on the radiometric resolution of the image and the distribution of gray values in the image histogram. For example in this project,
T = 150 for standard deviation of GeoEye image (
Figure 6).
Figure 6.
Fuzzy function for, or Standard deviation, which has the same shape, but with different T values.
Figure 6.
Fuzzy function for, or Standard deviation, which has the same shape, but with different T values.
Equation (11) presents the associated fuzzy set for, or Standard deviation.
Considering the above specifications for road, the produced fuzzy rule is:
Using this rule, some narrow elongated features not belonging to road class might also be miss-classified as road. Therefore, in this study after applying this rule, all the road segments so produced are merged. Then, those narrow features are removed using a width threshold. Considering that the minimum width of a road is 3 m and spatial resolution of the image is 0.5 m, all road segments which have width less than 6 pixels are unlikely to belong to roads and they are omitted from it. This procedure improves error of commission.
3.2.4. Building
All previously mentioned object classes can be specified by first level of segmentation. However, building detection needs further processing because of the particular specifications of buildings. For example in pitched-roof buildings, each side of a roof will be assigned to a different segment due the dissimilar amount of solar radiation it receives in different sides. Therefore, a second level of segmentation must be applied to unify those segments, which in this study, requires training data. Afterwards, using building specifications, building segments are classified.
Second Level Segmentation
[
31] presented a supervised method for optimal multi-resolution image segmentation. The method called FbSP optimizer (Fuzzy-based Segmentation Parameter optimizer), offers a fuzzy-based process with which optimized scale, shape, and compactness parameters of multi resolution segmentation are generated. The process is trained using the segments belonging to a specific training building; the information of the training segments such as texture, brightness, stability, rectangular fit, and compactness are used to train FbSP optimizer. Then, new scale, shape, and compactness values are generated for the second level of segmentation. Using the optimal parameters for image re-segmentation, precise building borders are delineated. The output segments have borders fairly fitting the real ones. The problem of this method is the requirement of training data. Therefore, this method is only used for building classification due to its complicated nature. The full description of FbSP optimizer can be found in [
32]. After finding the optimized segments for buildings, the next step is to detect building segments out of unclassified ones.
Building Classification
The specification for buildings in VHRSI is that buildings are typically rectangular shaped (mostly square shaped) objects with an elevation above the ground. These specifications are going to be used for building detection in this part. In this study 4 parameters are used for building detection: Rectangular Fit, Elliptic Fit, Area, and Shadow Neighborhood, which are explained in this section.
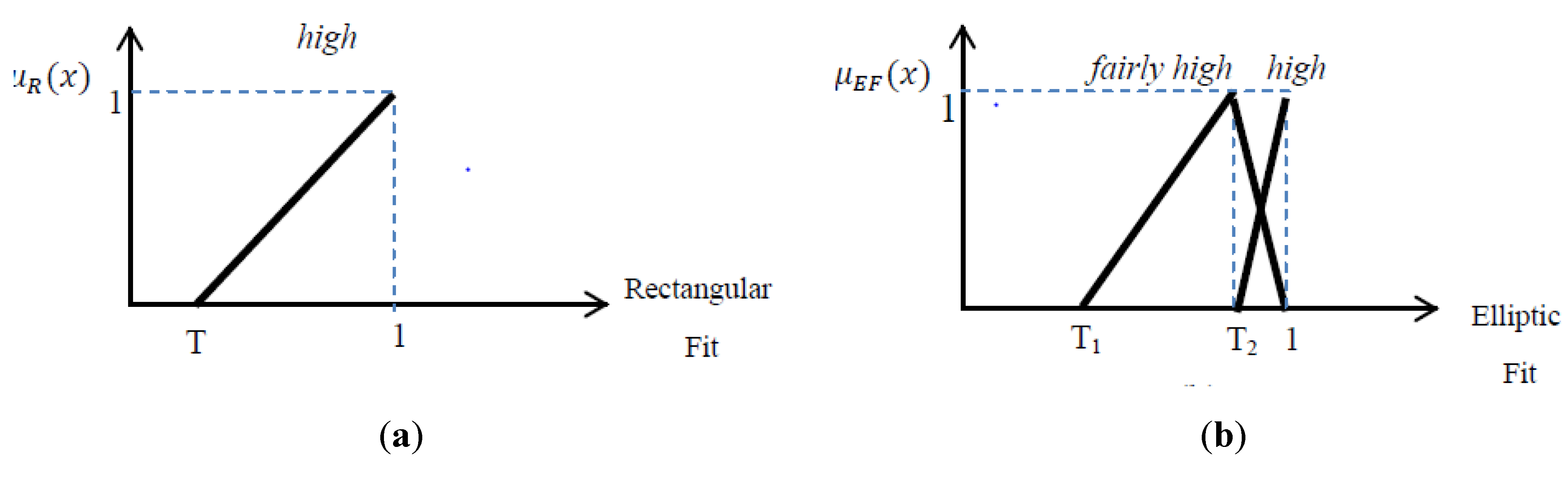
Rectangular Fit and Elliptic Fit: Rectangular Fit parameter describes how well an image object fits into a rectangle of similar size and proportions, while The Elliptic Fit feature describes how well an image object fits into an ellipse of similar size and proportions. They both range from 0 to 1, 0 meaning no fit and 1 meaning perfect fit [
28]. Having assessed the different building related image segments in this project, it is inferred that buildings have high similarities to rectangular shapes (
Figure 10a shows some typical buildings). Typically, buildings are square shaped which have a quite high Rectangular Fit and fairly high Elliptic Fit (not as high as circles). Therefore, Rectangular Fit and Elliptic Fit parameters can assist in building identification. If elliptic fit is omitted from the process, then elongated features which have rectangular shapes will also be miss-classified as buildings. Thus, both of the parameters must be used for building detection, simultaneously.
Figure 7 shows
high fuzzy membership for Rectangular Fit as well as
fairly high fuzzy membership of Elliptic Fit; high elliptic fit is used for round about detection in
Section 3.2.5.
Figure 7.
Fuzzy function for: (a) Rectangular Fit; (b) Elliptic Fit.
Figure 7.
Fuzzy function for: (a) Rectangular Fit; (b) Elliptic Fit.
The fuzzy set equations related to the high lingual value for rectangular fit are presented in Equation (12).
In addition, 2 fuzzy sets of elliptic fit for high and fairly high lingual values are presented in Equation (13) and (14).
fairly high elliptic fit:
Shadow Neighborhood: Using just Rectangular Fit and Elliptic fit for building detection, still, there might be parcels of bare land or any other classes which have approximately square shapes to be miss-classified as building reducing the classification accuracy. Therefore, there must be another parameter to extract buildings out of them. Here, shadows are of great importance. Considering the height of the building and Azimuth angle of sun at the time of exposure, a shadow with specific length and direction should be visible beside buildings.
Figure 8.
Direction of shadow in satellite images. Az is Azimuth angle of sun. Depending on the orientation of building, shadow is formed in side A (western side) or side B (southern side) or both.
Figure 8.
Direction of shadow in satellite images. Az is Azimuth angle of sun. Depending on the orientation of building, shadow is formed in side A (western side) or side B (southern side) or both.
The direction of the shadow depends on the azimuth angle of sun at the time of image capturing.
Figure 8 shows how azimuth angle of sun specifies the direction of shadow. Depending on the orientation of building, shadow is formed in the side A (in
Figure 8, western side), side B (in
Figure 8, southern side) or both. Therefore, whatever the sun azimuth angle is, the shadow of the building is formed in the opposite direction (in this research southern and/or western direction).
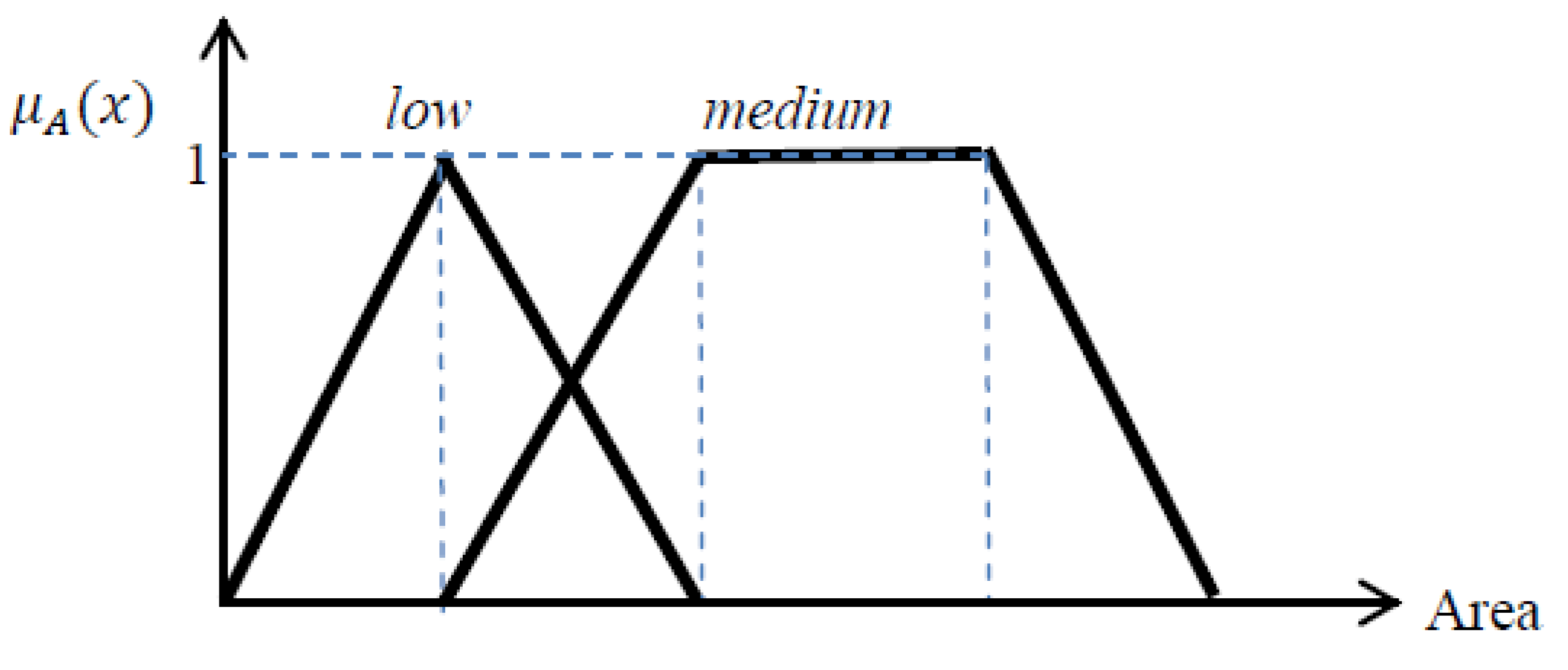
Area: Other than shape and shadow neighborhood in proper direction, buildings have another specification which is their area. In order to not misclassify other rectangular shaped features, such as vehicles, as building, the area limitation must also be considered. The smallest size for a building in this study is 3 m × 4 m and the biggest size is 25 m × 20 m. Regarding the image spatial resolution, area limit for building segments will be around 50 to 2000 pixels, within which, area from 100 to 1500 is the most probable range (membership degree equals to 1) and the remaining regions are the fuzzy areas. In
Figure 8, the
medium fuzzy function is used for delineating buildings; the
low fuzzy function will also be used for vehicle detection in
Section 3.2.5.
Figure 9.
Fuzzy functions for area, medium fuzzy function is used for building detection; low fuzzy function is used for vehicle detection.
Figure 9.
Fuzzy functions for area, medium fuzzy function is used for building detection; low fuzzy function is used for vehicle detection.
Equations related to low and medium lingual values for area.
where, a =
and
; also in this project
T1,
T2, and
T3 equal 50, 100, 1500, respectively.
In this research, Rectangular shapes with moderate area which are neighbors to shadows in the direction specified by sun azimuth angle are classified as buildings. The resulting fuzzy rule for building detection is:
3.2.5. Contextual Check
Having applied all the above mentioned rules to the image, still some unclassified segments might remain. Unclassified features are tested to see if they resemble specific classes. For example, since strict rules are applied for road detection, some parts of roads remain unclassified. Therefore, within unclassified objects those which are in the neighborhood of roads and have spectral similarity to roads are classified as Road. Also, some parts of the buildings might be remained unclassified. A similar rule is applied to them for a proper classification. The fuzzy rules used for further building or road classification are:
If spectral similarity to road is high and relative border to road is medium or relative border to road is high, then segment is Road.
If spectral similarity to building is high and relative border to building is medium or relative border to building is high, then segment is Building.
Other than the objects mentioned above, there are some other image objects which are not of interest of this study. For example, vehicles are irrelevant to this project, even though they might be the topic of other studies. Thus, using contextual information vehicles are removed. Courts and roundabouts must be assigned to road classification as well. In the following some of the contextual features with the related fuzzy rule are mentioned.
Vehicle removing: Considering the spatial resolution of the used satellite images, which is around 50 cm, and also the size of a typical vehicle which is approximately 1.5 m × 2.5 m, vehicles will be a rectangular shaped objects in satellite images with area around 15 pixels. The largest size vehicle that is counted in this study is a truck with size 2.5 m × 10 m. Therefore, objects which have an area between 15 to 100 pixels are probable to be vehicles. In addition, vehicles can be found in roads. Therefore, they must be connected to a road segment, which means their relative border with roads is greater than 50%.
Therefore the associated fuzzy rule is:
And since we do not deal with vehicles in this study, we assign it to road class.
Courts and Roundabouts: The segments of the image relating to courts and roundabouts fail to be classified as roads because of their round shapes or spectral reflectance different of that of roads. In this study, the unclassified segments are searched for circular or semi-circular features which are in neighborhood of the roads (covering roundabouts) or they have similar spectral reflectance to roads (covering courts). Here, these features are also classified as roads. The related rule is:
If Elliptic Fit is high and relative border to road is high, then segment is Road.
If Elliptic Fit is high and spectral similarity to road is high, then segment is Road.
3.2.6. Bare Land
Detecting parking lots from roads is a complicated issue which cannot be done without ancillary data [
2]. Here, the selected areas are so that they do not contain vast parking lots; just bare lands around the houses can be detected. The areas also contain no water bodies, therefore the remaining unclassified objects are assigned to bare land class.