Multi-Core Parallel Gradual Pattern Mining Based on Multi-Precision Fuzzy Orderings
Abstract
:1. Introduction
2. Related Work
2.1. Gradual Pattern Mining and Fuzzy Orderings
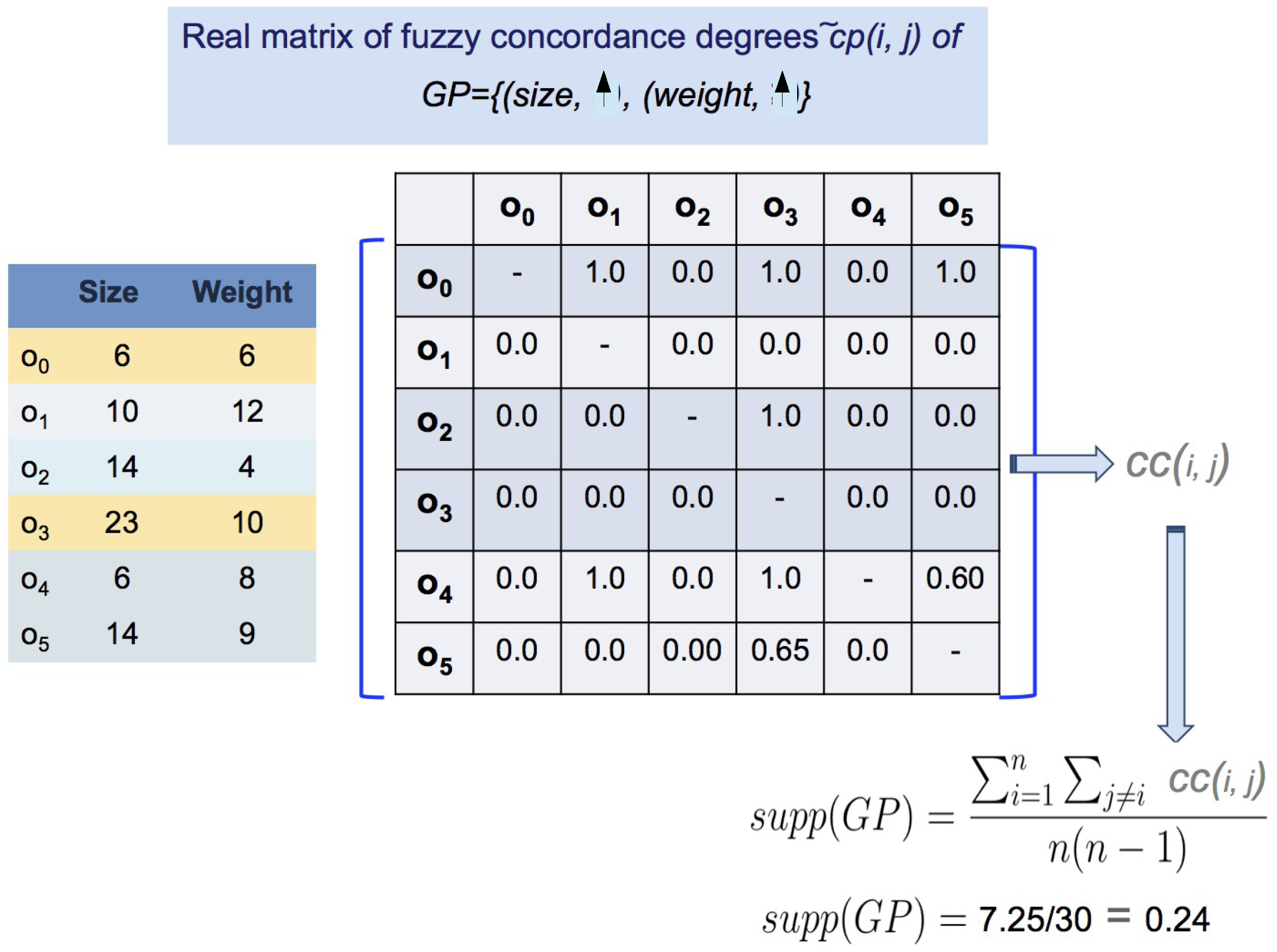
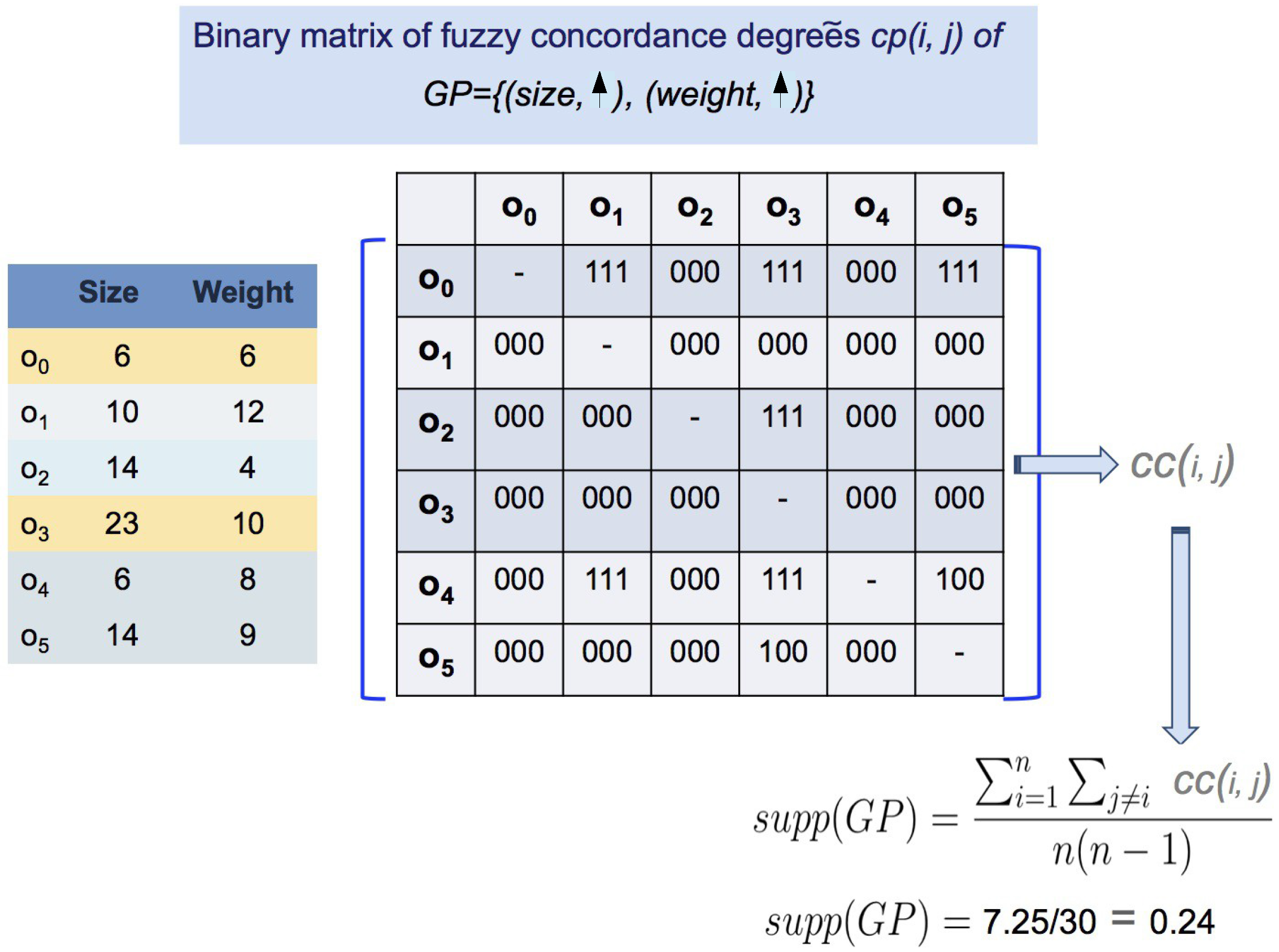
| :Size | :Weight | :Sugar Rate | |
|---|---|---|---|
| 6 | 6 | 5.3 | |
| 10 | 12 | 5.1 | |
| 14 | 4 | 4.9 | |
| 23 | 10 | 4.9 | |
| 6 | 8 | 5.0 | |
| 14 | 9 | 4.9 |
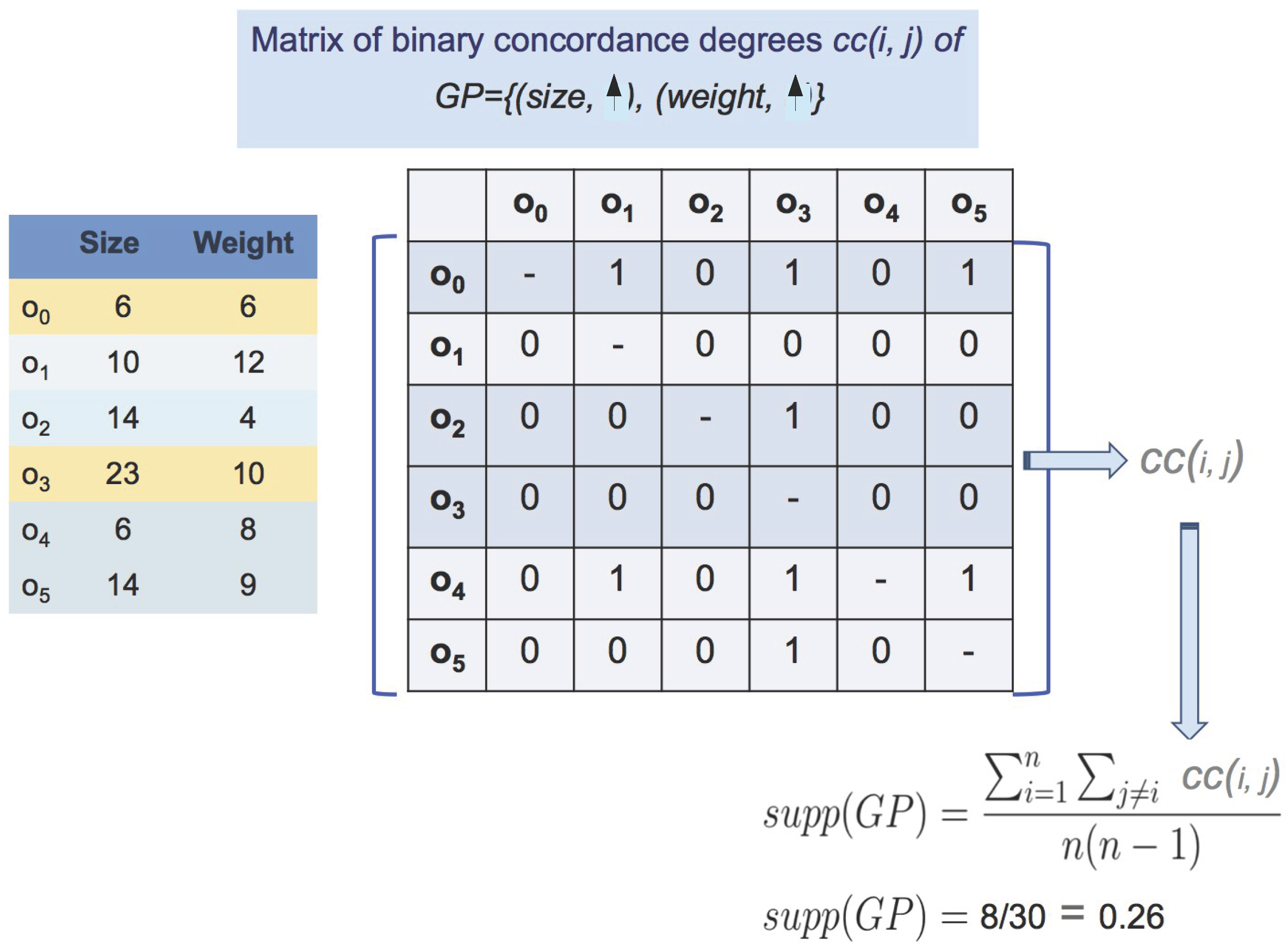
2.2. Parallel Data Mining
- Distributed memory systems (each processor has its own system memory that cannot be accessed by other processors, the shared data are transferred usually by message passing, e.g., sockets or message passing interface (MPI));
- Shared memory systems where processors share the global memory, they have direct access to the entire set of data. Here, accessing the same data simultaneously from different instruction streams requires synchronization and sequential memory operations;
- Hierarchical systems (a combination of shared and distributed models, composed by multiprocessor nodes in which memory is shared by intra-node processors and distributed over inter-node processors).
3. Parallel Fuzzy Gradual Pattern Mining Based on Multi-Precision Fuzzy Orderings
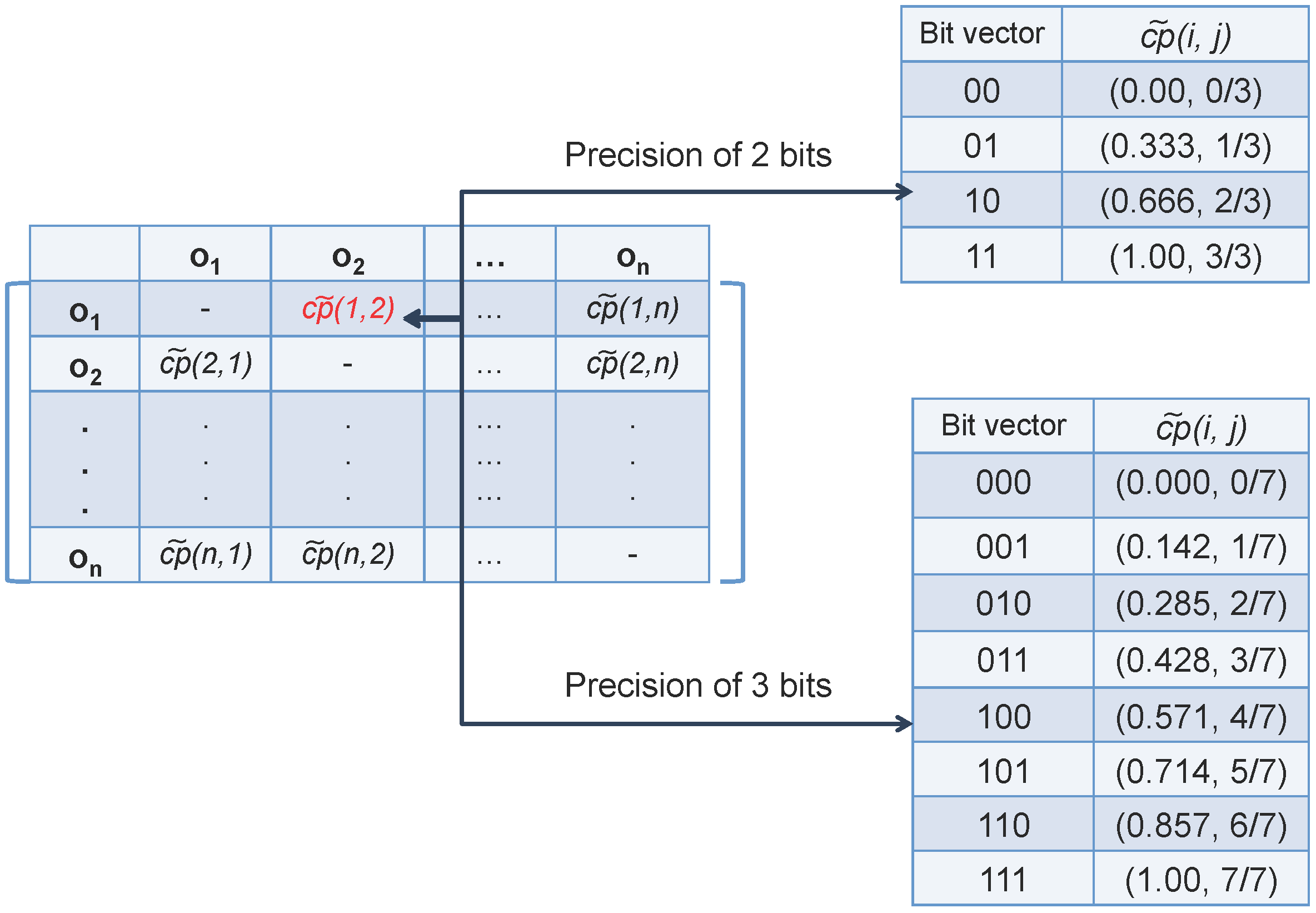
3.1. Managing Multi-Precision
| Algorithm 1 Fuzzy Orderings-based Gradual Itemset Mining |
 |
3.2. Coupling Multi-Precision and Parallel Programming
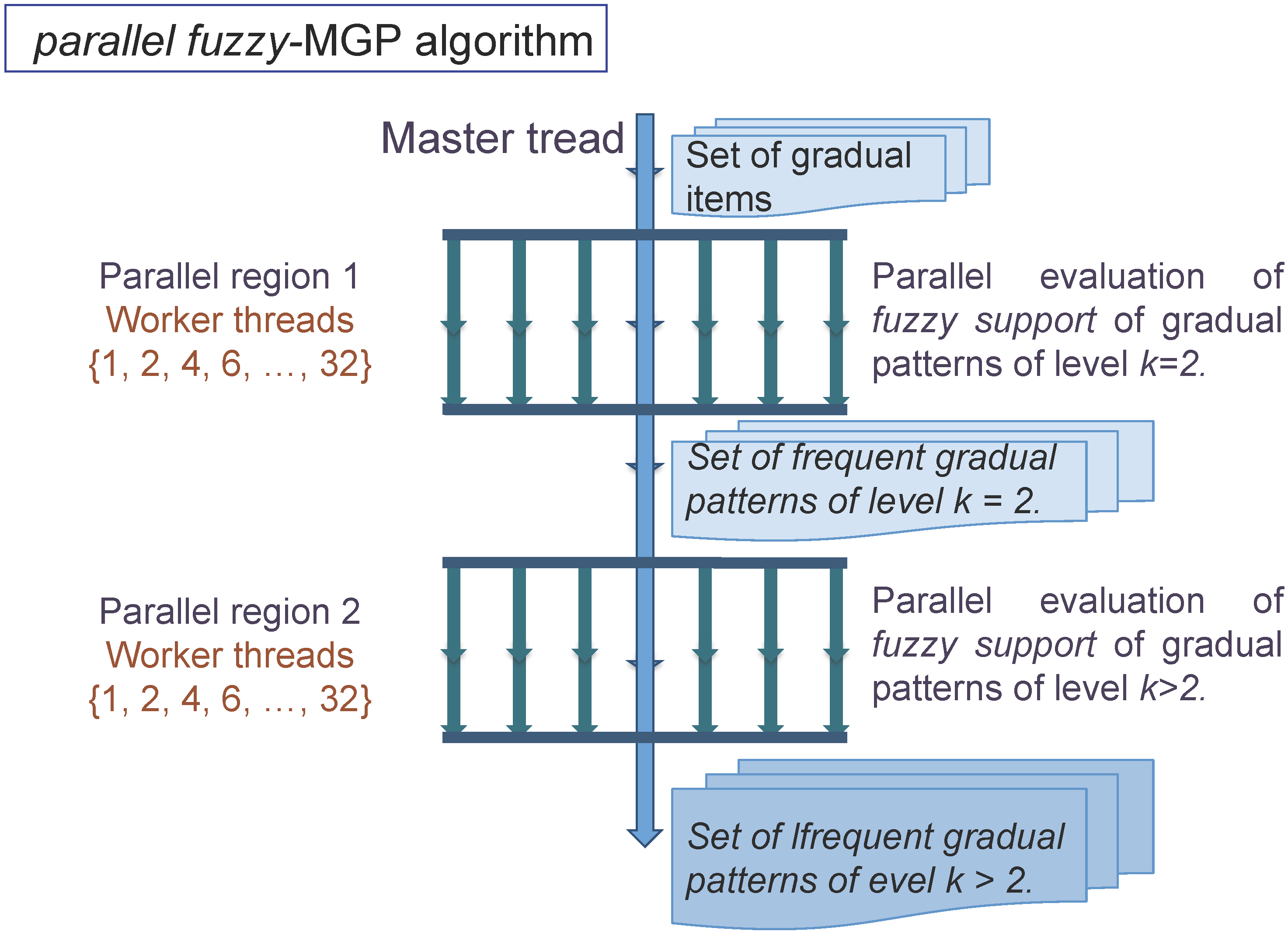
4. Experiments
4.1. Databases and Computing Resources
- an IBM dx360 M3 server embedding computing nodes configured with 2 × 2.66 GHx six core Intel (WESTMERE) processors, 24 Go DDR3 1,066 Mhz RAM and Infiniband (40 Gb/s) (reported as Intel); and
- an IBM x3850 X5 server running 8 processors embedding ten INTEL cores (WESTMERE), representing 80 cores at 2.26 GHz, 1 To DDR3 memory (1,066 Mhz) and Infiniband (40 Gb/s) reported as SMP (because of its shared memory).
4.2. Measuring Performances
- p is the number of processors/cores or threads;
- T(1) is the execution time of the sequential program (with one thread or core);
- T(p) is the execution time of the parallel program with p processors, cores, or threads.
4.3. Main Results
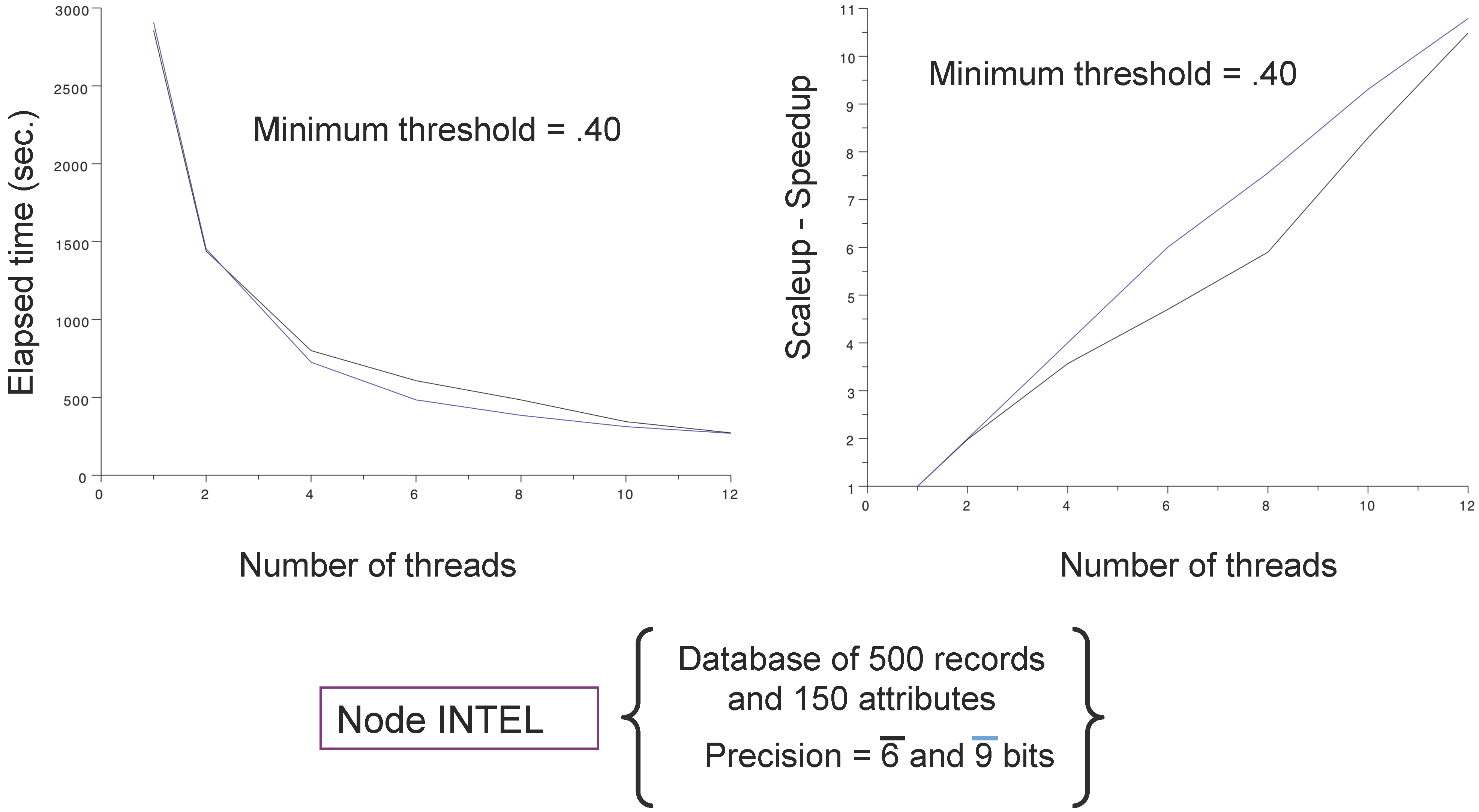
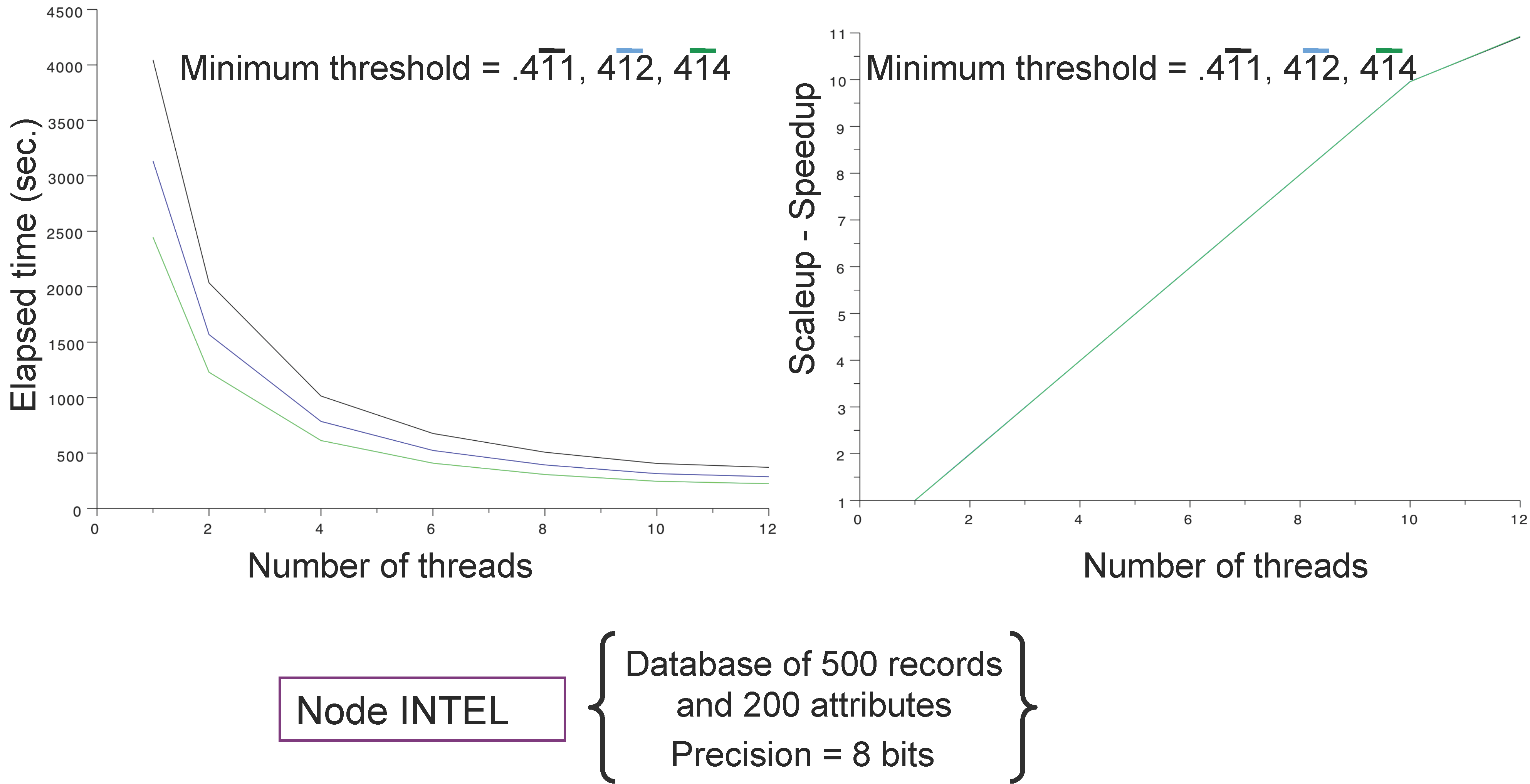
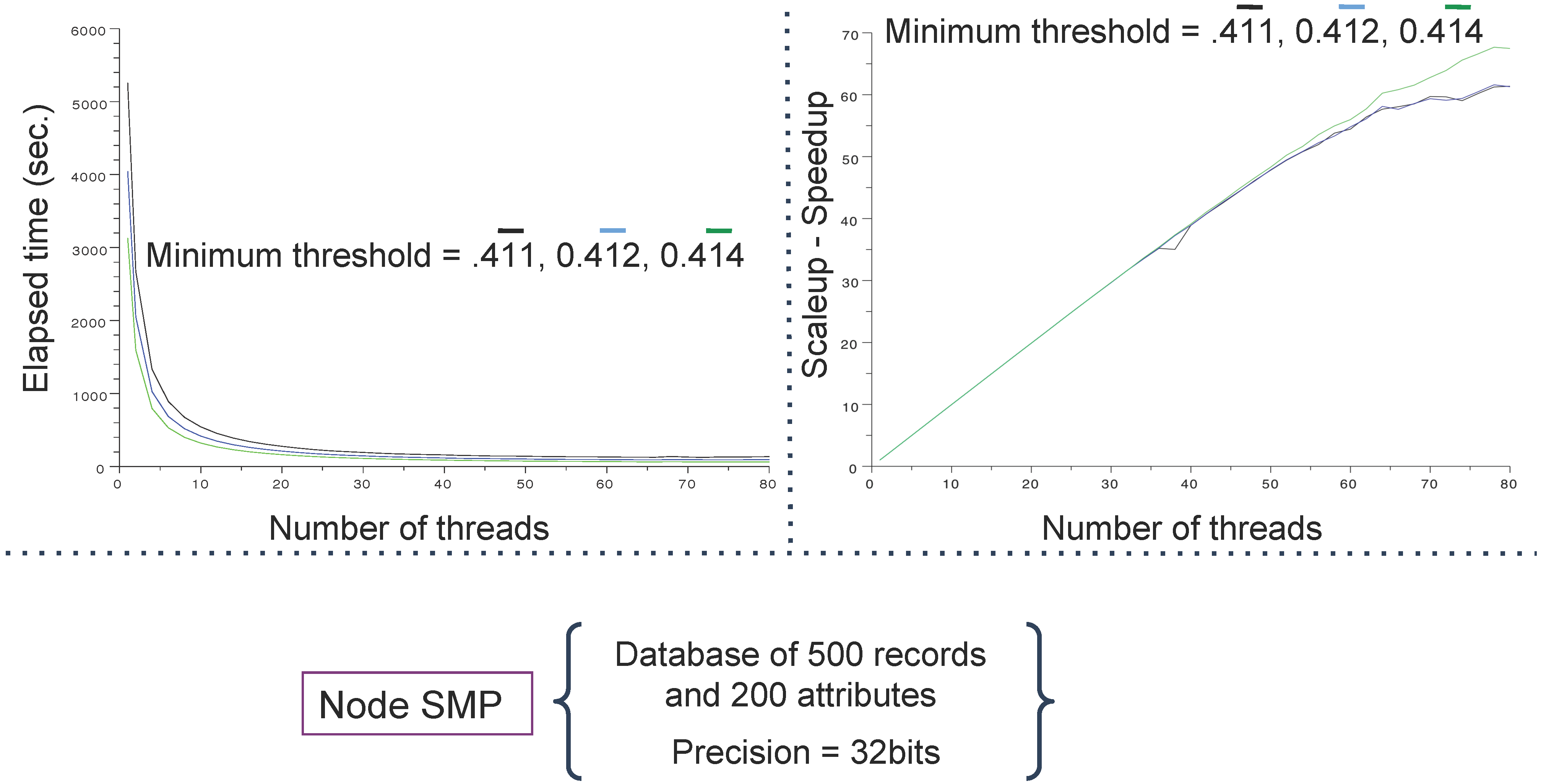
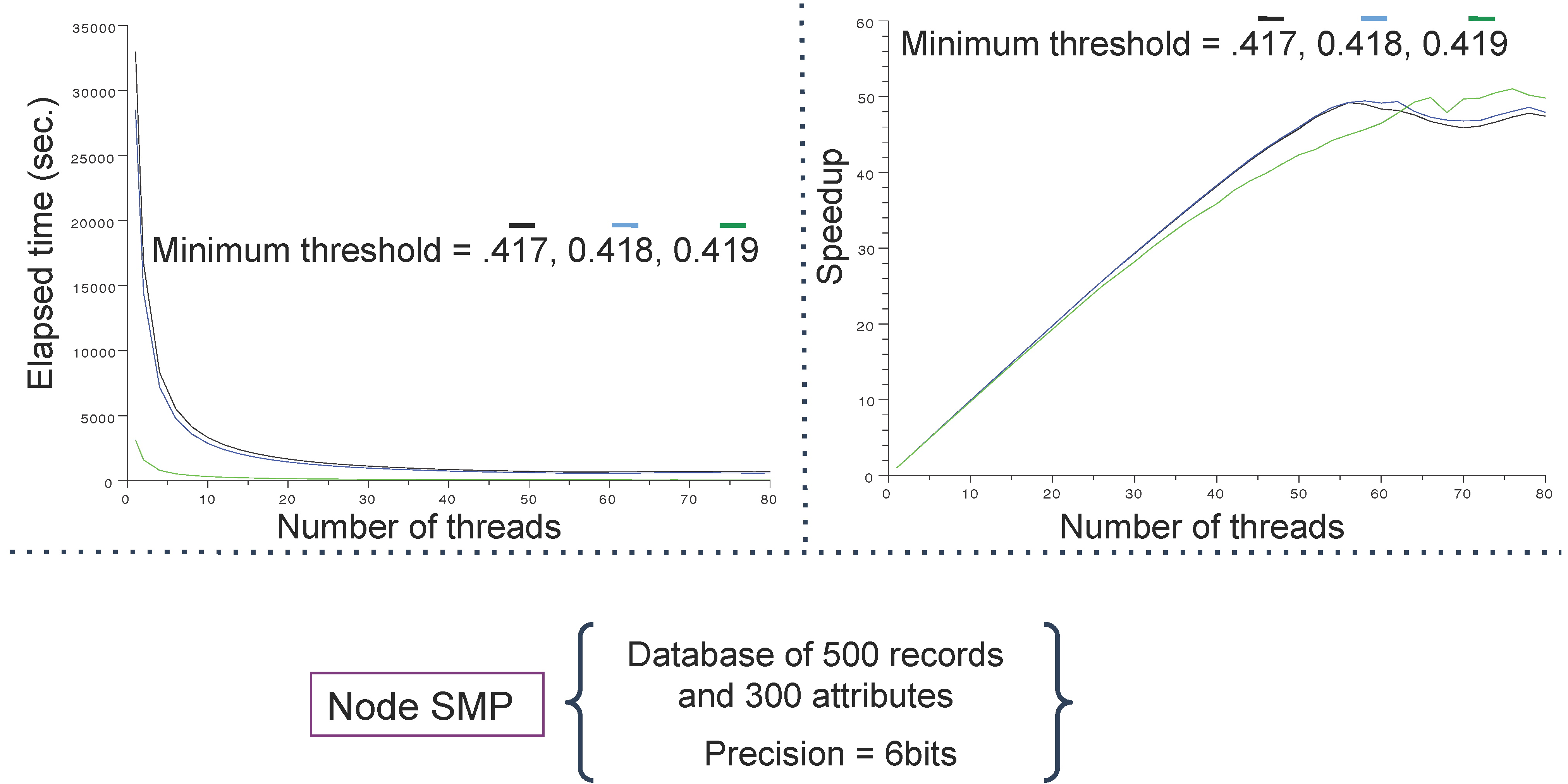
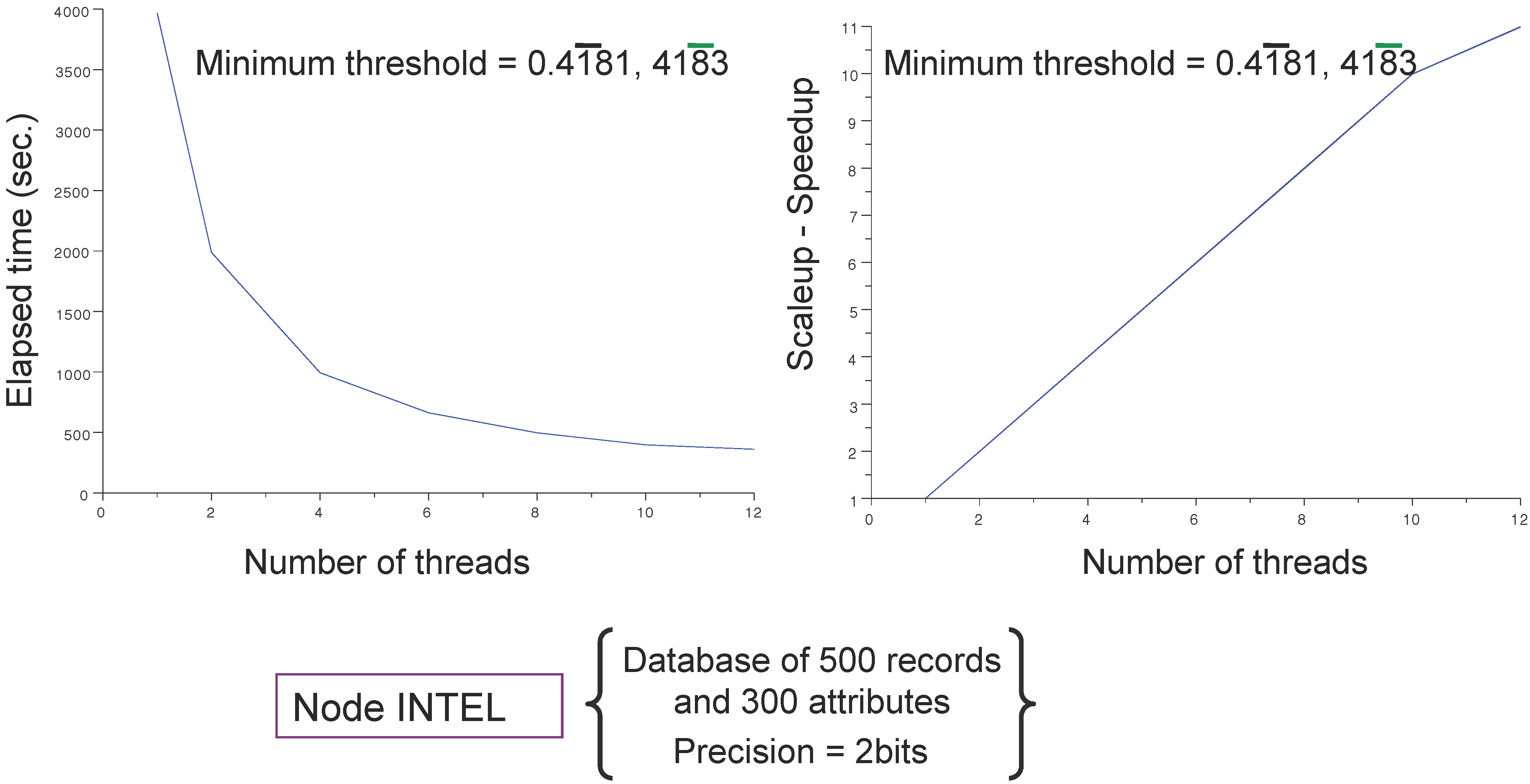
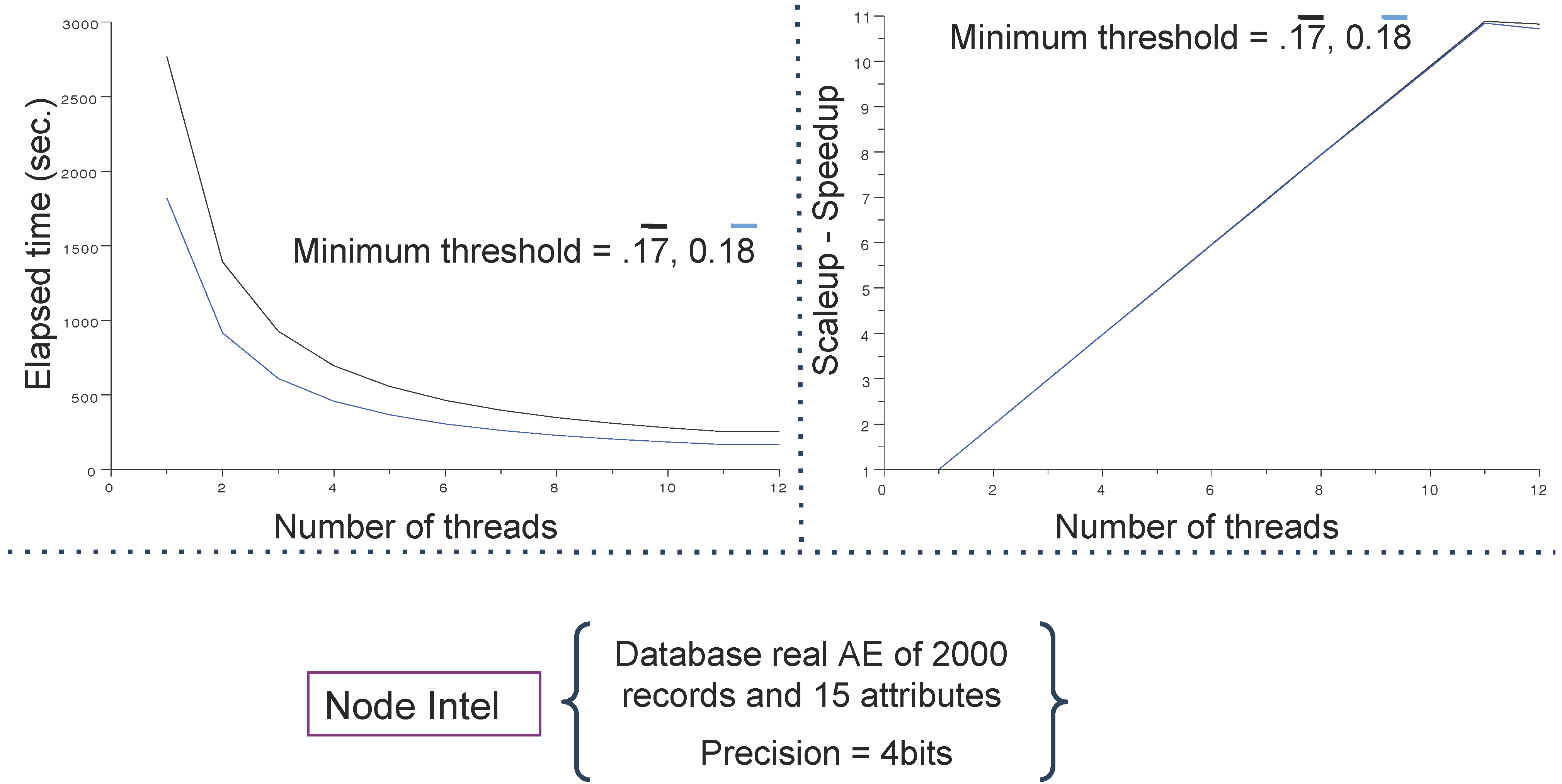
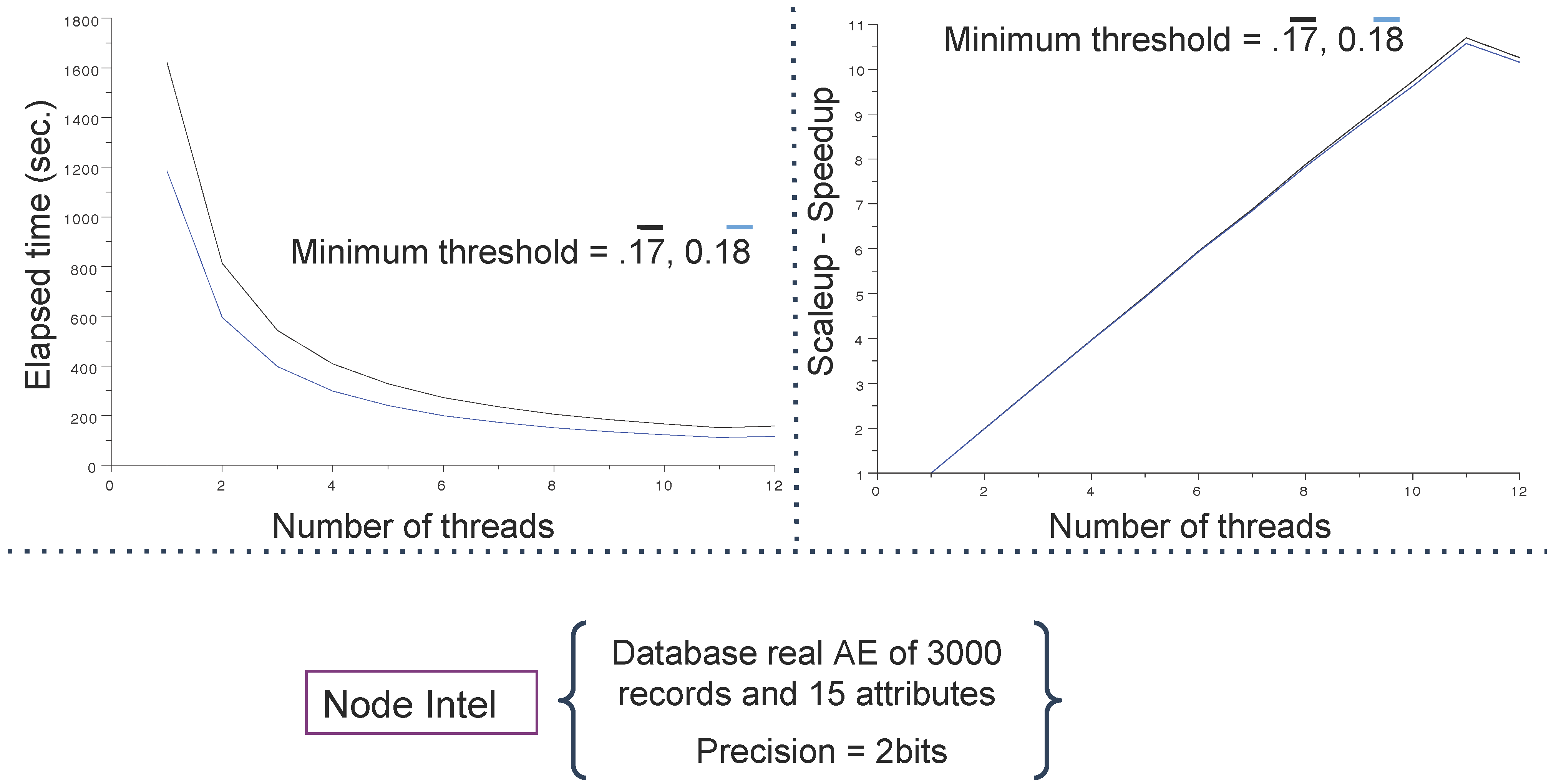
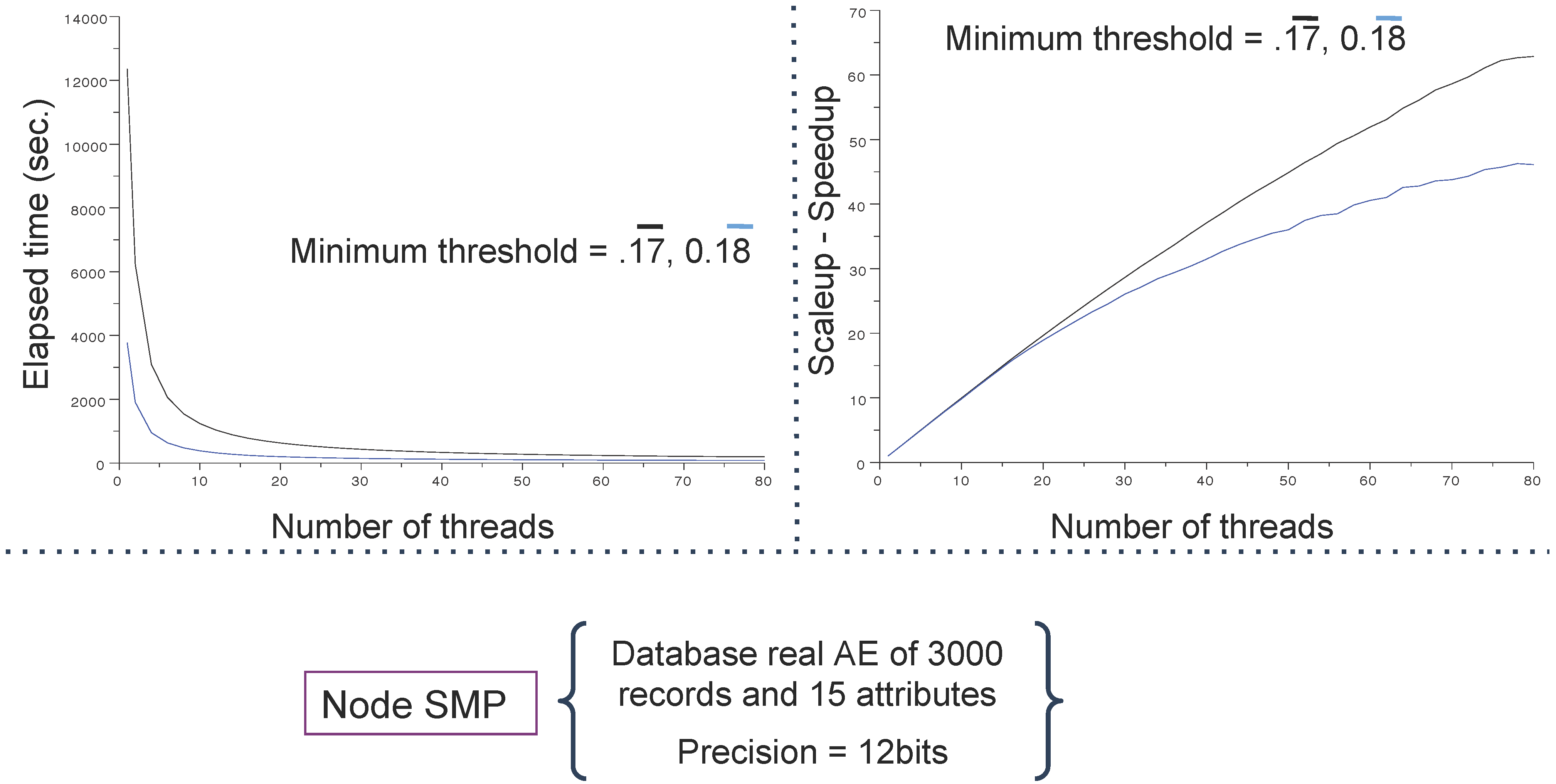
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Bodenhofer, U. Fuzzy Orderings of Fuzzy Sets. In Proceedings of the 10th IFSA World Congress, Istanbul, Turkey, 30 June–2 July 2003; pp. 500–5007.
- Koh, H.-W.; Hullermeier, E. Mining Gradual Dependencies Based on Fuzzy Rank Correlation. In Combining Soft Computing and Statistical Methods in Data Analysis; Volume 77, Advances in Intelligent and Soft Computing; Springer: Heidelberg, Germany, 2010; pp. 379–386. [Google Scholar]
- Lin, N.P.; Chueh, H. Fuzzy Correlation Rules Mining. In Proceedings of the 6th WSEAS International Conference on Applied Computer Science, Hangzhou, China, 15–17 April 2007; pp. 13–18.
- Laurent, A.; Lesot, M.-J.; Rifqi, M. GRAANK: Exploiting Rank Correlations for Extracting Gradual Itemsets. In Proceedings of the Eighth International Conference on Flexible Query Answering Systems (FQAS’09), Springer, Roskilde, Denmark, 26–28 October 2009; Volume LNAI 5822, pp. 382–393.
- Quintero, M.; Laurent, A.; Poncelet, P. Fuzzy Ordering for Fuzzy Gradual Patterns. In Proceedings of the FQAS 2011, Springer, Ghent, Belgium, 26–28 October 2011; Volume LNAI 7022, pp. 330–341.
- Di Jorio, L.; Laurent, A.; Teisseire, M. Mining Frequent Gradual Itemsets from Large Databases. In Proceedings of the International Conference on Intelligent Data Analysis (IDA’09), Lyon, France, 31 August–2 September, 2009.
- Quintero, M.; Laurent, A.; Poncelet, P.; Sicard, N. Fuzzy Orderings for Fuzzy Gradual Dependencies: Efficient Storage of Concordance Degrees. In Proceedings of the FUZZ-IEEE Conference, Brisbane, Australia, 10–15 June 2012.
- El-Rewini, H.; Abd-El-Barr, M. Advanced Computer Architecture Ans Parallel Processing; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Rauber, T.; Rünger, G. Parallel Programming: For Multicore and Cluster Systems; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Debosscher, J.; Sarro, L.M. Automated supervised classification of variable stars in the CoRoT programme: Method and application to the first four exoplanet fields. Astron. Astrophys. 2009, 506, 519–534. [Google Scholar] [CrossRef]
- Hill, M.D. What is scalability? ACM SIGARCH Comput. Archit. News 1990, 18, 18–21. [Google Scholar] [CrossRef]
- Bodenhofer, U.; Klawonn, F. Roboust rank correlation coefficients on the basis of fuzzy orderings: Initial steps. Mathw. Soft Comput. 2008, 15, 5–20. [Google Scholar]
- Calders, T.; Goethais, B.; Jarszewicz, S. Mining Rank-Correlated Sets of Numerical Attributes. In Proceedings of the KDD’06, 20–23 August 2006; ACM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Flynn, M. Some computer organizations and their effectiveness. IEEE Trans. Comput. 1972, C-21, 948–960. [Google Scholar] [CrossRef]
- Hüllermeier, E. Association Rules for Expressing Gradual Dependencies. In Proceedings of the PKDD Conference, Helsinki, Finland, 19–23 August 2002; Volume LNCS 2431, pp. 200–211.
- Zadeh, L.A. Similarity relations and fuzzy orderings. Inf. Sci. 1971, 3, 177–200. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sicard, N.; Aryadinata, Y.S.; Del Razo Lopez, F.; Laurent, A.; Flores, P.M.Q. Multi-Core Parallel Gradual Pattern Mining Based on Multi-Precision Fuzzy Orderings. Algorithms 2013, 6, 747-761. https://doi.org/10.3390/a6040747
Sicard N, Aryadinata YS, Del Razo Lopez F, Laurent A, Flores PMQ. Multi-Core Parallel Gradual Pattern Mining Based on Multi-Precision Fuzzy Orderings. Algorithms. 2013; 6(4):747-761. https://doi.org/10.3390/a6040747
Chicago/Turabian StyleSicard, Nicolas, Yogi Satrya Aryadinata, Federico Del Razo Lopez, Anne Laurent, and Perfecto Malaquias Quintero Flores. 2013. "Multi-Core Parallel Gradual Pattern Mining Based on Multi-Precision Fuzzy Orderings" Algorithms 6, no. 4: 747-761. https://doi.org/10.3390/a6040747
APA StyleSicard, N., Aryadinata, Y. S., Del Razo Lopez, F., Laurent, A., & Flores, P. M. Q. (2013). Multi-Core Parallel Gradual Pattern Mining Based on Multi-Precision Fuzzy Orderings. Algorithms, 6(4), 747-761. https://doi.org/10.3390/a6040747




