New Parallel Sparse Direct Solvers for Multicore Architectures
Abstract
:1. Background and Motivation
| Package | Year | Real/Complex | Positive definite | Indefinite | Out-of-core | Bit-compatible | Notes on parallelism |
|---|---|---|---|---|---|---|---|
| HSL_MA77 | 2006 | Real | √ | √ | √ | √ | Node-level parallelism only. |
| HSL_MA86 | 2011 | Both | √ | Fast task-based parallelism. | |||
| HSL_MA87 | 2009 | Both | √ | Fast task-based parallelism. | |||
| HSL_MA97 | 2011 | Both | √ | √ | √ | Constrained tree and | |
| node-level parallelism. |
- HSL_MA77 [2]: Solves very large sparse symmetric positive-definite and indefinite systems using a multifrontal algorithm; a key feature is out-of-core working, and there is an option to input the matrix A as a sum of (unassembled) finite elements.
- HSL_MA86 [3]: Solves sparse symmetric indefinite systems using a task-based algorithm; designed for multicore architectures.
- HSL_MA87 [4]: Solves sparse symmetric positive-definite systems using a task-based algorithm; designed for multicore architectures.
- HSL_MA97 [5]: Solves sparse symmetric positive-definite and indefinite systems using a multifrontal algorithm, optionally using OpenMP for parallel computation; a key feature is bit-compatibility.
2. Sparse Direct Algorithms
- An ordering phase that exploits the sparsity (non-zero) structure of A to determine a pivot sequence (that is, the order in which the Gaussian elimination operations will be performed). The choice of pivot sequence significantly influences both memory requirements and the number of floating-point operations required to carry out the factorization.
- An analyse phase that uses the pivot sequence to establish the work flow and data structures for the factorization. This phase generally works only with the sparsity pattern of A (this is the case for all the solvers in this study).
- A factorization phase that performs the numerical factorization. Following the analyse phase, more than one matrix with the same sparsity pattern may be factorized.
- A solve phase that performs forward elimination followed by back substitution using the stored factors. The solvers in this study all allow the solve phase to solve for a single right-hand side or for multiple right-hand sides on one call. Repeated calls to the solve phase may follow the factorization phase. This is typically used to implement iterative refinement (see, for example, [9]) to improve the accuracy of the computed solution.
2.1. Selecting an Ordering
2.2. The Analyse Phase
2.3. An Introduction to the Factorize Phase
2.4. The Importance of Scaling
2.5. The Issue of Bit Compatibility
3. Supernodal Task-Based Approach
3.1. Positive-Definite Case (HSL_MA87)
- factorize_block() This computes the traditional dense Cholesky factor of the triangular part of a block that is on the diagonal. If the block is trapezoidal, this is followed by a triangular solve of its rectangular part
- solve_block() This performs a triangular solve of an off-diagonal block by the Cholesky factor of the block on its diagonal, i.e.,
- update_internal(, ) This performs the update of the block by the block column belonging to the same nodal matrix, i.e.,where is a block within and is a submatrix in the same block column.
- update_between(, , ) This performs the update of the block by the block column of a descendant supernode i.e.,where and are submatrices of contiguous rows of that correspond to the rows and columns of , respectively.
3.2. Indefinite Case (HSL_MA86)

4. Multifrontal Approach
4.1. Supernodal Multifrontal (HSL_MA97)
- Tree-level parallelism that performs assembly and factorization work associated with different frontal matrices on different threads.
- Node-level parallelism that uses traditional dense linear algebra techniques to speed up the factorization of individual frontal matrices.
4.2. Out-of-Core Working (HSL_MA77)
5. Numerical Experiments
| Index | Name | n (103) | nz(A) (106) | nz(L) (106) | nflops (109) | Description |
|---|---|---|---|---|---|---|
| 1. | GHS_psdef/vanbody | 47.0 | 2.32 | 6.35 | 1.40 | Structural |
| 2. | GHS_psdef/oilpan | 73.8 | 2.15 | 7.00 | 2.90 | Structural |
| 3. | GHS_psdef/s3dkq4m2 | 90.4 | 4.43 | 18.9 | 7.33 | Structural |
| 4. | Wissgott/parabolic_fem | 525.8 | 3.67 | 31.0 | 7.46 | CFD |
| 5. | Schmid/thermal2 | 1,228 | 8.58 | 63.0 | 15.1 | Steady state thermal |
| 6. | Boeing/pwtk | 217.9 | 11.5 | 50.8 | 22.9 | Structural: wind tunnel |
| 7. | GHS_psdef/crankseg_1 | 52.8 | 10.6 | 34.0 | 32.5 | Structural |
| 8. | Rothberg/cfd2 | 123.4 | 3.09 | 40.0 | 33.0 | CFD |
| 9. | DNVS/shipsec1 | 140.9 | 3.57 | 40.5 | 38.3 | Structural: ship section |
| 10. | DNVS/shipsec5 | 179.9 | 4.60 | 55.3 | 57.7 | Structural: ship section |
| 11. | AMD/G3_circuit | 1,585 | 7.66 | 118.8 | 58.7 | Circuit simulation |
| 12. | GHS_psdef/bmwcra_1 | 148.8 | 10.6 | 71.8 | 61.5 | Structural |
| 13. | Schenk_AFE/af_5_k101 | 503.6 | 17.6 | 103.6 | 61.6 | Structural: sheet metal forming |
| 14. | Um/2cubes_sphere | 101.4 | 1.65 | 46.5 | 75.2 | Electromagnetics: 2 cubes in a sphere |
| 15. | GHS_psdef/ldoor | 952.2 | 42.5 | 154.7 | 79.9 | Structural |
| 16. | DNVS/ship_003 | 121.7 | 3.78 | 62.0 | 81.9 | Structural: ship structure |
| 17. | Um/offshore | 259.8 | 4.24 | 88.4 | 106.3 | Electromagnetics: transient field diffusion |
| 18. | GHS_psdef/inline_1 | 503.7 | 36.8 | 179.6 | 146.1 | Structural |
| 19. | GHS_psdef/apache2 | 715.2 | 4.82 | 148.6 | 176.0 | Structural |
| 20. | ND/nd24k | 72.0 | 28.7 | 321.7 | 2,057 | 2D/3D |
| 21. | Gupta/nastran-b (*) | 1,508 | 56.6 | 1,071 | 3,174 | Structural |
| 22. | Janna/Flan_1565 | 1,565 | 114.2 | 1,501 | 3,868 | Structural: steel flange |
| 23. | Oberwolfach/bone010 | 983.7 | 47.9 | 1,092 | 3,882 | Model reduction: trabecular bone |
| 24. | Janna/StocF-1465 | 1,465 | 21.0 | 1,149 | 4,391 | CFD: flow with stochastic permeabilities |
| 25. | GHS_psdef/audikw_1 | 943.7 | 77.7 | 1,259 | 5,811 | Structural |
| 26. | Janna/Fault_639 | 638.8 | 27.2 | 1,156 | 8,289 | Structural: faulted gas reservoir |
| 27. | Gupta/sgi_1M (*) | 1,522 | 63.6 | 2,049 | 9,017 | Structural |
| 28. | Janna/Geo_1438 | 1,438 | 60.2 | 2,492 | 18,067 | Structural: geo mechanical deformation model |
| 29. | Gupta/ten-b (*) | 1,371 | 54.7 | 3,298 | 33,095 | 3D metal forming |
| 30. | Gupta/algor-big (*) | 1,074 | 42.7 | 3,001 | 39,920 | Stress analysis |
| Index | Name | n (103) | nz(A) (106) | nz(L) (106) | nflops (109) | Description |
|---|---|---|---|---|---|---|
| 31. | GHS_indef/dixmaanl | 60.0 | 0.30 | 0.61 | 0.007 | Optimization |
| 32. | Marini/eurqsa | 7.3 | 0.007 | 0.29 | 0.03 | Time series |
| 33. | IPSO/HTC_336_4438 | 226.3 | 0.78 | 2.98 | 0.12 | Power network |
| 34. | TSOPF/TSOPF_FS_b39_c19 | 76.2 | 1.98 | 4.40 | 0.29 | Transient optimal power flow |
| 35. | GHS_indef/stokes128 | 49.7 | 0.56 | 2.98 | 0.37 | CFD |
| 36. | GHS_indef/mario002 | 389.9 | 2.10 | 8.09 | 0.55 | 2D/3D |
| 37. | Boeing/bcsstk39 | 46.8 | 2.06 | 7.92 | 2.20 | Structural: solid state rocket booster |
| 38. | GHS_indef/cont-300 | 180.9 | 0.99 | 11.7 | 2.96 | Optimization |
| 39. | GHS_indef/turon_m | 189.9 | 1.69 | 13.7 | 4.23 | 2D/3D: mine model |
| 40. | GHS_indef/bratu3d | 27.8 | 0.17 | 6.28 | 4.42 | Optimization |
| 41. | GHS_indef/d_pretok | 182.7 | 1.64 | 14.6 | 5.06 | 2D/3D: mine model |
| 42. | GHS_indef/copter2 | 55.5 | 0.76 | 10.4 | 5.49 | CFD: rotor blade |
| 43. | Cunningham/qa8fk | 66.1 | 1.66 | 24.3 | 21.3 | Acoustics |
| 44. | GHS_indef/bmw3_2 | 227.4 | 11.3 | 49.1 | 29.8 | Structural |
| 45. | Oberwolfach/t3dh | 79.2 | 4.35 | 48.1 | 69.1 | Model reduction: micropyros thruster |
| 46. | Dziekonski/gsm_106857 | 589.5 | 21.8 | 137.1 | 82.6 | Electromagnetics |
| 47. | Schenk_IBMNA/c-big | 345.2 | 2.34 | 52.0 | 115 | Optimization |
| 48. | Schenk_AFE/af_shell10 | 1,508 | 52.3 | 368 | 393 | Structural: sheet metal forming |
| 49. | Zaoui/kkt_power | 2,063 | 12.8 | 12.8 | 12.8 | Optimal power flow |
| 50. | Dziekonski/dielFilterV2real | 1,157 | 48.5 | 607 | 1,296 | Electromagnetics: dielectric resonator |
| 51. | PARSEC/Si34H36 | 97.6 | 5.16 | 486 | 4,267 | Quantum chemistry |
| 52. | PARSEC/SiO2 | 155.3 | 11.3 | 1.37 | 13,249 | Quantum chemistry |
| 53. | PARSEC/Si41Ge41H72 | 185.6 | 15.0 | 1,411 | 20,147 | Quantum chemistry |
| 54. | Schenk/nlpkkt80 | 1,062 | 28.2 | 2,282 | 29,265 | Optimization |
| 55. | Schenk/nlpkkt120 | 3,542 | 95.1 | 13,684 | 143,600 | Optimization |
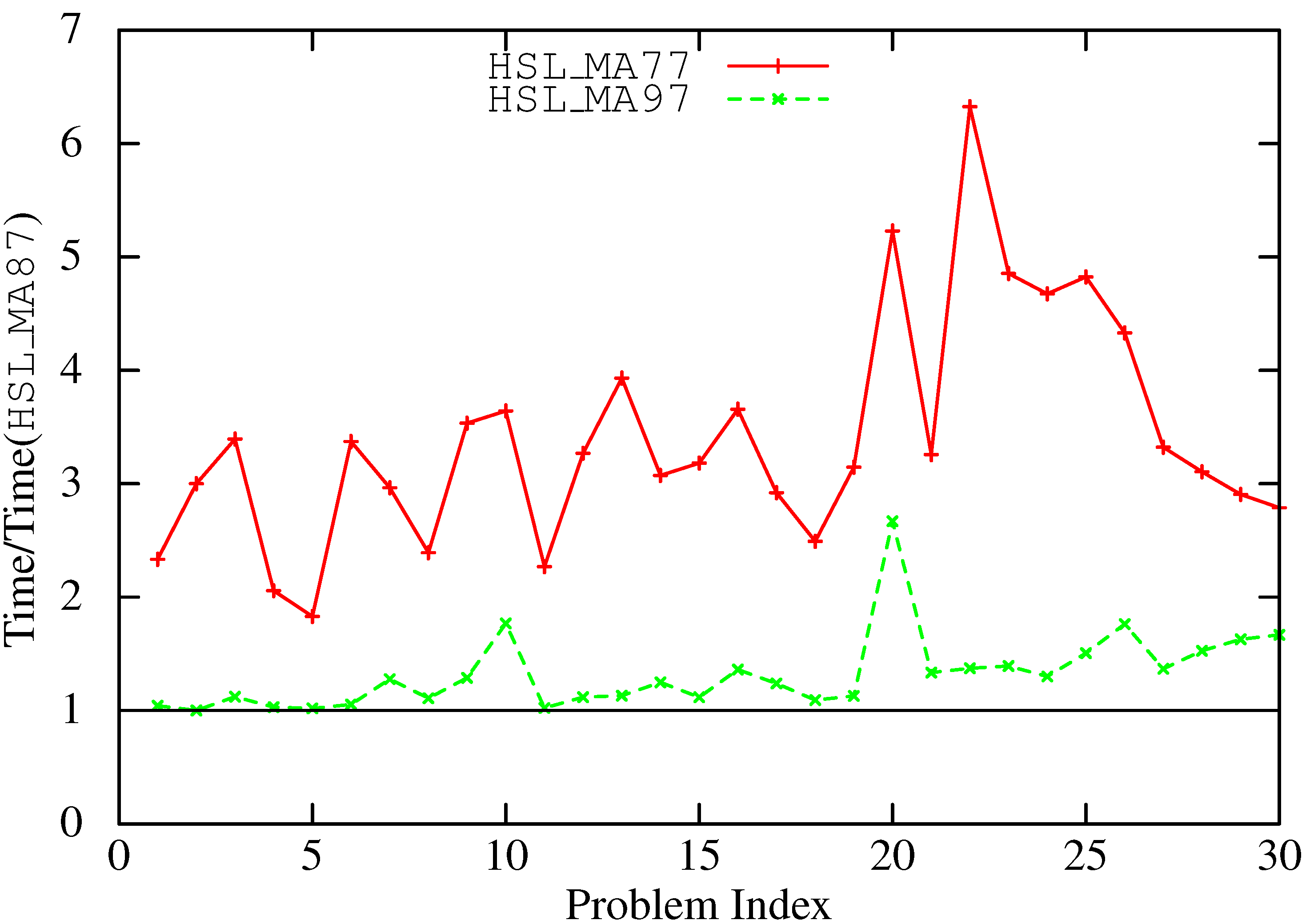
| Problem | MA57 | HSL_MA77 | HSL_MA87 | HSL_MA97 |
|---|---|---|---|---|
| 1. | 0.51 | 0.56 | 0.24 | 0.25 |
| 2. | 0.71 | 0.72 | 0.24 | 0.24 |
| 3. | 1.27 | 1.12 | 0.33 | 0.37 |
| 4. | 3.90 | 5.47 | 2.66 | 2.74 |
| 5. | 9.55 | 13.0 | 7.11 | 7.24 |
| 6. | 3.66 | 3.17 | 0.94 | 0.99 |
| 7. | 3.22 | 2.46 | 0.83 | 1.06 |
| 8. | 3.87 | 3.54 | 1.48 | 1.64 |
| 9. | 3.38 | 2.58 | 0.73 | 0.94 |
| 10. | 4.99 | 3.46 | 0.95 | 1.68 |
| 11. | 14.4 | 18.5 | 8.16 | 8.34 |
| 12. | 6.23 | 5.00 | 1.53 | 1.71 |
| 13. | 7.55 | 6.88 | 1.75 | 1.98 |
| 14. | 5.40 | 4.21 | 1.37 | 1.71 |
| 15. | 11.8 | 11.7 | 3.69 | 4.12 |
| 16. | 6.49 | 3.95 | 1.08 | 1.47 |
| 17. | 9.61 | 8.82 | 3.02 | 3.74 |
| 18. | 16.4 | 13.0 | 5.20 | 5.68 |
| 19. | 15.7 | 16.0 | 5.07 | 5.72 |
| 20. | 120 | 78.3 | 15.0 | 40.0 |
| 21. | 155 | 97.8 | 30.0 | 40.0 |
| 22. | 164 | 184 | 29.2 | 40.0 |
| 23. | 144 | 118 | 24.2 | 33.7 |
| 24. | 177 | 155 | 33.2 | 43.1 |
| 25. | 194 | 159 | 33.0 | 49.7 |
| 26. | 268 | 158 | 36.4 | 64.1 |
| 27. | + | 186 | 55.9 | 76.4 |
| 28. | + | 244 | 78.6 | 120 |
| 29. | + | 398 | 137 | 223 |
| 30. | + | 452 | 162 | 270 |
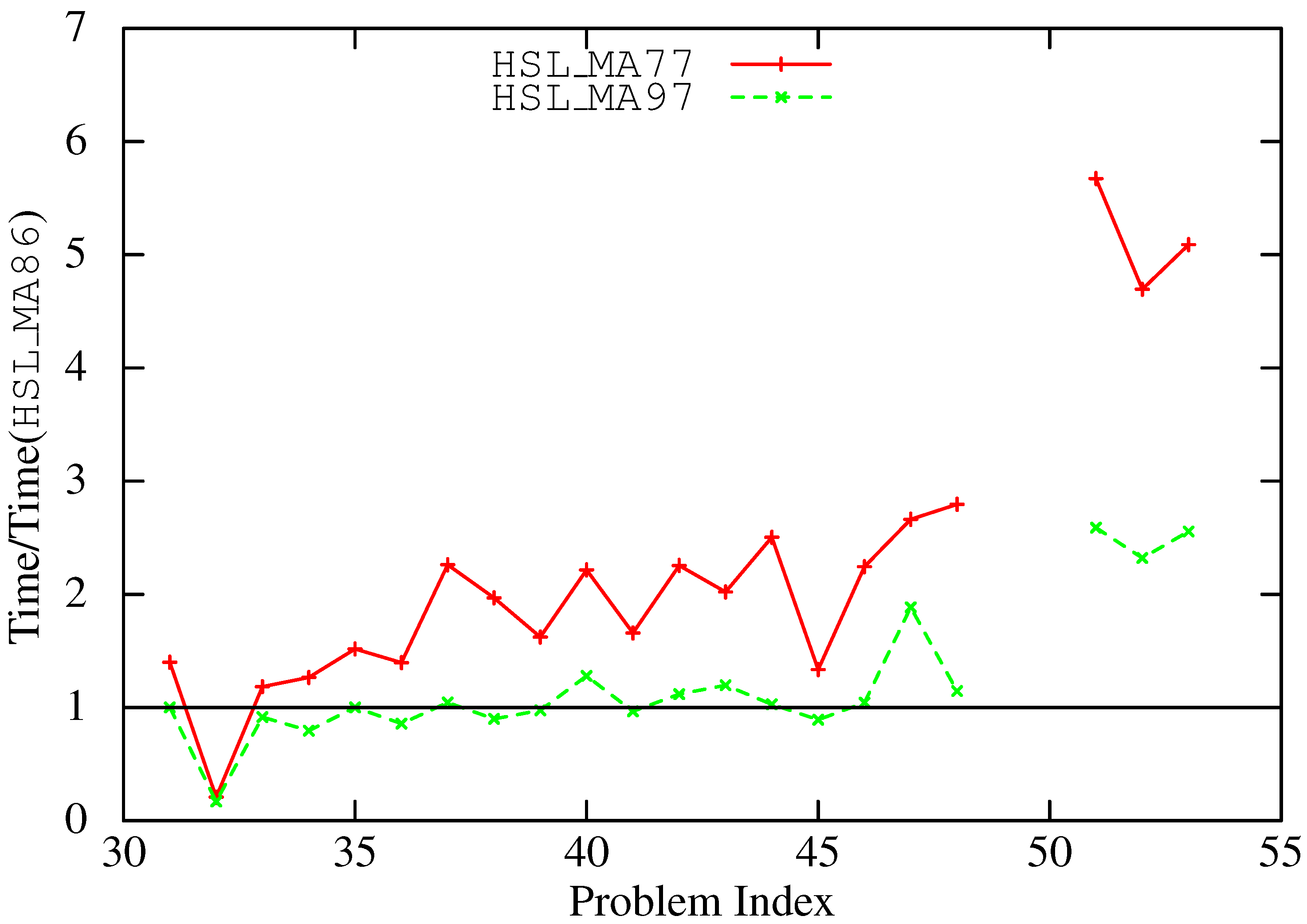
| Problem | MA57 | HSL_MA77 | HSL_MA86 | HSL_MA97 |
|---|---|---|---|---|
| 31. | 0.13 | 0.21 | 0.15 | 0.15 |
| 32. | - | 0.11 | 0.53 | 0.09 |
| 33. | 1.30 | 1.67 | 1.41 | 1.29 |
| 34. | 1.42 | 1.05 | 0.83 | 0.66 |
| 35. | 0.55 | 0.44 | 0.29 | 0.29 |
| 36. | 2.28 | 2.54 | 1.82 | 1.56 |
| 37. | 0.58 | 0.52 | 0.23 | 0.24 |
| 38. | 4.33 | 2.54 | 1.29 | 1.16 |
| 39. | 1.76 | 1.93 | 1.19 | 1.16 |
| 40. | 5.77 | 1.75 | 0.79 | 1.01 |
| 41. | 2.71 | 1.99 | 1.20 | 1.16 |
| 42. | 1.11 | 1.15 | 0.51 | 0.57 |
| 43. | 2.38 | 1.96 | 0.97 | 1.16 |
| 44. | †6.94 | †6.31 | †2.52 | †2.59 |
| 45. | 6.53 | 4.91 | †3.68 | †3.28 |
| 46. | 9.73 | 16.1 | 7.18 | 7.49 |
| 47. | 7.01 | 11.4 | 4.29 | 8.09 |
| 48. | 23.9 | 22.4 | 8.00 | 9.16 |
| 49. | - | †4,891 | - | - |
| 50. | 1,522 | 266 | - | 73.8 |
| 51. | 265 | 178 | 31.4 | 81.2 |
| 52. | 685 | 397 | 84.6 | 196 |
| 53. | 2,508 | 600 | 118 | 301 |
| 54. | - | 2,168 | - | - |
| 55. | - | 44,649 | - | - |
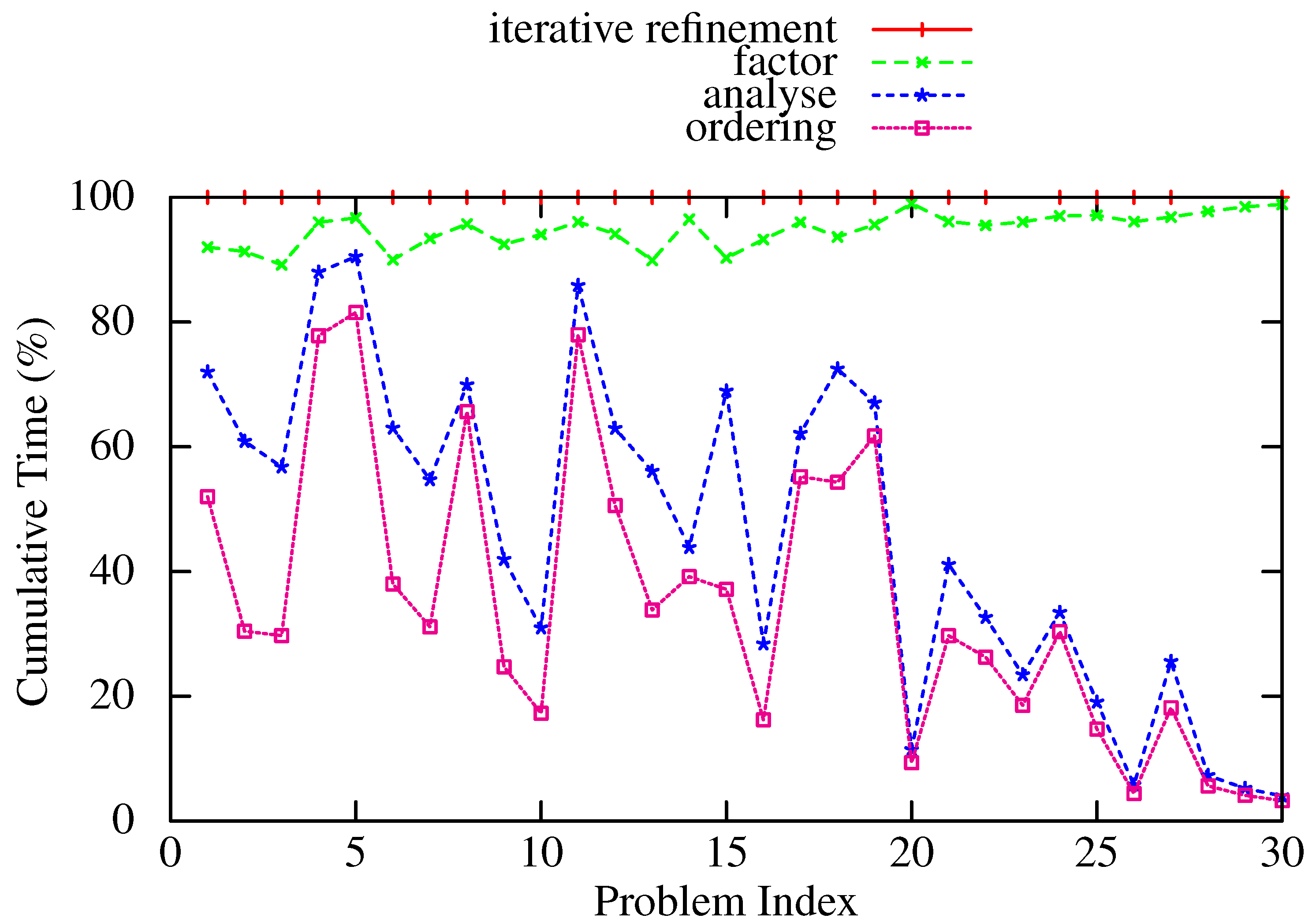
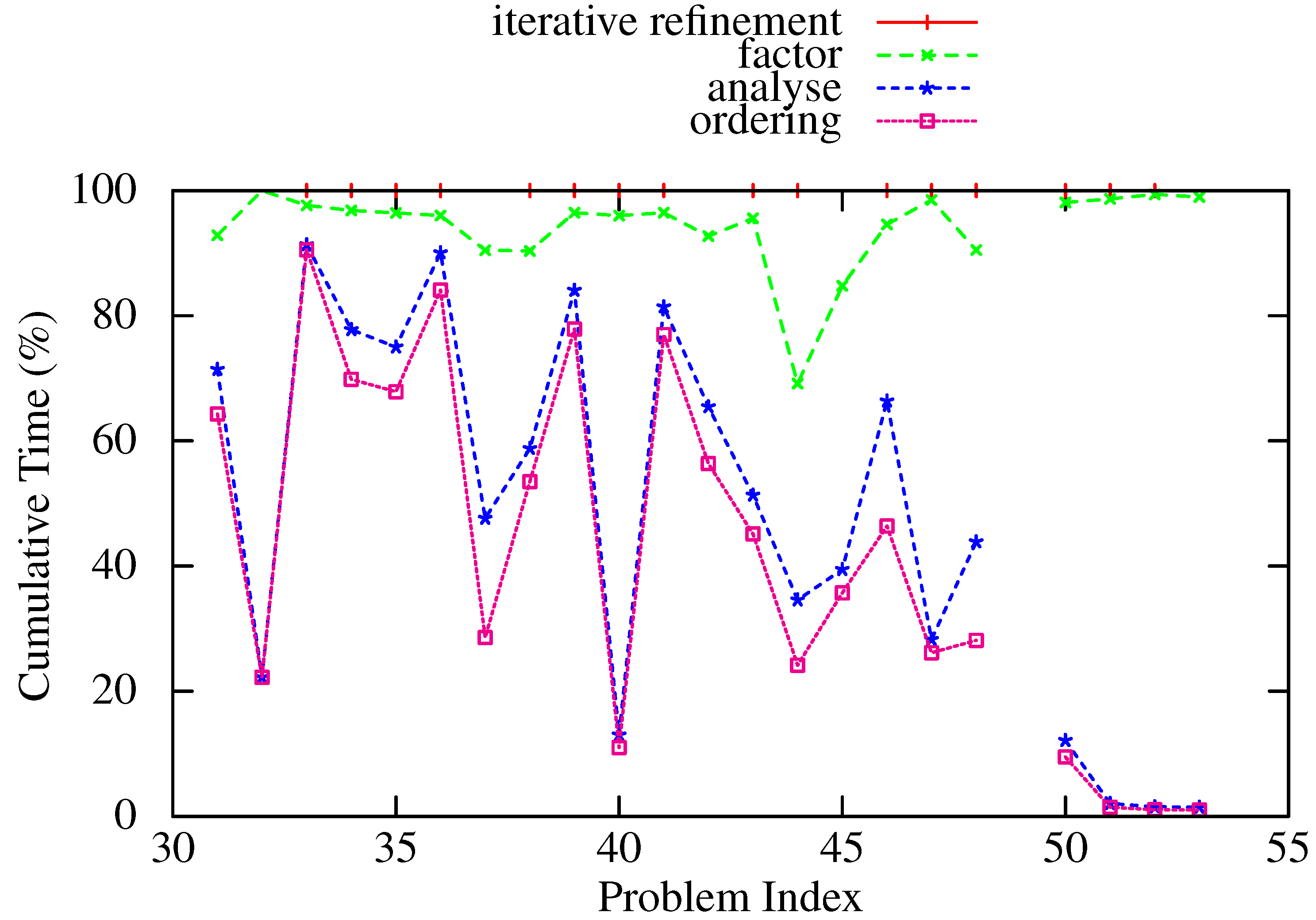
6. Concluding Remarks
Code Availability
Acknowledgements
Conflicts of Interest
References
- HSL. A collection of Fortran codes for large-scale scientific computation, 2013. Available online: http://www.hsl.rl.ac.uk/ (accessed on 28 October 2013).
- Reid, J.; Scott, J. An out-of-core sparse Cholesky solver. ACM Trans. Math. Softw. 2009, 36. [Google Scholar] [CrossRef]
- Hogg, J.; Scott, J. An Indefinite Sparse Direct Solver for Large Problems on Multicore Machines; Technical Report RAL-TR-2010-011; Rutherford Appleton Laboratory: Didcot, UK, 2010. [Google Scholar]
- Hogg, J.; Reid, J.; Scott, J. Design of a multicore sparse Cholesky factorization using DAGs. SIAM J. Sci. Comput. 2010, 32, 3627–3649. [Google Scholar] [CrossRef]
- Hogg, J.; Scott, J. HSL_MA97: A Bit-Compatible Multifrontal Code for Sparse Symmetric Systems; Technical Report RAL-TR-2011-024; Rutherford Appleton Laboratory: Didcot, UK, 2011. [Google Scholar]
- Davis, T. Direct Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Duff, I.; Erisman, A.; Reid, J. Direct Methods for Sparse Matrices; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Gould, N.; Hu, Y.; Scott, J. A numerical evaluation of sparse direct symmetric solvers for the solution of large sparse, symmetric linear systems of equations. ACM Trans. Math. Softw. 2007, 33. [Google Scholar] [CrossRef]
- Golub, G.; van Loan, C. Matrix Computations, 3rd ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Tinney, W.; Walker, J. Direct solutions of sparse network equations by optimally ordered triangular factorization. Proc. IEEE 1967, 55, 1801–1809. [Google Scholar] [CrossRef]
- Amestoy, P.; Davis, T.; Duff, I. An approximate minimum degree ordering algorithm. SIAM J. Matrix Anal. Appl. 1996, 17, 886–905. [Google Scholar] [CrossRef]
- Amestoy, P.; Davis, T.; Duff, I. Algorithm 837: AMD, an approximate minimum degree ordering algorithm. ACM Trans. Math. Softw. 2004, 30, 381–388. [Google Scholar] [CrossRef]
- Liu, J. Modification of the minimum-degree algorithm by multiple elimination. ACM Trans. Math. Softw. 1985, 11, 141–153. [Google Scholar] [CrossRef]
- George, A. Nested dissection of a regular finite-element mesh. SIAM J. Numer. Anal. 1973, 10, 345–363. [Google Scholar] [CrossRef]
- Gould, N.; Scott, J. A numerical evaluation of HSL packages for the direct solution of large sparse, symmetric linear systems of equations. ACM Trans. Math. Softw. 2004, 30, 300–325. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. METIS: A software package for partitioning unstructured graphs, partitioning meshes and computing fill-reducing orderings of sparse matrices—Version 4.0, 1998. Available online: http://www-users.cs.umn.edu/karypis/metis/ (accessed on 28 October 2013).
- Karypis, G.; Kumar, V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput. 1999, 20, 359–392. [Google Scholar] [CrossRef]
- Pellegrini, F. SCOTCH 5.1 User’s Guide; Technical Report. LaBRI, Universit/’e Bordeaux I: Frace, 2008. Available online: http://www.labri.fr/perso/pelegrin/scotch/ (accessed on 28 October 2013).
- Boman, E.; Devine, K.; Fisk, L.A.; Heaphy, R.; Hendrickson, B.; Vaughan, C.; Catalyurek, U.; Bozdag, D.; Mitchell, W.; Teresco, J. Zoltan 3.0: Parallel Partitioning, Load-balancing, and Data Management Services; User’s Guide; Technical Report SAND2007-4748W; SANDIA National Laboratory: Albuquerque, NM, USA, 2007. Available online: http://www.cs.sandia.gov/Zoltan/ug html/ug.html (accessed on 28 October 2013).
- Duff, I.; Scott, J. Towards an Automatic Ordering for a Symmetric Sparse Direct Solver; Technical Report RAL-TR-2006-001; Rutherford Appleton Laboratory: Didcot, UK, 2005. [Google Scholar]
- Liu, J. The role of elimination trees in sparse factorization. SIAM J. Matrix Anal. Appl. 1990, 11, 134–172. [Google Scholar] [CrossRef]
- Dongarra, J.; Croz, J.D.; Hammarling, S.; Duff, I.S. A set of level 3 basic linear algebra subprograms. ACM Trans. Math. Softw. 1990, 16, 1–17. [Google Scholar] [CrossRef]
- Ashcraft, C.; Grimes, R.G. The influence of relaxed supernode partitions on the multifrontal method. ACM Trans. Math. Softw. 1989, 15, 291–309. [Google Scholar] [CrossRef]
- Hogg, J.; Scott, J. A Modern Analyse Phase for Sparse Tree-Based Direct Methods; Technical Report RAL-TR-2010-031; Rutherford Appleton Laboratory: Didcot, UK, 2010. [Google Scholar]
- Duff, I.; Reid, J. The multifrontal solution of indefinite sparse symmetric linear systems. ACM Trans. Math. Softw. 1983, 9, 302–325. [Google Scholar] [CrossRef]
- Liu, J. The multifrontal method for sparse matrix solution: Theory and practice. SIAM Rev. 1992, 34, 82–109. [Google Scholar] [CrossRef]
- Ashcraft, C.; Grimes, R.G.; Lewis, J.G. Accurate symmetric indefinite linear equation solvers. SIAM J. Matrix Anal. Appl. 1999, 20, 513–561. [Google Scholar] [CrossRef]
- Bunch, J.R.; Kaufman, L. Some stable methods for calculating inertia and solving symmetric linear systems. Math. Comput. 1977, 31, 163–179. [Google Scholar] [CrossRef]
- Duff, I.S.; Gould, N.I.M.; Reid, J.K.; Scott, J.A.; Turner, K. Factorization of sparse symmetric indefinite matrices. IMA J. Numer. Anal. 1991, 11, 181–204. [Google Scholar] [CrossRef]
- Hogg, J.; Scott, J. Pivoting strategies for tough sparse indefinite systems. ACM Trans. Math. Softw. 2014, 40. to be published. [Google Scholar] [CrossRef]
- Hogg, J.; Scott, J. Compressed Threshold Pivoting for Sparse Symmetric Indefinite Systems; Technical Report RAL-P-2013-007; Rutherford Appleton Laboratory: Didcot, UK, 2013. [Google Scholar]
- Hogg, J.; Scott, J. The Effects of Scalings on the Performance of a Sparse Symmetric Indefinite Solver; Technical Report RAL-TR-2008-007; Rutherford Appleton Laboratory: Didcot, UK, 2008. [Google Scholar]
- Hogg, J.; Scott, J. Optimal weighted matchings for rank-deficient sparse matrices. SIAM J. Matrix Anal. Appl. 2013, 34, 1431–1447. [Google Scholar] [CrossRef]
- Hogg, J.; Scott, J. Achieving Bit Compatibility in Sparse Direct Solvers; Technical Report RAL-P-2012-005; Rutherford Appleton Laboratory: Didcot, UK, 2012. [Google Scholar]
- Buttari, A.; Dongarra, J.; Kurzak, J.; Langou, J.; Luszczek, P.; Tomov, S. The Impact of Multicore on Math Software. In Proceedings of Workshop on State-of-the-Art in Scientific and Parallel Computing (PARA’06), Umeå, Sweden, 18–21 July 2006.
- Buttari, A.; Langou, J.; Kurzak, J.; Dongarra, J. A Class of Parallel Tiled Linear Algebra Algorithms for Multicore Architectures; Technical Report UT-CS-07-600; Also LAPACK Working Note 191; ICL, University of Tennessee: Knoxville, TN, USA, 2007. [Google Scholar]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide, 3rd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Reid, J.; Scott, J. Partial Factorization of a Dense Symmetric Indefinite Matrix. ACM Trans. Math. Softw. 2011, 38. [Google Scholar] [CrossRef]
- Reid, J.; Scott, J. Algorithm 891: A Fortran virtual memory system. ACM Trans. Math. Softw. 2009, 36, 1–12. [Google Scholar] [CrossRef]
- Davis, T.; Hu, Y. The University of Florida sparse matrix collection. ACM Trans. Math. Softw. 2011, 38. [Google Scholar] [CrossRef]
- Ruiz, D.; Uçar, B. A Symmetry Preserving Algorithm of Matrix Scaling; Technical Report RR-7552; INRIA: Paris, France, 2011. [Google Scholar]
- Duff, I.S. MA57—a new code for the solution of sparse symmetric definite and indefinite systems. ACM Trans. Math. Softw. 2004, 30, 118–154. [Google Scholar] [CrossRef]
- Hogg, J.; Scott, J. A fast and robust mixed precision solver for the solution of sparse symmetric linear systems. ACM Trans. Math. Softw. 2010, 37. [Google Scholar] [CrossRef]
- Schenk, O.; Gärtner, K. Solving unsymmetric sparse systems of linear equations with PARDISO. J. Future Generation Comput. Syst. 2004, 20, 475–487. [Google Scholar] [CrossRef]
- Schenk, O.; Gärtner, K. On fast factorization pivoting methods for symmetric indefinite systems. Electron. Trans. Numer. Anal. 2006, 23, 158–179. [Google Scholar]
- Amestoy, P.; Duff, I.; L’Excellent, J.Y.; Koster, J. A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Appl. 2001, 23, 15–41. [Google Scholar] [CrossRef]
- Hénon, P.; Ramet, P.; Roman, J. PaStiX: A high-performance parallel direct solver for sparse symmetric definite systems. Parallel Comput. 2002, 28, 301–321. [Google Scholar] [CrossRef]
- Gupta, A.; Joshi, M.; Kumar, V. WSMP: A High-Performance Serial and Parallel Sparse Linear Solver; Technical Report RC 22038 (98932). IBM T.J. Watson Research Center, 2001. Available online: http://www.cs.umn.edu/∼agupta/doc/wssmp-paper.ps (accessed on 28 October 2013).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hogg, J.; Scott, J. New Parallel Sparse Direct Solvers for Multicore Architectures. Algorithms 2013, 6, 702-725. https://doi.org/10.3390/a6040702
Hogg J, Scott J. New Parallel Sparse Direct Solvers for Multicore Architectures. Algorithms. 2013; 6(4):702-725. https://doi.org/10.3390/a6040702
Chicago/Turabian StyleHogg, Jonathan, and Jennifer Scott. 2013. "New Parallel Sparse Direct Solvers for Multicore Architectures" Algorithms 6, no. 4: 702-725. https://doi.org/10.3390/a6040702
APA StyleHogg, J., & Scott, J. (2013). New Parallel Sparse Direct Solvers for Multicore Architectures. Algorithms, 6(4), 702-725. https://doi.org/10.3390/a6040702




