2.1. Parameterized Complexity
One of the decisions made when developing fixed-parameter algorithms is the choice of the parameter. Natural parameters occurring in the problem definition of
Pattern-Guided k-
Anonymity are the number
n of rows, the number
m of columns, the alphabet size
, the number
p of pattern vectors, the anonymity degree
k, and the cost bound
s. In general, the number of rows will arguably be large and, thus, also the cost bound
s, tends to be large. Since fixed-parameter algorithms are fast when the parameter is small, trying to exploit these two parameters tends to be of little use in realistic scenarios. However, analyzing the adult dataset [
22] prepared as described by Machanavajjhala
et al. [
23], it turns out that some of the other mentioned parameters are small: The dataset has
columns, and the alphabet size is 73. Furthermore, it is natural to assume that also the number of pattern vectors is not that large. Indeed, compared to the
rows, even the number of
all possible pattern vectors
is relatively small. Finally, there are applications where
k, the degree of anonymity, is small [
24]. Summarizing, we can state that fixed-parameter tractability with respect to the parameters
,
m,
k, or
p, could be of practical relevance. Unfortunately, by reducing from 3-
Set Cover, we can show that
Pattern-Guided k-
Anonymity is NP-hard in very restricted cases.
Theorem 1. Pattern-Guided k-Anonymity is NP-complete even for two pattern vectors, three columns, and .
Proof. We reduce from the NP-hard 3-
Set Cover [
25]: Given a set family
with
over a universe
and a positive integer
h, the task is to decide whether there is a subfamily
of size at most
h such that
. In the reduction, we need unique entries in the constructed input matrix
M. For ease of notation, we introduce the
▵-symbol with an unusual semantics. Each occurrence of a
▵-symbol stands for a
different unique symbol in the alphabet Σ. One could informally state this as “
”. We now describe the construction. Let
be the 3-
Set Cover instance. We construct an equivalent instance
of
Pattern-Guided k-
Anonymity as follows: Initialize
M and
P as empty matrices. Then, for each element
, add the row
twice to the input matrix
M. For each set
with
, add to
M the three rows
,
, and
. Finally, set
,
, and add to
P the pattern vectors (□, ☆, ☆), and (☆, □, □).
We show the correctness of the above construction by proving that is a yes-instance of 3-Set Cover, if and only if is a yes-instance of Pattern-Guided k-Anonymity.
“⇒:” If is a yes-instance of 3-Set Cover, then there exists a set cover of size at most h. We suppress the following elements in M: First, suppress all ▵-entries in M. This gives suppressions. Then, for each , suppress all -entries in M. This gives suppressions. Finally, for each , suppress the first column of all rows containing the entry . These are suppressions. Let denote the matrix with the suppressed elements. Note that contains suppressed entries. Furthermore, in each row in , either the first element is suppressed or the last two elements. Hence, each row of matches to one of the two pattern vectors of P. Finally, observe that is 3-anonymous: The three rows corresponding to the set are identical: the first column is suppressed, and the next two columns contain the symbol . Since is a set cover, there exists for each element a set such that . Thus, by construction, the two rows corresponding to the element , and the row in M coincide in : The first column contains the entry and the other two columns are suppressed. Finally, for each row in M that corresponds to a set , the row in coincides with the two rows corresponding to the element : Again, the first column contains the entry and the other two columns are suppressed.
“⇐:” If is a yes-instance of Pattern-Guided k-Anonymity, then there is a 3-anonymous matrix , that is obtained from M by suppressing at most s elements, and each row of matches to one of the two pattern vectors in P. Since M and, so, contain rows, contains at most suppressions and each pattern vector contains a ☆-symbol, there are at most rows in containing two suppressions and at least rows containing one suppression. Furthermore, since the rows in M corresponding to the elements of U contain the unique symbol ▵ in the last two columns in , these rows are suppressed in the last two columns. Thus, at most rows corresponding to sets of have two suppressions in . Observe that for each set the entries in the last two columns of the corresponding rows are . There is no other occurrence of this entry in M. Hence, the at least rows in with one suppression correspond to sets in . Thus, the at most rows in that correspond to sets of and contain two suppressions correspond to at most h sets of . Denote these h sets by . We now show that is a set cover for the 3-Set Cover instance. Assume by contradiction that is not a set cover, and hence, there is an element . However, since is 3-anonymous, there has to be a row r in that corresponds to some set such that this row coincides with the two rows and corresponding to u. Since all rows in corresponding to elements of U contain two suppressions in the last two columns, the row r also contains two suppressions in the last two columns. Thus, . Furthermore, r has to coincide with and in the first column, that is, r contains as the entry in the first column the symbol u. Hence, , a contradiction. ☐
Blocki and Williams [
7] showed that, while
3-Anonymity is NP-complete [
7,
8],
2-Anonymity is polynomial-time solvable by reducing it in polynomial time to the polynomial-time solvable,
Simplex Matching [
26], defined as follows:
Simplex Matching- Input:
A hypergraph
with hyperedges of size two and three, a positive integer
h, and a cost function,
, such that:
and
.
- Question:
Is there a subset of the hyperedges , such that for all , there is exactly one edge in containing v and ?
We slightly adjust their reduction to obtain polynomial-time solvability for Pattern-Guided 2-Anonymity, together with Theorem 1, yielding a complexity dichotomy for Pattern-Guided k-Anonymity with respect to the parameter k.
Theorem 2. Pattern-Guided 2-Anonymity is polynomial-time solvable.
Proof. We reduce Pattern-Guided 2-Anonymity to Simplex Matching. To this end, we first introduce some notation. Let be the Pattern-Guided 2-Anonymity instance. For a set A of rows and a pattern vector p in P the set is obtained from A by suppressing entries in the rows of A such that each row matches p (see Definition 2). The set contains all pattern vectors p such that is a set of identical rows. Intuitively, contains all “suitable” pattern vectors to make the rows in A identical.
Now, construct the hypergraph as follows: Initialize and . For each row r in M add a vertex to V. For a vertex subset let be the set of the corresponding rows in M. For each vertex subset of size add the hyperedge if . Let be a pattern vector in with the minimum number of ☆-symbols. Denote this number of ☆-symbols of by ℓ. Then, set . Note that this is exactly the cost to “anonymize” the rows in with the pattern vector p. Finally, set the cost bound . This completes the construction.
First, we show that Conditions 1 and 2 are fulfilled. Clearly, as each pattern vector that makes some row set
A identical also makes each subset of
A identical, it follows that for any
and any
, it holds
. Hence, Condition 1 is fulfilled. Furthermore, it follows that
for each
, implying:
Thus, Condition 2 is fulfilled.
Observe that the construction can be easily performed in polynomial time. Hence, it remains to be shown that is a yes-instance of Pattern-Guided 2-Anonymity, if and only if is a yes-instance of Simplex Matching.
“⇒:” Let be a 2-anonymous matrix obtained from M by suppressing at most s elements, and each row of matches a pattern vector in P. Let be the set of all row types in . We construct a matching for H as follows: First, partition the rows in each row type, such that each part contains two or three rows. For each part Q, add to the set of the vertices corresponding to the rows in Q. By construction, the cost bound is satisfied, and all vertices are matched.
“⇐:” Let be a matching, and let . Recall that denotes the set of rows corresponding to the vertices in e. By construction, . We construct from M by suppressing for each entries in the rows such that they match . Observe that is k-anonymous, and each row matches a pattern vector. Furthermore, by construction, there are at most s suppressions in . Thus, is a yes-instance. ☐
Contrasting the general intractability result of Theorem 1, we will show fixed-parameter tractability with respect to the combined parameter
. To this end, we additionally use as a parameter the number
t of different input rows. Indeed, we show fixed-parameter tractability with respect to the combined parameter
. This implies fixed-parameter tractability with respect to the combined parameter
, as
and
. This results from an adaption of combinatorial algorithms from previous work [
13,
27].
Before presenting the algorithm, we introduce some notation. We distinguish between the
input row types of the input matrix
M and the
output row types of the matrix
. Note that in the beginning, we can compute the input row types of
M in
time using a trie [
28], but the output row types are unknown. By the definition of
Pattern-Guided k-
Anonymity, each output row type
has to match a pattern vector
. We call
an
instance of
v.
Theorem 3. Pattern-Guided k-Anonymity can be solved in time, where p is the number of pattern vectors and t is the number of different rows in the input matrix M.
Proof. We present an algorithm running in two phases:
- Phase 1:
Guess for each possible output row type whether it is used in . Denote with the set of all output row types in according to the guessing result.
- Phase 2:
Check whether there exists a k-anonymous matrix that can be obtained from M by suppressing at most s elements, such that respects the guessing result in Phase 1; that is, the set of row types in is exactly .
As to Phase 1, observe that the number of possible output row types is at most
: For each pattern vector, there exist at most
t different instances—one for each input row type. Hence, Phase 1 can be realized by simply trying all
possibilities. On the contrary, Phase 2 can be computed in polynomial time using the so-called
Row Assignment problem [
27]. To this end, we introduce
and
, where
r is the number of used output row types according to the guessing result of Phase 1, formally,
. With this notation, we can state
Row Assignment.
Row Assignment- Input:
Nonnegative integers k, s, and with , and a function .
- Question:
Is there a function , such that:
We now discuss how we use Row Assignment to solve Phase 2. The function h captures the guessing in Phase 1: If the input row type i is “compatible” with the output row type j, then , otherwise, . Here, an input row type R is compatible with an output row type if the rows in both row types are identical in the non-☆-positions or, equivalently, if any row of R can be made identical to any row of by just replacing entries with the ☆-symbol. The integer is set to the number of stars in the output row type in ; that is, captures the cost of “assigning” a compatible row of M to . In , the size (number of rows) of the input row type is stored. The integers with the same names in Row Assignment and Pattern-Guided k-Anonymity also store the same values.
Next, we show that solving Row Assignment indeed correctly realizes Phase 2: Since the output row types of are given from Phase 1, it remains to specify how many rows each output row type contains, such that can be obtained from M by suppressing at most s entries, and is k-anonymous. Due to Phase 1, it is clear that each row in matches a pattern vector in P. To ensure that can be obtained from M by suppressing entries, we “assign” rows of M to compatible output row types. Herein, this assigning means to suppress the entries in the particular row, such that the modified row belongs to the particular output row type. This assigning is captured by the function g: The number of rows from the input row type that are assigned to the output row type is . Inequality (1) ensures that we only assign rows to compatible output row types. The k-anonymous requirement is guaranteed by Inequality (2). Equation (3) ensures that all rows of M are assigned. Finally, the cost bound is satisfied, due to Inequality (4). Hence, solving Row Assignment indeed solves Phase 2.
Analyzing the running time, we get the following: Computing the input row types in
M can be done in
. In Phase 1, the algorithm tries
possibilities. For each of these possibilities, we have to check which input row types are compatible with which output row types. This is clearly doable in
time. Finally,
Row Assignment can be solved in
(Lemma 1 in [
27]). Since
, we roughly upper-bound this by
. Putting all this together, we arrive at the statement of the theorem. ☐
In other words, Theorem 3 implies that Pattern-Guided k-Anonymity can be solved in linear time if t and p are constants.
2.3. Greedy Heuristic
In this section, we provide a greedy heuristic based on the ideas of the fixed-parameter algorithm of Theorem 3 presented in
Section 2.1. The fixed-parameter algorithm basically does an exhaustive search on the assignment of rows to pattern vectors. More precisely, for each row type
R and each pattern vector
v it tries both possibilities of whether rows of
R are assigned to
v or not. Furthermore, in the ILP formulation, all assignments of rows to pattern vectors are possible. In contrast, our greedy heuristic will just pick for each input row type
R the “cheapest” pattern vector
v and, then, assigns all compatible rows of
M to
v. This is realized as follows: We consider all pattern vectors, one after the other, ordered by increasing number of ☆-symbols. This ensures that we start with the “cheapest” pattern vector. Then, we assign as many rows as possible of
M to
v: We just consider every instance
of
v, and if there are more than
k rows in
M that are compatible with
, then, we assign all compatible rows to
. Once a row is assigned, it will not be reassigned to any other output row type, and hence, the row will be deleted from
M. Overall this gives a running time of
. See Algorithm 1 for the pseudo-code of the greedy heuristic.If at some point in time, there are less than
k remaining rows in
M, then, these rows will be fully suppressed. Note that this slightly deviates from our formal definition of
Pattern-Guided k-
Anonymity. However, since fully suppressed rows do not reveal any data, this potential violation of the
k-anonymity requirement does not matter.
| Algorithm 1 Greedy Heuristic () |
- 1:
Sort pattern vectors P by cost (increasing order) - 2:
for each do - 3:
for each instance of v do - 4:
if rows are compatible with then - 5:
Assign all compatible rows of M to - 6:
Delete the assigned rows from M.
|
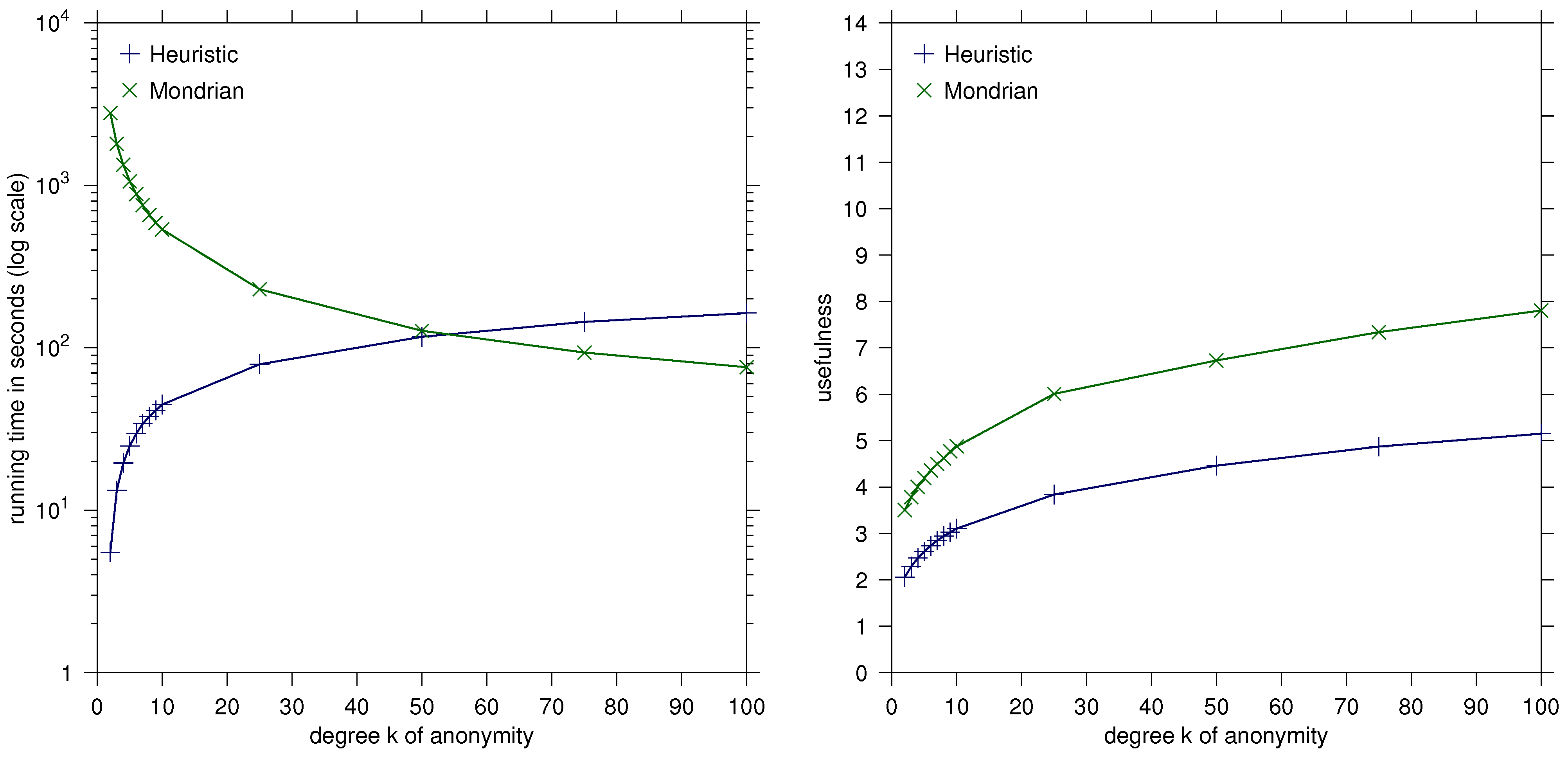
Our greedy heuristic clearly does not always provide optimal solutions. Our experiments indicate, however, that it is very fast and that it typically provides solutions close to the optimum and outperforms the Mondrian algorithm [
21] in most datasets we tested. While this demonstrates the practicality of our heuristic (Algorithm 1), the following result shows that from the viewpoint of polynomial-time approximation algorithmics, it is weak in the worst case.
Theorem 4. Algorithm 1 for Pattern-Guided k-Anonymity runs in time and provides a factor m-approximation. This approximation bound is asymptotically tight for Algorithm 1.
Proof. Since the running time is already discussed above, it remains to show the approximation factor. Let be the number of suppressions in a solution provided by Algorithm 1 and be the number of suppressions in an optimal solution. We show that for every instance, it holds that . Let M be a matrix, be the suppressed matrix produced by Algorithm 1, and be the suppressed matrix corresponding to an optimal solution. First, observe that for any row in not containing any suppressed entry, it follows that the corresponding row in also does not contain any suppression. Clearly, each row in has at most m entries suppressed. Thus, each row in has at most m times more suppressed entries than the corresponding row in and, hence, .
To show that this upper bound is asymptotically tight, consider the following instance. Set , and let M be as follows: The matrix M contains k-times the row with the symbol 1 in every entry. Furthermore, for each , there are rows in M, such that all but the entry contains the symbol 1. In the entry, each of the rows contains a uniquely occurring symbol. The pattern mask contains pattern vectors: For , the pattern vector contains □-symbols and one ☆-symbol at the position. The last two pattern vectors are the all-□ and all-☆ vectors. Algorithm 1 will suppress nothing in the k all-1 rows and will suppress every entry of the remaining rows. This gives suppressions. However, an optimal solution suppresses in each row exactly one entry: The rows containing in all but the entry the symbol 1 are suppressed in the entry. Furthermore, to ensure the anonymity requirement, in the submatrix with the k rows containing the symbol 1 in every entry, the diagonal is suppressed. Thus, the number of suppressions is equal to the number of rows; that is, . Hence, . ☐