Abstract
Nowadays, due to the concern regarding environmental issues, establishing pedestrian/bike friendly urbanism is widely encouraged. To promote safety-assured, mobile communication environments, efficient, reliable maintenance, and information integrity need to be designed, especially in highly possibly interfered places. For busy traffic areas, regular degree-3 dedicated short range communication (DSRC) networks are safety and information featured with availability, reliability, and maintainability in paths of multi-lanes. For sparsely populated areas, probes of wireless sensors are rational, especially if sensor nodes can be organized to enhance security, reliability, and flexibility. Applying alternative network topologies, such as spider-webs, generalized honeycomb tori, and cube-connected cycles, for comparing and analyzing is proposed in DSRC and cellular communications to enhance integrity in communications.
1. Introduction
Facing issues like energy conservation, the bicycle as a vital monetarily-conscious transportation mode is gaining attention. Travelers, on both business and leisure purposes, can better enjoy tourism-related activities by using bicycles; specifically, bicyclists do not move in a closed room, but, probably along some narrow paths, watch sceneries or historical assets, in a thoroughly relaxed, enjoyed, and even information-realized, yet fully exercised mood. Hence, serving bicyclists well is expected in many cities, including Amsterdam, Atlanta, and other global cities or aerotropolis [1,2], where synergistically incorporated multimodal transportation is essential.
Issues like bicycles being parked randomly, for example, can harm landscapes and pedestrians. In a multimodal urban transportation environment, especially for high-density places, related resource uses should be well planned. Consequently, bicyclists undertaking both business and leisure traveling, should be well informed and managed. In the last decade, electronic technologies have been advancing at startling rates with faster, more reliable and economical systems. New technological products, for example, can help bicyclists enjoy private amenities through solar powered i-phones. Moreover, the wireless communication infrastructure can help bicyclists get plenty of demanded mobile information for dealing with (nature or business) tasks and enjoying amenities, safely, orderly and in real-time. Hence, the serving level for bicyclists and pedestrians can be the feasible index for evaluating or governing cities in global perspectives.
In other words, to well support quality-assured traffic, and (bicycle/car) parking spaces, with possibilities of mobile business services along paths, interior and exterior, integrity should be seriously concerned. Hence, coordinating bipartite networks, i.e., the spider-web (SW) network, the generalized honeycomb torus (GHT) network, and the hypercube-derived network (CCC, cube-connected cycles), are proposed for establishing integrity assured platforms in dynamical, challenging environments to promote customer satisfaction ubiquitously is intended.
2. Literature Review
Except for occlusion and material interference, intentional radio intrusions such as those caused by truck drivers’ personal privacy devices (PPD) are gaining more attention [3,4]. To obtain better telecommunication integrity, using correlated data analysis is rational [5,6]. Hence, communication transceivers or sensors allocated and networked in complementary positions are basically prototyped, probably in a modular perspective—just like coordinated sensory mechanisms in two eyes or ears—promoting more diagnosing resilience and intelligence. Furthermore, such dual-surveillance can incorporate with allocation design concerning availability and maintainability in changing environments.
An effective, efficient sequential order for area inspection needs to be pondered, especially if available resources are limited [7]. Regarding networking, a Hamiltonian path (cycle) is a path (cycle) linking all nodes once. Such a sequentially ordered feature is essential in communication due to confidential needs in network inspection errands. Wireless communications have peer-to-peer connectivity. Hence, different mathematical performance can be assumed and inspected to help assure network reliability, and analyze the impact of communication interference confidentially.
On the strategy of tracing performance on different networks with the same wireless communication nodes, we show that the performance of mutually independent Hamiltonian paths (MIHP) in both GHT and SW [8] networks can be feasible approaches. Their topology can be adaptable in the dedicated short range communication (DSRC) and the cellular communication networks. Network topologies that have comprehensive information capability can be considered first.
Consequently, hypercube derived networks, e.g., cube-connected-cycle (CCC) graphs [9], which can have similar regular-degree-3 performance, with potentially packaged merits, are schemed to offer more adaptability and mathematical traits including fault-tolerance and Hamiltonian reliability/maintainability. Packaged nodes accommodating CCC or different network topologies may be concerned for maintainability to promote the application of wireless communication in less populated areas, where wireless information and communication is essential; however, they may potentially be significantly and adversely affected due to changing weather and other unexpected conditions.
3. Mathematical Preliminaries
Communication networks are usually illustrated by graphs, in which nodes represent processors and edges represent links between processors. Let G = (V, E) be a graph if V is a finite set and E is a subset of {(a, b) | (a, b) is an unordered pair of V}. A path is delimited by (x0, x1, x2,…xn−1). A path is called a Hamiltonian path if its nodes are distinct and span V. A cycle is a path of at least three nodes such that the first node is the same as the last node. A cycle is called a Hamiltonian cycle or Hamiltonian if its nodes are distinct except for the first node and the last node, and if they span V [10].
A bipartite graph G = (V, E) is a graph such that V = A ∪ B and E is a subset of {(a, b) | a ∈ A and b ∈ B}; if G-F remains Hamiltonian for any F = {a, b} with a ∈ A and b ∈ B, then G is 1p-Hamiltonian. A graph G is 1-edge Hamiltonian if G-e is Hamiltonian for any e ∈ E; moreover, if there is a Hamiltonian path between any pair of nodes {c, d} with c ∈ A and d ∈ B, then the bipartite graph G is Hamiltonian laceable.
The number of links connecting a node is called the degree; a network that regularly has fewer degrees is generally economical [11]. For DSRC’s functionality in busy traffic conditions, regular degree-3 is minimal for supporting availability, reliability, and maintainability in paths of multi-lanes; consequently, networks prototyped for DSRC are regular degree-3 based in this paper.
Assume that m and n are positive integers, where n is even and m ≥ 2. Let d be any integer such that (m − d) is even. The generalized honeycomb torus [12], GHT(m, n, d) is the graph with the node set {(i, j) | 0 ≤ i < m, 0 ≤ j < n} such that (i, j) and (k, l) are adjacent if they satisfy one of the following conditions: (1) i = k and j = l ± 1(mod n); (2) j = l and k = i − 1 if i + j is even; and (3) i = 0, k = m − 1, and l =j + d(mod n) if j is even.
The spider-web network, SW (m, n) is a graph with the node set {(i, j) | 0 ≤ i < m, 0 ≤ j < n}, where m, n ≥ 4 and even, such that (i, j) and (k, l) are adjacent if they satisfy one of the following conditions: (1) i = k and j = l ± 1; (2) j = l and k = i + 1(mod m) if i + j is odd or j = n − 1; and (3) j = l, k = i − 1(mod m) if i + j is even or j = 0. The configuration of SW(m, n) is shown in Figure 1(a,d).
It is proved that GHT(m, n, 0), also named HReT(m, n), is 1-edge Hamiltonian if n ≥ 4; 1p-Hamiltonian if n ≥ 6 or m = 2, n ≥ 4 [13]. When m and n are positive integers with n, m − n/2 being even, GHT(m, n, n/2) is proved 1-edge Hamiltonian if n ≥ 4; 1p-Hamiltonian if n ≥ 6 or m = 2, n ≥ 4 [14]. Besides, SW(m, n) is proved 1-edge Hamiltonian, 1p-Hamiltonian [15]. Thus, the fault-tolerance in which we are engaged is systematically based. Moreover, GHT(m, n, 0), GHT(m, n, n/2), and SW(m, n) are Hamiltonian laceable if m, n ≥ 4 integers [16,17].
Two Hamiltonian paths P1 = (u1, u2, …, un(G)) and P2 = (v1, v2, …, vn(G)) of G from u to v are independent if u = u1 = v1, v = un(G) = vn(G), and ui ≠ vi, for every 1 < i < n (G). A set of Hamiltonian paths, {P1, P2, …, Pk}, of G from u to v is mutually independent if any two different Hamiltonian paths are independent from u to v. The mechanism of mutually independent Hamiltonian paths (MIHP) can be applied to parallel processing [18]. Such a feature is also considered for secret communications [19,20]. It is proved that SW(m, n) has MIHP performance [8]; and it is believed that GHT(m, n, 0) and GHT(m, n, n/2) can have such performance if nodes are enough (e.g., more than 16).
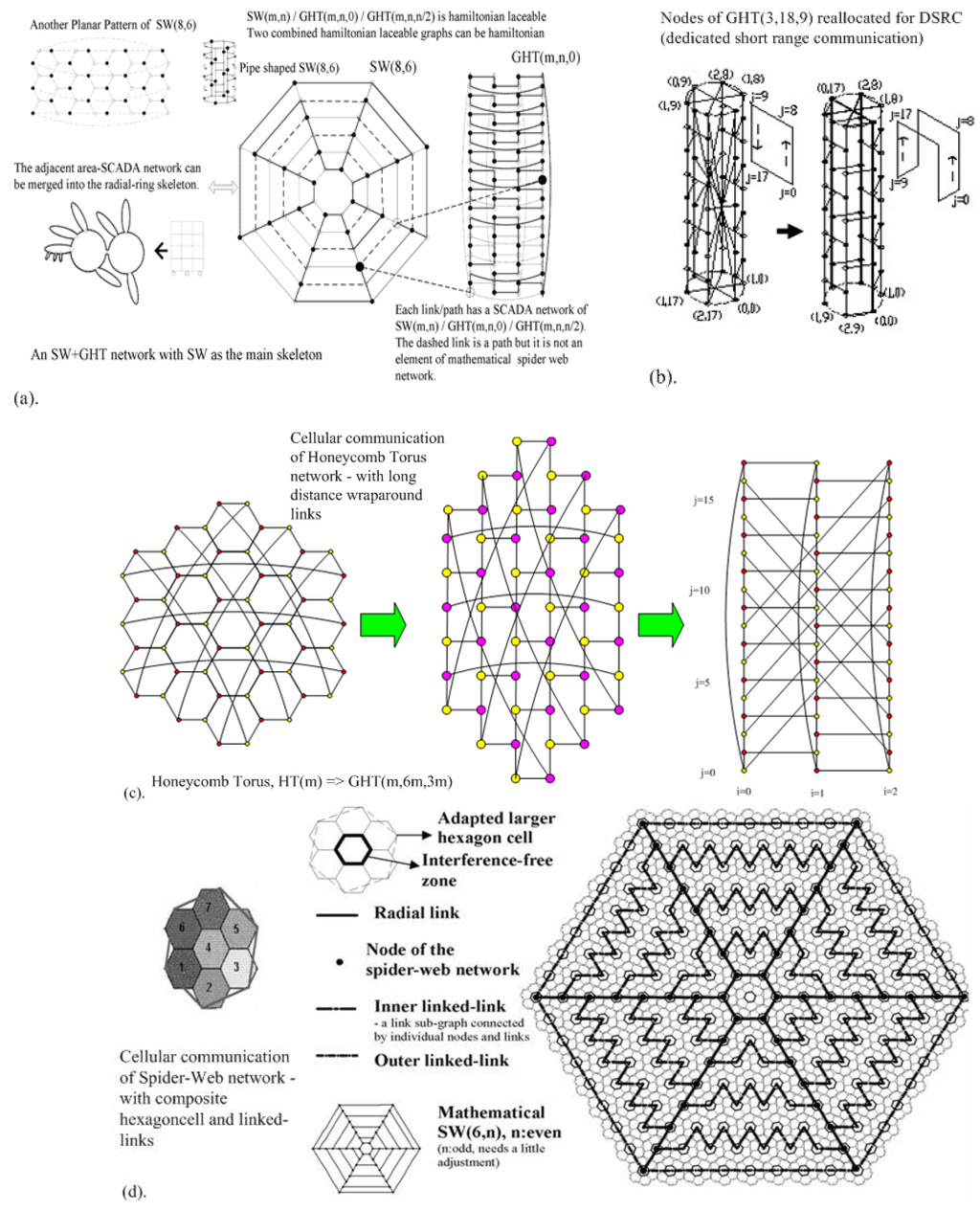
Figure 1.
Link adaptability in wide area communication network, (a) urban dedicated short range communication network with Spider-Web networks’ integration and fractal connectivity performances; (b) wireless communication quality affected by link adaptability; (c) cellular communication modeled by honeycomb tori, generalized honeycomb torus (GHT) networks; (d) cellular communication modeled by Spider-Web networks.
The definition of hypercubes is given as follows. Let u = bn−1 … bi … b0 be an n-bit binary string. For any j, 0 ≤ j ≤ n − 1, we use (u)j to denote the binary string bn−1 …bj … b0. Moreover, we use (u)j to denote the bit bj of u. The Hamming weight of u, denoted by wH(u), is the value of |{0 ≤ i ≤ n − 1|(u)i = 1}|. The n-cube (or hypercube) Qn consists of 2n nodes and n2n−1 links. Each node corresponds to an n-bit binary string. Two nodes, u and v, are adjacent if and only if v = (u)j for some j, and we call link (u, (u)j) j-dimensional. The Hamming distance between u and v, denoted by h(u, v), is defined to be the number of elements in {0 ≤ i ≤ n − 1|(u)i ≠ (v)i}. Hence, two nodes, u and v, are adjacent if and only if h(u, v) = 1.
The cube-connected-cycles graph CCCn has n2n nodes, labeled as (l, x), where l is an integer between 0 and n − 1, and x is an n-bit and x is the processor node with an n-bit binary string. Two vertices (l, x) and (l’, y) are adjacent if and only if x = y and |l − l’| = 1 or l = l’ and y = (x)l. In the latter case, x and y only differ in the position l. The edges that connect (l, x) to its neighbors (l + 1, x) and (l − 1, x) are called cycle-edges. Moreover these cycle-edges form a cycle of length n called a fundamental cycle defined by x (Figure 2), which can represent a node composed of ring networked processors. L(n) is the set offering all possible lengths of cycles in CCCn [9]; for n = 2, CCCn is just the cycle of length 8. The possible-length parameter can be applied for systematic checking and design on affiliated processors.
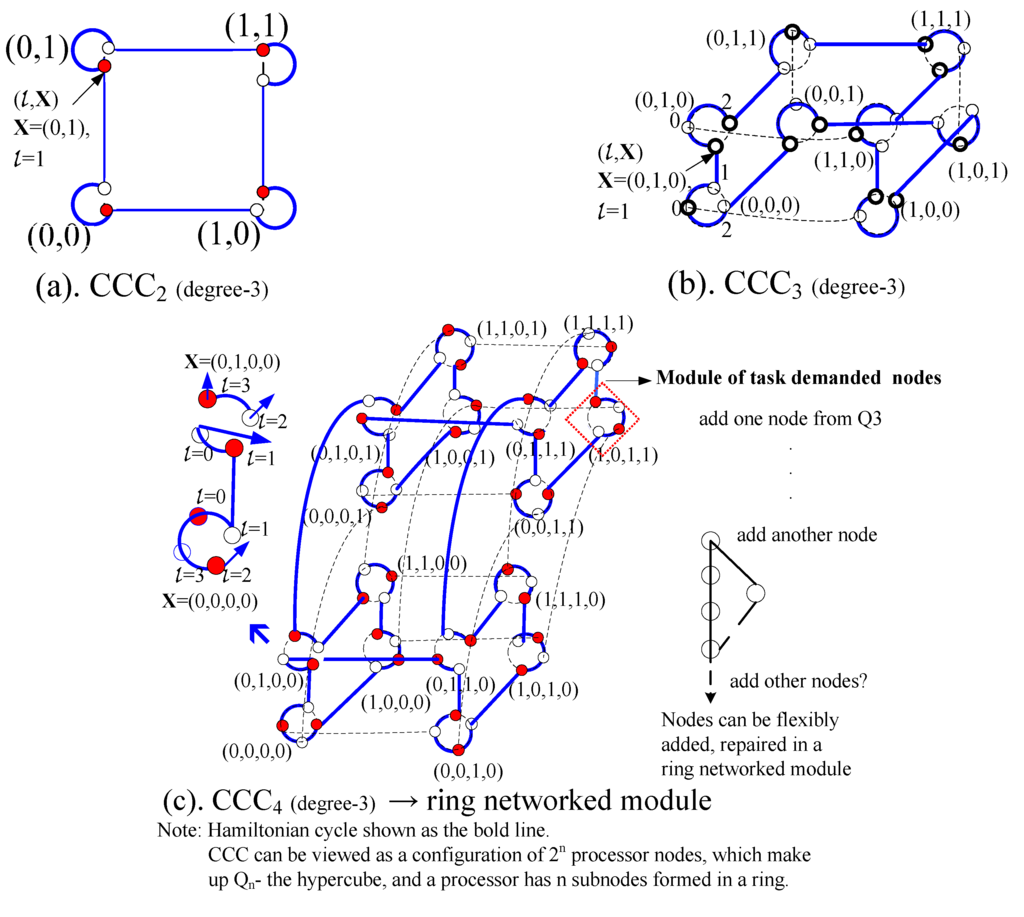
Figure 2.
Relationship between Hypercubes and Cube-Connected-Cycles. (a) CCC2; (b) CCC3; (c) CCC4 and ring networked module.
4. Proof Examples (two MIHP on GHT(m, n, n/2) )
GHT(m, n, n/2) can have scalable MIHP performance if its node quantity is reasonable enough. In this paper, an approach is introduced. We can establish basic two MIHP first, and then check their vertical extension and horizontal expansion. Assume (x1, y1) and (x2, y2) are two end nodes of the basic pattern, and they are based on the basic definition of GHT(m, n, n/2). (0, 0) is the left-lowest node’s coordinate, but an alternative node number sequence is used to show no collision in two Hamilton path patterns.
4.1. m Even, n ≥ 4; y1 = y2, Even; (x2 − x1) Odd
The two basic Lt. and Rt. Hamiltonian path patterns in a GHT(2, 4, 2) network shown below can have no collision except for end nodes. Assume n = 4 first to show the scalability performance of mutually independent Hamiltonian paths (MIHP) existed in GHT (m, 4, 2), m even, for end nodes with a same, even y coordinate. As below, the underline shows the location of L-embeddings and R-embeddings, and the italic underline is for the R-embedding. Coordinates (0, 0) and (1, 3) represent the lowest-left and highest-right positions of GHT(2, 4, 2). 03 is the coordinate (0, 2) and 04 is the coordinate (1, 2) in Figure 3(a).
03,01,02,08,06,05,07,04 Lt.
03,08,06,05,07,01,02,04 Rt.
For both Lt. and Rt. patterns, 01,02 and 06,05 have exactly same nodes and nodes’ sequence; hence they can be deemed as a special node. 08, 06,05 and 07 can be collisionfree, because basic patterns’ leading difference is 2 but the adding node differences between 01,02 and 03,08 are multiples of 4. Rt. 03,08 and Lt. 07,04 have enough separation to be collision free in accommodating their adding nodes, which have consistent sequence in both patterns.
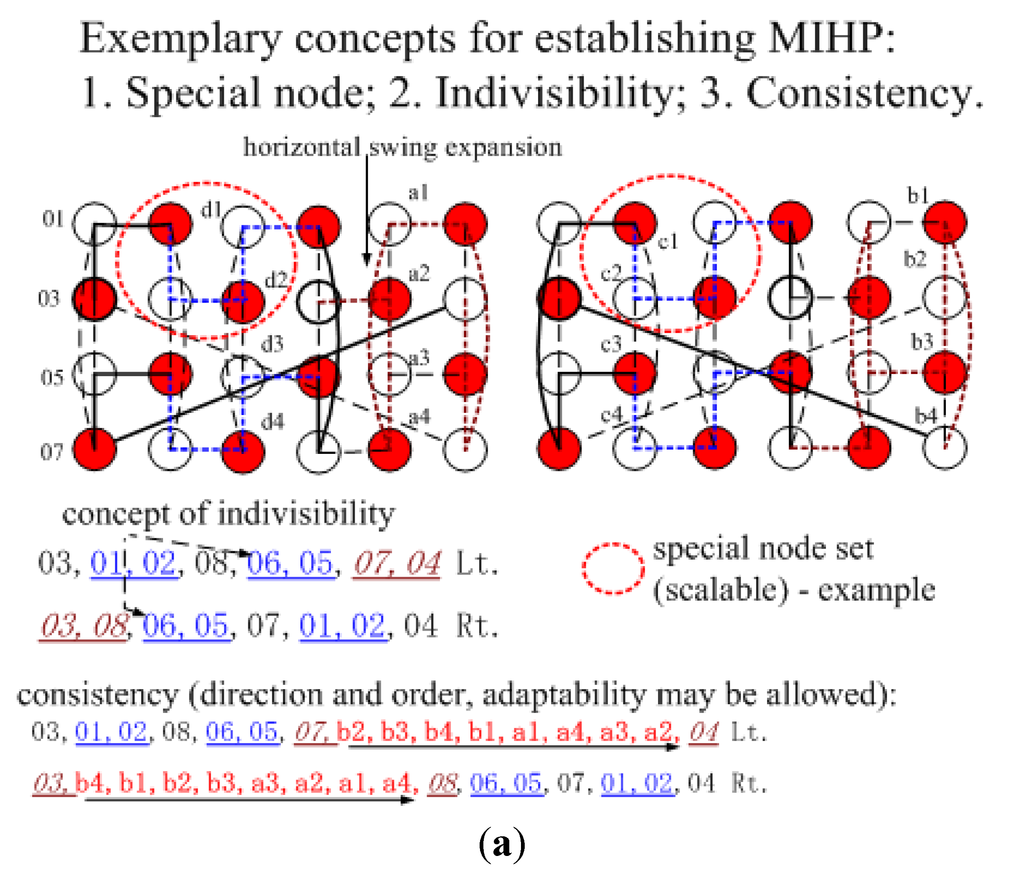
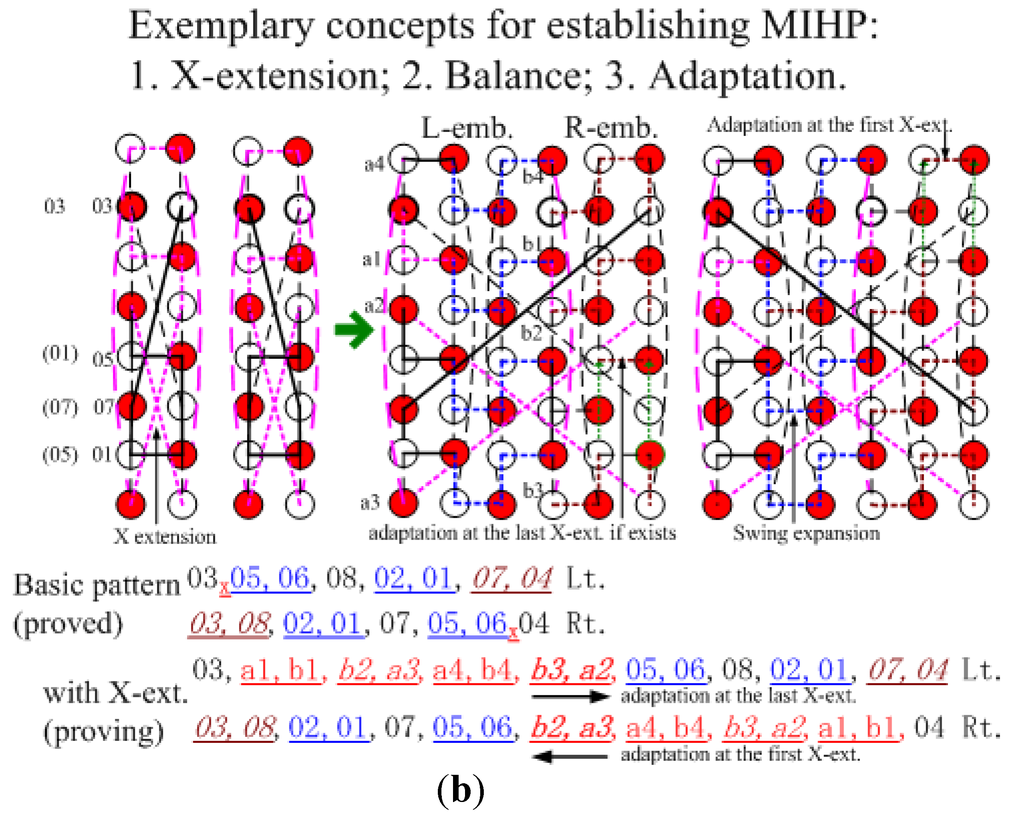
Figure 3.
Mutually independent Hamiltonian paths (MIHP) performance exist in GHT(2,4,2) (a) without vertical extension (X-ext.); (b) with vertical extension (X-ext.).
We then considered scalable vertical extension, as in Figure 3(b), and showed the vertex transitiveness. By the half vertical span nature of the third coordinate of GHT(m, n, n/2), scalable vertical extensions can be configured through the mechanism of continual symmetrical vertical extensions, X-shaped extensions, which do not affect the original nodes’ connections. We can find that the vertical extension can have the rhythm, incorporating with the horizontal embeddings, and the rhythm of both patterns will not collide, despite extension increases. It is noted that after the first extension, the compared nodes can get more separation spaces. Besides, the adaptation is applied in R-embeddings, and whether collisions exist can be easily checked.
4.2. m Even, n ≥ 4; y1 = y2, Odd; (x2 − x1) Odd
The basic Lt. and Rt. Hamiltonian path patterns in a GHT(2, 12, 6) network can have no collision except for end nodes such as Figure 4.
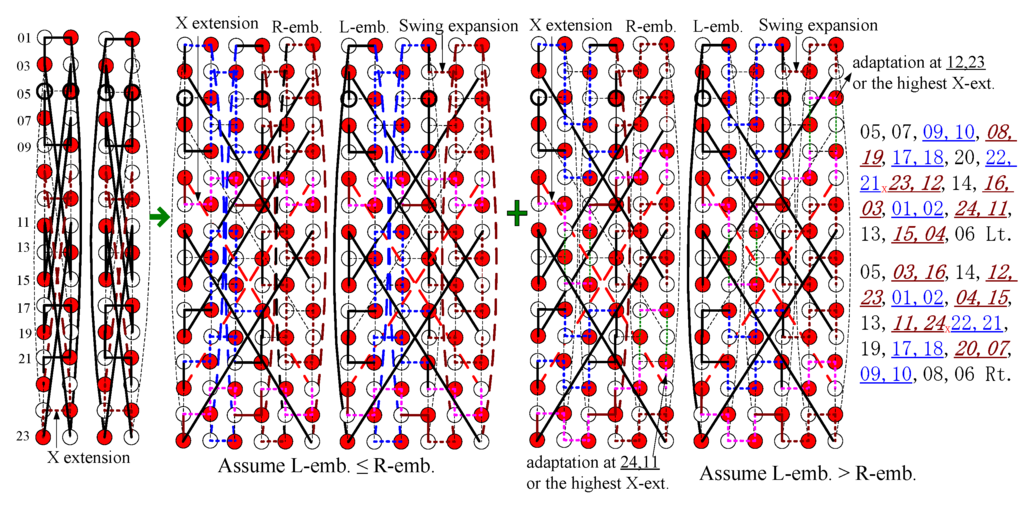
Figure 4.
MIHP performance may exist in HT(2)/GHT(2, 12, 6).
Both X-extensions, noted as the subscript x, are in consistent directions. Node blocks are deemed as special nodes. On the Lt. nodes 07, 09,10, 08, 19, 17,18, 20, 22,21 keep lagging, and nodes 23, 12, 14, 16, 03, 01,02, 24, 11, 13, 15, 04 keep leading. For nodes embedded, we need only check those of R-emb. Assume L-emb. ≤ R-emb. first. Nodes within 08,09 of the Lt. keep lagging behind their compared nodes within 04,15 of the Rt. Nodes within 15,04 of the Lt. keep leading their compared nodes within 04,15 of the Rt. Nodes within 20,07 of the Rt. keep leading their compared nodes within 16,03 of the Rt. Nodes within 03,16 of the Rt. keep lagging behind their compared nodes within 16,03 of the Lt. Nodes within 23,12 (24,11) of the Lt. keep leading their compared nodes within 12,23 (11,24) of the Rt. We change the direction of swing expansions (upward ↔ downward) of embeddings. If L-emb. ≥ R-emb. 01,02 can definitely get more nodes per embedding. It is noted that the swing expansion close to the location of X-ext. needs to be adapted to get more nodes in the highest or lowest extension.
This example of end nodes being adjacent, can have relatively fewer links to start establishing MIHP. Nevertheless, it shows the possibility of scalable MIHP performance in honeycomb tori, HT(m) or GHT(m, 6m, 3m) m ≥ 2.
5. Network Proposal
Recently, due to the concern about energy conservation, global warming, establishing pedestrian, bike friendly urbanism, tourism has been encouraged by a lot of countries. Depending on rural or urban areas, two approach directions are proposed. One is for occlusion and interference and concerns urban areas; the other is for maintainability and concerns less populated areas.
5.1. Along Streets—A Pedestrian/Bike DSRC Proposal
From small settlements to big cities, the traditional cities generally have relatively convenient accessibilities, and enough living resources, and then it can be developed step by step—inherently in a radial-ring configuration, probably including water ways, centered in the original settlement [21]. By inherent, real radial-ring motion flow, a grid urban pattern can enlarge its original scope of urban activities. In this perspective, a grid pattern can rationally be adapted to a radial-ring pattern; moreover, the grid can be illustrated to be the radial-ring [21]. It is found that bipartite spider-web networks have mathematical laceability (Figure 1 (a)) to sustain the ring performance of connected spider-web networks.
The proposed radial-ring configured DSRC network prototype is integrated via the spider-web network; in other words, it can be a spider-web (radial-ring) network of spider-web (radial-ring) networks. Furthermore, just as cities may be multi-centered, flexible amounts of radial-rings of radial rings can be composed or sub-divided (e.g., in a campus site, a large vehicle architecture); i.e., fractal. Such connected rings can have sequential order [7], fault-tolerance for maintenance, and fractal features for hierarchical management.
In another perspective, historical heritage and other cultural or natural assets are often resources for tourism development. However, such assets may affect flows of spatial development. Apart from adopting underground or overpass construction technologies, such assets can be more economically concerned with, or preserved if the proposed information network prototype can be applied to prevent adversary effects on traffic flows and spatial development—i.e., proposed information networks can be well connected either underground or overpass to help keep traffic moving.
Parallelism along paths is aimed to analyze spatial-tempo interference. Moreover, the system manager may use such parallelism for operating dynamic authentication/authorization in transporting privacy demanded tasks, which can be recorded through active RFID (radio frequency identification) systems. This paper proposes a network in which the sequence of such orderly operation can be both flexibly and logically adjusted in a Hamiltonian way, because the network has scalability and Hamiltonian laceability.
Hence, the aforementioned, highly reliable security-information networks can offer continuous and thoughtful protection for travelers. That is vital in planning future urban infrastructure. Such infrastructure can offer another benefit, specifically regarding bikes’ parking, which can be organized in parking spaces, definitely not on the sidewalks, ubiquitously. Moreover, enhancing more flexibility in infrastructure can be considered via networking; parking structures may provide an alternative place for freight distribution and economical synergies [22].
5.2. Probe Proposal
In detection of tasked areas, a processor’s maintenance needs to be highly concerned. Grouping a set of sensors in a probe can benefit scheduled maintenance errands. For energy saving and fault-tolerance, such wireless sensors in a probe can be linked in a cycle, which is like a row of nodes in the GHT graph. Hence, GHT(m, n, d) can be packaged in m probes (Figure 1 and Figure 2), and each probe has n nodes. Naturally, probes and their inner sensors can be configured in a network model.
The hypercube graph can be one of the most efficient networks for parallel computation. Yet, one drawback is that its degree (number of connections to each node) grows with the size of the network [23]. The regular degree-3 CCC network is a hypercube’s derivatives. In the CCC network, each probe is considered to have n sensing operations or n subnodes, which can be processed and integrated in a ring independently [24]. Each probe is represented as a node of a hypercube, which can be organized in an ad-hoc network of 2n sup-nodes, or n2n nodes totally in a planned zone. A probe integrates all its nodes’ operation, and then wirelessly transmits information to other probes, and other areas via cellular communication and global positioning systems.
5.3. Linking Alternatives
Proposed network prototypes can have different mathematical performances. Hence, a set of nodes can be linked differently to form or reside in different network topologies. Then, such performances can be compared and analyzed to enhance communication integrity and reliability. For example:
- (1)
- (2)
- On cellular communication, both SW(6, n) and GHT(m, 6m, 3m) are proposed (Figure 1(c,d)) with MIHP, fault-tolerance performances.
- (3)
- Radial-ring, SW networks, have more fault-tolerance than ring networks. The area DSRC network can be configured as an integral SW network. Naturally, radial-ring can be grouped, and even configured as a radial-ring of radial-rings (Figure 1(a)).
6. Conclusions
The bicycle as a vital energy conscious and tourist’s amenity transportation mode is gaining attention. Moreover, establishing pedestrian/bike friendly urbanism is widely encouraged. To promote comfort, safety-assured, mobile communication environments for cyclists, efficient and reliable maintenance and information integrity in communication networks need be considered, especially in highly possible interfered places, including parking garages.
Through dedicated short range communication (DSRC) in busy traffic conditions, regular degree-3 networks with Hamiltonian performances are suggested for supporting availability, reliability, and maintainability in paths of multi-lanes. In sparsely populated areas, applying probes of wireless sensors, such as regular degree-3 GHT and CCC graphs, with security, reliability, and flexibility, is proposed. SW networks having more fault-tolerance than ring networks are suggested as a mechanism to integrate paths’ DSRC networks. SW(6, n) and GHT(m, 6m, 3m) with fault-tolerance, MIHP performances are proposed to enhance reliability and integrity in cellular communications.
Scalable MIHP is an example that has been proven solvable in the honeycomb torus, which is the prototype for cellular communication network; researchers are still working to prove related cases. MIHP’s parallelism can naturally support more independent data for analyzing interference and other spatial-temporal information. Routinely maintained or replaced packaged probes can be accommodated in GHT and CCC graphs. The CCC network can easily be processed in an available hypercube-derived algorithm for parallel computation; its possible-length parameter can be applied for systematic checking and design on affiliated processors.
The network prototypes introduced in this paper are all regular degree-three (in optimal dual-surveillance perspectives); however, different typologies can potentially be applied to the same processing nodes for further analyzing spatial-temporal information.
Acknowledgment
The author deeply appreciates two anonymous reviewers’ constructive opinions; he presents his thankfulness here.
Conflict of Interest
The authors declare no conflict of interest.
References
- Teng, Y.-H.; Tan, J.; Ho, T.-Y.; Hsu, L.-H. On mutually independent hamiltonian paths. Appl. Math. Lett. 2006, 19, 345–350. [Google Scholar] [CrossRef]
- Ashford, N.; Mumayiz, S.; Wright, P. Airport Engineering: Planning, Design, and Development of 21st Century Airports; John Wiley: New York, NY, USA, 2011; pp. 660–665, 679–681, 684. [Google Scholar]
- Atlanta Regional Commission (ARC). Hartsfield-Jackson Atlanta International Airport—Issues and Opportunities around the “Worlds’ Busiest Airport”. ARC: Atlanta, GA, USA, 2011. Available online: http://www.atlantaregional.com/FileLibrary/LandUse/airport/HJAIAIssuesOpportunities.pdf (accessed on 4 August 2013).
- Leighton, F.T. Introduction to Parallel Algorithms and Architectures: Arrays, Trees, Hypercubes; Morgan Kaufmann: Burlington, MA, USA, 1992; pp. 389–392. [Google Scholar]
- Cho, H.-J.; Hsu, L.-Y. Ring embedding in faulty honeycomb rectangular Torus. Inform. Process. Lett. 2002, 84, 277–284. [Google Scholar] [CrossRef]
- Pivo, G.; Carson, D.; Kitchen, M.; Billen, D. Learning from truckers: Truck drivers’ view on the planning and design of urban and suburban centers. J. Archit. Plan. Res. 2002, 19, 13–29. [Google Scholar]
- Keeble, L. Principles and Practice of Town and Country Planning; Estates Gazette: London, UK, 1969; pp. 50, 102, 112. [Google Scholar]
- Hsu, L.-H.; Lin, C.-K. Graph Theory and Interconnection Networks; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2008; pp. 1–20. [Google Scholar]
- Hsu, L.-Y. Developing dual-surveillance and dual-tele-paths in surveillance-information networks of tunnel/mining spaces. J. Northeast. Univ. Nat. Sci. 2009, 30, 311–314. [Google Scholar]
- Damjanovski, V. CCTV Networking and Digital Technology; Elsevier: Amsterdam, The Netherlands, 2005; pp. 159–168. [Google Scholar]
- Preparata, F.; Vuillemin, J. The cube-connected cycles: A versatile network for parallel computation. Commun. ACM 1981, 24, 300–309. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, W.; Trappe, W.; Zhang, Y.-Y. Securing Emerging Wireless Systems: Lower-Layer Approaches; Springer: New York, USA, 2009; pp. 1–3. [Google Scholar]
- Cho, H.-J.; Hsu, L.-Y. Generalized honeycomb torus. Inform. Process. Lett. 2003, 86, 185–190. [Google Scholar] [CrossRef]
- Hsu, L.-Y. Scalable parallelism in spider-web networks. Int. J. Inf. Eng. 2012, 2, 169–183. [Google Scholar]
- Hsu, L.-Y.; Lin, T.-Y.; Kao, S.-S. Hamiltonian laceability of some generalized honeycomb tori. AIP Conf. Proc. 2008, 1060, 302–306. [Google Scholar]
- Hsu, L.-Y.; Hsu, L.-H.; Ho, Y.-H.; Tsay, C.-W.; Ho, T.-Y. Embedding Cycles in Cube-Connected-Cycles Graphs. In Proceedings of IET International Conference of Frontier Computing—Theory, Technologies and Applications, Xining, China, 16–18 August 2012; pp. 11–17.
- Kao, S.-S.; Hsu, L.-H. Spider-web networks: A family of optimal, fault tolerant, hamiltonian bipartite graphs. Appl. Math. Comput. 2005, 160, 269–282. [Google Scholar] [CrossRef]
- Stojmenovic, I. Honeycomb networks: Topological properties and communication algorithms. IEEE Trans. Parallel Distrib. Syst. 1997, 8, 1036–1042. [Google Scholar] [CrossRef]
- Hsu, L.-Y.; Ling, F.-I.; Kao, S.-S.; Cho, H.-J. Ring embedding in faulty generalized honeycomb tori—GHT(m, n, n/2). Int. J. Comput. Math. 2010, 87, 3344–3358. [Google Scholar] [CrossRef]
- Knezevic, J. Systems Maintainability—Analysis, Engineering and Management; Chapman Hall: London, UK, 1997; pp. 11, 221. [Google Scholar]
- Kao, S.-S.; Hsu, L.-H. Hamiltonian laceability of spider-web networks. Chung Yuan J. 2005, 33, 1–10. [Google Scholar]
- National Space-Based Positioning, Navigation, and Timing Advisory Board. National PNT Advisory Board comments on Jamming the Global Positioning System—A National Security Threat: Recent Events and Potential Cures, November 4, 2010. AIAA: Reston, VA, USA, 2010. Available online: http://www.gps.gov/governance/advisory/recommendations/2010-11-jammingwhitepaper.pdf (accessed on 4 August 2013). [Google Scholar]
- Lee, A.; Boyer, J.; Drexelius, C.; Naldurg, P.; Hill, R.; Campbell, R. Supporting Dynamically Changing Authorizations in Pervasive Communication Systems. In Security in Pervasive Computing, LNCS3450; Hutter, D., Ullmann, M., Eds.; Springer: New York, NY, USA, 2005; pp. 134–150. [Google Scholar]
- Polak, F.J.; Attfield, S.; Wallace, W.A. Compatibility of two 3D Kinematic motion analysis systems during simultaneous real time gait acquisition. Gait Posture 1996, 4, 167–208. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).