A Generic Two-Phase Stochastic Variable Neighborhood Approach for Effectively Solving the Nurse Rostering Problem
Abstract
1. Introduction and Related Work
1.1. Introduction
1.2. Related Work
2. Problem Definition
Constraints
- All shift type demands during the planning period must be met
- The shift coverage requirements must be fulfilled
- Each nurse should work at most one shift per day
- Maximum number of shifts that should be assigned to a nurse
- Minimum number of shifts that should be assigned to a nurse
- Maximum number of consecutive working days
- Minimum number of consecutive working days
- Maximum number of consecutive free days
- Minimum number of consecutive free days
- Maximum number of hours worked
- Minimum number of hours worked
- Maximum number of consecutive working weekends
- Maximum number of working weekends in four weeks
- Number of days off after a series of night shifts
- Complete weekends (i.e., if a nurse has to work only on some days of the weekend, then a penalty occurs)
- Identical shift types during the weekend (i.e., assignments of different shift types to the same nurse during a weekend are penalized)
- Unwanted patterns (i.e., an unwanted pattern is a sequence of assignments that is not in the preferences of a nurse, based on her contract)
- Unwanted patterns not involving specific shift types
- Unwanted patterns involving specific shift types
- Alternative skill (i.e., if assignments of a nurse to a shift type requiring a skill that she does not have occurs, then the solution is penalized accordingly)
- Day on/off request (i.e., requests by nurses to work or not to work on specific days of the week should be respected, otherwise solution quality is compromised)
- Shift on/off request (i.e., similar to the previous, but now for specific shifts on certain days)
3. Solution Approach
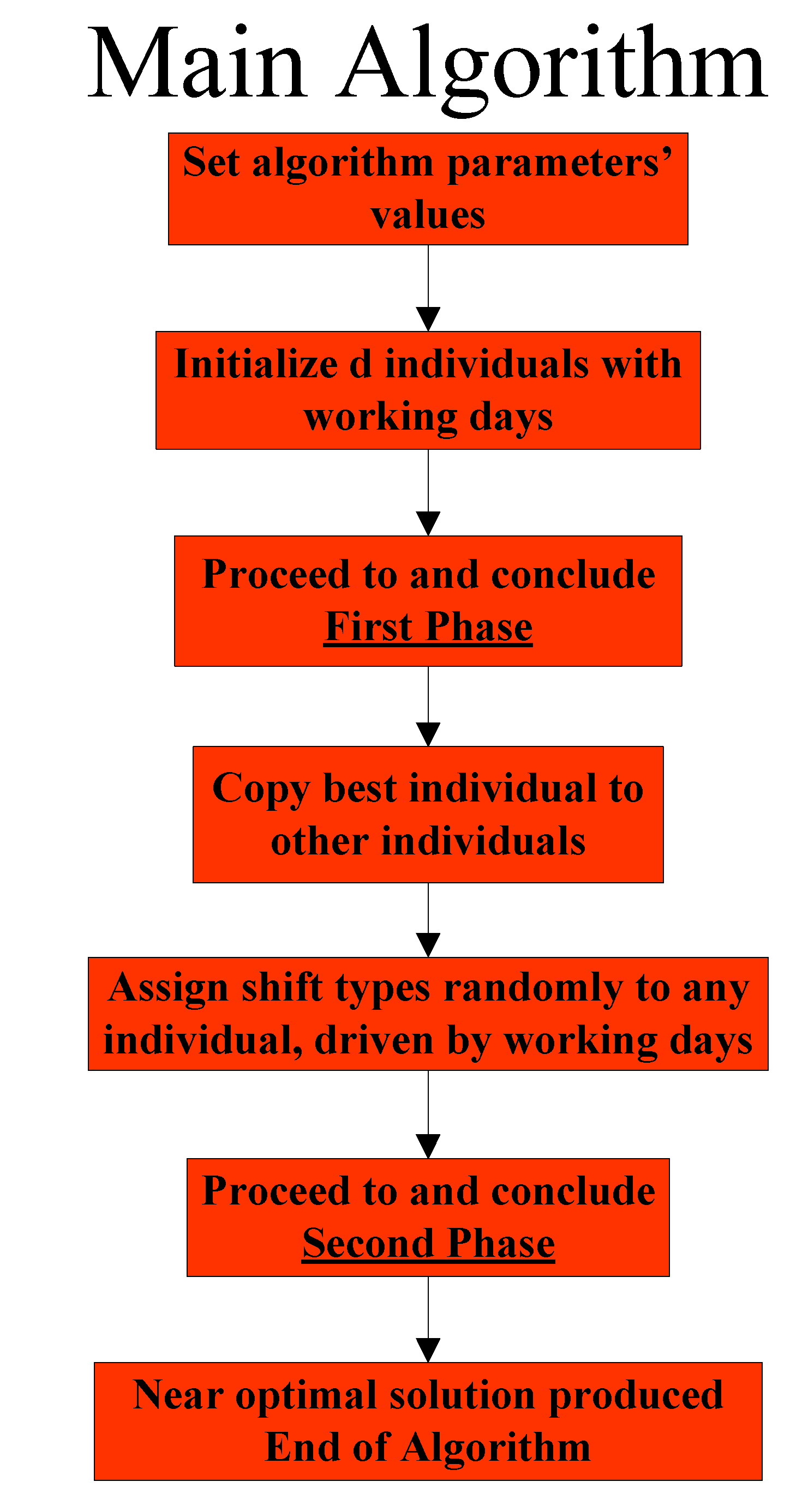
3.1. General Overview of the Stochastic Variable Neighborhood Algorithm
- (a)
- The first phase deals with the assignment of nurses to working days
- (b)
- The second phase deals with the assignment of nurses to shift types
| No | Input instance | Swapping probability (pswap) | Number of cycles in first phase | Maximum number of generations in second phase | Population size | Number of experiments needed to find the optimal parameters of the algorithm | Average time per experiment | Average time consumed |
|---|---|---|---|---|---|---|---|---|
| 1 | Valouxis-1 | 0.99995 | 1 | 100 | 2 | 22 | 2 min | 44 min |
| 2 | BCV3-46.2 | 0.97 | 1 | 100 | 2 | 22 | 11 min | 242 min |
| 3 | MUSA | 0.97 | 1 | 100 | 2 | 22 | 0.06 s | 1.32 s |
| 4 | LLR | 0.5 | 1 | 100 | 2 | 17 | 0.56 s | 9.52 s |
| 5 | BCV4-13.1 | 0.97 | 1 | 100 | 2 | 22 | 3 s | 66 s |
| 6 | WHPP | 0.45 | 1 | 100 | 2 | 17 | 7.7 s | 130.9 s |
| 7 | HED01 | 0.85 | 1 | 100 | 2 | 27 | 29 s | 13.05 min |
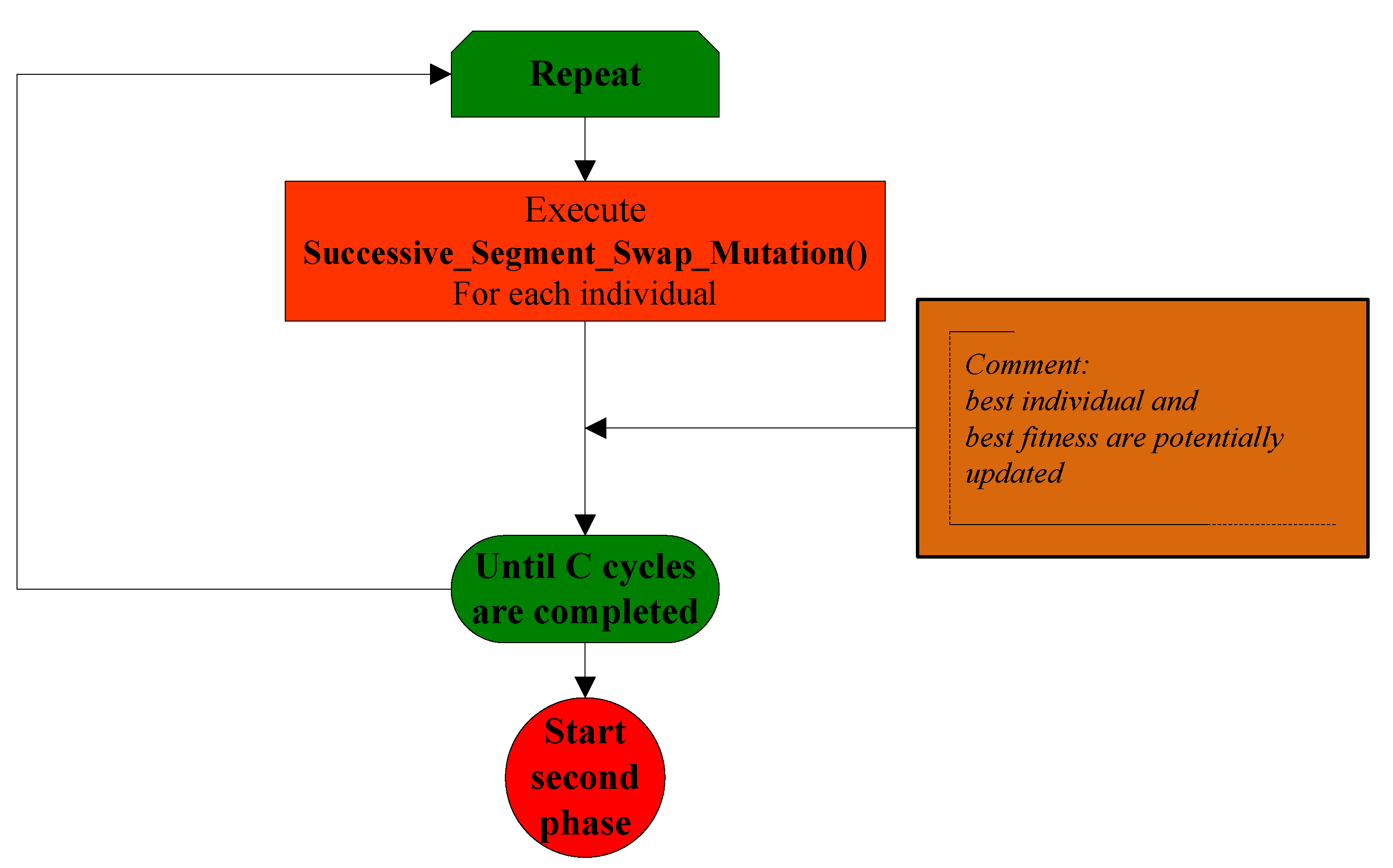
3.2. The First Phase of the Stochastic Variable Neighborhood Algorithm
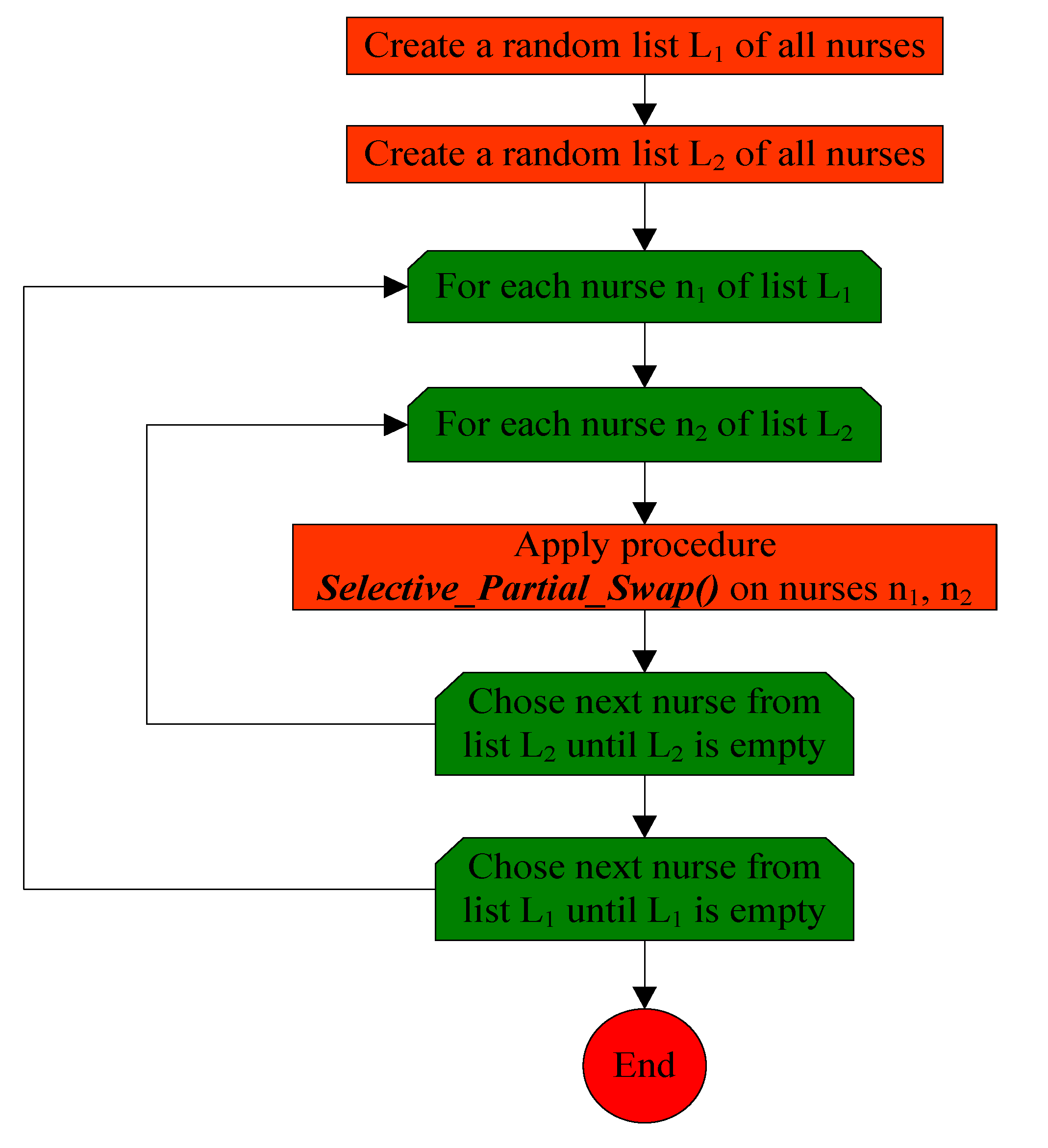
3.3. The Second Phase of the Algorithm
- (a)
- Selective_Day_Swap_Mutation()
- (b)
- Successive_Segment_Swap_Mutation()
- (c)
- Random_Segment_Swap_Mutation()
- ▪
- The total number of generations
- ▪
- The number of generations for which the fitness remains the same, that is, no improvement is reported
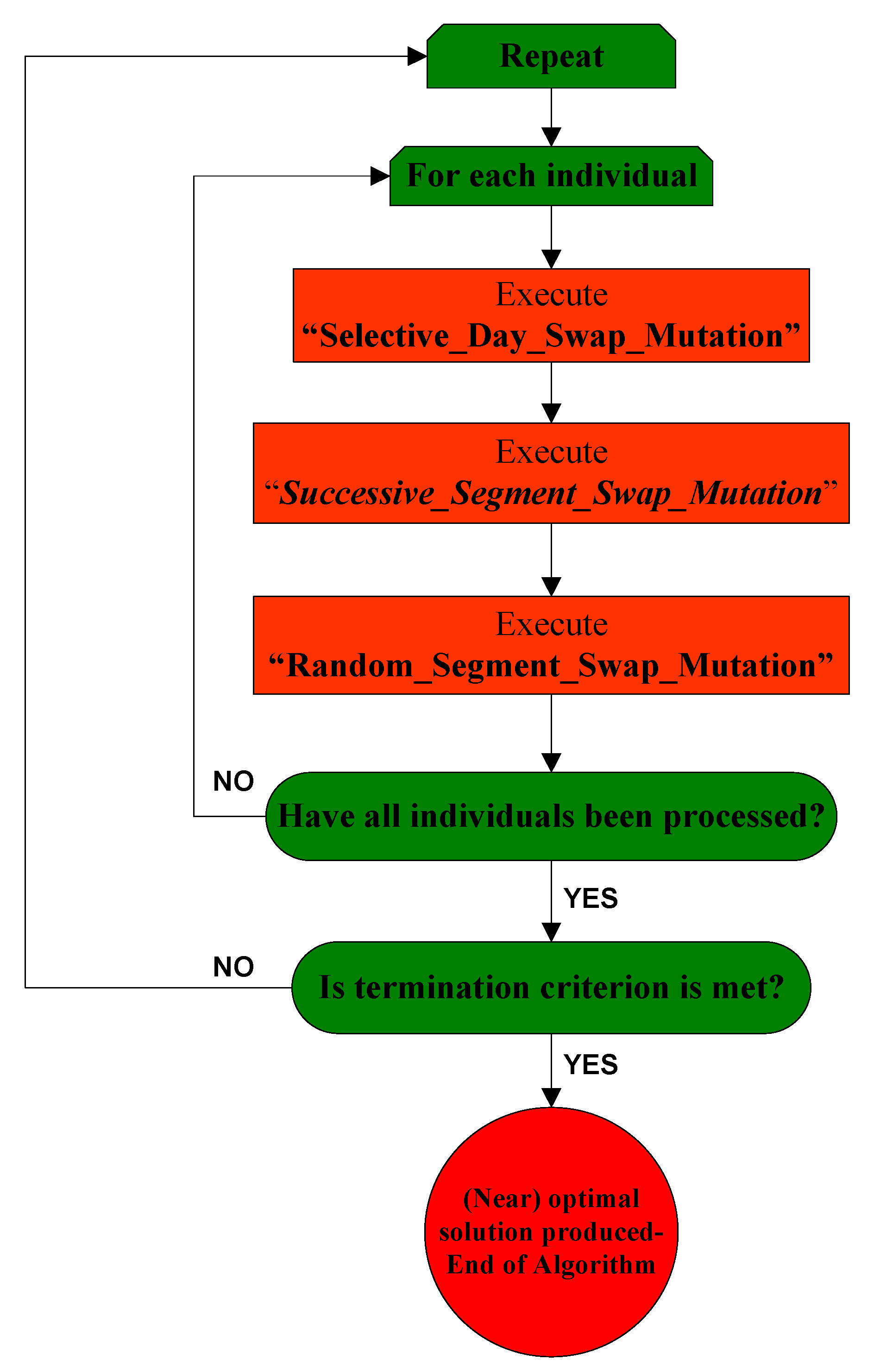
- If he/she chooses “the total number of generations”, next, he/she has to insert this number.
- If he/she chooses “the total number of generations for which the fitness remains the same”, next, he/she has to insert this number.
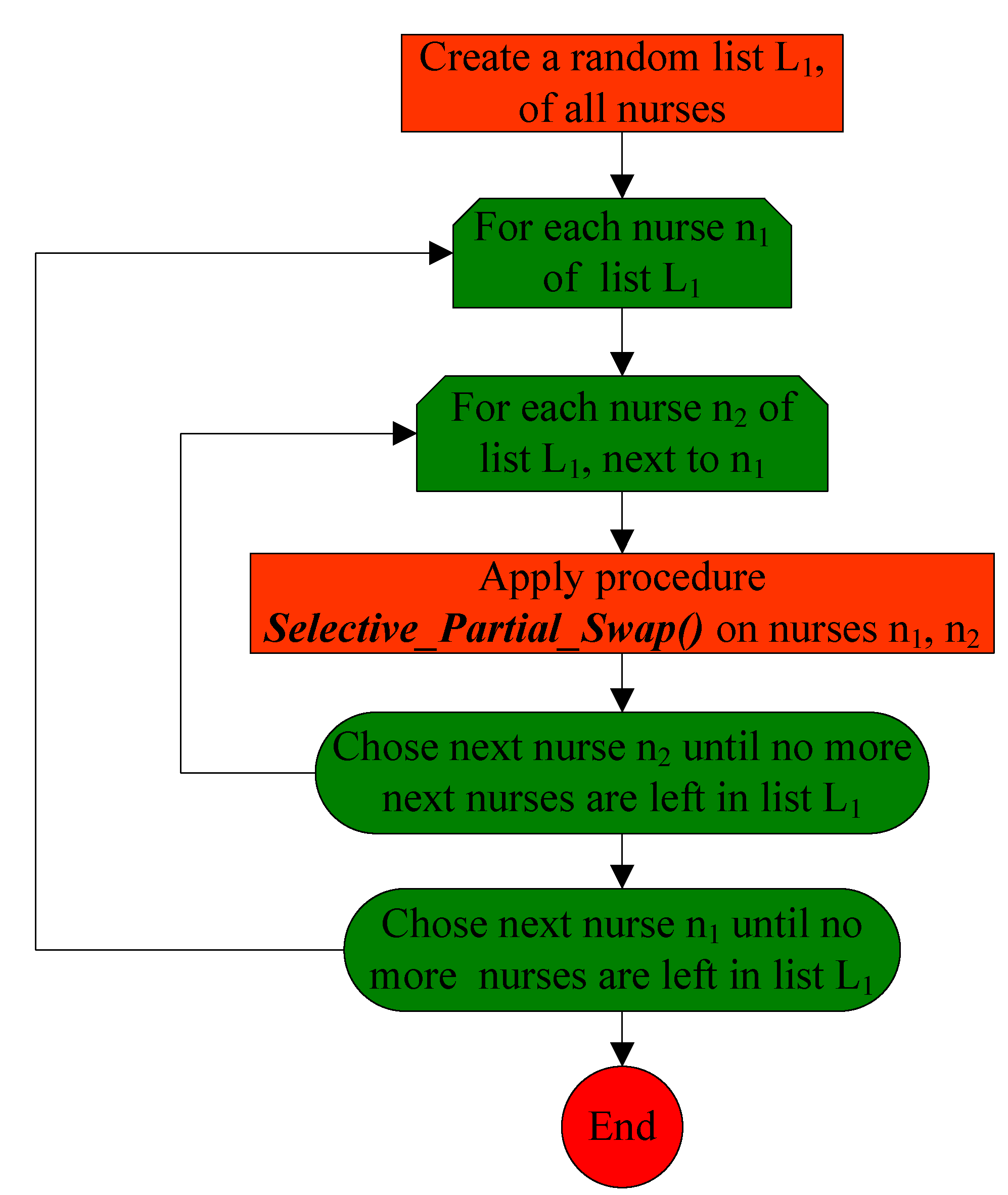
3.3.1. Procedure Selective_Day_Swap_Mutation()
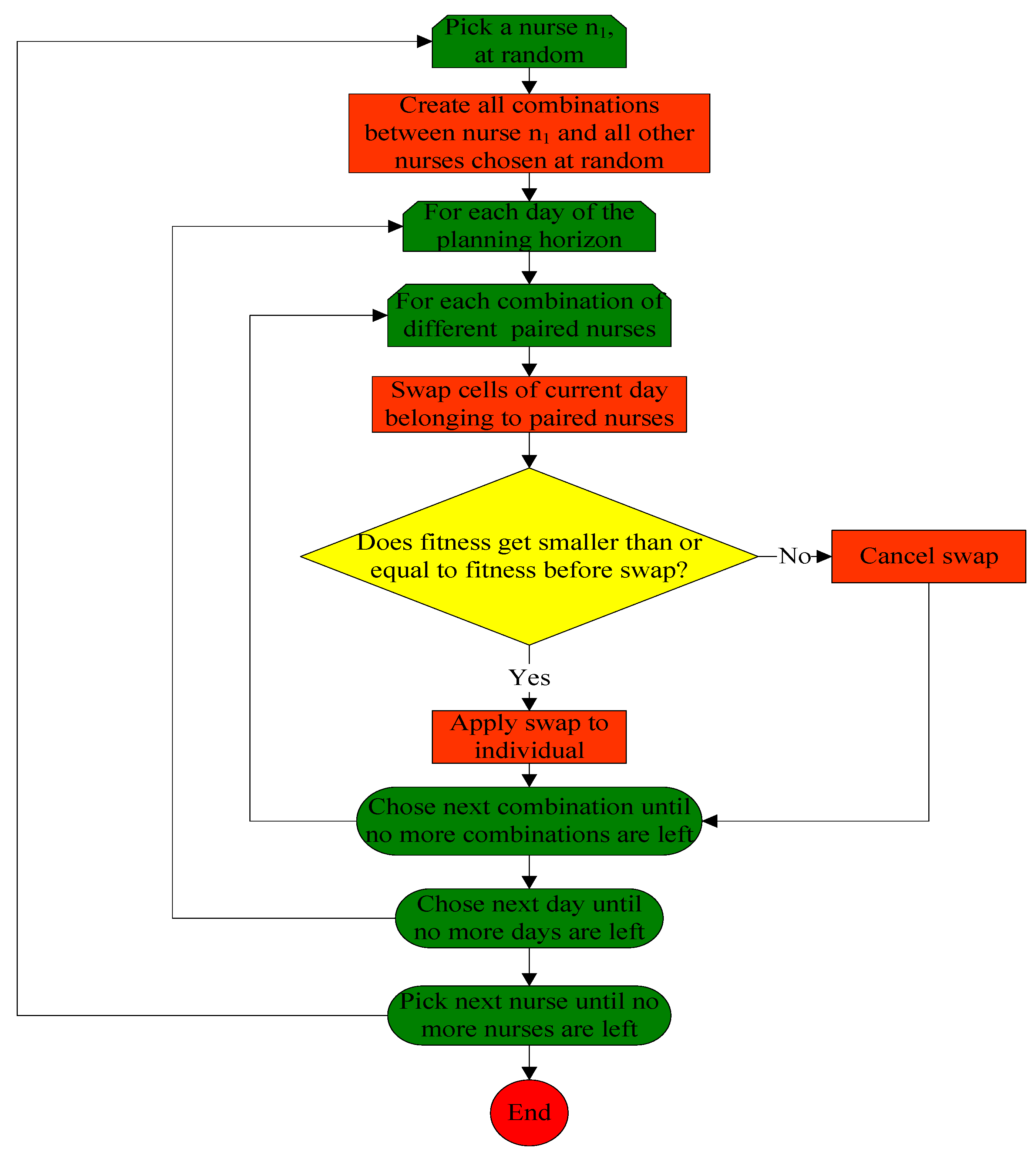
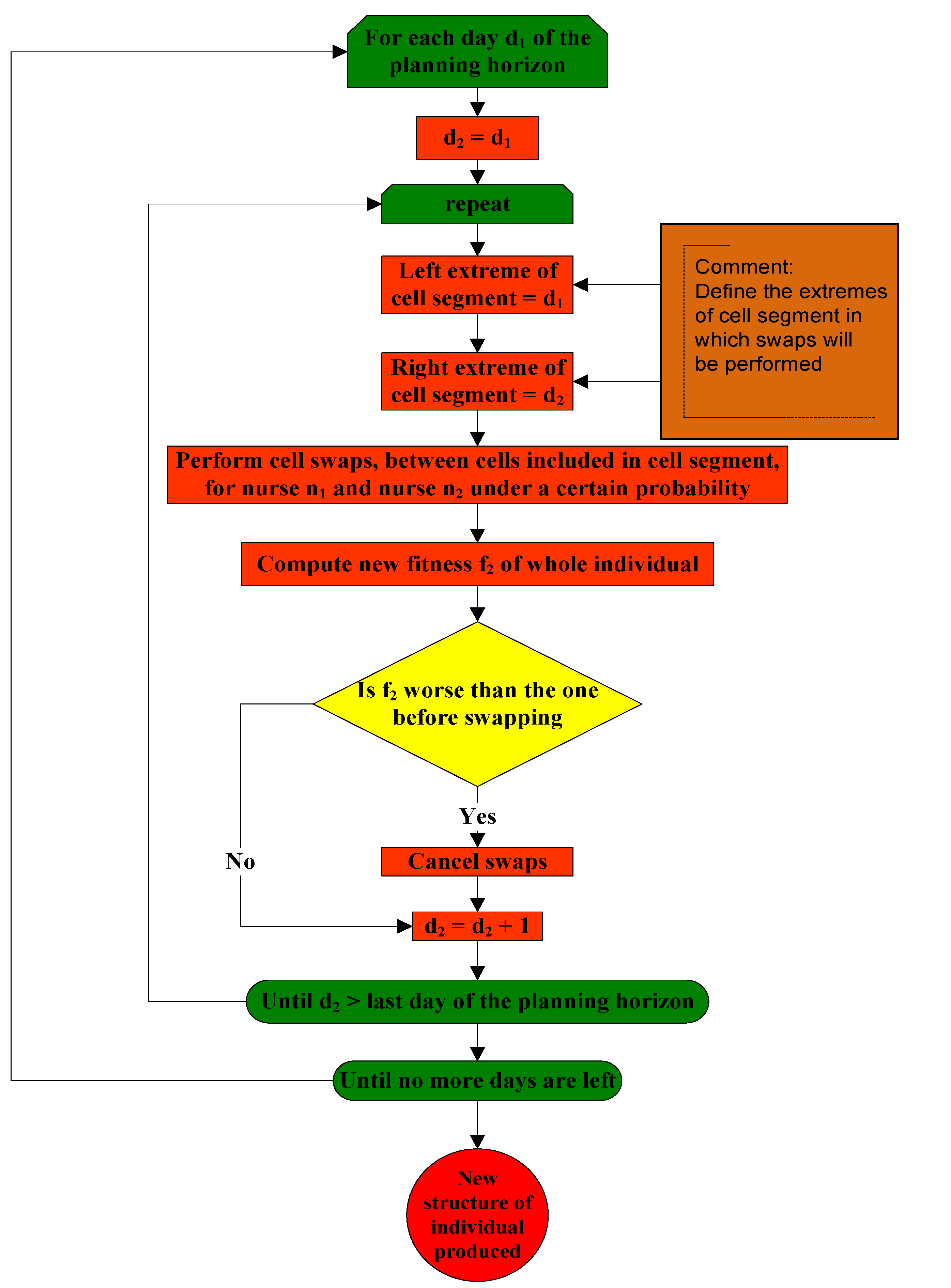
3.3.2. Procedure Random_Segment_Swap_Mutation()
4. Input Data
4.1. Input Instance, Valouxis-1
4.2. Input Instance, BCV3-46.2
4.3. Input Instance, MUSA
4.4. Input Instance, LLR
4.5. Input Instance, BCV4-13.1
4.6. Input Instance, WHPP
4.7. Input Instance, HED01
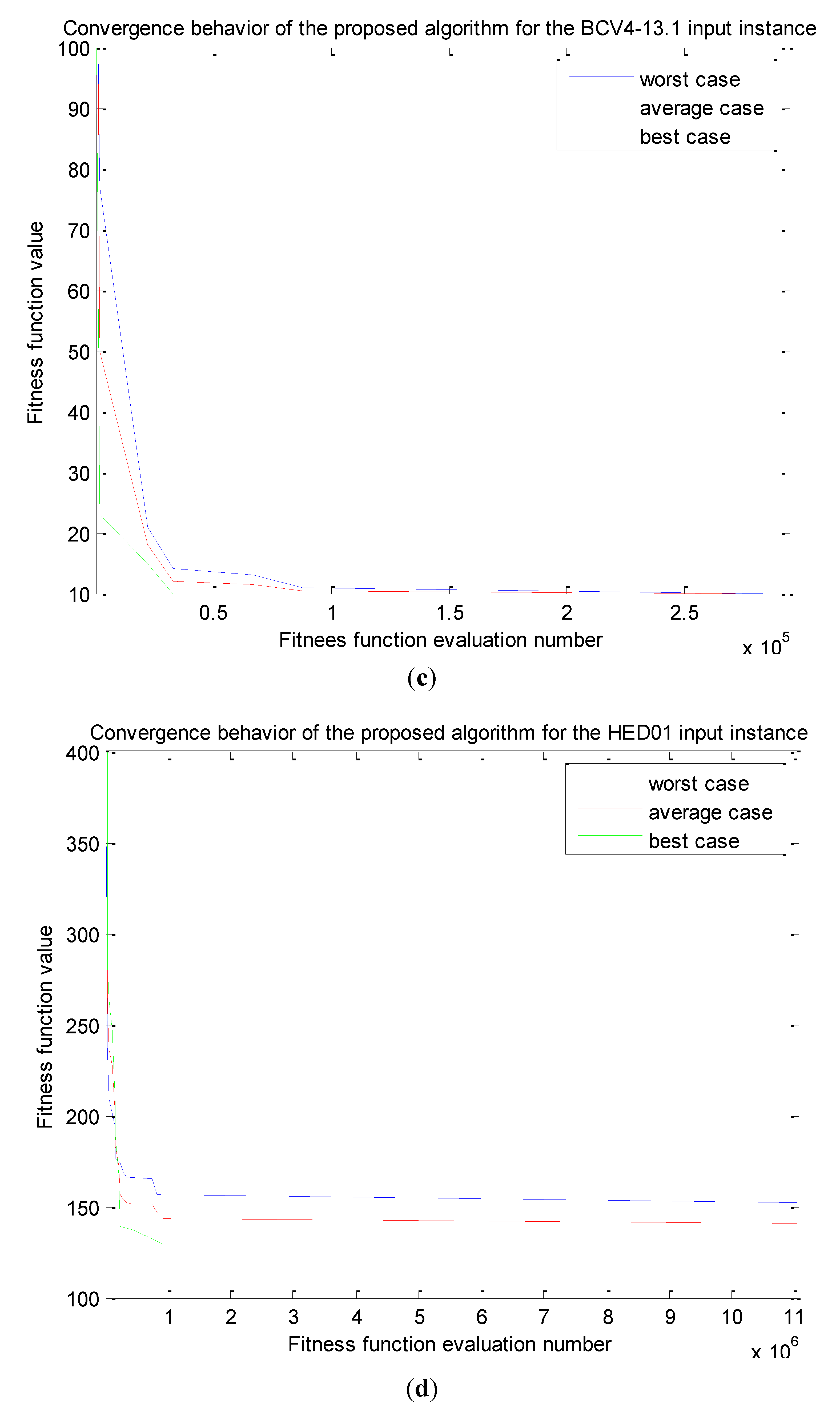
5. Computational Results
| Input instance | Published algorithm | Proposed algorithm | |||
|---|---|---|---|---|---|
| Description of algorithm | Fitness value | Execution time | Fitness value | Execution time | |
| Valouxis-1 | Integer linear programming approach [32] | 160 | 15 min | 20 | 17.64 s |
| BCV3-46.2 | A shift sequence based approach with greedy local search and adaptive ordering [34] | 3601 | 3 min, 4 s | 894 | 16 min |
| MUSA | Single phase goal programming model [36] | 199 | 28.3 s | 175 | 0.12 s |
| LLR | Two-phase hybrid approach [33] | 510 | 1 min, 36 s | 301 | 0.3 s |
| BCV4-13.1 | A shift sequence based approach with greedy local search without adaptive ordering [34] | 18 | 10 s | 10 | 3 s |
| WHPP | Linear programming formulation using column generation approach [37] | 5 | Not mentioned | 5 | 9.1 s |
| HED01 | Genetic algorithm [35] | 517 | Not mentioned | 129 | 29.1 s |
| Input Instance | Best roster reported ever [38] | Best roster found by the proposed algorithm | |||
|---|---|---|---|---|---|
| Found by | Fitness value | Execution Time | Fitness value | Execution Time | |
| Valouxis-1 | Tim Curtois, 3/9/2008 | 20 | Not mentioned | 20 | 17.64 s |
| BCV3-46.2 | F. Xue, C. Y. Chan and W. H. Ip, using a Hybrid VDS, 2/8/2008 | 894 | 4 h, 57 min | 894 | 16 min |
| MUSA | Not mentioned | 175 | Not mentioned | 175 | 0.12 s |
| LLR | Tim Curtois, using a variable depth search, 5/9/2008 | 301 | 10 s | 301 | 0.3 s |
| BCV4-13.1 | Not mentioned | 10 | Not mentioned | 10 | 3 s |
| WHPP | Weil et al., 5/4/2009 | 5 | Not mentioned | 5 | 9.1 s |
| HED01 | Tec on BEECHBONE (CS), 11/2/2010 | 136 | Not mentioned | 129 | 29.1 s |
| Input instance | Fitness value | Execution Time | Success Rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| Valouxis-1 | 20 | 120 | 73.33 | 30.55 | 41.7 | 17.64 s | 222.88 s | 90.19 s | 75.6 | 20% |
| BCV3-46.2 | 894 | 894 | 894 | 0 | 0 | 16 min | 31 min | 25 min | 4.37 | 100% |
| MUSA | 175 | 175 | 175 | 0 | 0 | 0.12 s | 0.52 s | 0.22 s | 0.13 | 100% |
| LLR | 301 | 305 | 301.48 | 0.93 | 0.3 | 0.3 s | 5.5 s | 1.85 s | 1.4 | 67% |
| BCV4-13.1 | 10 | 10 | 10 | 0 | 0 | 3 s | 14.2 s | 7.1 s | 0.7 | 100% |
| WHPP | 5 | 5 | 5 | 0 | 0 | 9.1 s | 27.2 s | 16.2 s | 5.9 | 100% |
| HED01 | 129 | 156 | 143.28 | 7.88 | 5.5 | 29.1 s | 5 min, 40 s | 2 min, 47 s | 2.13 | 6% |
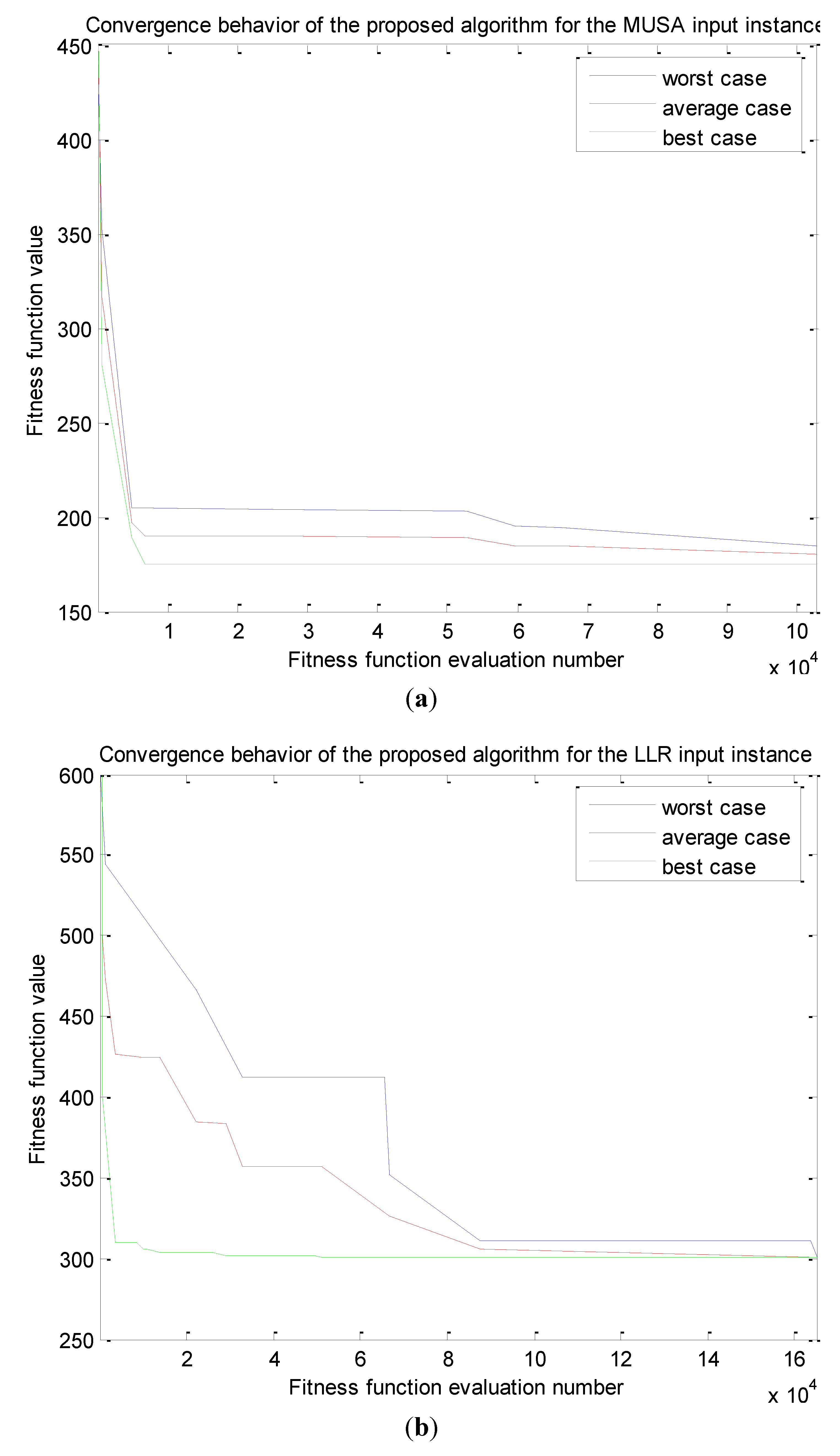
Investigating the Effect of Parameter Setting to Algorithms’ Performance
| Input instance Valouxis-1 | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| First phase cycles = 0 | 40 | 160 | 88 | 34.25 | 38.92 | 80 | 170 | 110 | 24.6 | 10% |
| First phase cycles = 1 | 20 | 120 | 73.33 | 30.55 | 41.7 | 17.64 | 222.88 | 90.19 | 75.6 | 20% |
| First phase cycles = 2 | 40 | 140 | 83 | 35.92 | 43.27 | 85 | 180 | 100 | 31.8 | 20% |
| First phase cycles = 3 | 40 | 160 | 86 | 34.06 | 39.6 | 90 | 180 | 150 | 27.6 | 10% |
| First phase cycles = 4 | 40 | 140 | 68 | 28.6 | 42.05 | 110 | 210 | 180 | 43.8 | 20% |
| First phase cycles = 5 | 40 | 120 | 68 | 21.5 | 31.62 | 78 | 290 | 232 | 34.08 | 10% |
| Input instance Valouxis-1 | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| POPSIZE = 1 | 60 | 140 | 88 | 30.11 | 34.21 | 61 | 180 | 130 | 36 | 30% |
| POPSIZE = 2 | 20 | 120 | 73.33 | 30.55 | 41.7 | 17.64 | 222.88 | 90.19 | 75.6 | 20% |
| POPSIZE = 3 | 60 | 160 | 83 | 34.01 | 40.97 | 62 | 246 | 135 | 57.3 | 30% |
| POPSIZE = 4 | 60 | 140 | 100 | 28.28 | 28.28 | 72 | 222.9 | 140 | 55 | 10% |
| POPSIZE = 5 | 60 | 100 | 84 | 20.66 | 24.59 | 80 | 200 | 150 | 62 | 30% |
| Input instance Valouxis-1 | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| Swapping probability = 0.85 | 40 | 120 | 82 | 25.73 | 31.37 | 100 | 190 | 150 | 33 | 10% |
| Swapping probability = 0.9 | 20 | 160 | 76 | 40.88 | 53.78 | 80 | 200 | 112 | 38.4 | 10% |
| Swapping probability = 0.95 | 40 | 100 | 68 | 19.32 | 28.41 | 66 | 253 | 129 | 60.9 | 20% |
| Swapping probability = 0.97 | 20 | 100 | 60 | 24.94 | 41.56 | 18 | 93.6 | 71 | 39.24 | 10% |
| Swapping probability = 0.99995 | 20 | 120 | 73.33 | 30.55 | 41.7 | 17.64 | 222.88 | 90.19 | 75.6 | 20% |
| Input instance BCV3-46.2 | Fitness value | Execution time (min) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| First phase cycles = 0 | 894 | 894 | 894 | 0 | 0 | 25 | 42 | 31 | 5.55 | 100% |
| First phase cycles = 1 | 894 | 894 | 894 | 0 | 0 | 16 | 31 | 25 | 4.37 | 100% |
| First phase cycles = 2 | 894 | 894 | 894 | 0 | 0 | 21 | 45 | 39 | 11.52 | 100% |
| First phase cycles = 3 | 894 | 894 | 894 | 0 | 0 | 19 | 57 | 35 | 11.94 | 100% |
| First phase cycles = 4 | 894 | 894 | 894 | 0 | 0 | 26 | 49 | 38 | 6.13 | 100% |
| First phase cycles = 5 | 894 | 894 | 894 | 0 | 0 | 30 | 49 | 40 | 5.6 | 100% |
| Input instance BCV3-46.2 | Fitness value | Execution time (min) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| POPSIZE = 1 | 894 | 894 | 894 | 0 | 0 | 16 | 48 | 28 | 8.71 | 100% |
| POPSIZE = 2 | 894 | 894 | 894 | 0 | 0 | 16 | 31 | 25 | 4.37 | 100% |
| POPSIZE = 3 | 894 | 894 | 894 | 0 | 0 | 16 | 38 | 28 | 7.64 | 100% |
| POPSIZE = 4 | 894 | 894 | 894 | 0 | 0 | 17 | 43 | 34 | 8 | 100% |
| POPSIZE = 5 | 894 | 894 | 894 | 0 | 0 | 25 | 42 | 33 | 5.55 | 100% |
| Input instance BCV3-46.2 | Fitness value | Execution time (min) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| Swapping probability = 0.85 | 894 | 894 | 894 | 0 | 0 | 16 | 57 | 36 | 11.67 | 100% |
| Swapping probability = 0.9 | 894 | 894 | 894 | 0 | 0 | 23 | 49 | 35 | 9.04 | 100% |
| Swapping probability = 0.95 | 894 | 894 | 894 | 0 | 0 | 27 | 51 | 39 | 8.46 | 100% |
| Swapping probability = 0.97 | 894 | 894 | 894 | 0 | 0 | 16 | 31 | 25 | 4.37 | 100% |
| Swapping probability = 0.99995 | 894 | 894 | 894 | 0 | 0 | 11 | 61 | 30 | 12.84 | 100% |
| Input instance Musa | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| First phase cycles = 0 | 175 | 185 | 177.8 | 4.25 | 2.4 | 0.13 | 0.52 | 0.3 | 0.12 | 75% |
| First phase cycles = 1 | 175 | 175 | 175 | 0 | 0 | 0.12 | 0.52 | 0.22 | 0.13 | 100% |
| First phase cycles = 2 | 175 | 180 | 175.7 | 3.9 | 2.2 | 0.33 | 0.58 | 0.43 | 0.12 | 80% |
| First phase cycles = 3 | 175 | 180 | 175.5 | 3.5 | 2 | 0.4 | 0.57 | 0.48 | 0.07 | 85% |
| First phase cycles = 4 | 175 | 180 | 177.6 | 4.2 | 2.4 | 0.39 | 0.62 | 0.54 | 0.11 | 90% |
| First phase cycles = 5 | 175 | 180 | 177.5 | 3.4 | 1.9 | 0.54 | 0.87 | 0.7 | 0.14 | 90% |
| Input instance MUSA | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| POPSIZE = 1 | 175 | 180 | 175.65 | 1.1 | 0.62 | 0.31 | 0.54 | 0.4 | 0.07 | 95% |
| POPSIZE = 2 | 175 | 175 | 175 | 0 | 0 | 0.12 | 0.52 | 0.22 | 0.13 | 100% |
| POPSIZE = 3 | 175 | 175 | 175 | 0 | 0 | 0.51 | 0.74 | 0.6 | 0.12 | 100% |
| POPSIZE = 4 | 175 | 175 | 175 | 0 | 0 | 0.19 | 0.82 | 0.5 | 0.24 | 100% |
| POPSIZE = 5 | 175 | 175 | 175 | 0 | 0 | 0.43 | 0.75 | 0.58 | 0.11 | 100% |
| Input instance MUSA | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| Swapping probability = 0.85 | 175 | 185 | 176.5 | 3.38 | 1.9 | 0.14 | 0.42 | 0.32 | 0.14 | 80% |
| Swapping probability = 0.9 | 175 | 185 | 176.5 | 3.38 | 1.9 | 0.12 | 0.38 | 0.2 | 0.1 | 80% |
| Swapping probability = 0.95 | 175 | 185 | 176 | 3.16 | 1.79 | 0.11 | 0.29 | 0.18 | 0.07 | 90% |
| Swapping probability = 0.97 | 175 | 175 | 175 | 0 | 0 | 0.12 | 0.52 | 0.22 | 0.13 | 100% |
| Swapping probability = 0.99995 | 175 | 185 | 177.62 | 3.75 | 2 | 0.06 | 0.56 | 0.23 | 0.14 | 62% |
| Input instance LLR | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| 1ST Phase cycles = 0 | 301 | 303 | 301.7 | 0.82 | 0.27 | 0.8 | 2.5 | 2 | 1.1 | 50% |
| 1ST Phase cycles = 1 | 301 | 305 | 301.48 | 0.93 | 0.3 | 0.3 | 5.5 | 1.85 | 1.4 | 67% |
| 1ST Phase cycles = 2 | 301 | 303 | 301.8 | 0.8 | 0.3 | 1 | 2.9 | 1.6 | 0.6 | 45% |
| 1ST Phase cycles = 3 | 301 | 303 | 301.6 | 0.8 | 0.26 | 1.3 | 3.8 | 2.4 | 0.8 | 58% |
| 1ST Phase cycles = 4 | 301 | 303 | 301.4 | 0.7 | 0.23 | 1.3 | 3.4 | 2.8 | 0.7 | 62% |
| 1ST Phase cycles = 5 | 301 | 303 | 301.5 | 0.7 | 0.23 | 1.4 | 4.6 | 2.9 | 1.1 | 47% |
| Input instance LLR | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| POPSIZE = 1 | 301 | 305 | 302.2 | 1.6 | 0.53 | 0.74 | 2.38 | 1.5 | 0.6 | 50% |
| POPSIZE = 2 | 301 | 305 | 301.48 | 0.93 | 0.3 | 0.3 | 5.5 | 1.85 | 1.4 | 67% |
| POPSIZE = 3 | 301 | 303 | 301.7 | 1.06 | 0.35 | 0.98 | 7.08 | 2.9 | 2.2 | 60% |
| POPSIZE = 4 | 301 | 303 | 301.8 | 0.8 | 0.27 | 0.23 | 3.21 | 1.32 | 0.9 | 45% |
| POPSIZE = 5 | 301 | 303 | 301.6 | 0.7 | 0.23 | 0.38 | 4.03 | 1.72 | 1.2 | 55% |
| Input instance LLR | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| Swapping probability = 0.4 | 301 | 303 | 301.6 | 0.9 | 0.29 | 0.85 | 5.23 | 2.1 | 0.33 | 55% |
| Swapping probability = 0.45 | 301 | 303 | 301.5 | 0.55 | 0.18 | 1.27 | 5.66 | 2.2 | 1.36 | 63% |
| Swapping probability = 0.5 | 301 | 305 | 301.48 | 0.93 | 0.3 | 0.3 | 5.5 | 1.85 | 1.4 | 67% |
| Swapping probability = 0.55 | 301 | 303 | 301.5 | 0.4 | 0.13 | 1.2 | 2.6 | 2.4 | 1.6 | 65% |
| Swapping probability = 0.6 | 301 | 303 | 301.5 | 0.7 | 0.23 | 1.1 | 4.9 | 2.2 | 1.1 | 64% |
| Input instance BCV4-13.1 | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| First phase cycles = 0 | 10 | 10 | 10 | 0 | 0 | 5.84 | 7.23 | 6.21 | 0.52 | 100% |
| First phase cycles = 1 | 10 | 10 | 10 | 0 | 0 | 3 | 14.2 | 7.1 | 2.65 | 100% |
| First phase cycles = 2 | 10 | 10 | 10 | 0 | 0 | 6.95 | 12.3 | 8.43 | 1.66 | 100% |
| First phase cycles = 3 | 10 | 10 | 10 | 0 | 0 | 7.46 | 14.4 | 10.36 | 1.99 | 100% |
| First phase cycles = 4 | 10 | 10 | 10 | 0 | 0 | 9.42 | 14.3 | 10.99 | 1.45 | 100% |
| First phase cycles = 5 | 10 | 10 | 10 | 0 | 0 | 9.35 | 15 | 13.15 | 1.77 | 100% |
| Input instance BCV4-13.1 | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| POPSIZE = 1 | 10 | 10 | 10 | 0 | 0 | 5.3 | 8.5 | 6.98 | 2.1 | 100% |
| POPSIZE = 2 | 10 | 10 | 10 | 0 | 0 | 3 | 14.2 | 7.1 | 2.65 | 100% |
| POPSIZE = 3 | 10 | 10 | 10 | 0 | 0 | 6.2 | 8 | 7.23 | 0.64 | 100% |
| POPSIZE = 4 | 10 | 10 | 10 | 0 | 0 | 6 | 8.3 | 6.95 | 0.9 | 100% |
| POPSIZE = 5 | 10 | 10 | 10 | 0 | 0 | 6.4 | 9.8 | 7.8 | 1.31 | 100% |
| Input instance BCV4-13.1 | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| Swapping probability = 0.85 | 10 | 10 | 10 | 0 | 0 | 5.72 | 7.8 | 7.3 | 0.51 | 100% |
| Swapping probability = 0.9 | 10 | 10 | 10 | 0 | 0 | 5.23 | 7.55 | 7.3 | 0.61 | 100% |
| Swapping probability = 0.95 | 10 | 10 | 10 | 0 | 0 | 5.14 | 7.45 | 7.2 | 0.69 | 100% |
| Swapping probability = 0.97 | 10 | 10 | 10 | 0 | 0 | 3 | 14.2 | 7.1 | 0.7 | 100% |
| Swapping probability = 0.99995 | 10 | 10 | 10 | 0 | 0 | 3.87 | 22.1 | 12.45 | 6.61 | 100% |
| Input instance WHPP | Fitness value | Execution time (s) | Success Rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| First phase cycles = 0 | 5 | 7 | 5.2 | 0.63 | 12.1 | 16.45 | 97.43 | 43.3 | 21.8 | 90% |
| First phase cycles = 1 | 5 | 5 | 5 | 0 | 0 | 9.1 | 27.2 | 16.2 | 5.9 | 100% |
| First phase cycles = 2 | 5 | 8 | 5.3 | 0.95 | 17.9 | 25.74 | 42.4 | 37 | 5.4 | 90% |
| First phase cycles = 3 | 5 | 5 | 5 | 0 | 0 | 23.43 | 51.6 | 33.8 | 9.35 | 100% |
| First phase cycles = 4 | 5 | 5 | 5 | 0 | 0 | 25.19 | 39.9 | 34.3 | 5.6 | 100% |
| First phase cycles = 5 | 5 | 5 | 5 | 0 | 0 | 21 | 54.3 | 38 | 9.7 | 100% |
| Input instance WHPP | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| POPSIZE = 1 | 5 | 8 | 5.3 | 0.95 | 17.9 | 9.9 | 78.2 | 34.5 | 20.84 | 90% |
| POPSIZE = 2 | 5 | 5 | 5 | 0 | 0 | 9.1 | 27.2 | 16.2 | 5.9 | 100% |
| POPSIZE = 3 | 5 | 7 | 5.2 | 0.63 | 12.12 | 12.4 | 58.1 | 31 | 16.8 | 90% |
| POPSIZE = 4 | 5 | 8 | 5.3 | 0.95 | 17.9 | 19.2 | 51.3 | 33.6 | 10.71 | 90% |
| POPSIZE = 5 | 5 | 5 | 5 | 0 | 0 | 18.5 | 89.8 | 37.6 | 21.9 | 100% |
| Input instance WHPP | Fitness value | Execution time (s) | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| Swapping probability = 0.4 | 5 | 8 | 5.3 | 0.95 | 38.4 | 87.3 | 55 | 14.76 | 90% | |
| Swapping probability = 0.45 | 5 | 5 | 5 | 0 | 0 | 9.1 | 27.2 | 16.2 | 5.9 | 100% |
| Swapping probability = 0.5 | 5 | 5 | 5 | 0 | 0 | 7.72 | 50.25 | 20 | 10.97 | 100% |
| Swapping probability = 0.55 | 5 | 5 | 5 | 0 | 0 | 19.23 | 98.2 | 37.3 | 22.7 | 100% |
| Swapping probability = 0.6 | 5 | 5 | 5 | 0 | 0 | 24.3 | 54.4 | 40.3 | 10.53 | 100% |
| Input instance HED01 | Fitness value | Execution time | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| First phase cycles = 0 | 131 | 144 | 136 | 4.24 | 1 min, 30 s | 4 min, 28 s | 3 min, 6 s | 0.97 | 8% | |
| First phase cycles = 1 | 129 | 156 | 143.28 | 7.88 | 5.5 | 29.1 s | 5 min, 40 s | 2 min, 47 s | 2.13 | 6% |
| First phase cycles = 2 | 131 | 146 | 135.9 | 5.82 | 1 min, 28 s | 5 min, 15 s | 3 min, 40 s | 1.37 | 8% | |
| First phase cycles = 3 | 130 | 142 | 134.7 | 4.34 | 1 min, 31 s | 6 min, 33 s | 4 min | 1.23 | 7% | |
| First phase cycles = 4 | 130 | 138 | 132.8 | 2.53 | 2 min, 6 s | 5 min, 36 s | 4 min | 1.13 | 9% | |
| First phase cycles = 5 | 132 | 150 | 140.7 | 5.17 | 2 min, 12 s | 5 min, 29 s | 4 min | 1.22 | 7% | |
| Input instance HED01 | Fitness value | Execution time | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| POPSIZE = 1 | 133 | 151 | 142 | 7.69 | 5.4 | 2 min, 57 s | 6 min | 4 min, 18 s | 1.1 | 12% |
| POPSIZE = 2 | 129 | 156 | 143.28 | 7.88 | 5.5 | 29.1 s | 5 min, 40 s | 2 min, 47 s | 2.13 | 6% |
| POPSIZE = 3 | 132 | 151 | 139.6 | 6.63 | 4.76 | 2 min, 20 s | 4 min, 50 s | 3 min, 30 s | 0.78 | 10% |
| POPSIZE = 4 | 131 | 146 | 139.5 | 5.15 | 3.77 | 1 min, 30 s | 5 min, 30 s | 3 min, 40 s | 1.04 | 9% |
| POPSIZE = 5 | 131 | 147 | 136.7 | 5.68 | 4.15 | 2 min, 45 s | 12 min, 25 s | 5 min | 2.79 | 11% |
| Input instance HED01 | Fitness value | Execution time | Success rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Average | STD | CV (%) | Best | Worst | Average | STD | ||
| Swapping probability = 0.8 | 131 | 151 | 137.9 | 7.31 | 1 min, 20 s | 4 min, 28 s | 2 min, 55 s | 0.93 | 5% | |
| Swapping probability = 0.82 | 132 | 148 | 138.5 | 5.28 | 2 min, 6 s | 6 min, 26 s | 3 min, 50 s | 1.34 | 6% | |
| Swapping probability = 0.85 | 129 | 156 | 143.28 | 7.88 | 5.5 | 29.1 s | 5 min, 40 s | 2 min, 47 s | 2.13 | 6% |
| Swapping probability = 0.88 | 131 | 135 | 133.4 | 1.84 | 1 min, 35 s | 2 min, 30 s | 2 min, 30 s | 1.01 | 7% | |
| Swapping probability = 0.9 | 130 | 153 | 134 | 7.05 | 1 min, 50 s | 3 min, 7 s | 2 min, 5 s | 1.62 | 5% | |
6. Conclusions and Future Work
References
- Cooper, T.B.; Kingston, J.H. The Complexity of Timetable Construction Problems; Technical Report No. 495; Basser Department of Computer Science, The University of Sidney: Sidney, Australia, 1995. [Google Scholar]
- White, G.; Xie, B.; Zonjic, S. Using tabu search with longer term memory and relaxation to create examination timetables. Eur. J. Oper. Res. 2004, 153, 80–91. [Google Scholar] [CrossRef]
- Yang, S.; Jat, S.N. Genetic algorithms with guided and local search strategies for university course timetabling. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2011, 41, 93–106. [Google Scholar] [CrossRef]
- Burke, E.K.; de Causmaecker, P.; Vanden Berghe, G.; van Landeghem, H. The state of the art of nurse rostering. J. Sched. 2004, 7, 441–499. [Google Scholar] [CrossRef]
- Van den Bergh, J.; Beliën, J.; de Bruecker, P.; Demeulemeester, E.; de Boeck, L. Personnel scheduling: A literature review. Eur. J. Oper. Res. 2013, 226, 367–385. [Google Scholar] [CrossRef]
- Aickelin, U.; Dowsland, K.A. An indirect genetic algorithm for a nurse-scheduling problem. Comput. Oper. Res. 2004, 31, 761–778. [Google Scholar] [CrossRef]
- Bai, R.; Burke, E.K.; Kendall, G.; Li, J.; McCollum, B. A hybrid evolutionary approach to the nurse rostering problem. Trans. Evolut. Comput. 2010, 14, 580–590. [Google Scholar] [CrossRef]
- Maenhout, B.; Vanhoucke, M. An evolutionary approach for the nurse rostering problem. Comput. Oper. Res. 2011, 38, 1400–1411. [Google Scholar] [CrossRef]
- Burke, E.; Soubeiga, E. Scheduling Nurses Using a Tabu-search Hyperheuristic. In Proceeding of the 1st Multidisciplinary International Scheduling Conference (MISTA 2003), Nottingham, UK, 13–16 August 2003; pp. 197–218.
- Oughalime, A.; Ismail, W.R.; Yeun, L.C. A Tabu Search Approach to the Nurse Scheduling Problem. In Proceeding of the International Symposium on Information Tecnhology 2008 (ITSim 2008), Kuala Lumpur, Malaysia, 26–28 August 2008; pp. 1–7.
- Parr, D.; Thompson, J.M. Solving the multi-objective nurse scheduling problem with a weighted cost function. Ann. Oper. Res. 2007, 155, 279–288. [Google Scholar] [CrossRef]
- Kundu, S.; Mahato, M.; Mahanty, B.; Acharyya, S. Comparative Performance of Simulated Annealing and Genetic Algorithm in Solving Nurse Scheduling Problem. In Proceeding of the International Multi Conference on Engineers and Computer Sciences 2008 (IMECS 2008), Hong Kong, 19–21 March 2008; pp. 19–21.
- Burke, E.K.; de Causmaecker, P.; Petrovic, S.; Vanden Berghe, G. Variable Neighborhood Search for Nurse Rostering Problems. In Metaheuristics: Computer Decision-Making; Resende, M.C.G., Pinho de Sousa, J., Eds.; Kluwer Academic Publishers B.V.: Dordrecht, The Netherlands, 2003; Chapter 7; pp. 153–172. [Google Scholar]
- Burke, E.K.; Curtois, T.; Post, G.; Qu, R.; Veltman, B. A hybrid heuristic ordering and variable neighbourhood search for the nurse rostering problem. Eur. J. Oper. Res. 2008, 188, 330–341. [Google Scholar] [CrossRef]
- Lü, Z.; Hao, J.-K. Adaptive neighborhood search for nurse rostering. Eur. J. Oper. Res. 2012, 218, 865–876. [Google Scholar] [CrossRef]
- Burke, E.K.; Curtois, T.; Qu, R.; Vanden Berghe, G. A scatter search methodology for the nurse rostering problem. J. Oper. Res. Soc. 2010, 61, 1667–1679. [Google Scholar] [CrossRef]
- Maenhout, B.; Vanhoucke, M. New computational results for the nurse scheduling problem: A scatter search algorithm. Lect. Notes Comput. Sci. 2006, 3906, 159–170. [Google Scholar]
- Bellanti, F.; Carello, G.; Della Croce, F.; Tadei, R. A greedy-based neighborhood search approach to a nurse rostering problem. Eur. J. Oper. Res. 2004, 153, 28–40. [Google Scholar] [CrossRef]
- Burke, E.K.; Curtois, T.; van Draat, L.F.; van Ommeren, J.K.; Post, G. Progress control in iterated local search for nurse rostering. J. Oper. Res. Soc. 2011, 62, 360–367. [Google Scholar] [CrossRef]
- Gunther, M.; Nissen, V. Particle swarm optimization and the agent-based algorithm for a problem of staff scheduling. Lect. Notes Comput. Sci. 2010, 6025, 451–461. [Google Scholar]
- Ozcan, E. Memetic algorithms for nurse rostering. Lect. Notes Comput. Sci. 2005, 3733, 482–492. [Google Scholar]
- Gutjahr, W.J.; Rauner, M.S. An ACO algorithm for a dynamic regional nurse-scheduling problem in Austria. Comput. Oper. Res. 2007, 34, 642–666. [Google Scholar] [CrossRef]
- Brimberg, J.; Hansen, P.; Mladenovic, N.; Taillard, E. Improvements and comparison of heuristics for solving the multisource Weber problem. Oper. Res. 2000, 48, 444–460. [Google Scholar] [CrossRef]
- Fleszar, K.; Hindi, K.S. Solving the resource-constrained project scheduling problem by a variable neighborhood search. Eur. J. Oper. Res. 2004, 155, 402–413. [Google Scholar] [CrossRef]
- Avanthay, C.; Hertz, A.; Zufferey, N. A variable neighborhood search for graph coloring. Eur. J. Oper. Res. 2003, 151, 379–388. [Google Scholar] [CrossRef]
- Lü, Z.; Hao, J.-K.; Glover, F. Neighborhood analysis: A case study on curriculum-based course timetabling. J. Heuristics 2011, 17, 97–118. [Google Scholar] [CrossRef]
- Di Gaspero, L.; Schaerf, A. Multi-neighborhood local search with application to course timetabling. Lect. Notes Comput. Sci. 2003, 2740, 262–275. [Google Scholar]
- Burke, E.K.; Li, J.; Qu, R. A hybrid model of integer programming and variable neighborhood search for highly-constrained nurse rostering problems. Eur. J. Oper. Res. 2010, 203, 484–493. [Google Scholar] [CrossRef]
- Burke, E.K.; Eckersley, A.; McCollum, B.; Petrovic, S.; Qu, R. Hybrid variable neighbourhood approaches to exam timetabling. Eur. J. Oper. Res. 2010, 206, 46–53. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenovic, N.; Pérez-Brito, D. Variable neighborhood decomposition search. J. Heuristics 2001, 7, 335–350. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenovic, N.; Perez, J.A.M. Variable neighbourhood search: Methods and applications. Ann. Oper. Res. 2010, 175, 367–407. [Google Scholar] [CrossRef]
- Valouxis, C.; Housos, E. Hybrid optimization techniques for the workshift and rest assignment of nursing personnel. Artif. Intell. Med. 2000, 20, 155–175. [Google Scholar] [CrossRef]
- Li, H.; Lim, A.; Rodrigues, B. A Hybrid AI Approach for Nurse Rostering Problem. In Proceeding of the ACM Symposium on Applied Computing (SAC 2003), Melbourne, FL, USA, 9–12 March 2003; ACM: New York, NY, USA, 2003; pp. 730–735. [Google Scholar] [Green Version]
- Brucker, P.; Burke, E.; Curtois, T.; Qu, R.; Vanden Berghe, G. A shift sequence based approach for nurse scheduling and a new benchmark dataset. J. Heuristics 2010, 16, 559–573. [Google Scholar] [CrossRef]
- Puente, J.; Gómes, A.; Fernández, I.; Priore, P. Medical doctor rostering problem in a hospital emergency department by means of genetic algorithms. Comput. Ind. Eng. 2009, 56, 1232–1242. [Google Scholar] [CrossRef]
- Musa, A.A.; Saxena, U. Scheduling nurses using goal-programming techniques. AIEE Trans. 1984, 13, 216–221. [Google Scholar] [CrossRef]
- Weil, G.; Heus, K.; Francois, P.; Poujade, M. Constraint programming for nurse scheduling. IEEE Eng. Med. Biol. Mag. 1995, 14, 417–422. [Google Scholar] [CrossRef]
- Automated employee scheduling benchmark instances. Available online: http://www.cs.nott.ac.uk/~tec/NRP/ (accessed on 1 April 2013).
- Roster::Valouxis-1. Available online: http://www.cs.nott.ac.uk/~tec/NRP/data/solutions/html/Valouxis-1.Solution.20.html (accessed on 1 April 2013).
- Burke, E.K.; de Causmaecker, P.; van den Berghe, G. Novel Meta-Heuristic Approaches to Nurse Rostering Problems in Belgian Hospitals. In Handbook of Scheduling: Algorithms, Models and Performance Analysis; Leung, J., Ed.; CRC Press: Boca Raton, FL, USA, 2004; Chapter 44; pp. 1–18. [Google Scholar]
- Roster::BCV-3.46.2. Available online: http://www.cs.nott.ac.uk/~tec/NRP/data/solutions/html/BCV-3.46.2.Solution.894.html (accessed on 1 April 2013).
- Roster::BCV-4.13.1. Available online: http://www.cs.nott.ac.uk/~tec/NRP/data/solutions/html/BCV-4.13.1.Solution.10.html (accessed on 1 April 2013).
- Roster::HED01. Available online: http://www.cs.nott.ac.uk/~tec/NRP/data/solutions/html/HED01.Solution.136.html (accessed on 1 April 2013).
- Roster LLR. Available online: http://www.cs.nott.ac.uk/~tec/NRP/data/solutions/html/LLR.Solution.301.html (accessed on 1 April 2013).
- Roster::Musa. Available online: http://www.cs.nott.ac.uk/~tec/NRP/data/solutions/html/Musa.Solution.175.html (accessed on 1 April 2013).
- Roster::WHPP. Available online: http://www.cs.nott.ac.uk/~tec/NRP/data/solutions/html/WHPP.Solution.5.html (accessed on 1 April 2013).
- Applying a stochastic variable neighborhood search algorithm on nurse rostering benchmark instances. Executables and results. Available online: http://www.deapt.uwg.gr/nurse_rostering/nurse_rostering.html (accessed on 1 April 2013).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Solos, I.P.; Tassopoulos, I.X.; Beligiannis, G.N. A Generic Two-Phase Stochastic Variable Neighborhood Approach for Effectively Solving the Nurse Rostering Problem. Algorithms 2013, 6, 278-308. https://doi.org/10.3390/a6020278
Solos IP, Tassopoulos IX, Beligiannis GN. A Generic Two-Phase Stochastic Variable Neighborhood Approach for Effectively Solving the Nurse Rostering Problem. Algorithms. 2013; 6(2):278-308. https://doi.org/10.3390/a6020278
Chicago/Turabian StyleSolos, Ioannis P., Ioannis X. Tassopoulos, and Grigorios N. Beligiannis. 2013. "A Generic Two-Phase Stochastic Variable Neighborhood Approach for Effectively Solving the Nurse Rostering Problem" Algorithms 6, no. 2: 278-308. https://doi.org/10.3390/a6020278
APA StyleSolos, I. P., Tassopoulos, I. X., & Beligiannis, G. N. (2013). A Generic Two-Phase Stochastic Variable Neighborhood Approach for Effectively Solving the Nurse Rostering Problem. Algorithms, 6(2), 278-308. https://doi.org/10.3390/a6020278






