Laplace–Fourier Transform of the Stretched Exponential Function: Analytic Error Bounds, Double Exponential Transform, and Open-Source Implementation “libkww”
Abstract
:1. Introduction
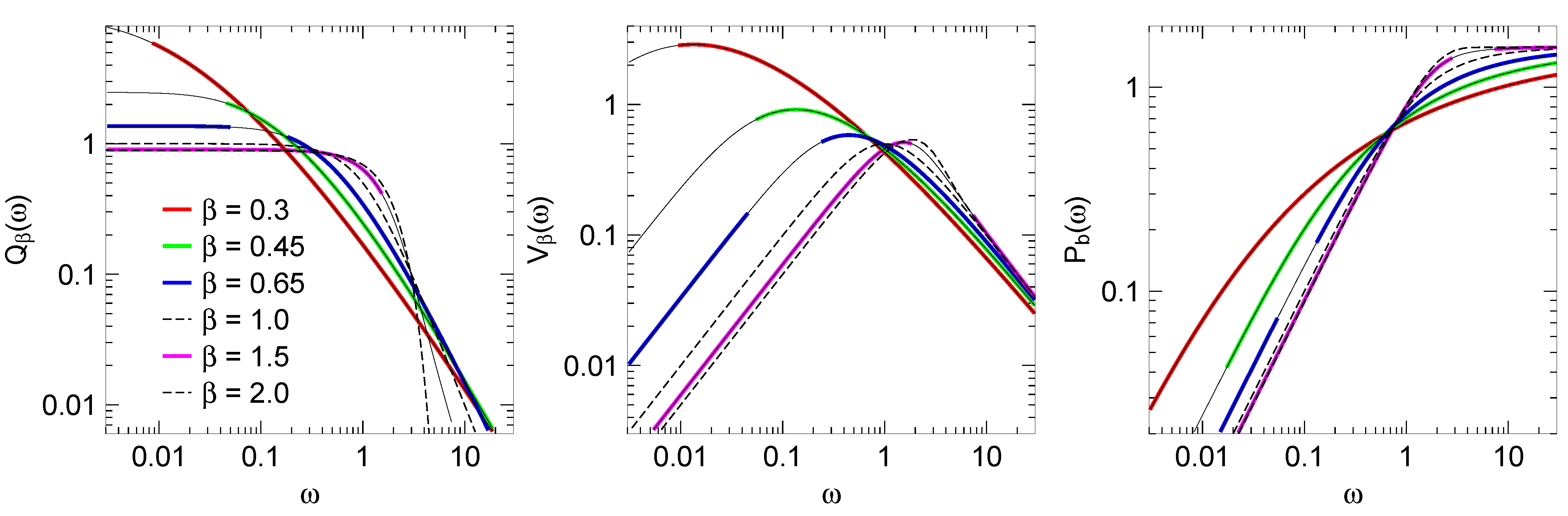
2. Applications
2.1. The Stretched Exponential
2.2. The Kohlrausch–Williams–Watts Function
3. Notation
4. Series Expansions
4.1. Small-ω Expansion
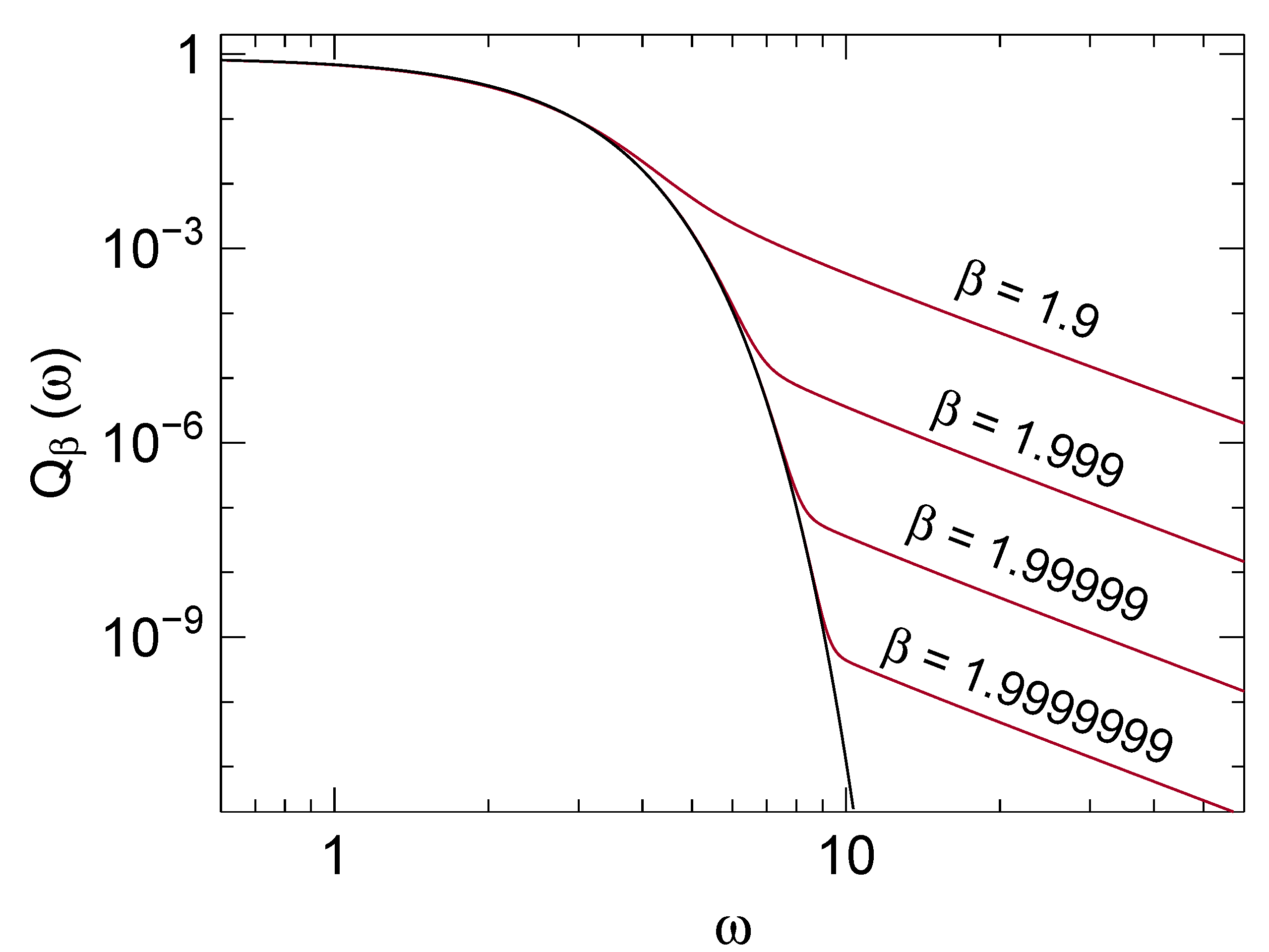
4.2. Large-ω Expansion
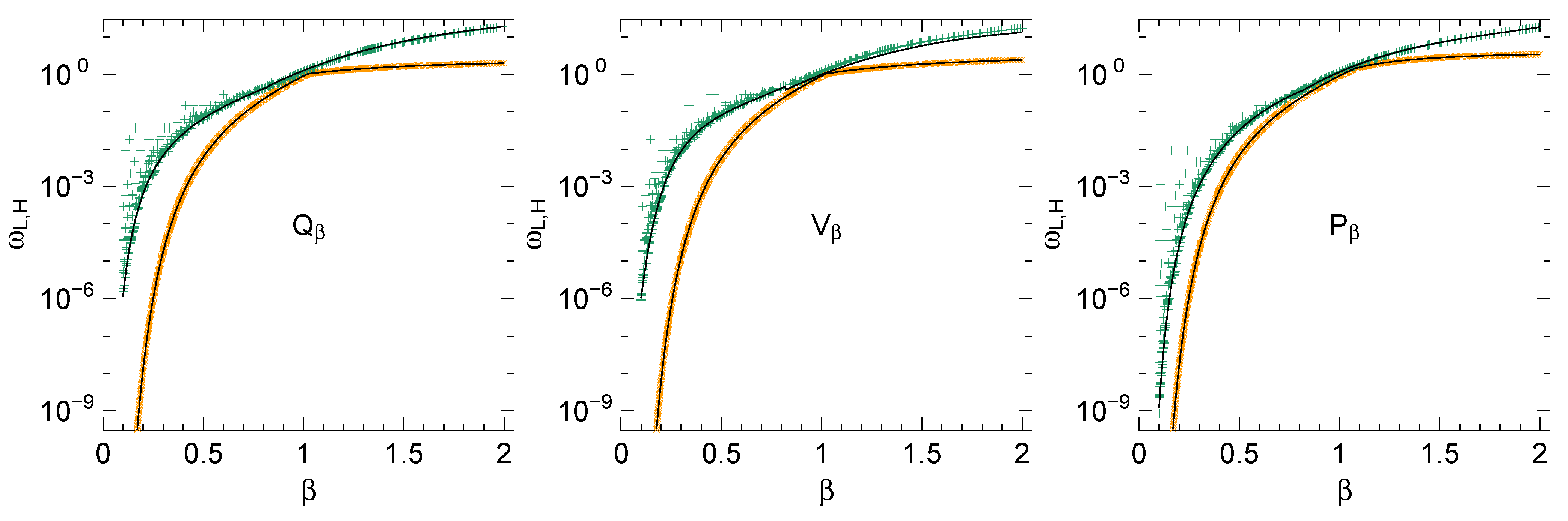
4.3. Cross-Over Frequencies
4.4. Error Bounds and Algorithm
4.5. Application Domains
5. Numeric Integration
5.1. Notation
5.2. Integrating on a Double-exponential Grid
5.3. Choosing a Double-exponential Transform
5.4. Truncation Error and Mesh Width
5.5. Iterative Integration
5.6. Special Case
6. Implementation
6.1. Download and Installation
6.2. Application Programming Interface, Error Handling
The letters c and s stand for cosine and sine transform, respectively; p stands for the primitive of the cosine transform.#include <kww.h> double kwwc (double omega, double beta);double kwws (double omega, double beta);double kwwp (double omega, double beta);
6.3. Low-level Functions
and similar for kwws and kwwp. If or , the appropriate series expansion is tried. If it returns an error code (return value below 0) the computation falls back to numeric integration. If ω lies between and , the numeric integration is invoked from the outset.double kwwc_lim_low( double b ); double kwwc_lim_hig( double b );
and similar for kwws and kwwp. For test purposes, these low-level functions can also be called directly.double kwwc_low( double w, double b );double kwwc_mid( double w, double b );double kwwc_hig( double w, double b );
where the actual computations are carried out, following the algorithms described above (Section 4.4, Section 5.5), with .double kww__low( double w, double b, int kappa, int mu);double kww__mid( double w, double b, int kind, int mu);double kww__hig( double w, double b, int kappa, int mu);
6.4. Diagnostic Variables and Test Programs
The variable kww_algorithm is set to 1, 2, or 3, to indicate whether the low-ω expansion, the numeric integration, or the high-ω expansion has been used. The variable kww_num_of_terms counts the evaluations of .extern int kww_algorithm; extern int kww_num_of_terms;
Acknowledgments
References
- Dishon, M.; Weiss, G.H.; Bendler, J.T. Stable Law Densities and Linear Relaxation Phenomena. J. Res. N. B. S 1985, 90, 27–40. [Google Scholar] [CrossRef]
- Chung, S.H.; Stevens, J.R. Time-dependent correlation and the evaluation of the stretched exponential or Kohlrausch-Williams-Watts function. Am. J. Phys. 1991, 59, 1024–1029. [Google Scholar] [CrossRef]
- Cardona, M.; Chamberlin, R.V.; Marx, W. The history of the stretched exponential function. Ann. Phys. (Leipzig) 2007, 16, 842–845. [Google Scholar] [CrossRef]
- Böhmer, R.; Ngai, K.L.; Angell, C.A.; Plazek, D.J. Nonexponential relaxations in strong and fragile glass formers. J. Chem. Phys. 1993, 99, 4201–4210. [Google Scholar] [CrossRef]
- Phillips, J.C. Anomalous glass transitions and stretched exponential relaxation in fused salts and polar organic compounds. Phys. Rev. E 1996, 53, 1732–1739. [Google Scholar] [CrossRef]
- Ngai, K.L. Relaxation and Diffusion in Complex Systems; Springer: New York, NY, USA, 2011. [Google Scholar]
- Wiebel, S.; Wuttke, J. Structural relaxation and mode coupling in a non-glassforming liquid: depolarized light scattering in benzene. New J. Phys. 2002, 4, 56. [Google Scholar] [CrossRef]
- Torre, R.; Bartolini, P.; Righini, R. Structural relaxation in supercooled water by time-resolved spectroscopy. Nature 2004, 428, 296–299. [Google Scholar] [CrossRef] [PubMed]
- Turton, D.A.; Wynne, K. Crossover from Stretched to Compressed Exponential Relaxations in a Polymer-Based Sponge Phase. J. Chem. Phys. 2009, 131, 201101. [Google Scholar] [CrossRef] [PubMed]
- Berberan-Santos, M.N.; Bodunov, E.N.; Valeur, B. Mathematical functions for the analysis of luminescence decays with underlying distributions 1. Kohlrausch decay function (stretched exponential). Chem. Phys. 2005, 315, 171–182. [Google Scholar]
- Phillies, G.D.J.; Peczak, P. The ubiquity of stretched-exponential forms in polymer dynamics. Macromolecules 2002, 21, 214–220. [Google Scholar] [CrossRef]
- Nakamura, H.K.; Sasai, M.; Takano, M. Scrutinizing the squeezed exponential kinetics observed in the folding simulation of an off-lattice Go-like protein model. Chem. Phys. 2004, 307, 259–267. [Google Scholar] [CrossRef]
- Falus, P.; Borthwick, M.A.; Narayanan, S.; Sandy, A.R.; Mochrie, S.G.J. Crossover from Stretched to Compressed Exponential Relaxations in a Polymer-Based Sponge Phase. Phys. Rev. Lett. 2006, 97, 066102. [Google Scholar] [CrossRef] [PubMed]
- Hamm, P.; Helbing, J.; Bredenbeck, J. Stretched versus compressed exponential kinetics in α-helix folding. Chem. Phys. 2006, 323, 54–65. [Google Scholar] [CrossRef]
- Xi, H.; Franzen, S.; Guzman, J.I.; Mao, S. Degradation of magnetic tunneling junctions caused by pinhole formation and growth. J. Magn. Magn. Mat. 2007, 319, 60–63. [Google Scholar] [CrossRef]
- Laherrère, J.; Sournette, D. Stretched exponential distributions in nature and economy: “fat tails” with characteristic scales. Eur. Phys. J. B 1998, 2, 525–539. [Google Scholar] [CrossRef]
- Davies, J.A. The individual success of musicians, like that of physicists, follows a stretched exponential distribution. Eur. Phys. J. B 2002, 27, 445–447. [Google Scholar] [CrossRef]
- Sinha, S.; Raghavendra, S. Hollywood blockbusters and long-tailed distributions—An empirical study of the popularity of movies. Eur. Phys. J. B 2004, 42, 293–296. [Google Scholar] [CrossRef]
- Götze, W.; Sjögren, L. The glass transition singularity. Z. Phys. B 1987, 65, 415–427. [Google Scholar] [CrossRef]
- Fuchs, M. The Kohlrausch law as a limit solution to mode coupling equations. J. Non-Cryst. Solids 1994, 172–174, 241–247. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. From stretched exponential to inverse power-law: fractional dynamics, Cole¨CCole relaxation processes, and beyond. J. Non-Cryst. Solids 2002, 305, 81–87. [Google Scholar] [CrossRef]
- Götze, W. Complex Dynamics of Glass-Forming Liquids. A Mode-Coupling Theory; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Anderssen, R.S.; Husain, S.A.; Loy, R.J. The Kohlrausch function: properties and applications. ANZIAM J. 2004, 45, C800–C861. [Google Scholar]
- Husain, S.A.; Anderssen, R.S. Modelling the relaxation modulus of linear viscoelasticity using Kohlrausch functions. J. Non-Newton. Fluid Mech. 2005, 125, 159–170. [Google Scholar] [CrossRef]
- Williams, G.; Watts, D.C. Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans. Faraday Soc. 1970, 66, 80–85. [Google Scholar] [CrossRef]
- Williams, G.; Watts, D.C.; Dev, S.B.; North, A.M. Further considerations of non symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans. Faraday Soc. 1971, 67, 1323–1335. [Google Scholar] [CrossRef]
- Lindsey, C.P.; Patterson, G.D. Detailed comparison of the Williams¨C-Watts and Cole-¨CDavidson functions. J. Chem. Phys. 1980, 73, 3348–3347. [Google Scholar] [CrossRef]
- Montroll, E.W.; Bendler, J.T. On Lévy (or stable) distributions and the Williams-Watts model of dielectric relaxation. J. Stat. Phys. 1984, 34, 129–162. [Google Scholar] [CrossRef]
- Macdonald, J.R. Accurate fitting of immittance spectroscopy frequency-response data using the stretched exponential model. J. Non-Cryst. Solids 1997, 212, 95–116. [Google Scholar] [CrossRef]
- Alvarez, F.; Alegría, A.; Colmenero, J. Relationship between the time-domain Kohlrausch-Williams-Watts and frequency-domain Havriliak-Negami relaxation functions. Phys. Rev. B 1991, 44, 7306–7312. [Google Scholar] [CrossRef]
- Alvarez, F.; Alegría, A.; Colmenero, J. Interconnection between frequency-domain Havriliak-Negami and time-domain Kohlrausch-Williams-Watts relaxation functions. Phys. Rev. B 1993, 47, 125–130. [Google Scholar] [CrossRef]
- Copson, E.T. Asymptotic Expansions; Cambridge University Press: Cambridge, UK, 1965. [Google Scholar]
- Bleistein, N.; Handelsman, R.A. Asymptotic Expansion of Integrals; Dover Publications: London, UK, 1986. [Google Scholar]
- Wintner, A. The singularities of Cauchy¡¯s distributions. Duke Math. J. 1941, 8, 678–681. [Google Scholar] [CrossRef]
- Tuck, E.O. A Simple “Filon-trapezoidal” rule. Math. Comput. 1967, 21, 239–241. [Google Scholar] [CrossRef]
- Mori, M.; Sugihara, M. The double-exponential transformation in numerical analysis. J. Comp. Appl. Math. 2001, 127, 287–296. [Google Scholar] [CrossRef]
- Mori, M. Discovery of the double exponential transformation and its developments. Publ. RIMS, Kyoto Univ. 2005, 41, 897–935. [Google Scholar] [CrossRef]
- Ooura, T.; Mori, M. The double exponential formula for oscillatory functions over the half infinite interval. J. Comp. Appl. Math. 1991, 38, 353–360. [Google Scholar] [CrossRef]
- Ooura, T.; Mori, M. A robust double exponential formula for Fourier-type integrals. J. Comp. Appl. Math. 1999, 112, 229–241. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Progr. Phys. 1966, 29, 255–284. [Google Scholar] [CrossRef]
- Doster, W.; Busch, S.; Gaspar, A.M.; Appavou, M.S.; Wuttke, J.; Scheer, H. Dynamical transition of protein-hydration water. Phys. Rev. Lett. 2010, 104, 098101. [Google Scholar] [CrossRef] [PubMed]
- Scarborough, J.B. Numerical Mathematical Analysis; John Hopkins Press: Baltimore, ML, USA, 1930; The statement about usual truncation errors in asymptotic series is on p. 158 of the 2nd edition (1950), and on p. 164 of the 5th edition (1962). [Google Scholar]
- Charlier, C.L. Die Mechanik des Himmels. Zweiter Band; Veit & Comp.: Leipzig, Germany, 1907. [Google Scholar]
- NIST Digital Library of Mathematical Functions. Available online: http://dlmf.nist.gov, 7.2.5 and 7.7.3 (accessed on 20 November 2012).
- GNU Scientific Library, version GSL-1.15 of 6 May 2011, chapter 7.9. Available online: http://www.gnu.org/software/gsl/manual/html_node/Dawson-Function.html (accessed on 20 November 2012).
Appendix
A. Description of Relaxation in Time and Frequency
B. Convolution with a Resolution Function
C. Truncation Error in Small-ω Expansion
D. Truncation Error in Large-ω Expansion

E. Analytic Solutions for
© 2012 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wuttke, J. Laplace–Fourier Transform of the Stretched Exponential Function: Analytic Error Bounds, Double Exponential Transform, and Open-Source Implementation “libkww”. Algorithms 2012, 5, 604-628. https://doi.org/10.3390/a5040604
Wuttke J. Laplace–Fourier Transform of the Stretched Exponential Function: Analytic Error Bounds, Double Exponential Transform, and Open-Source Implementation “libkww”. Algorithms. 2012; 5(4):604-628. https://doi.org/10.3390/a5040604
Chicago/Turabian StyleWuttke, Joachim. 2012. "Laplace–Fourier Transform of the Stretched Exponential Function: Analytic Error Bounds, Double Exponential Transform, and Open-Source Implementation “libkww”" Algorithms 5, no. 4: 604-628. https://doi.org/10.3390/a5040604
APA StyleWuttke, J. (2012). Laplace–Fourier Transform of the Stretched Exponential Function: Analytic Error Bounds, Double Exponential Transform, and Open-Source Implementation “libkww”. Algorithms, 5(4), 604-628. https://doi.org/10.3390/a5040604




