Alpha-Beta Pruning and Althöfer’s Pathology-Free Negamax Algorithm
Abstract
:1. Introduction
Yet, it should come as a surprise that the minimax method works at all. The static evaluation function does not exactly evaluate the positions at the search frontier, but, only provides estimates of their strengths; minimaxing these estimates as if they are true payoffs amounts to committing one of the deadly sins of statistics, computing a function of the estimates instead of an estimate of the function.
2. Review of Althöfer’s Algorithm
3. Review of Alpha-Beta Pruning
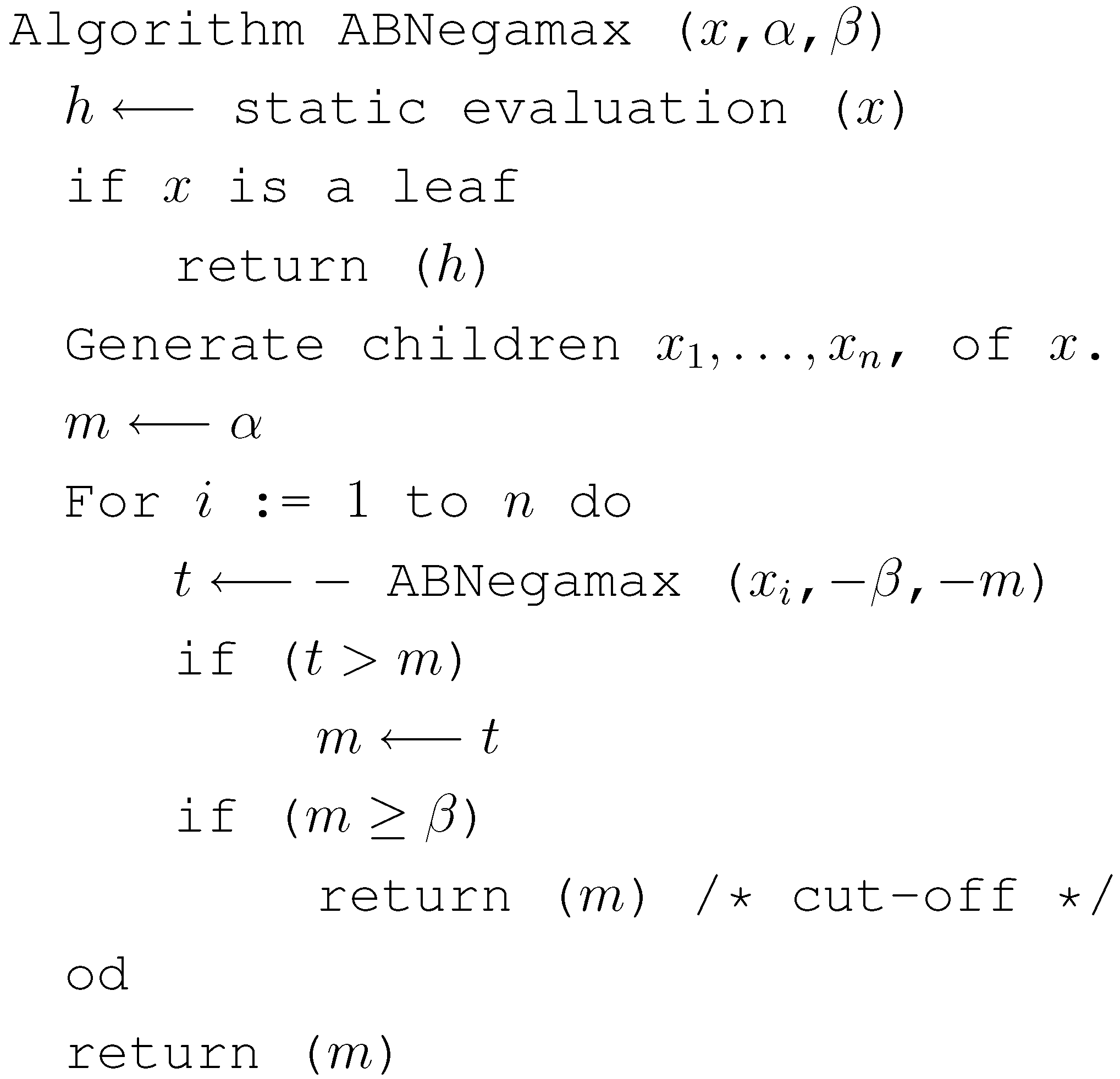
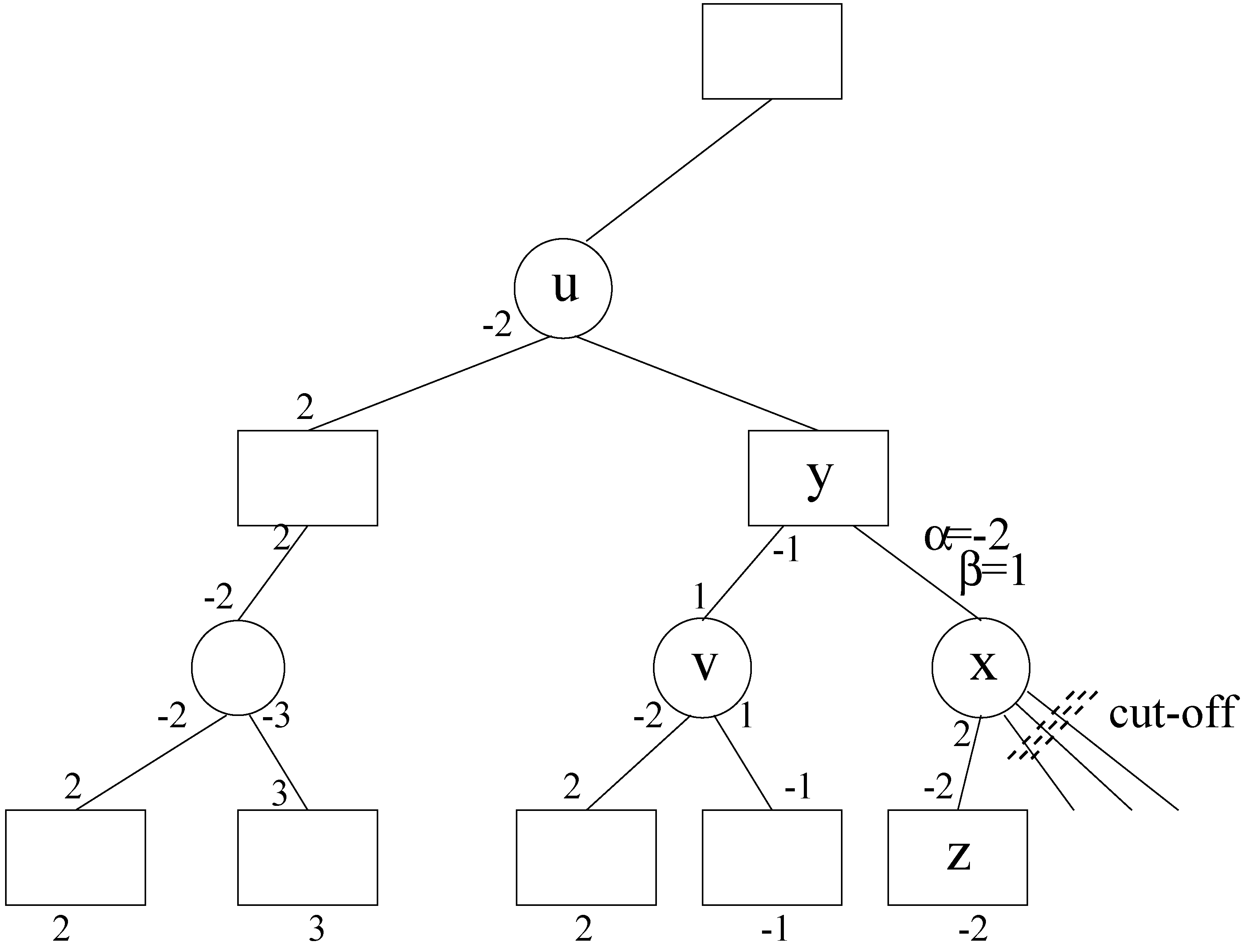
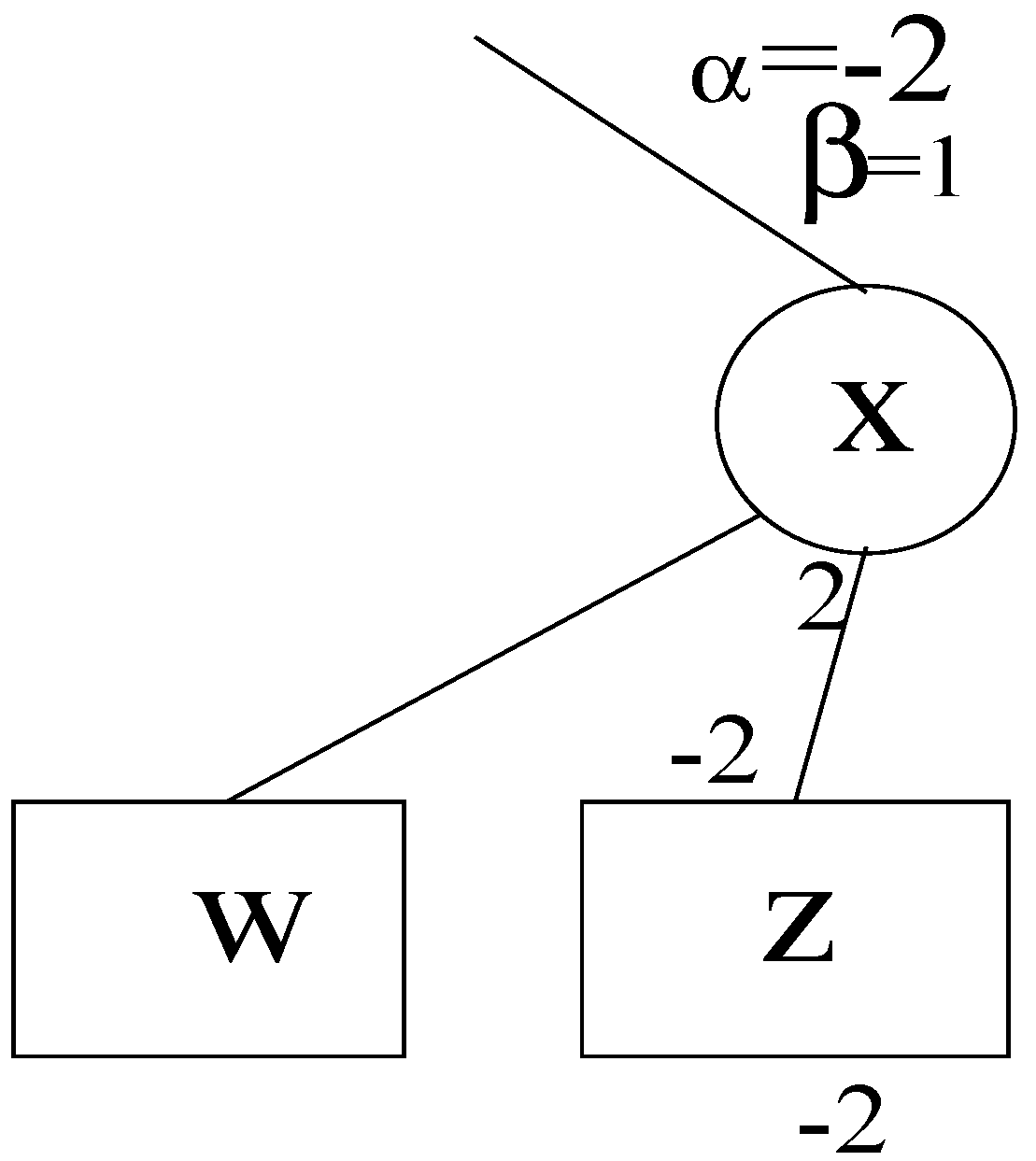

4. Applying Alpha-Beta Pruning to Althöfer’s Algorithm
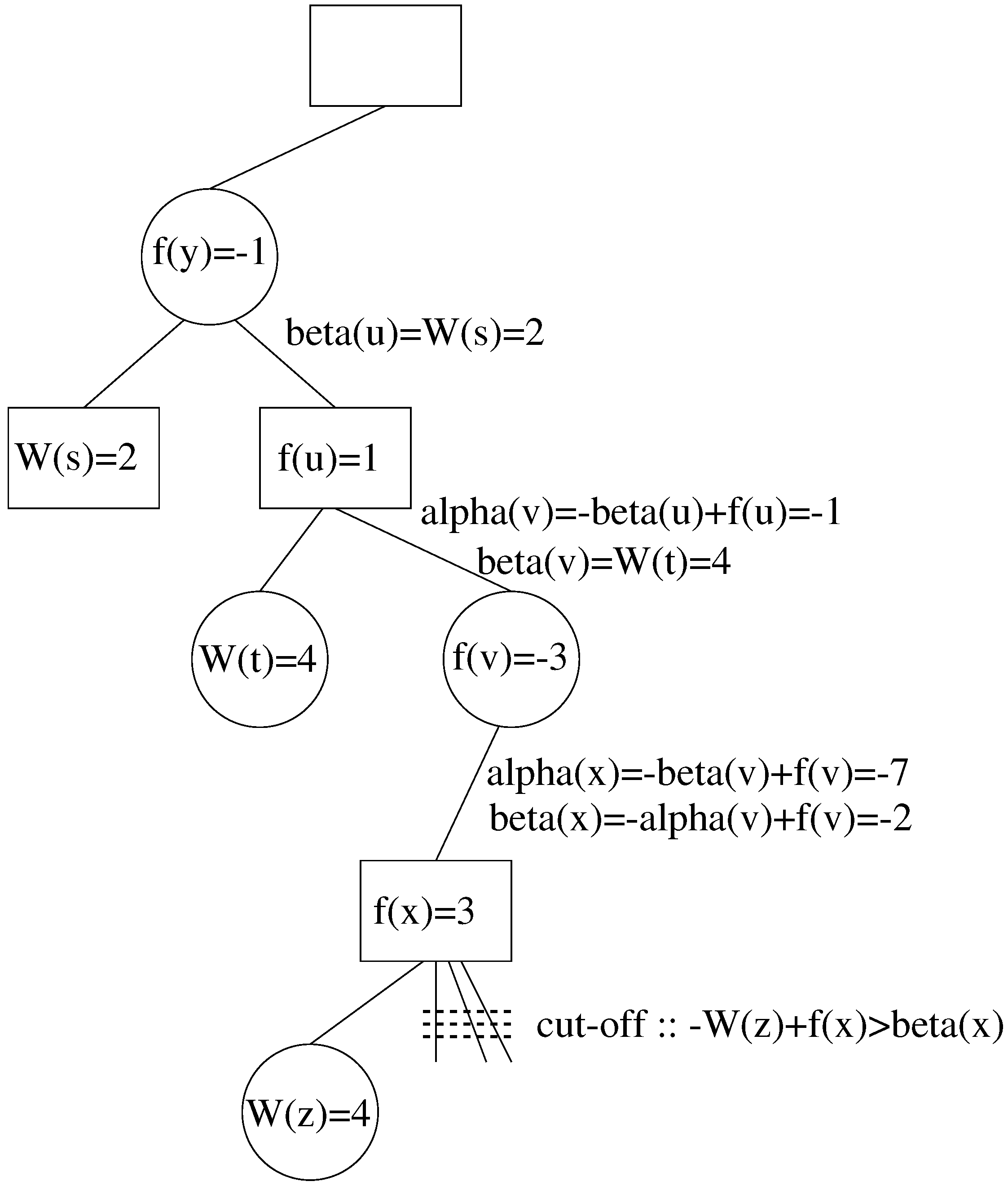
5. Concluding Remarks
References
- Pearl, J. On the nature of pathology in game searching. Artif. Intell. 1983, 20, 427–453. [Google Scholar] [CrossRef]
- Delcher, A.; Kasif, S. Improved Decision-Making in Game Trees: Recovering from Pathology. In Proceedings of the National Conference on Artificial Intelligence, San Hose, CA, USA, September 1992; pp. 513–518.
- Luštrek, M.; Gams, M.; Bratko, I. Is real-valued minimax pathological. Artif. Intell. 2006, 170, 620–642. [Google Scholar] [CrossRef]
- Luštrek, M.; Bulitko, V. Thinking too much: Pathology in Pathfinding. In Proceedings of the 2008 Conference on ECAI, Patras, Greece, July 2008; pp. 899–900.
- Luštrek, M. Pathology in heuristic search. AI Commun. 2008, 21, 211–213. [Google Scholar]
- Mutchler, D. The multiplayer version of minimax displays game-tree pathology. Artif. Intell. 1993, 64, 323–336. [Google Scholar] [CrossRef]
- Nau, D.S. An investigation of the causes of pathology in games. Artif. Intell. 1982, 19, 257–278. [Google Scholar] [CrossRef]
- Nau, D.S. Pathology on game trees revisited and an alternative to minimaxing. Artif. Intell. 1983, 21, 221–244. [Google Scholar] [CrossRef]
- Nau, D.S.; Luštrek, M.; Parker, A.; Bratko, I.; Gams, M. When is it better not to look ahead. Artif. Intell. 2010, 174, 1323–1338. [Google Scholar] [CrossRef]
- Pearl, J. Asymptotic properties of minimax trees and game-searching procedures. Artif. Intell. 1980, 14, 113–138. [Google Scholar] [CrossRef]
- Piltaver, R.; Luštrek, M.; Gams, M. The pathology of heuristic search in the 8-puzzle. J. Exp. Theor. Artif. Intell. 2012, 24, 65–94. [Google Scholar] [CrossRef]
- Sadikov, A.; Bratko, I.; Konenenko, I. Bias and pathology in minimax search. Theor. Comput. Sci. 2005, 349, 261–281. [Google Scholar] [CrossRef]
- Schrufer, G. Presence and Absence of Pathology on Game Trees. In Advances in Computer Chess; Beal, D.F., Ed.; Pergamon: Oxford, UK, 1986; volume 4, pp. 101–112. [Google Scholar]
- Wilson, B.; Parker, A.; Nau, D. Error Minimizing Minimax: Avoiding Search Pathology in Game Trees. In Proceedings of International Symposium on Combinatorial Search (SoCS-09), Los Angeles, CA, USA, July 2009.
- Althöfer, I. An incremental negamax algorithm. Artif. Intell. 1990, 43, 57–65. [Google Scholar] [CrossRef]
- Karp, R.M.; Pearl, J. Searching for an optimal path in a tree with random costs. Artif. Intell. 1983, 21, 99–116. [Google Scholar] [CrossRef]
- Knuth, D.E.; Moore, R.W. An analysis of alpha-beta pruning. Artif. Intell. 1975, 6, 293–326. [Google Scholar] [CrossRef]
- Müller, M. Computer Go. Artif. Intell. 2002, 134, 145–179. [Google Scholar] [CrossRef]
© 2012 by the authors licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Abdelbar, A.M. Alpha-Beta Pruning and Althöfer’s Pathology-Free Negamax Algorithm. Algorithms 2012, 5, 521-528. https://doi.org/10.3390/a5040521
Abdelbar AM. Alpha-Beta Pruning and Althöfer’s Pathology-Free Negamax Algorithm. Algorithms. 2012; 5(4):521-528. https://doi.org/10.3390/a5040521
Chicago/Turabian StyleAbdelbar, Ashraf M. 2012. "Alpha-Beta Pruning and Althöfer’s Pathology-Free Negamax Algorithm" Algorithms 5, no. 4: 521-528. https://doi.org/10.3390/a5040521
APA StyleAbdelbar, A. M. (2012). Alpha-Beta Pruning and Althöfer’s Pathology-Free Negamax Algorithm. Algorithms, 5(4), 521-528. https://doi.org/10.3390/a5040521



