Recognizing the Repeatable Configurations of Time-Reversible Generalized Langton’s Ant Is PSPACE-Hard
Abstract
: Chris Langton proposed a model of an artificial life that he named “ant”: an agent- called ant- that is over a square of a grid moves by turning to the left (or right) accordingly to black (or white) color of the square where it is heading, and the square then reverses its color. Bunimovich and Troubetzkoy proved that an ant's trajectory is always unbounded, or equivalently, there exists no repeatable configuration of the ant's system. On the other hand, by introducing a new type of color where the ant goes straight ahead and the color never changes, repeatable configurations are known to exist. In this paper, we prove that determining whether a given finite configuration of generalized Langton's ant is repeatable or not is PSPACE-hard. We also prove the PSPACE-hardness of the ant's problem on a hexagonal grid.1. Introduction
1.1. Generalized Langton's Ant
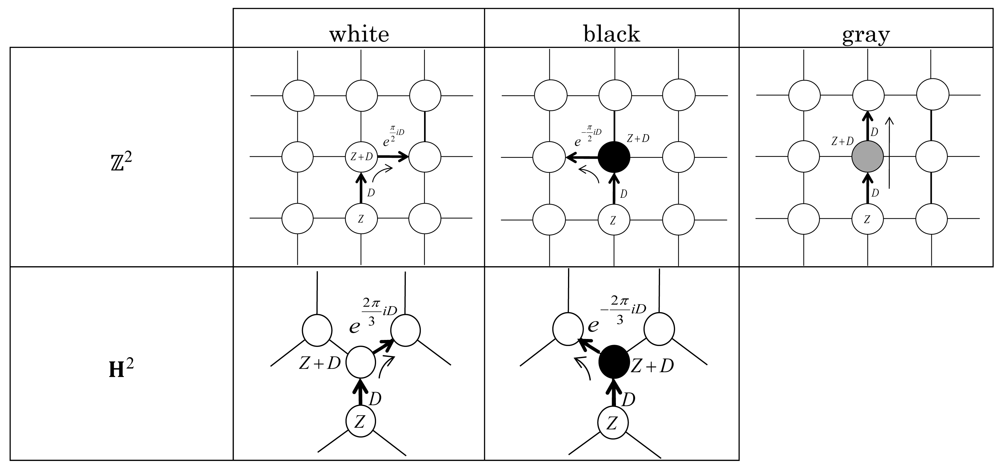
The virtual ant defined by Chris Langton [1-3] is the following cellular automaton. The “ant”, represented by a pair (z, D) of a lattice point z ∈ ℤ2 ≔ ℤ + iℤ and a direction , moves around on a two-dimensional square lattice ℤ2, where each lattice point, referred to as a “cell”, is colored by white or black (later we will also introduce gray cells). Initially, the ant is sitting on a given cell with a given direction, say z = 0 and D = 1. It proceeds to travel from cell to cell according to the following rule (see Figure 1): the ant (z, D) moves to when z + D is a white cell, and to when z + D is a black cell; the cell z + D then reverses its color. In other words, the ant moves in the direction it is heading; when it lands on a white (or black) cell it rotates its direction 90° to the right (left); after that, the color of the cell changes to black (or white).
Langton's ant has been investigated independently as one model of Lorentz Lattice Gas Cellular Automata (LLGCA). Langton's ant corresponds to the Flipping Rotator (FR) model on ℤ2 [4]. In more general terms, the FR model was investigated on a triangular lattice [5] and on a hexagonal lattice [6], too. On H2 the ant (z, D), where z ∈ H2 and , moves to and when z + D is white and black, respectively (see Figure 1), and the cell z + D then reverses its color. Another generalization of Langton's ant on ℤ2 is to introduce a third type of cell, called “gray” cell [7]. The ant (z, D) moves to (z + D, D) if z + D is a grey cell, and the cell z + D never changes its color but remains gray forever (see Figure 1). In LLGCA models, gray cells were introduced naturally as empty lattice points. We remark that the H2 topology does not allow having such a gray cell.
We denote by R, L and S the ant's valid moves corresponding to the Right-turn, Left-turn and Straight-ahead respectively under these transaction rules; e.g., by R, L and S, the ant (z, D) on ℤ2 moves to , and (z + D, D), respectively.
1.2. Recognizing the Repeatable Configurations of GLA
These transaction rules assure that Generalized Langton's Ant (GLA) is a time-reversible cellular automaton: the current configuration of GLA, consisting of a coloring of the cells and an ant's starting cell and direction, determines the past configurations as well as the future ones. As a consequence, the configurations of GLA are divided into the following two kinds: an ant's trajectory starting from a configuration of one kind is unbounded, never repeating the same configuration again; an ant's trajectory starting from a configuration of the other kind is bounded, repeating a finite series of configurations an infinitive number of times.
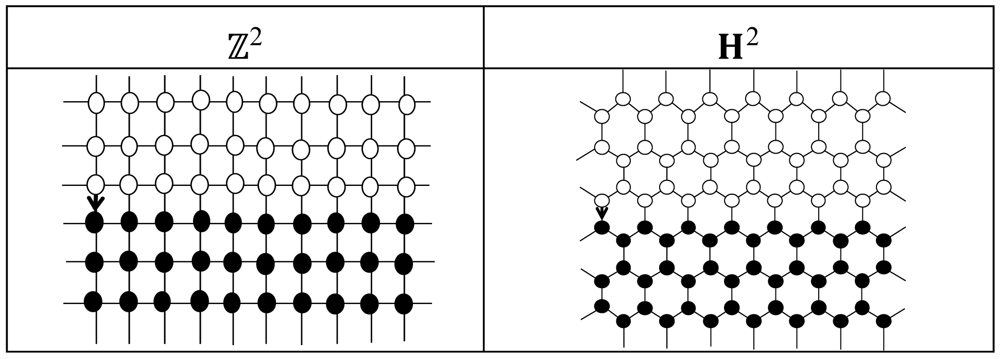
A “finite” configuration of GLA is defined by a finite coloring of the cells and an ant's starting cell and direction. Here, a coloring is finite if it has only a finite number of non-background-color cells. In this paper, we use the all white, all black, and half-and-half coloring as the background, where the half-and-half coloring gives white (black) color to the cells on the upper-half (lower-half) plane (see Figure 2Figure 2). We define size of a configuration by the minimum size of a closed square which contains the ant's starting cell and the all non-background-color cells. In this paper, we study the computational complexity of determining whether a given finite configuration of GLA is repeatable or not.
1.3. Previous Results
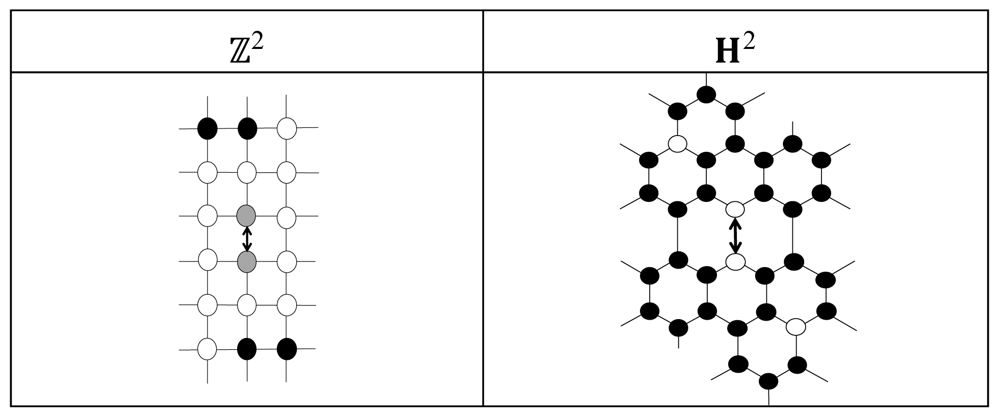
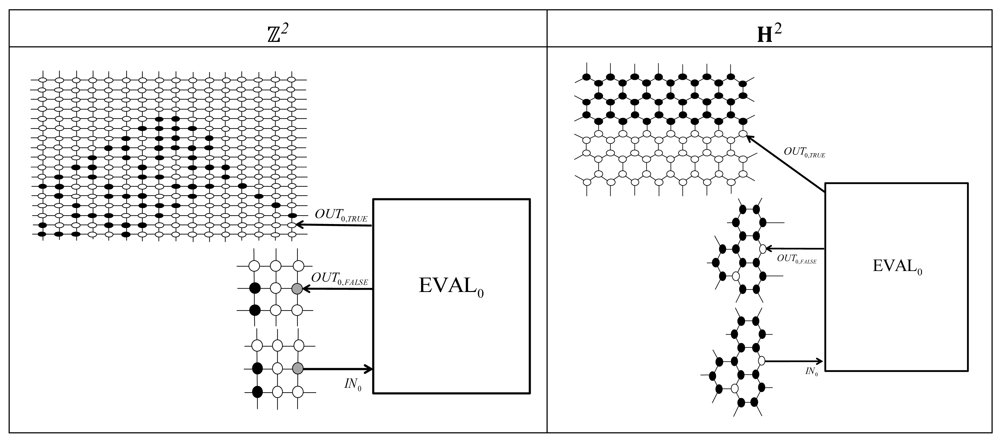
Bunimovch and Troubetskoy [4] proved the following: when there is no gray cell, an ant's trajectory on ℤ2 is always unbounded, or equivalently, there exists no repeatable configuration of the ant's system. As a matter of fact, the set of repeatable configurations of GLA on ℤ2 with no gray cell is empty, hence its recognition problem is trivial. On the other hand, repeatable configurations exist of GLA on ℤ2 with some gray cells (see Figure 3, see also [8]). The H2 model is also known to have repeatable configurations (see Figure 3, see also [6]).
The long-run behavior of Langton's ant on ℤ2 has been studied using both theories and experiments for more than two decades, yet it is still highly unpredictable. As a result, indicating hardness of the prediction, Gajardo, Moreira and Goles [9] proved that the following problem on ℤ2 with no gray cell is PTIME-hard: “Does the ant ever visit this given cell?”.
1.4. New Results
In this paper, we prove the following theorems:
Theorem 1
Recognizing the repeatable configurations of GLA on ℤ2 with gray cells is PSPACE-hard.
Theorem 2
Recognizing the repeatable configurations of GLA on H2 is PSPACE-hard.
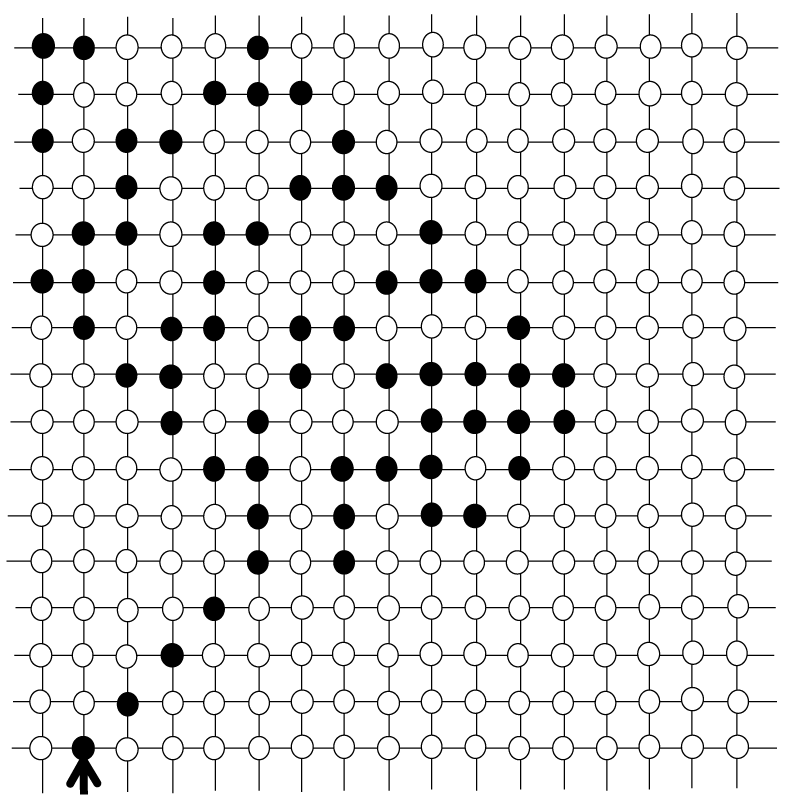
To prove these theorems, we should have unbounded trajectories of the ant on each of the topologies. For the half-and-half background, Figure 2 shows such unbounded trajectories where the ant, starting from the arrow, walks from left to right by repeating the LLRR (LLLRRR) moves forever on ℤ2 (H2). On the other hand, for the monochromatic background, we do have the famous diagonal highway on ℤ2 (see Figure 4), but no provable unbounded trajectory is known on H2 [6]. For this reason, we can prove Theorem 1 for both of the monochromatic and half-and-half backgrounds, but Theorem 2 for only the half-and-half background.
We will prove Theorem 1 for “everywhere sparse” gray cells. For a given function f: ℕ → ℕ, we say that a configuration is colored by f-sparse gray cells if the configuration size is n and its coloring has no more than one gray cell within any closed square of size no more than . For example, a configuration colored by k-sparse gray cells, for any constant k ∈ ℕ, contains no more than k gray cells, and a configuration colored by n2-sparse gray cells could have an arbitrary number of gray cells. We prove the following theorem:
Theorem 3
For any ε > 0 recognizing the repeatable configurations of GLA on ℤ2 colored by nε-sparse gray cells is PSPACE-complete.
1.5. Reduction
To prove Theorems 1–3, it is enough to reduce a known PSPACE-hard problem to the ant's problems on square and hexagonal grids. In this paper, we will reduce QBF (Quantified Boolean Formula) evaluation problem to the ant's problems. An instance of QBF is given by a closed CNF (Conjunctive Normal Form) formula, which is written as Q1x1Q2x2…Qnxnϕ(x1,…,xn) by an open CNF formula ϕ(x1,…,xn) and arbitrary Boolean quantifiers Qi ∈ {∃, ∀}. Then, QBF evaluation problem asks the truth value of a given closed CNF formula. QBF evaluation problem is a well known PSPACE-complete problem [10].
1.6. Preparation
A (ant's walking) course is a sequence of ant's consecutive valid moves; it also represents a sequence of the induced coloring. When a coloring S of the ant's system turns to a coloring T by an ant's walking course w, we write as . When the ant, at a place I, moves to another place O by w, we write it as . The reverse of the ant (z, D) is (z + D, − D). By time reversibility, we can define the reverse w−1 of w by the following walking course: reverse the order of the coloring in w, and reverse the ants therein. We write , meaning that S turns to T by w, and T turns to S by w−1.
2. Gadgets
A gadget is a collection of GLA's coloring written on the all white background with an associated transition diagram and several input and output marked arrows. A polynomial number of gadgets are seamlessly connected to form an entire coloring of GLA, where some gadgets may be used after rotation or reflection. Note that the colors of reflected gadgets should be switched.
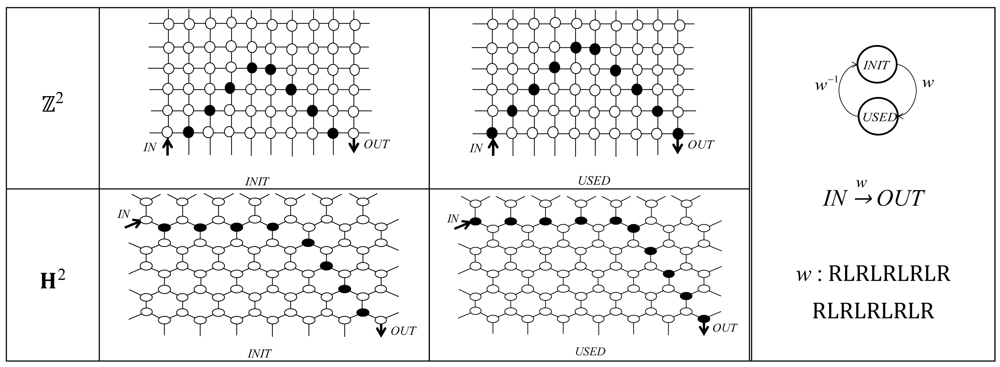
2.1. Path
We connect the rotations and reflections of PATH gadgets (see Figure 5) to form a long path along which the ant is guided. Its coloring is initially INIT, which turns to USED by a course .
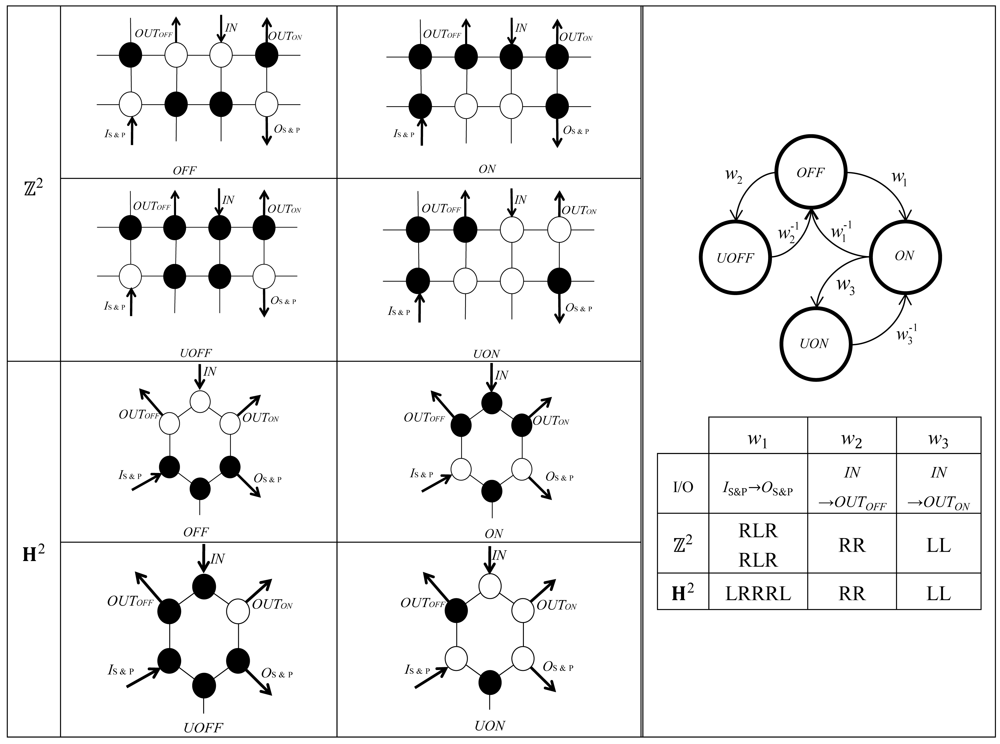
2.2. Switch & Pass
A Switch & Pass (S&P) gadget (see Figure 6) can memorize 1 bit information by its coloring state. The coloring is initially OFF, which turns to ON by a walking course ; in other words, the ant is “Switching” the coloring state and “Passing” through it. When the coloring is OFF, the ant entering at IN walks along w2 and exits at OOFF, changing the coloring to UOFF. When the coloring is ON, the ant entering at IN walks along w3 and exits at OON, changing the coloring to UON.
2.3. Switch & Turn
A Switch & Turn (S&T) gadget (see Figure 7) can memorize 1 bit information by its coloring state, too. The coloring is initially OFF, which turns to ON by an ant's walking course ; in other words, since OS&T is the reverse of IS&T, the ant is “Switching” the coloring state and “Turning” around. When the coloring is OFF, the ant entering at IN walks along w2 and exits at OUTOFF. When the coloring is ON, the ant entering at IN walks along w3 and exits at OUTON.
2.4. Conjunction
The CONJunction (CONJ) gadget (see Figure 8, see also [9]) has two entrances and one exit. The coloring is initially INIT. The ant entering at INj walks along wj and exits at OUT, for each j =1, 2.
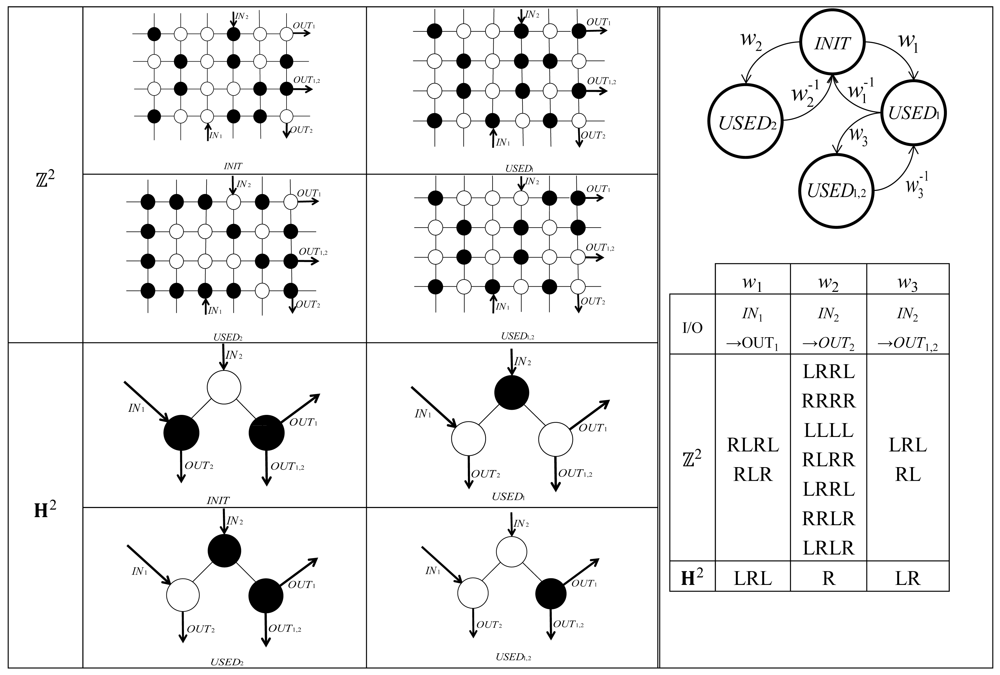
2.5. Pseudo-Crossing
A Pseudo-Crossing (PC) gadget (see Figure 9, see also [9]) has two entrances IN1 and IN2 and two exits OUT1 and OUT2 such that the ant entering at INj walks along wj and exits at OUTj for each j = 1, 2. Since IN1, IN2, OUT1, OUT2 are placed clockwise in this order in 2D plane, these two walking courses w1 and w2 should be mutually crossing. Beginning from the initial coloring INIT, the ant can take mutually intersecting courses, first and secondly order, changing the coloring to .
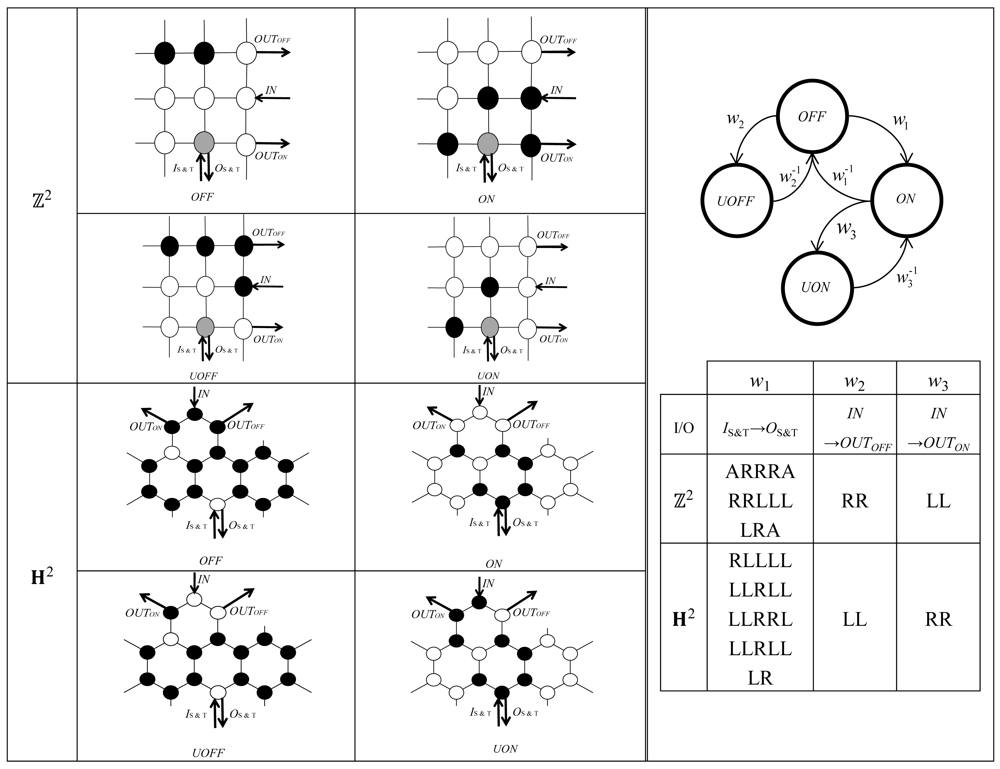
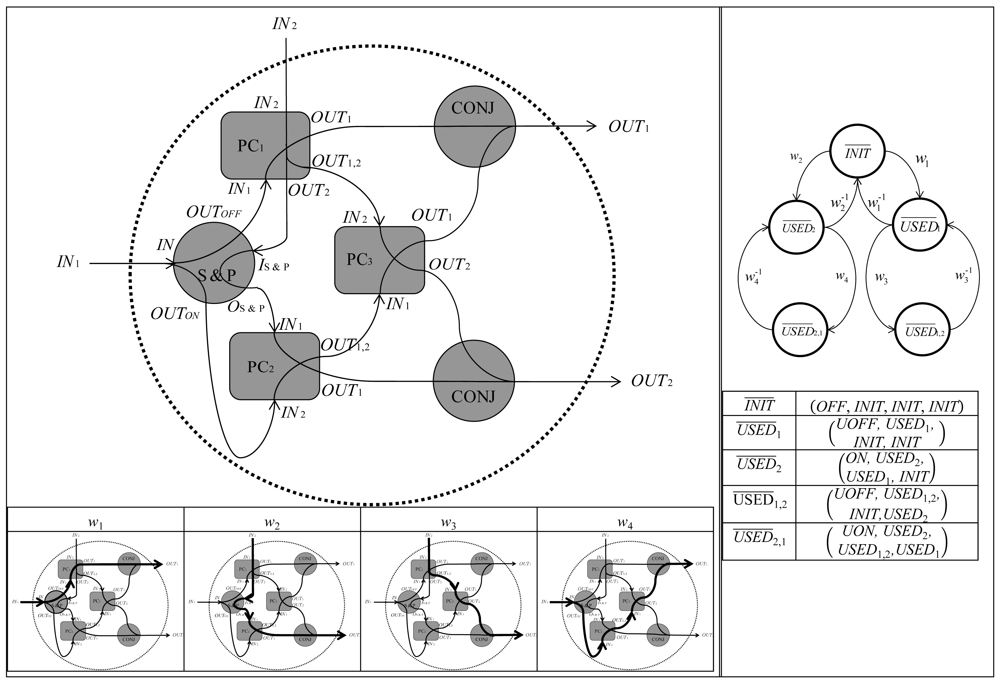
2.6. Crossing
A CROSSing (CROSS) gadget (see Figure 10) is placed at each crossing point of two intersecting paths on 2D plane. It is built by one S&P gadget and three PC gadgets, named PC1, PC2 and PC3. The coloring of a CROSS gadget can be represented by the coloring of all gadgets composing it, that are S&P, PC1, PC2, PC3, two CONJ gadgets and many PATH gadgets connecting them. We indicate the coloring of a CROSS gadget only by those of (S&P, PC1, PC2, PC3). The coloring of CONJ (PATH) gadgets and PATH gadgets are initially INIT, that turn to USEDj (USED) when the ant has passed through them. The ant can take mutually intersecting courses by first and secondly , as well as by first and secondly . In Figure 10, each of these paths are depicted by thick lines, where those gadgets that passed through are shown by the thick lines that have turned to used coloring, while the other gadgets remain in their initial coloring.
3. CNF Formulae Evaluation
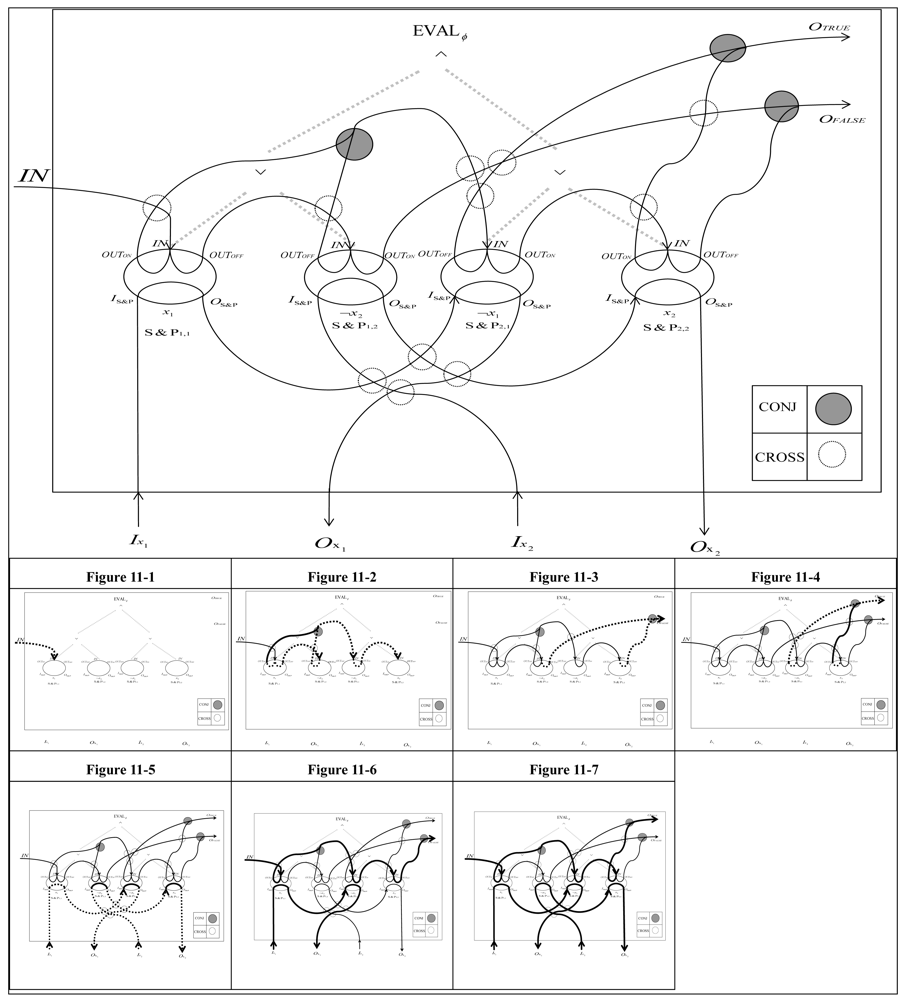
In this section, we construct an EVALϕ gadget for evaluating the truth value of a CNF formula ϕ by inputting a given truth-value assignment a. It has one entrance IN and two exits OUTFALSE and OUTTRUE. The ant entering at IN is routed to exit at OUTFALSF (OUTTRUE) if ϕ(a) is FALSE (TRUE).
Let POS = {x1,…,xn} and NEG = {−x1,…, −xn}. Let yi,j ∈ POS ∪ NEG be the jth literal in the ith term of ϕ(x1,…,xn), where 1 ≤ i ≤ m and 1 ≤ j ≤ ki. These literals yi,j are implemented in EVALϕ, by S&P gadgets, named S&Pi,j. Then, draw PATHs between S&Pi,j in the following manner to define an evaluator EVALϕ of ϕ: IN → IN of S&P1,1 (see Figure 11-1). When yi,j ∈ POS (NEG), OUTOFF (OUTON) of S&Pi,j → IN of S&Pi,j+1 (see Figure 11-2). When yi,ki ∈ POS(NEG), OUTOFF (OUTON) of S&Pi,ki → OUTFALSE (see Figure 11-3). When ym,j ∈ POS (NEG), OUTON (OUTOFF) of S&Pm,j → OUTTRUE (see Figure 11-4).
For each xk ∈ POS, EVALϕ has an entrance Ixk and an exit Oxk such that the ant entering at Ixi switches the coloring states of all S&P gadgets corresponding to the literals yi,j ∈ {xk, -xk} from OFF to ON, and exits at Oxi. Figure 11-5 is drawing such PATHs, where the ports Ix1, Ox1, Ix2, Ox2,…,Ixn, Oxn should be placed in this order for further development in the next section.
Suppose that the coloring of the composing gadgets of EVALϕ are all initialized. For every a ∈ {FALSE, TRUE}n, we denote by INITa the coloring of EVALϕ after taking the walking courses Ixk → Oxk for all xk such that axk = TRUE in the descending order of k. Consequently, INITa sets the coloring of every S&Pi,j, with yi,j ∈ {xk, −xk} OFF(ON) if ak = FALSE (TRUE).
Lemma 1
If the coloring of EVALϕ is INITa and ϕ(a) = FALSE (TRUE), then the ant entering at IN exits at OUTFALSE (OUTTRUE).
Proof
First, suppose that ϕ (a) = FALSE. We can assume that the ℓth term of ϕ is FALSE and the ith term of ϕ is TRUE for every 1 ≤ i < l. So, we can assume that for every 1 ≤ j ≤ kℓ, if yℓ,j ∈ POS (NEG) then S&Pℓ,j is OFF (ON), and for every 1 ≤ i < l there exits 1 ≤ ji ≤ ki such that if yi,ji ∈ POS (NEG) then S&Pi,ji, is ON(OFF); in addition, for every 1 ≤ j < ji, if yi,j ∈ POS (NEG) then S&Pi,j is OFF (ON). Given these colorings of the S&Ps, the ant walks from IN to OUTFALSE in the following way: IN → IN of S&P1,1; IN of S&Pi,j → OUTOFF (OUTON) of S&Pi,j → IN of S&Pi,j+1; IN of S&Pi,ji → OUTON (OUTOFF) of S&Pi,ji → IN of S&Pi+1,1; IN of S&Pℓ,j → OUTOFF (OUTON) of S&Pℓ,j → IN of S&Pℓ,j+1; IN of S&Pℓ,kℓ → OUTOFF (OUTON) of S&Pℓ,kℓ → OUTOFF. Figure 11-6 illustrates this walking course by a thick line when ϕ = (x1 V −x2) Λ (−x1 V x2) and (a1, a2) = (TRUE, FALSE), where the gadgets have passed through, shown by the thick line, have turned to used coloring states, while the other gadgets still remain in their initial coloring.
Secondly, suppose that ϕ(a) = TRUE. Then, all terms of ϕ are TRUE. So, we can assume that for every 1 ≤ i ≤ m there exits 1 ≤ ji ≤ ki such that if yi,ji ∈ POS (NEG) then S&Pi,ji is ON(OFF); in addition, for every 1 ≤ j < ji, if yi,j ∈ POS (NEG) then S&Pi,j is OFF (ON). Given these colorings of the S&P s, the ant walks from IN to OUTTRUE in the following way: IN → IN of S&P1,1; IN of S&Pi,j → OUTOFF (OUTON) of S&Pi,j → IN of S&Pi,j+1; IN of S&Pi,ji → OUTON (OUTOFF) of S&Pi,ji → IN of S&Pi+1,1; IN of S&Pm,j → OUTOFF (OUTON) of S&Pm,j → IN of S&Pm,j+1; IN of S&Pm,jm → OUTON (OUTOFF) of S&Pm,jm → OUTON. Figure 11-7 illustrate this walking course when ϕ = (x1 V −x2) Λ (−x1 V x2) and (a1, a2) = (TRUE, TRUE).
Let USEDa be the coloring of an EVALϕ gadget derived from INITa by the ant's walking course from the entrance to an exit of EVALϕ.
4. Boolean Quantifiers Evaluation
Let ϕ(x1,…,xn) be an arbitrary CNF formula of the variables x1,…,xn. For arbitrary taken quantifiers Qi ∈ {∃, ∀}, let ϕi(x1,…,xi) ≔ Qi+1xi+1Qi+2xi+2 … Qnxnϕ(x1,…,xn). In particular, ϕn(x1,…,xn) = ϕ(x1,…,xn). Let EVALn ≔ EVALϕ built in the previous section. We have already defined INITn,a ≔ INITa as a coloring of EVALn for every a ∈ {FALSE, TRUE}n. In the following, for each i = n, n − 1,…,0, we define inductively an EVALi, gadget and its coloring INITi, a for every a ∈ {FALSE, TRUE}i. Figure 12 depicts our construction of an EVALi gadget when Qi+1 = ∀, containing an already constructed EVALi+1 gadget. We describe the coloring of EVALi by those of the (S&T, S&P, CONJ, EVALi+1) gadgets therein. For a ∈ {FALSE, TRUE}i and b ∈ {FALSE, TRUE}, let (a,b) = (a1,…,ai,b) ∈ {FALSE, TRUE}i+1. Let INITi,a be the coloring of EVALi, that sets the coloring of the (S&T, S&P, CONJ, EVALi+1) gadgets as (UOFF, OFF, INIT, INITi+1 (a, FALSE)); the coloring of the other gadgets are set to be initialized. Then, we denote by USEDi, a the coloring derived from INITi, a by the ant's walking course from the entrance to an exit of EVALi. We have already defined USEDn, a ≔ USEDa. In the following lemma, USEDi, a are inductively defined, too.
Lemma 2
For every a ∈ {FALSE, TRUE}i, if the coloring of EVALi is INITi, a and ϕi(a1,…,ai) = FALSE (TRUE) then the ant entering to the EVALi gadget at INi exits at OUTi, FALSE (OUTi, TRUE).
Proof
Lemma 1 proves the i = n case of Lemma 2. Let a ∈ {FALSE, TRUE}i. By the backward induction hypothesis, Lemma 2 is assumed to hold for both ϕi+1(a, FALSE) and ϕi+1(a, TRUE). In the following proof, we prove Lemma 2 for ϕi(a) when Qi = Q∀.
Case 1
Suppose that ϕi+1(a, FALSE) = FALSE. The ant walks as follows (Figure 12-1): INi → S&T → CONJ → INi+l, changing the coloring of (S&T, CONJ) from (UOFF, INIT) to (OFF, USED1); next, since the coloring of EVALi+1 is INITi+1,(a, FALSE), by Lemma 2 for ϕi+1(a, FALSE), the ant starting from INi+1 reaches to OUTi+1, FALSE, which changes the coloring of EVALi+1 from INITi+1, (a, FALSE) to USEDi+1, (a, FALSE); finally, the ant walks from OUTi+1, FALSE to OUTi, FALSE.
Case 2
Suppose ϕi+1(a, FALSE) = TRUE and ϕi+1(a, TRUE) = FALSE. First, the ant walks as follows (see Figure 12-2): INi → S&T → CONJ → INi+1; next, since ϕi+1(a, FALSE) = TRUE, the ant entering EVALi+1 at INi+1 reaches to OUTi+1, TRUE, changing the coloring of EVALi+1 from INITi+1, (a, FALSE) to USEDi+1 (a, FALSE); after that, the ant walks as OUTi+1, TRUE → IN of S&P → OUTOFF of S&P → IS&T, which change the coloring of the S&P gadget from OFF to ON, and the coloring of the PATHs taken from INIT to USED; then, getting into the S&T gadget, the ant turns around and exits at OS&T, switching the coloring of the S&T gadget from OFF to ON.
Secondly, the ant takes the following reversed walking course (see Figure 12-3): OS&T → S&P → EVALi+1 → CONJ → IN of S&T, changing the colorings of (S&P, EVALi+1, CONJ) from (UOFF, USEDi+1, (a, FALSE), USED1) to (ON, INIT(a, FALSE), INIT); the coloring of the taken PATH taken and CROSS gadgets are initialized, too.
We remark that the gadgets that passed through, shown by the dotted line in Figure 12-3, are those gadgets that changed to the used color by the ant's forward walking, but then initialized by the ant's backward walking. These gadgets can be used again without violating the rules of the transition diagram given in Section 2; in other words, the already completely used gadgets, e.g., USED PATH gadgets or USED1,2 CROSS gadgets, will never be used without being initialized in this manner.
Finally, the ant walks as follows (see Figure 12-4): IN of S&T → OUTON of S&T → IS&P → OS&P → Ixi of EVALϕ → Oxi of EVALϕ → CONJ → INi+1, changing the coloring of (S&T, S&P, EVALi+1, CONJ) from (ON, OFF, INIT(a, FALSE), INIT) to (UON, ON, INIT(a, TRUE), USED2); we remark that, as shown in Figure 11, the walking course Ixi → Oxi going through the EVALϕ gadget have polynomially many crossing points with other such courses Ixj → Oxj inside the EVALϕ gadget; next, since ϕi+1(a, TRUE) = FALSE, the ant entering to EVALi+1 at INi+1 reaches OUTi+1,FALSE; finally, the ant walks as OUTi+1, FALSE → OUTi, FALSE.
Case 3
Suppose ϕi+1(a, FALSE) = TRUE and ϕi+1(a, TRUE) = TRUE. First, the ant walks as in Case 2: INi → S&T → CONJ → INi+1 → OUTi+1,TRUE → IN of S&P → OUTOFF of S&P → IS&T → OS&T → S&P → EVALi+1 → CONJ → IN of S&T → OUTON of S&T → IS&P → OS&P → Ixi of EVALϕ → Oxi of EVALϕ → CONJ → INi+1.
Secondly, the ant walks as follows (see Figure 12-5): since the coloring of EVALi+1 has become INIT(a, TRUE) and ϕi+1 (a, TRUE) = TRUE, the ant reaches OUTi+1,TRUE; after that, since the coloring of the S&P gadget has become ON, the ant walks as OUTi+1,TRUE → IN of S&P → OUTON of S&P → OUTi,TRUE.
By these three Cases, Lemma 2 has shown to hold for ϕi(a) when Qi = ∀. Since ∃ is a logical dual of ∀, a gadget of the Qi = ∃ case is obtained from Figure 12 by switching the labels OUTi′,TRUE and OUTi′, FALSE for i′ = i and i+1. Accordingly, rewriting the above proof attains that of the Qi = ∃ case.
5. Polynomial-Time Reduction
For a given closed QBF formula ϕ0, Lemma 2 and its proof gives a polynomial-time construction of an EVAL0 gadget such that if ϕ0 = FALSE (TRUE) then the ant placed at IN0 of INIT0, FALSEn coloring of EVAL0 finally reaches OUT0, FALSE (OUT0,TRUE). So, as illustrated in Figure 13, plugging reflectors (see Figure 3) in both IN0 and INIT0, FALSEn and a diagonal highway (see Figure 4) in OUT0,TRUE gives an initial configuration of GLA such that ϕ0 = FALSE (TRUE) if, and only if, the ant stays in a bounded area (goes out of any bounded area). This establishes an efficient reduction from the QBF evaluation problem to the recognition problem of the repeatable coloring of GLA on ℤ2 with gray cells, proving Theorem 1. For the H2 model, plugging a highway along the horizon of the half-and-half background (see Figure 1) to OUT0,TRUE gives an efficient reduction, too, proving Theorem 2.
Among our gadgets on ℤ2 given in Section 2, only Switch & Turn gadget uses gray cell. In addition, the Switch & Turn gadget contains only one gray cell. So, putting these Switch & Turn gadgets mutually away from each other makes a size-n configuration of GLA colored by nε-sparse gray cells for the reduction, proving Theorem 3.
6. Open Questions
We can construct all gadgets shown in Section 2 on the T2 (triangular lattice) model with gray cells, excepting the Switch & Turn gadget. Although we are lacking the Switch & Turn gadget, we believe that the recognition problem of the repeatable configurations of GLA on T2 with gray cells is PSPACE-hard. The experimental results by Wang and Cohen [6] showed that randomly generated configurations of GLA on H2 for the monochromatic background, fall into the repeatable configurations with high probability. As far as we know, it is challenging to find even one provably unrepeatable configuration of GLA on H2 for the monochromatic background. Perhaps it is more challenging to prove the following: “an ant's trajectory starting from a repeatable size- n configuration of GLA is always at most a polynomial of n”. If this were true, then the recognition problem of the repeatable configurations of GLA would belong to PSPACE.


References
- Langton, C.G. Studying artificial life with cellular automata. Physica D 1986, 22, 120–149. [Google Scholar]
- Gale, D. Tracking the Automatic Ant and Other Mathematical Explorations; Springer-Verlag: New York, NY, USA, 1998. [Google Scholar]
- Langton, C.G. Artificial Life; Addison-Wesley: Redwood, CA, USA, 1989. [Google Scholar]
- Bunimovich, L.A.; Troubetzkoy, S.E. Recurrence properties of Lorentz lattice gas cellular automata. J. Stat. Phys. 1992, 67, 289–302. [Google Scholar]
- Kong, X.P.; Cohen, E.G.D. Diffusion and propagation in triangular Lorentz lattice gas cellular automata. J. Stat. Phys. 1991, 62, 737–757. [Google Scholar]
- Wang, F.; Cohen, E. Diffusion in Lorentz lattice gas cellular automata: The honeycomb and quasi-lattices compared with the square and triangular lattices. J. Stat. Phys. 1995, 81, 467–495. [Google Scholar]
- Gale, D. The Industrious Ant. Math. Intell. 1993, 15, 54–58. [Google Scholar]
- Bunimovich, L.A.; Troubetzkoy, S.E. Rotators, periodicity, and absence of diffusion in cyclic cellular automata. J. Stat. Phys. 1994, 74, 1–10. [Google Scholar]
- Gajardo, A.; Moreira, A.; Goles, E. Complexity of Langton's ant. Discrete Appl. Math. 2002, 117, 41–50. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W.H. Freeman & Co.: San Francisco, CA, USA, 1979. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tsukiji, T.; Hagiwara, T. Recognizing the Repeatable Configurations of Time-Reversible Generalized Langton’s Ant Is PSPACE-Hard. Algorithms 2011, 4, 1-15. https://doi.org/10.3390/a4010001
Tsukiji T, Hagiwara T. Recognizing the Repeatable Configurations of Time-Reversible Generalized Langton’s Ant Is PSPACE-Hard. Algorithms. 2011; 4(1):1-15. https://doi.org/10.3390/a4010001
Chicago/Turabian StyleTsukiji, Tatsuie, and Takeo Hagiwara. 2011. "Recognizing the Repeatable Configurations of Time-Reversible Generalized Langton’s Ant Is PSPACE-Hard" Algorithms 4, no. 1: 1-15. https://doi.org/10.3390/a4010001
APA StyleTsukiji, T., & Hagiwara, T. (2011). Recognizing the Repeatable Configurations of Time-Reversible Generalized Langton’s Ant Is PSPACE-Hard. Algorithms, 4(1), 1-15. https://doi.org/10.3390/a4010001




