1. Introduction
L1 splines have been shown to provide superior shape preservation for interpolation and approximation of multiscale data, that is, data with sudden large changes in magnitude and/or spacing used for modeling of natural and urban terrain, geophysical features, biological objects, robotic paths and many other irregular surfaces, processes and functions ([
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15]). The minimization principles for
L1 splines have typically (but not uniformly) been based on the
L1 norm of the second derivative (rather than on the
L1 norm of expressions involving other levels of derivatives). The resulting non-differentiable convex generalized geometric programs have been solved by active set [
3], primal affine [
5,
6,
7,
10,
11] and primal-dual [
12,
14] algorithms.
In the literature, there are a few indications of limitations of the primal affine and primal-dual algorithms for bivariate
L1 splines for large data sets [
9,
12]. There is also unpublished computational experience of the authors and others who have noticed issues of incomplete convergence or not completely correct convergence of the active set, primal affine and primal-dual algorithms for both univariate and bivariate
L1 splines. It is in this context that we seek in this paper a new algorithmic approach for calculating
L1 splines. Auquiert, Gibaru and Nyiri [
16] have developed a subdifferential-based procedure for calculating second-derivative-based
L1 splines on 5-point windows. We propose here an algorithm for second-derivative-based 5-point-window
L1 splines based on the analysis in
Section 2 of [
17], which links, via analytical properties of the spline functional, local geometric properties of 5-point windows of the data set with geometric properties of the
L1 spline interpolant.
In considering second-derivative-based 5-point-window
L1 splines, three types of information are needed for full “situational awareness,” namely, 1) information about whether use of 5-point windows is superior to use of windows of other sizes and to use of global data sets, 2) information about whether use of the second derivative in the spline functional is superior to use of the first derivative, function value or antiderivative and 3) information about whether the new, analysis-based algorithm mentioned above can achieve computational results superior to those of the primal affine algorithm, which was the previously most widely used algorithm for calculating
L1 splines. The third item here has not yet been considered in the literature and the information in the literature on the first and second items is sketchy at best. The computational and analytical results in [
2,
16,
17] do suggest that 5-point windows have advantages vs. global calculations. However, it is not yet known whether windows of other sizes might also have advantages. Results presented in [
10,
11] indicate that first-derivative-based and function-value-based
L1 splines may have advantages over standard second-derivative-based
L1 splines. However, these two publications considered only the behavior of
L1 splines on the global scale and did not consider behavior on the fine, interval-to-interval scale.
The present paper addresses these needs. In
Section 2, we give a brief description of the primal affine algorithm that has previously been widely used to calculate
L1 splines. In
Section 3, we compare
L1 splines calculated by minimizing, on 5-point windows, on 7-point windows and on global data sets, four different spline functionals, namely, ones based on the second derivative, the first derivative, the function value and the antiderivative. These
L1 splines are calculated by the primal affine algorithm. The results of this section provide motivation for the development of a new, analysis-based algorithm for calculating 5-point-window, second-derivative-based
L1 splines. In
Section 4, we present this new algorithm, which is based on the analysis in
Section 2 of [
17]. In
Section 5, we show that, while the results of both the new algorithm and the primal affine algorithm look good on the macro level, there are differences on the micro level. Specifically, the results of the new algorithm are accurate on the micro level while those of the primal affine algorithm are occasionally only approximate. Finally, in
Section 6, we summarize the results presented in the previous sections and point out the potential for future algorithms for locally calculated univariate
L1 approximating splines and locally calculated bivariate
L1 interpolating and approximating splines.
All of the quantities in this paper are real quantities. The nodes
,
, are a strictly monotonic but otherwise arbitrary partition of the finite interval
. Let
. At each node
, the function value
is given,
. The slope of the line segment connecting
and
is
The local and global cubic
L1 splines discussed in this paper are cubic polynomials in each interval
,
, and are
C1 continuous at the nodes. The first derivative of the spline at node
,
, is denoted by
(to be determined by minimization of the
L1 spline functional). We use
to denote the slope of the chord between neighboring points:
We use
ζ to denote the linear spline:
For the interpolation problem under consideration in the present paper, the nodes and the function values at the nodes are given. Minimization of a spline functional means “determination of the first derivatives that yield the minimum.” The first derivatives determined from the minimization along with the fixed nodal and functional values yield the piecewise cubic
L1 spline by the standard Hermite interpolation formula. For reference, we present here the spline functionals that define traditional, globally calculated
L1 splines (“global
L1 splines”). Second-derivative-based, first-derivative-based, function-value-based and antiderivative-based cubic
L1 splines are calculated by minimizing
and
respectively, over the finite-dimensional spline space of
C1 piecewise cubic polynomials
z that interpolate the data. The
L1 splines that minimize these functionals can be nonunique, a situation that will be handled by adding “regularization terms” to the functionals when they are minimized by the primal affine algorithm or, in the new algorithm proposed in this paper, by applying a “choice procedure” as described below in
Section 4. Second-derivative-based
L1 splines are the
L1 splines commonly encountered in the literature. First-derivative-based
L1 splines have been investigated in [
10,
11]. Function-value-based
L1 splines have been treated in [
11]. Antiderivative-based
L1 splines are newly introduced in this present paper to provide additional insight into how the order of the derivative in the spline functional affects the geometric shape preservation properties of the
L1 spline.
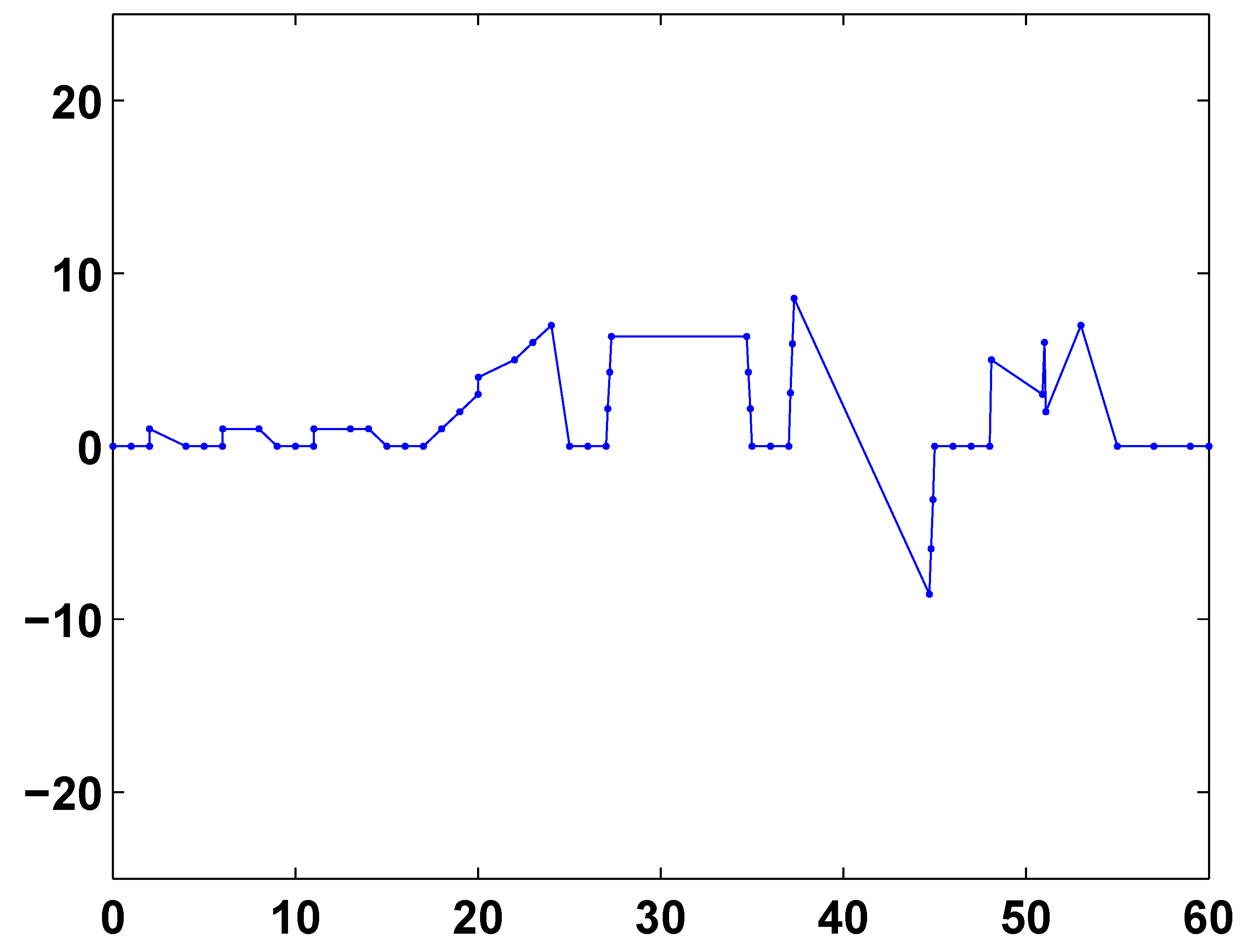
In the present paper, computations of different algorithms are based on the following challenging data set consisting of 56 irregular data points that lie on flat, linear, quadratic, cubic and oscillatory functions and on protuberances, patched together with discontinuities of function values and first derivatives and with extreme irregular spacing—with lengths of neighboring intervals differing by up to a factor of 100:
This data set was used in [
11]. The data
,
, in the region from
x = 27 to
x = 45 lie on the the quadratic function 44 − 2.75(
x − 31)
2. The data
,
, in the region from
x = 37 to
x = 45 lie on the cubic function −16(
x − 41) + (
x − 41)
3. Note the large gaps in the intervals
and
. In the figures, the data will be represented by dots “·”. The linear spline for these data is given in
Figure 1.
2. Primal Affine and Other Previously Available Algorithms for L1 Splines
Minimization of the global
L1 spline functionals (4), (5), (6) and (7) is a nonlinear programming problem. Direct minimization of (4) has been accomplished by an active set method [
3]. Active set algorithms for minimizing (5), (6) and (7) have not been developed, but these functionals and functional (4) have been minimized by primal affine algorithms and primal-dual algorithms [
12,
14]. Primal affine and primal-dual algorithms are linear (not nonlinear) programming procedures. To create a linear program suitable for application of these algorithms, the integrals in the
L1 spline functionals need to be discretized. For the primal affine algorithm used in the present paper and in [
5,
6,
8,
10,
11], the spline functionals were discretized by the midpoint rule with
K equal subintervals in each interval
. In this paper,
K = 100. For a detailed description of the primal affine algorithm, see [
7].
Figure 1.
Data set and linear spline.
Figure 1.
Data set and linear spline.
For calculation of
L1 splines by the primal affine method using the global functionals (4), (5), (6) and (7), we add to these functionals the regularization terms
When
ε is sufficiently small, the
L1 spline that minimizes the functional with the regularization term is unique. For the computational experiments of the present paper,
ε = 10
−4.
In addition to calculating
L1 splines by minimizing the global functionals (4), (5), (6) and (7) by the primal affine method, we will calculate
L1 splines using these functionals on 5-point and 7-point windows. To calculate the derivative
of a “windowed”
L1 spline at node
, we minimize functionals that are the same as (4), (5), (6) and (7) except that the integral is over a local set of intervals (“window”) rather than over the global domain. For 5-point-window
L1 splines, the window
is used for nodes
,
, the window
is used for nodes
,
and the window
is used for nodes
,
. For 7-point-window
splines, the window
is used for nodes
,
, the window
is used for nodes
,
and the window
is used for nodes
,
. When minimizing a “windowed”
L1 spline functional for node
by the primal affine algorithm, we add to the spline functional the regularization term
For the computational experiments of the present paper,
ε = 10
−4.
3. Computational Results for Windowed and Global L1 Splines
A window with an odd number of points is desirable, since it has a “middle point” at which one can use a locally calculated derivative as the derivative of the global interpolant. Conversely, a window with an even number of points is not desirable, because it lacks a middle point. Using the primal affine algorithm described in the previous section, we generated computational results for 5-point-window and 7-point-window L1 splines as well as for global L1 splines.
In the literature, there have been reports [
10,
11] about
L1 splines based on spline functionals involving first derivatives and function values, that is, derivatives of degree lower than the standard second degree. Results in [
10,
11] suggest that, for global
L1 splines, spline functionals based on the first derivative or function value (that is, on functional (5) or (6)) result in improved shape preservation. Those results emphasized overall global preservation of shape on the macro scale but did not treat local preservation of shape on the fine, interval-to-interval scale. Following up on these prior investigations, we revisit here the comparison of
L1 splines based on derivatives of degree 2, 1 and 0, add to the comparison
L1 splines based on derivatives of degree −1 (antiderivatives) and add the new dimension of considering the window size (5 points, 7 points or global). For this comparison, we use the primal affine algorithm described in
Section 2.
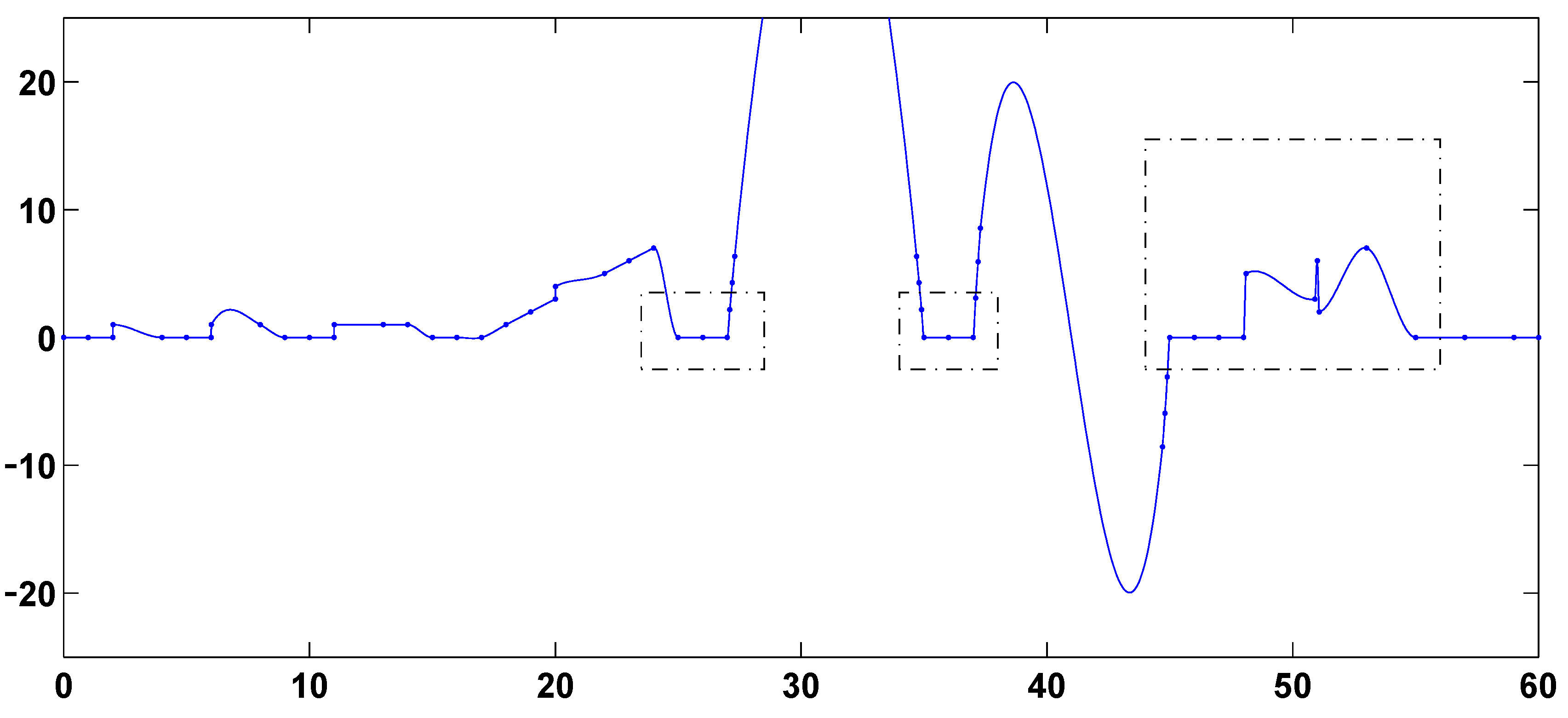
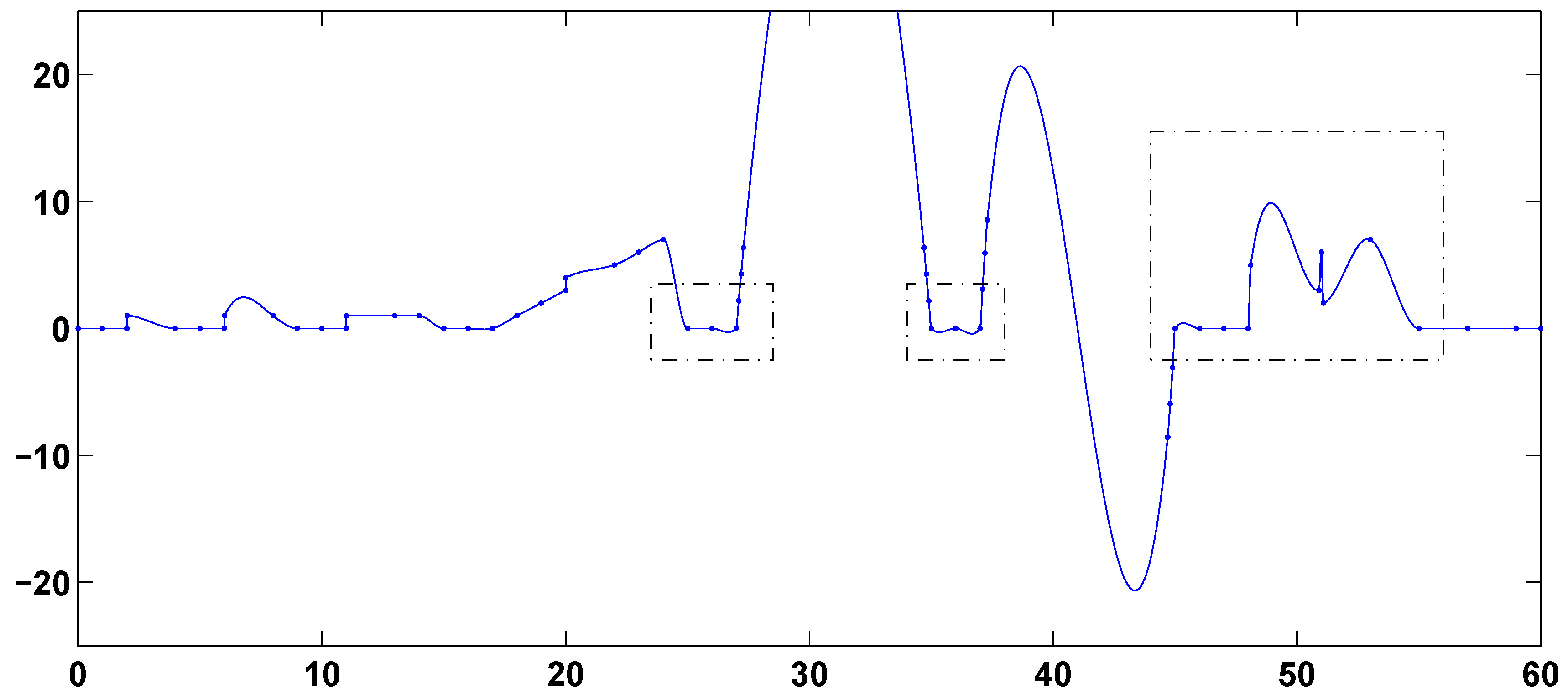
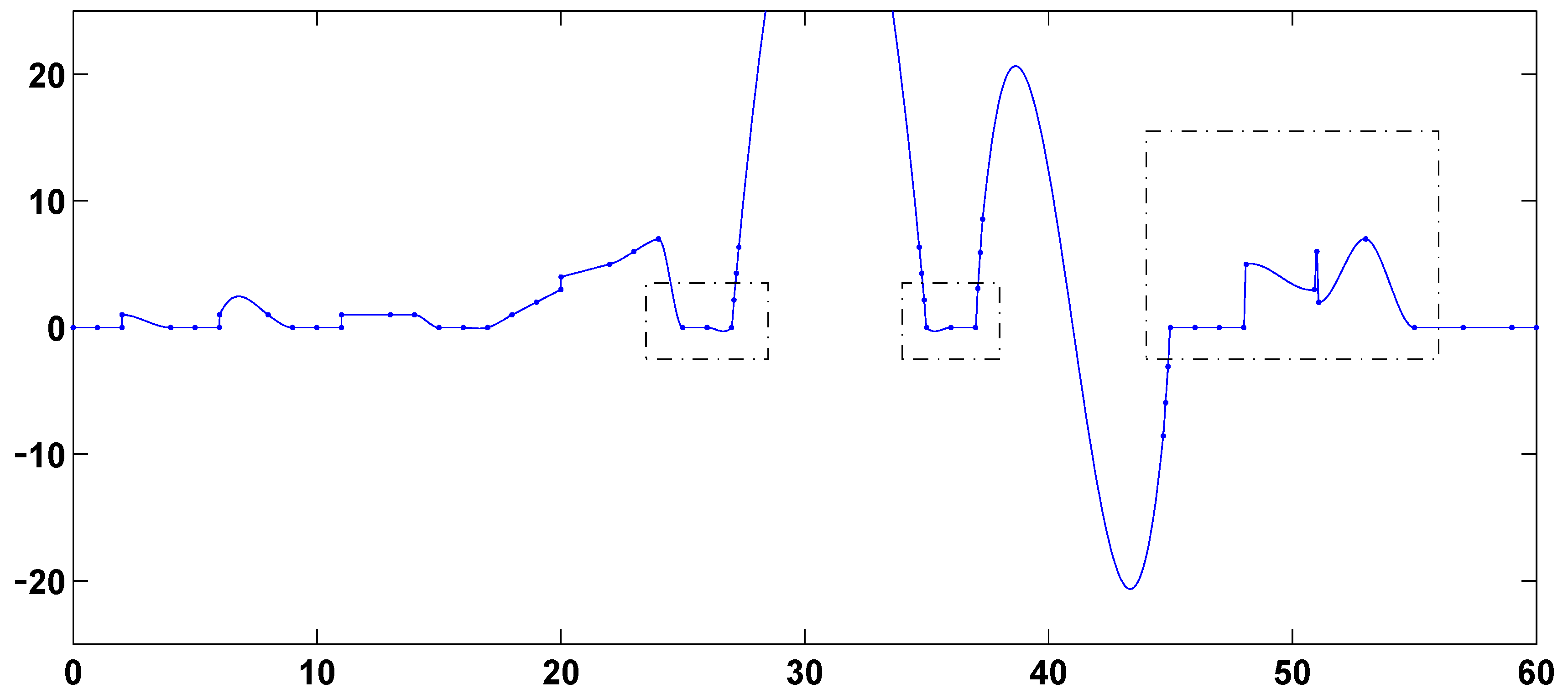
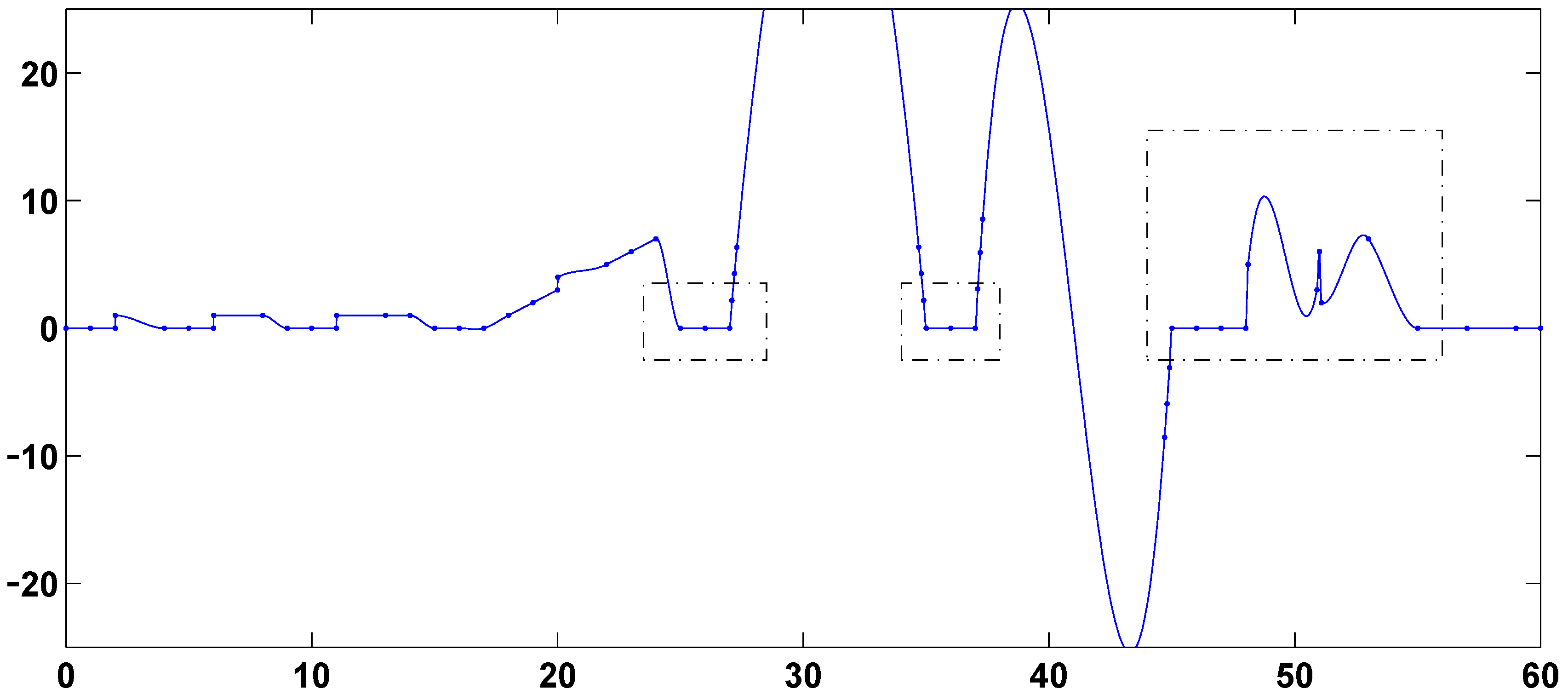
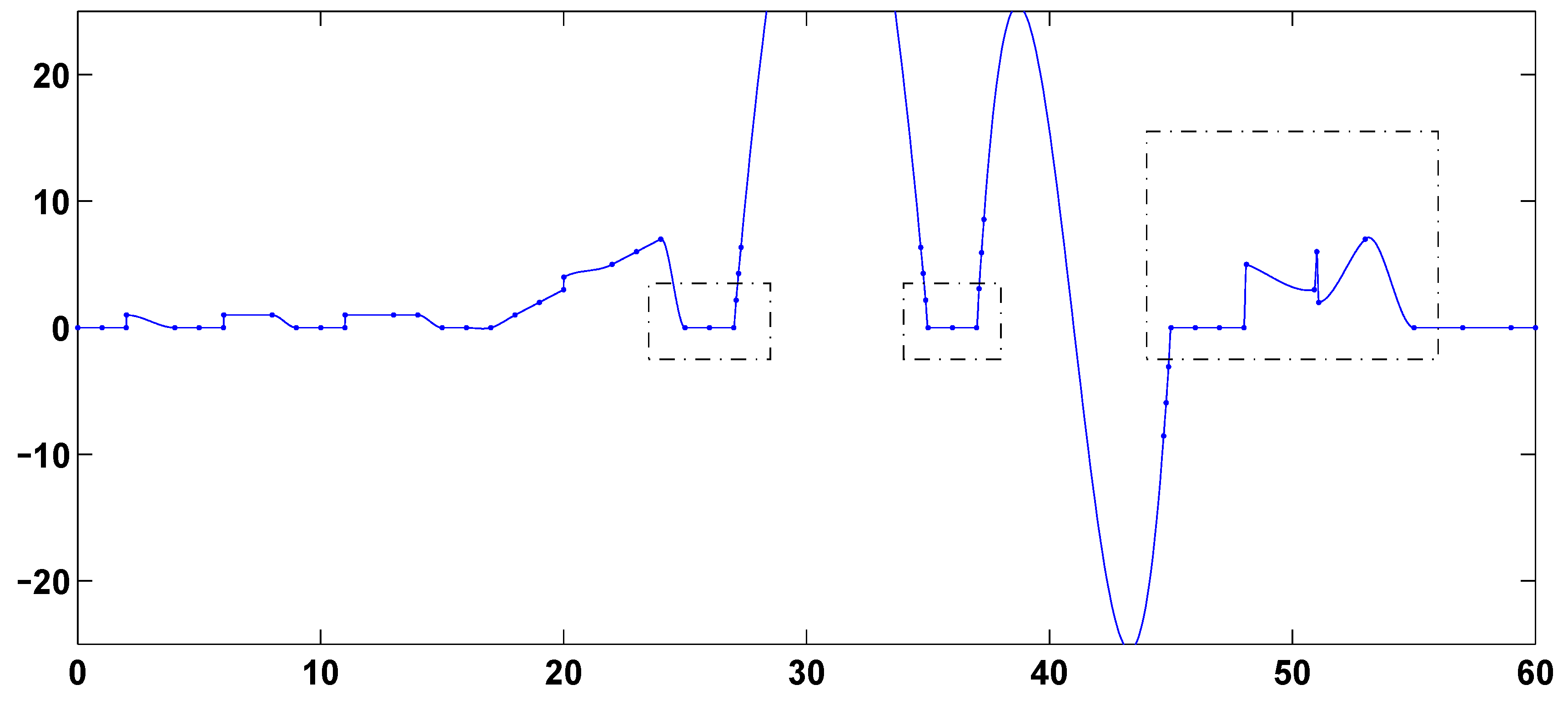
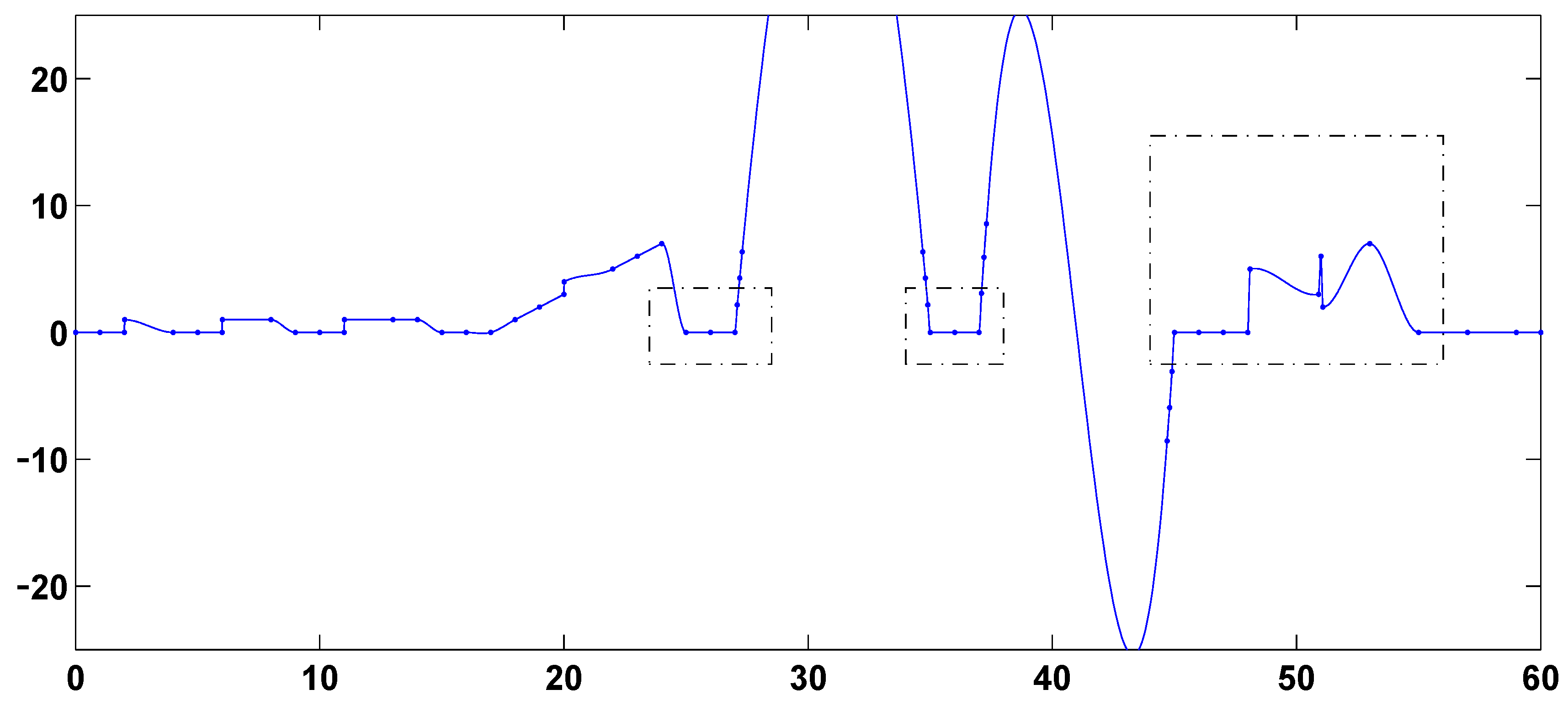
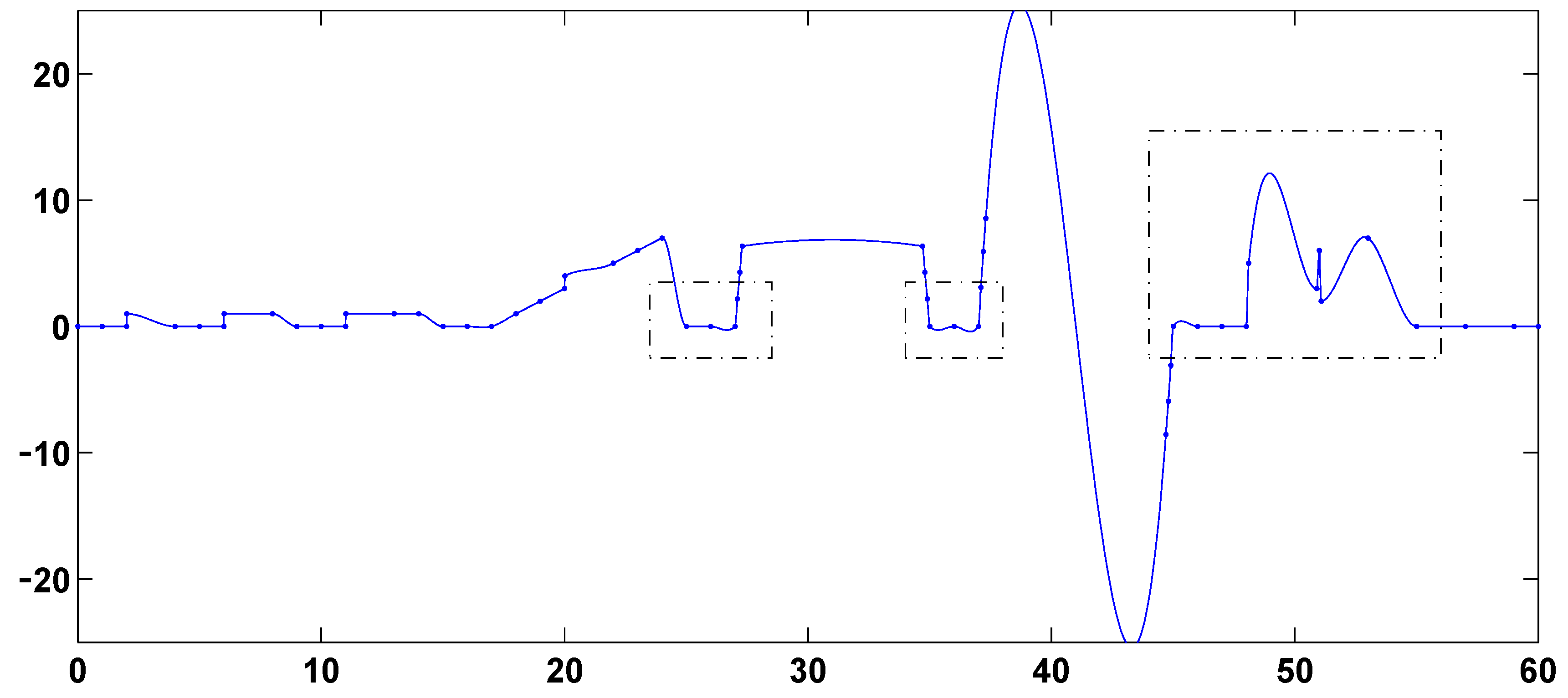
Computational results are presented in
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
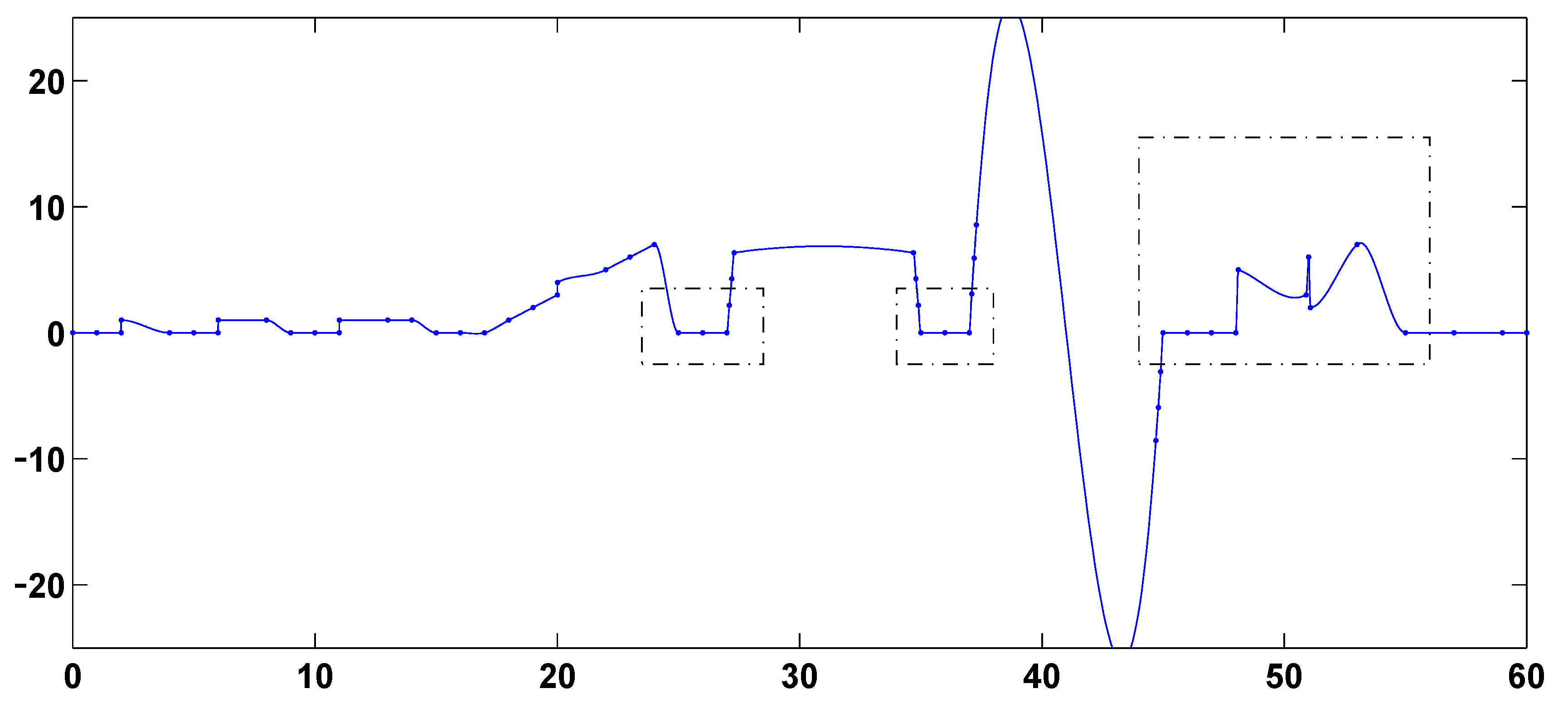
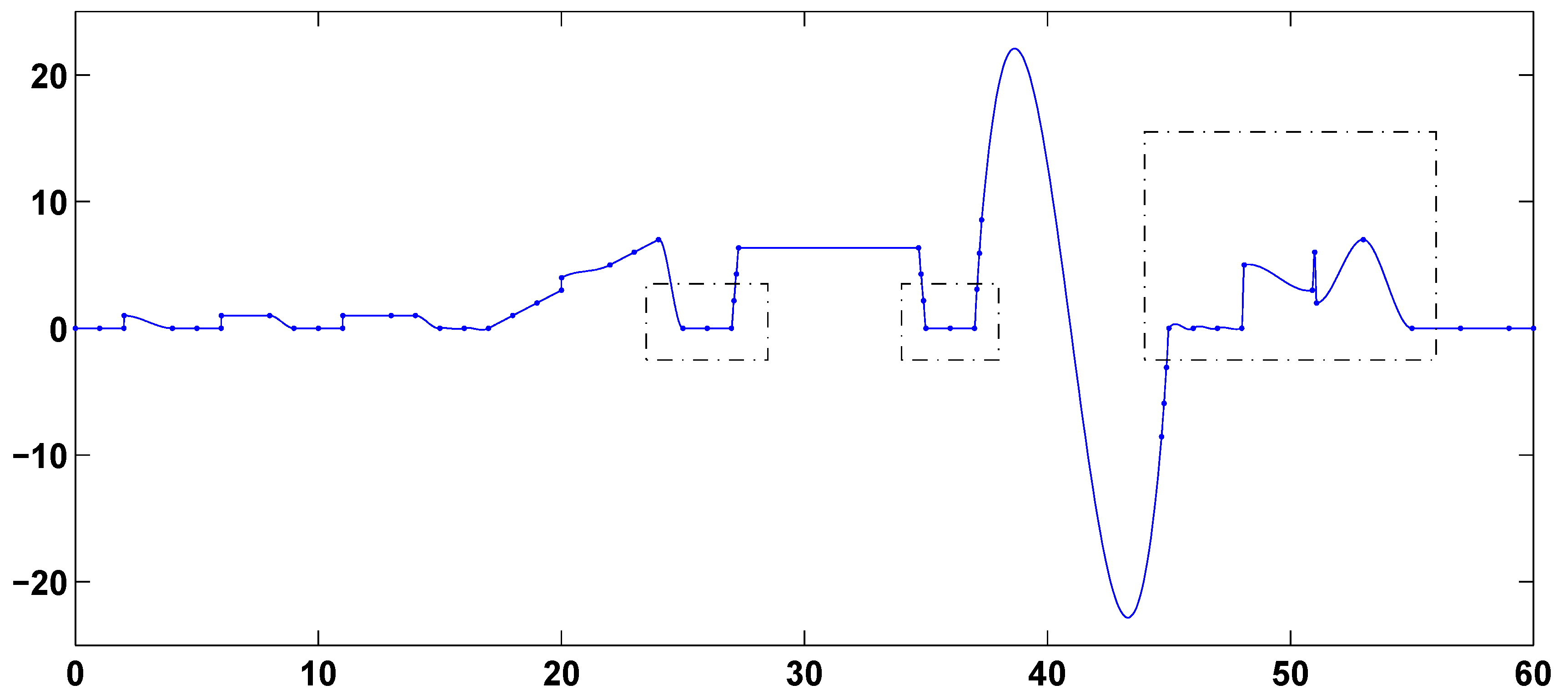
Figure 13. In each figure, we highlight in dashed boxes the intervals [25, 27]; [35, 37] and [45, 55], where differences among the various splines are most prominent. The second-derivative-based 5-point-window spline of
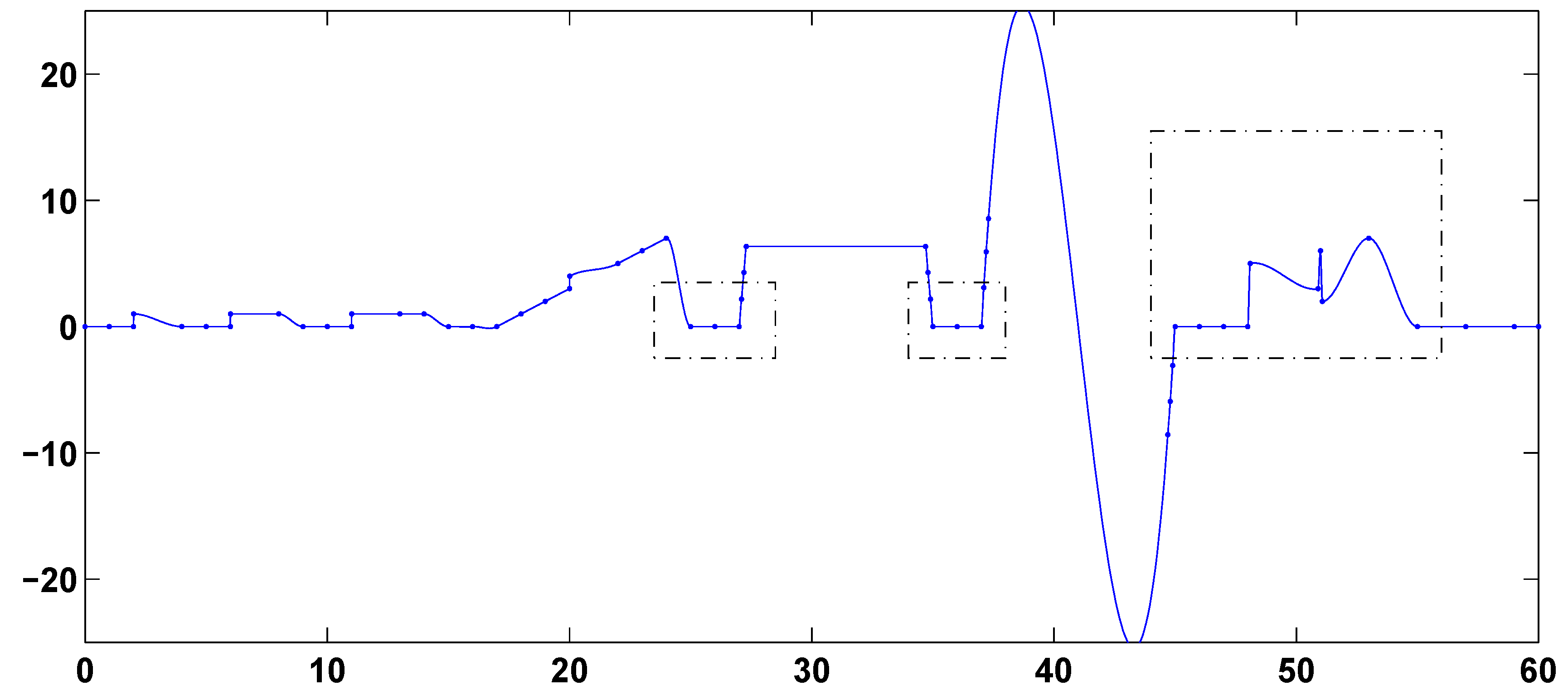
Figure 2 and the first-derivative-based and function-value-based global splines of
Figure 7 and
Figure 10 preserve linearity in the intervals [25, 27], [35, 37] and [45, 48] and avoid extraneous overshoot, extraneous undershoot and extraneous oscillation in the interval [48.1, 55]. None of the other nine splines of
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13 is able to preserve linearity and avoid extraneous overshoot, undershoot and oscillation in all of these intervals. In particular, the splines of
Figure 3,
Figure 4,
Figure 8,
Figure 11,
Figure 12 and
Figure 13 do not preserve linearity well on the intervals [25, 27], [35, 37] and/or [45, 48]. The splines of
Figure 3,
Figure 5,
Figure 8 and
Figure 11 have extraneous oscillation on the interval [48.1, 50.9]. The splines of
Figure 6,
Figure 9 and
Figure 12 have undershoot in [48.1, 50.9]. The differences in the large intervals [27.3, 34.7] and [37.3, 44.7] is a separate issue that is discussed in the remark below.
Remark The data points immediately to the right and left of the large intervals [27.3, 34.7] and [37.3, 44.7] lie on a quadratic and a cubic function, respectively. The second- and first-derivative-based splines of
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6 and
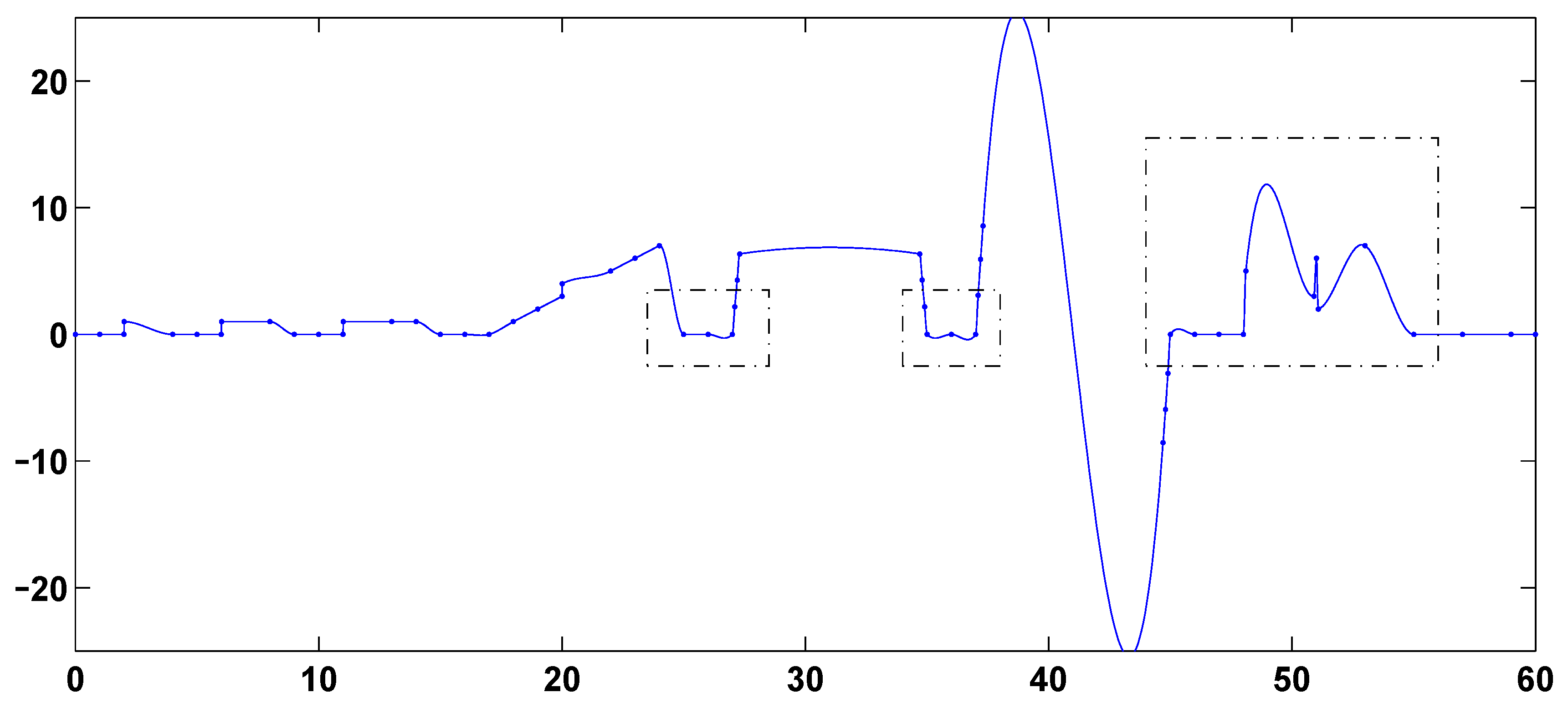
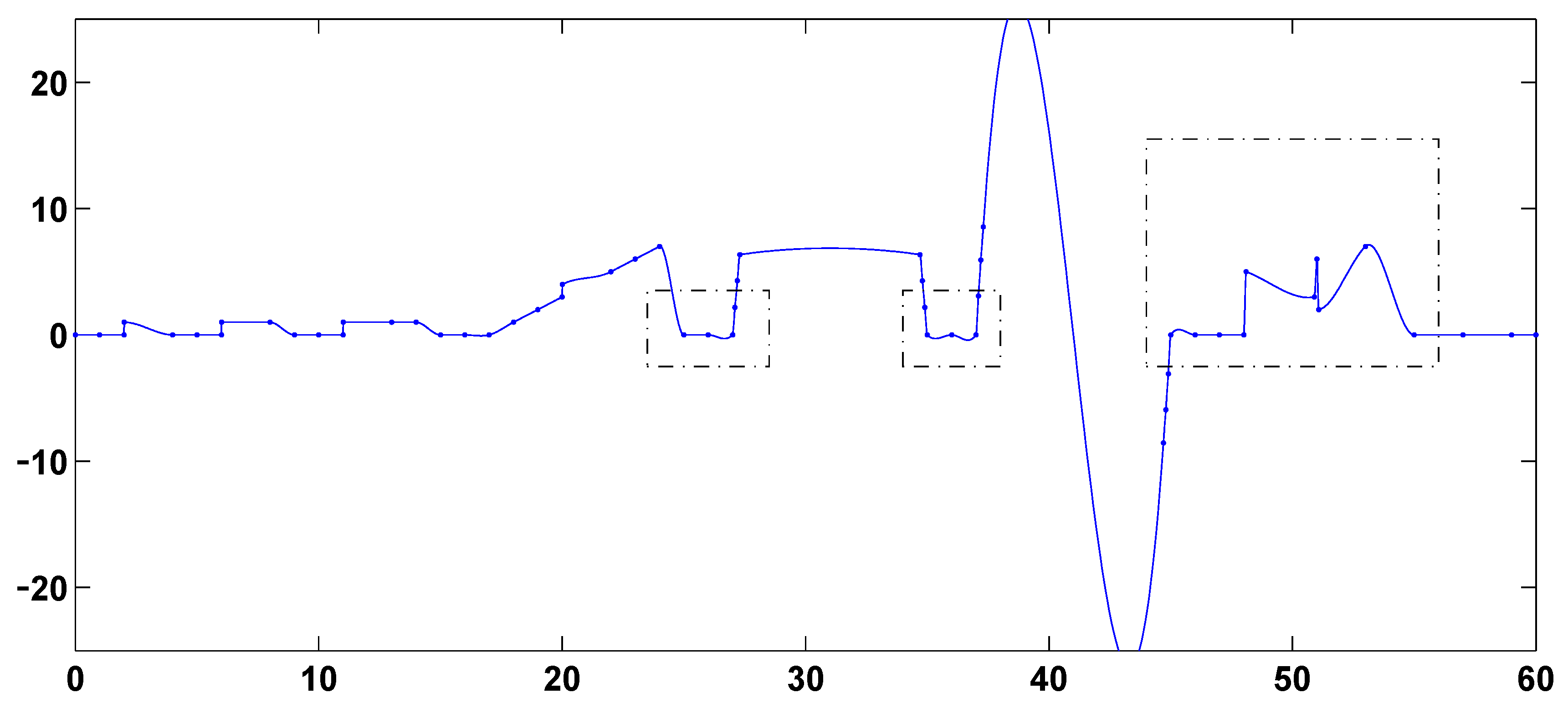
Figure 7 approximate both the quadratic and the cubic function. In contrast, the function-value-based and antiderivative-based splines of
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13 avoid approximating the quadratic function in [27.3, 34.7], even though they do approximate the cubic function in [37.3, 44.7]. In classical approximation theory, the ability to approximate or even reproduce quadratic, cubic and higher-degree functions is a goal. In geometric modeling of irregular data, however, reproducing any function of degree higher than 1 is generally considered disadvantageous because it leads to extraneous oscillation, overshoot or undershoot. It is not yet known how to construct
L1 splines that generically avoid approximating functions of degree higher than 1. In the present article, we acknowledge this issue but we do not take it into account when assessing the shape-preservation capabilities of the various types of
L1 splines.
Figure 2.
Second-derivative-based 5-point-window L1 spline
Figure 2.
Second-derivative-based 5-point-window L1 spline
Figure 3.
Second-derivative-based 7-point-window L1 spline
Figure 3.
Second-derivative-based 7-point-window L1 spline
Figure 4.
Second-derivative-based global L1 spline
Figure 4.
Second-derivative-based global L1 spline
Figure 5.
First-derivative-based 5-point-window L1 spline
Figure 5.
First-derivative-based 5-point-window L1 spline
Figure 6.
First-derivative-based 7-point-window L1 spline
Figure 6.
First-derivative-based 7-point-window L1 spline
Figure 7.
First-derivative-based global L1 spline
Figure 7.
First-derivative-based global L1 spline
Figure 8.
Function-value-based 5-point-window L1 spline
Figure 8.
Function-value-based 5-point-window L1 spline
Figure 9.
Function-value-based 7-point-window L1 spline
Figure 9.
Function-value-based 7-point-window L1 spline
Figure 10.
Function-value-based global L1 spline
Figure 10.
Function-value-based global L1 spline
Figure 11.
Antiderivative-based 5-point-window L1 spline
Figure 11.
Antiderivative-based 5-point-window L1 spline
Figure 12.
Antiderivative-based 7-point-window L1 spline
Figure 12.
Antiderivative-based 7-point-window L1 spline
Figure 13.
Antiderivative-based global L1 spline
Figure 13.
Antiderivative-based global L1 spline
We do not claim here that the results presented in
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13 should yet be broadly interpreted as general descriptions of the shape-preservation capabilities of the various types of
L1 splines. However, these results do provide insight into the shape-preservation capabilities of these types of
L1 splines as well as a piece of evidence supporting the use of second-derivative-based 5-point-window
L1 splines. In these computational results, the performance of second-derivative-based
L1 splines, the hitherto most widely used variant of
L1 splines is improved by using 5-point windows. The other two “top performers” of
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13, namely, the first-derivative-based and function-value-based global
L1 splines of
Figure 7 and
Figure 10 are computationally much more expensive than second-derivative-based 5-point-window
L1 splines. No theory has been published for function-value-based
L1 splines. Elementary theory has been published for first-derivative-based
L1 splines but only for the global case [
15]. Based on these considerations, we choose the second-derivative-based 5-point-window
L1 spline as the
L1 spline to be used in the remainder of this paper.
4. Algorithm for Minimization of Second-derivative-based 5-point-window Spline Functional
We propose here an algorithm for generation of second-derivative-based 5-point-window
L1 splines based on the analytical results of
Section 2 of [
17]. Recall that, in the interpolation situation of interest in this paper, the task of calculating an
L1 spline is the task of calculating the first derivatives
by minimization of a spline functional with given nodes
and given function values
at the nodes. In the
ith 5-point window, 2 ≤
i ≤
I − 2, an objective function
is minimized:
In [
17], minimization of
is treated as a bilevel minimization problem by representing
,
,
and
as functions of
. The optimal
, called
, is determined by solving
where
and
G1(
bi) and
G2(
bi) have similar structure, which leads to the representation
where
G(
q;
c) is a function that is defined and analyzed in [
17].
The analysis of [
17] is based on the signs of
,
and
. There are 27 cases, as shown in
Table 1. For the simple cases, the optimal
are listed in the last column of the table. For cases 14, 15, 17, 18, 23, 24, 26 and 27, the
will be discussed in Algorithm 1.
Table 1.
27 cases used in the 5-point window algorithm (see [
17])
Table 1.
27 cases used in the 5-point window algorithm (see [17])
| Case | Sign of | Same as Case | |
| | |
| 1 | 0 | 0 | 0 | | |
| 2 | 0 | 0 | + | | |
| 3 | 0 | 0 | − | 2 | |
| 4 | 0 | + | 0 | | |
| 5 | 0 | + | + | | |
| 6 | 0 | + | − | | |
| 7 | 0 | − | 0 | 4 | |
| 8 | 0 | − | + | 6 | |
| 9 | 0 | − | − | 5 | |
| 10 | + | 0 | 0 | 2 | |
| 11 | + | 0 | + | | |
| 12 | + | 0 | − | | |
| 13 | + | + | 0 | 5 | |
| 14 | + | + | + | | [see text] |
| 15 | + | + | − | | [see text] |
| 16 | + | − | 0 | 6 | |
| 17 | + | − | + | | [see text] |
| 18 | + | − | − | 15 | [see text] |
| 19 | − | 0 | 0 | 2 | |
| 20 | − | 0 | + | 12 | |
| 21 | − | 0 | − | 11 | |
| 22 | − | + | 0 | 6 | |
| 23 | − | + | + | 15 | [see text] |
| 24 | − | + | − | 17 | [see text] |
| 25 | − | − | 0 | 5 | |
| 26 | − | − | + | 15 | [see text] |
| 27 | − | − | − | 14 | [see text] |
Whenever the optimal
is non-unique at a node
, 2 ≤
i ≤
I − 2, we choose the solution
to be the real number in the optimal set closest to
, that is,
. In all 27 cases, the solution is either uniquely determined by a simple expression or lies inside the interval
and can be found by a line search. The expression
is always continuously differentiable on
. When line search is required, the solution of (10) is obtained by solving
. (The explicit form of this expression is provided in [
17].) For the results generated in this paper, we used the secant method (previously used in an analogous way in [
3]). Calculation of
for
i = 0, 1,
I − 1 and
I is carried out differently, as described in Step 3 of Algorithm 2.
The complete algorithm for calculating second-derivative-based 5-point-window L1 splines consists of a subroutine (Algorithm 1) for the local window calculation embedded in an “outer loop” (Algorithm 2) as described in the remainder of this section. Recall that the quantities are defined in (2).
Algorithm 1 (Subroutine(
;
)).
- STEP 1
Calculate , and and determine the case to which these quantities correspond.
- STEP 2
Calculate using information from [17] contained in Table 1 or described below in this step. Here, and .
- -
In Cases 1, 2, 3, 5, 6, 8, 9, 11, 12, 20 and 21, return .
- -
In Cases 10, 13, 16, 19, 22 and 25, return .
- -
In Cases 4 and 7, return .
- -
Case 14:- ∙
Subcase 14-1: If ,
then - ∙
Subcase 14-2: If ,
then lies in the intervalUse a line search to find such that in this interval.
- ∙
Subcase 14-3: If ,
then - ∙
Subcase 14-4: If ,
then lies in the intervalUse a line search to find such that in this interval.
Return .
- -
Case 15:- ∙
Subcase 15-1: If , then .
- ∙
Subcase 15-2: If , then .
- ∙
Subcase 15-3: If ,
then lies in the intervalUse a line search to find such that in this interval.
Return .
- -
Case 17:- ∙
Subcase 17-1: If ,
then lies in the intervalUse a line search to find such that in this interval.
- ∙
Subcase 17-2: If ,
then
Return .
- -
In Case 18, letThis transforms Case 18 into Case 15. Obtain the optimal solution of the transformed problem. Return .
- -
In Case 23, letThis transforms Case 23 into Case 15. Obtain the optimal solution of the transformed problem. Return .
- -
In Case 24, letThis transforms Case 24 into Case 17. Obtain the optimal solution of the transformed problem. Return .
- -
In Case 26, letThis transforms Case 26 into Case 15. Obtain the optimal solution of the transformed problem. Return .
- -
In Case 27, letThis transforms Case 27 into Case 14. Obtain the optimal solution of the transformed problem. Return .
- STEP 3
Stop.
The “outer loop” (Algorithm 2) consists of repeated or parallel application of Algorithm 1.
Algorithm 2 (Analysis-based Algorithm).
- STEP 1
Given a set of points , , calculate , , and , , by formulas (1) and (2).
- STEP 2
For , calculate using Subroutine(;) (Algorithm 1).
- STEP 3
- STEP 4
Stop.
5. Analysis-based Algorithm vs. Primal Affine Algorithm for 5-pointWindows
In this section, we compare computational results generated by the analysis-based algorithm introduced in
Section 4 and the widely used primal affine algorithm described in
Section 2. These results differ significantly (by more than 10
−4) at a number of nodes as shown in
Table 2. It was confirmed by hand calculation that the results for the analysis-based algorithm are accurate for the original nondiscretized
L1 spline functional (a confirmation of both the analysis-based algorithm and the code). The differences in the results produced by the primal affine algorithm and the analysis-based algorithm are due mainly to the discretization (midpoint rule with 100 subintervals, as described in
Section 2).
Remark On 5-point windows, the primal affine algorithm converges well. However, for global
L1 splines on large data sets, the primal affine algorithm can converge slowly or not at all, especially in bivariate situations, as indicated in Section 6 of [
9], a conclusion supported by additional unpublished computational experience of the authors. In such situations, the
L1 spline functional may result in a nearly degenerate nonlinear program and this near degeneracy is retained in the discretized version.
Table 2.
generated by primal affine algorithm and analysis-based algorithm.
Table 2.
generated by primal affine algorithm and analysis-based algorithm.
| i | | from primal affine algorithm | from analysis-based algorithm |
| 7 | 6.01 | 3.4096 | 3.3874 |
| 29 | 27.2 | 20.9698 | 20.9729 |
| 30 | 27.3 | 19.5166 | 19.5250 |
| 31 | 34.7 | -19.5166 | -19.5250 |
| 32 | 34.8 | -20.9698 | -20.9729 |
| 38 | 37.2 | 27.5971 | 27.6099 |
| 39 | 37.3 | 18.4160 | 18.4667 |
| 40 | 44.7 | 18.4160 | 18.4667 |
| 41 | 44.8 | 27.5971 | 27.6099 |
The analysis-based algorithm introduced in this paper does not require discretization of the
L1 spline functional and does not require regularization terms to be added to this functional. The algorithm is simple, accurate and inherently parallelizable. Moreover, it is computationally much cheaper than the primal affine algorithm. Both of the algorithms were implemented in C++ 6.0. Computational results for the data set of
Section 1 were generated on an IBM laptop running under the Windows XP operating system at 1.66 GHz CPU with 1.50 GB RAM and were presented in
Section 3. The computing times of the primal affine algorithm were
177.7 milliseconds for a 5-point window (sequential calculations),
335.2 milliseconds for a 7-point window (sequential calculations),
94.9 milliseconds for global
for the second-derivative-based
L1 splines of
Figure 2,
Figure 3 and
Figure 4, respectively. The computing time of the analysis-based algorithm was
for the second-derivative-based
L1 spline that corresponds to
Figure 2. In these computational experiments, the sequential analysis-based algorithm is thus 177.7/0.0531 = 3347 times faster than the sequential primal affine algorithm. The speed-up for the parallel versions of these algorithms would be roughly the same, since each parallel version would be faster than the corresponding sequential version by a factor roughly equal to the number of points in the data set (56 in this case). The sequential analysis-based algorithm is faster than the global primal affine algorithm by a factor of 94.9/0.0531 = 1787. The speed-up of the parallel analysis-based algorithm vs. the global primal affine algorithm would, therefore, be roughly a factor of 1787.2 × 56 ≈ 10
5, an impressive amount. For larger data sets, the speed-up is correspondingly larger.
Remark The computing time for the primal affine algorithm could be reduced by decreasing the number of subintervals K for discretization (via the midpoint rule) of the spline functional from 100, as was used for the results generated for this paper, to, say, 10, or less. However, since the degree to which a discretized spline functional approximates the continuum spline functional decreases as the number of subintervals is decreased, using only a few subintervals is generally not an advantageous choice when accuracy is an issue, as it is here.