A Clinical Decision Support Framework for Incremental Polyps Classification in Virtual Colonoscopy
Abstract
:1. Introduction
2. Multi-Classification LS-SVM Survey
3. Proposed multi-classification WP-SVM
3.1. Proposed Multi-Classification
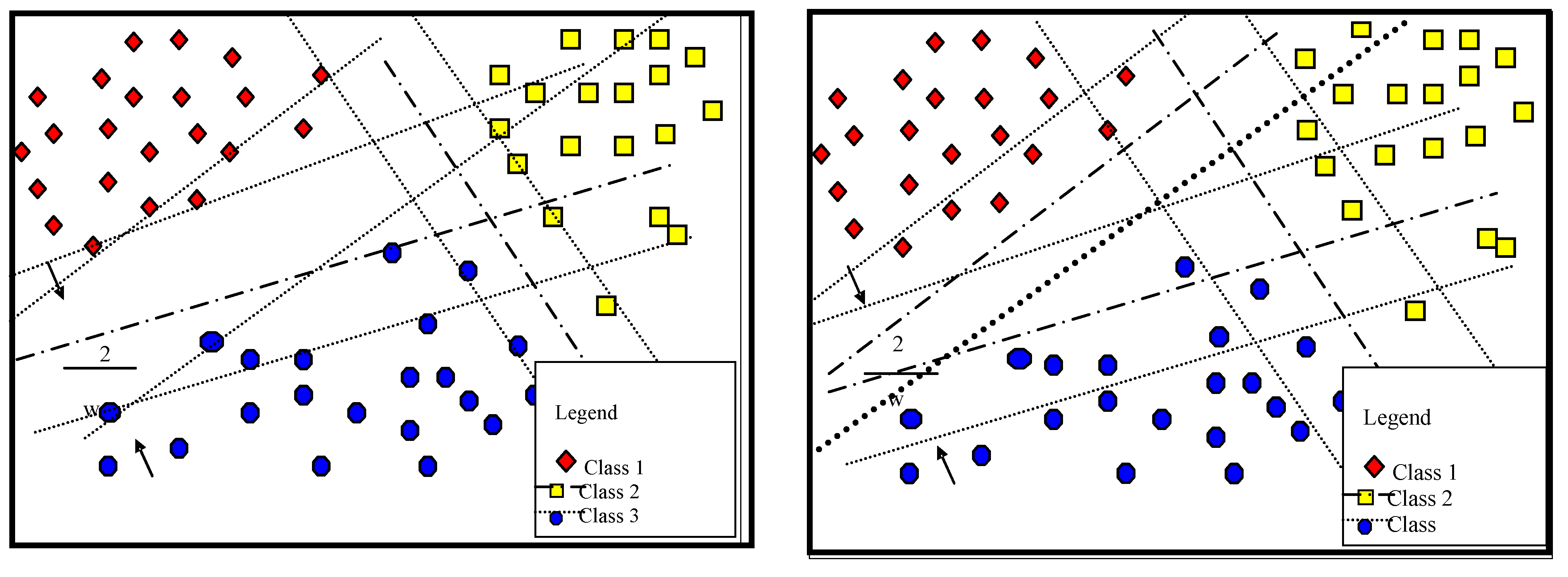
| Matrix Symbol | Matrix Element |
| C | Diagonal matrix of size (f*c) by (f*c), the diagonal elements are composed of the square matrix cn which is of size f: |
| D | Diagonal matrix of size (f*c) by c, the diagonal elements are the column vector dn of length f |
| E | Column vector of size c made from |
| H | Matrix of size (f*c) by c. The row vector is hn of length c and of the form |
| G | Square matrix of size (f*c) by (f*c), composed of matrix gn of size f by c such that |
| Q | Square matrix of size c, made from the row vector qn of length c qn = [(q(1)+q(n)) ... (q(c)+q(n))] |
| U | Column vector of size c, made from un such that un = −2(N −cq(n)) |
| R | Square diagonal matrix of size c, the diagonal elements rn are as follows |
3.2. Proposed WP-SVM
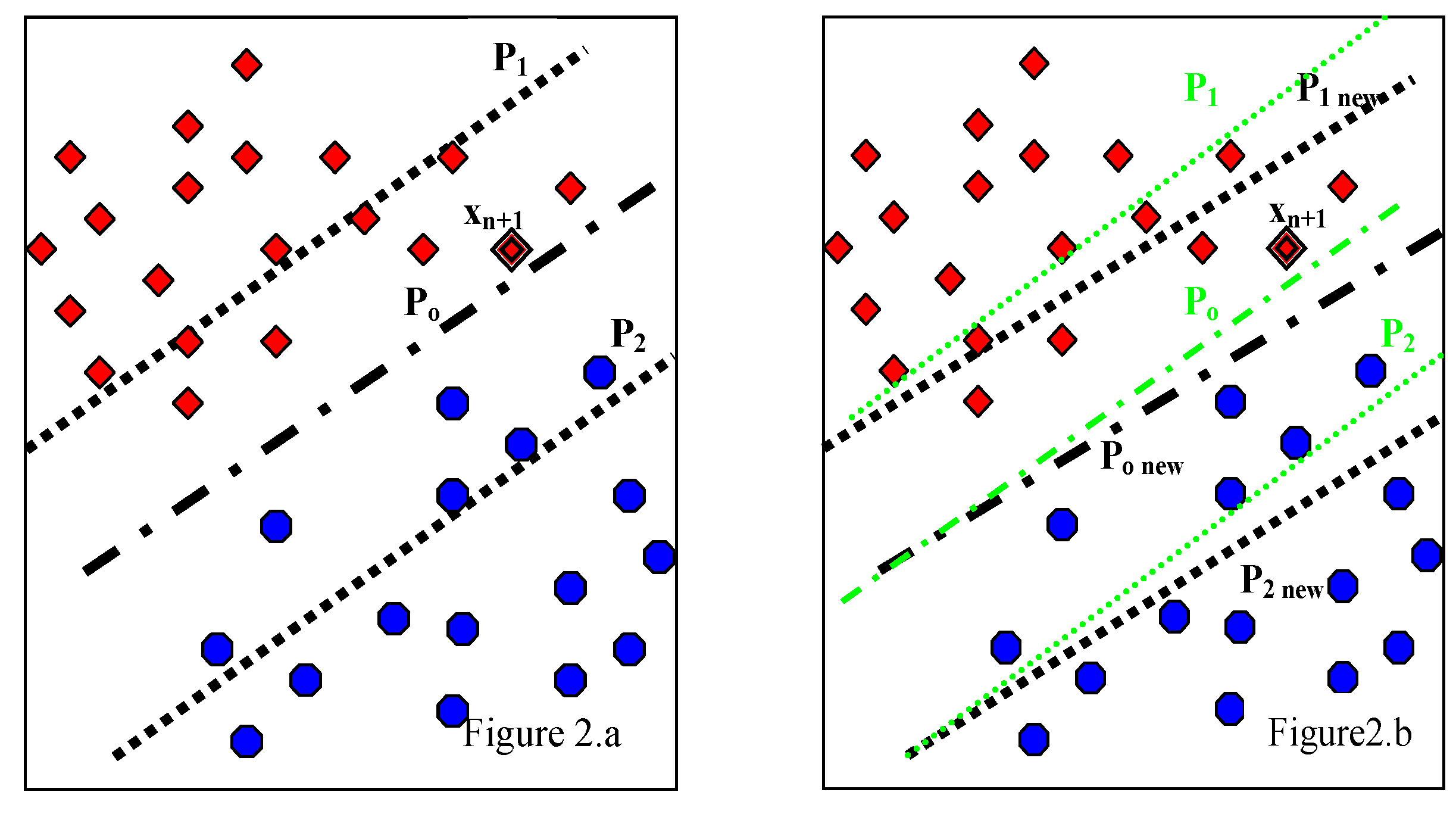
| Step # | Algorithm |
| Step 1 | Train initial model using TrainSet which consists of N patient data each having f features. Store only W and B as Initial_Model. Discard TrainSet |
| Step 2 | Acquire incremental data IncSet. |
| Step 3 | Validate the generalization performance using decision function of Initial_Model with the independant TestSet
|
4. Experimental Results
4.1. Data Set Details and Feature Selection
| Symbol | Name | Count |
| DB1 | Database 1 | Class 1 (FP) = 8008 Class 2 (TP1) = 43 Class 3 (TP2) = 84 |
| VOI=16*16*16=4096 Features |

4.2. Performance and validation criteria for WP-SVM
4.3. WP-SVM Performance in Processing Chunk versus Sequential Data
| Inc_Model | INC_SEQ_MODEL | Incremental SVM | |
| Confusion Rate | 1.2 | 1.07 | 1.24 |
| CPU Time | 0.62 | 0.675 | 0.687 |
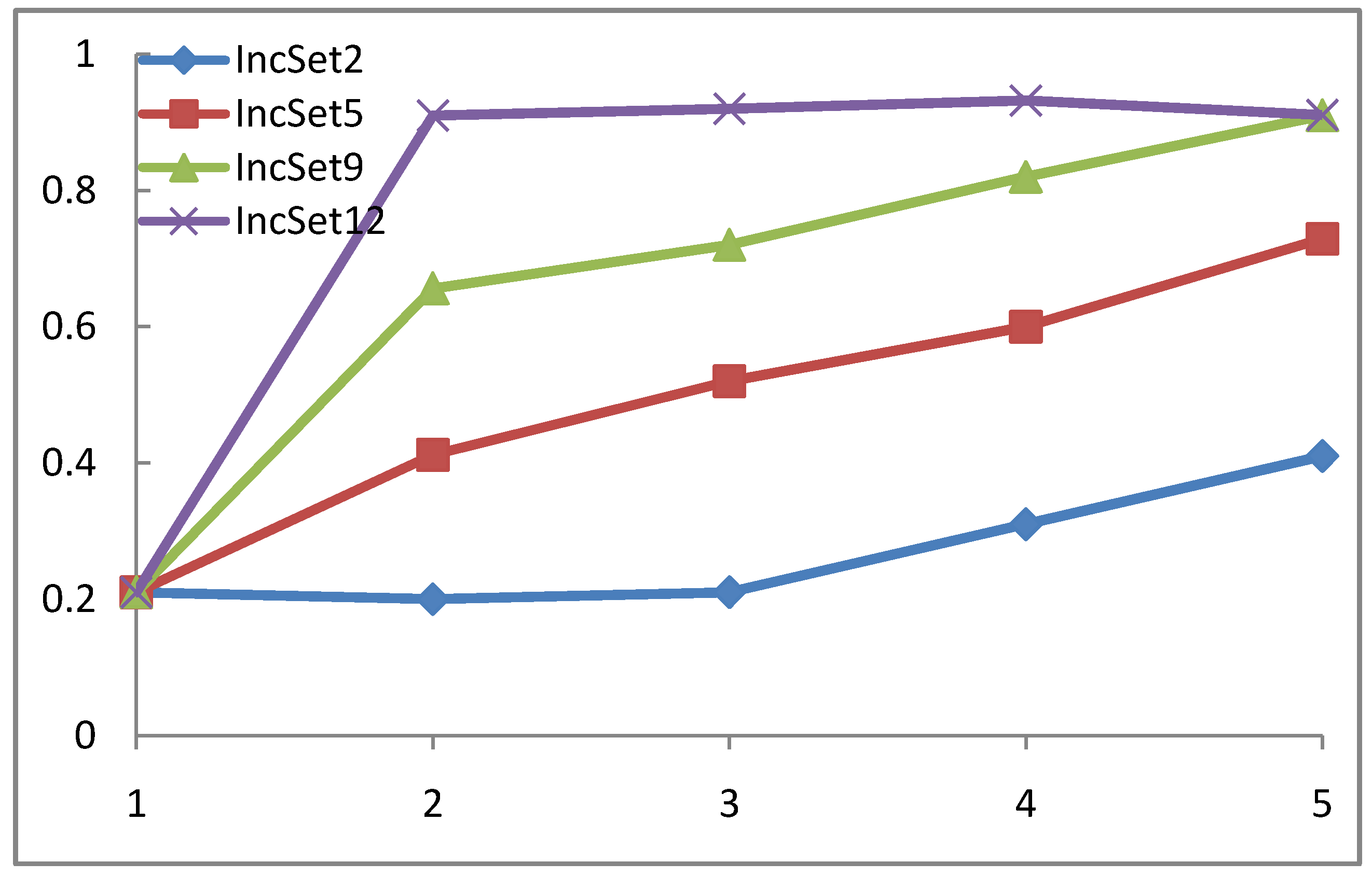
4.4. WP-SVM Specificity and Storage Requirements
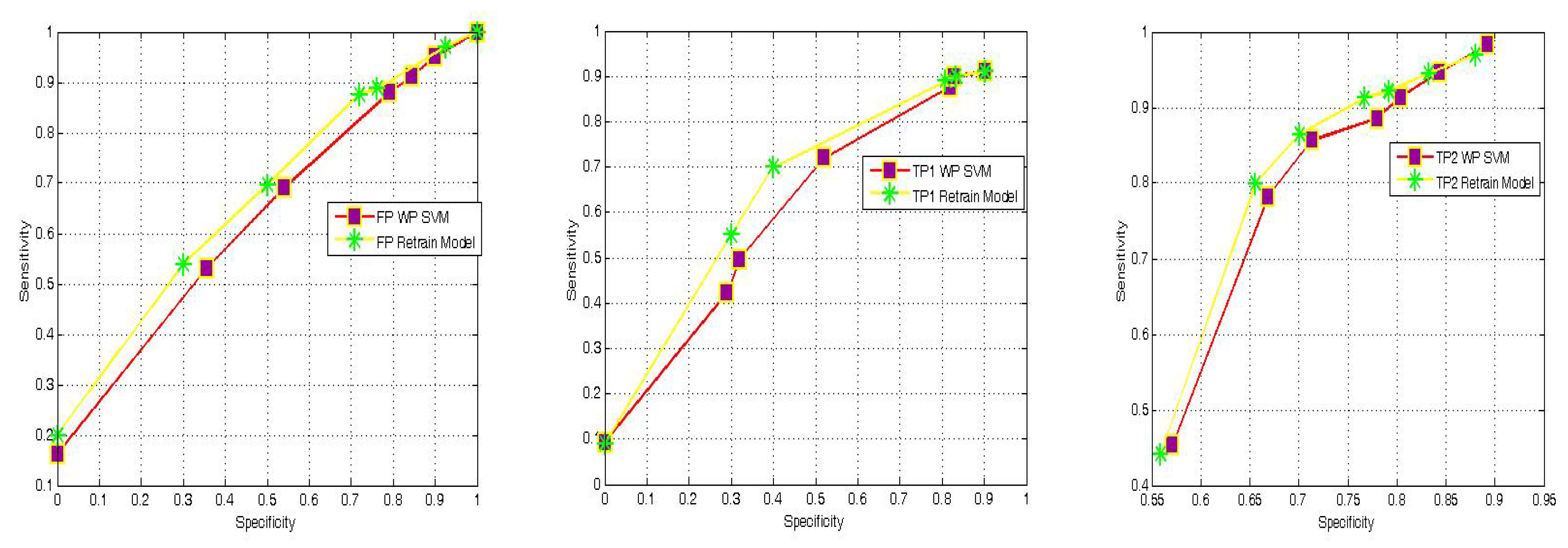
| Reference | Results | Settings |
| [33] | 95%, average of 1.5 false positive per patient | 72 patients, 144 data sets, 21 polyps >=5 mm in 14 patients |
| [34] | 90.5%, average of 2.4 false positive per patient | 121 patients, 242 data sets, 42 polyps >=5 mm in 28 patients |
| [35] | 80%, average of 8.2 false positive per patient | 18 patients, 15 polyps >= 5mm in 9 patients |
| [36] | 100%, average of 7 false positive per patient | 8 patients, 7 polyps>=10 mm in 4 patients |
| 50%, average of 7 false positive per patient | 8 patients, 11 polyps measuring between 5 – 9 mm in 3 patients | |
| [37] | 90%, average of 15.7 false positive per patient | 40 patients, 80 data sets,39 polyps>=3 mm in 20 patients |
| WP-SVM | 93.4% average of 3.2 false positive per patient | 169 patients, 28 polyps measuring between 6-9 mm and 33 polyps >10mm |
| Classifier Type | Data Structure Size |
| Retrain_Model | 1- a permanent storage of size (N+incnum)*f that is always increasing. |
| Inc_Model | 1- f by c for classifier parameters 2-temporary memory of size incnum*f for dynamic data if classifier is not updated. |
5. Conclusions
Acknowledgements
References and Notes
- Macari, M.; Bini, E.J. CT Colonography: Where Have We Been And Where Are We Going? Radiology 2005, 237, 819–833. [Google Scholar]
- Yoshida, H.; Näppi, J. Three-Dimensional Computer-Aided Diagnosis Scheme for Detection of Colonic Polyps. IEEE T. Med. Imaging 2001, 20, 1261–1274. [Google Scholar]
- Duda, R.; Hart, P.; Stork, D. Pattern Classification, 2nd Ed. ed; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction To Support Vector Machines And Other Kernel-Based Learning Methods; Cambridge University Press: New York, NY, USA, 2000; pp. 64–87. [Google Scholar]
- Basu, S.; Bilenko, M.; Banerjee, A.; Mooney, R. Probabilitic Semi-Supervised Clustering With Constraints, in Semi-Supervised Learning; Chapelle, O., Scholkopf, B., Zien, A., Eds.; The MIT Press: New York, NY, USA, 2006; p. 72. [Google Scholar]
- Zou, A.; Wu, F.X.; Ding, J.R.; Poirier, G.G. Quality Assessment Of Tandem Mass Spectra Using Support Vector Machine. BMC Bioinformatics 2009, 10 Suppl. 1. [Google Scholar]
- Isa, D.; Lee, L.H.; Kallimani, V.P.; RajKumar, R. Text Document Preprocessing with the Bayes Formula for Classification Using the Support Vector Machine. IEEE T. Knowl. Data En. 2008, 20, 1264–1272. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, Y.; Wang, Z. Prediction on Ecological Water Demand Based on Support Vector Machine. International Conference on Computer Science and Software Engineering 2008, 5, 1032–1035. [Google Scholar]
- Chen, S.H. A Support Vector Machine Approach For Detecting Gene-Gene Interaction. Genet. Epidemiol. 2007, 32, 152–167. [Google Scholar] [CrossRef] [PubMed]
- Yao, X.; Tham, L.G.; Dai, F.C. Landslide Susceptibility Mapping Based on Support Vector Machine: A Case Study On Natural Slopes of Hong Kong, China. Geomorphology 2008, 101, 572–582. [Google Scholar] [CrossRef]
- Cheng, J.; Baldi, P. Improved Residue Contact Prediction Using Support Vector Machines And A Large Feature Set. BMC Bioinformatics 2007, 8, 113. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, B. Support Vector Machines For Quality Monitoring In A Plastic Injection Molding Process. IEEE T. Syst. Man Cy. C 2005, 35, 401–410. [Google Scholar] [CrossRef]
- Valentini, G. An Experimental Bias-Variance Analysis of SVM Ensembles Based on Resampling Techniques. IEEE T. Syst. Man Cy. B 2005, 35, 1252–1271. [Google Scholar] [CrossRef]
- Waring, C.; Liu, X. Face Detection Using Spectral Histograms and SVMs. IEEE T. Syst. Man Cy. B 2005, 35, 467–476. [Google Scholar] [CrossRef]
- Chakrabartty, S.; Cauwenberghs, G. Sub-Microwatt Analog VLSI Support Vector Machine for Pattern Classification and Sequence Estimation. Adv. Neural Information Processing Systems (NIPS'2004) 2005, 17. [Google Scholar]
- Dacheng, T.; Tang, X.; Li, X.; Wu, X. Asymmetric Bagging and Random Subspace for Support Vector Machines-Based Relevance Feedback in Image Retrieval. IEEE T. Pattern Anal. 2006, 28, 1088–1099. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.X.; Krzyzak, A.; Suen, C.Y. Fast SVM Training Algorithm With Decomposition On Very Large Data Sets. IEEE T. Pattern Anal. 2005, 27, 1088–1099. [Google Scholar]
- Mao, K. Feature Subset Selection For Support Vector Machines Through Discriminative Function Pruning Analysis. IEEE T. Syst. Man Cy. B 2004, 34, 60–67. [Google Scholar] [CrossRef]
- Fung, G.; Mangasarian, O. Proximal Support Vector Machine Classifiers. In Proceedings of the 7th ACM SIGKDD, International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 26–29, 2001; pp. 77–86.
- Song, Q.; Hu, W.; Xie, W. Robust Support Vector Machine With Bullet Hole Image Classification. IEEE T. Syst. Man Cy. C 2002, 32, 440–448. [Google Scholar] [CrossRef]
- Hua, S.; Sun, Z. A Novel Method of Protein Secondary Structure Prediction With Light Segment Overlap Measure: Support Vector Machine Approach. J. Mol. Biol. 2001, 308, 397–407. [Google Scholar] [CrossRef] [PubMed]
- Matas, J.; Li, Y. P.; Kittler, J.; Jonsson, K. Support Vector Machines For Face Authentication. Image Vis. Comput. 2002, 20, 369–375. [Google Scholar]
- Chiu, D.Y.; Chena, P.J. Dynamically Exploring Internal Mechanism of Stock Market by Fuzzy-Based Support Vector Machines With High Dimension Input Space and Genetic Algorithm. IEEE Expert 2009, 36, 1240–1248. [Google Scholar] [CrossRef]
- Guoa, X.; Yuan, Z.; Tian, B. Supplier Selection Based On Hierarchical Potential Support Vector Machine. IEEE Expert 2009, 36, 6978–6985. [Google Scholar]
- Yu, L.; Chen, H.; Wang, S.; Lai, K.K. Evolving Least Squares Support Vector Machines for Stock Market Trend Mining. IEEE T. Evolut. Comput. 2009, 13, 87–102. [Google Scholar]
- Gao, Z.; Lu, G.; Gu, D. A Novel P2P Traffic Identification Scheme Based on Support Vector Machine Fuzzy Network. Knowledge Discovery and Data Mining 2009, 909–912. [Google Scholar]
- Diehl, C.; Cauwenberghs, G. SVM Incremental Learning, Adaptation and Optimization. Proceedings of the International Joint Conference on Neural Networks 2003, 4, 2685–2690. [Google Scholar]
- Vapnik, V. H. The Nature of Statistical Learning Theory, 2nd Ed. ed; Springer: New York, NY, USA, 2000. [Google Scholar]
- Hsu, C.; Lin, C. A Comparison of Methods For Multi-Class Support Vector Machines. IEEE T. Neural Networ. 2002, 13, 415–425. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; John Hopkins University Press: London, UK, 1996. [Google Scholar]
- Chen, S. C.; Lu, D.S.; Hecht, J. R. CT Colonography: Value of Scanning in Both the Supine and Prone Positions. AJR 1999, 172, 595–599. [Google Scholar] [CrossRef] [PubMed]
- Nappi, J.; Okamura, A.; Frimmel, H.; Dachman, A.H.; Yoshida, H. Region Based Supine-Prone Correspondence For The Reduction Of False-Positive Cad Polyp Candidates in CT Colonography. ACAD Radiol. 2005, 12, 695–707. [Google Scholar] [CrossRef] [PubMed]
- Nappi, J.; Yoshida, H. Feature-Guided Analysis For Reduction of False Positives in Cad of Polyps for Computed Tomographic Colonography. Med. Phys. 2003, 30, 1592–1601. [Google Scholar] [CrossRef] [PubMed]
- Kiss, G.; Cleynenbreugel, J.; Thomeer, M.; Suetens, P.; Marchal, G. Computer–aided Diagnosis in Virtual Colonography Via Combination of Surface Normal and Sphere Fitting Methods. Eur. Radiol. 2002, 12, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Paik, D.S.; Beaulieu, C.F.; Rubin, G.D.; Acar, B.; Jeffrey, R.B., Jr.; Yee, J.; Dey, J.; Napel, S. Surface Normal Overlap: a Computer Aided Detection Algorithm with Application to Colonic Polyps and Lung Nodules in Helical CT. IEEE Trans. Med. Imaging 2004, 23, 661–675. [Google Scholar] [CrossRef] [PubMed]
- Jerebko, A.K.; Summers, R.M.; Malley, J.D.; Franaszek, M.; Johnson, C.D. Computer Assisted Detection of Colonic Polyps with CT Colonography Using Neural Networks and Binary Classification Trees. Med. Phys. 2003, 30, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Masutani, Y.; Yoshida, H.; MacEneaney, P.; Dachman, A. Automated Segmentation of Colonic Walls for Computerized Detection of Polyps in CT Colonography. J. Comput. Assist. Tomogr. 2001, 25, 629–638. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Awad, M.; Motai, Y.; Näppi, J.; Yoshida, H. A Clinical Decision Support Framework for Incremental Polyps Classification in Virtual Colonoscopy. Algorithms 2010, 3, 1-20. https://doi.org/10.3390/a3010001
Awad M, Motai Y, Näppi J, Yoshida H. A Clinical Decision Support Framework for Incremental Polyps Classification in Virtual Colonoscopy. Algorithms. 2010; 3(1):1-20. https://doi.org/10.3390/a3010001
Chicago/Turabian StyleAwad, Mariette, Yuichi Motai, Janne Näppi, and Hiroyuki Yoshida. 2010. "A Clinical Decision Support Framework for Incremental Polyps Classification in Virtual Colonoscopy" Algorithms 3, no. 1: 1-20. https://doi.org/10.3390/a3010001




