CADrx for GBM Brain Tumors: Predicting Treatment Response from Changes in Diffusion-Weighted MRI
Abstract
:1. Introduction
| Authors | Technique | Type | Image sequences | # of tumors |
|---|---|---|---|---|
| Liu et al. [16] | Semi-automated fuzzy clustering | GBM | T1w, T1w+c, Flair | 5 |
| Philips et al. [4] | Fuzzy clustering | GBM | PD,T2w, T1w+c | 1 |
| Clark et al. [5] | Fuzzy clustering and knowledge-based analysis | GBM | PD,T2w, T1w+c | 7 |
| Fletcher-Heath et al. [6] | Fuzzy clustering and knowledge-based analysis | Brain tumor | PD,T2w, T1w with no contrast | 4 |
| Prastawa et al. [7] | Learn distribution of normal tissues/outlier detection as tumors | Brain tumors | T2w, T1w (with or without contrast) | 3 |
| Kaus et al. [8] | Adaptive template -moderate technique with atlas prior | LGG/MG | T1w+c, sagittal view | 20 |
| Lee et al. [11] | Conditional random field and support vector machine | Brain tumors | T1w, T1w+c, T2w | 7 |
| Ho et al. [9] | 3D level set | GBM | T1w+c, T1w, T2w | 3 |
| Vinitski et al. [10] | k-nearest neighbor | MS and MG | PD, T2w, T1w, magnetization transfer | 9 |
| Zhu & Yan et al. [12] | Hopfield neural network | Brain tumors | NA | 2 |
| Zhang et al. [13] | Support vector machine | NC | T1w, T1w+c | 9 |
| Corso et al. [15] | SWA-segmentation by weighted aggregation. | GBM | T2w, T1w, T1w+c, Flair | 20 |
| Dube et al. [17] | SWA with texture features | GBM | T1w+c | NA |
| Nie et al. [14] | Spatial accuracy-weighted hidden Markov field and EM to solve the problem of high and low resolution problem | Gliomas | High:T1w, T1w+c Low:T2w, Flair | 15 |
| Authors | # Of Patients |
|---|---|
| Chenevert et al. [20] | 2 |
| Ross et al. [2] | 2 |
| Mardor et al. [21] | 10 |
| Moffat et al. [22] | 20 |
| Hamstra et al. [23] | 34 |
2. Image Acquisition
2.1. Patient cohort
2.2. ADC map derivation
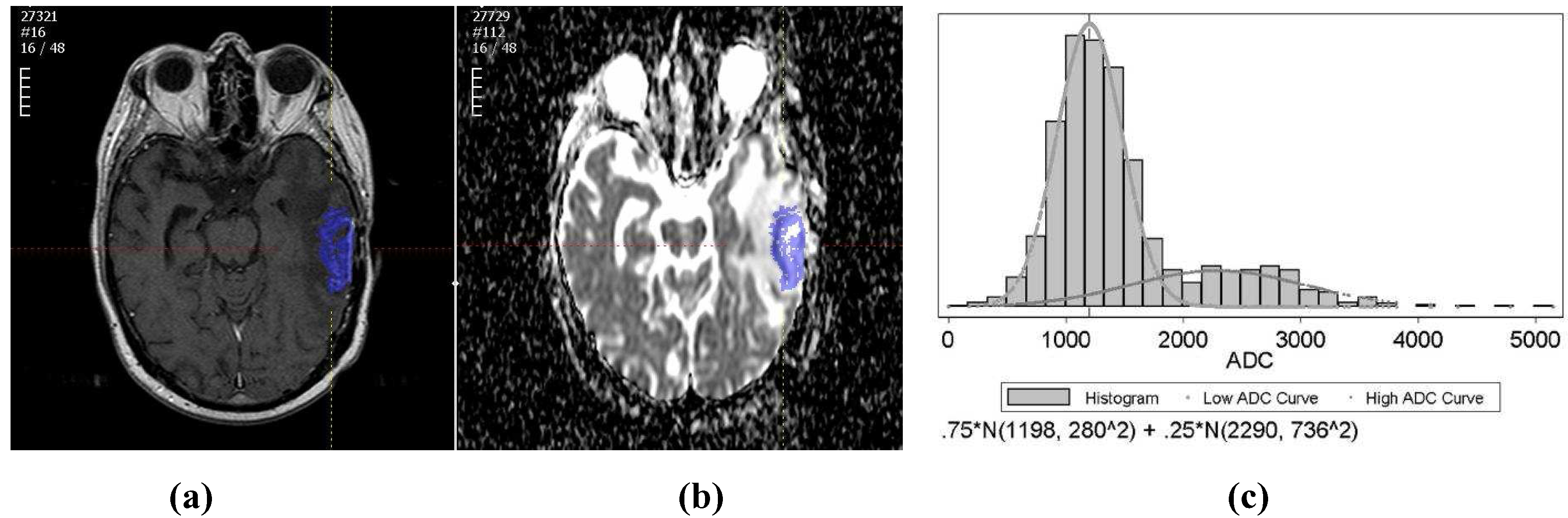
3. Semi-Automated Image Analysis on ADC Maps
3.1. Tumor segmentation on T1wCE MR images

3.2. Tumor mapping from T1wCE images to ADC maps

4. Feature Extraction and Classification
4.1. Observations
4.2. General histogram features

4.3. Features from GMM



4.4. Earth Mover’s Distance
4.5. Classification
5. Results
5.1. Segmentation Performance

| Overlap ratio | 100% | 95~100% | 90~95% | 80~90% | 60~80% | 0~60% |
| Number of patients | 10 | 7 | 3 | 2 | 5 | 4 |
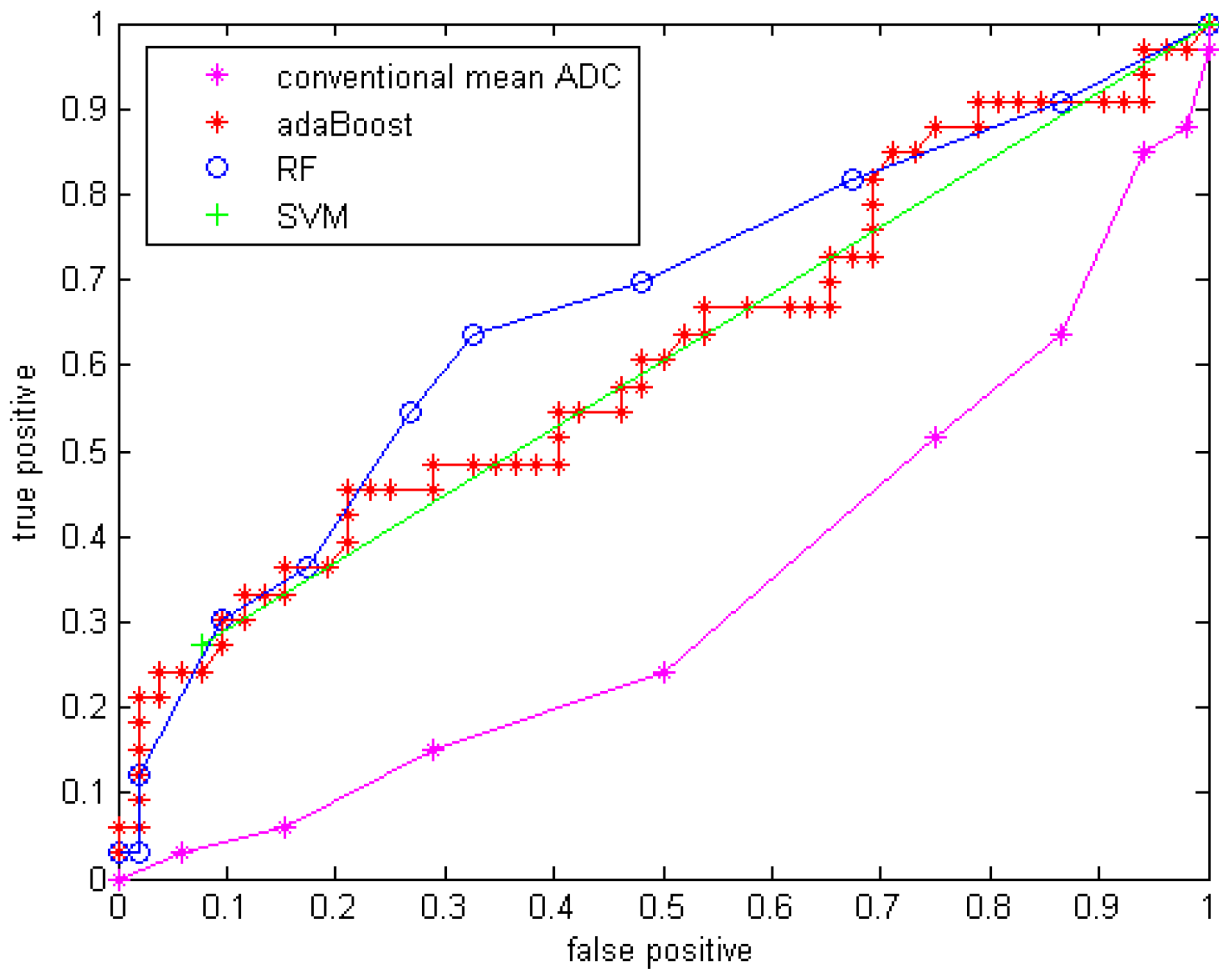
5.2. Classification Performance
| Classifier | Sensitivity | Specificity | Accuracy | Az |
|---|---|---|---|---|
| Mean ADC change | 17.95% | 60.87% | 29.4% | 0.33 |
| Classifier | Sensitivity | Specificity | Accuracy | Az |
|---|---|---|---|---|
| AdaBoost | 45.45% | 75% | 63.53%* | 0.61 |
| Random forest | 54.55% | 73% | 65.88%* | 0.66 |
| SVM | 27.27% | 92.3% | 67.06%* | 0.60 |
| Classifier | Sensitivity | Specificity | Accuracy | Az |
|---|---|---|---|---|
| AdaBoost | 39.39% | 80.77% | 64.7%* | 0.60 |
| Random forest | 51.52% | 80.77% | 69.41%* | 0.70 |
| SVM | 27.27% | 92.3% | 67.06%* | 0.60 |

6. Discussion
References
- Giger, M.L. Computer-aided diagnosis in medical imaging — A new era in image interpretation; Technical Report; World Markets Research Centre: London, UK, 2000; pp. 75–78. [Google Scholar]
- Ross, B.D.; Moffat, B.A.; Lawrence, T.S.; Mukherji, S.K.; Gebarski, S.S.; Quint, D.J.; Johnson, T.D.; Junck, L.; Robertson, P.L.; Muraszko, K.M.; Dong, Q.; Meyer, C.R.; Bland, P.H.; McConville, P.; Geng, H.; Rehemtulla, A.; Chenevert, T.L. Evaluation of cancer therapy using diffusion magnetic resonance imaging. Mol. Cancer Ther. 2003, 2, 581–587. [Google Scholar] [PubMed]
- Padhani, A.R.; Liu, G.; Mu-Koh, D.; Chenevert, T.L.; Thoeny, H.C.; Takahara, T.; Dzik-Jurasz, A.; Ross, B.D.; Cauteren, M.V.; Collins, D.; Hammoud, D.A.; Rustin, G.J.S.; Taouli, B.; Choyke, P.L. Diffusion-weighted magnetic imaging as a cancer biomarker: consensus and recommendations. Neoplasia 2009, 11, 102–125. [Google Scholar] [CrossRef] [PubMed]
- Phillips, W.E.; Velthuizen, R.P.; Phupanich, S.; Hall, L.O.; Clarke, L.P.; Silbiger, M.L. Applications of fuzzy C-means segmentation technique for tissue differentiation in MR images of a hemorrhagic glioblastoma multiforme. J. Magn. Reson. Imaging 1995, 13, 277–290. [Google Scholar] [CrossRef]
- Clark, M.C.; Hall, L.O.; Goldgof, D.B.; Velthuizen, R.; Murtagh, R.; Silbiger, M.S. Automatic tumor segmentation using knowledge-based techniques. IEEE Trans. Med. Imaging 1998, 17, 187–201. [Google Scholar] [CrossRef] [PubMed]
- Fletcher-Heath, L.M.; Hall, L.O.; Goldgof, D.B.; Murtagh, R.F. Automatic segmentation of non-enhancing brain tumors in magnetic resonance images. Artif. Intell. Med. 2001, 21, 43–63. [Google Scholar] [CrossRef]
- Prastawa, M.; Bullitt, E.; Moon, N.; Leemput, K.V.; Gerig, G. Automatic brain tumor segmentation by subject specific modification of atlas priors. Acad. Radiol. 2003, 10, 1341–1348. [Google Scholar] [CrossRef]
- Kaus, M.; Warfield, S.; Nabavi, A.; Black, P.M.; Jolesz, F.A.; Kikinis, R. Automated segmentation of mr images of brain tumors. Radiology 2001, 218, 586–591. [Google Scholar] [CrossRef] [PubMed]
- Ho, S.; Bullitt, E.; Gerig, G. Level set evolution with region competition: Automatic 3-d segmentation of brain tumors. In Proceedings of International Conference on Pattern Recognition, Quebec, Canada, August, 2002; pp. 532–535.
- Vinitski, S.; Gonzalez, C.F.; Knobler, R.; Andrews, D.; Iwanaga, T.; Curtis, M. Fast tissue segmentation based on a 4D feature map in characterization of intracranial lesions fast tissue segmentation based on a 4D feature map in characterization of intracranial lesions. J. Magn. Reson. Imaging 1999, 9, 768–776. [Google Scholar] [CrossRef]
- Lee, C.H.; Schmidt, M.; Murtha, A.; Bistritz, A.; Sander, J.; Greiner, R. Segmenting brain tumor with conditional random fields and support vector machines. In Proceedings of Workshop on Computer Vision for Biomedical Image Applications at International Conference on Computer Vision, Beijing, China, October, 2005; Vol. 3765, pp. 469–478.
- Zhu, Y.; Yan, H. Computerized tumor boundary detection using a hopfield neural network. LEEE Trans. Med. Imaging 1997, 16, 55–67. [Google Scholar]
- Zhang, J.; Ma, K.; Er, M.H.; Chong, V. Tumor segmentation from magnetic resonance imaging by learning via one-class support vector machine. In Proceedings of International Workshop on Advanced Image Technology, Singapore, January, 2004; pp. 207–211.
- Niea, J.; Xue; Liu, T.; Young, G.S.; Setayesh, K.; Guo, L.; Wong, S.T.C. Automated brain tumor segmentation using spatial accuracy-weighted hidden Markov Random Field. Comput. Med. Imaging Graph. 2009, 33, 431–441. [Google Scholar] [CrossRef] [PubMed]
- Corso, J.J.; Sharon, E.; Dube, S.; El-Saden, S.; Sinha, U.; Yuille, A. Efficient Multilevel Brain Tumor Segmentation with Integrated Bayesian Model Classification. IEEE Trans. Med. Imaging 2008, 27, 629–640. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Udupa, J.; Odhner, D.; Hackney, D.; Moonis, G. A system for brain tumor volume estimation via mr imaging and fuzzy connectedness. Comput. Med. Imaging Graph. 2005, 29, 21–34. [Google Scholar] [CrossRef] [PubMed]
- Dube, S.; Corso, J.J.; Yuille, A.; Cloughesy, T.F.; El-Saden, S.; Sinha, U. Hierarchical Segmentation of Malignant Gliomas via Integrated Contextual Filter Response. Proc. SPIE 2008, 6914, 69143Y. [Google Scholar]
- Dube, S.; Corso, J.J.; Cloughesy, T.F.; El-Saden, S.; Yuille, A.; Sinha, U. Automated MR image processing and analysis of malignant brain tumors: enabling technology for data mining. In Data Mining Systems Analysis and Optimization in Biomedicine; American Institute of Physics Proceedings: New York, NY, USA, 2007; Vol. 953, pp. 64–84. [Google Scholar]
- US Food and Drug Administration. Guidance for industry: clinical trial endpoints for the approval of cancer drugs and biologics. Federal Register 2007, 72, No. 94. [Google Scholar]
- Chenevert, T.L.; Stegman, L.D.; Taylor, J.M.; Robertson, P.L.; Greenberg, H.S.; Rehemtulla, A.; Ross, B.D. Diffusion magnetic resonance imaging: an early surrogate marker of therapeutic efficacy in brain tumors. J. Natl. Cancer Inst. 2000, 92, 2029–2036. [Google Scholar] [CrossRef] [PubMed]
- Mardor, Y.; Pfeffer, R.; Spiegelmann, R.; Roth, Y.; Maier, S.E.; Nissim, O.; Berger, R.; Glicksman, A.; Baram, J.; Orenstein, A.; Cohen, J.S.; Tichler, T. Early detection of response to radiation therapy in patients with brain malignancies using conventional and high b-value diffusion-weighted magnetic resonance imaging. J. Clin. Oncol. 2003, 21, 1094–1100. [Google Scholar] [CrossRef] [PubMed]
- Moffat, B.A.; Chenevert, T.L.; Meyer, C.R.; Mckeever, P.E.; Hall, D.E.; Hoff, B.A.; Johnson, T.D.; Rehemtulla, A.; Ross, B.D. The functional diffusion map: a noninvasive MRI biomarker for early stratification of clinical brain tumor response. PANS 2005, 102, 5524–5529. [Google Scholar] [CrossRef] [PubMed]
- Hamstra, D.A.; Chenevert, T.L.; Moffat, B.A.; Johnson, T.D.; Meyer, C.R.; Mukherji, S.K.; Quint, D.J.; Gebarski, S.S.; Fan, X.; Tsien, C.I.; Lawrence, T.S.; Junck, L.; Rehemtulla, A.; Ross, B.D. Evaluation of the functional diffusion map as an early biomarker of time-to-progression and overall survival in high-grade glioma. PNAS 2005, 102, 16759–16764. [Google Scholar] [CrossRef] [PubMed]
- Huo, J.; Kim, H.J.; Pope, W.B.; Okada, K.; Alger, J.R.; Wang, Y.; Goldin, J.G.; Brown, W.S. Histogram-based classification with Gaussian mixture modeling for GBM tumor treatment response using ADC map. Proc. SPIE 2009, 7260, 72601Y. [Google Scholar]
- Pope, W.B.; Kim, H.J.; Huo, J.; Alger, J.R.; Brown, W.S.; Gjertson, D.; Sai, V.; Young, J.R.; Tekchandani, L.; Cloughesy, T.; Mischel, P.S.; Lai, A.; Nghiemphu, P.; Rahmanuddin, S.; Goldin, J.G. Recurrent glioblastoma multiforme: ADC histogram analysis predicts response to bevacizumab treatment. Radiology 2009, 252, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Sajda, P. Machine learning for detection and diagnosis of disease. Annu. Rev. Biomed. Eng. 2006, 8, 537–65. [Google Scholar] [CrossRef] [PubMed]
- Freund, Y.; Schapire, R.E. A short introduction to boosting. J. Jpn. Soc. For. Artif. Intell. 1999, 14, 771–780. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.H. Pattern classification; Wiley Interscience: Malden, MA, USA, 2000. [Google Scholar]
- Ho, T.K. Random decision forest. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, Canada, August, 1995; pp. 278–282.
- Breiman, L. Random decision forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Vapnik, V. Estimation of Dependencies Based on Empirical Data; Nauka: Moscow, Russia, 1979. [Google Scholar]
- Bishop, C. Neural Networks for Pattern Recognition; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- http://en.wikipedia.org/wiki/Support_vector_machine (accessed November 10, 2009).
- Burbidge, R.; Trotter, M.; Buxton, B.; Holden, S. Drug design by machine learning: support vector machines for pharmaceutical data analysis. Comput. And. Chem 2001, 26, 5–14. [Google Scholar] [CrossRef]
- Huo, J.; Alger, J.R.; Kim, H.J.; Pope, W.B.; Okada, K.; Goldin, J.G.; Brown, M.S. Between-scanner variation in normal white matter ADC in the setting of a multi-center clinical trial. Ismrm 2009, (in press). [Google Scholar]
- Otsu , N. A threshold selection method from gray level histograms. IEEE Trans. Syst. Man. Cybern. 1979, 9, 62–66. [Google Scholar]
- Adams, R.; Bischof, L. Seeded region growing. IEEE Trans. Syst. Man. Cybern. Int. 1994, 16, 641–647. [Google Scholar] [CrossRef]
- Rubner, Y.; Tomasi, C.; Guibas, L.J. A metric for distributions with applications to image databases. In Proceedings of ICCV, Bombay, India, January, 1998; pp. 59–66.
- Ling, H.; Okada, K. An efficient Earth mover's distance algorithm for robust histogram comparison. IEEE Trans. Patt. Anal. Mach. Intell. 2007, 29, 840–853. [Google Scholar] [CrossRef] [PubMed]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: San Francisco, CA, USA, 2005. [Google Scholar]
- Yamasaki, F.; Sugiyama, K.; Ohtaki, M.; Takeshima, Y.; Abed, N.; Akiyamad, Y.; Takabad, J.; Amatyac, V.J.; Saitoa, T.; Kajiwaraa, Y.; Hanayaa, R.; Kurisua, K. Glioblastoma treated with postoperative radio-chemotherapy: Prognostic value of apparent diffusion coefficient at MR imaging. Eur.J. Aiol. 2009, (in press). [Google Scholar] [CrossRef] [PubMed]
- Marzban, C. The ROC curve and the area under it as a performance measure. Weather Forecast. 2004, 19, 1106–1114. [Google Scholar] [CrossRef]
- Huhn, S.L.; Mohapatra, G.; Bollen, A.; Lamborn, K.; Prados, M.D.; Feuerstein, B.G. Chromosomal abnormalities in glioblastoma multiforme by comparative genomic hybridization: correlation with radiation treatment outcome. Clin. Cancer Res. 1999, 5, 1435–1443. [Google Scholar] [PubMed]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Huo, J.; Okada, K.; Kim, H.J.; Pope, W.B.; Goldin, J.G.; Alger, J.R.; Brown, M.S. CADrx for GBM Brain Tumors: Predicting Treatment Response from Changes in Diffusion-Weighted MRI. Algorithms 2009, 2, 1350-1367. https://doi.org/10.3390/a2041350
Huo J, Okada K, Kim HJ, Pope WB, Goldin JG, Alger JR, Brown MS. CADrx for GBM Brain Tumors: Predicting Treatment Response from Changes in Diffusion-Weighted MRI. Algorithms. 2009; 2(4):1350-1367. https://doi.org/10.3390/a2041350
Chicago/Turabian StyleHuo, Jing, Kazunori Okada, Hyun J. Kim, Whitney B. Pope, Jonathan G. Goldin, Jeffrey R. Alger, and Matthew S. Brown. 2009. "CADrx for GBM Brain Tumors: Predicting Treatment Response from Changes in Diffusion-Weighted MRI" Algorithms 2, no. 4: 1350-1367. https://doi.org/10.3390/a2041350
APA StyleHuo, J., Okada, K., Kim, H. J., Pope, W. B., Goldin, J. G., Alger, J. R., & Brown, M. S. (2009). CADrx for GBM Brain Tumors: Predicting Treatment Response from Changes in Diffusion-Weighted MRI. Algorithms, 2(4), 1350-1367. https://doi.org/10.3390/a2041350




