Incentive Compatible and Globally Efficient Position Based Routing for Selfish Reverse Multicast in Wireless Sensor Networks

Abstract

We consider the problem of all-to-one selfish routing in the absence of a payment scheme in wireless sensor networks, where a natural model for cost is the power required to forward, referring to the resulting game as a Locally Minimum Cost Forwarding (LMCF). Our objective is to characterize equilibria and their global costs in terms of stretch and diameter, in particular finding incentive compatible algorithms that are also close to globally optimal. We find that although social costs for equilibria of LMCF exhibit arbitrarily bad worst-case bounds and computational infeasibility of reaching optimal equilibria, there exist greedy and local incentive compatible heuristics achieving near-optimal global costs.

1. Introduction

Incentive-compatible topology control protocols play a central role in selfish wireless networking. These protocols determine which links are to be used for forwarding data packets from sources to destinations. Non-selfish topology control involves selecting a subset of possible communication edges such that the resulting induced subgraph satisfies a number of desirable properties, such as being a single component, having small maximum degree, and preserving shortest paths within a small factor (see [1,2] for an overview of topology control results). Incentive-compatible topology control has only recently received attention from the wireless network research community, with the two traditional game-theoretic approaches being to characterize Nash equilibria [3,4,5] and to design VCG-based mechanisms for ad-hoc networks [3,4,6,7,8,9].

A wireless sensor node is capable of monitoring the environment or sensing an occurrence of a particular event. A collection of such nodes is called a wireless sensor network [10]. Sensor nodes are often deployed in an ad-hoc manner and they send the sensed information to a base-station or a cluster head which acts as a data collection point. As often sensor nodes are deployed on a far off location and are battery-powered, they are highly energy-constrained. Thus energy efficiency is an important parameter in evaluating the performance of any protocol designed for sensor networks. Reverse multicast traffic is more common in a wireless sensor network as multiple nodes send the sensed information to a single data collection point and due to the energy constraint, a sensor node will often choose to send the data in a multihop fashion so as to avoid transmission over a long distance [11]. Thus a sensor network can be modelled as a collection of selfish nodes with reverse multicast traffic.

We study selfish topology control where all participating nodes need to have a path to a single destination. This might be a central processing node in a sensor network, the access point (AP) that allows the nodes to connect to the Internet, or a base station in a hybrid cell phone network. Our cost and utility model is as follows.

Individual nodes care only about minimizing their own power consumption given that they must forward what has been given to them in this reverse-multicast scenario, and adopt their strategies accordingly, whereas the global objective is to minimize the total energy used. In other words, the social goal is to minimize the expected amount of power consumed by transmitting a single message from source to destination. Assuming fixed routing tables (pure strategy) this will also be the cost-per-message in the long term. We assume that messages are generated at random sources. For simplicity we will assume uniformly at random, but all our results will hold for any probability distribution, which guarantees that each node has a non-zero probability of being a message source. Specifically, define:

• $q_v=$ load generated at node v
• $Q_v=$ total outgoing load at v from all data passing through v
• $c_v=$ cost per-bit of forwarding from v to v’s chosen neighbor
• $PAT{H}_v=$ sum of $c_i$ along the path from v to the destination

Player v wants to minimize $Q_v{c}_v$, but has no control over $Q_v$ and can only minimize $c_v$. The global objective is to minimize the total induced load times the forwarding cost, ${\sum }_v{Q}_v{c}_v={\sum }_v{q}_{v}PAT{H}_v$. Given an aggregate load ${\sum }_v{q}_v$, the worst-case distribution would be concentrated along the most costly path, with exactly one nonzero $q_v$. The global objective is therefore to keep that longest directed path short.

Since a node’s interest is limited to having a path to the destination, and it does not care how long that path is, so long as its individual or local forwarding cost is minimized, we refer to this setting as a Locally Minimum Cost Forwarding Game (LMCF). Of course, from a system-wide perspective, short paths are desirable, as explained above so that our social optimum objectives are the following: (i) minimize the maximum stretch factor1 in the resulting topology with respect to true shortest path distances, or (ii) minimize the cost of the longest path in the resulting topology. Our aim is to find and to characterize Nash equilibria that optimize the social objective. The ratio of the objective value achieved by the best Nash equilibrium and the (non-selfish) value of the social optimum is called the price of stability, whereas that ratio for the worst Nash equilibrium is called the price of anarchy[12,13,14].

The prices of stability and anarchy have been extensively investigated in other network settings under other objectives, particularly for congestion-based games and fair-allocation games (for example [12,13,14,15]). The problem of finding good Nash equilibria in the context of topology-control for ad-hoc networks has also been investigated [3,4,6,7,8,9]. We note that the LMCF game differs from previously considered games in its objectives, both individually and socially. Our work is related to the non-game-theoretic results of [16] that construct spanning structures balancing edge costs, i.e., Minimum Spanning Trees(MSTs), and path costs, i.e., Shortest Path Trees (SPTs). However the game-theoretic aspect of this work, in particular the locality of individual preferences, makes a crucial difference as the algorithms of [16] do not directly relate to Nash equilibria for LMCF.

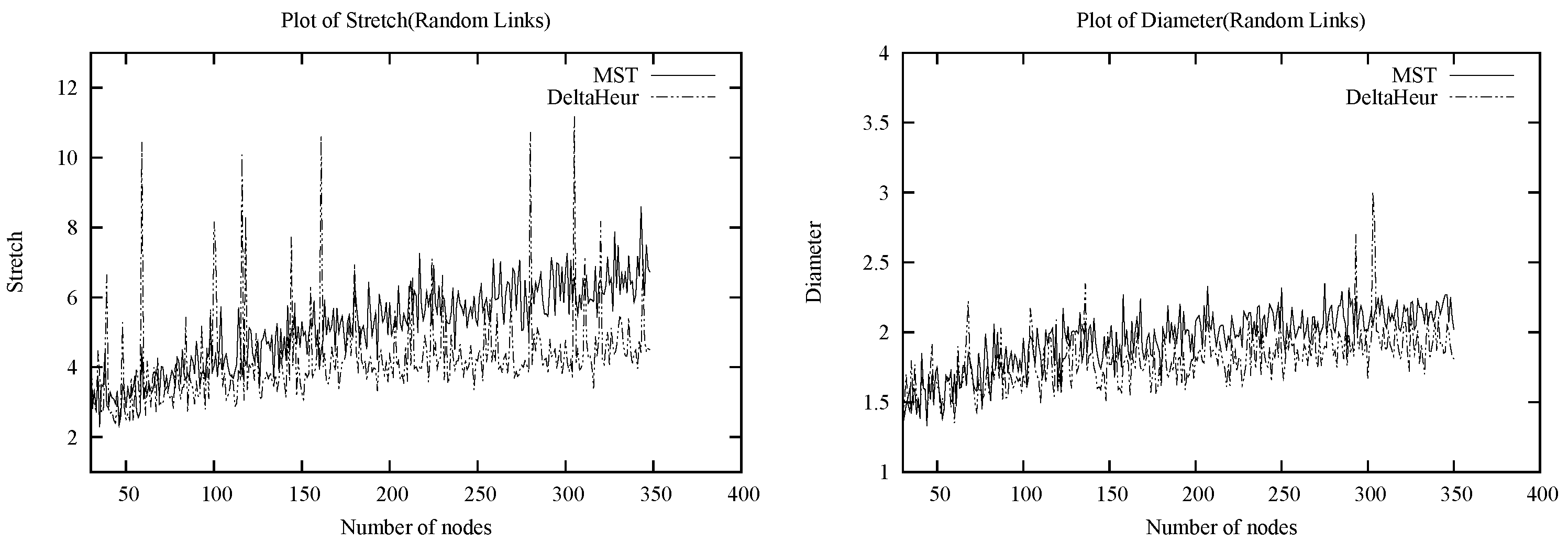
We prove that Nash equilibria always exist for LMCF, and that in fact a minimum spanning tree is always a Nash, albeit rarely a socially optimal one. We give examples showing that both the prices of anarchy and stability can be linear with respect to the stretch-based social cost objective and $\omega \left(n^c\right)$ for any $c<1$ for the maximum-distance-based cost function. We show NP-hardness and inapproximability results for the problem of finding the socially optimal Nash equilibrium. We observe that there is hope for positive average results in various random graph models, such as Euclidean power cost functions, which is a common model for communication costs in ad-hoc networks (Section 3.), in view of previous work indicating that many nodes are involved in mutual nearest neighbor pairs in the relevant random models [17,18]. We propose a greedy heuristic, DeltaHeur, that we test in simulation, and find that the quality of the Nash equilibria found appear independent of the instance size (this is not true for a straight-forward MST heuristic). Our experiments suggest a plausible $\omega \left(1\right)$ average price of anarchy and $\Theta \left(1\right)$ average price of stability, and supports the use of our heuristic as a topology-control protocol for selfish all-to-one routing in ad-hoc networks.

However, as DeltaHeur requires complete information of node locations, which may be unrealistic in some wireless scenarios (in particular in the presence of mobility), in this work we consider a new locally computable heuristic “recommendation algorithm”, which we refer to as LocalHeur for convenience. LocalHeur lies within the class of location based routing methods [19,20,21,22] with particular similarity to the Nearest Forward Progress (NFP) algorithm [22] though from the perspective of game-theoretic reverse multicast routing.

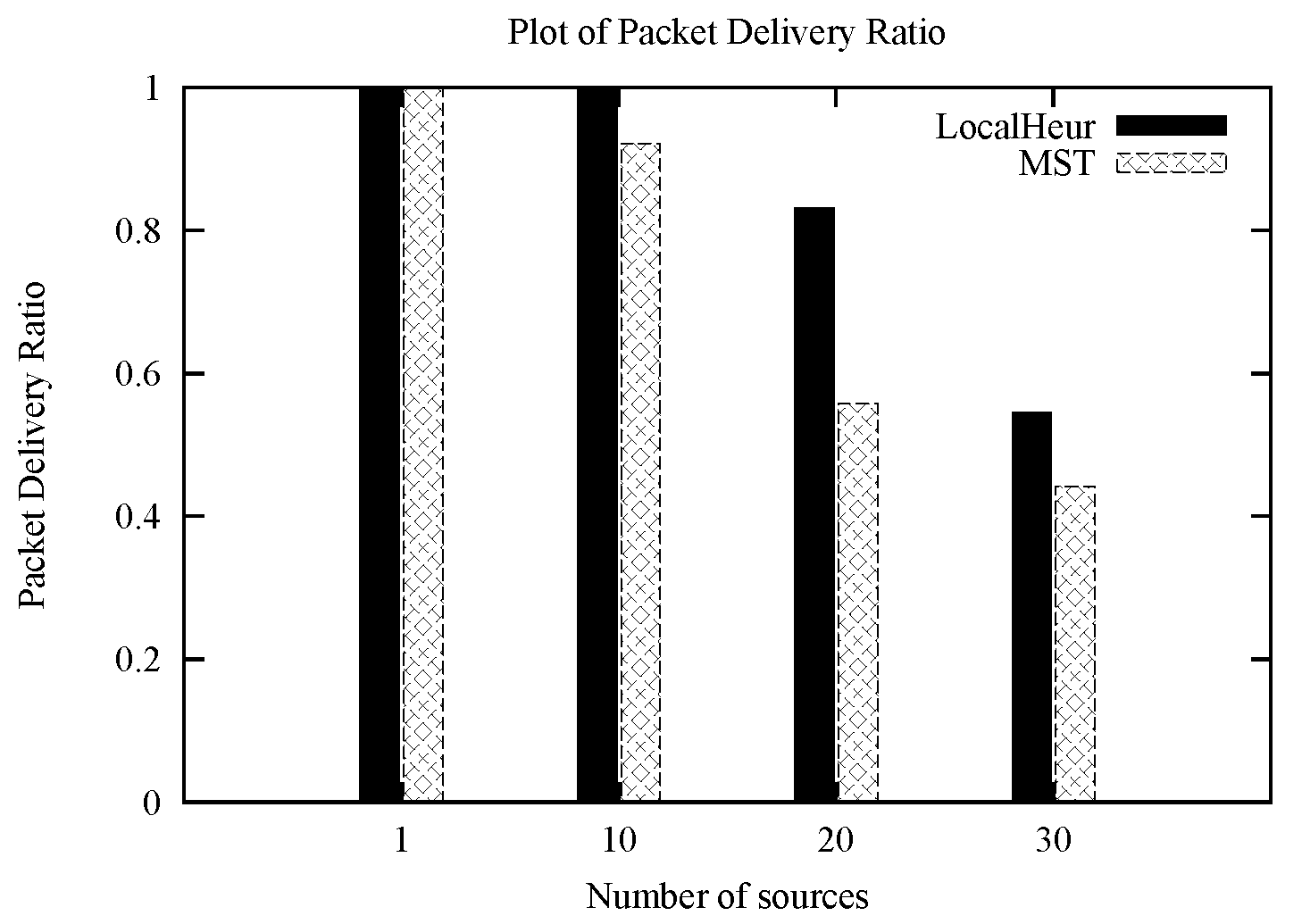
We find that LocalHeur actually outperforms DeltaHeur in terms of global optimality in random Euclidean power instances that model wireless networks, though at the expense of loosening the Nash equilibrium condition. Nonetheless, we find that the relaxation of the Nash condition is strongly bounded in multiple ways, with high probability: The vast majority of players are provably playing a best response, while simulation results demonstrate that the average deviation ratio from a best response is within a decimal point of 1. Furthermore, the player deviating most from his best response is provably still within $O(logn)$2 of the cost of his best response, while simulation results support a much smaller maximum deviation from the best response. Finally, under the assumption of local information, it may be more costly for a player to check whether forwarding to a closer player who is behind him would create a cycle than it would be to simply forward to the closest player ahead of him, thus making LocalHeur configurations candidates for equilibria under incomplete information.

2. Model and Background

Definition 2..1 (LMCF Game).

Given a connected, undirected, edge-weighted graph $G=(V,E)$ (with $V=(1,2,\dots ,n)$, weight function $w:E\to R$3 and designated destination node t, $LMCF(G,w,t)$ consists of the following: Players are nodes $v\in V\backslash \left\{t\right\}$, each player v with strategy set $N\left(v\right)=\{$ one-hop neighbors of $v\}$. Given a pure strategy-tuple $S=(s_1,s_2,\dots ,s_{n-1})$ refer to $G_S$, the graph induced by S, as the directed graph formed by the set of directed edges of the form $(u,s_u)$. Finally, the cost $c_S\left(v\right)$ of strategy-tuple S to player v is $c_S\left(v\right)=w(v,s_v)$ if $G_S$ contains a path from v to t and ∞ otherwise.

For any node v and any strategy-tuple S, at most one path may exist from v to t in $G_S$. Denote by $dis{t}_S\left(v\right)$ the total weight of that path if such exists and ∞ otherwise. Clearly, this distance is minimum in a shortest path tree (SPT) rooted at t. Denote the shortest path distance by $dist\left(v\right)$. Now, we present two alternative formulations for the Social Cost of a strategy-tuple S for the LMCF Game. The first is based on the stretch factor of node-destination paths in $G_S$, the second based directly on the maximum distance of any node to the destination in $G_S$.

$$S{C}_{stretch}\left(S\right)=ma{x}_{v\in V\backslash \left\{t\right\}}\frac{dis{t}_S\left(v\right)}{dist\left(v\right)}$$

(1)

$$S{C}_{md}\left(S\right)=ma{x}_{v\in V\backslash \left\{t\right\}}dis{t}_S\left(v\right)$$

(2)

As we are concerned with the relative social optimality of a strategy-tuple, in a manner consistent with the literature we denote the price of a strategy tuple S to be the ratio of the social cost of S over the social cost of the globally optimal strategy, which for the LMCF game is the SPT. In an incentive compatible topology control problem, the goal is to find a “recommendation algorithm” for selfish nodes to forward such that the nodes are in a Nash equilibrium or approximate Nash equilibrium configuration that also performs well socially. A Nash equilibrium is a fixed-point best-response strategy profile: a strategy-tuple from which no agent has a unilateral incentive to deviate, i.e., any such deviation would not improve the cost to the agent. The price of anarchy, $PoA$, with respect to a social cost function on a given instance is the maximum (worst) ratio of the social cost of a Nash equilibrium to the best possible social cost (that for the SPT). The price of stability, $PoS$, is the minimum (best) such ratio. We investigate the price of anarchy and price of stability, as well as their computability, for Nash equilibria of the Locally Minimum Cost Forwarding (LMCF) Game. We study these quantities in both the worst-case and average-case. Since by definition $S{C}_{stretch}\left(S\right)=1$ for the SPT, $PoA$ and $PoS$ over $S{C}_{stretch}$ are precisely the maximum and minimum social cost over all Nash equilibria.

We will focus on the prices of anarchy and stability on Euclidean power graphs and random link graphs. A Euclidean p-power graph in dimension d is a complete graph consisting of nodes embedded into d-dimensional Euclidean space with edge weights defined by $w(i,j)=d^p(i,j)$, the $p^{th}$ power of the distance.4 Random Euclidean power graphs are induced by placing each node uniformly at random into the d-dimensional unit-cube. These are especially relevant models of wireless ad-hoc sensor networks due to the randomness of placement and the modeling of energy, when $p=d=2$.

Given that our reverse multicast problem is motivated by incentive compatible topology control for wireless sensor networks, we consider “recommendation algorithms” to achieve good Nash equilibria, or good near-equilibria, for random Euclidean power graphs. We shall first discuss the Minimum Spanning Tree, which we shall show to be an equilibrium configuration for the LMCF game, though with poor global performance. Then, after a series of negative worst-case results, we look to heuristics which perform well in expectation. The first heuristic we consider, DeltaHeur, guarantees Nash equilibrium and exhibits good global performance. However, as information locality constraints are quite reasonable to expect in a wireless sensor network5, we then look to extending DeltaHeur into a local algorithm, proposing the conveniently named LocalHeur. Local algorithms are algorithms with running time and informational requirements are independent of n. While the locality of the extension of DeltaHeur into LocalHeur shall demonstrate similarly good global performance, this is at the expense of loosening the Nash equilibrium condition. However, nonetheless we shall demonstrate that LocalHeur is close to equilibrium in multiple ways, both theoretically and experimentally.

Intuitively, the location-based protocol Nearest Forward Progress (NFP) of [22], where each node forwards to its nearest neighbor that minimizes the distance to the destination, is closest in spirit to DeltaHeur with the additional advantage of locality, so LocalHeur bears fundamental resemblance to NFP. Location-aware protocols [19] or position based protocols [20] are protocols proposed for mobile ad-hoc networks and sensor networks where location information helps a node in adjusting its transmit power according to the position of its neighbors. In this way, a node can optimize its energy utilization. But, the cost incurred in this process is the overhead involved in propagating the location information. This becomes even more cumbersome when the nodes are mobile. Thus the gain in the expenditure of energy should better this overhead involved which is one of the criteria on which this class of protocols are evaluated. [20,21] presents a good survey of such protocols. Out of the various location based protocols the greedy forwarding technique matches our assumption of a network with selfish nodes, as all nodes forward to one of its in range neighbor and does not worry about the delivery of the packets [21]. This is similar to our model with an additional constraint that the nodes forward to the nearest of the in-range neighbor. LocalHeur may be considered an application of NFP to a reverse multi-cast scenario. By forwarding to the the nearest neighbor that is in the direction of the destination there is not much deviation from the best-response and also the global performance tends towards optimum. [22] studies NFP and shows better local throughput and normalized average progress (hops per slot) results when compared with MFR (Most Forward with Fixed Radius) and MVR (Most Forward with Variable Radius).

3. Preliminary Results

3.1. Examples and Lower Bounds

We first present examples of Nash equilibria that provide some intuition on the nature of the problem, as well as lower bounds on $PoA$ and $PoS$.

Example 3..1 (MST).

Given a graph G and destination t, construct a minimum spanning tree T of G and direct its edges towards t. Note that this forms a Nash equilibrium: If a node u has an incentive to switch from its current forwarding choice v to a new node $v^{\prime }$, forming $T^{\prime }$, then doing so does not introduce a cycle and $w(u,v^{\prime })<w(u,v)$. But then $T^{\prime }$ is also a spanning tree, with total cost less than that of T, contradicting that T is a MST.

Now consider the MST for the Euclidean “Horseshoe” graph $G_H$ of Figure 1 given in [16]. This example immediately gives a $\Omega \left(n\right)$ lower bound on $PoA$ with respect to $S{C}_{stretch}$, since both a clockwise and a counterclockwise path to t are Nash equilibria. Further, it can inductively be checked that the best Nash equilibria for this case with respect to both $S{C}_{stretch}$ and $S{C}_{md}$ is that of Figure 1, thus also giving a $\Omega \left(n\right)$ lower bound on $PoS$ for $S{C}_{stretch}$. We note the contrast with [16]’s approximate solution for balancing MST cost and SPT cost which yields a constant bound for $G_H$ (by actually connecting the dots as a horseshoe) but is not a Nash equilibrium. Thus, we have:

Example 3..2 (Horseshoe).

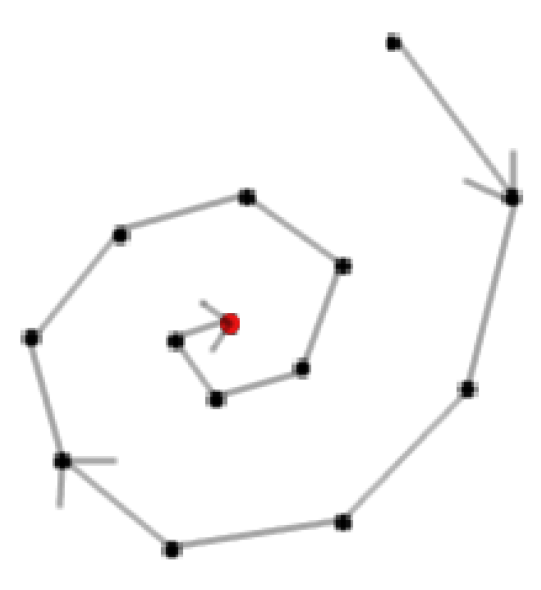
The Euclidean “Horseshoe” graph given in [16] yields linear lower bounds on both $PoA$ and $PoS$ under $S{C}_{stretch}$, the optimal Nash being the counter-intuitive one of Figure 1 (unlike [16]’s constant stretch approximation for a non-game-theoretic scenario).

Now consider a Euclidean Spiral graph $G_{spiral}$ with t at center such as the nodes of Figure 2. The spiral is formed such that each new node has a distance from the previous node that is greater than the previous node’s distance to its previous node, and also shorter than the new node’s distance to the closest neighbor in the inner layer of the spiral. It can be checked that the unique Nash in such a class of instances is that of directing the Spiral inward towards t as shown in the Figure. Moreover, precise parameters may be set such that the number of spiral layers is proportional to $\Omega \left(n^c\right)$ for any constant $0<c<1$, leading to the following (see [23] for details):

Example 3..3 (Spiral).

The Euclidean “Spiral” graph of Figure 2 yields a $\omega \left(n^c\right)$ (for any constant $c<1$) lower bound on $PoA$ and $PoS$ under $S{C}_{md}$.

Figure 1. Euclidean Horseshoe and its Optimal Nash.

Figure 1. Euclidean Horseshoe and its Optimal Nash.

Figure 2. Euclidean Spiral.

Figure 2. Euclidean Spiral.

3.2. Observations on the Structure of Nash Equilibria

It is not a coincidence that the Nash equilibria examples thus far have been trees. We briefly return to consideration of general Nash, including the mixed case:

Remark 3..4.

In any connected graph G, Nash equilibria always exist (guaranteed via MST), and all Nash equilibria form an acyclic spanning graph with destination t as sink. In particular every pure Nash equilibria forms a spanning tree directed towards t.

Note that mixed Nash can be viewed as flows in G and that any non-zero flow through a cycle will have infinite cost. Now, given any Nash-induced sub-graph $G_S$, denote as $T_t$ the maximal acyclic sub-graph in $G_S$ that contains t. Due to connectedness, if there are any cycles in $G_S$, then there is always some node on some cycle that has a neighbor in $T_t$, thus giving finite rather than infinite flow weighted cost (an infinite flow weighted cost is still infinite), and an incentive to switch. So, there can be no cycles and $T_t$ spans G. And, due to the single out-degree nature of pure Nash, if $G_S$ is a pure Nash then $T_t$ is a spanning tree.

It is without loss of generality to consider pure Nash equilibria with respect to maxima and minima of our social cost functions, for the following reason. For any branching out (i.e., a node forwarding in a mixed manner to more than one neighbor) that occurs in a mixed Nash, the multiple options must have identical cost to the branching node (and given that, the branching node may distribute the probability flow in any manner). Any mixed flow achieving some relevant minima or maxima (with respect to $PoS$ or $PoA$) can therefore be converted into a directed tree achieving the same such minima or maxima by continuously shifting the flow to a path that induces the extreme value. Thus, from now on we discuss Nash trees without loss of generality.

We may further state the following regarding the structure of Nash trees:

Remark 3..5.

In a weighted graph G, if i is j’s unique nearest neighbor and j is also i’s unique nearest neighbor, then we refer to i and j as mutual nearest neighbors. Edges between mutual nearest neighbors (excluding t) are always used in some direction, in any Nash tree.

To see this, consider a mutual nearest neighbor pair $i,j$ and Nash tree T such that edge $(i,j)$ is not used in either direction. Since the weight of this edge is minimal amongst all neighbors for both i and j, the only way it cannot be present in a Nash equilibrium is if it lies on a cycle. But if directing from i to j would create a cycle, then there must already be a path from j to i in T, and likewise for the opposite direction. So there must already be a cycle in T, namely from i to j and back to i, contradicting that T is a Nash tree. Thus, $(i,j)$ must be used in some direction in every Nash tree.

As a corollary, we may also relate this to generating Nash equilibria. Due to the uniqueness condition in the above definition, any set of mutual nearest neighbor edges must be an independent set. Moreover, noting that in a complete graph we may always complete a spanning tree after fixing any independent set of edges as a subgraph, we have the following:

Corollary 3..6.

In any complete graph, for every directionality of the set of mutual nearest neighbor edges (excluding t) there exists a corresponding Nash equilibrium.

Euclidean graphs are especially relevant cases for analysis of the LMCF Game. While we have already noted that a restriction to Euclidean graphs is rich enough to generate arbitrarily bad examples, this class also has some further structural properties:

Remark 3..7.

For any Nash tree in any 2-dimensional Euclidean power graph of any power6, the incoming node degree is at most 6.

The reason is as follows: Consider a set of seven nodes incoming to a vertex v in some Nash tree T. By a regular hexagonal decomposition into 6 parts, it may be seen that at least one of these incoming neighbors u must be strictly closer to another incoming neighbor w than to v. Moreover, if by switching u’s forwarding choice from v to w a cycle was created in the graph, then w and hence w’s own forwarding choice v must have already had a path to u in T. But since u forwards to v in T, there must already be a cycle through u in T, contradicting that T is a Nash tree.

Of course, the smallest edge in any graph must consist of a mutual nearest neighbor pair. Exactly how many we may expect? To address this question, we may say something in the case of random instances based on results of [17,18] on random Euclidean graphs of any dimension and on results of [18] on random link graphs.

Remark 3..8.

For random Euclidean power instances of any dimension and any power, and for random link graphs, at least half the nodes are expected to be involved in some mutual nearest neighbor relation.

Recall that the “bad” Euclidean examples, Figure 1 and Figure 2, each had at most $O\left(1\right)$ nodes involved in a mutual nearest neighbor and a sparse set of possible Nash equilibria. As such situations are highly unlikely, it is reasonable to hope that greater optimism is warranted for random instances. We discuss this further in Section 5. and beyond.

4. Hardness of Optimal Nash Equilibria

We now provide hardness results for computing and approximating optimal Nash equilibria.

Theorem 4..1.

The optimal Nash equilibrium for the LMCF Game is NP-Hard to approximate to any constant factor for both the $S{C}_{md}$ and $S{C}_{stretch}$ social cost functions.

Proof.

We start by showing that finding the optimal Nash equilibrium for $S{C}_{md}$ is NP-hard. Following arguments from [16], a related construction then shows NP-hardness for $S{C}_{stretch}$ as well as hardness of approximation for both social cost functions.

The proof of Theorem 4..1 is based on the 3-SAT reduction of [16] for the minimal-stretch MST problem, modified with appropriate “choice” gadgets between positive and negative literals of the same variable. For the purpose of showing NP-Hardness, the constructed graph G is 3-SAT represented as the union of the clause-literal bipartite graph with edges of length B, along with additional paths E between the positive and negative literals of each variable, as well as a destination S connected to every literal by edges of length $A\le B$. The choice gadget for E is simply a symmetric path of edges with small (meaning even the heaviest edge has small cost) decreasing cost then increasing cost. This replaces the edges of path E in [16]’s construction. Note that for every positive and negative variable nodes, say x and $\overline{x}$, the choice gadget enforces that every Nash tree has either a path from x to $\overline{x}$ or vice versa. This is shown in Figure 3. Since each literal is directly connected to S by an edge shorter than the edge to a clause, the literal with the incoming path from its corresponding choice gadget must necessarily then forward to S in every Nash tree as well. Moreover, each clause must choose one of its corresponding literals to forward to. Therefore, there are only two possible kinds of paths from a clause to the destination depending on the choice gadget’s direction: Zigzagging $B\to E\to A$ or bypassing E via $B\to A$. For every pair of literals, directing E from $\overline{x}$ to x if the corresponding 3-SAT variable assignment is true and from x to $\overline{x}$ if it is false, we see that a clause node that directs into its chosen literal does not zigzag. Since every Nash equilibrium for G uniquely specifies the direction of all paths E between literals and vice versa, the reduction is clear: The 3-SAT instance is satisfiable if there exists a choice of all path directions for E such that no clause zigzags. For sufficiently long B, zigzagging is the only way to increase the directed diameter, and so NP-hardness for optimal $S{C}_{md}$ follows.

For demonstrating NP-hardness for $S{C}_{stretch}$ as well as hardness of approximation, the construction is augmented by an additional node R connected to S by a path of length D and to the clause nodes via edges of length W. By making W sufficiently long and D sufficiently short, we can ensure that zigzagging is the only way to increase the maximum stretch for any Nash equilibrium, from which NP-hardness for optimal $S{C}_{stretch}$ follows. Finally, following the identical method as [16], we can set edge and path length to induce an arbitrary constant approximation gap, from which NP-hardness of approximation follows for both social cost functions. We refer the reader to [16] for details and Figure 3 for illustration.☐

Figure 3. 3-SAT reduction akin to [16] with additional directionality gadgets.

Figure 3. 3-SAT reduction akin to [16] with additional directionality gadgets.

Note that the theorem above also holds under the restriction to complete graphs, by ensuring that any edges added to this construction are large enough not to be used in any Nash equilibrium.

More specifically, we show that it is hard to compute optimal Nash equilibria even when we restrict ourselves to the 3-dimensional Euclidean case.

Theorem 4..2.

The social cost of the optimal Nash equilibrium for the LMCF Game on 3-dimensional Euclidean graphs is NP-Hard to compute for both the $S{C}_{md}$ and $S{C}_{stretch}$ social cost functions.

Proof. Here, it suffices to modify the 3-SAT construction G in the previous proof so that it can be embedded into 3-dimensional Euclidean space. Place the destination node t at the origin. For each variable $x_i$ connect its positive and negative literal via a choice gadget E as in the previous proof, and place each such connected pair equidistant from neighboring pairs on a sufficiently large circle about S. This is shown in Figure 4. We introduce a new gadget here as well, which we call the “directionality” gadget: a sequence of nodes $<v_0,v_1,\cdots ,v_q>$ such that for each $0\le i<q$ the nearest neighbor of $v_i$ is uniquely $v_{i+1}$. Namely, the distances of consecutive points is strictly decreasing and chosen small enough to guarantee that there are no closer points elsewhere in the remaining construction. Now, for each literal, draw a directionality gadget from the literal to S along the line connecting those two points, identical for every pair. These replace the A-edges in the previous proof, so let us refer to these as A as well. Note that the choice gadget E is simply two directionality gadgets mirroring each other about the central shortest edge. Whereas in a Nash equilibrium E has two choices of direction, A has only one choice of direction: all $v_i$ except possibly $v_0$ direct towards $v_{i+1}$. We retain the caveat that the longest edge of E is still shorter than its neighboring edges outside of E. Now, for the placement of clauses, and the paths connecting clauses to literals: Place clause nodes on a sufficiently large sphere about the origin, sufficiently far apart from each other. For each clause node $c_i$ place three identical directionality gadgets connecting $c_i$ to its corresponding literals, replacing the edges B in the previous construction. Note that this can certainly be accomplished in 3-dimensional space without any two paths B coming too close by choosing the sufficiently large sphere. Moreover, these gadgets B can be made identical in total length as well by elongating short lines by a curve. This completes the specifications for the construction of the embedding: let us call it $G_{3D}$. What remains is this. Every Nash equilibrium for the LMCF game on $G_{3D}$ is uniquely determined by the choice of literal to which $c_i$ connects via a B-gadget and the choice of direction for each E gadget. Again note: The maximum possible stretch factor and weighted-hop-distance to S in a Nash equilibrium are achieved by a zigzagging of $B\to E\to A$. Identically to the previous proof, such zigzagging is only necessary for unsatisfiable 3-SAT instances. The NP-Hardness then follows. We refer the reader to Figure 4 for illustration.

Figure 4. 3-SAT reduction embedded in 3-dimensional Euclidian space.

Figure 4. 3-SAT reduction embedded in 3-dimensional Euclidian space.

☐

5. Heuristics

Given the hardness results, we seek to find an intuitive heuristic to compute Nash trees for LMCF with low Social Cost. First, we present a meta-heuristic, LMHeur, to compute general Nash equilibria for the LMCF Game. The main idea behind the meta-heuristic is that since equilibria are directed trees, for any Nash tree there exists a forwarding order such that, maintaining a forest of directed edges for nodes already chosen, the next chosen node forwards to its nearest neighbor that does not introduce a cycle into the forest. The choice of forwarding order may be dictated by whichever global cost function we wish to optimize, or which kind of Nash we are looking for.

As we have proposed $S{C}_{stretch}$ and $S{C}_{md}$ as reasonable social cost functions to consider for the LMCF Game, we propose the DeltaHeur, a member of the LMHeur class, to compute good Nash trees. The ordering priority for DeltaHeur is based on maximal progress towards shortest path. A priority queue is kept holding the nodes that have yet to forward, sorted by the difference between the candidate node’s shortest path distance to the destination and its available nearest neighbor’s shortest path distance to the destination (“available” means not introducing a cycle within the current forest). The description is shown in Algorithm 5..1. It is straightforward to show in the Euclidean case that the ordering induced by the DeltaHeur corresponds exactly to a “maximum projection” heuristic, which we call ProjHeur, where the projection in question is that of the vector from the candidate node to its available nearest neighbor projected onto the vector from the candidate node to the destination t.

Algorithm 5..1 DeltaHeur

Require: Position of all the nodes is known to all other nodes; for given nodes (numnodes), $numnodes\ne 0$ // Q: Priority Queue initially contains indices from 1 to numnodes  while Q is not empty do   for all $i=1$ to $numnodes$ do       for all $j=1$ to $numnodes$-1 do             if (cyclecheck$(i,Nbrs[i].j)\ne 1$) then                     // cyclecheck(i,j) returns 1 if Node i forwarding to Node j forms a cycle                     // Nbrs[i].j refers to jth nearest neighbor of i                     i.cnn → j // i.cnn refers to the current nearest neighbor of i that does not create a cycle                     break             end if       end for   end for   for all $i=1$ to $numnodes$ do       i.delta=d2d(i)-d2d(i.cnn) // d2d refers to the shortest distance to destination       update(Q) // Q is updated with the node indices(i) in decreasing order of delta   end for   [Q.top()].pointTo → Nbrs[Q.top()].cnn // pointTo refers to the node to which the node with maximum delta forwards to   Q.pop() end while

The extension of ProjHeur to a local algorithm, LocalHeur, is simply that each node forwards to its nearest neighbor that is closer in the Euclidean space to the destination than itself (thus also being in the direction of the destination). The description is shown in Algorithm 5..2. Trivially, any such configuration is guaranteed to be cycle-free without need of an explicit cycle check, nor computation of shortest paths, since Euclidean metrics are used. However, unlike ProjHeur, LocalHeur does not guarantee Nash equilibrium. We provide results later on closeness of LocalHeur to Nash equilibrium. Note furthermore, that while the Euclidean power graph of power $p=2$ is not a metric graph, it is a closely bounded approximation of the underlying Euclidean metric, particularly in random instances.

Algorithm 5..2 LocalHeur

Require: Position of the destination is known to all the nodes; each node knows the position of its one-hop neighbors, $numnodes\ne 0;\vee i,numnbrs\left(i\right)\ge 1$  for all $i=1$ to $numnodes$ do   // numnbrs(i) is the total number of neighbors of i   for all $j=1$ to $numnbrs\left(i\right)$ do       // dist(i,j)computes the distance between Node i and j       // dest refers to the destination node       // Nbrs[i].j refers to jth nearest neighbor of i       if (dist$(i,dest)$ - dist($Nbrs\left[i\right].j,dest)\ge 0$) then             i.pointTo → Nbrs[i].j // pointTo refers to the node to which i forwards to             break       end if   end for end for

6. Theoretical Analysis of Expected Social Costs on Random Graphs

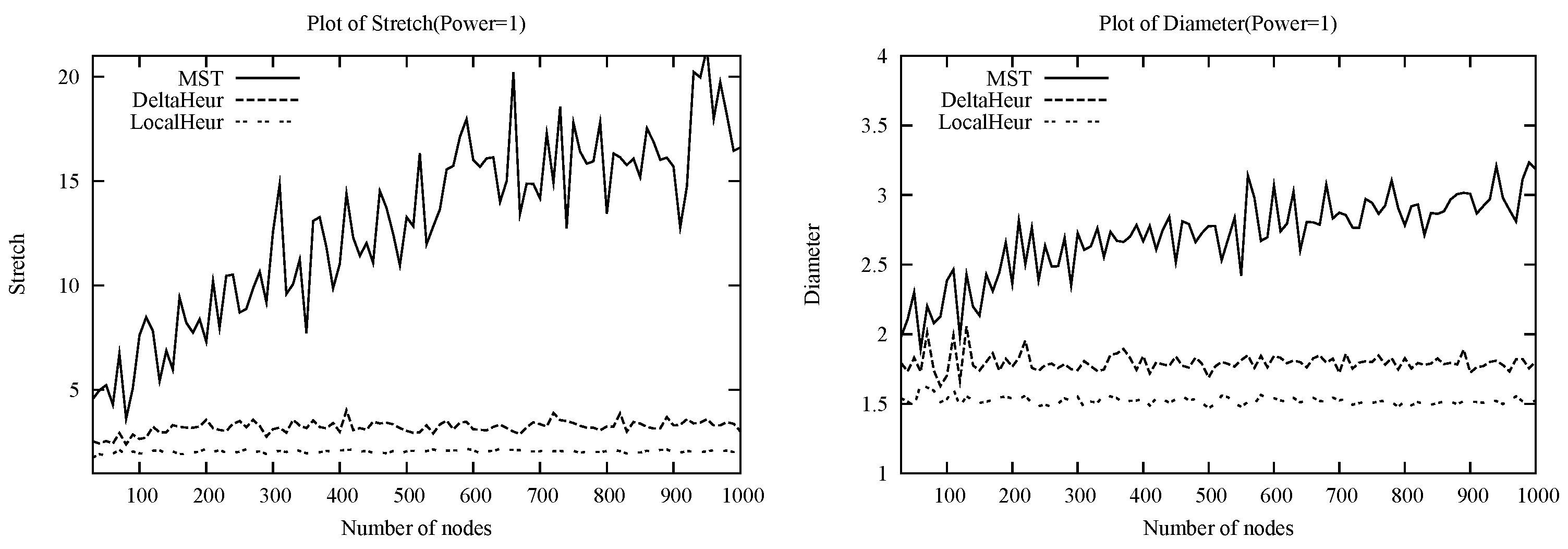
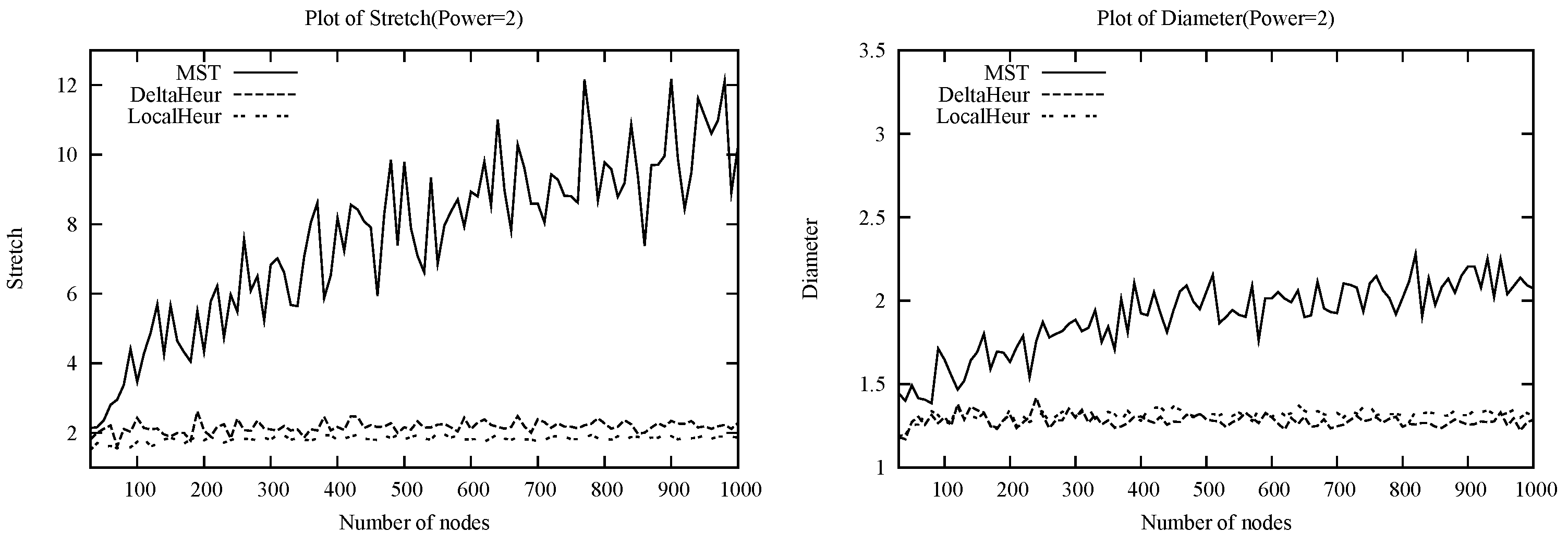
While we have given worst-case lower bounds on $PoA$ and $PoS$, it is also of practical interest to consider the expected values of these quantities for classes of random graphs. Here we discuss the case of random Euclidean instances, arguing that based on the structure of the MST, $PoA$ is likely to be $\omega \left(1\right)$, whereas based on the behavior of DeltaHeur, $PoS$ may be $\Theta \left(1\right)$.

The argument for $PoA$ (at least under $S{C}_{stretch}$) is as follows. Consider the MST on nodes placed uniformly at random in a d-dimensional unit hypercube. Now consider a $(d-1)$-dimensional hyperplane that cuts one of the edges incident on t in the spanning tree, but none of the others. Because of the uniform density of nodes, we expect that this (curved) hyperplane will pass between many pairs of nodes separated by distance $\Theta \left(n^{-1/d}\right)$, i.e., the typical distance between a node and its close neighbors. The hyperplane continues to the boundaries of the hypercube, and so some of these pairs of nodes are likely to be at constant distance from t. However, since the nodes in the pair are on opposite sides of the hyperplane, the shortest MST path between them must pass through the cut edge, and thus be of constant length. While we are concerned with the maximum stretch factor of a node to t rather than between two arbitrary nodes on the graph, note that in the random case, t is in fact equally likely to be any of the nodes in the MST. This suggests the maximum stretch factor could be $\Theta \left(n^{1/d}\right)$, so $PoA$ would then be $\Omega \left(n^{1/d}\right)$ under $S{C}_{stretch}$. The argument is qualitatively similar for Euclidean power graphs.

Now consider the behavior of DeltaHeur in constructing Nash equilibria on the same random Euclidean instances. Not all directed edges in the Nash tree will point towards t, but we expect there to be a distinct positive bias in favor of this: it is easy to show, for instance, that the algorithm orients all mutual nearest neighbors in the direction of t. Given that mutual nearest neighbors pairs are a constant fraction of edges and their angles of orientation are uniform at random, at each step the expected progress towards destination (the criterion on which DeltaHeur ranks edge) is likely to be a constant fraction of the edge length. The typical distance on the Nash tree from a node to t is then a constant, giving an average (not maximum) social cost of $\Theta \left(1\right)$. Moreover, if it turns out that the random variables representing the progress towards destination along a path to t are only weakly correlated, the distribution of these distances will be close to a Gaussian with constant mean and variance $\Theta \left(n^{-1/d}\right)$. The maximum of n such Gaussian variables has mean $\Theta (\alpha +\sqrt{logn}{n}^{-1/d})$ [24] where α is a constant independent of d, suggesting that this too might be the expected maximum distance. A very similar argument holds for maximum stretch factor, leading to the possible scenario that $PoS$ is $\Theta \left(1\right)$.

Finally, we note that the above argument bounding the expected stretch and diameter of DeltaHeur holds strongly for LocalHeur when $d=2,p=1$ due to the clear satisfaction of the assumption of directed edges pointing towards t with independent forwards. For the case of $d=p=2$, we note that the result is similar due to the approximation of the underlying metric.

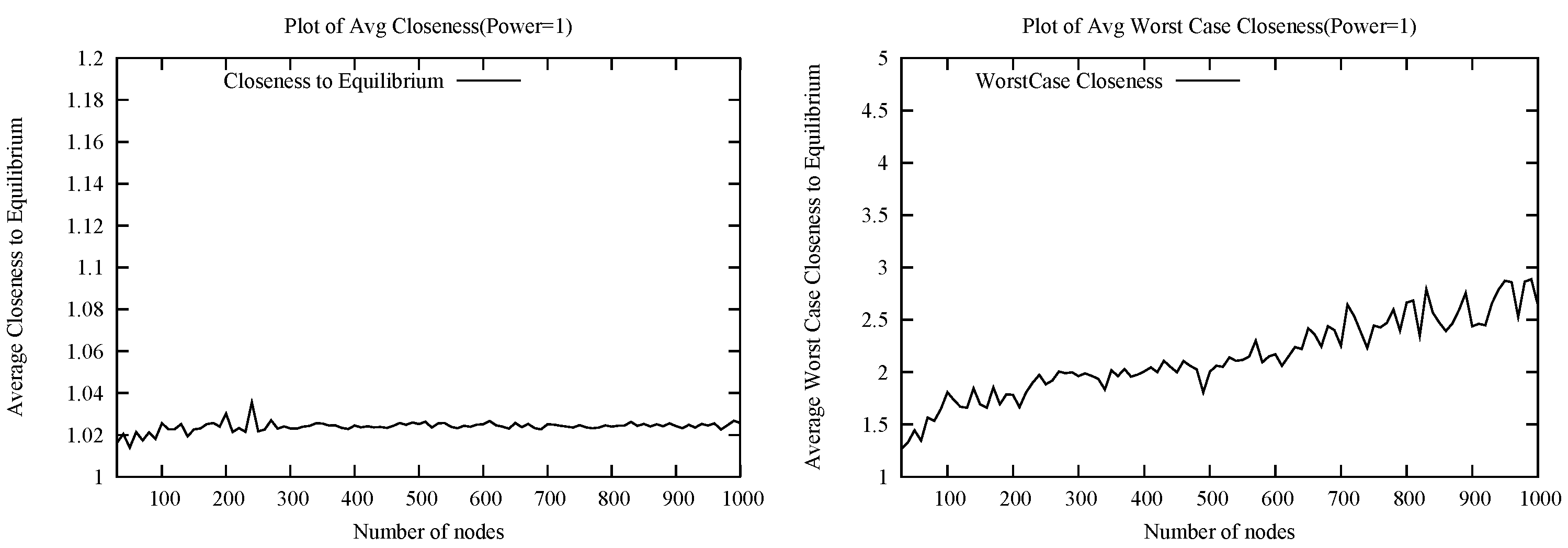
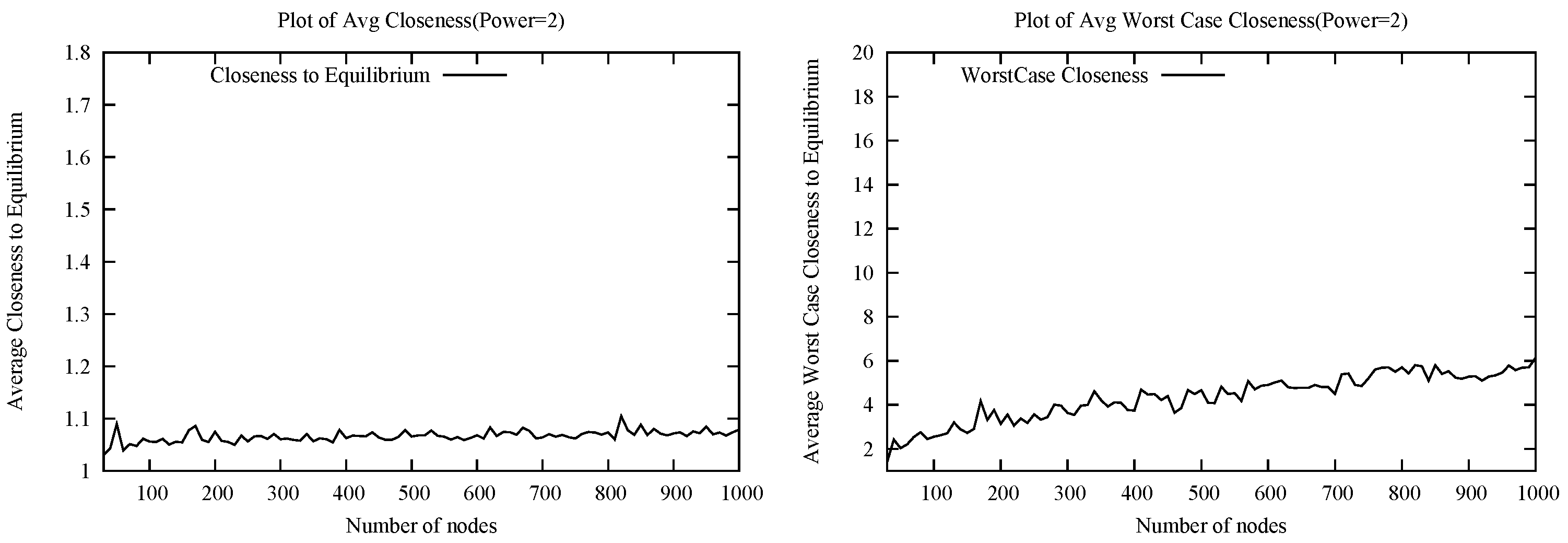
7. Theoretical Bounds on Closeness to Equilibrium for LocalHeur

In this section, we prove bounds on the closeness of the LocalHeur configurations to the Nash equilibrium condition. The main theorems concern the non-deviation from equilibrium for a majority of the nodes and the worst case approximation to a Nash equilibrium. When referring to random Euclidean instances, we restrict our consideration only to points distributed uniformly at random in the two-dimensional unit square.

Theorem 7..1.

[Majority Non-Deviation] In any configuration induced by LocalHeur on a random Euclidean instance, with high probability at least half of the players are playing a best response.

Theorem 7..2.

[Approximation to Nash] In any configuration induced by LocalHeur on a random Euclidean instance, with high probability the worst player’s cost is within $O\left(\sqrt{logn}\right)$ of the cost of his best response.

Before proceeding to prove the theorems, we introduce some notational convenience: Let $H\left(x\right)$ denote the half-plane through x defined by all points y such that vector $<x,y>$ has a positive projection onto the vector $<x,t>$, for destination t. Let $n{n}_i\left(x\right)$ denote the $i^{th}$ nearest neighbor of x, and let $n{n}_{i,H}\left(x\right)$ for function H denote the $i^{th}$ nearest neighbor of x restricted to half-plane $H\left(x\right)$ 7. Note that, except within a negligible constant neighborhood of the destination t for which relevant results hold anyway, $n{n}_{1,H}\left(x\right)$ is with high probability the neighbor to which x forwards under the LocalHeur algorithm. Thus w.l.o.g. we denote $LocalHeur\left(x\right)=n{n}_{1,H}\left(x\right)$.

Finally to make appropriate game-theoretic analysis, let $BR\left(x\right)$ denote the set of points y for which the act of x forwarding to y would constitute a best response for x given the current configuration of all other players. Since $BR\left(x\right)$ will be a singleton with probability 1 for random Euclidean instances, we refer to the best response as a single point w.l.o.g.. Note that player x is playing a best response iff x is forwarding to his nearest neighbor which does not already have a path to x (in which case the forwarding would induce a cycle, giving infinite cost). Now we proceed to prove our theorems:

Proof of Theorem 7..1. It suffices to show that, for any player x, the probability that x is playing a best response is at least $\frac{1}{2}+c$ for some constant $c>0$, as the probability distribution of players playing best response is then bounded below by an i.i.d. binomial distribution with $p=\frac{1}{2}+c$ for which the corresponding result on biased coin flips inducing majority w.h.p. is well known8. Thus, we proceed to show that for any player x, which is of course a random position in our Euclidean space, the probability that x is playing a best response is at least $\frac{5}{8}$.

Clearly, if $n{n}_1\left(x\right)\in H\left(x\right)$ then x is trivially playing a best response. Since there is no bias induced by either half-plane, we thus have that $Pr[LocalHeur\left(x\right)=BR\left(x\right)]\ge \frac{1}{2}$. What remains now is to demonstrate a constant bias towards choosing a best response. This is accomplished by noting just another disjoint situation, namely the situation that although $n{n}_1\left(x\right)\notin H\left(x\right)$, that $n{n}_2\left(x\right)\in H\left(x\right)$ and $x=n{n}_1\left(n{n}_1\left(x\right)\right)$. If we may show that the probability of this situation is bounded below by a constant $c>0$ then we are done, and in particular we demonstrate that the probability of this situation is bounded below by $\frac{1}{8}$. For convenience, let us denote the relevant events as follows:

• Let A denote the event that $n{n}_2\left(x\right)\in H\left(x\right)$.
• Let B denote the event that $n{n}_1\left(x\right)\notin H\left(x\right)$.
• Let C denote the event that $x=n{n}_1\left(n{n}_1\left(x\right)\right)$.

Now we show that $Pr[A\wedge B\wedge C]\ge \frac{1}{8}$:

First note that $Pr\left[A\right|B\wedge C]>\frac{1}{2}$ as the events $B\wedge C$ serve to mark out a slightly larger area of $\overline{H\left(x\right)}$ from consideration than the area marked out from consideration within $H\left(x\right)$. Namely, two areas become impossible for $n{n}_2\left(x\right)$ to lie within, one area being the circle centered at x with radius $dist(x,n{n}_1\left(x\right))$, and the second area (not disjoint) being the circle centered at $n{n}_1\left(x\right)$ with same radius. The first circle blots out from consideration equal sizes areas in $H\left(x\right)$ and $\overline{H\left(x\right)}$, but the second circle lies wholly within $\overline{H\left(x\right)}$.

Secondly, note that event C, a reciprocity or mutuality event, is entirely independent of event B. Thus, $Pr[B\wedge C]=Pr\left[B\right]Pr\left[C\right]$. As mentioned previously, $Pr\left[B\right]=Pr\left[\overline{B}\right]=\frac{1}{2}$. It can be shown that $Pr\left[C\right]\ge \frac{1}{2}$ . Intuitively if points are assumed to be uniformly distributed in a n-dimensional Eucledian space, their reciprocity relationship follows a geometric distribution whose expectation cannot exceed 2. The reader is referred to [17,18] for a detailed understanding. Thus, combining via Bayes’ Rule, we obtain that $Pr[A\wedge B\wedge C]=Pr\left[A\right|B\wedge C]Pr[B\wedge C]=Pr\left[A\right|B\wedge C]Pr\left[B\right]Pr\left[C\right]\ge \frac{1}{2^3}$ completing our proof. ☐

Proof of Theorem 7..2. Let x be a player. From [25] it follows that the distance $dist(x,n{n}_1\left(x\right))=\Theta \left(\frac{1}{\sqrt{n}}\right)$ with high probability 9, yielding a lower bound on the cost of the best response. Thus, if we demonstrate that $dist(n{n}_{1,H}\left(x\right),x)=O\left(\frac{\sqrt{logn}}{\sqrt{n}}\right)$ w.h.p., then we are done: For some constant c, consider a radius $r=c\sqrt{\frac{logn}{\pi n}}$ circle of area $A=\frac{2logn}{n}$ about point x. We complete the proof by showing that the probability $P{r}_{empty}$ that the intersection of this area with $H\left(x\right)$ is empty (excluding x) is vanishing:

$$\begin{array}{cc}\hfill P{r}_{empty}& ={(1-\frac{A}{2})}^{n-1}\approx {(1-\frac{logn}{n})}^n\\ & ={\left({(1-\frac{logn}{n})}^{\frac{n}{logn}}\right)}^{logn}\\ & \approx e^{-logn}=\frac{1}{n}\to 0\end{array}$$

☐

Lastly we derive corollaries to the more general case of random Euclidean power graphs, as we especially care to model such graphs of power $p=2$ for more realistic wireless applications. From the above proofs and the observation that relative proximity relation remain unchanged upon powering the distance, as well as the result from [25] on moments of the nearest neighbor distance distributions, the following corollaries immediately follow:

Corollary 7..3 (following from Thm. 7..1).

For any power p, in any configuration induced by LocalHeur on a random Euclidean power p instance, with high probability at least half of the players are playing a best response.

Corollary 7..4 (following from Thm. 7..2).

For any power p, in any configuration induced by Local-Heur on a random Euclidean power p instance, with high probability the worst player’s cost is within $O\left({(logn)}^{\frac{p}{2}}\right)$ of the cost of his best response.

8. Simulations on Social Cost and Closeness to Equilibrium

8.1. Setup

Euclidean power graphs of size n and powers p=1,2 were generated by uniformly distributing n nodes on a 560 × 560 grid. n was varied from 30 to 1,000 in steps of 10 thus varying the density of nodes in the grid.For the random link case n was varied from 30 to 350. In the computation of worst case closeness to best response, a diminishing fraction (square root of the sample size) of maximum and minimum outliers were removed. The results thus obtained are shown in Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 and Table 1.

8.2. Results

From Figure 5 we can infer that prices in terms of both stretch and diameter are asymptotically increasing in case of MST while they are concentrated about small constants for DeltaHeur and LocalHeur. The stretch results of LocalHeur outperforms DeltaHeur almost always by an additive factor of 2. The cost of achieving this is minimal, considering that in all cases only at most 10 percent of the nodes deviate from their best-response (Table 1) and the deviation from best-response is only about 3 percent, which can be inferred by the constant shown in the average closeness to equilibrium plot (Figure 6). This is consistent with Theorem 7..1. For power $p=2$, the performance becomes comparable to DeltaHeur, but still there are only 10 percent of nodes deviating, and the worst case deviation is a very slowly growing function consistent with the theoretical upper-bound from Theorem 7..2. An explanation for comparable stretch and diameter results upon powering the distance is that SPT tends to choose shorter edges at higher powers [26] thus tending towards closer neighbor, while the choice of the next forwarding neighbor in the case of LocalHeur remains the same for all powers. For the random link models under both social cost functions, both DeltaHeur and MST prices appear growing, though for the stretch-based pricing (Figure 8), again MST appears growing asymptotically faster, and there is too much variance in the DeltaHeur plot to make further inferences. The primary consistent observation applying here is that the DeltaHeur is still an improvement over MST (whether by a constant or asymptotically growing factor), and that the md-prices are still quite small.

Figure 5. Plot of stretch and diameter for the MST, DeltaHeur and LocalHeur case when power = 1.

Figure 5. Plot of stretch and diameter for the MST, DeltaHeur and LocalHeur case when power = 1.

Figure 6. Plot of average and worst-case closeness to equilibrium for LocalHeur when power = 1.

Figure 6. Plot of average and worst-case closeness to equilibrium for LocalHeur when power = 1.

Figure 7. Plot of stretch and diameter for the MST,DeltaHeur and LocalHeur case when power = 2.

Figure 7. Plot of stretch and diameter for the MST,DeltaHeur and LocalHeur case when power = 2.

Figure 8. Plot of stretch and diameter for the MST and DeltaHeur scheme with random link costs.

Figure 8. Plot of stretch and diameter for the MST and DeltaHeur scheme with random link costs.

Figure 9. Plot of average closeness to equilibrium and average worst-case closeness to equilibrium for LocalHeur when power = 2.

Figure 9. Plot of average closeness to equilibrium and average worst-case closeness to equilibrium for LocalHeur when power = 2.

Table 1. Count of deviating nodes.

Worst Case no. of nodes deviating from best-response
No of nodes	power = 1	power = 2
100	10	8
500	62	59
1,000	98	103

Table 1. Count of deviating nodes.

Worst Case no. of nodes deviating from best-response
No of nodes	power = 1	power = 2
100	10	8
500	62	59
1,000	98	103

9. NS-2 Simulations

9.1. Simulation Parameters

The LocalHeur and the MST scheme were implemented and comparatively studied using the ns-2 simulator [27]. A realistic wireless environment is modelled using the parameters specified in [28]. Nodes were uniformly distributed on a 1,500 m by 300m grid. Instances where the node density has to be varied were obtained by changing the number of nodes (50,100,250) in the above grid and instances where traffic-load has to be varied were obtained by fixing the sending rate at 4 packets per second and varying the number of sources (1,10,20,30). To nullify the effects of congestion, CBR traffic was used and the packet size was kept as low as 64 bytes. Each node adapts its transmit power after the next-hop forwarding decision is made and the receiver sensitivity of all the nodes are fixed. IEEE 802.11 was the underlying MAC, using the Distributed Coordination Function (DCF). In our energy model, to eliminate the MAC effects, we do not consider the energy expenditure for idle listening. Each simulation was carried for 150 s and averaged over 10 runs for different node distributions and connectivity patterns.

9.2. Analysis

Figure 10, Figure 11, Figure 12 and Figure 13 presents the results obtained. From Figure 12 it can be observed that the MST requires almost 50 percent more energy than LocalHeur for a single traffic source. As consistent with bounds on stretch and diameter, MST has a longer path length and more number of hops and thus greater is the cost of per packet transmission. LocalHeur outperforms MST for 20 sources too but becomes comparable to MST for 30 sources, where the expected starting time between sources is less than 2.5 seconds, given that CBR traffic is turned on randomly in the first 50 seconds of the simulation. These results are for a packet size of 64 bytes at a rate of 4 packets per second. Thus it can be observed that under the assumption of selfish nodes, for events that has to be sensed below this expected time, Localheur can give a considerable energy gain compared to MST. For more frequent sensing of data, the LocalHeur can still provide a good end-to-end delay performance and a better packet delivery ratio with its energy performance tending towards the MST in the worst case. Also having 30 sources transmitting at less than 2.5 s interval between them will cause a significant MAC level contention especially when there are many sources lying within the interference range of the currently transmitting source. Even though this level of contention is bounded by a maximum degree of 6 for both MST and the heuristics as we noted of any Euclidean Nash tree, 802.11 performance is considerably influenced under such levels of contention especially when there are multiple hops to destination [29]. This makes a considerable impact both on energy performance as well as the packet delivery ratio considering the fact that for every failed packet there were 7 attempts to retransmit a packet. Thus the effects of MAC are not fully eliminated at high contention, even though we eliminated the effects of idle listening.

The forwarding decisions of both LocalHeur and MST are very simple with each node just deciding on the next-hop neighbor thus eliminating the cost of having complex routing tables at the intermediate nodes and also very low route computation costs. LocalHeur will have an initial overhead associated with the discovery of the local neighbors which in turn is very much insignificant compared to the costs of cycle check and global neighbor discovery phase of MST. Thus it can be stated that under the constraints of selfish behavior, LocalHeur shows a good energy performance and a better packet delivery ratio compared with the MST scheme under moderate levels of contention, thus providing a global optimal performance with a minimum deviation from equilibrium condition.

Figure 10. Plot of average hopcount to destination for MST and LocalHeur for 50,100,250 nodes.

Figure 10. Plot of average hopcount to destination for MST and LocalHeur for 50,100,250 nodes.

Figure 11. Plot of PacketDelivery ratio for MST and LocalHeur for 100 nodes and 1,10,20,30 sources.

Figure 11. Plot of PacketDelivery ratio for MST and LocalHeur for 100 nodes and 1,10,20,30 sources.

Figure 12. Plot of Average Energy Utilization per node (at the end of 150s) for MST and LocalHeur for 100 nodes and 1,10,20,30 sources.

Figure 12. Plot of Average Energy Utilization per node (at the end of 150s) for MST and LocalHeur for 100 nodes and 1,10,20,30 sources.

Figure 13. Plot of Average End-to-end delay per node for MST and LocalHeur for 50,100,250 nodes and 1 source.

Figure 13. Plot of Average End-to-end delay per node for MST and LocalHeur for 50,100,250 nodes and 1 source.

10. Conclusion

We have considered the LMCF model of all-to-one (reverse multicast) selfish routing in the absence of a payment scheme in wireless sensor networks, where a natural model for cost is the power required to forward. Whereas each node requires a path to the destination, it does not care how long that path is, so long as its own individual or local forwarding cost is minimized, yielding two related social objectives of finding topologies that minimize: (i) the maximum stretch factor, and (ii) the directed weighted diameter. We proved that Nash equilibria always exist for LMCF, in particular the directed MST always being one, and we analyzed price of anarchy and the price of stability (PoS) of this game restricted to wireless scenarios.

For the maximum stretch factor we present a $\Omega \left(n\right)$ worst-case bound on $PoA$ and $PoS$, and for the directed weighted diameter we have presented a $\omega \left(n^c\right)$ worst-case bound on $PoA$ and $PoS$ for all $c<1$, even when restricted to Euclidean instances. We proved hardness of computing the optimal Nash equilibrium in three-dimensional Euclidean instances as well as approximation hardness in arbitrary instances.

Given the negative worst case results, we presented heuristics that are fully or approximately close to Nash equilibria while also approximating the optimum social cost with good likelihood in relevant random instances. The first heuristic, DeltaHeur guarantees Nash equilibria and is extendable to general graphs. However, as the issue of local computation (or computation with local information) may be important under many wireless scenarios, we propose a modification of DeltaHeur that is locally computable, LocalHeur, which we prove approximates Nash equilibrium with high probability: at least half of the players are provably playing a best response with high probability, while simulation results demonstrate that majority of the players are playing a best response and the average deviation ratio from a best response is within a decimal point of 1. Furthermore, the player deviating most from his best response is provably still within $O(logn)$ of the cost of his best response with high probability, while simulation results support a much smaller maximum deviation from the best response. LocalHeur lies within the class of location based routing methods with particular similarity to the Nearest Forward Progress algorithm [22] though from the perspective of game-theoretic reverse multicast routing.

We analyzed, via simulations and probabilistic arguments, the social costs given by the heuristics and by the MST on random Euclidean power instances, and found that both DeltaHeur and LocalHeur significantly outperform MST. In particular, both heuristics proposed exhibit concentration about small constants to the global optimum experimentally. These results suggest that for random Euclidean power instances, the expected $PoA$ is $\omega \left(1\right)$ while the expected $PoS$ is $\Theta \left(1\right)$.