RFI Mitigation in Microwave Radiometry Using Wavelets
Abstract
:1. Introduction
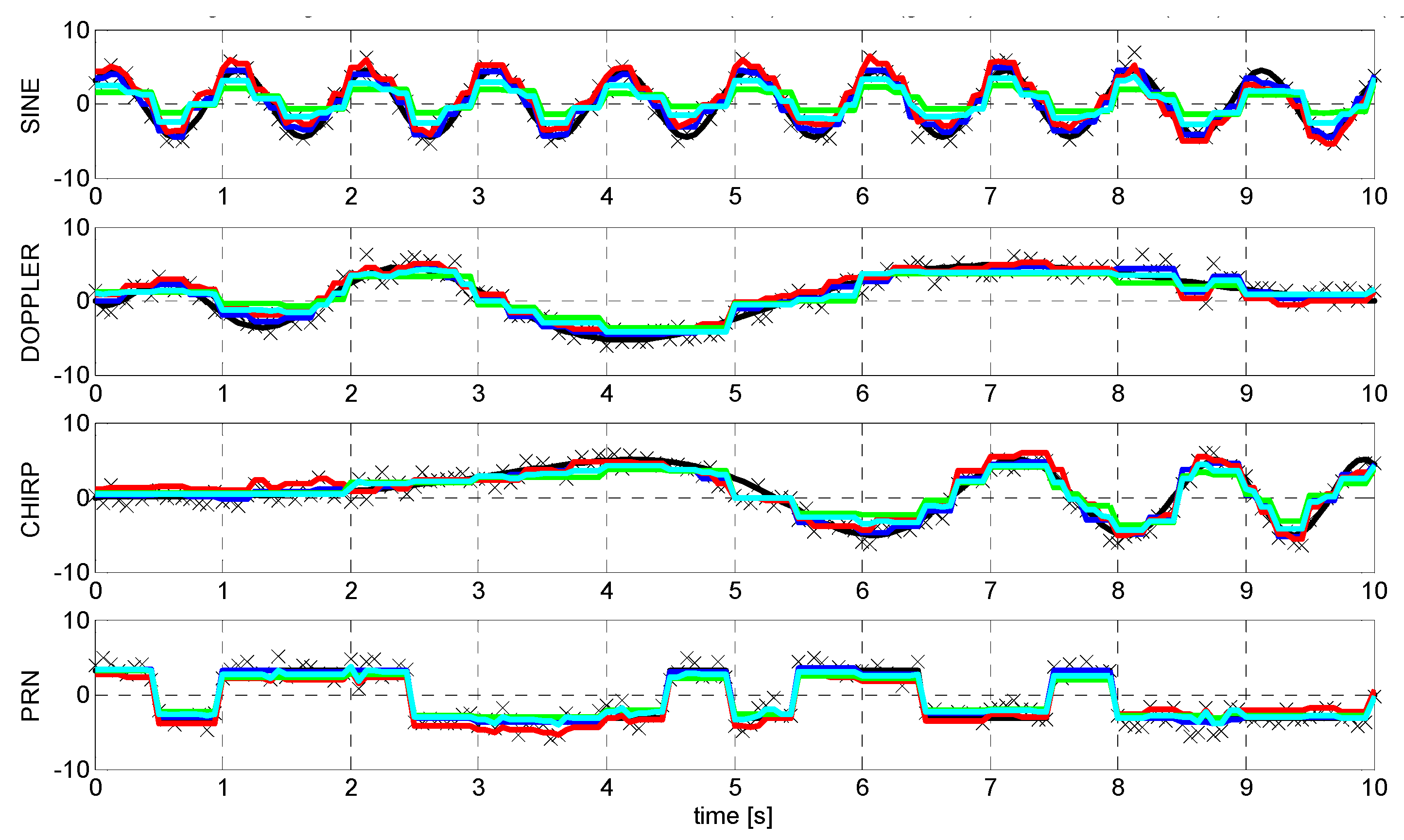
- the maximum instantaneous frequency has been set to be equal to 1 Hz for all of them, so that the sequence length corresponds to the number of samples per signal period, and
- the amplitude of the different interfering signals has been properly scaled so that their power is also the same, and so the interference-to-noise (INR) ratio.
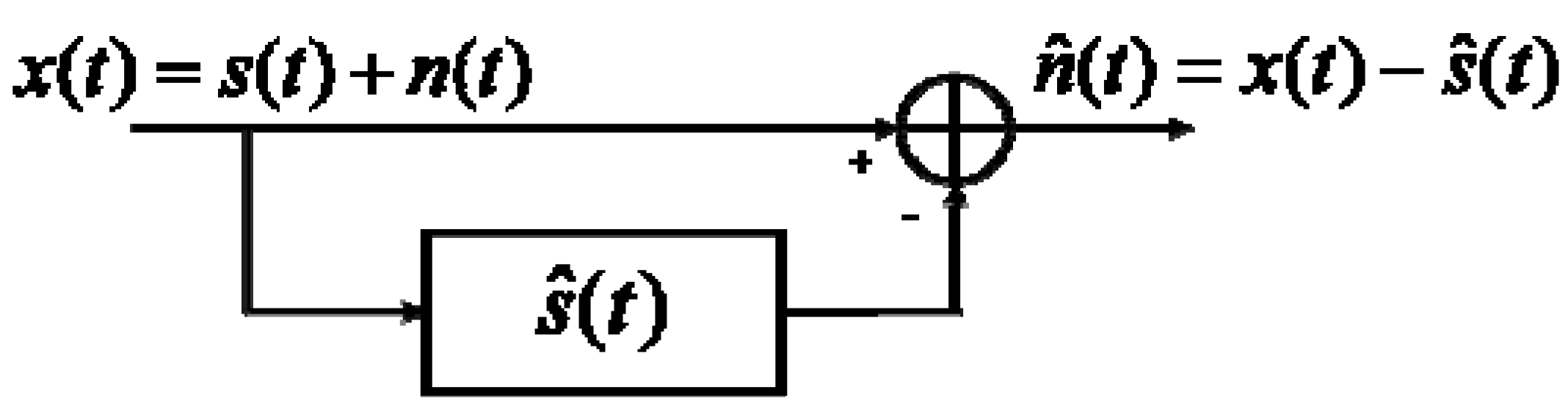
2. Principles of Denoising
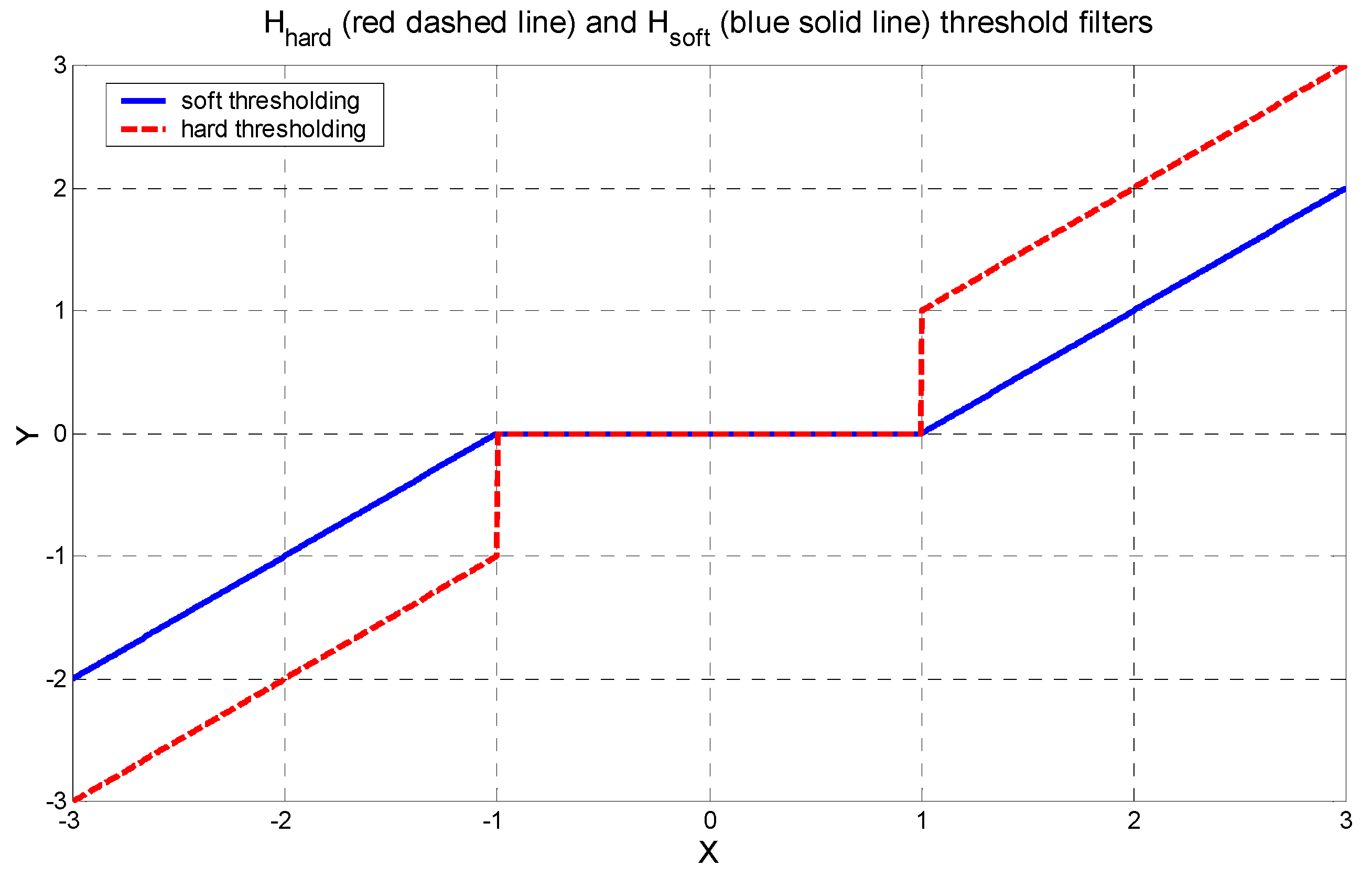
- The hard threshold filter Hhard removes the coefficients below a threshold value T, determined by the noise variance and keeps the others to the same value:
- The soft threshold filter Hsoft shrinks the wavelet coefficients above, and below the threshold reduces them towards zero:
- One approach utilizes a selection rule based on Stein's Unbiased Risk Estimate or SURE (quadratic loss function). If the signal to noise ratio is very small, the SURE estimate is very noisy.
- The Universal method assigns a threshold level equal to the noise variance times , where M is the sample size [21].
- The heuristic approach is a mixture of the two previous ones, and if the signal to noise ratio is detected to be very small, the fixed threshold is used.
- The fourth method uses a fixed threshold selected to yield the minimax performance for mean square error against an ideal procedure (minimum of the maximum mean square error).
3. Optimum Parameters Selection
3.1. Threshold Selection and Sequence Length
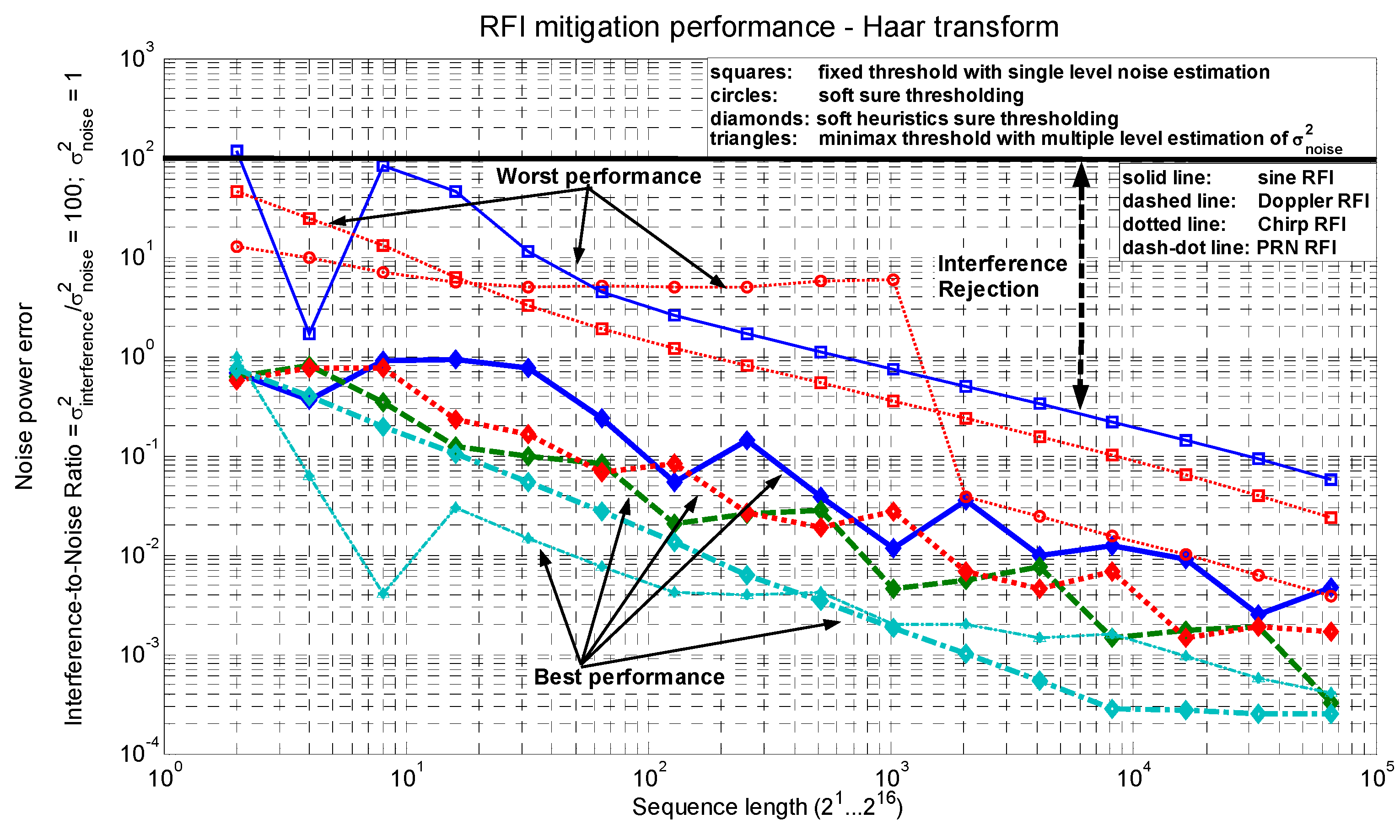
3.2. Decomposition Level
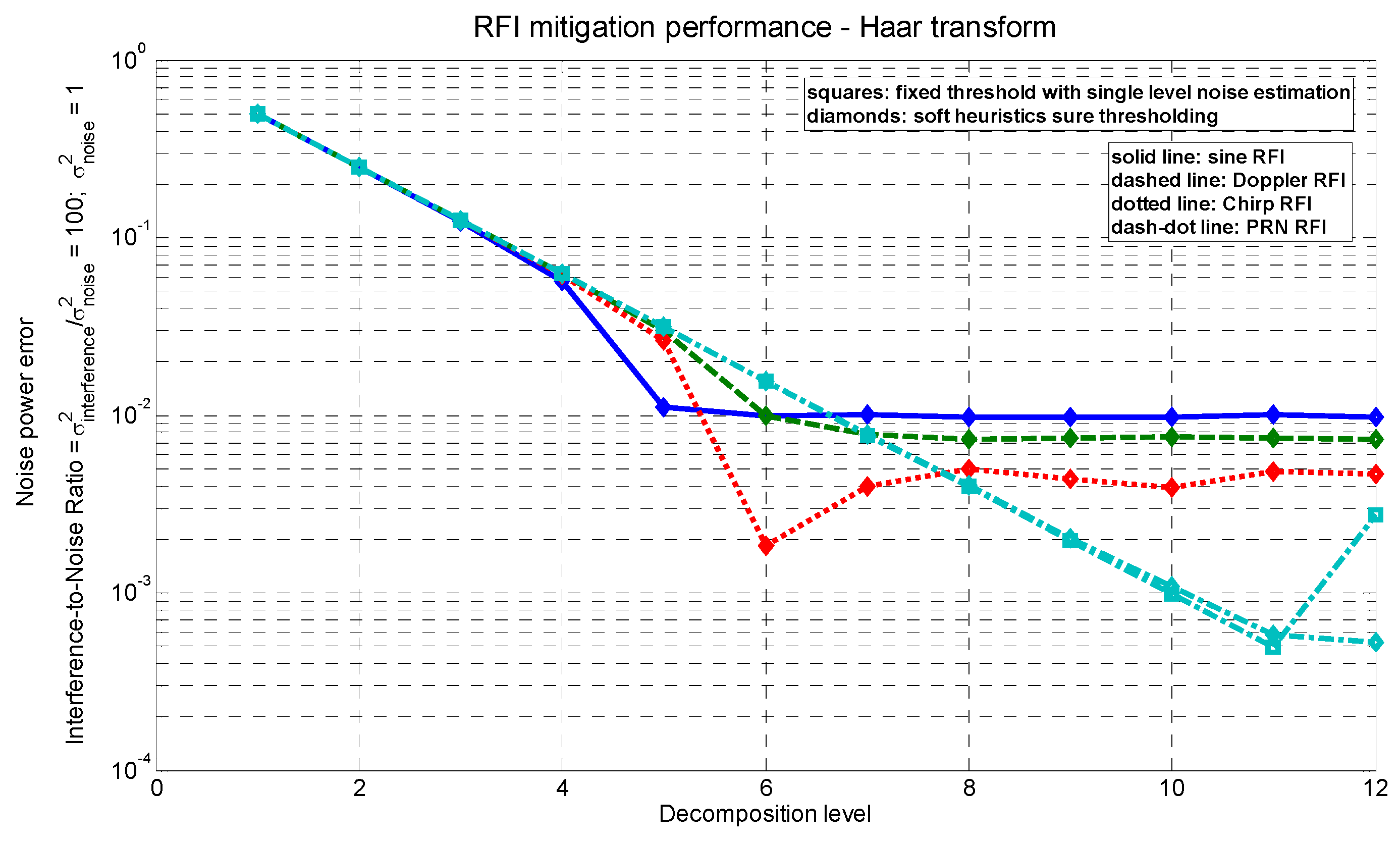
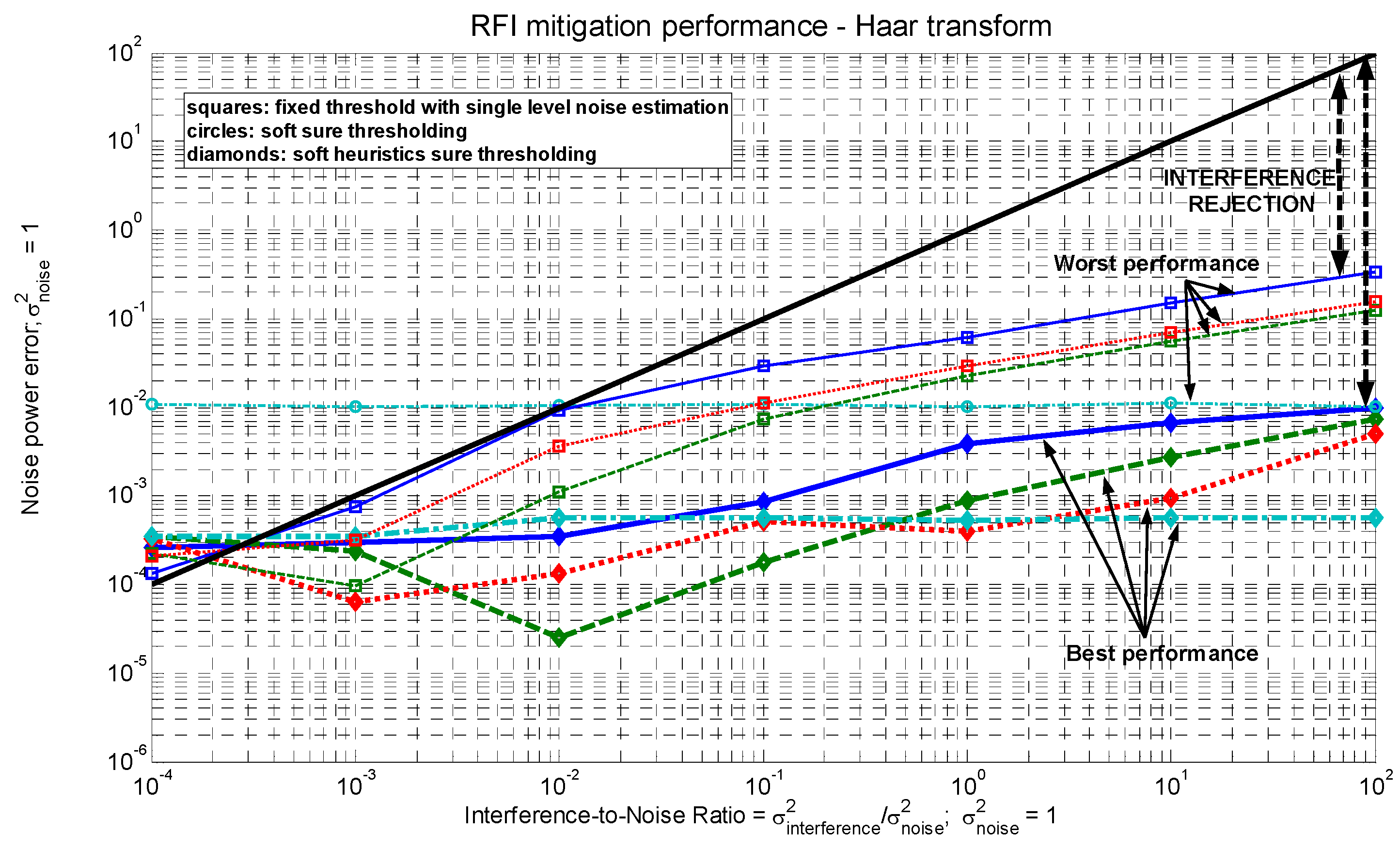
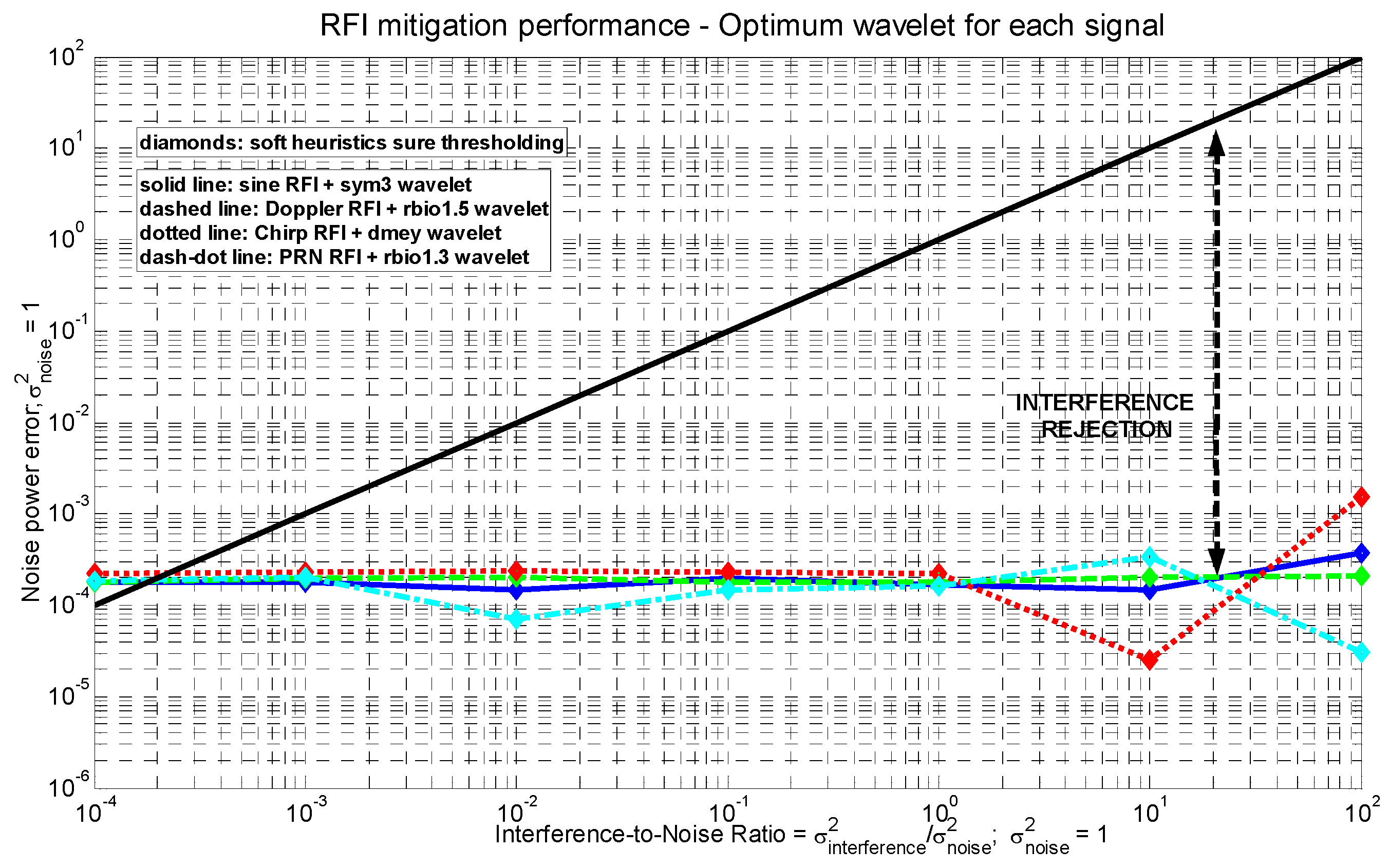
3.3. RFI Mitigation Performance vs. Interference-to-Noise Ratio (INR)
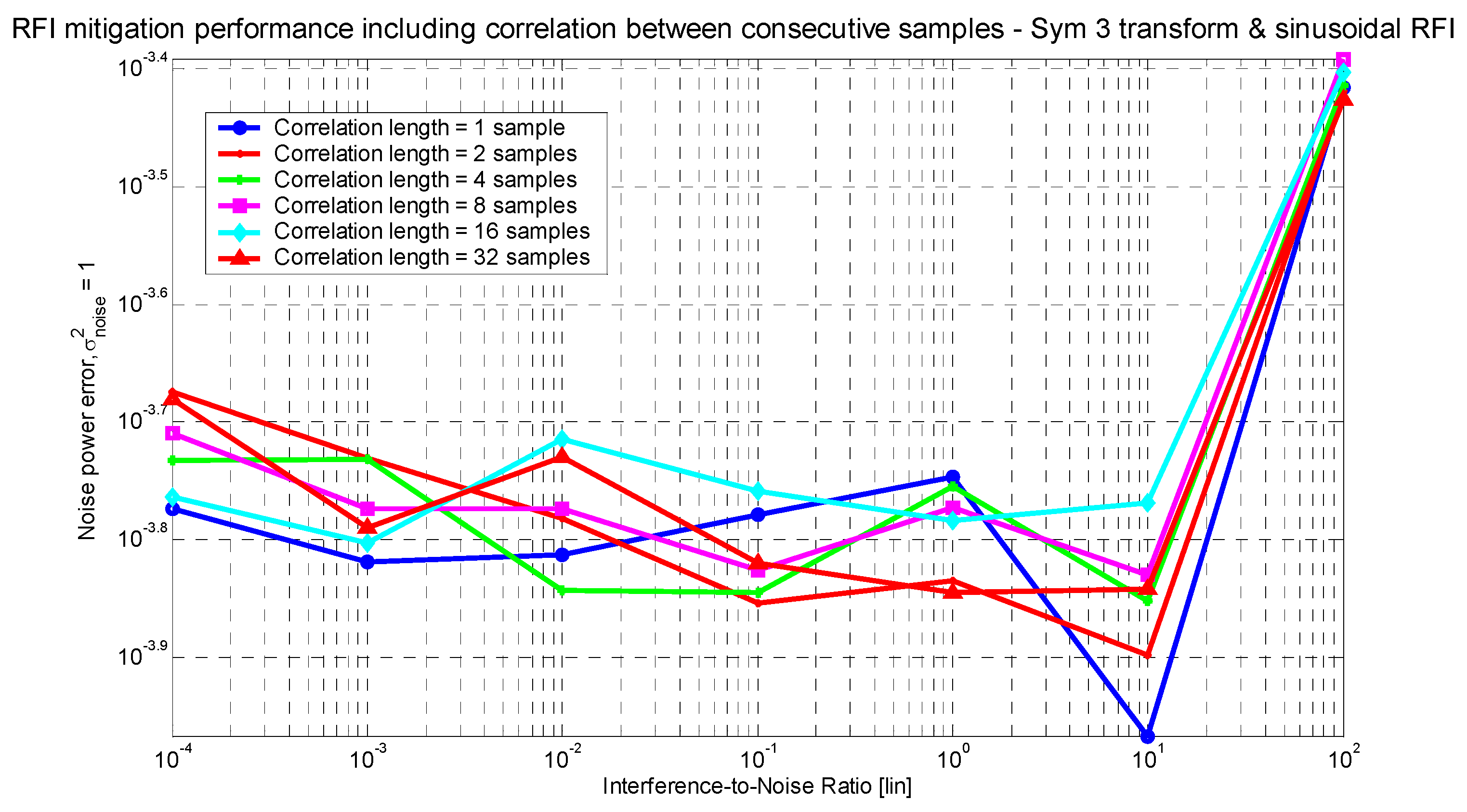
3.4. Noise Correlation Effects
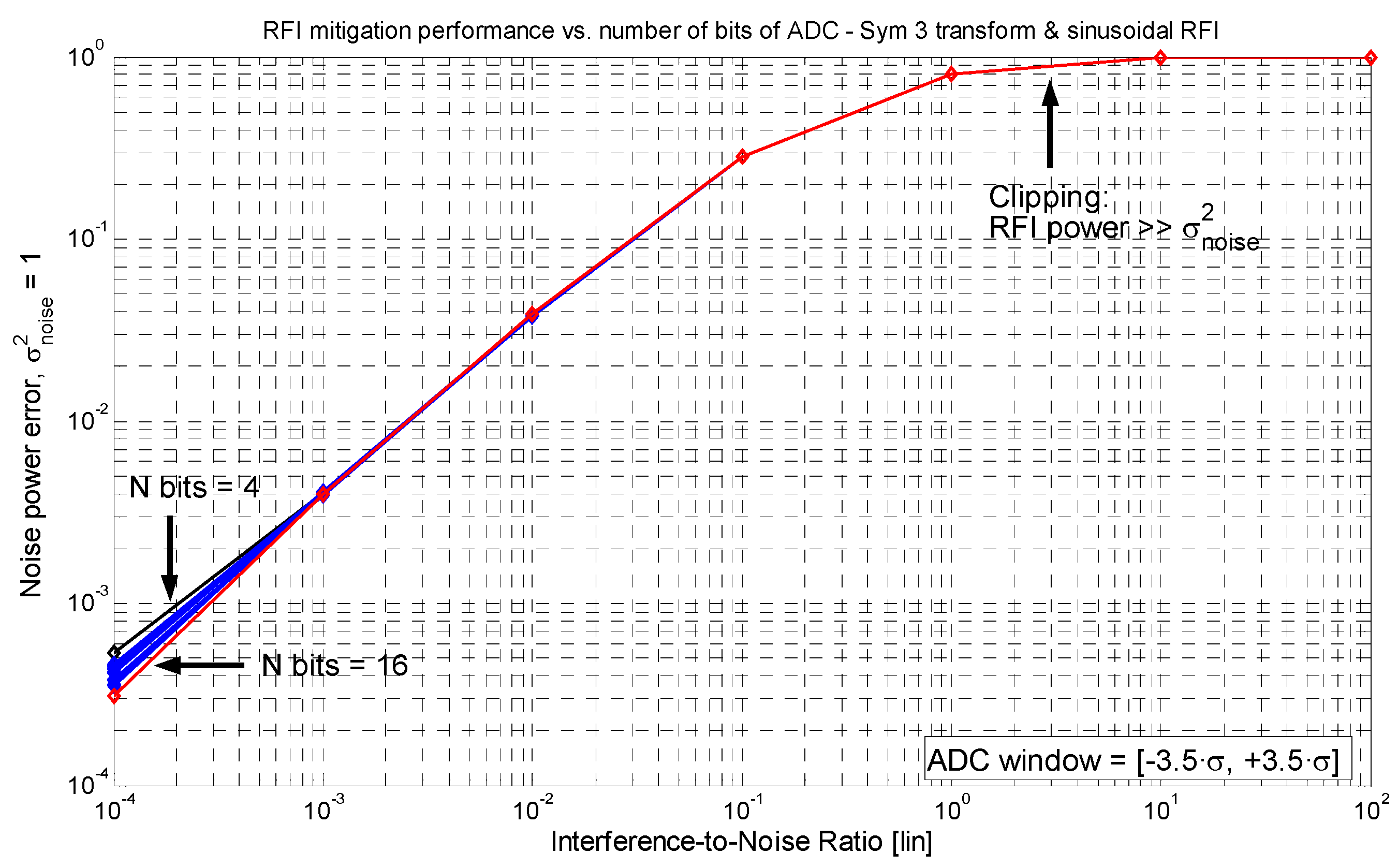
3.5. Quantization Effects
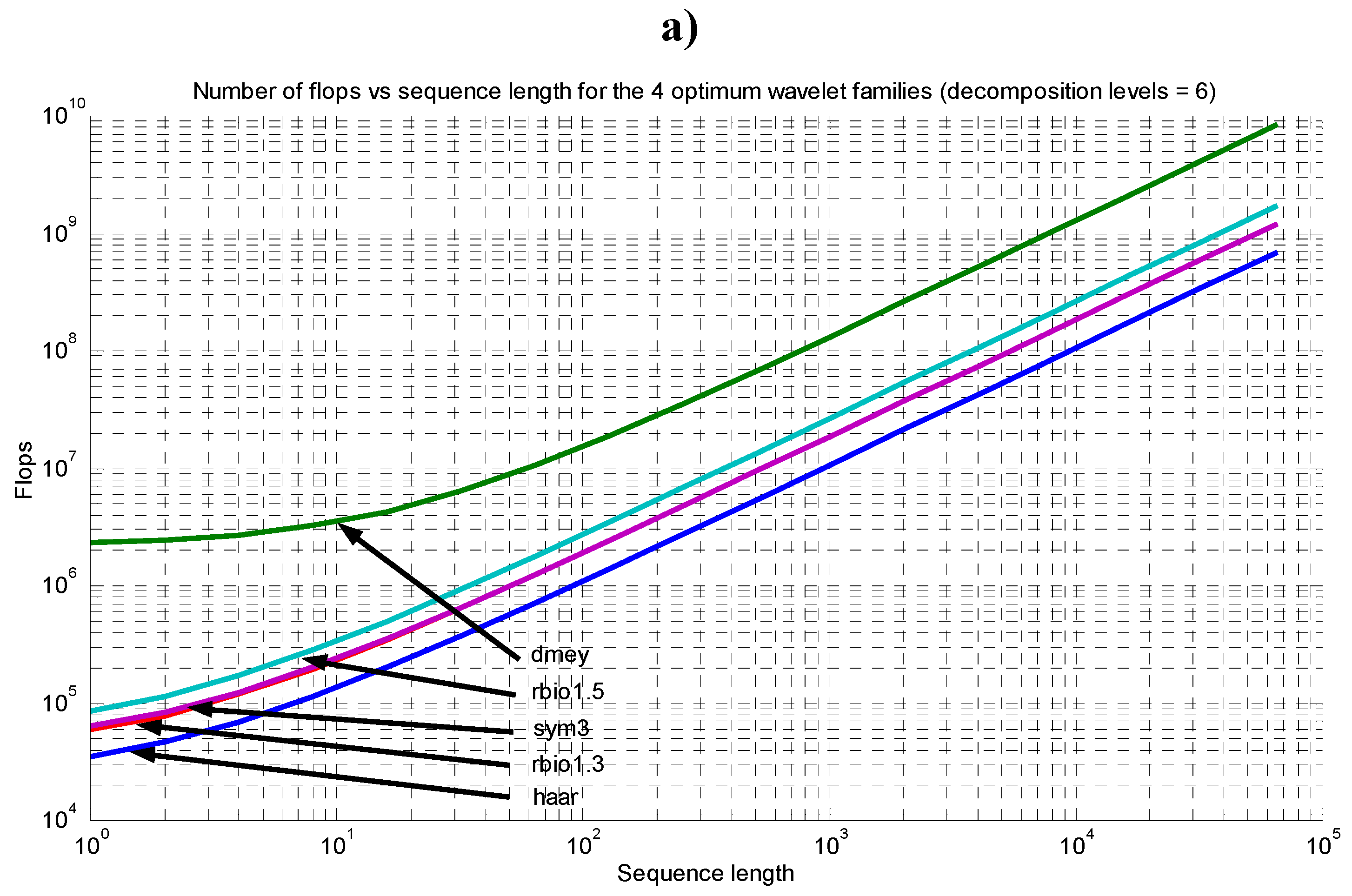
4. Computing Requirements
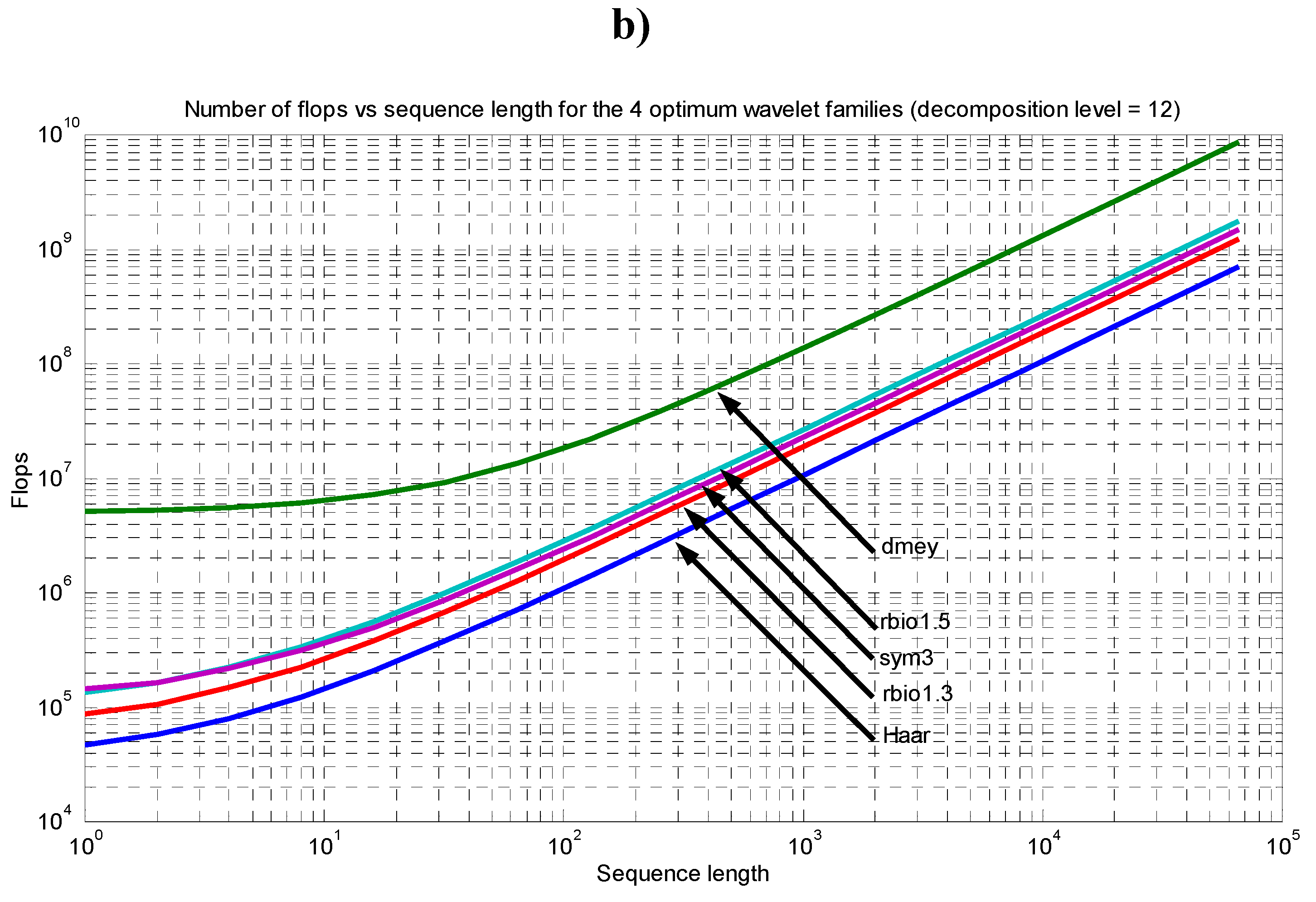
5. Conclusions
- 1.A Doppler signal exhibits an amplitude modulation associated to the different paths of the transmitter and receiver and a frequency modulation that is not linear, only around a time interval around the time in which transmitter and receiver are in their closest positions.
- 2.A chirp signal exhibits a constant amplitude and a constant linear frequency shift.
Acknowledgements
References and Notes
- Njoku, E.G.; Ashcroft, P.; Chan, T.K.; Li, L. Global survey and statistics of radio-frequency interference in AMSR-E land observations. IEEE T. Geosci. Remote 2005, 43, 938–947. [Google Scholar] [CrossRef]
- Ellingson, S.W.; Johnson, J.T. A Polarimetric Survey of Radio-Frequency Interference in C- and X-Bands in the Continental United States Using WindSat Radiometry. IEEE T. Geosci. Remote 2006, 44, 540–548. [Google Scholar] [CrossRef]
- Younis, M.; Maurer, J.; Fortuny-Guasch, J.; Schneider, R.; Wiesbeck, W.; Gasiewski, A.J. Interference from 24-GHz Automotive Radars to Passive Microwave Earth Remote Sensing Satellites. IEEE T. Geosci. Remote 2007, 42, 1387–1398. [Google Scholar] [CrossRef]
- Ellingson, S.W.; Hampson, G.A.; Johnson, J.T. Design of an L-Band Microwave Radiometer with Active Mitigation of Interference. In Proceedings of IEEE International Geoscience and Remote Sensing Symposium IGARSS 2003; Volume 3, pp. 1751–1753.
- Guner, B.; Johnson, J.T.; Niamswaun, N. Time and frequency blanking for radio frequency interference mitigation in microwave radiometry. IEEE T. Geosci. Remote 2007, 45, 3672–3679. [Google Scholar] [CrossRef]
- Johnson, J.T.; Gasiewski, A.J.; Guner, B.; Hampson, G.A.; Ellingson, S.W.; Krishnamachari, R.; Niamsuwan, N.; McIntyre, E.; Klein, M.; Leuski, V.Y. Airborne radio-frequency interference studies at C-band using a digital receiver. IEEE T. Geosci. Remote 2006, 44, 1974–1985. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gross, S.M.; Misra, S. RFI detection and mitigation for microwave radiometry with an agile digital detector. IEEE T. Geosci. Remote 2006, 44, 694–706. [Google Scholar] [CrossRef]
- De Roo, R.D.; Misra, S.; Ruf, C.S. Sensitivity of the Kurtosis Statistic as a Detector of Pulsed Sinusoidal RFI. IEEE T. Geosci. Remote 2007, 45, 1938–1946. [Google Scholar]
- Misra, S.; Ruf, C.S. Detection of Radio-Frequency Interference for the Aquarius Radiometer, IEEE T. Geosci. Remote 2008, 46, 3123–3128. [Google Scholar] [CrossRef]
- De Roo, R.D.; Misra, S. Effectiveness of the Sixth Moment to Eliminate a Kurtosis Blind Spot in the Detection of Interference in a Radiometer. IEEE International Geoscience and Remote Sensing Symposium 2008, IGARSS 2008. Volume 2, 331–334. [Google Scholar]
- Johnson, J.T.; Potter, L.C. Performance Study of Algorithms for Detecting Pulsed Sinusoidal Interference in Microwave Radiometry. IEEE T. Geosci. Remote 2009, 47, 628–636. [Google Scholar] [CrossRef]
- Piepmeier, J.R.; Mohammed, P.N.; Knuble, J.J. A Double Detector for RFI Mitigation in Microwave Radiometers. IEEE T. Geosci. Remote 2008, 46, 458–465. [Google Scholar] [CrossRef]
- Fridman, P.A.; Baan, W.A. RFI methods in radiastronomy. Astronomy and Astrophysics 2001, 378, 327–344. [Google Scholar] [CrossRef]
- Middleton, D. Non-Gaussian noise models in signal processing for telecommunications: New methods and results for Class A and Class B noise models. IEEE T. Inform. Theory 1999, 45, 1129–1149. [Google Scholar] [CrossRef]
- Evans, B.L. Mitigation of Radio Frequency Interference from the Computer Platform to ImproveWireless Data Communication. Intel Labs Seminar – University of Texas. 16 April 2007. http://users.ece.utexas.edu/~bevans/projects/rfi/talks/April2007.html.
- Walker, J.S. A Primer on Wavelets and Their Scientific Applications, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2008; Chapters 1-2. [Google Scholar]
- Donoho, D.L. De-Noising by soft-thresholding. IEEE T. Inform. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- MATLAB tutorial on denoising: http://www.mathworks.com/access/helpdesk/help/toolbox/ wavelet/index.html?/access/helpdesk/help/toolbox/wavelet/ch06_a12.html&http://www.mathworks.com/access/helpdesk/help/toolbox/wavelet/ch06_a10.html#62573.
- Misiti, M.; Misiti, Y.; Oppenheim, G.; Poggi, J.M. Wavelet Toolbox User's Guide; The MathWorks Inc.: Natick, MA, USA, 1996. [Google Scholar]
- Aboufadel, E.; Schlicker, S. Discovering Wavelets; John Wiley and Sons: New York, NY, USA, 1999; p. 14. [Google Scholar]
- Donoho, D.L.; Johnstone, I.M. Ideal spatial adaption by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Ghael, S.P.; Sayeed, A.M.; Baraniuk, R.G. Improved Wavelet Denoising via Empirical Wiener Filtering. In Proceedings of SPIE, Mathematical Imaging, San Diego, CA, USA, July 1997; Vol. 3169, pp. 389–399.
- Lang, M.; Guo, H.; Odegard, E.; Burrus, C.S.; Wells, R.O. Nonlinear processing of a shift-invariant discrete wavelet transform (DWT) for noise reduction. Harold, H. Szu, Ed.; 1995; Vol. 2491, pp. 640–651. [Google Scholar]
- Resnikoff, H.; Wells, R.O. Wavelet Analysis: The Scalable Structure of Information; Springer-Verlag: New York, NY, USA, 2002; p. 365. [Google Scholar]
- Summary of wavelet families and properties: http://www.mathworks.com/access/helpdesk/help/ toolbox/wavelet/index.html?/access/helpdesk/help/toolbox/wavelet/ch06_a12.html&http://www.mathworks.com/access/helpdesk/help/toolbox/wavelet/ch06_a10.html#62573/.
- Leon 3 description: http://www.gaisler.com/cms/index.php?option=com_content&task=view& id=196&Itemid=172.
- Bosch-Lluis, X.; Ramos-Pérez, I.; Camps, A.; Marchan-Hernandez, J.F.; Rodríguez-Álvarez, N.; Valencia, E.; Vericat, M.; Guerrero, M. A. The Impact of the Number of Bits in Digital Beamforming Real Aperture and Synthetic Aperture Radiometers. In Proceedings of the Microwave Radiometry and Remote Sensing of the Environment, MICRORAD 2008, Florence, Italy, 11–14 March 2008.
- Elfouly, F.E.; Mahmoud, M.I.; Dessouky, M.I.M.; Deyab, S. Comparison between Haar and Daubechies Wavelet Transformations on FPGA Technology. IJCISSE 2008, 2, 37–42. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Camps, A.; Tarongí, J.M. RFI Mitigation in Microwave Radiometry Using Wavelets. Algorithms 2009, 2, 1248-1262. https://doi.org/10.3390/a2031248
Camps A, Tarongí JM. RFI Mitigation in Microwave Radiometry Using Wavelets. Algorithms. 2009; 2(3):1248-1262. https://doi.org/10.3390/a2031248
Chicago/Turabian StyleCamps, Adriano, and José Miguel Tarongí. 2009. "RFI Mitigation in Microwave Radiometry Using Wavelets" Algorithms 2, no. 3: 1248-1262. https://doi.org/10.3390/a2031248
APA StyleCamps, A., & Tarongí, J. M. (2009). RFI Mitigation in Microwave Radiometry Using Wavelets. Algorithms, 2(3), 1248-1262. https://doi.org/10.3390/a2031248




