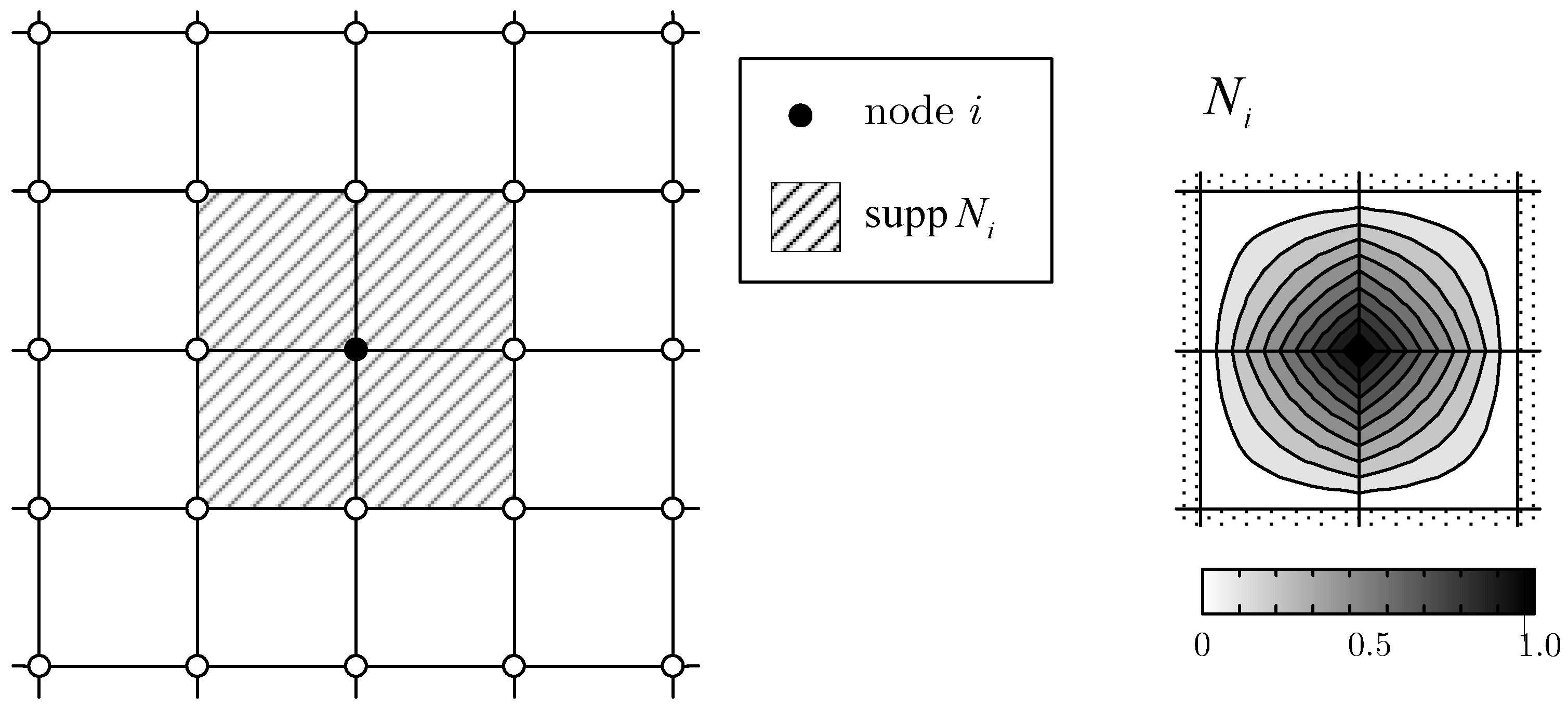
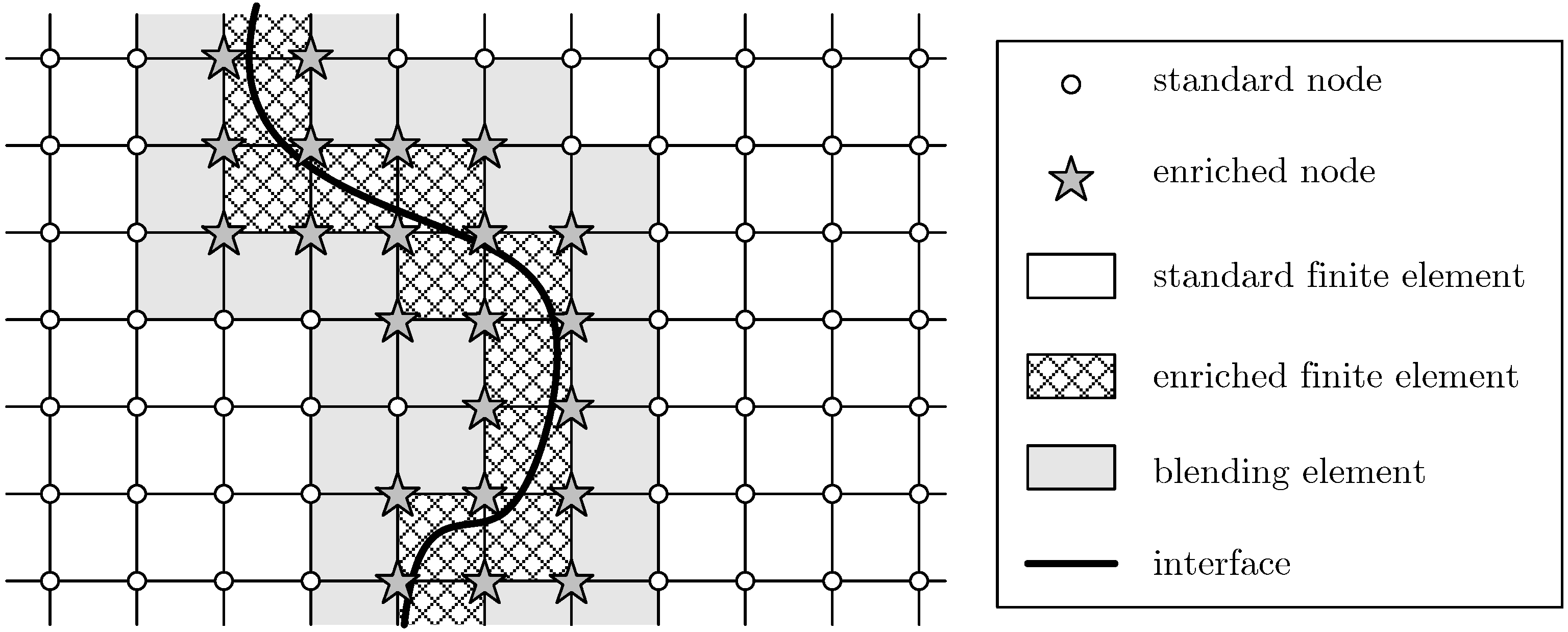
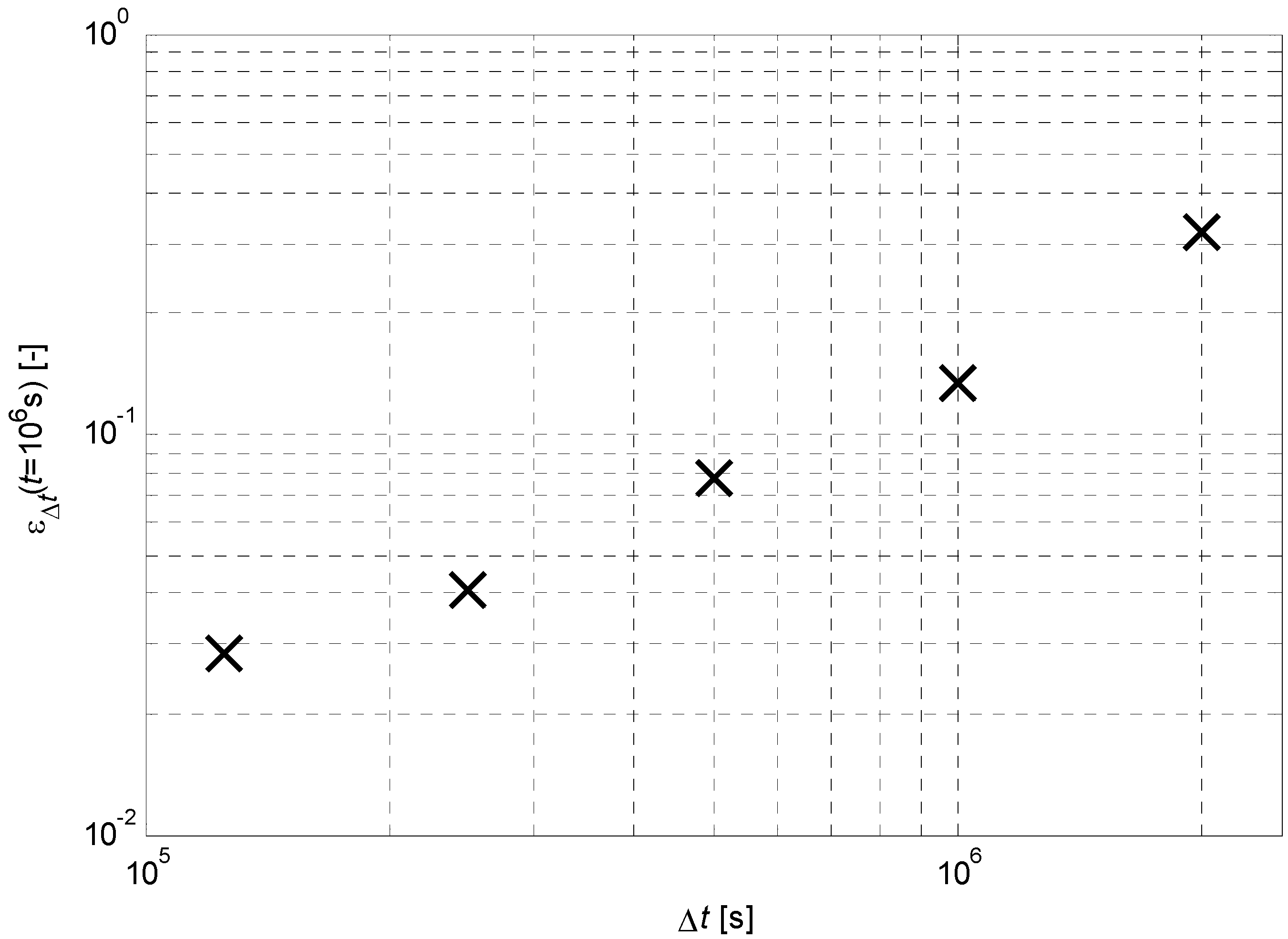1. Introduction
In its original formulation, the
Stefan problem is a representation of (temperature-driven) first-order phase transitions in matter through a boundary value problem for PDEs in which a discontinuity surface, internal to the domain, can move with time. Indeed, the problem was originally formulated in relation to ice formation and melting. However, the same mathematical framework can be applied to a variety of problems arising in different areas of science and technology, such as the diffusion of gasses in biologic tissues, biofilm and hydrogel growth [
1,
2], the penetration of solvents in polymers, the flow in porous media, filtration problems, free surface flows, etching, shock propagation, and financial mathematics (e.g. [
3]). For the formulation details of some of the physical problems mentioned above, and for further examples, see Reference [
4].
Since the topic of this paper is the numerical treatment of the problem, we select a specific physical case, that is the solid-liquid phase transition (e.g. [
5]). Applicative examples are the casting of metals, the freezing and thawing of foods, the production of ice, or ice formation on pipes. As in all the first-order phase transitions, a discontinuity in the first derivative of the free energy with respect to a thermodynamic variable is exhibited and a latent heat is involved. In a solid-liquid transition at constant volume, the pressure, i.e. the first derivative of the free energy with respect to the specific volume, is discontinuous. During the transition, the system either absorbs or releases a fixed amount of energy at a constant temperature. Since the heat cannot be exchanged instantly, a front of solidification or melting is present and moves according to the heat transport across the front itself.
From the mathematical point of view, the solid and liquid regions are subdomains in which the coefficients (representing the physical properties of the medium in each phase) of the underlying PDEs are continuous and differentiable up to the order of the PDEs. The coefficients are discontinuous across the surfaces that separate the adjacent phases and the PDEs are not valid there, so that additional equations are needed for closure. These are derived from energy conservation, namely by the Stefan condition that expresses the local velocity of the moving freezing/melting front as a function of the heat flux evaluated at both sides of the phase boundary. Therefore, the solution of the heat-conduction equations are required within unknown subdomains (the liquid and the solid regions) and their interface must be determined as part of the solution.
Existence and uniqueness of the solution to Stefan problem are demonstrated in References [
6] and [
7], respectively. However, analytical solutions are available in a close form only for a restricted number of simple, particular cases, all characterised by a high degree of symmetry in the geometry and in the boundary and initial conditions. For all the other cases a numerical treatment is required.
For developing a numerical scheme for Stefan problem, two issues must be solved. Firstly, the evolving geometry of the phase-interface must be suitably described with a discrete model; secondly, the temperature field must be discretised in such a way as the jump in the heat flux, i.e. in the temperature gradient, at the phase interface can be reproduced. The description of the phase-interface can be done explicitly or implicitly.
In the explicit methods, a Lagrangian approach is followed and some marker points (finite in number) on the phase interface are selected and tracked explicitly. This is the case, for instance, in which the temperature field is discretised by standard Finite Element Method (FEM); the mesh is generated at the initial time instant in such a way as the element boundaries lay on the phase interface. The finite element nodes on the interface are used as marker points and, at each time step, are displaced according to the solution of the heat-transfer problem within each phase. Eventually, the initial FE mesh will become too distorted and a new mesh must be generated in the solid and liquid regions.
In the implicit methods, on the other hand, the computational grid is usually fixed and the position of the interface is obtained indirectly from some field defined over the whole domain (and suitably discretised). Examples of implicit methods are the enthalpy method, the phase field method, and the level set method. In the
enthalpy method (e.g. [
8,
9]), the enthalpy field is considered and the position of the interface is determined in a smeared way by a jump of such field. In the
phase field method (e.g. [
10]) a phase function is defined over the domain; it assumes fixed values in each of the phases (e.g. 1 in solid and -1 in liquid) and varies smoothly between these values in the interface region. In order to allow such smooth variation, an artificial ‘interface thickness’ must be added to the model. Hence, the interface position is not defined exactly, although it can be chosen conventionally as the surface where the phase field assumes an average value (e.g. zero) or as some kind of ‘average surface’ of the interface region; hence, a sufficiently fine mesh is required in order to resolve the interface zone. Of course, it is necessary to provide additional governing equation for the phase field evolution in a thermodynamically-consistent way. Finally, in the
level set method a function is defined all over the domain and the position of the phase interface is obtained as a level set of this function. In comparing the last two methods, we see that, although the level set function is artificial, the physics of the problem is fully respected; on the other hand, the phase field has a physical meaning, but it necessitates of an artificial ‘thickness’ of the interface. Some comparative analyses in Reference [
11] lead to the conclusion that methods based on the level set are the most promising and general. For these reasons, and since it allows a general, elegant formulation of the extended finite element method, the level set method is chosen here for the numerical analyses and it is reviewed in
Section 3.
The second issue in the numerical treatment of the Stefan problem is the discretisation of the temperature field. The crucial feature, in order to account for the evolution of the phase interface, is the discontinuity in the temperature gradient across the interface itself.
In the aforementioned enthalpy method the problem is reformulated in terms of enthalpy instead of temperature. Although this approach has the advantage of offering a straightforward discretisation of the problem, it has two main disadvantages, as the discrete set of equation in terms of enthalpy becomes nonlinear and the phase interface is smeared throughout a finite thickness. In the so-called
boundary immobilisation method, a new set of coordinates is defined in which the phase-boundary is fixed. Caldwell and Kwan, in their comparative analysis [
12], highlight the effectiveness of this method for one-dimensional problems, but discard it for planar or spatial cases because of the difficulties in defining the coordinate transform with respect to a reference coordinate system fixed in time. Other methods, which are not discussed in depth here due to their lack of generality, are the
perturbation method, which requires hints from a partial analytical solution, the
nodal integral method, which only applies to plane symmetric geometries, and the
heat balance integral method, which is restricted to time-independent boundary conditions. For details on these methods, we remand to the last quoted reference and further references therein.
More general approaches to the temperature field discretisation are based on standard techniques, such as the
finite difference method with a moving grid (e.g. [
11]), the
boundary element method, and, above all, the
finite element method with adaptive mesh (for references on the last two methods applied to Stefan problem, see in Reference [
13]). As already mentioned while discussing the interface tracking methods, Stefan problem can be treated by using standard FEM and a mesh which conforms to the phase interface (e.g. [
14]). The heat-conduction problem is then solved separately in the solid and liquid domains by imposing essential boundary conditions on the phase-interface, i.e. by prescribing the phase-transition temperature. Then, the evolution of the interface is obtained from the jump in the heat flow across the interface, and the position of the nodes belonging to the interface is updated accordingly. The jump in the temperature gradient across the phase interface is possible thanks to the adapted mesh but, of course, remeshing is required every few discrete time-steps. Moreover, each time a new mesh is generated, the nodal values of the temperature must be recomputed by using the interpolated values from the older mesh.
In order to avoid remeshing it is possible to enhance the FEM by allowing for discontinuities that cross the elements. This can be achieved either by embedding the discontinuity directly within the finite elements intersected by the phase-interface and controlling it by additional elemental degrees of freedom, or by enriching the interpolation by means of nodal extended shape functions controlled by additional nodal degrees of freedom. The former approach we call embedded-discontinuity FEM, while the latter is well known as eXtended Finite Element Method (XFEM). In this paper, we focus on these two methods by reviewing the XFEM and adapting it to a specific case, and by developing an original embedded-discontinuity FEM. In both methods, the nodes of the discretisation are fixed and no remeshing is required. It is then natural to adopt an Eulerian approach for the interface description, so that the level set method is used.
The XFEM has been applied to Stefan problem by Merle and Dolbow (2002) [
15], who focus on the one-dimensional case, by Chessa et al. (2002) [
16], who develop the general method that is adapted here for the use with different constraint enforcement methods, and by Zabaras et al. (2006) [
17], who introduce a simplified case of fluid motion and dendritic solidification by using a smeared-interface model. An application of XFEM to the problem of biofilm growth in two dimensions is developed in Reference [
18]. No applications of the embedded-discontinuity FEM to Stefan problem are known to the writers.
Though, as it has been shown, the research is currently tackling planar and spatial cases, the one-dimensional Stefan problem is the subject of several recent research works [
11,
12,
15] and of a monographic book [
19]. Also the examples that are presented in this paper are developed for cases that can be treated as one dimensional due to planar, cylindrical, or spherical symmetry. This is done for the sake of simplicity in exposition, implementation, and result visualisation, which allow concentrating on the differences between different approaches of the XFEM and between XFEM and embedded-discontinuity FEM. Moreover, exact analytical solutions are available in some one-dimensional cases, so that error and convergence can be studied. In further cases, it is possible to develop, as it is done in
Section 6 and
Section 7, simple approximated analytical solutions in the so-called pseudo steady state approximation, in which the heat-conduction problem and the evolution of the interface can be decoupled. Though the aim of the present one-dimensional analyses is basically heuristic, they may also find practical applications. Examples in planar, cylindrical, and spherical symmetry are, respectively, the maintenance of ice surface of skating facilities, the freezing of water into pipelines, or the solidification of droplets of liquid metal into cooling fluid. The initial review provided in this paper includes details that are not strictly necessary for the subsequent one-dimensional applications but that are advisable for a clearer understanding and propaedeutical for the discussion.
This paper is organised as follows. In
Section 2, the governing equations of the melting/solidification problem are briefly recalled.
Section 3 and
Section 4 are review sections, dedicated to the level set method for the geometrical description of the phase interface and its evolution, and to the extended finite element method, respectively. In
Section 5, a method for embedding the gradient discontinuity into finite elements is developed and a specific element is formulated. In
Section 6, the XFEM is thoroughly discussed by means of numerical applications to planar-symmetric problems; spatial and temporal discretisation errors, the enforcement of the interface condition, and the treatment of the so-called blending elements are studied; moreover, the XFEM is compared to the embedded-discontinuity FEM. In
Section 7, polar-symmetric problems are analysed and the relevant XFEM results are compared to analytical solutions.
2. Governing Equations
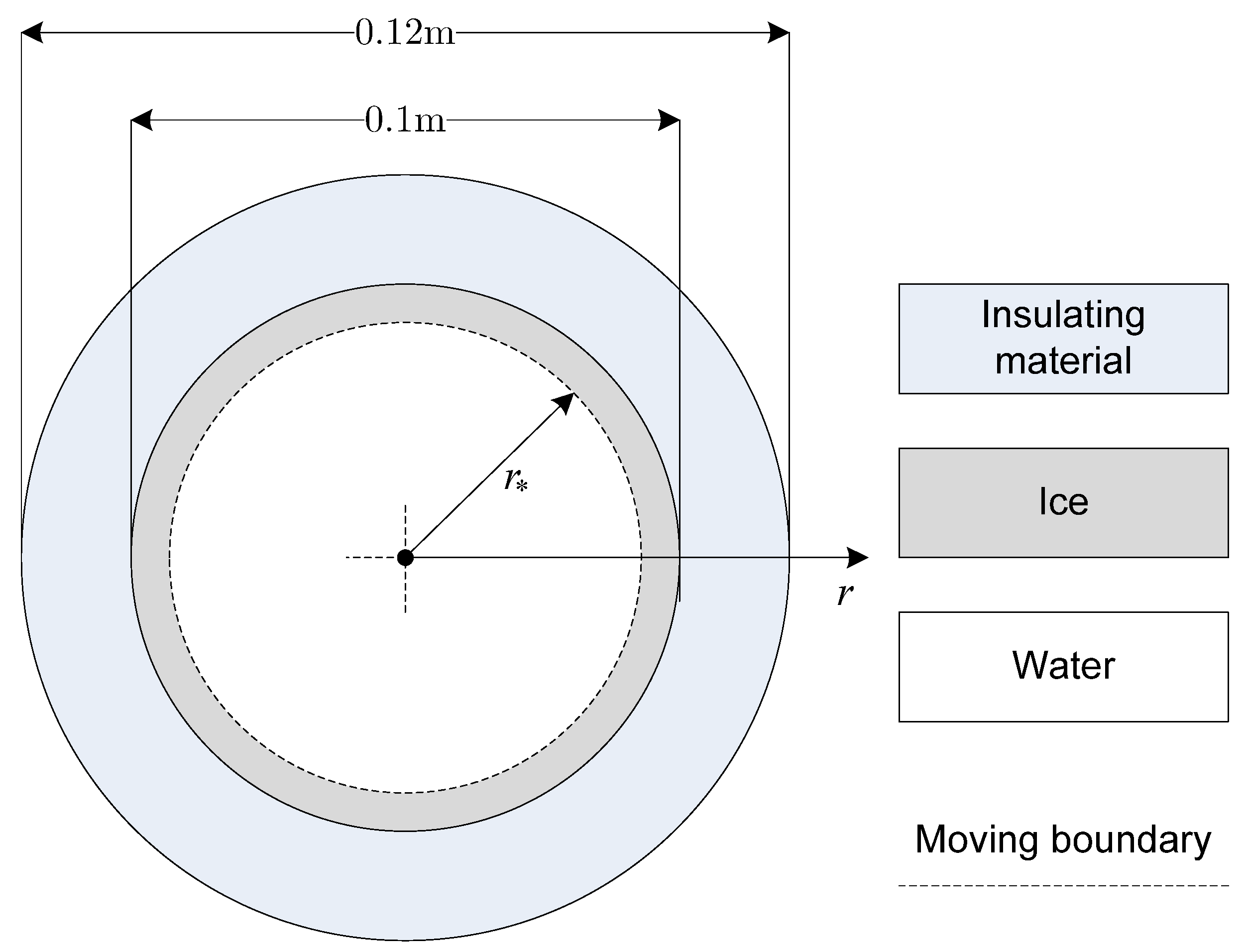
The
Stefan problem of melting/solidification in absence of material transport is considered. For the case of the melting/solidification of a two-phase flow, see Reference [
20].
Let
be the domain shown in
Figure 1 and
its boundary with outward normal unit vector
. The domain is composed of a solid region
and a liquid region
. We denote by
the interface between the two regions and by
the outward normal from
. The temperature in the point
at time
is
.
Figure 1.
Schematic representation of the domain.
Figure 1.
Schematic representation of the domain.
The model accounts for the heat transferred by conduction only; therefore, convection, thermal expansion, and buoyancy are not considered. Since deformations are excluded, the mass density
is the same in the solid and liquid phases. The energy conservation equation in the domain reads
where
is the heat capacity,
the heat flux vector, and
the volumetric heat source.
The constitutive equation which characterises the conductivity within the material is given by Fourier law,
where
is the thermal conductivity second-order tensor. In the following, we assume isotropy with respect to heat conduction, so that
, where
denotes the identity tensor and
the scalar thermal conductivity.
and
are taken as constants in each phase and their values in the solid and in the liquid are indicated by subscripts ‘sol’ and ‘liq’ respectively.
The essential and natural boundary conditions are
where
and
are assigned functions defined over
and
respectively, with
and
.
The phase-interface is characterised by the constant temperature
, so that the condition
holds. It is noted that the temperature field must be continuous through the interface; this requirement must be included (or enforced) in the numerical models as discussed in
Section 4.
It is also possible to consider more complicate interface conditions which involve the velocity of the interface or its geometrical properties. An example is Gibbs-Thomson relation, which describes the unstable dendritic growth of crystals into an undercooled melt, and modifies Eq. (4) as , where and are the surface tension and the kinetic mobility coefficients, is the mean curvature of the interface, and its normal speed (negative for melting and positive for solidification).
The evolution of the interface is governed by the Stefan equation, which expresses the energy balance of the interface,
where
is the latent heat of the phase transition and
the jump in the heat flux normal to
given by
The initial condition for the transient problem is provided by the knowledge of the temperature field at time
,
where
is a known continuous function over
. The initial conditions are completed by the knowledge of the position of the interface at
.
3. Description of the interface through level set
The
level set method (e.g. [
21]) is a numerical scheme used to describe implicitly geometrical objects such as surfaces and lines. The basic concept is to represent a surface
, of co-dimension one, in the domain
as the isocontour of some function
defined over
. The method can be extended to model objects with higher co-dimensions by considering multiple level set functions (as many as the co-dimension of the object); for instance, a curve in the three-dimensional space can be represented as the intersection of two surfaces, i.e. the isocontours of two functions
and
.
In the case of Stefan problem we need to represent the phase-transition interface, i.e. a surface
of co-dimension one, which evolves with the time. Therefore we need one level set function that depends also on the time. Let
be the distance of the point
from the transition interface at time
; we define the level set function as the signed distance function from the interface,
where the arbitrary sign convention in which
is positive in the liquid, negative in the solid, and vanishes on the phase interface, is adopted.
Eq. (9) allows the construction of
, when the position of the interface is known. Vice versa, when
is given, the interface
is the zero isocontour of
,
Take note that, whereas the function is not differentiable in space across the interface, the gradient of is defined everywhere in (provided that the interface is sufficiently regular) and on the interface it points in the direction of the outward normal from the solid region. Therefore, although the interface is obviously the zero level set of , itself is not suitable for describing the interface position since it is not sufficiently regular and, in the numerically approximated form used in computational models, would not reach the zero level in certain parts or would cross the zero twice in others.
Besides its position, the level set allows one to describe further geometrical properties of the interface. The normal unit vector is given by
Since the level set function has been chosen as the signed distance function,
, so that Eq. (11) simplifies to
. The interface mean curvature, which may have a physical interest in the case of Gibbs-Thomson diffusion (see
Section 2), can be computed as
which simplifies to
in the case of signed distance function.
In order to track the movement of the interface it is necessary to define suitable evolution equations for the level-set update. An Eulerian approach is followed by letting the level-set field be advected by a suitable velocity field
. The relevant evolution equation is then given in the Hamilton-Jacobi form by requiring the material derivative of the level set to vanish,
In particular, Eq. (13) requires that
be constant on the interface. The field
represents an extension of the interface velocity, which is physically defined only on
, to the whole domain
. In fact, whereas in a Lagrangian approach, where the position of the interface is tracked explicitly, the velocity on
suffices for its evolution, in an Eulerian approach, it is necessary to extend the velocity field to the entire domain so that the level set function, which controls the interface position and is defined everywhere in
, can be advected by such extended velocity field. It is convenient to introduce the scalar normal velocity
that is the component of
in the direction of
; Eq. (13) rewrites then as
The field
is the extension of the normal interface velocity to the entire domain, and it is known only on the interface, where it is physically meaningful and can be obtained by Eq. (5),
Since the velocity field in
is artificial, there is a certain freedom in its construction, the only requirements being that
be continuous through the interface and satisfy Eq. (16). It can be demonstrated [
22] that, if
and
are smooth and their gradients are orthogonal,
then
tends to preserve the initial signed-distance properties of the level set.
The evolution of
is controlled by Eq. (15), with the initial condition
Practically, in the initial time instant,
is constructed by the knowledge of
by using the definition in Eq. (9), whereas in the subsequent time instants, the updated position of the interface is obtained from
by Eq. (10). The field
is constructed by solving Eq. (17) with the essential boundary conditions provided by Eq. (16). The problem can be casted in a discrete form by using standard finite element techniques developed from the weak forms of Eqs (15) and (17),
where
and
are test fields belonging to
. Essential boundary conditions are provided by a discretised version of Eq. (16), which can be obtained, for instance, by considering the projection of the interface velocity onto the finite element nodes whose support is intersected by the interface. The complete procedure is thoroughfully derived in Reference [
16], where the numerical issues arising in the integration of first order hyperbolic equations are solved by adding stabilisation and shock-capturing terms; further stabilisation techniques for the update of the level set function are described in Reference [
21]. In the numerical analyses, the discretised field
progressively diverges from a signed distance function, so that every few steps a reinitialisation must be performed; some relevant procedures based on the fast marching algorithm are described in References [
22] and [
17].
5. Finite elements with embedded gradient discontinuity
An alternative approach to model localised discontinuities within the FEM consists in embedding the discontinuity directly into the elements by adding degrees of freedom at elemental level instead of nodal level (as in the XFEM). The resulting methods appear in the literature with different names and they can be considered somehow as precursors of the XFEM (e.g. [
59,
60]). Further references, mainly focusing on fracture mechanics, can be retrieved in the comparative study by Jirásek [
61].
The basic idea is to use standard FE interpolation as from Eq. (20) in all the elements but those intersected by
. In these latter, the standard interpolation is enriched by suitable functions
(
), which vanish at the nodes and reproduce the desired discontinuity. The resulting interpolation can be written as
where
are element-level parameters. The enrichment functions
depend on the time through the interface-position, which, in turn, is described by the time-evolving level set function. Eq. (45) is the embedded-discontinuity version of XFEM’s Eq. (31) and can be rewritten in matrix form as
where the matrix
collects the standard and discontinuity-embedding shape functions, and the vector
the standard nodal degrees of freedom and the additional elemental ones.
The numerical model is developed by following the same steps as in
Section 4.2 and
Section 4.3, so that the same formal expressions obtained there for the XFEM hold for the embedded-discontinuity FEM, once Eq. (31) is replaced by Eq. (45).
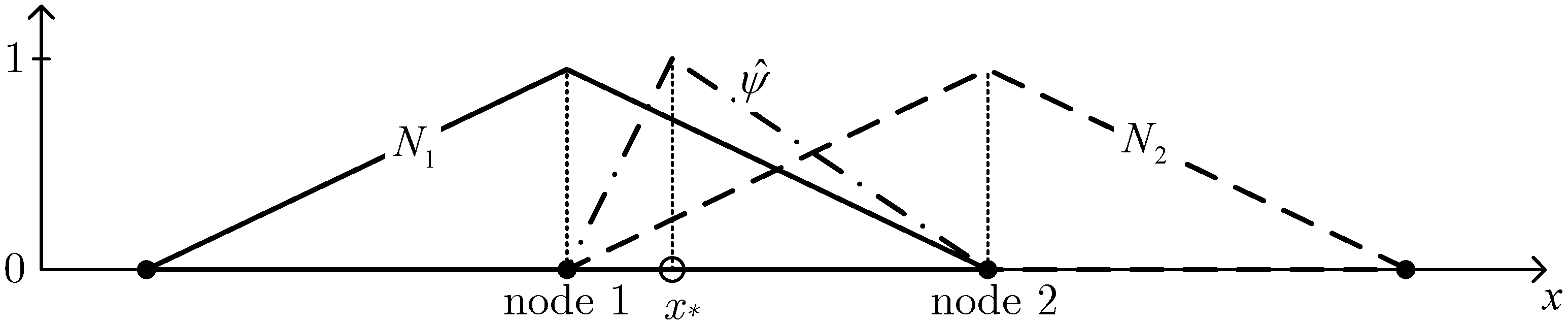
In order to explain the procedure, a two-node element with an embedded gradient discontinuity for the one-dimensional Stefan problem (see also
Section 6) is developed here. In this simple case the standard FE shape functions are linear (
Figure 4a) and the enrichment of the element containing the phase interface can be obtained by a piecewise-linear hat-shaped function
(
Figure 4c), whose contribution vanishes at the nodes, assumes a unit value at the discontinuity, and it is controlled by the elemental degree of freedom
.
Figure 4.
Shape functions within one element in local coordinate ξ: (a) standard, (b) enriched in XFEM, and (c) enriched in embedded-discontinuity FEM.
Figure 4.
Shape functions within one element in local coordinate ξ: (a) standard, (b) enriched in XFEM, and (c) enriched in embedded-discontinuity FEM.
It can be observed that the definition of
given above does not cover the case in which the phase interface coincides with a node. When the interface reaches the local
i-th node (
), the function
coincides with
, in the element that last contained the interface. However,
is still linearly independent from
at the global level, as visualised in
Figure 5, and no particular indeterminacy arises, unless the interface reaches the domain boundary. In the last, quite particular case, the loss of linear independency may also compromise the convergence of the gradient discontinuity at the phase boundary, as observed by Merle and Dolbow [
15], and, in any case, the conditioning of the system matrixes deteriorates as the phase interface gets closer to a boundary node.
Figure 5.
Standard FE shape functions and embedded-discontinuity function.
Figure 5.
Standard FE shape functions and embedded-discontinuity function.
The case discussed here is particularly simple and further difficulties arise in two and three dimensions or in case of stronger discontinuities, as in fracture mechanics. For these reasons, XFEM is usually preferred to embedded-discontinuity methods in those fields. However, in the case of one-dimensional Stefan problem, the approach developed above proves quite effective, as shown by the examples in
Section 6.6.
6. Numerical study on the error and applications to planar-symmetric problems
Exact solutions to Stefan problem exist in a very small number of cases such as those of planar symmetry with semi-infinite domain, in which the interface position is proportional to the square root of the time (similarity solutions). These cases are reviewed in this Section, so that the numerical results can be compared to exact values. The accuracy of XFEM is evaluated with respect to space and time discretisations. Penalty and Lagrange multiplier methods to enforce the interface temperature condition are compared, and the treatment of the blending elements is discussed. XFEM and embedded-discontinuity FEM are compared too. Finally, a second planar-symmetric example with finite domain is presented.
Besides exact solutions and for the cases in which such solutions are not available, we also consider the so-called pseudo steady state (PSS) approximations. These are based on the assumption that the rate of the interface movement is much slower than the rate of the temperature diffusion within the domain, so that the temperature field at a given time instant can be approximated with the steady-state field corresponding to a fixed phase-interface, and the interface position can be, in turn, updated from the resulting steady-state temperature field. It follows that the PSS solution is a suitable approximation for large values of the Stefan number
, defined as
where
is some temperature difference, characteristic of the specific problem (e.g. the temperature difference between two thermostats providing essential boundary conditions). A PSS approximation provides a limit behaviour, useful for comparisons where no exact analytical solution is available, such as the cases considered in
Section 6.7 and
Section 7. For further details on the exact and PSS analytical solutions, the Reader is referred to Reference [
19].
From here on, planar-, cylindrical-, and spherical-symmetric problems are considered. These can be treated as spatially one-dimensional, allowing for some simplifications in the interface-position tracking. In particular, with the phase-transition interface reduced to one point in the one-dimensional space (representing a planar, cylindrical, or spherical surface in the original three-dimensional space), one coordinate suffices for individuating the interface position and generating the level set.
In the examples below, we consider one-dimensional extended finite elements with two-nodes and linear shape functions, enriched as in Eq. (31). The relevant enriched shape functions are shown in
Figure 4b. In
Section 6.6, we also consider the embedded-discontinuity FEM described in
Section 5. Where it is not differently stated, the temperature condition on the phase interface is enforced through Lagrange multiplier method and no enrichment is used in the XFEM blending elements.
6.1. One-phase freezing problem
A planar-symmetric freezing problem in a semi-infinite domain is considered. Due to symmetry and material isotropy, the problem can be reduced to one dimension and the coordinate
in the direction orthogonal to the constant-temperature planes suffices to the problem description. The one-dimensional domain
is initially at the freezing/melting temperature, with
,
, and
. The boundary condition is
, whereas the initial position of the interface is
. The values used in the numerical examples are reported in
Table 1. Stefan number is computed with the temperature difference between phase-transition and coolant thermostat,
Table 1.
Data used in the numerical examples.
Table 1.
Data used in the numerical examples.
| One-phase | Two-phase | Polar-symmetric | Water-pipe |
| example data | example data | example data | example data |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | | |
With these initial and boundary conditions, no heat flow occurs in the liquid domain, which remains at a constant temperature, and the interface is driven only by the temperature gradient in the solid domain, so that the problem can be considered as a one-phase problem with moving boundary.
Neumann’s exact solution is available for this case. The temperature field in the solid region is given by
where the non-dimensional coefficient
is the positive real root of
and the position of the freezing front is given by
As further comparison, we also consider the PSS solution, although the Stefan number of the specific example, see Eq. (48), is not large enough for the PSS solution to constitute a good approximation [
19]. Under the PSS assumption, the one-dimensional governing equation becomes
with the boundary conditions
Integration of Eq. (52) leads to
The further integration of Eq. (5), with
and the initial condition
, results in
Eqs (54) and (55) are the PSS versions of Eqs (49) and (51) respectively. All of them are written into a form in which mutual comparison is straightforward; in particular it is noted that the temperature profile becomes linear in the case of PSS solutions, whereas the expression of the position of the freezing front only differs on a time scale-factor.
In the numerical analyses, we use a finite domain , with . Since no heat flux occurs in the liquid phase as long as the position of the interface is contained into , the numerical set-up is completely equivalent to the one studied analytically, provided that the natural boundary condition is imposed.
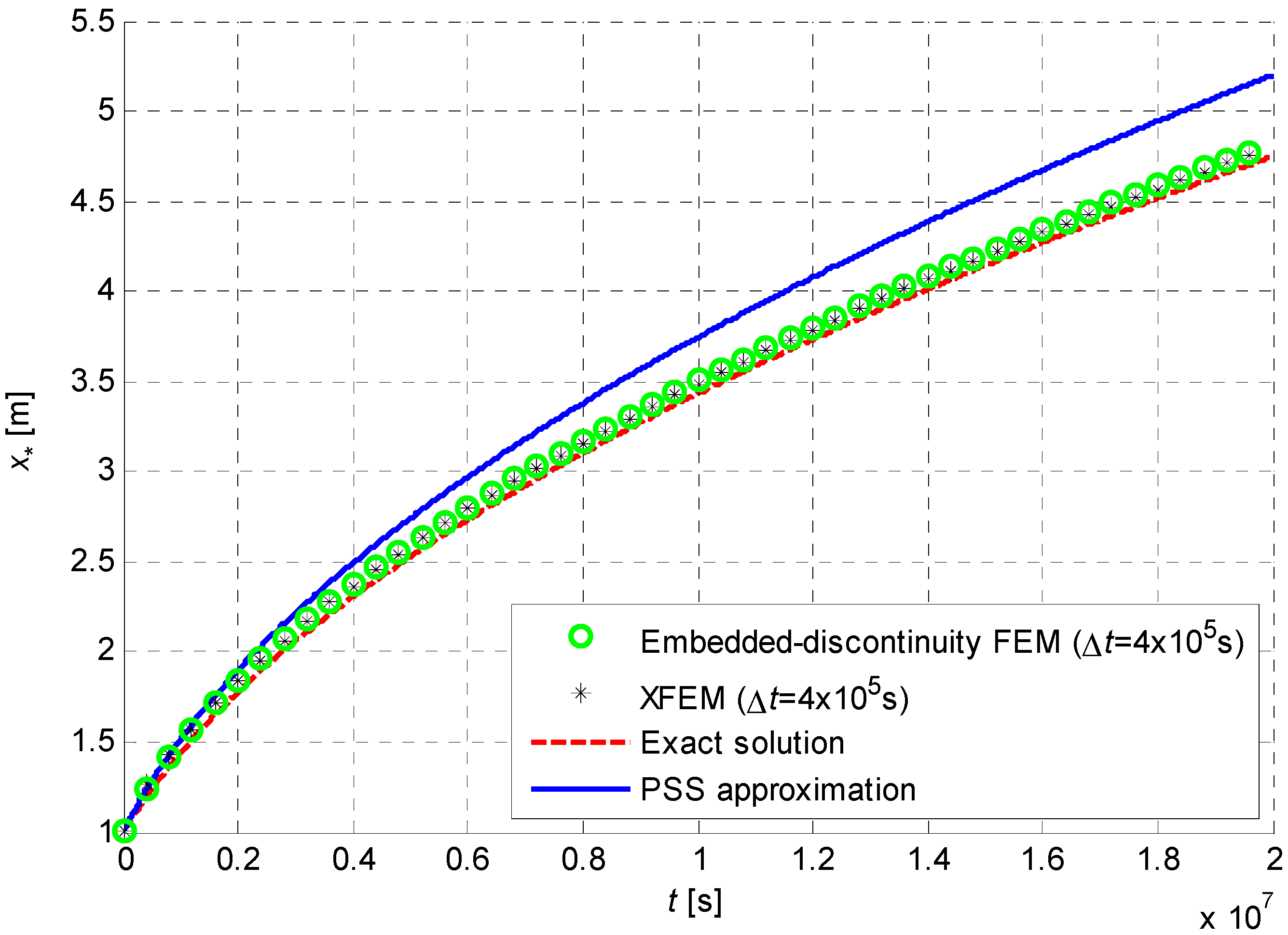
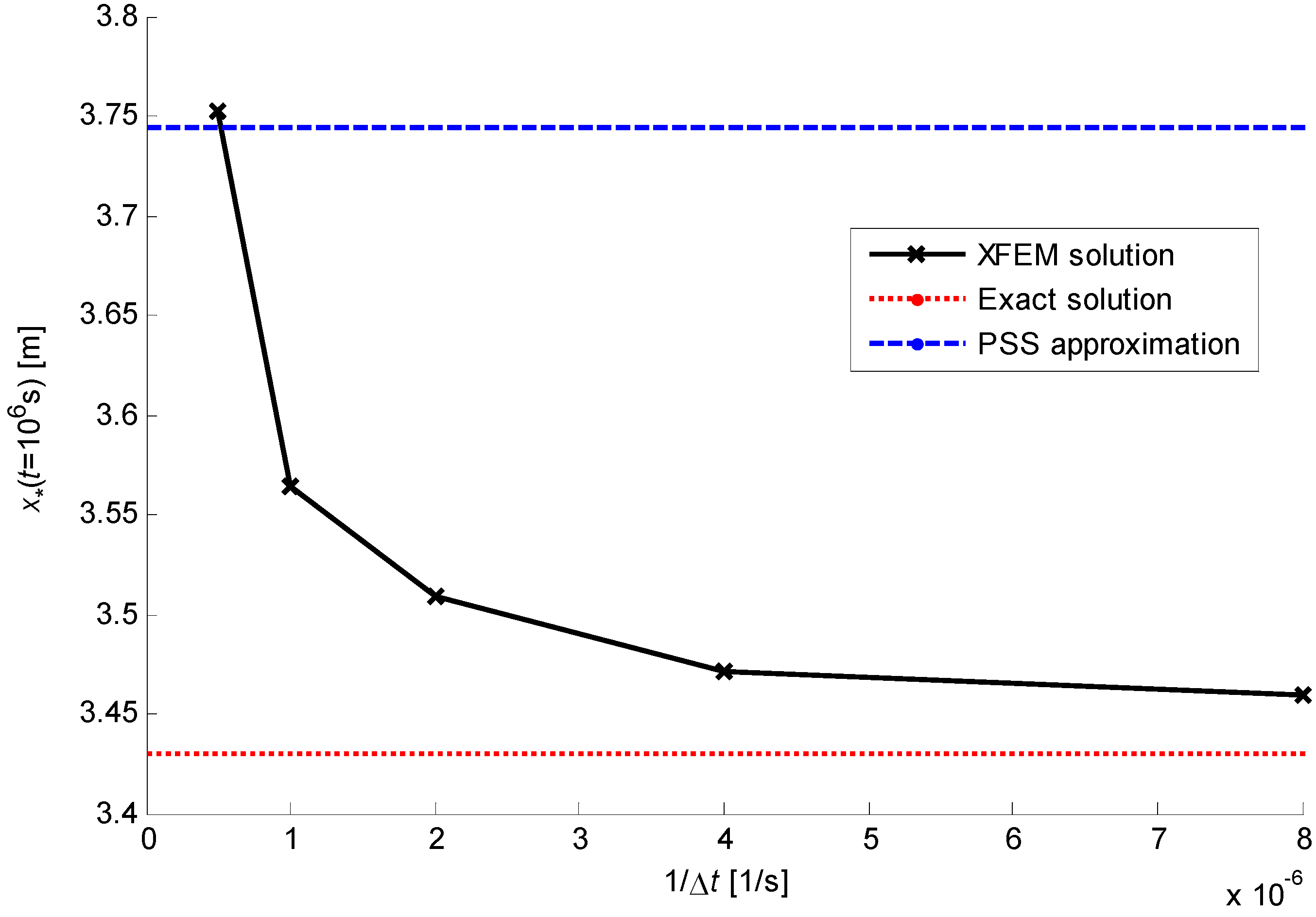
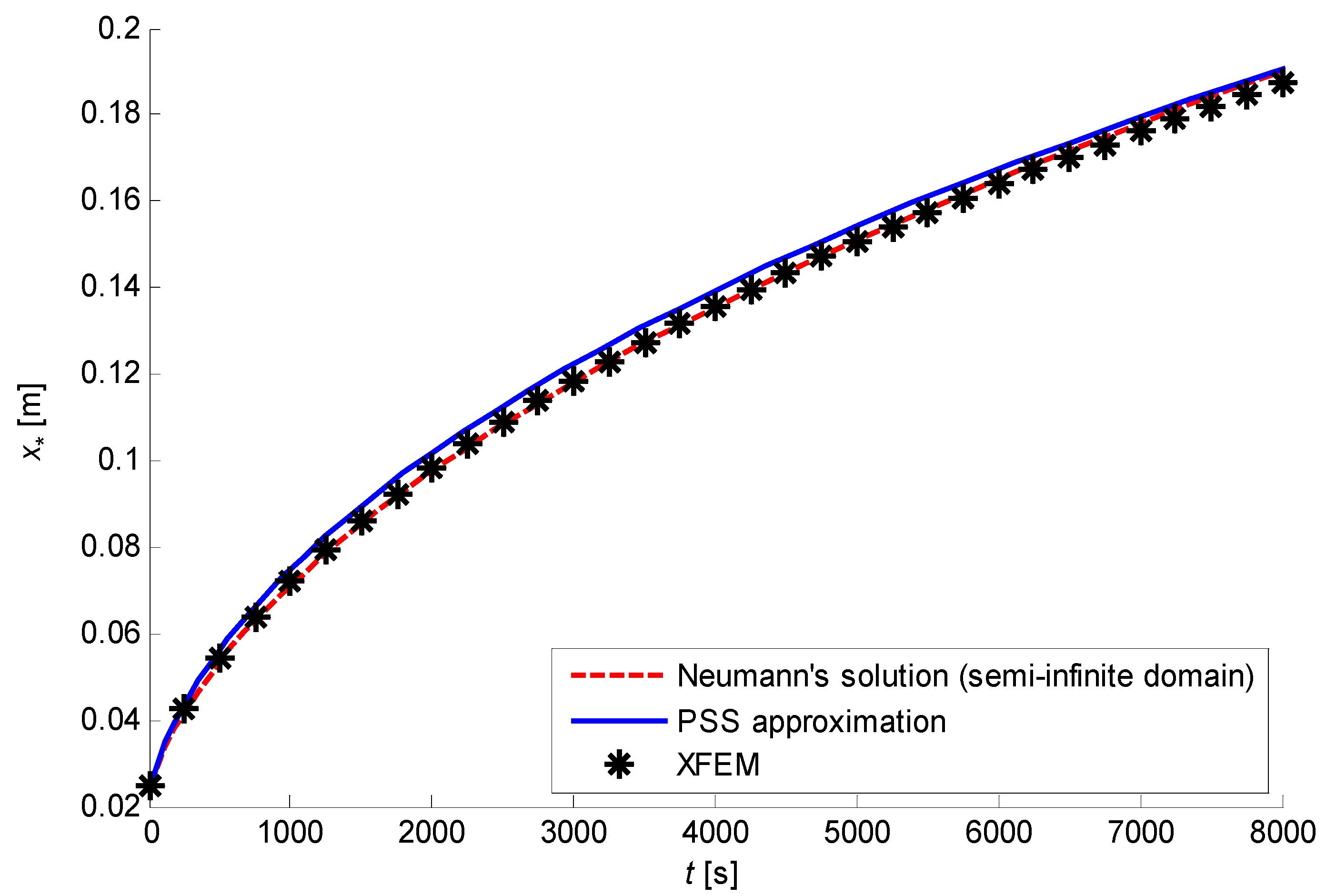
In
Figure 6, the interface position calculated through Neumann’s and PSS analytical solutions are compared with the XFEM simulations obtained with a spatial discretisation in 10 equally-sized elements and a time-step
. The numerical results are very close to the exact ones, whereas the PSS solution overestimates the freezing-front velocity because it does not account for the thermal inertia. At a closer look, the numerical solution lies slightly above the exact one, due to the use of backward Euler integration scheme, in which the interface position at current time-step is updated with the velocity of the previous time-step, i.e. a slightly overestimated one in this example. Of course, this effect is reduced with smaller time-steps and the XFEM solution converges to the exact one as the temporal and spatial discretisations are refined (see
Section 6.2 and
Section 6.3). The temperature field at some different time-steps is shown in
Figure 7, where the numerical and the exact solutions superimpose quite well one to the other, whereas the PSS approximation overestimates the phase-interface positions.
Figure 6.
Interface position for the one-phase planar-symmetric example.
Figure 6.
Interface position for the one-phase planar-symmetric example.
Figure 7.
Temperature field for the one-phase planar-symmetric example.
Figure 7.
Temperature field for the one-phase planar-symmetric example.
6.2. Time discretisation
As mentioned above, backward Euler integration evaluates the interface position at every time step with the temperature gradient computed through finite differences in the previous time-step, so that the computed gradient is slightly larger, in the considered example, than the exact one.
Figure 8 shows the interface position obtained with different time discretisations at a fixed time instant
. The interface position converges to the exact one as
goes to zero. The non-dimensional relative error
is represented versus the time-step size in
Figure 9.
Figure 8.
Convergence of the interface position.
Figure 8.
Convergence of the interface position.
Figure 9.
Relative error in the interface position.
Figure 9.
Relative error in the interface position.
6.3. Space discretisation
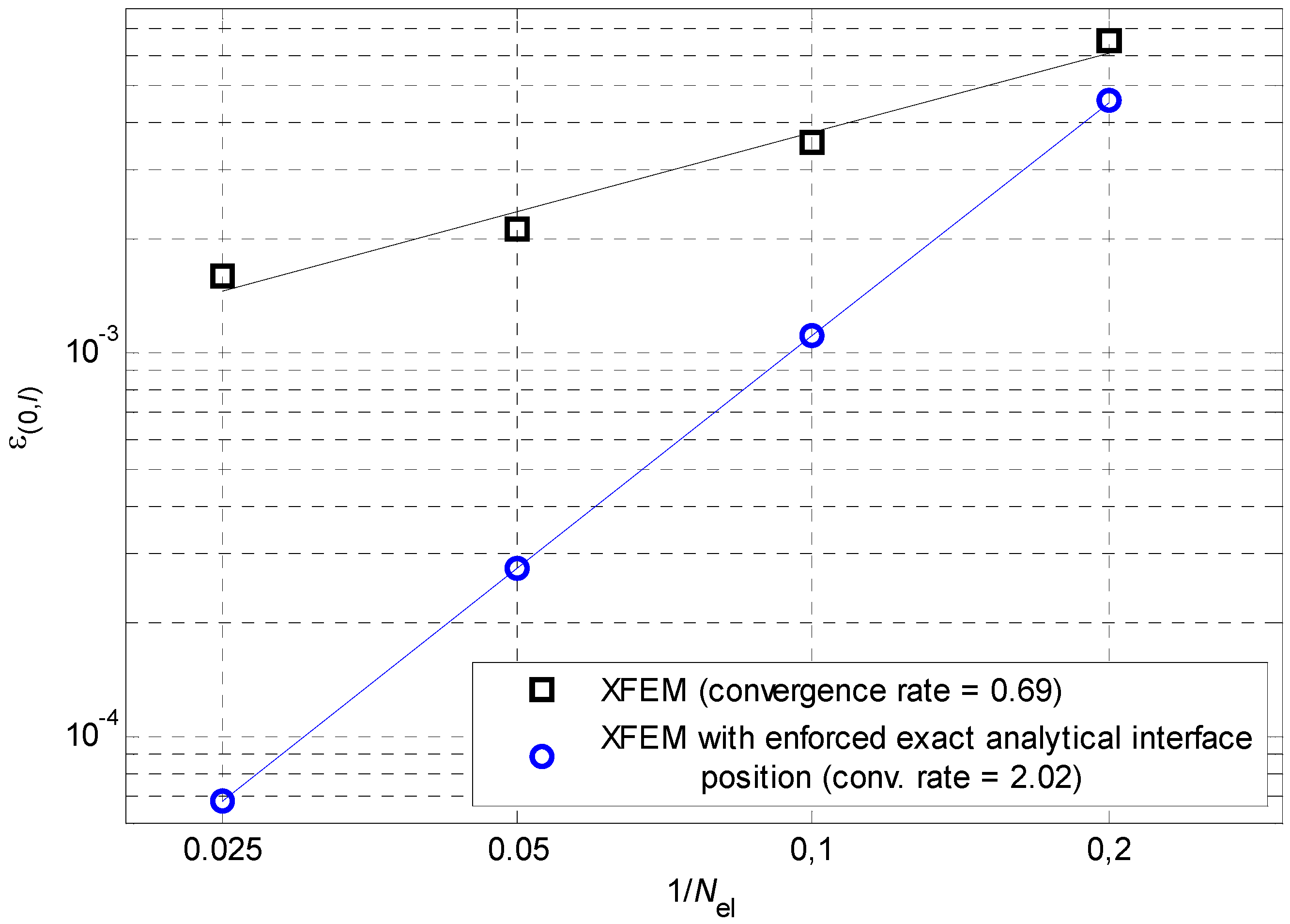
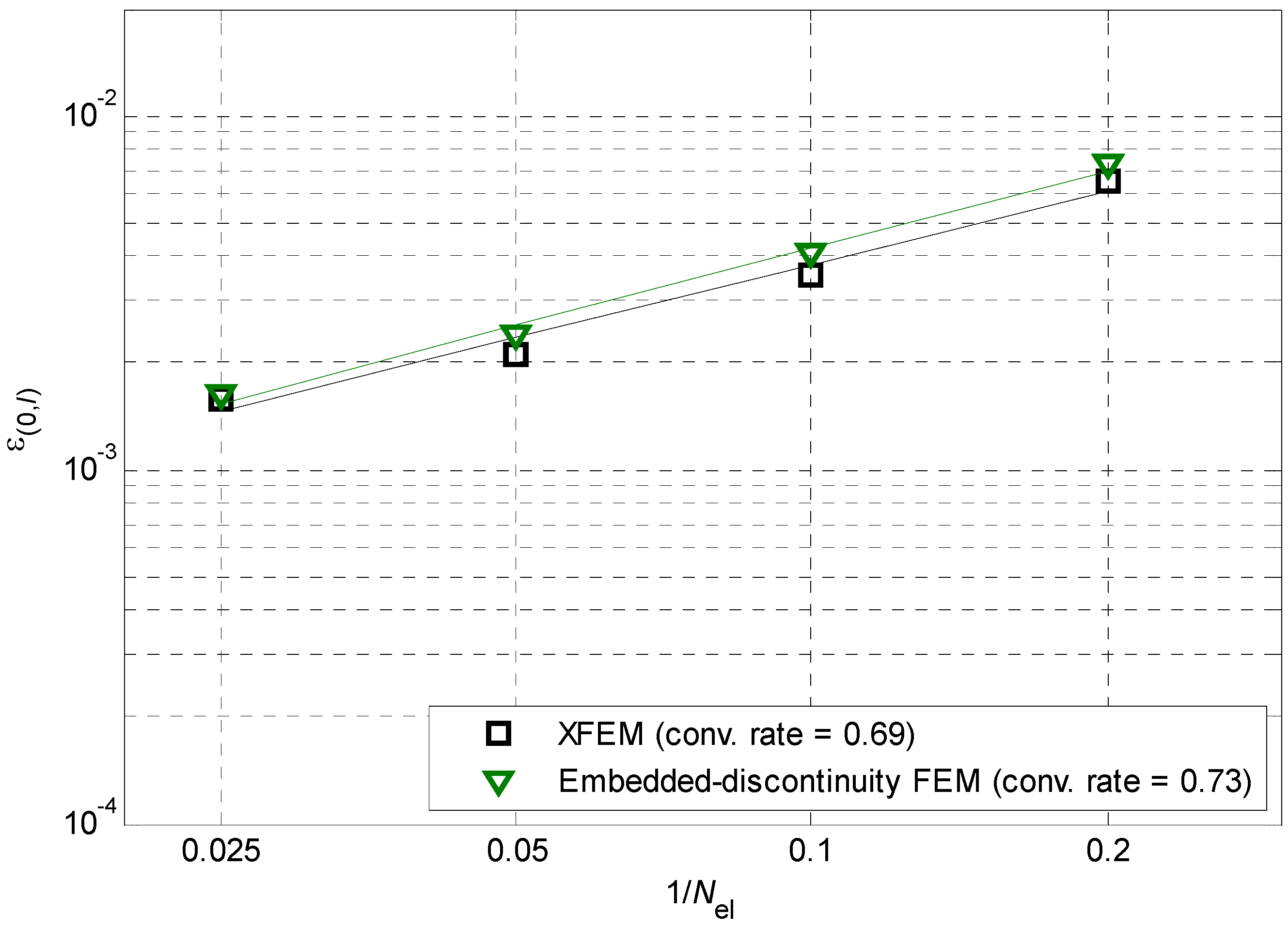
The dependence on the spatial discretisation of the error in XFEM simulations with respect to the exact solution is studied by considering the same example of
Section 6.1 with a fixed time step and a domain subdivision into different numbers of equally-sized elements.
The error in a spatial subdomain
at time
is evaluated as
which, for the convergence study, is equivalent to the square-root of the non-dimensional error in the energy. The convergence to exact solution is shown in
Figure 10, where the error in the whole domain is averaged on the time and plotted as a function of the normalised element size (i.e. the inverse of the number of elements in which the spatial domain is subdivided). Of course, the error on the spatial discretisation is increased by the error on the interface position (and vice versa), which is responsible of the apparent scatter in the error values, as well as of a reduced convergence rate. In order to highlight this effect, the error on the spatial discretisation can be somehow ‘depurated’ from the time-discretisation error by enforcing the exact analytical interface position in the numerical simulations. In this way a higher convergence rate and no ‘scatter’ are obtained, as also shown in
Figure 10.
Figure 10.
Error in temperature field versus element size.
Figure 10.
Error in temperature field versus element size.
6.4. Constraint enforcement
The enforcement of the phase-transition temperature at the interface, described in
Section 4.3, is discussed here in the same settings of
Section 6.1.
We consider first the penalty method, which is used in most of the research works on XFEM and Stefan problem [
15,
16,
17], because of its robustness and simplicity of implementation. As discussed in
Section 4.3, the main disadvantage of this method is that high values of the penalty coefficient
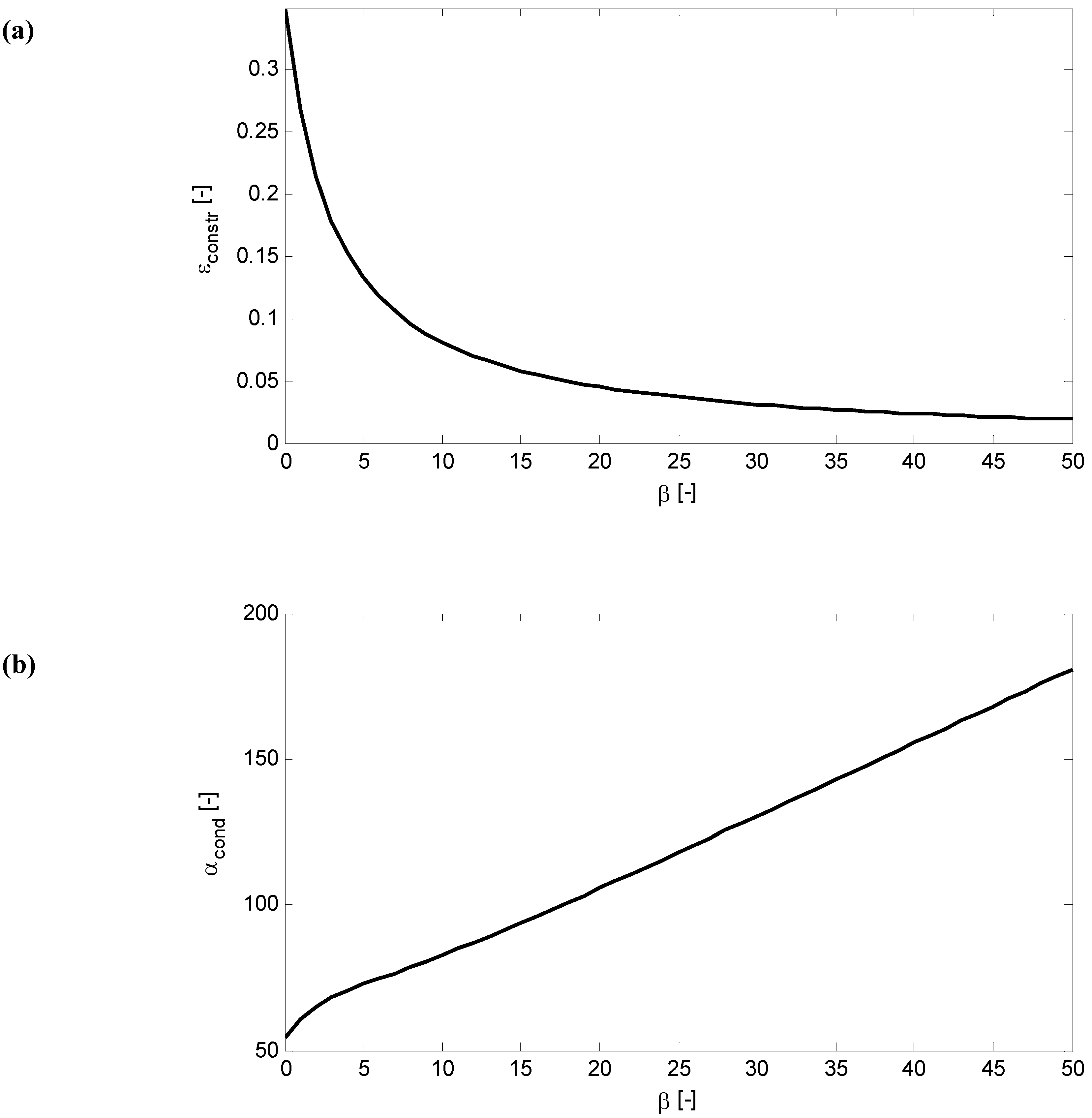
, while accurately enforcing the constraint, may lead to a poor conditioning of the numerical problem of Eq. (42). We define the error in the enforcement of the constraint at a given time instant as
Figure 11.
Penalty method: relative error (a) and condition number (b).
Figure 11.
Penalty method: relative error (a) and condition number (b).
The conditioning of the linear system in Eq. (42) is measured by the condition number with respect to inversion,
, defined as the ratio between the maximum and the minimum singular values of the system matrix
; the higher is
and the worse is the conditioning of the numerical problem. The error and the numerical conditioning are studied as functions of the non-dimensional penalty coefficient, which we define as
with
and
the average cross-sectional area and length of the one-dimensional elements, respectively. Since
is dimensionless, the term in parentheses in Eq. (59) contains the physical dimension and the average magnitude of the coefficients of the stiffness matrix
, which, in turn, contributes to
. In this way,
is expected to be less problem-dependent than its dimensional version
.
Figure 11 shows the influence of the penalty coefficient on the quality of the constraint enforcement and of the numerical solution (both averaged over several time-steps); low values of
result in a poor enforcement of the interface condition, whereas high values lead to a progressive increase of the condition number. It is then evident that in practical cases the value of
must be chosen as a compromise between accuracy of the constraint enforcement and quality of the numerical solution.
The error in the constraint enforcement vanishes if Lagrange Multiplier method is used. The temperature field in the vicinity of the phase-interface at time
as obtained with penalty (
) and Lagrange multiplier methods is shown in
Figure 12 (position and temperature are indicated by solid dots for the nodes and by a circle for the interface).
In the analysed case, the condition number with the Lagrange multiplier method is 104.5 with an exact enforcement of the constraint; the same condition number can be obtained with the penalty method for , with an error in the constrain enforcement exceeding 5%.
Figure 12.
Temperature field in the vicinity of the interface.
Figure 12.
Temperature field in the vicinity of the interface.
6.5. On the interpolation in the blending elements
The treatment of blending elements (i.e. those whose nodal support is only partially enriched, see
Section 4.1) is discussed here by means of a numerical example. Different approaches to the temperature interpolation in this region are possible: (i) the partial enrichment by routinely applying Eq. (31), (ii) the adoption of special strategies such as the use of hierarchical functions (e.g. [
62]), and (iii) the use of standard FE shape functions only (as in the non-enriched elements).
The XFEM strategy consists in enriching the nodes whose support is intersected by the discontinuity. In this way the subset
of the standard FE shape functions constitutes a local partition of unity in the region
surrounding the discontinuity and does not affect the region far from the enriched nodes (where standard FE interpolation holds). However, by following approach (i), the enrichment involves a region
and is only partial in the region
, i.e. in the blending elements. In a blending element, only some nodes are enriched and the subset of the standard shape functions used to weight the discontinuity does not represent a partition of unity. This leads to the appearance of pathological terms and, in general, to a sub-optimal convergence rate [
62].
One possible cure, the approach (ii), is the use of hierarchical, higher-order shape functions as proposed in Reference [
62]. The idea is that the enrichment functions are obtained by the product of the standard FE shape functions (linear, in our case) and the enrichment functions (also linear); therefore, it is possible to compensate their pathological contributions by using higher order FE shape functions in the blending elements (second grade polynomials). This approach proves very effective as demonstrated by their proposer. However, in those cases in which the interface is not fixed, local modifications of the topology are required as the interface evolves. When the interface moves from one element to another one, new nodes must be enriched and, consequently, some standard elements become blending elements. There, in a topological approach, new hierarchical nodes must be added. This may complicate the implementation of the method, even though the result is computationally cheaper than the remeshing required by standard FEM with adaptive mesh. Tarancón et al. [
62], shows that the approximation error
in a two-node one-dimensional blending element satisfies the inequality
where
and
are points inside the element and
is the extended degree of freedom of the enriched node. It is clear that the second term in the right-hand side of Eq. (60), which is not present in the standard FE case, may lead to an increased error. This pathological term can be compensated by using higher-order (second grade, in our case) standard shape functions for the blending element, controlled by additional standard degrees of freedom (hierarchical approach).
Alternatively, as in the approach (iii), it is possible to eliminate the pathological term by considering the enrichment functions only in those elements whose support is completely enriched and simply using the standard FE shape functions in the blending elements. In fracture mechanics, where the XFEM has been originally developed, this approach causes problems, as the displacement field may not be well reproduced in the vicinity of the interface boundaries (the crack tips) and conformity between enriched and blending elements may be lost. In the case of Stephan problem, however, these are not concerns. In fact, the phase-interface has no boundaries inside the body (either it is a closed surface or its boundary belongs to the domain boundary) and the considered discontinuity is weaker (gradient discontinuity). Incidentally, we observe that non-conforming elements (sometimes called ‘incompatible’) are not uncommon, and the loss of conformity can be traded for an improved accuracy in secondary (but sometimes more relevant for technical applications) variables such as strains and stresses (e.g. [
63,
64,
65]).
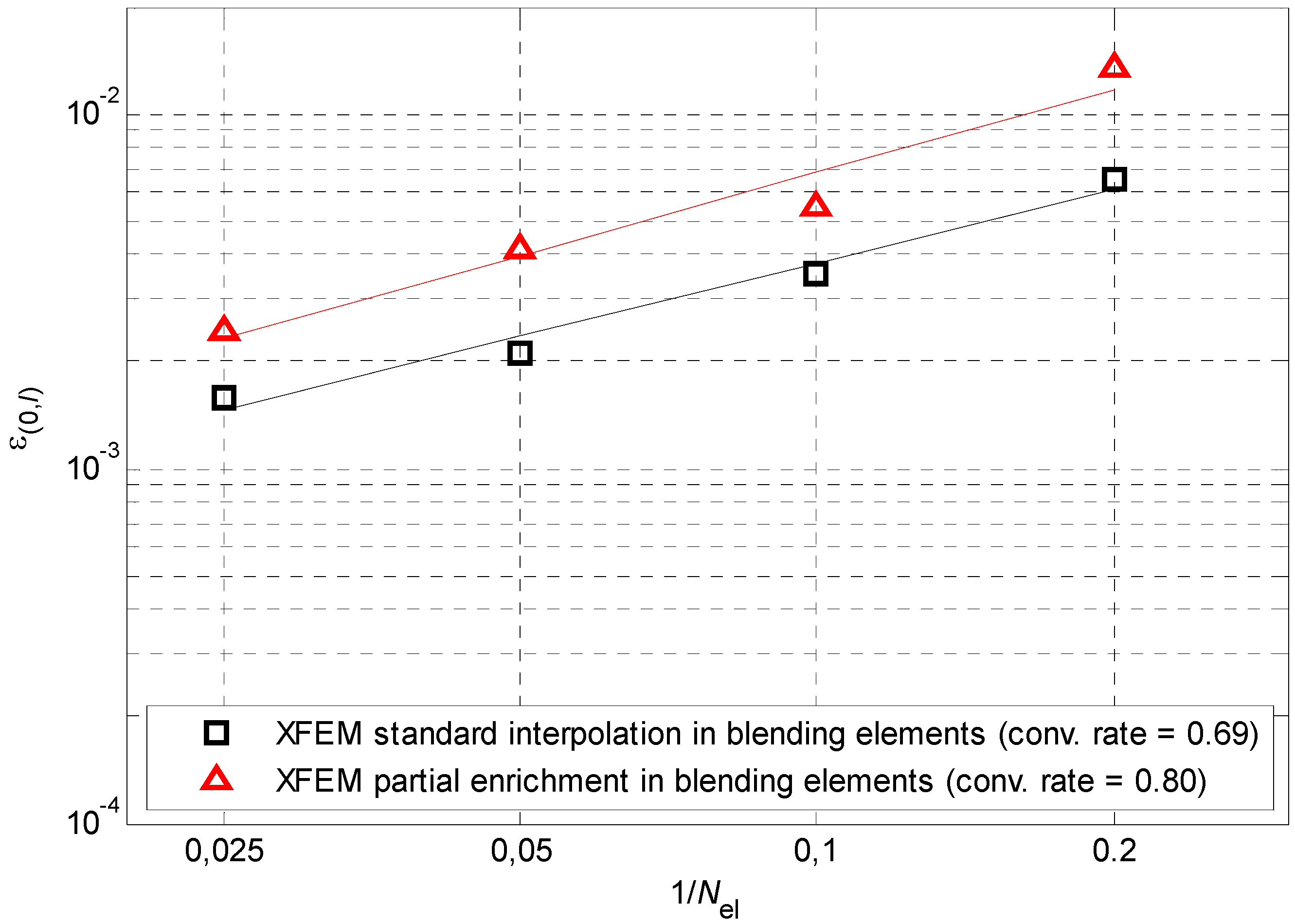
With that said, the approach (iii) seems optimal in the case of phase transitions and it is used in all the examples of the present paper. Only in this Section we compare the approaches (i) and (iii).
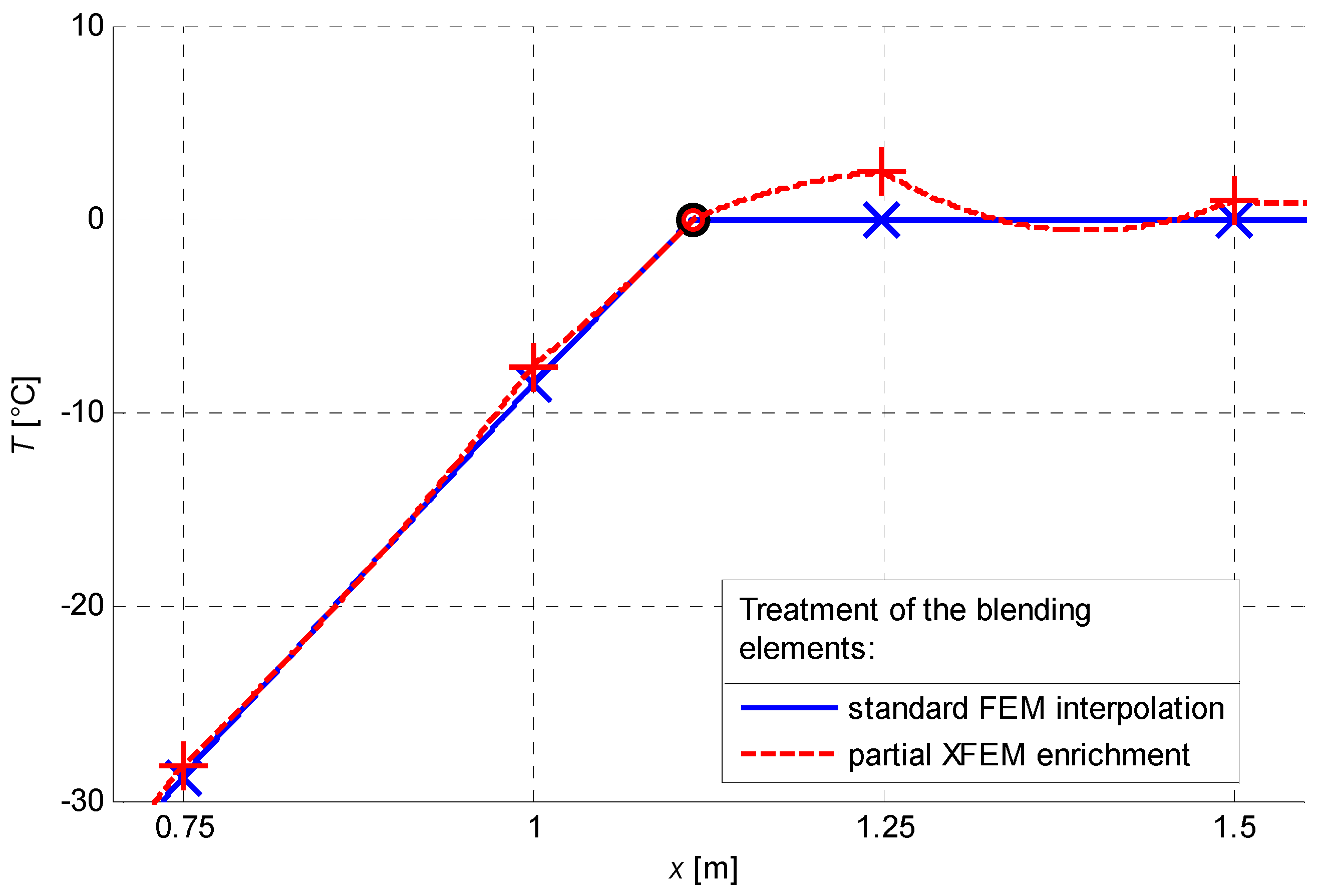
Figure 13 shows the error as a function of the spatial discretisation, computed as in
Section 6.3. The temperature fields obtained in the two cases at the same time instant are shown in
Figure 14 (where the crosses denote the nodal positions and temperatures, and the circle the phase interface). It is noted that, not only approach (i) is less accurate than approach (iii), which confirms the estimates by Tarancón et al. [
62], but it also leads to a poor estimate of the left- and right-gradients of the temperature at the interface, altering the rate of its movement.
Figure 13.
Error versus element size with different kind of blending elements.
Figure 13.
Error versus element size with different kind of blending elements.
Figure 14.
Temperature field with different kind of blending elements.
Figure 14.
Temperature field with different kind of blending elements.
6.6. Comparison with embedded-discontinuity finite elements
The one-phase problem of
Section 6.1 is now analysed by means of the one-dimensional embedded-discontinuity FEM developed in
Section 5. The simulations are performed by using the penalty method for the enforcement of the interface condition, with
.
As a first analysis, we discretise the spatial domain into 10 equally-sized elements and time with
, the same discretisations used with XFEM in
Section 6.1.
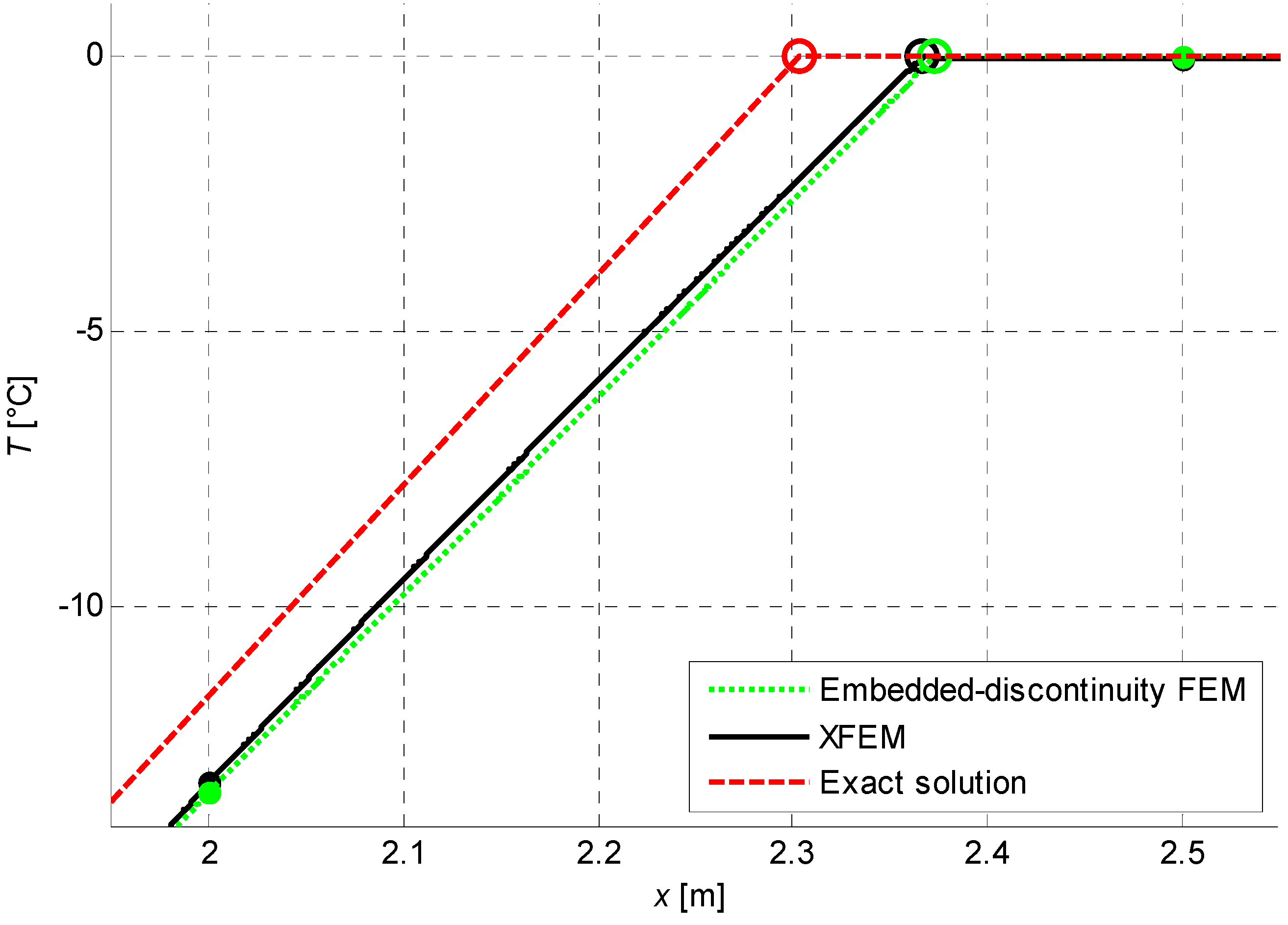
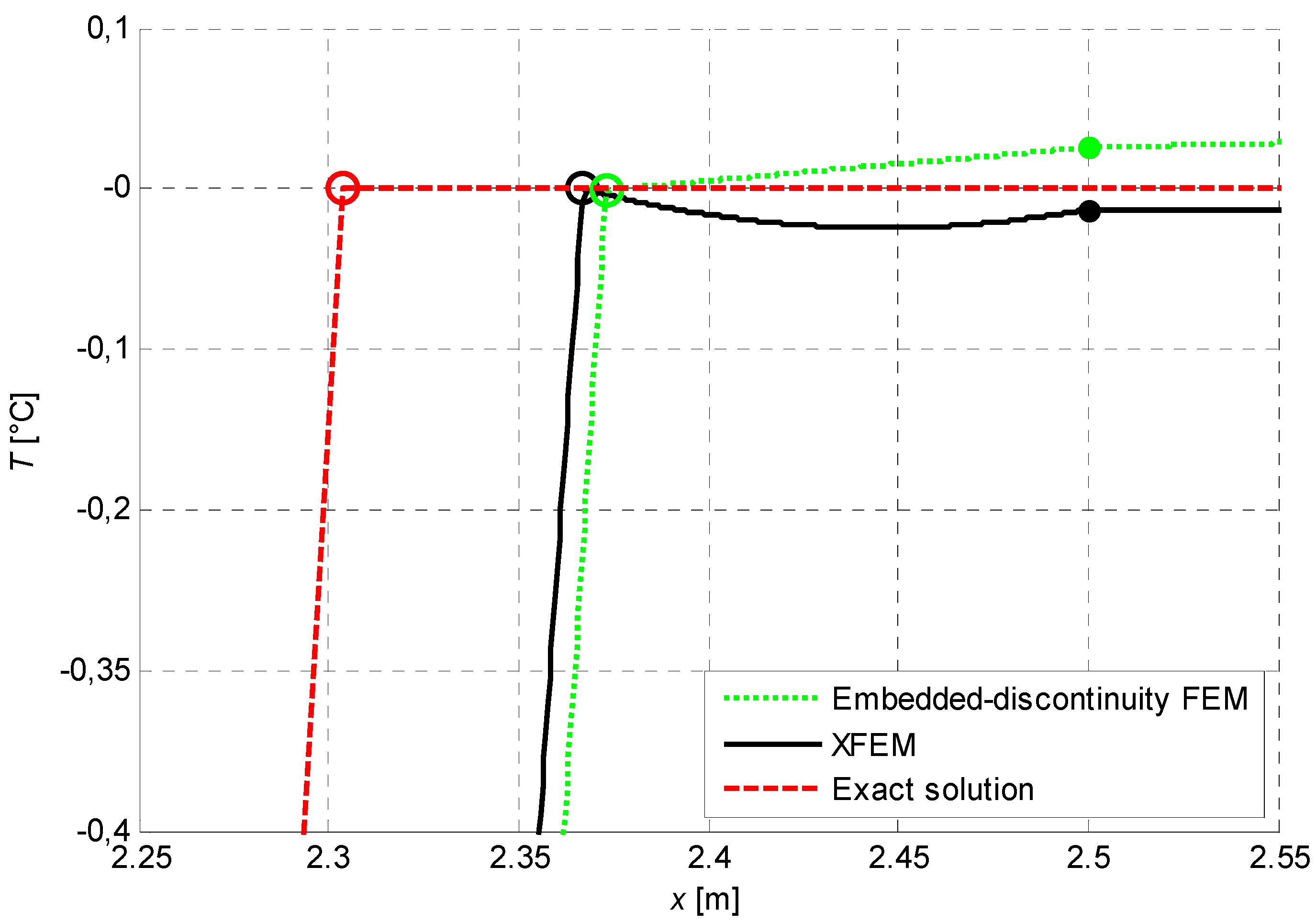
Figure 6 shows the evolution of the melting front computed with embedded-discontinuity FEM in comparison with XFEM results and analytical calculations. The two numerical techniques provide comparable results, with only a slightly smaller accuracy in the embedded-discontinuity FEM. The temperature field in the element containing the discontinuity at
is shown in
Figure 15, where the two numerical methods appear as quite equivalent. A particular of the same plot is shown in
Figure 16, where the differences in the interpolation (linear for embedded-discontinuity FEM and quadratic for XFEM) can be appreciated thanks to a strong magnification on the temperature axis. In
Figure 15 and
Figure 16, the dots denote nodal positions and temperatures and the circles highlight the phase interface.
As a second analysis, the convergence with spatial discretisation is studied in the same way of
Section 6.3. The results are summarised by the plot in
Figure 17, where embedded-discontinuity FEM and XFEM are compared. The two methods show, in the present case, comparable accuracy and convergence rate.
Figure 15.
Temperature field in the element containing the discontinuity.
Figure 15.
Temperature field in the element containing the discontinuity.
Figure 17.
Error in temperature field versus element size for embedded-discontinuity FEM.
Figure 17.
Error in temperature field versus element size for embedded-discontinuity FEM.
6.7. Two-phase solidification problem
The planar-symmetric solidification process of aluminium in a case in which the heat conduction occurs in both the solid and the liquid phases is considered. The one-dimensional domain is , with , , and . The boundary conditions are and ; both phases are initially at the temperature .
Under these conditions, no exact analytical solution is available. Then, Neumann’s solution for the case in which the domain is unbounded on the side of positive (i.e. when tends to infinity) and the PSS solutions are used to compare the numerical results. Neumann’s solution is exact in the semi-infinite domain; therefore, in the finite domain it provides a good approximation only in the earliest instants of the melting process. On the other hand, the PSS solution is expected to provide a better and better approximation as the system approaches the steady state.
For the two-phase problem described above, the interface position calculated through Neumann’s analytical solution is
where
gamma is the positive root of
being
the solid-to-fluid thermal diffusivity ratio.
The PSS approximation is developed analogously to the one-phase case of
Section 6.1. From Eq. (52) we obtain linear temperature fields in the solid and liquid phases, and the evolution of the melting front is obtained (in an implicit form) as
where the constants
,
, and
are introduced for the sake of conciseness.
The numerical data used in the example are reported in
Table 1 and the resulting Stefan number is
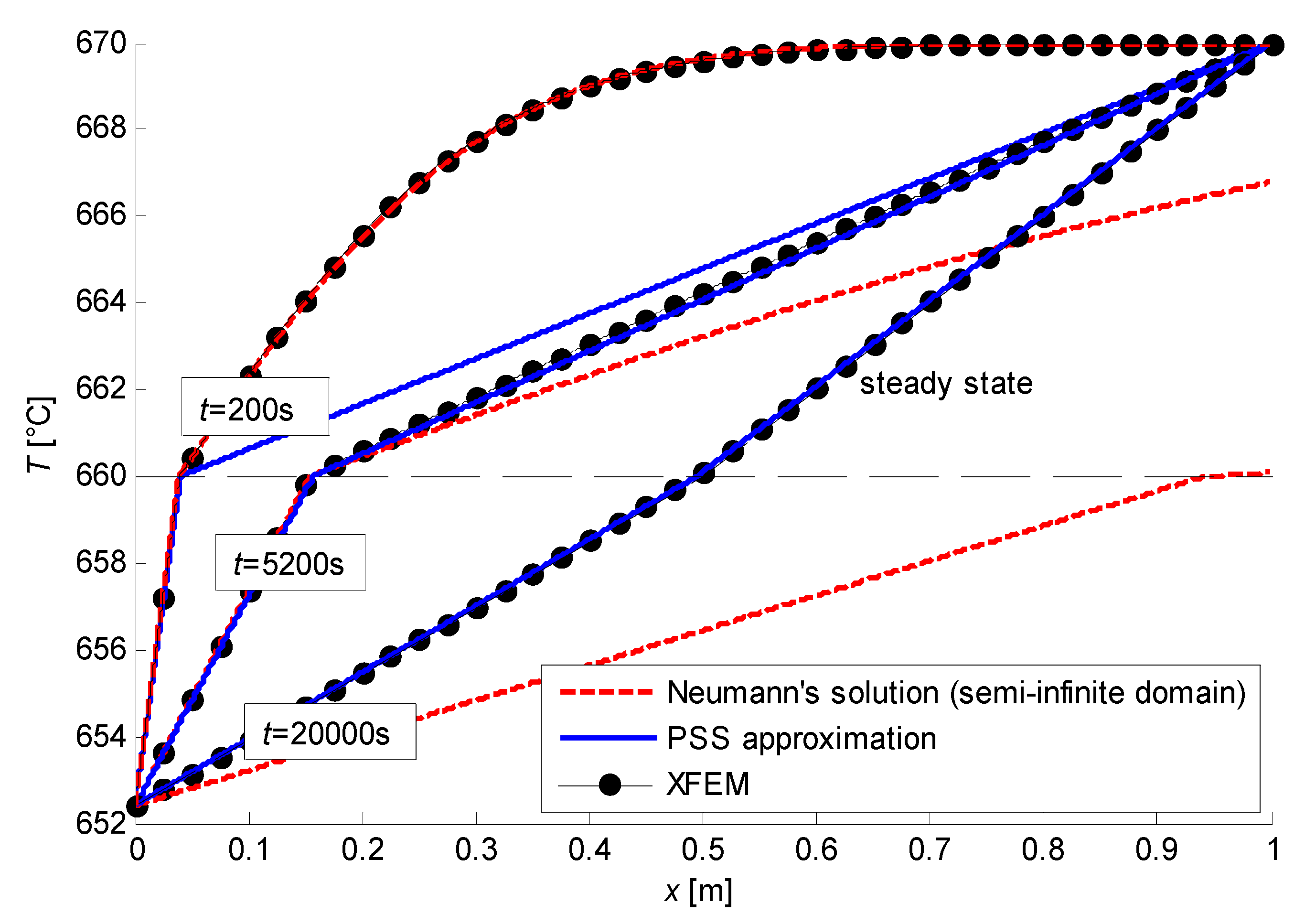
As it can be evinced from
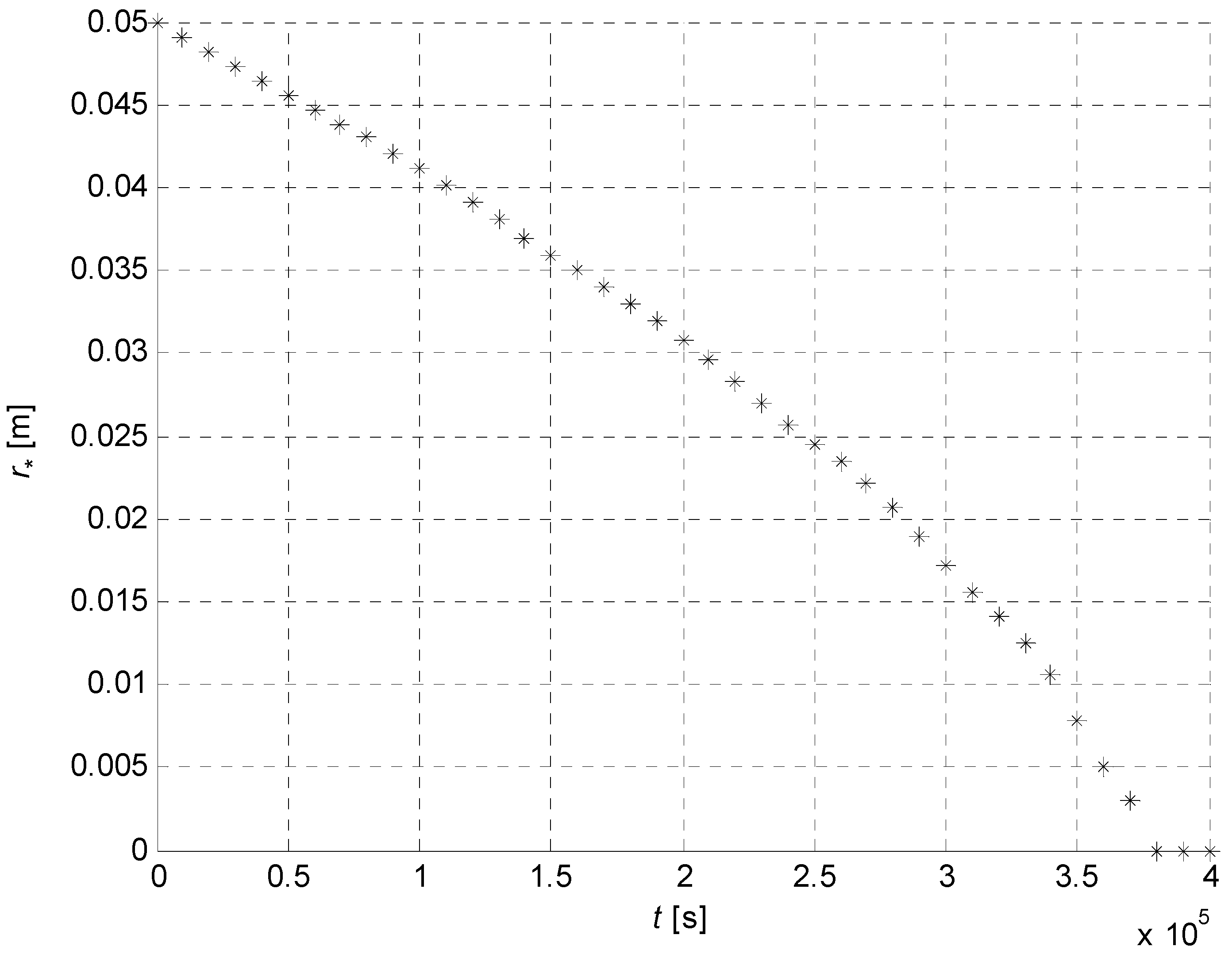
Figure 18, the interface positions evaluated by the XFEM and the two analytical models are close in the initial time instants. Afterwards, the numerical solution and the PSS approximation converge to the steady state, whereas Neumann’s solution (which matches different boundary conditions) diverges. However, in the initial instants, when the position of thermostat
makes little difference, Neumann’s solution should be considered as reference, since it includes thermal inertia, contrarily to the PSS solution. The position of the phase-interface in such initial instants is represented in
Figure 19, where the better agreement of the numerical simulation to Neumann’s results is highlighted.
The temperature fields within the domain at some time instants are plotted in
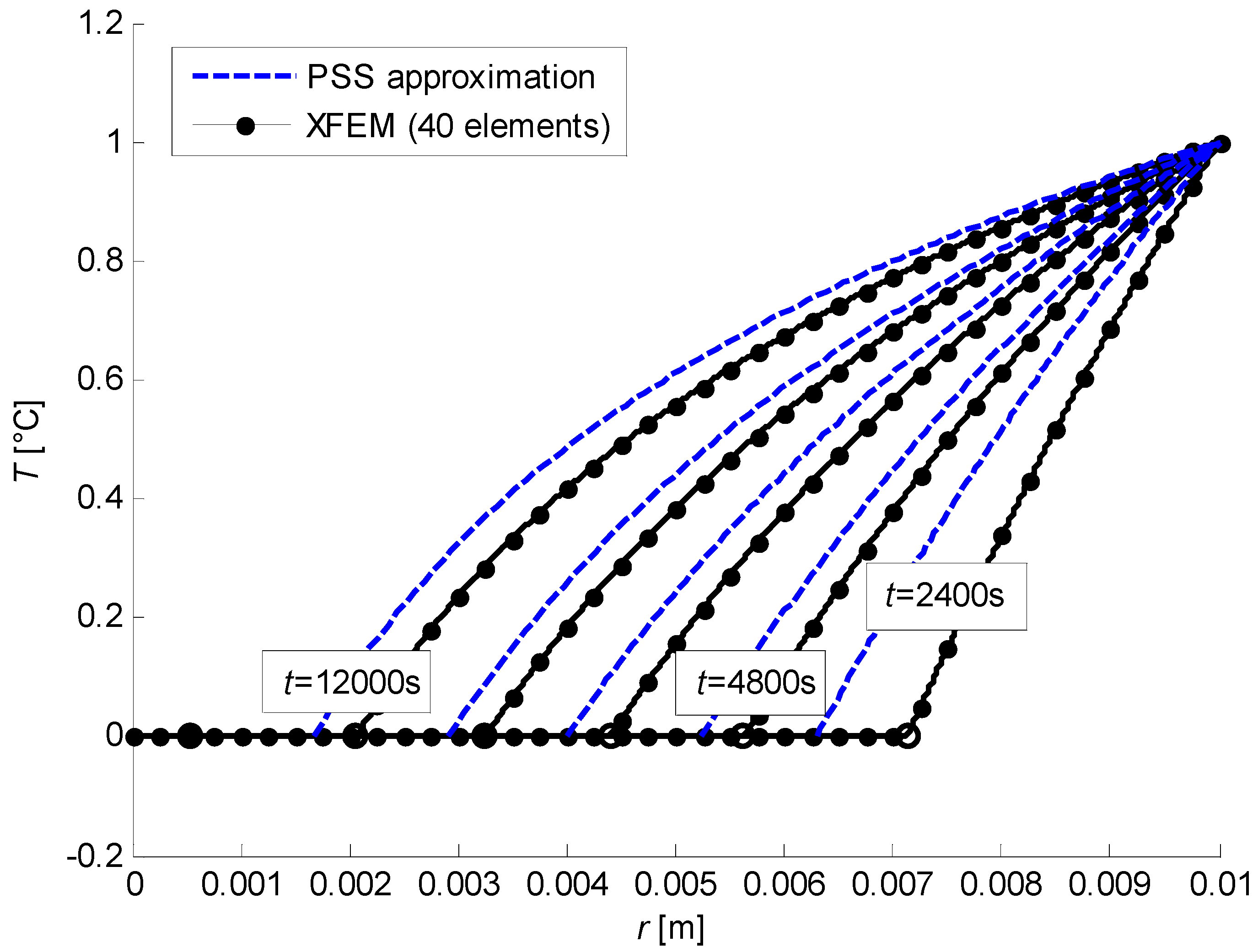
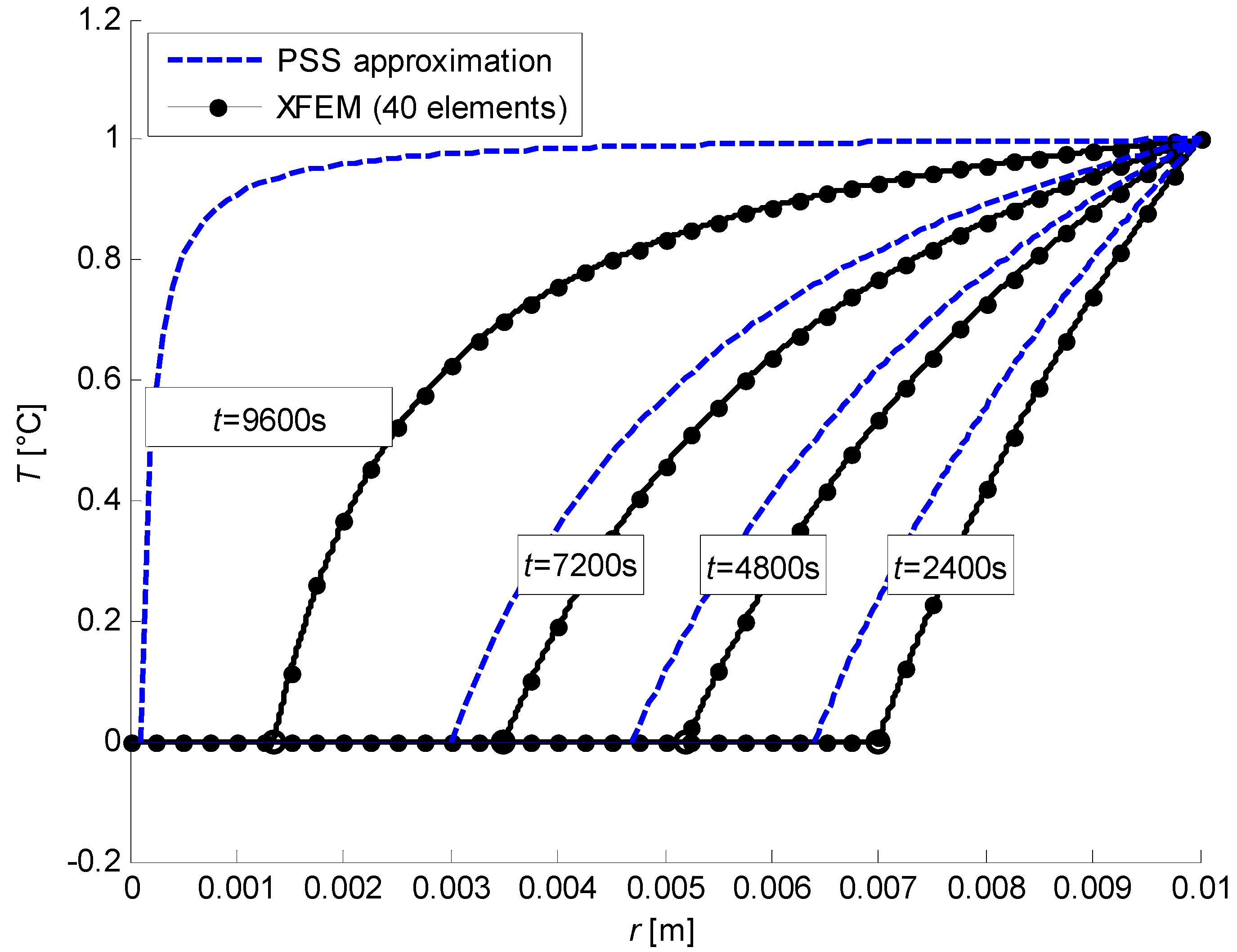
Figure 20. Initially, when the effects of thermal inertia are larger, the PSS (piecewise linear) temperature field poorly approximates the expected physical behaviour, which is more suitably represented by Neumann’s solution. On the other hand, as the system approaches the steady state (represented by the dashed lines, almost superimposed with the fields at
), the thermal inertia becomes less and less significant so that the PSS approximation can be considered as reference (we remind that Neumann’s solution is computed with a semi-infinite domain so that no steady state can be reached in this case).
As a conclusion, the numerical simulations appear quite satisfactory since they stick to Neumann’s solution in the initial time steps and to the PSS solution in later stages of the process.
Figure 18.
Interface position.
Figure 18.
Interface position.
Figure 20.
Temperature field at different time instants.
Figure 20.
Temperature field at different time instants.