An Image Pattern Tracking Algorithm for Time-resolved Measurement of Mini- and Micro-scale Motion of Complex Object

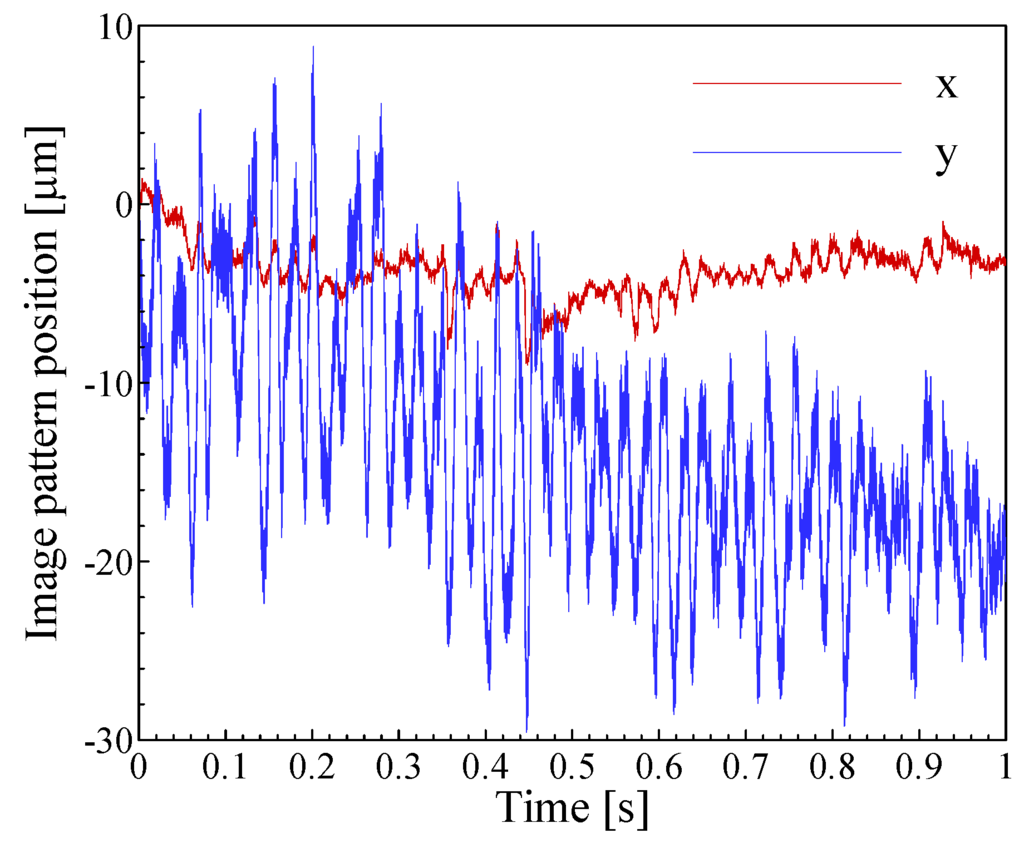
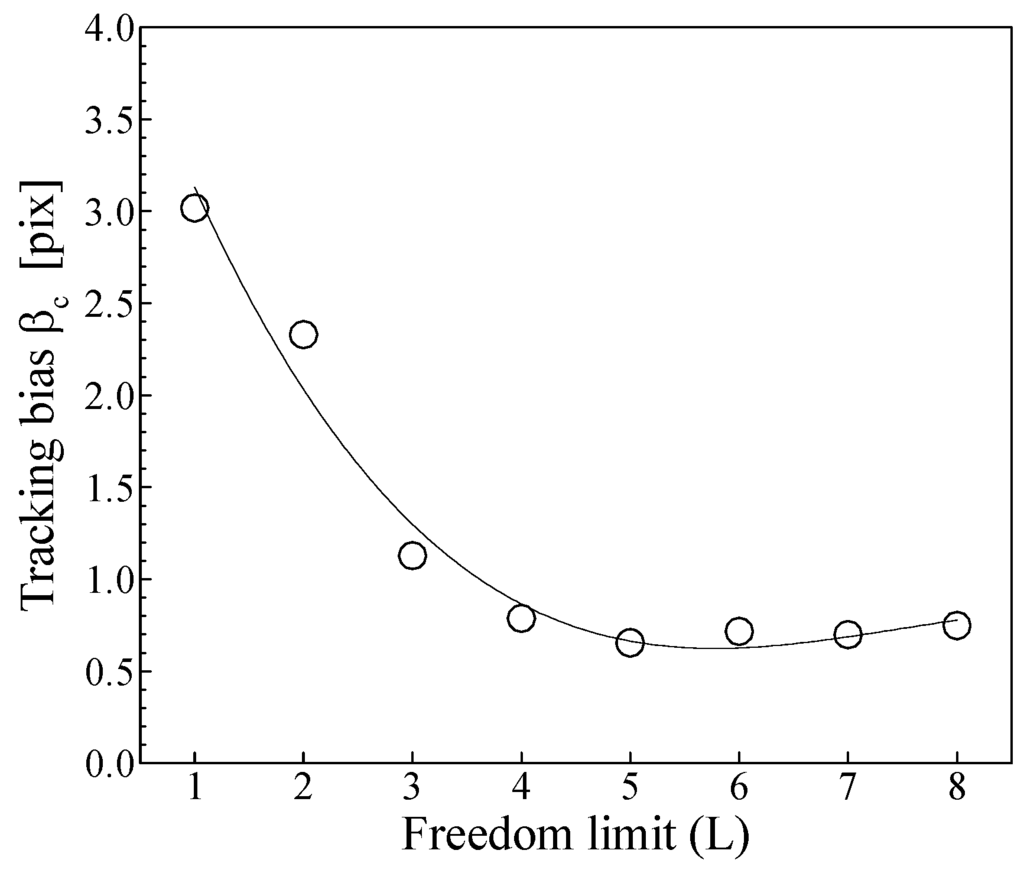
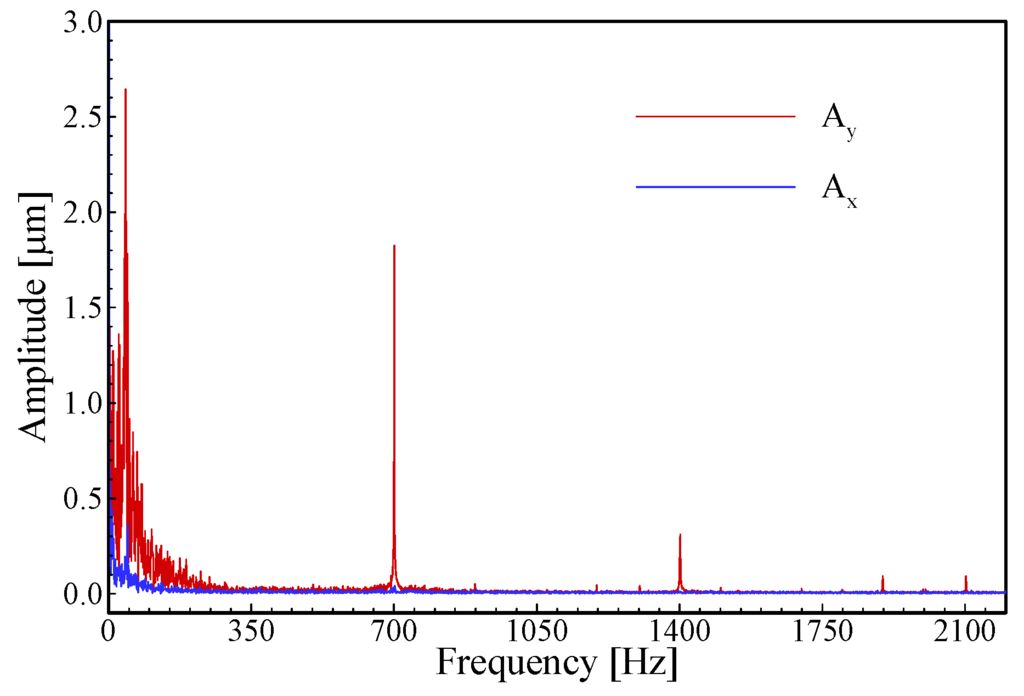
Abstract

An image pattern tracking algorithm is described in this paper for time-resolved measurements of mini- and micro-scale movements of complex objects. This algorithm works with a high-speed digital imaging system, which records thousands of successive image frames in a short time period. The image pattern of the observed object is tracked among successively recorded image frames with a correlation-based algorithm, so that the time histories of the position and displacement of the investigated object in the camera focus plane are determined with high accuracy. The speed, acceleration and harmonic content of the investigated motion are obtained by post processing the position and displacement time histories. The described image pattern tracking algorithm is tested with synthetic image patterns and verified with tests on live insects.

1. Introduction

Imaging techniques including photography, cinematography and analog/digital video techniques are always favorite tools for research scientists to investigate motion of fluids and solid objects. For example, one of the imaging techniques, i.e. the particle image velocimetry (PIV), are widely used to measure complex fluid flows and quantify motion of large solid particles and bubbles in fluids [1, 2]. Recent advances in high‑speed digital imaging system and digital image evaluation algorithm have made it possible to measure mini- and micro-scale motion of insect body parts with high accuracy and high temporal resolution. The time resolved quantification of insect body part motion is of great interest because the insect body part (head, wing, antenna, hairs etc.) motion is usually related to the communication between insects or the reaction of insects under environment excitations. Currently, some commercially available high-speed imaging systems are capable of capturing more than 10,000 frames per second (fps) with sufficient digital resolution, e.g. 256×256 pixels, with which an image pattern of 32×32 pixels can be tracked in a displacement range of up to 200 pixels. According to publications on the particle image velocimetry (PIV), i.e. an image pattern tracking technique for fluid flow measurements, the uncertainties for determining the displacement of image pattern of 32×32 pixels may be less than 0.1 pixels [3,4,5,6,7] that ensures the high accuracy of determining the insect body part motion. In addition, by using a high-speed imaging system, thousands of image frames can be consecutively captured with a constant time interval between frames, so that a temporal analysis of the inset body motion can be conducted.

Most of the particle image pattern tracking algorithms in PIV can directly be used to track the image pattern of insect body part for determining the displacement between two or a few more frames. Difficulties arise when tracking the image pattern of insect body part among hundreds to thousands of image frames. At first, as mentioned in many publications on PIV, the most PIV algorithms were designed to track a group of image patterns of very small particles with an optimal particle image diameter around 3 pixels [8]; however, the equivalent diameter of the tracked insect image pattern is usually more than 10 pixels. The algorithm for the insect body motion tracking should be insensitive to the image pattern size or should work well for larger particle images. The second difficulty is that an insect body part can not be assumed as a point light source like a tracer particle in PIV experiments. The image pattern of an insect body part may have a complex structure, may rotate in the objective plane and may deform because of the off-plane motion. The image pattern distortion were considered in PIV algorithms by using particle image displacements near to the tracked image pattern [9,10,11], but those ideas cannot be applied in the insect body part tracking because no neighborhood information is available to correct the distorted image pattern of the insect body part. It seems that the only effective way to solve the problem of strong image pattern distortion is to use a high frame rate so that the image pattern distortion between two neighbored frames may be small enough. When tracking the image pattern among a great number of image frames, the bias errors will be accumulated frame by frame so that the tracked image pattern may deviate from the originally chosen one, and consequently, a false tracking result may finally be resulted in. Therefore, the algorithm for the insect body motion should have a very low bias error level, and the bias error should properly be controlled to ensure that the tracking procedure can be completed with high reliability. Considering above factors, the image pattern tracking algorithm presented in this paper for the insect body motion tracking is developed on the basis of the correlation-based interrogation algorithm with continuous window-shift (CCWS) that is a PIV algorithm described by Gui and Wereley [12], because the CCWS has the minimal bias error among PIV algorithms and works very well for large particle images. In addition, a multi-pass scheme is used to control the image tracking bias to ensure a reliable and accurate result.

In the following we shall first describe the algorithm and the multi-pass procedure. Then the algorithm is tested with synthetic image patterns. Finally, two application examples from termite and fire ant, respectively, are used to verify the described algorithm.

Figure 1. Tracking image pattern (24×24 pixels) on a termite head in a 33-ms head-banging period.

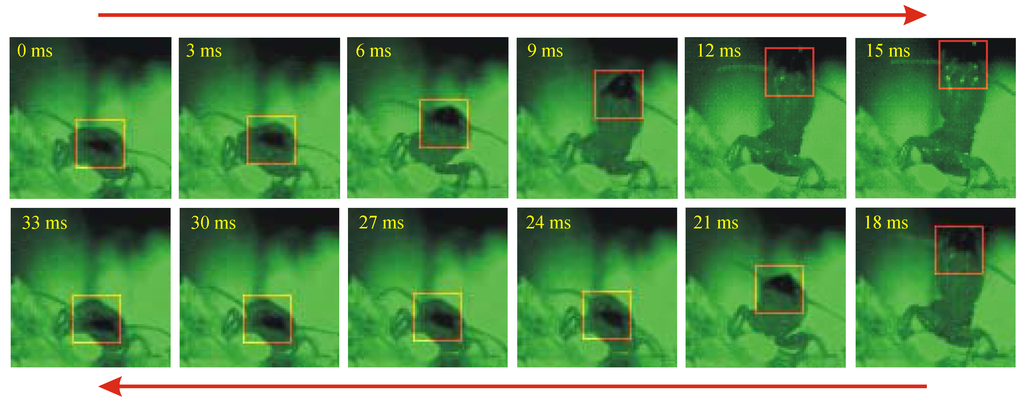
Figure 1. Tracking image pattern (24×24 pixels) on a termite head in a 33-ms head-banging period.

2. Description of the algorithm

2.1 Sample images

Some sample images are given in Fig. 1 for investigating the head-banging behavior of a termite. These images were taken at a frame rate of 10,000 fps with a digital resolution of 256×256 pixels. The brightness of the image is resolved with 10-bit for each pixel in the CMOS sensor of the used Photron’s ultima APX high-speed camera, and it is saved with 16-bit in raw image files. The object to image ratio is 40 µm/pixel. In order to show the tracked image pattern on the termite head more clearly, only portions (i.e. 81×81 pixels) of the selected raw image frames are displayed in Fig. 1 in green color. The tracked image patterns are indicated with square boxes of 24×24 pixels, i.e. 0.96×0.96 mm2 in the objective plane. As shown in Fig. 1, the image pattern of the termite head is deformed strongly during the termite head rising and falling. Nevertheless, it is still possible to correctly determine the movement of the termite head, because the image pattern deformation is resolved with a large number of image frames. For example, the largest image pattern deformation is observed between the 18th and the 21st ms, however, since there are 31 frames to resolve this deformation, as shown in Fig. 2, the image pattern distortion cannot be seen between two neighbored frames at both the 18th and 21st ms.

Figure 2. Neighbored image patterns at the 18^th and 21^st ms.

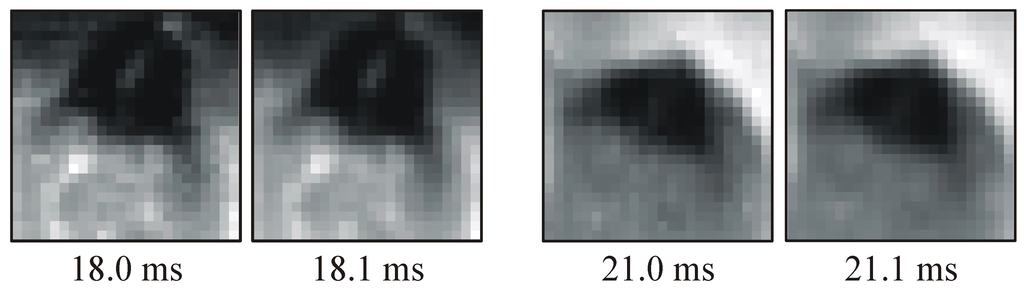
Figure 2. Neighbored image patterns at the 18^th and 21^st ms.

2.2 Image pattern

When a group of successively recorded images has a frame size of I×J pixels and a total frame number of K, the gray value distribution of each image frame is represented here as G_k(i,j) for i = 1, 2 , …, I; j = 1, 2, …, J; and k = 1, 2, …, K. In order to track an insect body part from frame to frame, image patterns restricted in a square or rectangular interrogation window of M×N pixels are evaluated. When the center position of an image pattern (x, y) is divided into integer pixel portion (i₀, j₀) and positive sub‑pixel portion (a, b), i.e. $x=i_0+a$, $y=j_0+b$, the gray value distribution in the interrogation window can be determined with a bilinear interpolation as

$$\begin{gathered} \begin{array}{ll}{g}_{x,y}^k\left(p,q\right)& =\left(1-a\right)\cdot \left(1-b\right)\cdot G_k\left(i_0-\frac{M}{2}+p,j_0-\frac{N}{2}+q\right)\\ & +a\cdot \left(1-b\right)\cdot G_k\left(i_0-\frac{M}{2}+p+1,j_0-\frac{N}{2}+q\right)\\ & +b\cdot \left(1-a\right)\cdot G_k\left(i_0-\frac{M}{2}+p,j_0-\frac{N}{2}+q+1\right)\\ & +a\cdot b\cdot G_k\left(i_0-\frac{M}{2}+p+1,j_0-\frac{N}{2}+q+1\right)\end{array} \\ forp=1,2,\cdot \cdot \cdot ,Mandq=p=1,2,\cdot \cdot \cdot ,N \end{gathered}$$

(1)

2.3 Reference image pattern and tracking freedom pattern

During the image pattern tracking, a reference image pattern g^r(p,q) is chosen to scan every image frame in the recording group, to determine the position of the image pattern that has the highest likeness to the reference image pattern. There are three different ways to select the reference image pattern:

1)

Fixed reference pattern – The reference image pattern is chosen in the first frame, and it will not be changed during the tracking.

2)

Reference pattern with maximal freedom – At first the reference image pattern is chosen in the first frame, and then, it is replaced with the tracked image pattern after the tracking for each frame is completed.

3)

Reference pattern with limited freedom – At first the reference image pattern is chosen in the first frame, and then it is replaced with the tracked image pattern of every L frames. L is referred to the tracking freedom limit in the followed text.

The position of the reference image pattern in the first frame (x_o,y_o) is the start point of the image pattern tracking, and it is set as the coordinate origin in the following tests.

2.4 Tracking function

A correlation-based tracking function is given for each image frame as below.

$${\Phi }^k\left(m,n\right)={\displaystyle \sum _{q=1}^N{\displaystyle \sum _{p=1}^M{g}^r\left(p,q\right)\cdot g_{x,y}^k\left(p+m,q+n\right)}}$$

(2)

where g^r(p,q) and g^k_x,y (p,q) are gray value distributions of the reference and tracked image pattern, respectively. When the computation of the correlation function Φ ^k(m,n) is accelerated with the fast Fourier transformation (FFT), g^r(p,q) and g^k_x,y(p,q) are assumed to be distributed periodically in the p-q plane with the periodicity M, N. The position of the highest peak (m*,n*) determines the position deviation of the tracked image pattern from the reference pattern image pattern in the interrogation window coordinate system, i.e. the pq-plane. Since (p,q) and (m,n) are integer pixel values, the high-peak position (m*,n*) is determined with sub-pixel accuracy by using a three-point Guassian fit.

2.5 Tracking criterion and basic steps

When the image pattern tracking is completed, it is expected that the reference image pattern and the tracked image pattern will match to each other at the interrogation window center. Since the high-peak position (m*, n*) of correlation function Φ ^k(m,n) reflects the position deviation of the tracked image pattern from the reference image pattern in the pq-plane, the criterion for the tracked image pattern to match the reference pattern is set as (m^*)² + (n^*)² ≤ ε², where ε is the position error tolerance limit. The basic procedure of the image pattern tracking at each frame (except for k = 1) is given below:

• Estimate initial position of the tracked image pattern (x, y). Usually the tracked image pattern position in the previous frame can be used as the initial image pattern position.
• Compute the correlation function Φ ^k(m,n) with FFT acceleration.
• Determine the high peak position of the correlation function, i.e. (m^*,n^*), with a three-point Guassian curve fit to achieve a sub-pixel accuracy.
• Check the tracking criterion (m^*)² + (n^*)² ≤ ε², to see whether or not it is fulfilled. If the criterion is fulfillled, stop the tracking and accept (x, y) as the position of the tracked image pattern in the current frame; If not, continue to the next step.
• Add the correlation high peak position (m*, n*) to the image pattern position (x, y), and then iterate step 2 to 4.

The position error tolerance limit ε is given according to precision requirement of the experiment. Smaller ε ‑value usually needs a higher iteration number. Usually, an iteration number around 6 is enough to fulfill the precision requirement. In the tests presented in this paper, the iteration number is set as 6 to control the multi-pass tracking procedure.

2.6 Accumulated tracking bias

In order to quantify the accumulated bias for tracking an image pattern among a group of image frames of number K, a reverse tracking is conducted in the first frame with following function:

$${\Phi }^R\left(m,n\right)={\displaystyle \sum _{q=1}^N{\displaystyle \sum _{p=1}^M{g}^K\left(p,q\right)\cdot g_{x,y}^1\left(p+m,q+n\right)}}$$

(3)

Wherein g^K(p,q) is the tracked image pattern in the last (K‑th) frame, whereas g¹_x,y (p,q) is the image pattern located at (x, y) in the first frame. The initial position of the tracked image pattern in the first frame is set at the start point of the image pattern tracking, i.e. (x_o,y_o). Following the same steps as described in section 2.5, the position of the tracked image pattern is determined as (x_r,y_r). The accumulated bias of the image pattern tracking is defined as

$${\beta }_c=\sqrt{{\left(x_r-x_o\right)}^2+{\left(y_r-y_o\right)}^2}$$

(4)

Figure 3. Synthetic image pattern and its motion.

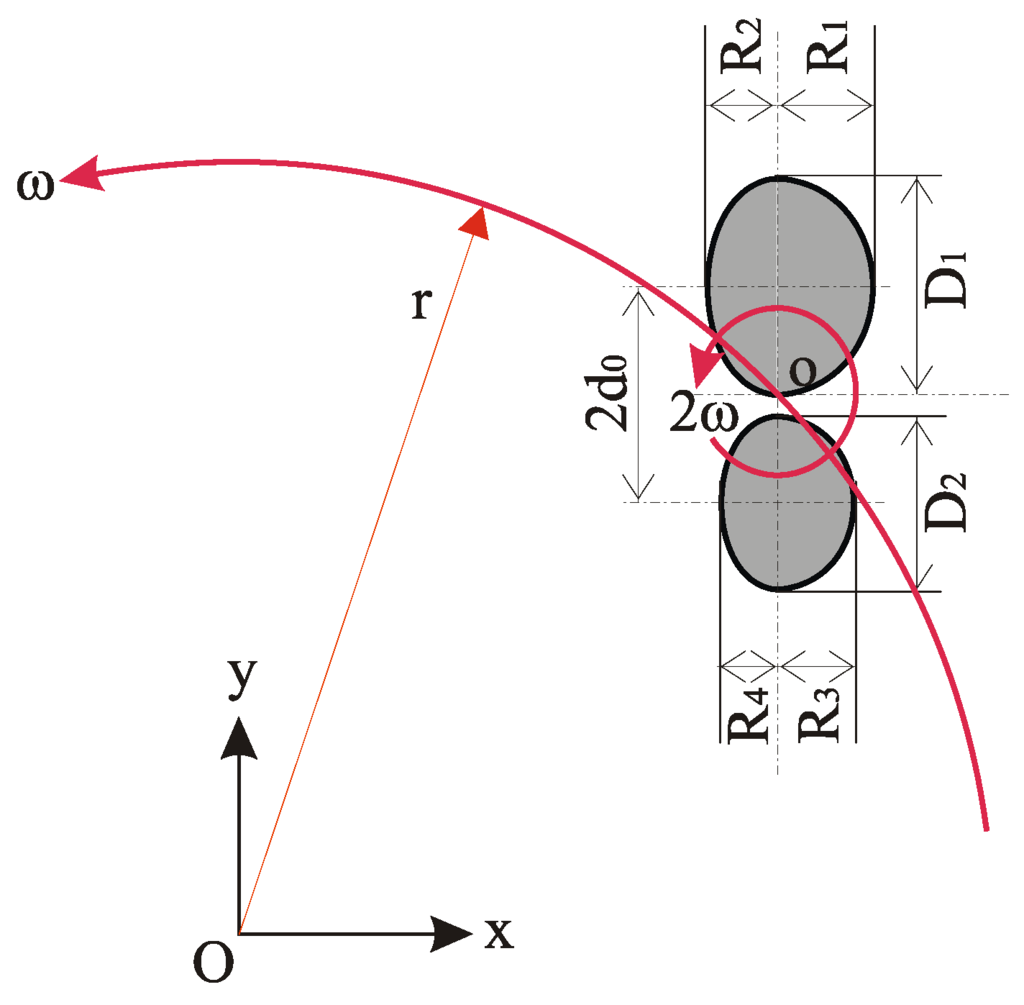
Figure 3. Synthetic image pattern and its motion.

3. Test with simulation

3.1 Synthetic image pattern

In order to test the described algorithm in complicated situations, synthetic image patterns are created with a given motion. The sketch in Fig. 3 illuminates the cross-section of the image pattern used in the following tests and the motion in the image plane. The image pattern consists of two asymmetric ellipses of different sizes, and they are separated with a distance of 2d₀. Each ellipse has two halves of different dimensions that are determined with parameters R and D. The gray value distribution of each half ellipse is determined with an exponential function as below.

$$g\left(x,y\right)=G_o\cdot \exp \left(-2{\left(\frac{x-x_c}{D}\right)}^2-2{\left(\frac{y-y_c}{2R}\right)}^2\right)$$

(5)

Wherein (x_c,y_c) is the center of the ellipse. The image pattern rotates at the center point (o) of the line that connects the two ellipse centers with an angular speed of 2ω. With the half of the angular speed (i.e. ω), the center of the image pattern o rotates around the origin point O in the xy-plane with radius r. In the current tests, d₀ is used as a basic parameter to determine the size of the image pattern, and other related parameters are determined accordingly:

$$\begin{array}{l}{D}_1=d_0,D_2=0.618D_1,\\ R_1=0.5D_1\left(1-0.4\frac{\left|y\right|}{r}\right),R_2=0.5D_1\left(1-0.6\frac{\left|y\right|}{r}\right),\\ R_3=0.5D_2\left(1-0.4\frac{\left|y\right|}{r}\right),R_4=0.5D_2\left(1-0.6\frac{\left|y\right|}{r}\right).\end{array}$$

(6)

According to equations (6) the ellipse image pattern shrinks in one axis with increasing |y|, so that the off-plane effect of the insect body part motion is simulated. To simplify the tests, the sample images shown in Fig. 1 are used as a reference for generating the synthetic image patterns, i.e. the radius r is set to 24 pixels to match the termite head-banging rising distance; the rotation circle is resolved with 600 frames (i.e. ωΔt = 0.6 degree) so that the half of the rotation circle have similar fames to that of the termite head-banging; the synthetic images have the same random noise level in the background as those given in Fig. 1, i.e. gray value standard deviation of 9 around average of 230. As an example, Fig. 4 shows the image patterns of d₀ = 6 at 11 different positions in the image plane.

Figure 4. Synthetic image patterns of d₀ = 6 pixels at 11 different positions.

Figure 4. Synthetic image patterns of d₀ = 6 pixels at 11 different positions.

3.2 RMS tracking errors

Since the center of the simulated image pattern goes along a perfect circular path of radius r with center at the coordinate origin O, the deviation of the distance between the tracked image pattern center o and the circle center O from the known radius is considered as a position error. The overall position error of tracking the image pattern in a group of K frames is quantified here with the root-mean-square (RMS) difference between the given and tracked radiuses, i.e.

$${\delta }_r=\sqrt{\frac{1}{K}{\displaystyle \sum _{k=1}^K{\left(r_k-r\right)}^2}}\text{ for }{r}_k=\sqrt{x_k^2+y_k^2}$$

(7)

Wherein (x_k, y_k) is the tracked image pattern position in each frame. In order to determine the instantaneous speed of the insect body part, the image pattern displacement is determined with a central difference for each frame as below.

$$\begin{array}{l}\Delta x_k=\frac{x_{k+1}-x_{k-1}}{2}\\ \Delta y_k=\frac{y_{k+1}-y_{k-1}}{2}\\ S_k=\sqrt{\Delta x_k^2+\Delta y_k^2}\end{array}$$

(8)

Wherein S_k is the tangential displacement along the circular path of the image pattern in the current tests, and the true value is a constant of rωΔt = 0.2513 pixels. Here, Δt is the time interval between two successive frames. Thus the RMS error of the tangential displacement is determined as

$${\delta }_s=\sqrt{\frac{1}{K-2}{\displaystyle \sum _{k=2}^{K-1}{\left(S_k-r\omega \Delta t\right)}^2}}$$

(9)

3.3 Influences of freedom limit

In order to investigate the influences of the image pattern tracking freedom limit L on the accumulated bias β_c and the position error δ_r, 601 synthetic frames with an image pattern of d₀ = 6 are tracked with 600 different freedom limit, i.e from L = 1 to L = 600 with increasing step of 1. The image pattern in the last (601st) frame is exactly the same as that in the first frame, and the only difference between the two frames is that the random background noise distributions are not identical. This synthetic image group is evaluated by using the image pattern tracking algorithm described in section 2 with an image pattern window of 32×32 pixels. The errors of the image pattern tracking are given in Fig. 5.

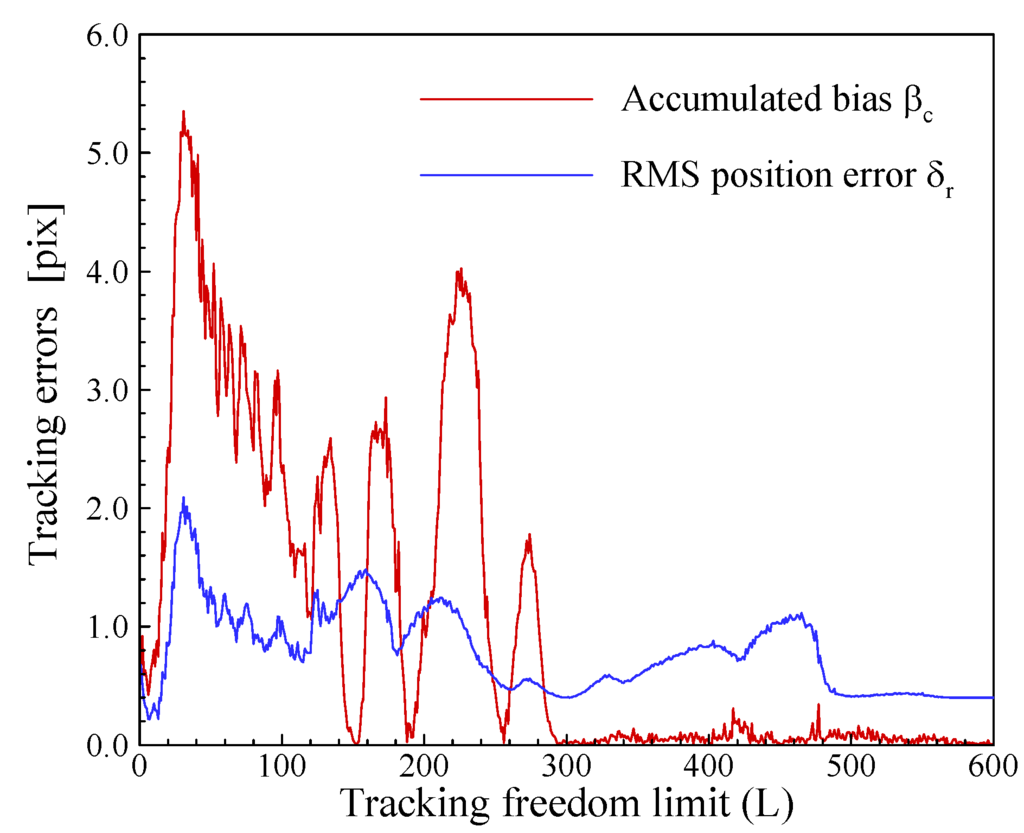
Figure 5. Errors of image pattern tracking for synthetic image pattern of d₀ = 6 pixels.

Figure 5. Errors of image pattern tracking for synthetic image pattern of d₀ = 6 pixels.

Fig. 5 indicates that in the current test case the RMS position error δ_r has the minimum (δ_r ≈ 0.2 pixels) between L = 1 and L = 20, and it rise up to the highest peak of more than 2 pixels at L = 30. After the highest peak the RMS position error is significant large, i.e. δ_r > 0.4 pixels. The accumulated bias error β_c also has a local minimum in the freedom limit range of 1 to 20, and it goes up to the highest peak of more than 5 pixels at L = 30. After the highest peak, the accumulated bias error β_c has some local minima that are much smaller than the minimum before the highest peak. The reason for small β_c at high L-number is that the reference pattern is chosen with a large skip, so that relatively few bias errors are accumulated to the end of the image pattern tracking. It can be seen that the local minima of β_c after the first high-peak can be smaller than the first local minimum, e.g. at L≈150, 190, 260 etc. The possible reason is that the rotation and the asymmetric shrink of the image pattern result in both positive and negative biases during the tracking, so that the accumulated bias can occasionally be very small at certain L-numbers. Fig. 5 confirms that the two first high-peaks for β_c and δ_r, respectively, appear at the same L number, i.e. the maximal position error occurs at the maximal accumulate bias. The purpose of current test is to find a way for determining an optimal tracking freedom limit L_opt. Obviously, it is reasonable to determine L_opt at minimal RMS position error. Unfortunately, the RMS position error cannot be quantified in real experiments because the true values are unknown. However, Fig. 5 indicates that the position error δ_r has a similar distribution to the accumulate bias β_c before its first high peak that is also the highest peak of β_c among all the possible freedom limits. Since accumulate bias β_c can be obtained by tracking real image patterns, the distribution of accumulate bias β_c before the first high peak may be used to determine the optimal tracking freedom limit L_opt.

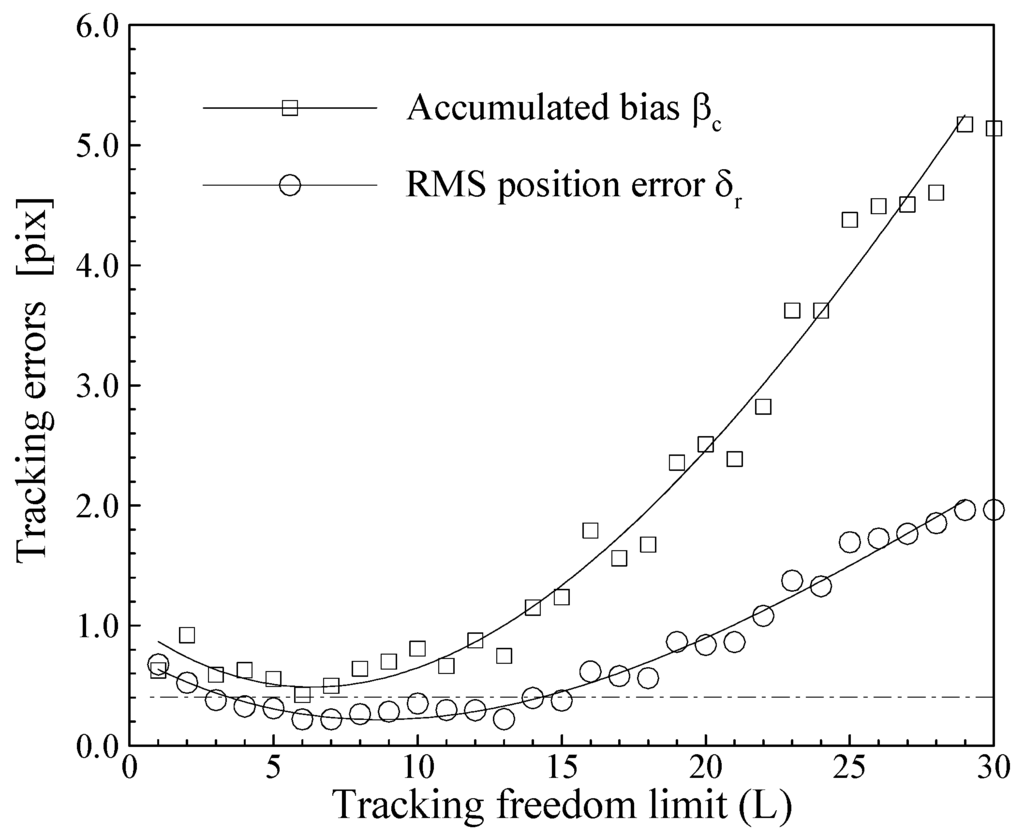
Figure 6. Tracking error distributions before the highest peaks for synthetic image pattern of d₀ = 6 pixels.

Figure 6. Tracking error distributions before the highest peaks for synthetic image pattern of d₀ = 6 pixels.

Fig. 6 shows the distributions of accumulate bias β_c and position error δ_r before the first high-peak, i.e. L ≤ 30. The dash-dot line indicates the minimal position error in the region of L > 30. In the current case the position error at minimal β_c, i.e. L = 6, is very close to the minimal position error at L = 7, and it is much smaller than the minimal position error in the region of L > 30.

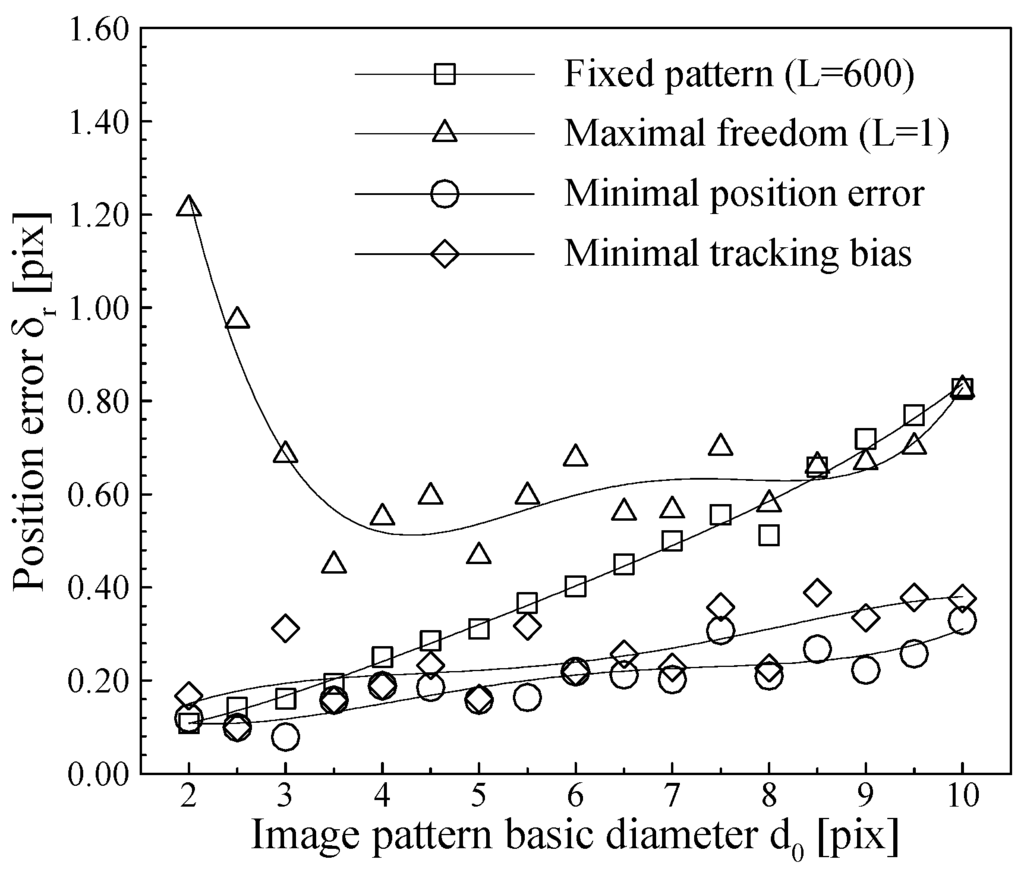
Figure 7. Position error distributions on image pattern size for different tracking freedom limits.

Figure 7. Position error distributions on image pattern size for different tracking freedom limits.

Figure 8. Displacement error distributions on image pattern size for different tracking freedom limits.

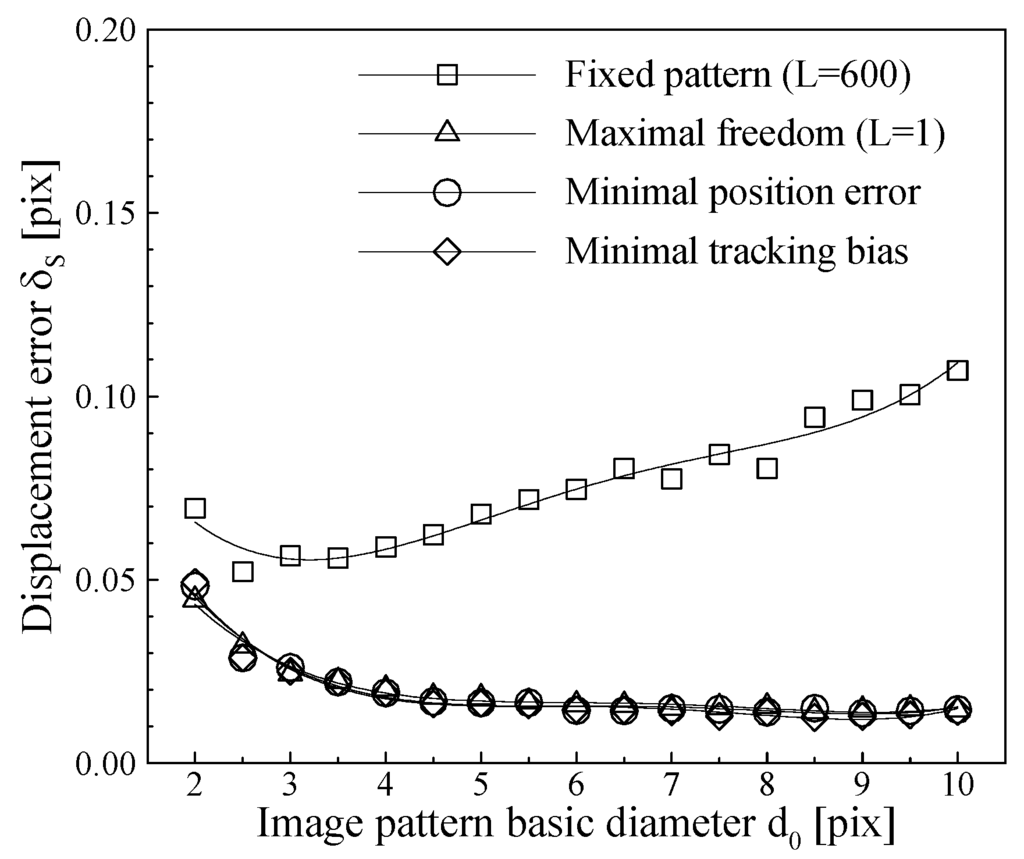
Figure 8. Displacement error distributions on image pattern size for different tracking freedom limits.

3.4 Influences of image pattern size

The followed tests are conduced with synthetic image pattern groups of 17 different basic diameters, i.e. from d₀ = 2 to 10 with a step of 0.5 pixels. The position error distributions on the image pattern basic diameter (d₀) for four different tracking freedom limits are given in Fig. 7. Fig. 7 shows that the position errors of maximal tracking freedom (L = 1) are significantly larger than those in other cases for most image pattern sizes, especially for small image patterns. The reason for the overall large bias distribution is that the bias errors are added from frame to frame to finally obtain a large accumulated bias. The position error of the fixed image pattern (L = 600) is small at small image pattern, but it increases with increasing image pattern size because the effects of the image pattern rotation and asymmetric shrink become stronger when the image pattern size increases. The minimal position error has a relatively flat distribution and raises a little at large image patterns. The position error distribution of the minimal tracking bias is close to the minimal position error distribution.

The displacement error distributions on the image pattern basic diameter (d₀) for the four different tracking freedom limits are given in Fig. 8. It is shown in Fig. 8 that the displacement error of the fixed image pattern (L = 600) is much larger than those of the other three cases for all tested image pattern sizes, and it has a minimum around d₀ = 3 pixels and increases almost linearly with increasing image pattern size. The displacement errors of the other three cases are large with the smallest image pattern, reduce quickly with increasing image pattern to a large enough size (d₀ = 5), and then converge to a constant level. No obvious differences can be identified between the displacement error distributions of the other three cases in Fig. 8.

According to the above discussions, an optimal image tracking freedom limit can be determined with the minimal accumulate tracking bias before the first high peak. With the optimal freedom limit determined with the minimal accumulated tracking bias, an image pattern tracking result of position and displacement errors close to the minima can be obtained.

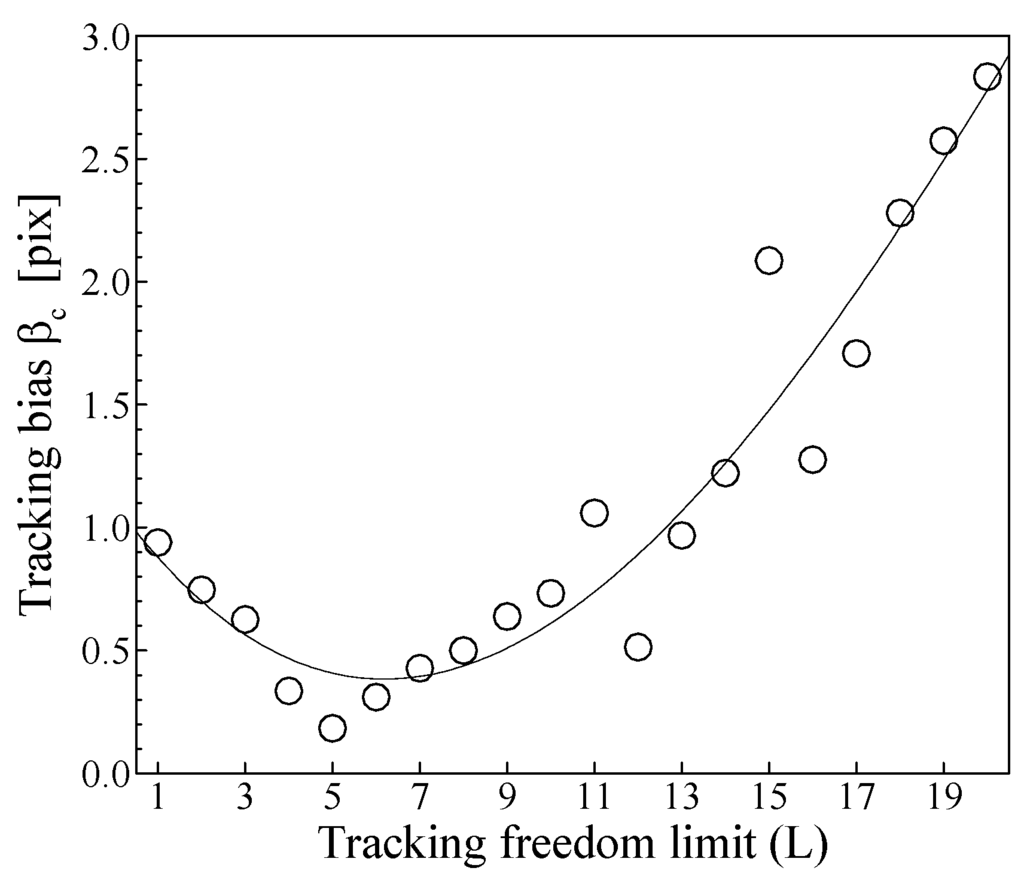
Figure 9. Tracking bias distribution on the freedom limit for termite head-banging case at the 225^th frame.

Figure 9. Tracking bias distribution on the freedom limit for termite head-banging case at the 225^th frame.

Figure 10. Time histories of the termite head position in a 33‑ms head-banging period.

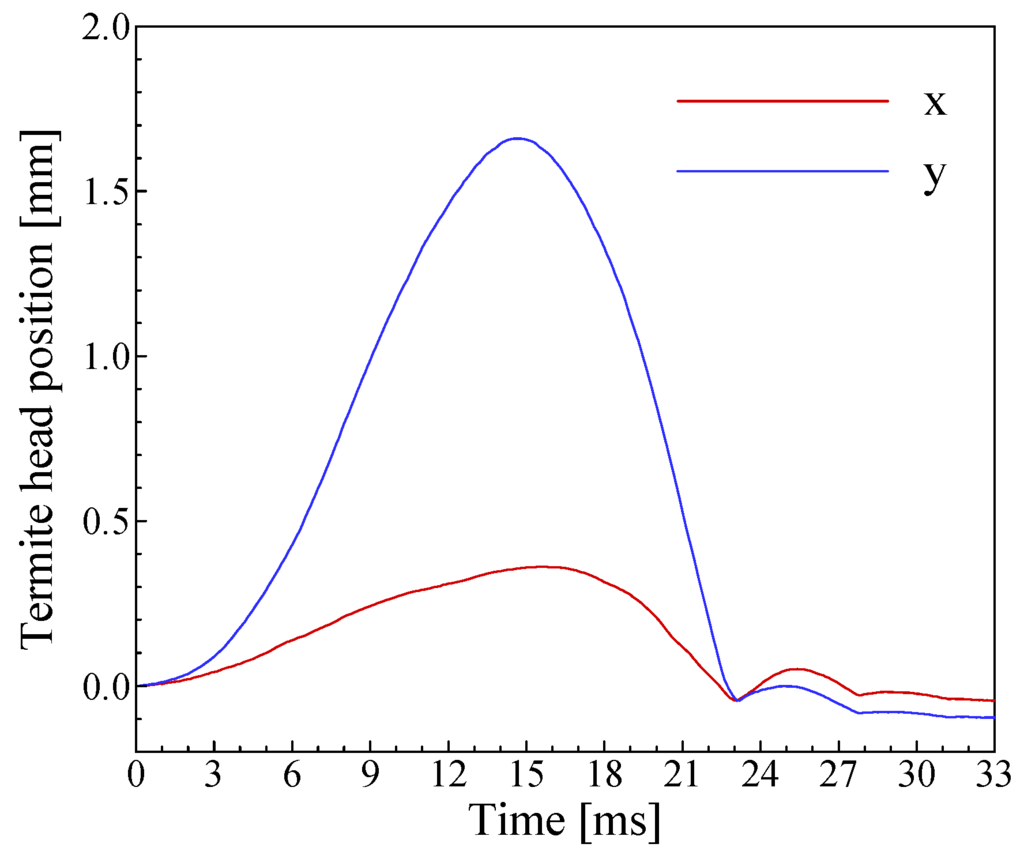
Figure 10. Time histories of the termite head position in a 33‑ms head-banging period.

4. Application examples

4.1 Termite head-banging experiment

A typical application of the described image pattern tracking algorithm is to quantitatively investigate the termite head-banging behavior, which induces sound waves that can be used to detect and identify different termites behind the wall. Head-banging in termite soldiers in response to some disturbance is well known [13,14,15]. The head-banging movements of termites can be captured with a standard (PAL/NTCS) video system, i.e. 25/30 full frames or 50/60 interlaced frames per second. However, a high-speed imaging system is required to map the details of the head-banging movement, because the head-banging period is around 30 ms that cannot be resolved with standard video systems. In the present work a head-banging behavior is resolved with more than 300 frames at 10,000 fps by using a Photron’s ultima APX high-speed imaging system, so that the temporally dependent termite head displacement, instantaneous velocity and acceleration can be determined. Image frames of 256×256 were taken with a scale of 0.04 mm/pixel. Some sample images obtained in this experiment are given in Fig. 1. During the tracking, image patterns were chosen on the termite head in size of 24×24 pixels, i.e. 0.96×0.96 mm². The physical coordinate origin is set to the image pattern position in the first frame.

In order to determine the optimal image pattern tracking freedom limit, the first 225 frames in the termite head-banging recording group are selected for a multi-pass tracking test. At the 225th frame (i.e. t = 22.4 ms), the termite head falls almost to the same position as in the 1st frame, so that the image pattern in these two frames are very similar. That allows a reliable tracking of the last (i.e. in the 225th frame) image pattern back to the first frame, so that the accumulated tracking bias can reasonably be determined. The accumulated tracking bias distribution on the tracking freedom limit for the test case is given in Fig. 9, and it is shown that the minimal tracking bias can be obtained with L = 5.

The image pattern tracking results, i.e. the time histories of the termite head position in a 33‑ms head-banging period, are given in Fig. 10 for a tracking freedom limit of 5. It is shown that the termite raises its head slowly in 15 ms to accumulate potential energy, and then releases the potential energy quickly in 8 ms by moving the head down until it strikes the substrate. Then the termite head passively rebounds up and down (striking the substrate) again for several more times until the energy is completely released. The main head-bang is completed in 24 ms with a rising magnitude of 1.67 mm, and the following secondary head bangs have a much smaller magnitude (≈ 0.2 mm) and shorter period (≈ 5 ms). The time histories of the termite head velocity are determined with the image pattern displacement and time interval, and the results are given in Fig. 11. The figure shows that the maximal velocity in the head raising period is 0.2 m/s at t =8 ms, and the maximal velocity in the head falling period is 0.34 m/s at t =21 ms.

As shown in Fig. 12, the acceleration time histories of the tracked termite head can further be computed according to the velocity time histories shown in Fig. 11. The total acceleration (i.e. “a” in Fig. 12) has a high peak of 362 m/s² at the main head-bang, i.e. at t = 22.8 ms. The corresponding striking force of the termite head with known weight (mass) of 1.37 mg is estimated as 0.5 mN. Note that the support force of the termite neck and the gravity should also be considered when using the estimated striking force value. It should also be mentioned that the measured valuables are two-dimensional in the camera focus plane. The out of plane component, i.e. in z-direction, cannot be determined with the described image pattern tracking system.

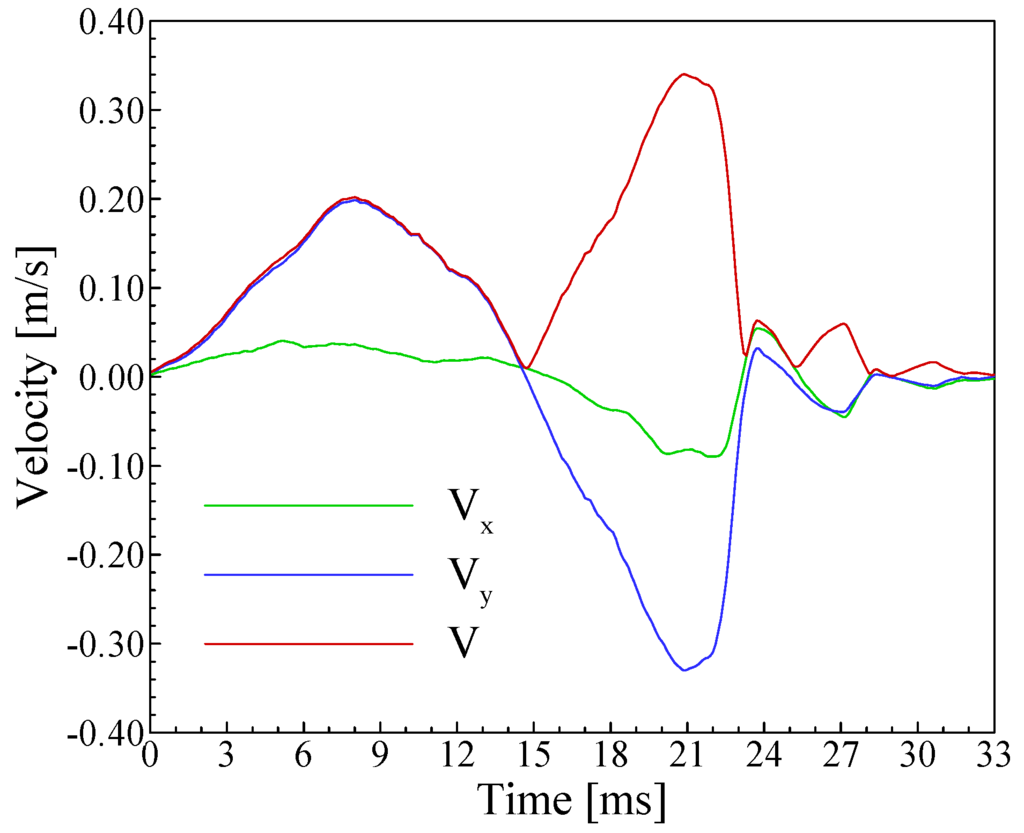
Figure 11. Time histories of the termite head velocity in a 33‑ms head-banging period.

Figure 11. Time histories of the termite head velocity in a 33‑ms head-banging period.

Figure 12. Time histories of the termite head acceleration in a 33‑ms head-banging period.

Figure 12. Time histories of the termite head acceleration in a 33‑ms head-banging period.

4.2 Fire ant antenna vibration in near-field sound

Another experiment was conducted with a live fire ant in a sound field, to verify the capability of the described image pattern tracking algorithm. The purpose of the test is to determine the possibility for fire ants to detect sound waves. During this experiment, a pipe guided a sound wave of 700 Hz from a loudspeaker to a nozzle of 3-mm diameter. The ant was made unconscious with CO₂ and then put within 10 mm to the nozzle with head directed to the nozzle. The camera view was centered at one of the two antennas of the fire ant and the focus was put on some tiny hairs on the antenna. Shadow images were taken with a back lighting at a frame rate of 4000 fps. Totally 4000 successive frames of size of 512×256 pixels were recorded in one second at a scale of 2.58 μm/pixel. The first frame of this image group is given on the left in Fig. 13. As marked in picture “A” on the left with a yellow box, an image pattern of size of 16×16 pixels (i.e. 41×41 μm²) is selected at a hair tip on the fire ant antenna, an enlarged picture of which is shown in picture “B” on the top right.

Figure 13. Image pattern of a vibrating hair tip on a fire ant antenna: (A) first frame of 4000 consecutive images, (B) selected image pattern in the 1st frame, (C) tracked image pattern in the 805th frame.

Figure 13. Image pattern of a vibrating hair tip on a fire ant antenna: (A) first frame of 4000 consecutive images, (B) selected image pattern in the 1st frame, (C) tracked image pattern in the 805th frame.

Figure 14. Position time histories of a fire ant antenna hair tip.

Figure 14. Position time histories of a fire ant antenna hair tip.

Figure 15. Tracking bias distribution on the freedom limit for the fire ant case at the 805th frame.

Figure 15. Tracking bias distribution on the freedom limit for the fire ant case at the 805th frame.

Test run results shown in Fig. 14 indicate that the investigated hair tip drifts away from the original position after 200 ms, possibly because the ant was not completely unconscious, and it moved the antenna slowly. In order to determine the optimal tracking freedom limit, the accumulated tracking bias is tested at the 805th frames for t = 201.25 ms, at which the tracked image pattern goes almost back to the original position so that the image pattern deformation is small between the first and last frame in the test period, see picture B and C in Fig. 13. The accumulated tracking biases at the 805th frame are given in Fig. 15 for the freedom limit up to 8. Fig. 15 shows that the accumulated image tracking bias reduces from L = 1 to L = 5, and it begins to increase at L = 6, so that the optimal tracking freedom limit is determined as L = 5 for this test case.

A Fourier analysis is conducted on time histories of the fire ant antenna hair tip position given in Fig. 14, and the frequency responses are given in Fig. 16. The figure shows that low frequency responses to different sources are limited in the region of 0‑350 Hz. The first and second harmonic responses to the exciting sound wave of 700 Hz have peak amplitudes of 1.82 and 0.25 μm, respectively. The third harmonic response is very weak but can be identified as an amplitude peak of 90 nm at 2100 Hz. Because of the periodicity assumption of the Fourier transformation, a peak can be seen at 1900 Hz, which has the same height as that at 2100 Hz. The test results illuminates that the hairs on the fire ant antenna may be able to detect the near-field sound. However, whether or not the detected mechanical signal can be interpreted biologically and used to influence the behavior of the fire ant is under study and out of the scope of this paper.

Figure 16. Frequency response of an antennal hair of a fire ant to a vibration signal of 700 Hz.

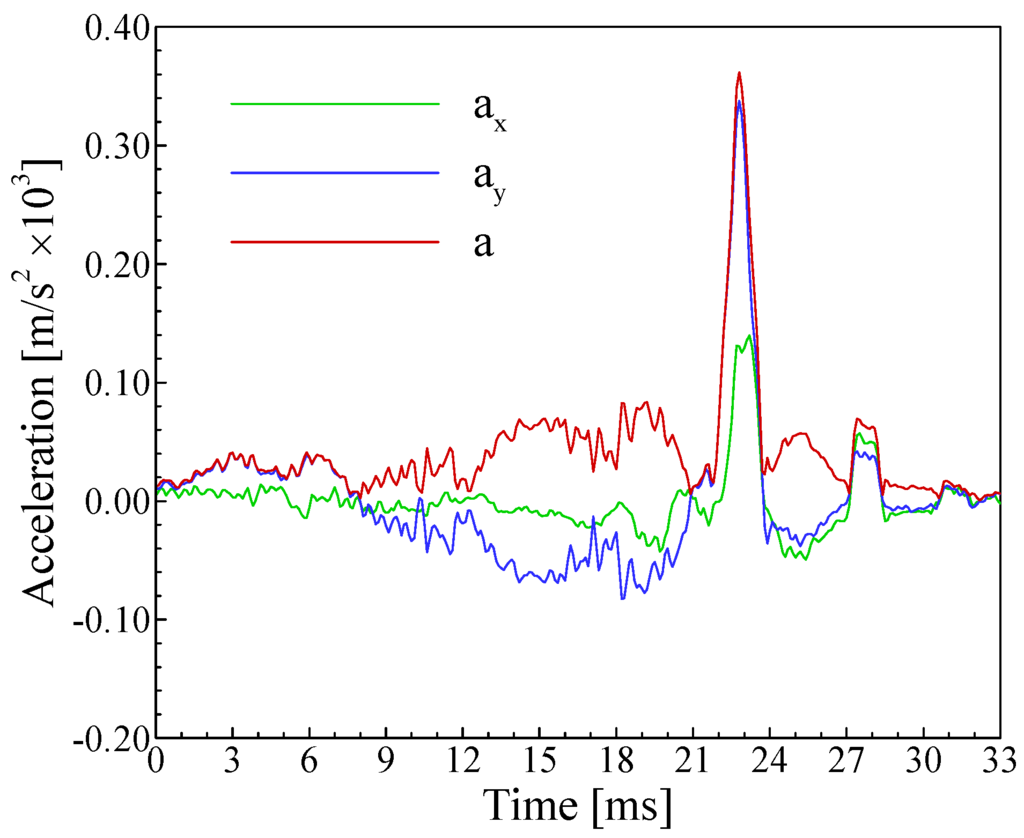
Figure 16. Frequency response of an antennal hair of a fire ant to a vibration signal of 700 Hz.

5. Summary and conclusion

The presented method consists of a high-speed digital imaging system and a multi-pass, correlation-based image pattern tracking algorithm. The high-speed digital imaging system resolves strong distortion of insect image pattern with enough number of image frames and enables a time resolved analysis of insect body part motion. The described image pattern tracking algorithm is developed on the basis of the correlation-based interrogation with continuous window-shift (CCWS), which is an algorithm for digital PIV recording evaluation. Since the CCWS algorithm has very low bias error level and is insensitive to the image pattern size, it makes tracking of complex image patterns possible among hundreds and even thousands of successively recorded frames.

Tests with synthetic image patterns demonstrate that a proper selection of the reference image pattern is very important for an image pattern tracking. When a fixed reference pattern is used, i.e. it is chosen in the first frame and does not change anymore, there will be a large error for determining the image pattern displacement between frames, and consequently, the instantaneous insect body moving velocity cannot be measured at high accuracy. On the other hand, when the tracking is conducted at the maximal image pattern freedom, i.e. the reference image pattern for tracking in the next frame is replaced with every tracked image pattern; a large error will appear by determining the image pattern position. Therefore, an optimal image pattern freedom limit should be setup for the image pattern tracking to avoid the large errors for determining both position and displacement of the tracked image pattern. The optimal freedom limit can be determined with a multi-pass test on the accumulated bias at a selected image frame in the following way: (1) At first, a time period is select that starts at the first frame and includes frames of the most strong image pattern distortion, and the last frame in the selected period should have the most similar image pattern as the first frame. (2) Then, the image pattern tracking runs with increasing freedom limit from L = 1 with step 1. (3) When the accumulated bias frame begins to rise, it is time to stop the test runs. (4) Finally, the freedom limit L is chosen with the minimal accumulated bias.

The described algorithm has been successfully applied to investigate the head-banging behavior of a termite. The position and velocity of the termite head in a head-banging period was determined in the camera focus plane with a high temporal resolution. The acceleration time history was deduced by post processing of the velocity time history, so that the striking force of a termite head-bang on the substrate was estimated. The application for the fire ant antenna in sound waves demonstrates that the described algorithm can be used to detect micro scale, high frequency vibration of an inset body part.

The authors would like to state here that the presented algorithm is one out of several effective algorithms for image pattern tracking, and others may be more suitable for the presented application cases. The authors will try to conducted comparison of possible alternative algorithms in the near future. It should also be mentioned that image tracking of solid objects are much different from tracking tracer particles in fluid flows with particle image velocimetry (PIV), for instance, window deformation and rotation methods in PIV require known particle image displacements at several neighbored evaluation points, so that they cannot be used for the presented cases. Therefore, a high-speed imaging system is essential with the presented algorithm to resolve rotation and deformation of the tracked image pattern.