Resonance in Interacting Induced-Dipole Polarizing Force Fields: Application to Force-Field Derivatives

Abstract

The Silberstein model of the molecular polarizability of diatomic molecules, generalized by Applequist et al. for polyatomic molecules, is analyzed. The atoms are regarded as isotropically polarizable points located at their nuclei, interacting via the fields of their induced dipoles. The use of additive values for atom polarizabilities gives poor results, in some cases leading to artificial predictions of absorption bands. The molecular polarizability of methane and its derivative are computed. The agreement with experimental mean molecular polarizabilities is within 1–5%. A hypothesis is indispensable for a suitable representation of polarizability derivative.

1. Introduction

A simple way to understand the origin of various optical effects in many substances is based on an atom-dipole interaction model. The atoms in a molecule are regarded as isotropic particles, which interact by way of the dipole moments induced in them by an external field.

In a diatomic molecule AB whose atoms have isotropic polarizabilities α_A and α_B, respectively, the additive model of polarizability allows calculating the isotropic molecular polarizability α_mol = α_A + α_B. The diagonal form of α_mol has only one component:

$${\alpha }_{\text{mol}}=\left[\begin{array}{ccc}{\alpha }_{\text{A}}+{\alpha }_{\text{B}}& 0& 0\\ 0& {\alpha }_{\text{A}}+{\alpha }_{\text{B}}& 0\\ 0& 0& {\alpha }_{\text{A}}+{\alpha }_{\text{B}}\end{array}\right]$$

(1)

In the interacting induced-dipole polarization model, the molecular polarizability of AB can be placed in a simple and explicit form. The diagonal form of anisotropic α_mol has two distinct components α_|| and α_⊥, parallel and perpendicular, respectively, to the bond axis. Siberstein’s equations for this case follow [1,2,3]:

$${\alpha }_{\left|\right|}=\frac{{\alpha }_{\text{A}}+{\alpha }_{\text{B}}+4{\alpha }_{\text{A}}{\alpha }_{\text{B}}/r^3}{1-4{\alpha }_{\text{A}}{\alpha }_{\text{B}}/r^6}$$

(2)

$${\alpha }_{\perp }=\frac{{\alpha }_{\text{A}}+{\alpha }_{\text{B}}-2{\alpha }_{\text{A}}{\alpha }_{\text{B}}/r^3}{1-{\alpha }_{\text{A}}{\alpha }_{\text{B}}/r^6}$$

(3)

$${\mathbf{\alpha }}_{\text{mol}}=\left[\begin{array}{ccc}{\alpha }_{\perp }& 0& 0\\ 0& {\alpha }_{\perp }& 0\\ 0& 0& {\alpha }_{\left|\right|}\end{array}\right]$$

(4)

The mean polarizability $\overline{\alpha }$ and anisotropy δ are defined by:

$$\overline{\alpha }=\left({\alpha }_{\text{||}}+2{\alpha }_{\perp }\right)/3$$

(5)

$$\delta =\left({\alpha }_{\text{||}}-{\alpha }_{\perp }\right)/\overline{\alpha }$$

(6)

As an example of the manner in which the molecular polarizability depends on the atom polarizabilities, the isotropic molecule methane (CH₄) is considered [4]. Certain features of the dependence are illustrated by the surface in Figure 1. Additivity of atom polarizabilities would require that the surface be a plane, which is approximately true in the vicinity of the origin, where interactions are small. However, the experimental polarizability of CH₄ is 2.62ų, which is reached in only regions of the surface where the influence of interactions is quite marked. Notice a curve of discontinuity along which the polarizability approaches ±∞. The behaviour is seen in the polarizability surfaces of several molecules that have been similarly explored. Its origin for diatomic molecules can be seen in Equations (2) and (3), where the denominators vanish when α_Aα_B approaches r⁶/4 or r⁶, respectively. For this case the α_A and α_B are inversely related along the curve of discontinuity, which in the α_H–α_C plane follows the relation α_Hα_C = 0.193Å⁶, which is of the form expected for diatomic molecules, though the numerical constant is not predictable from Equations (2) or (3).

The significance of a polarizability of ±∞ is that the molecule is in a state of resonance and absorbs energy from the applied field, which occurs in spite of the fact that any absorption properties of the atoms are not introduced [4]. The behaviour of the model can be understood from its close relation to the classical system of N coupled oscillators, which likewise shows resonance under conditions other than the resonance conditions of the isolated oscillators [5]. The absorption properties [6,7,8] of some types of systems can be predicted from the point-dipole interaction approach used in the present report, but it seems doubtful that this could be done reliably for molecules with the model [7]; the neglect of electron exchange between atoms is probably serious. In the immediate vicinity of the resonance condition, the polarizability is bound to be in error because the model does not take into account damping effects, which would prevent the polarizability from going to infinity. The resonance conditions, wherever they appear, are regarded simply as indications that the coupling between atoms far exceeds the extent that can be treated by the model.

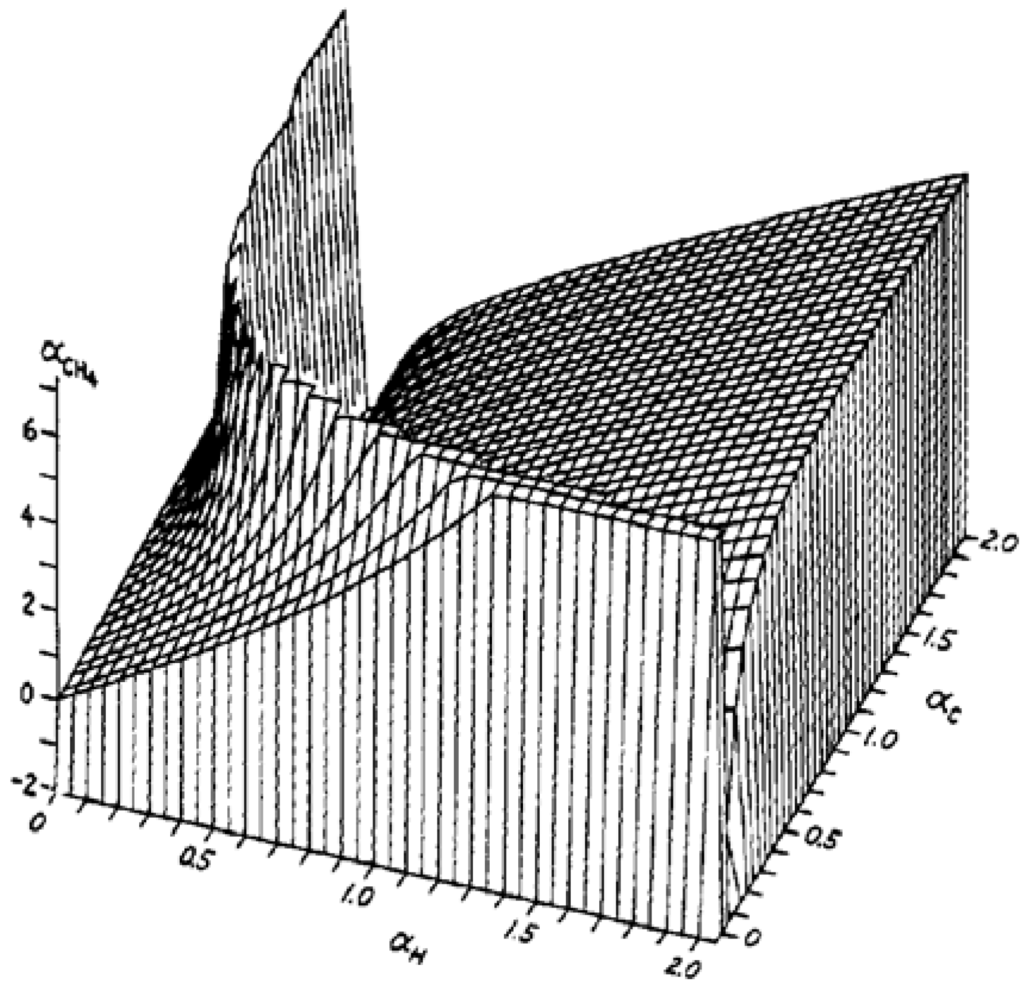
Figure 1. Polarizability of CH₄ as a function of polarizabilities of H and C [4]. Units are ų. Drawn with subroutine THREED (H. Jespersen, Iowa State University Computation Center). The vertical coordinate was truncated at 7 and –2.

Figure 1. Polarizability of CH₄ as a function of polarizabilities of H and C [4]. Units are ų. Drawn with subroutine THREED (H. Jespersen, Iowa State University Computation Center). The vertical coordinate was truncated at 7 and –2.

The purpose of the present report is to present some new derivations of fundamental equations relating molecular electric multipole moments, polarizabilities and their derivatives to the electrostatic energy, and to draw some new conclusions regarding the general characteristics of the polarizability tensors and derivatives.

2. Results and Discussion

2.1. Molecular Dipolar Polarizability Model

The derivative of a molecular dipolar-polarizability tensor α’, with respect to the normal coordinates of vibration Q, is obtained as:

$$\alpha ’=-{\displaystyle \sum _{i,j,k,l}{B}^{ij}\cdot \left(A^{jk}\right)n\cdot B^{kl}}$$

(7)

where (A^jk)’ is the derivative of A^jk with respect to Q, A^jk the inverse polarizability matrix Aμ = E, μ the induced dipole moment vector, E the applied electric field vector, and B = A^–1 the many-body polarizability matrix. The (A^jk)’ can be calculated for j ≠ k, from the matrix of transformation from a Cartesian coordinate system in normal coordinates, for the considered vibration mode (A^jk = T^jk; ∀j ≠ k, where T^jk is the gradient tensor of the electric field E.

However, the diagonal elements (Aⁱⁱ)’ will be calculated, since the model must take into account the dependence of the atomic polarizabilities vs. the length of the bonds between atoms, which leads us to impose an indispensable supplementary hypothesis: the use of the vibrational correction of atomic polarizabilities to average molecular vibrational stretching modes. The modified atomic polarizabilities are calculated as:

$${\alpha }_j={\alpha }_j^{\text{o}}+{\displaystyle \sum _n\left(\frac{d{\alpha }_j}{d{R}_n}\right)R_n}$$

(8)

where R_n is the displacement of the n-th bond length from its experimental value in equilibrium, and α_jº the atomic polarizability of the j unit at the rest configuration of the molecule.

By optimizing the dα_j/dR_n relations to represent the best the experimental values of the derivative of the molecular polarizability tensor α’, to model the molecular polarizability variations during bond vibrations is possible.

2.2. Molecular Dipolar Polarizability of Methane

Equation (8) is an indispensable hypothesis for a suitable representation of α’, without which the registered variations will be of opposite sign to the experimental magnitudes (cf. Figure 2).

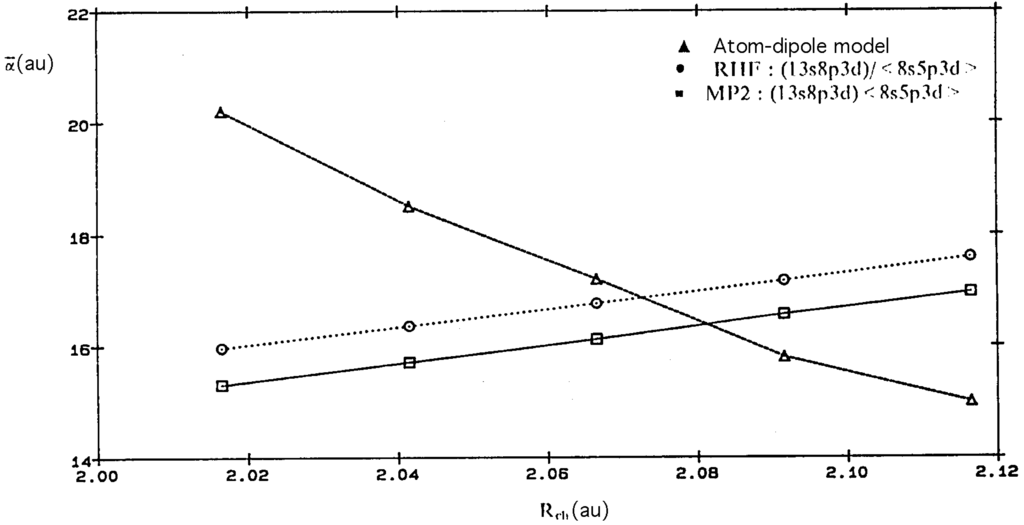
Figure 2. CH₄ gradient of mean dipolar polarizability: ∆ atom-dipole model, ○ RHF (13s8p3d)/<8s5p3d>, □ MP2 (13s8p3d)/<8s5p3d>.

Figure 2. CH₄ gradient of mean dipolar polarizability: ∆ atom-dipole model, ○ RHF (13s8p3d)/<8s5p3d>, □ MP2 (13s8p3d)/<8s5p3d>.

Table 1 lists the vibrational corrections for CH₄ effective atomic and mean molecular polarizabilities.

Table 1. Vibrational corrections for methane effective atomic and mean molecular polarizabilities.

Atom	αa	RH–Cb	α(CH4)c	RvibH–Cd	α’e	αvibf	αvib(CH4)g
H	0.135	–	0.123	–	1.233	0.159	0.146
C	0.878	–	1.288	–	–2.081	0.838	1.308
CH4	1.418	1.113	1.779	1.094	–	1.474	1.892

^a Atomic isotropic and mean additive molecular polarizabilities (ų).^b Bond length C–H (Å).^c Mean effective atomic and mean molecular polarizabilities (ų).^d Reference bond length C–H (Å) to calculate α’.^e Polarizability derivatives for vibrational modes H–C and C–H (Ų).^f Vibration-corrected atomic isotropic and mean additive molecular polarizabilities (ų).^g Vibration-corrected mean effective atomic and mean molecular polarizabilities (ų).

Table 1. Vibrational corrections for methane effective atomic and mean molecular polarizabilities.

Atom	αa	RH–Cb	α(CH4)c	RvibH–Cd	α’e	αvibf	αvib(CH4)g
H	0.135	–	0.123	–	1.233	0.159	0.146
C	0.878	–	1.288	–	–2.081	0.838	1.308
CH4	1.418	1.113	1.779	1.094	–	1.474	1.892

^a Atomic isotropic and mean additive molecular polarizabilities (ų).^b Bond length C–H (Å).^c Mean effective atomic and mean molecular polarizabilities (ų).^d Reference bond length C–H (Å) to calculate α’.^e Polarizability derivatives for vibrational modes H–C and C–H (Ų).^f Vibration-corrected atomic isotropic and mean additive molecular polarizabilities (ų).^g Vibration-corrected mean effective atomic and mean molecular polarizabilities (ų).

A set of strategies devised for applications to large systems is reported. The following improvements are implemented in the model:

1. To build up the many-body polarizability matrix A, the atomic polarizability tensors given by α_i = α_i^σ + α_i^π have been used instead of the scalar polarizability α_i.

2. Damping functions are used in the calculation of the interaction tensor to prevent the polarizability from going to infinity in the models by Applequist and Birge.

a.

Böttcher proposed [25]:

$$T_{pq,\alpha \beta }^{(2)}=\frac{3r_{pq,\alpha }{r}_{pq,\beta }}{r_{pq}^5}-\frac{{\delta }_{\alpha \beta }}{r_{pq}^3}$$

(9)

where T⁽²⁾ is the gradient tensor of the electric field E and δ represents the Kronecker delta function: δ(α,β) = 1 if α = β, and δ(α,β) = 0 if α ≠ β.

b.

Thole proposed [26]:

$$T_{pq,\alpha \beta }^{(2)}=\frac{3v_{pq}^4{r}_{pq,\alpha }{r}_{pq,\beta }}{r_{pq}^5}-\frac{\left(4v_{pq}^3-3v_{pq}^4\right){\delta }_{\alpha \beta }}{r_{pq}^3}$$

(10)

where v_pq = r_pq/s_pq if r_pq < s_pq, otherwise v_pq = 1. The term s is defined as s = 1.662(α_pα_q)^1/6. The values of α_p are parametrized by ab initio coupled Hartree–Fock.

c.

Miller proposed [27,28]:

$$T_{pq,\alpha \beta }^{(2)}=\left(\frac{3r_{pq,\alpha }{r}_{pq,\beta }}{r_{pq}^5}-\frac{{\delta }_{\alpha \beta }}{r_{pq}^3}\right)\left\{1-\exp \left[-{\left(\frac{r_{pq}}{0.7{\rho }_{pq}}\right)}^{10}\right]\right\}$$

(11)

with ρ_pq = ρ_p + ρ_q (sum of the van der Waals radii).

3. The interactions between bonded atoms and between atoms within a distance lying in an interval defined by [r^inf, r^sup] is neglected. The starting values for this interval are [0, 10³⁰] a.u. and r^inf is incremented if resonance conditions are detected.

4. The following tests indicating a resonance condition are implemented:

a.

test whether matrix B^–1 is singular, where B is the many-body polarizability matrix;

b.

test whether matrix B^–1 is not defined positive;

c.

test whether matrix B is not defined positive;

d.

test whether some effective matrix B_p is not defined positive.

5. Atomic polarizabilities are improved with vibrational corrections to average molecular vibrational stretching modes.

6. The atomic polarizabilities allow selecting between optimized ab initio and experimental values.

7. The atomic classes can be either read from input or assigned by the program.

8. The molecule can be reoriented by its principal axes of inertia.

9. The polarization parameters have been included in the database for He, Li, Be, B, Ne, Na, Mg, Al, Si, P, S, Ar, K, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Ga, Ge, As, Se, Kr, Rb, Sr, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, Cd, In, Sn, Sb, Te and Xe.

10. The optimized experimental polarization parameters have been included in the database for the following atomic classes: H (alkane, alcohol, aldehyde, amide, amine and aromatic), C (alkane, carbonyl, nitrile and aromatic), N (amide, amine and nitrile), O (alcohol, ether and carbonyl), F (halomethanes), Cl (halomethanes), Br (halomethanes) and I (halomethanes).

Applications are carried out for the following systems. (1) Clusters: Si_n, Ge_n (1 ≤ n ≤ 10), Ga_nAs_m (1 ≤ n, m ≤ 4), Sc_n (1 ≤ n ≤ 74), C_n-graphene (1 ≤ n ≤ 96), C_n-fullerene (1 ≤ n ≤ 82), endohedral metallofullerenes Sc_n@C_m (1 ≤ n ≤ 3, 60 ≤ m ≤ 82). (2) Single-wall carbon nanotubes: zigzag (n,0) (4 ≤ n ≤ 20) (16 ≤ atoms ≤ 180), armchair (n,n) (5 ≤ n ≤ 10) (90 ≤ atoms ≤ 200), chiral (n,m) (5 ≤ n ≤ 19, 1 ≤ m ≤ 9) (16 ≤ atoms ≤ 250), as well as n → ∞ and ∞-long extrapolations. Deformed (8,0) (28 ≤ atoms ≤ 48) with elliptical radial deformation. (3) Benzothiazole (A)–benzobisthiazole (B) A–B_n–A (0 ≤ n ≤ 13) linear oligomers and n → ∞ extrapolations in three conformations: (a) fully planar (000), (b) a rotational isomer in which each unit is rotated by a fixed angle ∅ with respect to the previous one, all rotations performed in the same direction (+++) (0º ≤ ∅ ≤ 10º), and (c) rotations performed in the alternate directions (+–+) (0º ≤ ∅ ≤ 10º).

3. Conclusions

From the present results and discussion, the following conclusions can be drawn:

1. The determined atom polarizabilities are suitable for calculating reasonably accurate molecular polarizabilities of polyatomic molecules and, probably, have greater validity in general than additive values for calculating interactions among atoms in molecules. The anisotropies of a wide variety of polyatomic molecules can be largely attributed to atom dipole interactions, in support of Silberstein’s [1,2,3] and Applequist’s [4] suggestions. The variety of molecular properties, which can be accounted for, at least approximately suggests that the atom-dipole interaction model is a reasonable facsimile of real molecules. The model is appealing because it requires relatively little information for practical calculations. It is to be expected that further research on the model will deal to refinements and extensions to other properties; e.g., the theory has been extended to include effects because of the nonlinear response of atoms to an applied field, and to consider the role of higher multipole interactions in optical rotation. Both of these developments may well have significant effects on the properties discussed in this report. Even if one is interested in only the dipole response of the system, which is expressed by appropriate elements of the A^–1 matrix, that response is influenced by all orders of multipole response, by virtue of the dependence of each element of A^–1 on all elements of A.

2. A hypothesis is indispensable for a suitable representation of polarizability derivative, without which the registered variations will be of opposite sign to the experimental magnitudes.

3. The point-atom model is not only a mathematical approximation for real molecules, but also a well-defined system, whose behaviour can be calculated to a high degree of accuracy on the basis of known physical laws. Where the behaviour of a real molecule is similar to that of the model, an insight is gained into the origins of the behaviour. Where discrepancies, e.g., resonances, are found, it can be concluded that the molecule is not like the model.

4. The results of the present work clearly indicate that, because of the observed differences between the molecular polarizability results of our program POLAR and our version of program PAPID, it may become necessary to recalibrate POLAR. The values calculated with POLAR are quite larger than those obtained with the reference program PAPID, and POLAR polarizability values do not increase monotonically with bond distances. The recalibration means to obtain better atomic polarizabilities to start with in Equation (13). It appears that the results of good-quality ab initio calculations might be suitable as primary standards for such a calibration.

Work is in progress on the recalibration of POLAR. The difference between POLAR polarizability and PAPID polarizability results is because of the different parametrization schemes used for the initial atomic polarizabilities. PAPID uses atomic polarizability values fitted to high-quality calculations, while POLAR performs a simpler individual computation for each molecule, in order to exploit the difference among different atoms in different functional groups in different molecular environments.

4. Experimental Section

The dipole–dipole polarizability α is calculated with the interacting induced-dipole polarization model [1,2,3], which calculates effective anisotropic point polarizability tensors by the method of Applequist et al. [4]. The molecular polarizability, α_ab^mol, is defined as the linear response to an external electric field:

$${\mu }_a^{\text{ind}}={\alpha }_{ab}^{\text{mol}}{E}_b^{\text{ext}}$$

(12)

where μ_a^ind is the induced molecular dipole moment and a, b, c… denote Cartesian components [9,10,11,12,13,14,15,16,17,18,19]. Considering a set of N interacting atomic polarizabilities, the atomic induced-dipole moment has a contribution also from the other atoms:

$${\mu }_{p,a}^{\text{ind}}={\alpha }_{p,ab}\left(E_b^{\text{ext}}+{\displaystyle \sum _{q\ne p}^N{T}_{pq,bc}^{(2)}{\mu }_{q,c}^{\text{ind}}}\right)$$

(13)

where T_pq,bc⁽²⁾ is the gradient tensor of the electric field:

$$T_{pq,ab}^{(2)}=\frac{3r_{pq,a}{r}_{pq,b}}{r_{pq}^5}-\frac{{\delta }_{ab}}{r_{pq}^3}$$

(14)

where r_pq is the distance between atoms p and q, and δ represents the Kronecker delta function: δ(a,b) = 1 if a = b, and δ(a,b) = 0 if a ≠ b. The molecular polarizability can then be written as:

$${\alpha }_{ab}^{\text{mol}}={\displaystyle \sum _p^N{\alpha }_{p,ab}^{\text{eff}}}={\displaystyle \sum _{q,p}^N{B}_{pq,ab}}$$

(15)

where α^eff_p is the effective polarizability of atom p and B is the relay matrix defined as (in supermatrix notation):

$$B={\left({\alpha }^{-1}-T^{(2)}\right)}^{-1}$$

(16)

The difference between our program POLAR and our version of program PAPID is in the different parametrization scheme used for the initial atomic polarizabilities. PAPID uses atomic α_p values fitted to high-quality calculations, while POLAR performs a simpler individual computation for each molecule, in order to exploit the difference among different atoms in different functional groups in different molecular environments. The following improvements have been implemented in the polarization model:

1. In order to build the relay matrix B, the atomic polarizability tensor α_p = α_p^σ + α_p^π has been used instead of the scalar polarizability α_p. The σ-atomic polarizability tensor is calculated according to:

$${\mathbf{\alpha }}^{\sigma }={\displaystyle \sum _{\text{bonds}}\frac{3{\alpha }^{\sigma }}{{\alpha }_{\left|\right|}^{\sigma }+2{\alpha }_{\perp }^{\sigma }}\left[\begin{array}{ccc}{\alpha }_{\perp }^{\sigma }& 0& 0\\ 0& {\alpha }_{\perp }^{\sigma }& 0\\ 0& 0& {\alpha }_{\left|\right|}^{\sigma }\end{array}\right]}={\displaystyle \sum _{\text{bonds}}\frac{3{\alpha }^{\sigma }}{3.676}\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1.676\end{array}\right]}$$

(17)

where the z-axis is defined as the bond direction for each bond. The diagonal form of α^σ has two distinct components noted as α^σ_|| and α^σ_⊥, parallel and perpendicular to the bond axis, respectively. The parameter α^σ_||/α^σ_⊥ = 1.676 has been obtained fitting the isotropic bonding polarizabilities of Vogel [20]. The bonding polarizabilities have been implemented in the database of program SIBFA [21]. The scalar π-atomic polarizabilities have been evaluated with a modified Hückel molecular orbital (HMO) method. A wave-like scheme is assumed for the variation of the Hückel β-parameter with the torsion angle. In first approximation, β between p_z orbitals twisted from coplanarity by an angle θ can be evaluated as β = β_ocosθ, where β_o is taken as the β value for benzene. An improved estimate of the β function is β = β_ocos^1.15θ [22]. The π-atomic polarizability tensor is calculated as:

$${\mathbf{\alpha }}^{\pi }={\displaystyle \sum _{\text{bonds}}\frac{3{\alpha }^{\pi }}{2{\alpha }_{\left|\right|}^{\pi }+{\alpha }_{\perp }^{\pi }}\left[\begin{array}{ccc}{\alpha }_{\left|\right|}^{\pi }& 0& 0\\ 0& {\alpha }_{\left|\right|}^{\pi }& 0\\ 0& 0& {\alpha }_{\perp }^{\pi }\end{array}\right]}={\displaystyle \sum _{\text{bonds}}\frac{3{\alpha }^{\pi }}{3.741}\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1.741\end{array}\right]}$$

(18)

where the xy plane is the σ-plane. The α^π_|| and α^π_⊥ are parallel and perpendicular to the σ-plane, respectively. The parameter α^π_⊥/α^π_|| = 1.741 has been obtained fitting the experimental polarizabilities of aromatic molecules.

2. Damping functions have been used in the calculation of the interaction tensor to prevent the polarizability from going to infinity [23,24,25]. Thole proposed:

$$T_{pq,\alpha \beta }^{(2)}=\frac{3v_{pq}^4{r}_{pq,\alpha }{r}_{pq,\beta }}{r_{pq}^5}-\frac{\left(4v_{pq}^3-3v_{pq}^4\right){\delta }_{\alpha \beta }}{r_{pq}^3}$$

(19)

where v_pq = r_pq/s_pq if r_pq < s_pq; otherwise v_pq = 1 [26]. The term s is defined as s = 1.662(α_pα_q)^1/6. Miller proposed:

$$T_{pq,\alpha \beta }^{(2)}=\left(\frac{3r_{pq,\alpha }{r}_{pq,\beta }}{r_{pq}^5}-\frac{{\delta }_{\alpha \beta }}{r_{pq}^3}\right)\left\{1-\exp \left[-{\left(\frac{r_{pq}}{0.7{\rho }_{pq}}\right)}^{10}\right]\right\}$$

(20)

with ρ_pq = ρ_p + ρ_q (sum of the van der Waals radii) [27,28].

3. The interactions between bonded atoms and between atoms within a distance lying in an interval defined by [r^inf,r^sup] have been neglected. The starting values for this interval are [0, 10³⁰] a.u. The calculation can start from a predefined value of r^inf (e.g., r^inf = 0) and increment r^inf by one atomic unit (Δr = 1 a.u.), each time resonance conditions are detected, up to r^sup.

4. Four tests indicating a resonance condition have been implemented: test whether matrix B^-1 is singular, whether matrix B^-1 is not positive definite, whether matrix B is not defined positive and whether some effective matrix B_p is not defined positive.

5. Vibrational corrections are obtained by a modification of atomic polarizability increments (Equation 8).

6. The optimized experimental polarization parameters have been included in the database for a number of atomic classes [29].

An optimized version of our program POLAR, including the whole interacting induced-dipole polarization model, has been implemented in the MM2 molecular mechanics program [30], in its extension to the coordination complexes of transition metals (MMX) [31] and in the empirical conformational energy program for peptides (ECEPP2) [32]. The new versions are called MMID2 [33,34], MMXID [35,36,37,38,39] and ECEPPID2 [39,40].