Recognizing Human Activities from Sensors Using Hidden Markov Models Constructed by Feature Selection Techniques

Abstract

In this paper a method for selecting features for Human Activity Recognition from sensors is presented. Using a large feature set that contains features that may describe the activities to recognize, Best First Search and Genetic Algorithms are employed to select the feature subset that maximizes the accuracy of a Hidden Markov Model generated from the subset. A comparative of the proposed techniques is presented to demonstrate their performance building Hidden Markov Models to classify different human activities using video sensors

1. Introduction

Sensors allow computers to perceive the world that surrounds them. By the use of sensors, like thermostats or photocells, computers can meassure the temperature or lighting conditions of a room. In the last years,the deployment of multisensor networks has become popular due to the cut down on sensor prizes. This networks can include different kind of sensors, maybe more complex, like cameras, indoor location systems (ILS), microphones, etc …By the use of sensor networks computer systems can take more accurate decissions due to the richer information about the environment that they have.

A common task in sensor processing is the recognition of situations in the environment perceived. If these situations to recognize are known a priori, i.e. there is a set of labels that describe each situation, the problem can be tackled as a classification task. Then, the problem to solve is to find a model relating the data from sensor readings with situation labels. Some sensor data may be too noisy, and other not provide any information for label prediction. Relevant sensor data has to be identified to build the model from them, not including irrelevant data.

An application where the use of sensor networks can be useful is Human Activity Recognition, i.e., the understanding by the computer of what humans are doing. This field has received increasing attention in the last years, due to their promising applications that have in surveillance, human computer interaction or ambient intelligence, and the interests that governments and commercial organizations have placed in the area. Human Activity Recognition systems can be integrated with existing systems as the proposed by Corchado et al. [1] to monitor alzehimer patients. If a patient falls to the floor, the system can alert a nurse to attend the accident. Human Activity Recognition systems can also be integrated with the system proposed by Pavón et al. [2], detecting forbidden activities being performed and alerting security staff.

Human activity recognition may be considered as a classification task, and human activity recognizers can be created using supervised learning. A set of activities to recognized has to be defined a priori. Different observations about the activities to recognize are extracted using different sensors. Then, the problem to solve is to find the function that best relates observations to activity labels. Data from sensors is not free from noise, so relevant attributes have to be identified before training the activity recognizer. Better results are expected to be obtained when this previous step is performed.

The sensors that provides the most information for Human Activity Recognition are video cameras. Works in activity recognition from video could be divided in two groups [3]: (1) those that are centered in small duration activities (i.e. walking, running,…); and (2) those that deal with large duration activities (i.e. leaving place, going to living room,…). The former are centered in choosing good features for activity recognition, whereas the latter usually tackle the temporal structure in the classifier.

Regarding small duration activities, Neural networks, Neuro-fuzzy systems and C4.5 have been succesfully employed [4]. Also, time delay neural networks have been used to recognize the case where the activities are hand gestures [5]. In [6] is shown how to perform feature extraction, feature selection and classification using a simple bayesian classifier to solve the small duration activity recognition problem. In their approach, they use ground truth data from CAVIAR* dataset of people bounding boxes instead of a blob tracker output. Perez et al. [7] use different time averaged speed measures to classify the activities present in the CAVIAR dataset using HMM.

Robertson et al. [3] uses trajectory and velocity concatenated data for five frames, and blob optical flow, to decide what is the current small duration activity. This small duration activity is then introduced in a Hidden Markov Model (HMM) to decide which is the small duration activity performed.

To classify large duration activities, Brand et al. [8] have used HMMs for modelling activities performed in an office. They use different spatial meassures taken from the blob bounding ellipse.The HMM approach has been extended in [9] to model activities involving two agents, using a Coupled-HMM. They use different velocity meassures as features, being all of them invariant with respect to camera rotations and translations, providing camera independent recognizers.

HMMs are recognized as one effective technique for activity classification, because they offer dynamic time warping, have clear bayesian semantics and well-understood training algorithms. In this paper a method to adapt them, selecting the best features in the observation space, is defined, trying to maximize its accuracy for classifying short durative activities. HMMs will be incrementally built using both heuristic search and genetic algorithms. A comparative of the performance obtained using these algorithm for HMM construction will be shown. Our approach differs from the proposed by Ribeiro et al. in some aspects: (1) blob tracker output is used instead of ground truth data; (2) the foreground mask of the blob tracker is used to extract features; (3) the classifier used for the recognition of activities is an HMM; (4) we use different temporal window sizes; and (4) we use different search methods for feature selection.

This paper is organized as follows: on section 2, an overview of the activity recognition system where the feature selection is going to be performed is given; on section 3, the feature selection algorithms that are used to build HMMs are presented; on section 4, experiments selecting good features for human activity recognition are performed and results are discussed; finally, on section 5 conclusions of this work are presented and future lines are discused.

2. Definition of Activity Recognition problem

2.1. Functional description

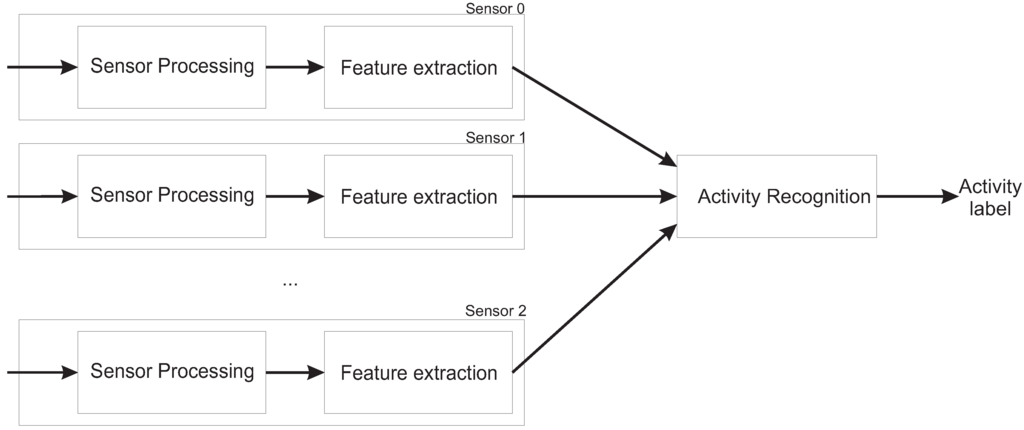
Figure 1. Overview of the activity recognition process from multiple sensors

Figure 1. Overview of the activity recognition process from multiple sensors

In the proposed human activity recognition architecture (see Figure 1), the objective is to select from a set of activity labels $A=\{a_1,\dots ,a_N\}$ the one that is the most likely according to the signal $p\left(t\right)$ retrieved by the sensors at each time step. Sensors could be video cameras, thermal cameras or indoor localization systems, depending of the available resources and the conditions of the environment. In case of imaging sensors, they get a frame on each time step, $p\left(t\right)\equiv I\left(t,x,y\right)$. Using $p\left(t\right)$, the system needs to extract the position and size $b_i\left(t\right)$ of each human i in the environment. When using imaging sensors, $b_i\left(t\right)$ may be obtained using a blob tracker [10]. Blob tracker takes an image sequence and provides the location of each object i moving in the scene, mantaining a temporal coherence of objects between frames. Human tracking is a hard task and, despite of the advances in the last years, tracking methods still provide a noisy output, caused in part by scene illumination changes or by the complexity of object movements [11]. Using $p\left(t\right)$ and $b_i\left(t\right)$, a set of additional features ${\zeta }_i\left(t\right)$ may have to be extracted to be able to differenciate between the activities to be recognized. Finally, using ${\zeta }_i\left(t\right)$, a function $\Lambda \left({\zeta }_i\left(t\right)\right)$, $\Lambda :\zeta \to A$ is used to decide wich is the activity being performed.

Activity recognition solves the correspondence:

$$q_{it}=\arg \underset{a_k}{\max }P\left({\zeta }_i\left(t\right),{\zeta }_i\left(t-1\right)\dots ,{\zeta }_i\left(1\right)\mid a_k\right)$$

(1)

where $q_{i}t$ is the activity that maximizes the probability of the observations ${\zeta }_i\left(t\right)$,${\zeta }_i\left(t-1\right)$,…,${\zeta }_i\left(0\right)$ at instant t by individual i.

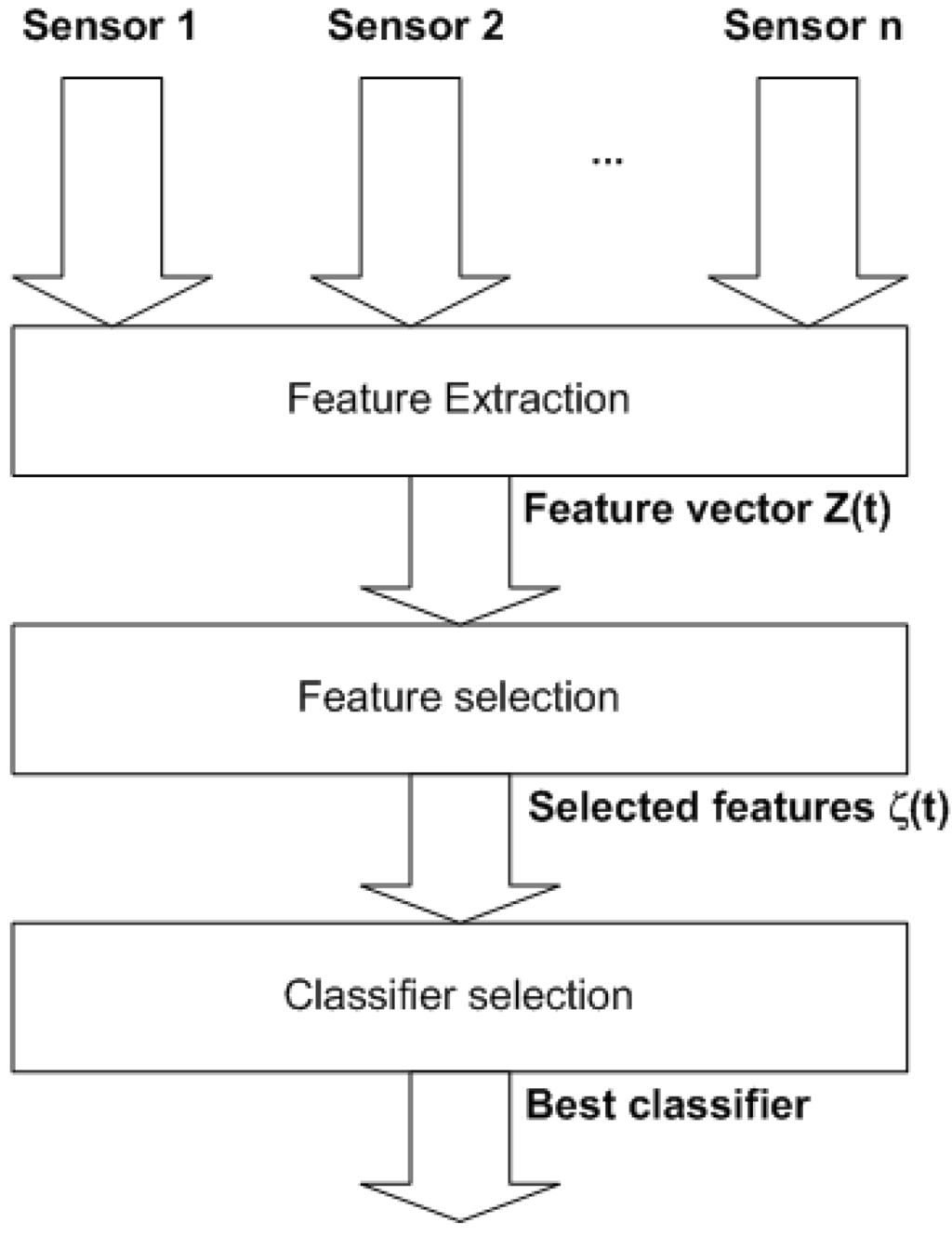
Figure 2. The three steps to create an activity recognizer

Figure 2. The three steps to create an activity recognizer

To build an activity recognition system, three processes have to be performed (see Figure 2). First, an extensive feature set $Z_i\left(t\right)$ has to be extracted from $b_i\left(t\right)$ and $I\left(t,x,y\right)$. On a second step, the subset ${\zeta }_i\left(t\right)$ has to be selected from $Z\left(t\right)$, selecting the subset with the most predictive power for A. The last problem to solve is to select the best classifier architecture for activity recognition.

2.2. Feature extraction for activity representation using video sensors

The features that can be used for activity representation depend of the type of sensor inputs to be processed. The most common sensor used for Human Activity recognition are video cameras, so all the features presented here are computed from image sequences.

The objective of this section is to present a large set of features to characterize the activities to classify as complete as possible. The input to the feature extraction process includes the original frame $I\left(t,x,y\right)$, its foreground mask $Fg\left(t,x,y\right)$, and the blob bounding box $b\left(t\right)$ given by a blob tracker, that represents the human (see Figure 3). Using these information, different type of features are going to be derived. Most of the features presented here have been proposed in [6]. The first group of extracted features comes from the blob bounding box properties and its time evolution, taking first order derivatives and time averaged derivatives, using a temporal window of T frames, as shown on Table 1

Figure 3. Inputs for the feature extraction process

Figure 3. Inputs for the feature extraction process

Table 1. First feature group: blob bounding box properties

#	Feature name	Definition
Bounding box properties at time t
1	Position	$p\left(t\right)=\left(x\left(t\right),y\left(t\right)\right)$
2	Size	$size\left(t\right)=\left(w\left(t\right),h\left(t\right)\right)$
3	Velocity	$s\left(t\right)=\frac{\partial p\left(t\right)}{\partial t}=\left(\frac{\partial x\left(t\right)}{\partial t},\frac{\partial y\left(t\right)}{\partial t}\right)$
4	Size derivative	$\frac{\partial size\left(t\right)}{\partial t}=\frac{\partial w\left(t\right)}{\partial t},\frac{\partial h\left(t\right)}{\partial t}$
5	Speed	$s\left(t\right)=\sqrt{{\left(\frac{\partial x\left(t\right)}{\partial t}\right)}^2+{\left(\frac{\partial y\left(t\right)}{\partial t}\right)}^2}$
6	Area	$s\left(t\right)=w\left(t\right)*h\left(t\right)$
Properties averaged over T frames
7	Mean speed	${\displaystyle {\overline{s}}_T\left(t\right)=\frac{1}{T}\sum _{i=t-T+1}^{T}s\left(i\right)}$
-	Mean velocity norm	$∥{\overline{\overrightarrow{s}}}_T\left(t\right)∥$ 3 different methods:
8	Averaging vectors	${∥{\overline{\overrightarrow{s}}}_T\left(t\right)∥}_1=∥{\displaystyle \frac{1}{T}\sum _{i=t-T}^{t-1}\frac{\overrightarrow{p}\left(t\right)-\overrightarrow{p}\left(i\right)}{t-i}}∥$
9	Mean vectors	${∥{\overline{\overrightarrow{s}}}_T\left(t\right)∥}_2=∥\frac{\overrightarrow{p\left(t\right)}-\overrightarrow{p\left(t-T+1\right)}}{T}∥$
10	Linear fitting	${∥{\overline{\overrightarrow{s}}}_T\left(t\right)∥}_3=$ Linear Least Squares Fitting
11..13	speed/velocity ratio	$R_{\overrightarrow{s_T},i}\left(t\right)={\frac{s_T\left(t\right)}{∥{\overrightarrow{s}}_T\left(t\right)∥}}_i$ $i=1,2,3$
Second order moments
14	speed	${\displaystyle {\sigma }_{v,T}^2{\left(t\right)}_1=\frac{1}{T-1}\sum _{i=t-T+1}^t{s}^2\left(i\right)}$
15..17	speed (centered)	${\displaystyle {\sigma }_{v,T}^2{\left(t\right)}_{1+j}=\frac{1}{T-1}\sum _{i=t-T+1}^t{\left(s\left(i\right)-{\overline{s}}_T\left(t\right)\right)}_j}$ j=1,2,3
-	velocity	${\displaystyle {\Sigma }_{\overrightarrow{s},T}{\left(t\right)}_1=\frac{1}{T-1}\sum _{i=t-T+1}^t\overrightarrow{s}\left(i\right)\overrightarrow{s}{\left(i\right)}^{\prime }}$
-	velocity centered	${\displaystyle {\Sigma }_{\overrightarrow{s},T}{\left(t\right)}_{1+j}=\frac{1}{T-1}\sum _{i=t-T+1}^t\left(\overrightarrow{s}\left(i\right)-{\overline{\overrightarrow{s}}}_T{\left(t\right)}_j\right){\left(\overrightarrow{s}\left(i\right)-{\overline{\overrightarrow{s}}}_T{\left(t\right)}_j\right)}^{\prime }}$ j=1,2,3
18..21	trace	$t{r}_{{\Sigma }_{\overrightarrow{s},T}}{\left(t\right)}_i=trace\left({\Sigma }_{\overrightarrow{v},T}\left(t\right)\right)$ i=1,2,3,4
22..25	eigenvalues ratio	$R_{{\Sigma }_{\overrightarrow{s},T}}{\left(t\right)}_i=\frac{{\lambda }_{min}}{{\lambda }_{max}}\left({\Sigma }_{\overrightarrow{v},T}\left(t\right)\right)$ i=1,2,3,4

Table 1. First feature group: blob bounding box properties

#	Feature name	Definition
Bounding box properties at time t
1	Position	$p\left(t\right)=\left(x\left(t\right),y\left(t\right)\right)$
2	Size	$size\left(t\right)=\left(w\left(t\right),h\left(t\right)\right)$
3	Velocity	$s\left(t\right)=\frac{\partial p\left(t\right)}{\partial t}=\left(\frac{\partial x\left(t\right)}{\partial t},\frac{\partial y\left(t\right)}{\partial t}\right)$
4	Size derivative	$\frac{\partial size\left(t\right)}{\partial t}=\frac{\partial w\left(t\right)}{\partial t},\frac{\partial h\left(t\right)}{\partial t}$
5	Speed	$s\left(t\right)=\sqrt{{\left(\frac{\partial x\left(t\right)}{\partial t}\right)}^2+{\left(\frac{\partial y\left(t\right)}{\partial t}\right)}^2}$
6	Area	$s\left(t\right)=w\left(t\right)*h\left(t\right)$
Properties averaged over T frames
7	Mean speed	${\displaystyle {\overline{s}}_T\left(t\right)=\frac{1}{T}\sum _{i=t-T+1}^{T}s\left(i\right)}$
-	Mean velocity norm	$∥{\overline{\overrightarrow{s}}}_T\left(t\right)∥$ 3 different methods:
8	Averaging vectors	${∥{\overline{\overrightarrow{s}}}_T\left(t\right)∥}_1=∥{\displaystyle \frac{1}{T}\sum _{i=t-T}^{t-1}\frac{\overrightarrow{p}\left(t\right)-\overrightarrow{p}\left(i\right)}{t-i}}∥$
9	Mean vectors	${∥{\overline{\overrightarrow{s}}}_T\left(t\right)∥}_2=∥\frac{\overrightarrow{p\left(t\right)}-\overrightarrow{p\left(t-T+1\right)}}{T}∥$
10	Linear fitting	${∥{\overline{\overrightarrow{s}}}_T\left(t\right)∥}_3=$ Linear Least Squares Fitting
11..13	speed/velocity ratio	$R_{\overrightarrow{s_T},i}\left(t\right)={\frac{s_T\left(t\right)}{∥{\overrightarrow{s}}_T\left(t\right)∥}}_i$ $i=1,2,3$
Second order moments
14	speed	${\displaystyle {\sigma }_{v,T}^2{\left(t\right)}_1=\frac{1}{T-1}\sum _{i=t-T+1}^t{s}^2\left(i\right)}$
15..17	speed (centered)	${\displaystyle {\sigma }_{v,T}^2{\left(t\right)}_{1+j}=\frac{1}{T-1}\sum _{i=t-T+1}^t{\left(s\left(i\right)-{\overline{s}}_T\left(t\right)\right)}_j}$ j=1,2,3
-	velocity	${\displaystyle {\Sigma }_{\overrightarrow{s},T}{\left(t\right)}_1=\frac{1}{T-1}\sum _{i=t-T+1}^t\overrightarrow{s}\left(i\right)\overrightarrow{s}{\left(i\right)}^{\prime }}$
-	velocity centered	${\displaystyle {\Sigma }_{\overrightarrow{s},T}{\left(t\right)}_{1+j}=\frac{1}{T-1}\sum _{i=t-T+1}^t\left(\overrightarrow{s}\left(i\right)-{\overline{\overrightarrow{s}}}_T{\left(t\right)}_j\right){\left(\overrightarrow{s}\left(i\right)-{\overline{\overrightarrow{s}}}_T{\left(t\right)}_j\right)}^{\prime }}$ j=1,2,3
18..21	trace	$t{r}_{{\Sigma }_{\overrightarrow{s},T}}{\left(t\right)}_i=trace\left({\Sigma }_{\overrightarrow{v},T}\left(t\right)\right)$ i=1,2,3,4
22..25	eigenvalues ratio	$R_{{\Sigma }_{\overrightarrow{s},T}}{\left(t\right)}_i=\frac{{\lambda }_{min}}{{\lambda }_{max}}\left({\Sigma }_{\overrightarrow{v},T}\left(t\right)\right)$ i=1,2,3,4

Second feature group consist of the seven Hu invariant moments [12] $\{h{u}_1,h{u}_2,h{u}_3,h{u}_4,h{u}_5,h{u}_6,h{u}_7\}$ of the foreground mask enclosed by the blob bounding box. These seven moments are shape descriptors invariant under translation, rotation and scaling. Each Hu moment is numbered from 26 to 32.

Table 2. Third and fourth group: Optical flow measures

# $I\left(t,x,y\right)$	# $Fg\left(t,x,y\right)$	Feature name	Definition
-	-	target pixels	$P\left(t\right)=\left\{(x,y)\in boundingbox\left(t\right)\right\}$
Instantaneous
-	-	optical flow	$\overrightarrow{F}\left(t,x,y\right)=\left(f_x\left(t,x,y\right),f_y\left(t,x,y\right)\right),\left(x,y\right)\in P\left(t\right)$
-	-	mean flow	${\displaystyle \overline{\overrightarrow{F}}{\left(t\right)}_1=\frac{1}{N}\sum _{\left(x,y\right)\in P\left(t\right)}\overrightarrow{F}\left(t,x,y\right)}$
-	-	mean flow (centered)	$\overline{\overrightarrow{F}}{\left(t\right)}_2=\overrightarrow{F}{\left(t\right)}_1-{\overrightarrow{v}}_t$
-	-	flow norm	$f{\left(t,x,y\right)}_1=∥\overrightarrow{F}\left(t,x,y\right)∥$
-	-	flow norm (centered)	$f{\left(t,x,y\right)}_2=∥\overrightarrow{F}\left(t,x,y\right)-\overrightarrow{v}\left(t\right)∥$
Spatial energy / 2nd order moments
33, 34	37, 38	motion energy	${\displaystyle f{\left(t\right)}_i=\frac{1}{N}\sum _{\left(x,y\right)\in P\left(t\right)}{\overrightarrow{f}}^2{\left(t,x,y\right)}_i}$$i=1,2$
-	-	flow cov.	${\displaystyle {\Sigma }_{\overrightarrow{F}}{\left(t\right)}_1=\frac{1}{N}\sum _{\left(x,y\right)\in P\left(t\right)}\overrightarrow{F}\left(t,x,y\right)\overrightarrow{F}{\left(t,x,y\right)}^{\prime }}$
-	-	flow cov. centered	${\displaystyle {\Sigma }_{\overrightarrow{F}}{\left(t\right)}_2=\frac{1}{N}\sum _{\left(x,y\right)\in P\left(t\right)}\left(\overrightarrow{F}\left(t,x,y\right)-\overline{\overrightarrow{F}}{\left(t\right)}_1\right){\left(\overrightarrow{F}\left(t,x,y\right)-\overline{\overrightarrow{F}}{\left(t\right)}_1\right)}^{\prime }}$
35,36	39, 40	eigenvalues ratio	$R_{{\Sigma }_{\overrightarrow{F}}}{\left(t\right)}_i=\frac{{\lambda }_{min}}{{\lambda }_{max}}\left({\Sigma }_{\overrightarrow{F}}\left(t\right)\right)$ i=1,2
Time averaged over T frames
-	-	mean flow	${\displaystyle \overline{\overrightarrow{F}}{\left(t\right)}_{i+2}=\overline{\overrightarrow{F}}{\left(t\right)}_i-\frac{1}{T}\sum _{j=t-T+1}^t\overline{\overrightarrow{F}}{\left(j\right)}_i}$ $i=1,2$
41	42	motion energy	${\displaystyle \overline{f_T}\left(T\right)=\frac{1}{T}\sum _{i=t-T+1}^{t}f{\left(i\right)}_1}$
Temporal energy / 2nd order moments
-	-	mean flow	${\displaystyle {\Sigma }_{\overline{\overrightarrow{F}}}{\left(t\right)}_i=\frac{1}{T}\sum _{j=t-T+1}^t\overline{\overrightarrow{F}}{\left(j\right)}_i\overline{\overrightarrow{F}}{\left(j\right)}_i^{\prime }}$ $i=1,2,3,4$
43…46	51…54	trace	$t{r}_{{\Sigma }_{\overline{\overrightarrow{F}}}}{\left(t\right)}_i=trace\left({\Sigma }_{\overline{\overrightarrow{F}}}{\left(t\right)}_i\right)$ $i=1,2,3,4$
47 …50	55…58	eigenvalues ratio	$R_{{\Sigma }_{\overline{\overrightarrow{F}}}}{\left(t\right)}_i=\frac{{\lambda }_{min}}{{\lambda }_{max}}\left({\Sigma }_{\overline{\overrightarrow{F}}}{\left(t\right)}_i\right)$ $i=1,2,3,4$

Table 2. Third and fourth group: Optical flow measures

# $I\left(t,x,y\right)$	# $Fg\left(t,x,y\right)$	Feature name	Definition
-	-	target pixels	$P\left(t\right)=\left\{(x,y)\in boundingbox\left(t\right)\right\}$
Instantaneous
-	-	optical flow	$\overrightarrow{F}\left(t,x,y\right)=\left(f_x\left(t,x,y\right),f_y\left(t,x,y\right)\right),\left(x,y\right)\in P\left(t\right)$
-	-	mean flow	${\displaystyle \overline{\overrightarrow{F}}{\left(t\right)}_1=\frac{1}{N}\sum _{\left(x,y\right)\in P\left(t\right)}\overrightarrow{F}\left(t,x,y\right)}$
-	-	mean flow (centered)	$\overline{\overrightarrow{F}}{\left(t\right)}_2=\overrightarrow{F}{\left(t\right)}_1-{\overrightarrow{v}}_t$
-	-	flow norm	$f{\left(t,x,y\right)}_1=∥\overrightarrow{F}\left(t,x,y\right)∥$
-	-	flow norm (centered)	$f{\left(t,x,y\right)}_2=∥\overrightarrow{F}\left(t,x,y\right)-\overrightarrow{v}\left(t\right)∥$
Spatial energy / 2nd order moments
33, 34	37, 38	motion energy	${\displaystyle f{\left(t\right)}_i=\frac{1}{N}\sum _{\left(x,y\right)\in P\left(t\right)}{\overrightarrow{f}}^2{\left(t,x,y\right)}_i}$$i=1,2$
-	-	flow cov.	${\displaystyle {\Sigma }_{\overrightarrow{F}}{\left(t\right)}_1=\frac{1}{N}\sum _{\left(x,y\right)\in P\left(t\right)}\overrightarrow{F}\left(t,x,y\right)\overrightarrow{F}{\left(t,x,y\right)}^{\prime }}$
-	-	flow cov. centered	${\displaystyle {\Sigma }_{\overrightarrow{F}}{\left(t\right)}_2=\frac{1}{N}\sum _{\left(x,y\right)\in P\left(t\right)}\left(\overrightarrow{F}\left(t,x,y\right)-\overline{\overrightarrow{F}}{\left(t\right)}_1\right){\left(\overrightarrow{F}\left(t,x,y\right)-\overline{\overrightarrow{F}}{\left(t\right)}_1\right)}^{\prime }}$
35,36	39, 40	eigenvalues ratio	$R_{{\Sigma }_{\overrightarrow{F}}}{\left(t\right)}_i=\frac{{\lambda }_{min}}{{\lambda }_{max}}\left({\Sigma }_{\overrightarrow{F}}\left(t\right)\right)$ i=1,2
Time averaged over T frames
-	-	mean flow	${\displaystyle \overline{\overrightarrow{F}}{\left(t\right)}_{i+2}=\overline{\overrightarrow{F}}{\left(t\right)}_i-\frac{1}{T}\sum _{j=t-T+1}^t\overline{\overrightarrow{F}}{\left(j\right)}_i}$ $i=1,2$
41	42	motion energy	${\displaystyle \overline{f_T}\left(T\right)=\frac{1}{T}\sum _{i=t-T+1}^{t}f{\left(i\right)}_1}$
Temporal energy / 2nd order moments
-	-	mean flow	${\displaystyle {\Sigma }_{\overline{\overrightarrow{F}}}{\left(t\right)}_i=\frac{1}{T}\sum _{j=t-T+1}^t\overline{\overrightarrow{F}}{\left(j\right)}_i\overline{\overrightarrow{F}}{\left(j\right)}_i^{\prime }}$ $i=1,2,3,4$
43…46	51…54	trace	$t{r}_{{\Sigma }_{\overline{\overrightarrow{F}}}}{\left(t\right)}_i=trace\left({\Sigma }_{\overline{\overrightarrow{F}}}{\left(t\right)}_i\right)$ $i=1,2,3,4$
47 …50	55…58	eigenvalues ratio	$R_{{\Sigma }_{\overline{\overrightarrow{F}}}}{\left(t\right)}_i=\frac{{\lambda }_{min}}{{\lambda }_{max}}\left({\Sigma }_{\overline{\overrightarrow{F}}}{\left(t\right)}_i\right)$ $i=1,2,3,4$

Third and Fourth feature groups have been extracted from optical flow meassures from the enclosed blob bounding box of $I\left(t,x,y\right)$ and $Fg\left(t,x,y\right)$. Optical flow is a meassure of the motion of each one of the pixels of a given frame with respect to a previous one. In our work, it is obtained using the Lucas-Kanade method [13]. Again, some properties are taken from the time averaged meassures of different optical flow properties, using a temporal window of size T.

2.3. Feature selection for activity recognition problems

Feature selection could be described as a single objective optimization problem where given a set of features F, a subset $f^{*}$ has to be determined, such:

$$J\left(f^{*},E\right)=\underset{f\subseteq F}{\max }J\left(f,E\right)$$

(2)

where $J:F\times \Psi \to \mathbb{R}$ is an utility function that meassures how good is a feature subset $f\subseteq F$ for classiffing a set of points $E\in \Psi$, being Ψ the space of training examples. In a supervised context, where the class of the points in E is known, the goodness of the subset f could be interpreted as the accuracy of a classifier built using the attributes in f, while in an unsupervised context the goodness of f could be interpreted as the quality of the generated clusters.

The need for feature selections comes from the fact that available training instances usually contain highly correlated and/or noise-dominated attributes. These attributes have to be identified and removed, because they don’t provide useful information for classification and their use only increase the classification cost, even dropping the classification accuracy.

The feature selection problem has been widely studied in the literature. A taxonomy of the existing techniques could be established according to the evaluation criteria used to score the candidate feature subsets [14]: (1) wrapper methods, where a classifier is trained to evaluate the predictive accuracy of the candidate subset; and (2) filter methods, where a meassure of the predictive power of the feature subset is calculated, without training any classifiers. Filter methods are quicker and more general than wrapper methods, but the optimality of the obtained feature subsets could not be ensured even using exhaustive search methods.

2.4. Classifiers for activity recognition

To solve general classification problems, different algorithms have been proposed, supervised and non supervised [15]. Supervised methods build class models using labelled data, whereas non supervised methods try to discover the structure of the data. Examples of supervised methods are kNN, Neural Networks and Classification Trees. Examples of non supervised methods are clustering techniques. In Human Activity Recognition, the most accepted classification techniques are Hidden Markov Models (HMMs), because activities have temporal structure and HMMs can tackle with this kind of processes. However, others methods have been succesfully used [4]: Neural Networks, Neuro-Fuzzy systems, C4.5. etc.

Be a system that can be described using a set of N different states, where random transitions are produced over time, according to a given probability distribution for each state. The state on the system on each moment depends on the state that it was in the previous moments. This kind of stochastic process is called ”Markov Model”. Additionally, if the present state of the system can not be observed, i.e., it could be only measured by an effect that it produces, the system is called ”Hidden Markov Model”.

A Hidden Markov Model λ [16] is defined by the tuple $\lambda \equiv \left(S,M,A,B,\Pi \right)$ where:

• $S=\{S_0,\dots ,S_N\}$ is the set of hidden states of the model. The state at time t is denoted by $q_t$.
• M is the set of observation symbols of the model.
• $A=\left\{a_{ij}\right\}$ is the state transition probability distribution:

  $$a_{ij}=p\left(q_{t+1}=S_j\mid q_t=S_i\right)$$

  (3)
• $B=\left\{b_j\right\}$ is the observation symbol probability distribution in state j:

  $$b_j=p\left(v\mid q_t=j\right)$$

  (4)
• $\Pi =\left\{{\pi }_j\right\}$ is the initial state probability distribution:

  $$p{i}_j=p\left(q_0=j\right)$$

  (5)

One of the most powerful features of HMMs is that it can model both large duration and small duration activities. To model large duration activities, an HMM is defined for each activity. Given a sequence $O=o\_1\dots o\_k$ of observations to classify as a large duration activity, and a set of HMM activity models $\Lambda =\{{\lambda }_1\dots {\lambda }_n\}$, the sequence is associated to the HMM with the highest probability of generating O:

$$\arg \underset{i}{\max }P\left(m_i\mid O\right)$$

(6)

$P\left(O\mid m_i\right)$ can be estimated using Forward-Backward algorithm [16].

When the recognition target are small duration activities, only one HMM is used, with one state per activity to classify. Given a sequence $O=o\_1\dots o_k$ of observations to classify as small duration activities, the problem to solve is the association of each observation with the state most likely of generating it:

$$q_t=\arg \underset{i}{\max }P\left(S_i\mid o_t,q_{t-1}\right)$$

(7)

The solution to estimate the current state of the HMM can be found using Viterbi algorithm [16]. Viterbi algorithm computes the most likely state sequence that has generated the observed output. The algorithm proceeds as fallows:

• Initialization:

  $$\begin{array}{cccc}\hfill {\delta }_1\left(i\right)& ={\pi }_i{b}_i\left(o_1\right)\hfill & \hfill 1& \le i\le N\hfill \end{array}$$

  (8)

  $$\begin{array}{ccc}\hfill {\psi }_1\left(i\right)& =0\hfill & \end{array}$$

  (9)
• Recursion:

  $$\begin{array}{cc}\hfill {\delta }_t\left(j\right)=\underset{1\le i\le N}{\max }\left[{\delta }_{t-1}\left(i\right)a_{ij}\right]b_j\left(o_t\right)& 2\le t\le K\hfill \\ & 1\le j\le N\hfill \end{array}$$

  (10)

  $$\begin{array}{cc}\hfill {\psi }_t\left(j\right)=\arg \underset{1\le i\le N}{\max }\left[{\delta }_{t-1}\left(i\right)a_{ij}\right]& 2\le t\le N\hfill \\ \hfill 1& \le j\le N\hfill \end{array}$$

  (11)
• Finalization:

  $$\begin{array}{cc}\hfill p^{*}& =\max 1\le i\le N\left[{\delta }_K\left(i\right)\right]\hfill \end{array}$$

  (12)

  $$\begin{array}{cc}\hfill q_K^{*}& =\arg \max 1\le i\le N\left[{\delta }_K\left(i\right)\right]\hfill \end{array}$$

  (13)
• Path Backtracking:

  $$q_t^{*}={\psi }_{t+1}\left(q_{t+1}^{*}\right)t=K-1,K-2,\dots ,1$$

  (14)

The algorithm give us the optimal state sequence stored in vector $q^{*}$. $p^{*}$ is the probability of $q^{*}$ generating O.

3. Feature selection for HMMs using Heuristic and Genetic Algorithms

Discriminant features have to be used in any classification problem to obtain good results. Also, HMMs have been widely used for activity classification, because activities can be easily represented using this abstraction. It seems to be of interest to study how HMMs could be built using feature selection techniques, because it is not clear that some commonly used features [7] provide the necessary separability of the activities.

3.1. Feature subset evaluation

To evaluate the utility of a given feature subset an HMM wrapper is going to be used. The utility of the feature subset will be the accuracy of the HMM for classifying some small duration activity sequences. Given a set of training sequences $O=\{O_1\dots O_N\}$, $O_i=\{o_{i}1\dots o_{i}k\}$ containing m different activities, and their corresponding set of hidden states $A=\{A_1\dots A_N\}$, $A_i=\{a_{i1}\dots a_{ik}\}$, the estimation of HMM parameters is straightforward. The HMM will have m hidden states, one per activity. To estimate he initial state probability distribution, the frequency of each state to be the first in each training sequence has to be computed. The state transition probability distribution is going to be computed using the frequency of each state transition along the training sequences. To simplify even more the estimation of parameters, the observation symbol robability distribution is supposed to be a single multivariate gaussian distribution. Other type of distributions, like Gaussian Mixtures or KDE [17] can be used, but the construction of the HMM will be harder, and it is not important for the objective of this work. The parameters of each state emission distribution to be estimated are the mean and covariance matrices.

Once that the Hidden Markov Model has been estimated, a test sequence $O=\{o_1,\dots ,o_K\}$ can be classified using Viterbi Algorithm. The obtained state sequence $q^{*}$ is compared to ground truth data, and the accuracy of the model for predicting each hidden state is taken as the subset utility.

3.2. Searching the feature space

Given a set of N features, the number of possible feature subsets to evaluate is $2^N$. As N grows, the feature selection problem becomes intractable and exhaustive search methods become unpractical. To avoid this course of dimensionality, suboptimal search methods have to be employed. In this paper two different methods are proposed: Best First Search and Genetic Search.

Best First Search (BFS) [18] is a tree search method that explores the search tree expanding the best node at each level. In this case, the best node is the one who has the best accuracy on its level. Algorithm pseudocode is shown on 1. This search method does not guarantee to find the optimal solution, only a local optima, because when selecting only the best child, the path to the optimal solution could be left unexplored.

Algorithm 1 Best First Search

$Open\leftarrow root$ while $Open\ne \varphi$ do     Pick the best node of $Open$     $Open\leftarrow \varphi$     Generate its children and introduce into $Open$ end while

To search the feature subset space using Best First Search, the root node of the tree will be the empty feature set. The successors of a node will be that nodes that contain the same features that its parent plus a new one that its parent does not have. The search will finish were the accuracy of children is equal or smaller than the accuracy of their parent.

Genetic Algorithms (GA) [19] are powerful search techniques inspired in the Darwinian Evolution Theory. Populations of individuals, where each one represents a different solution to the problem, are evolved using crossover and mutation operators. The pseudocode of a simple genetic algorithm can be seen on 2. Again, this search method does not guarantee to find the optimal solution, and even if it is found, there is no way to ensure that is the optimum.

Algorithm 2 Genetic Algorithm

$Population\leftarrow init$ while stop condition is not satisfied do     $Evaluate\left(Population\right)$     $NextPopulation\leftarrow selection\left(Population\right)$     $NextPopulation\leftarrow reproduction\left(Population\right)$     $Population\leftarrow replacement\left(Population,NextPopulation\right)$ end while $Solution\leftarrow best\left(Population\right)$

The individual that is going to be used to explore the feature subset space is a bit string of length N, being N the total number of given features. If the ith bit is set to 1, it means that the ith feature is selected, whereas if it is set to 0, it means that the ith feature is not selected.

4. Experimental validation

4.1. Experimental setup

A video has been recorded at 25 fps on a corridor using a Sony SSC-DC598P video surveillance camera located about 3 meters from the ground. An actor has performed six different small duration activities: walking, stopped, bending, falling, lied down and rising (see Figure 4). A blob tracker has been used to extract the actor bounding box on each frame where the actor appears. Using the bounding box, all the features presented on section 2.2. have been extracted, using temporal windows from 3 to 25 frames, giving 780 different features per frame. The blob tracker has divided the original video on 11 video sequences where the activity being performed on each frame has been manually annotated. The content of each sequence could be seen on Table 3.

The blob tracker has produced some erroneous outputs, where the bounding box does not contain the actor for some frames (see Figure 5. These errors may be produced by scene illumination changes, or by the initialization of a false track that is associated to the actor later. In this cases, the frame has been annotated with the especial activity error. It has been considered that is important to have that label to be able to detect these type of false alarms when the system is working.

An HMM is going to be build for each set of small duration activities to be recognized using both BFS and GA. To evaluate the utility of a candidate feature subset, leave-one-out cross-validation (LOOCV) of the generated HMM is going to be performed with the sequences to be employed on each experiment. LOOCV consist on generate the model with all the sequences unless one and test the model with that sequence. This process is repeated for every sequence to be employed. Using this training strategy, possible overfittings are minimized, because the model has not been built with the sequence used to meassure its quality.

Figure 4. Examples of the activities to recognize. First row, walking. Second row, stopped. Third row, lowing. Fourth row, falling. Fifth row, lied down. Last row, rising

Figure 4. Examples of the activities to recognize. First row, walking. Second row, stopped. Third row, lowing. Fourth row, falling. Fifth row, lied down. Last row, rising

Table 3. Content of the sequences used. W stands for walking, S for stopped, F for falling, D for lyed down, R for rising, L for bending and E for error. The number of frames that the activity last is shown between parenthesis

Sequence	Content
1	W(220), S(214), W(113), E(197), S(161), W(221)
2	W(107), S(172), W(116), S(268), W(12)
3	W(50), S(134), W(112), S(202), W(224), S(181), W(145), S(239), E(5), S(30), W(269), S(190), W(250), E(55)
4	W(56), S(131), W(215), F(27), D(211), R(64), W(174), F(57), D(171), R(97), W(115), S(69), W(156), F(68), D(58), R(61)
5	W(139), F(57), D(79), R(88), W(130), F(54), D(172), R(80), W(176), F(52), D(52), R(82), W(236), E(22)
6	L(281), W(283), L(208), W(213), L(173), W(156), L(168), W(167), E(23)
7	W(62), L(134), W(146), L(43), W(222), L(157), W(158), L(110), W(80), L(180), W(133), L(168), W(28), E(18)
8	W(733), E(10)
9	W(760), E(48)
10	E(155), W(271), E(307)
11	W(65), E(1)

Table 3. Content of the sequences used. W stands for walking, S for stopped, F for falling, D for lyed down, R for rising, L for bending and E for error. The number of frames that the activity last is shown between parenthesis

Sequence	Content
1	W(220), S(214), W(113), E(197), S(161), W(221)
2	W(107), S(172), W(116), S(268), W(12)
3	W(50), S(134), W(112), S(202), W(224), S(181), W(145), S(239), E(5), S(30), W(269), S(190), W(250), E(55)
4	W(56), S(131), W(215), F(27), D(211), R(64), W(174), F(57), D(171), R(97), W(115), S(69), W(156), F(68), D(58), R(61)
5	W(139), F(57), D(79), R(88), W(130), F(54), D(172), R(80), W(176), F(52), D(52), R(82), W(236), E(22)
6	L(281), W(283), L(208), W(213), L(173), W(156), L(168), W(167), E(23)
7	W(62), L(134), W(146), L(43), W(222), L(157), W(158), L(110), W(80), L(180), W(133), L(168), W(28), E(18)
8	W(733), E(10)
9	W(760), E(48)
10	E(155), W(271), E(307)
11	W(65), E(1)

Figure 5. Example of the error activity. Bounding box (in green) does not contain the actor.

Figure 5. Example of the error activity. Bounding box (in green) does not contain the actor.

GA has been employed using a configuration of 780 individuals and a mutation rate of $\frac{1}{780}$. The selection technique employed has been tournament selection of 3 individuals. The population of the genetic algorithm is initialized with one random gen set to true. As the length of the individual is 780 and the population 780, it is expected to have each bit set to true in the population at least one time. Population evolution has stopped when the fitness value of the best individual has been without changing for 10 generations. The algorithm has been run 20 times for each experiment, because GAs are random search techniques and different results may be achieved in different trials. The result shown is the best one found.

4.2. Experiment I: three activities

A first attempt to solve the problem will be done using a set of sequences containing sequences 1, 2 and 3. It contains three different activities: stopped, walking and noise. Results obtained with GA and BFS can be seen on Table 4. Relative confusion matrix for the solution obtained by BFS is shown on Table 5 and relative confusion matrix of the solution obtained by GA is shown on Table 6. Relative confusion matrices show the frequency of predicting errors per class. The HMM induced can be seen on Figure 6

Table 4. Features found by by Best First Search (BFS) and Genetic Algorithm(GA) for classificating three activities

Algorithm	Accuracy	Selection
BFS	0.8699	$f\left(t,F\right),R_{{\Sigma }_{\overline{\overrightarrow{F_4}}}}{\left(t,F\right)}_1,R_{{\Sigma }_{\overline{\overrightarrow{F_3}}}}{\left(t,F\right)}_1,R_{{\Sigma }_{\overline{\overrightarrow{F_4}}}}{\left(t,I\right)}_2,R_{{\Sigma }_{\overline{\overrightarrow{F_5}}}}{\left(t,I\right)}_1$
GA	0.9046	$\frac{\partial y\left(t\right)}{\partial t},R_{{\Sigma }_{\overline{\overrightarrow{F_3}}}}{\left(t,F\right)}_1,f_8{\left(t,F\right)}_1,$

Table 4. Features found by by Best First Search (BFS) and Genetic Algorithm(GA) for classificating three activities

Algorithm	Accuracy	Selection
BFS	0.8699	$f\left(t,F\right),R_{{\Sigma }_{\overline{\overrightarrow{F_4}}}}{\left(t,F\right)}_1,R_{{\Sigma }_{\overline{\overrightarrow{F_3}}}}{\left(t,F\right)}_1,R_{{\Sigma }_{\overline{\overrightarrow{F_4}}}}{\left(t,I\right)}_2,R_{{\Sigma }_{\overline{\overrightarrow{F_5}}}}{\left(t,I\right)}_1$
GA	0.9046	$\frac{\partial y\left(t\right)}{\partial t},R_{{\Sigma }_{\overline{\overrightarrow{F_3}}}}{\left(t,F\right)}_1,f_8{\left(t,F\right)}_1,$

The solution found by GA is better than the solution found by BFS according to the global accuracy. Also, taking a look in the confusion matrices of both classifiers (Table 5 and Table 6) reveals that the solution found by GA is better than the solution found by BFS for the accuracy of all the classes to predict. In both cases, the hardest class to predict is the error class, maybe because it is the class with less examples.

Solution obtained by BFS algorithm includes different meassures of the optical flow. Solution obtained by GA includes velocity along y axes and different optical flow meassures.

Table 5. Relative Confusion matrix for the HMM generated using BFS to classify the activities walking, stopped and error

	prediction	error	walking	stopped
class
error		0.5869	0.4161	0
walking		0.0505	0.8984	0.0511
stopped		0.0531	0.0796	0.8673

Table 5. Relative Confusion matrix for the HMM generated using BFS to classify the activities walking, stopped and error

	prediction	error	walking	stopped
class
error		0.5869	0.4161	0
walking		0.0505	0.8984	0.0511
stopped		0.0531	0.0796	0.8673

Figure 6. Structure of the HMM used in experiment 1

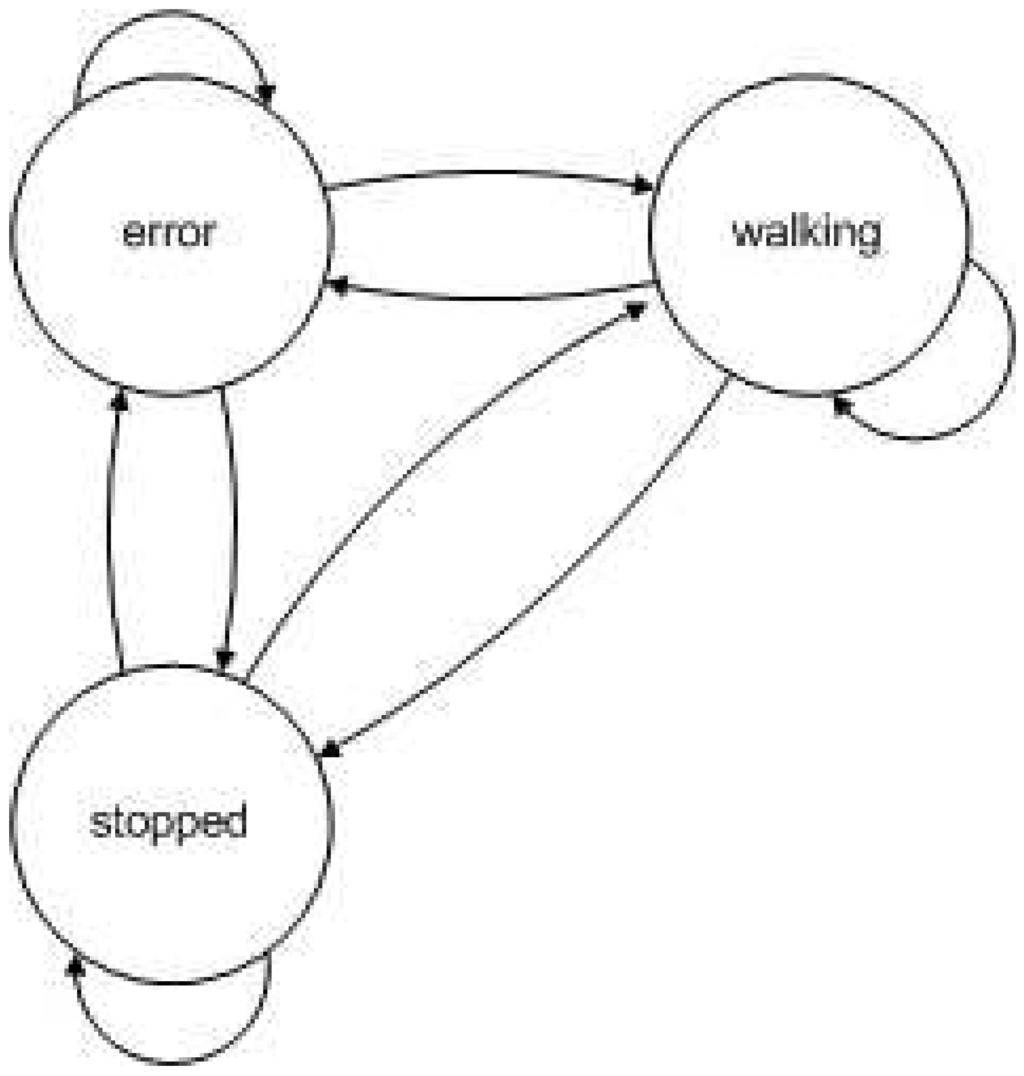
Figure 6. Structure of the HMM used in experiment 1

Table 6. Relative Confusion matrix for the HMM generated using GA to classify the activities walking, stopped and error

	prediction	error	walking	stopped
class
error		0.7521	0.0427	0.2051
walking		0.0238	0.9260	0.0502
stopped		0.0828	0.0251	0.8921

Table 6. Relative Confusion matrix for the HMM generated using GA to classify the activities walking, stopped and error

	prediction	error	walking	stopped
class
error		0.7521	0.0427	0.2051
walking		0.0238	0.9260	0.0502
stopped		0.0828	0.0251	0.8921

4.3. Experiment II: six activities

Two more sequences have been added to the set previously used: X and Y. Three new activities are going to be classified: falling,rising, and lyed down. Results obtained with GA and BFS can be seen on Table 7.

Table 7. Features found by by Best First Search (BFS) and Genetic Algorithm(GA) for classificating six activities

Algorithm	Accuracy	Selection
BFS	0.7051	$\overline{f_8}\left(t,F\right);R_{\overrightarrow{s_6},1}\left(t\right),R_{\overrightarrow{s_6},2}\left(t\right),t{r}_{{\Sigma }_{\overline{\overrightarrow{F_{2}5}}}}{\left(t,F\right)}_3,R_{{\Sigma }_{\overrightarrow{s},6}}{\left(t\right)}_2,R_{{\Sigma }_{\overline{\overrightarrow{F_3}}}}{\left(t\right)}_2$
GA	0.7779	$hu1,R_{{\Sigma }_{\overrightarrow{s},4}}{\left(t\right)}_2,R_{\overrightarrow{s_9},1}\left(t\right),R_{\overrightarrow{s_{1}1},1}\left(t\right),R_{\overrightarrow{s_{1}4},1}\left(t\right),\overline{f_{1}7}\left(t,F\right),t{r}_{{\Sigma }_{\overline{\overrightarrow{F_{2}2}}}}{\left(t,F\right)}_3$

Table 7. Features found by by Best First Search (BFS) and Genetic Algorithm(GA) for classificating six activities

Algorithm	Accuracy	Selection
BFS	0.7051	$\overline{f_8}\left(t,F\right);R_{\overrightarrow{s_6},1}\left(t\right),R_{\overrightarrow{s_6},2}\left(t\right),t{r}_{{\Sigma }_{\overline{\overrightarrow{F_{2}5}}}}{\left(t,F\right)}_3,R_{{\Sigma }_{\overrightarrow{s},6}}{\left(t\right)}_2,R_{{\Sigma }_{\overline{\overrightarrow{F_3}}}}{\left(t\right)}_2$
GA	0.7779	$hu1,R_{{\Sigma }_{\overrightarrow{s},4}}{\left(t\right)}_2,R_{\overrightarrow{s_9},1}\left(t\right),R_{\overrightarrow{s_{1}1},1}\left(t\right),R_{\overrightarrow{s_{1}4},1}\left(t\right),\overline{f_{1}7}\left(t,F\right),t{r}_{{\Sigma }_{\overline{\overrightarrow{F_{2}2}}}}{\left(t,F\right)}_3$

Table 8. Relative Confusion matrix for the HMM generated using BFS to classify the activities walking, stopped, falling, lyed down, rising and error

	prediction	error	walking	stopped	falling	lyed down	rising
class
error		0.2760	0.5082	0.0820	0.0984	0.0027	0.0328
walking		0.0098	0.8134	0.0225	0.0640	0.0060	0.0843
stopped		0.0050	0.1267	0.8092	0.0056	0.0195	0.0340
falling		0.0957	0.0319	0.0106	0.6596	0.2021	0
lyed down		0.0687	0.0102	0.3163	0.0037	0.5793	0.0219
rising		0.1588	0.5829	0.0118	0	0.0024	0.2441

Table 8. Relative Confusion matrix for the HMM generated using BFS to classify the activities walking, stopped, falling, lyed down, rising and error

	prediction	error	walking	stopped	falling	lyed down	rising
class
error		0.2760	0.5082	0.0820	0.0984	0.0027	0.0328
walking		0.0098	0.8134	0.0225	0.0640	0.0060	0.0843
stopped		0.0050	0.1267	0.8092	0.0056	0.0195	0.0340
falling		0.0957	0.0319	0.0106	0.6596	0.2021	0
lyed down		0.0687	0.0102	0.3163	0.0037	0.5793	0.0219
rising		0.1588	0.5829	0.0118	0	0.0024	0.2441

Figure 7. Structure of the HMM used in experiment 2

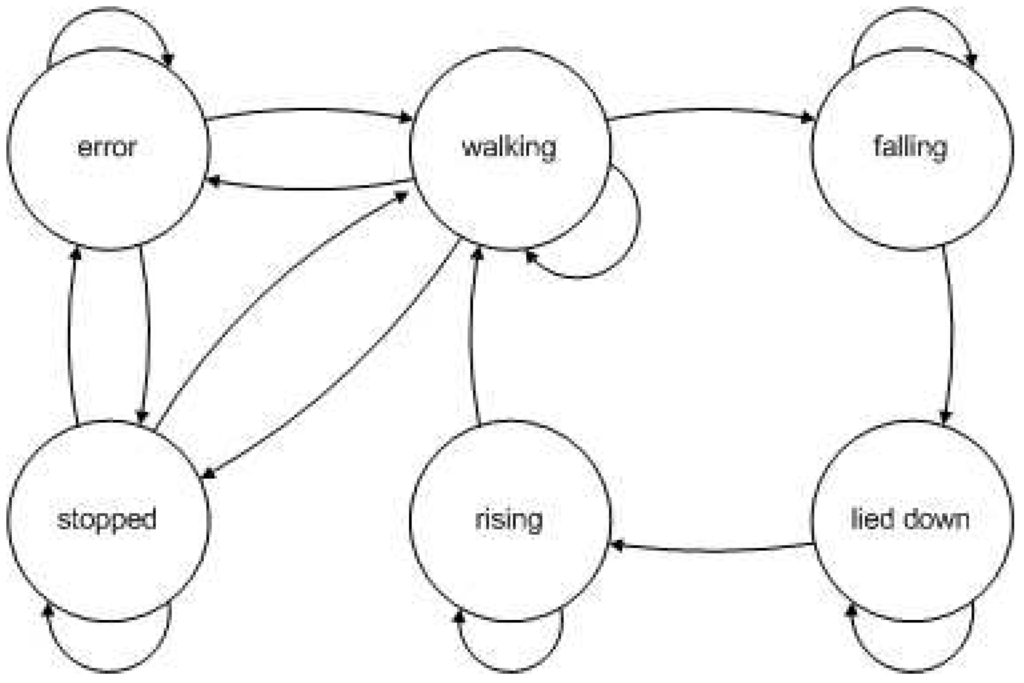
Figure 7. Structure of the HMM used in experiment 2

Again, the solution found by GA is better than the solution found by BFS if the global accuracy of the HMM induced (see Figure 7 ) by the feature subset is considered. But now, taking a look into the

Table 9. Relative Confusion matrix for the HMM generated using GA to classify the activities walking, stopped, falling, lyed down, rising and error

	prediction	error	walking	stopped	falling	lyed down	rising
class
error		0.2509	0.5818	0.0982	0.04	0.0036	0.0255
walking		0.0163	0.8656	0.0291	0.0404	0.0041	0.0445
stopped		0.0671	0.0439	0.7803	0.0044	0.0623	0.0421
falling		0.0939	0.0712	0.0421	0.5243	0.1165	0.1521
lyed down		0.0012	0.0731	0.0899	0.0024	0.8046	0.0288
rising		0.0227	0.4434	0.0097	0.0032	0.0162	0.5049

Table 9. Relative Confusion matrix for the HMM generated using GA to classify the activities walking, stopped, falling, lyed down, rising and error

	prediction	error	walking	stopped	falling	lyed down	rising
class
error		0.2509	0.5818	0.0982	0.04	0.0036	0.0255
walking		0.0163	0.8656	0.0291	0.0404	0.0041	0.0445
stopped		0.0671	0.0439	0.7803	0.0044	0.0623	0.0421
falling		0.0939	0.0712	0.0421	0.5243	0.1165	0.1521
lyed down		0.0012	0.0731	0.0899	0.0024	0.8046	0.0288
rising		0.0227	0.4434	0.0097	0.0032	0.0162	0.5049

confusion matrices of both classifiers (Table 8 and Table 9) reveals that the solution found by BFS is better for predicting classes error, stopped and falling, while the solution found by GA is better for walking, lyed down and rising.

Solution found by BFS includes optical flow and trajectory eccentricity meassures. GA includes also a shape descriptor.

Table 10. Results obtained by Best First Search (BFS) and Genetic Algorithm(GA) using all the training sequences

Algorithm	Accuracy	Selection
BFS	0.7442	$h{u}_1,f\left(t,F\right),R_{\overrightarrow{s_4},1}\left(t\right),R_{{\Sigma }_{\overrightarrow{s},3}}{\left(t\right)}_2,R_{\overrightarrow{s_6},1}\left(t\right),R_{\overrightarrow{s_{2}2},2}\left(t\right),R_{\overrightarrow{s_3},1}\left(t\right),R_{\overrightarrow{s_{1}8},1}\left(t\right)$
GA	0.7501	$h{u}_1,R_{\overrightarrow{s_3},1}\left(t\right),R_{\overrightarrow{s_8},2}\left(t\right),R_{{\Sigma }_{\overrightarrow{s},11}}{\left(t\right)}_1,\overline{f_8}\left(t,F\right),R_{\overrightarrow{s_{1}2},2}\left(t\right),t{r}_{{\Sigma }_{\overline{\overrightarrow{F_{1}3}}}}{\left(t,F\right)}_1$

Table 10. Results obtained by Best First Search (BFS) and Genetic Algorithm(GA) using all the training sequences

Algorithm	Accuracy	Selection
BFS	0.7442	$h{u}_1,f\left(t,F\right),R_{\overrightarrow{s_4},1}\left(t\right),R_{{\Sigma }_{\overrightarrow{s},3}}{\left(t\right)}_2,R_{\overrightarrow{s_6},1}\left(t\right),R_{\overrightarrow{s_{2}2},2}\left(t\right),R_{\overrightarrow{s_3},1}\left(t\right),R_{\overrightarrow{s_{1}8},1}\left(t\right)$
GA	0.7501	$h{u}_1,R_{\overrightarrow{s_3},1}\left(t\right),R_{\overrightarrow{s_8},2}\left(t\right),R_{{\Sigma }_{\overrightarrow{s},11}}{\left(t\right)}_1,\overline{f_8}\left(t,F\right),R_{\overrightarrow{s_{1}2},2}\left(t\right),t{r}_{{\Sigma }_{\overline{\overrightarrow{F_{1}3}}}}{\left(t,F\right)}_1$

Table 11. Relative Confusion matrix for de HMM generated using Best First Search

	prediction	error	walking	bending	stopped	falling	lied down	rising
class
error		0.5514	0.1479	0.0210	0.1189	0.0040	0.0999	0.0569
walking		0.0111	0.8676	0.0603	0.0136	0.0118	0.0035	0.0320
bending		0.0318	0.3043	0.6304	0.0093	0.0039	0.0202	0
stopped		0.0606	0.0818	0.0596	0.7513	0.0139	0.0176	0.0153
falling		0.1293	0.2239	0.1139	0.0656	0.3301	0.0676	0.0695
lied down		0.0058	0.0361	0.2300	0.0926	0.0039	0.6218	0.0097
rising		0.0108	0.3459	0.1811	0.0405	0.0622	0.0216	0.3378

Table 11. Relative Confusion matrix for de HMM generated using Best First Search

	prediction	error	walking	bending	stopped	falling	lied down	rising
class
error		0.5514	0.1479	0.0210	0.1189	0.0040	0.0999	0.0569
walking		0.0111	0.8676	0.0603	0.0136	0.0118	0.0035	0.0320
bending		0.0318	0.3043	0.6304	0.0093	0.0039	0.0202	0
stopped		0.0606	0.0818	0.0596	0.7513	0.0139	0.0176	0.0153
falling		0.1293	0.2239	0.1139	0.0656	0.3301	0.0676	0.0695
lied down		0.0058	0.0361	0.2300	0.0926	0.0039	0.6218	0.0097
rising		0.0108	0.3459	0.1811	0.0405	0.0622	0.0216	0.3378

4.4. Experiment III: seven activities

Finally, the eleven available sequences have been used to train the HMM models, adding a new activity to the previous experiment configurations: bending (see HMM on Figure 8). Results obtained with GA and BFS can be seen on Table 10.

Table 12. Relative Confusion matrix for de HMM generated using a Genetic Algorithm

	prediction	error	walking	bending	stopped	falling	lied down	rising
class
error		0.4881	0.1512	0.0148	0.1413	0.0267	0.1176	0.0603
walking		0.0101	0.8562	0.0701	0.0174	0.0166	0.0032	0.0264
bending		0.0196	0.2844	0.6815	0.0116	0.0029	0	0
stopped		0.0571	0.0421	0.0870	0.7758	0.0086	0.0122	0.0172
falling		0.0874	0.6053	0.0390	0.0031	0.2059	0.0265	0.0328
lied down		0.0692	0.0125	0.0999	0.0011	0.0170	0.7753	0.0250
rising		0.1486	0.2635	0.0203	0.0034	0.0304	0.0034	0.5304

Table 12. Relative Confusion matrix for de HMM generated using a Genetic Algorithm

	prediction	error	walking	bending	stopped	falling	lied down	rising
class
error		0.4881	0.1512	0.0148	0.1413	0.0267	0.1176	0.0603
walking		0.0101	0.8562	0.0701	0.0174	0.0166	0.0032	0.0264
bending		0.0196	0.2844	0.6815	0.0116	0.0029	0	0
stopped		0.0571	0.0421	0.0870	0.7758	0.0086	0.0122	0.0172
falling		0.0874	0.6053	0.0390	0.0031	0.2059	0.0265	0.0328
lied down		0.0692	0.0125	0.0999	0.0011	0.0170	0.7753	0.0250
rising		0.1486	0.2635	0.0203	0.0034	0.0304	0.0034	0.5304

Figure 8. Structure of the HMM used in experiment 3

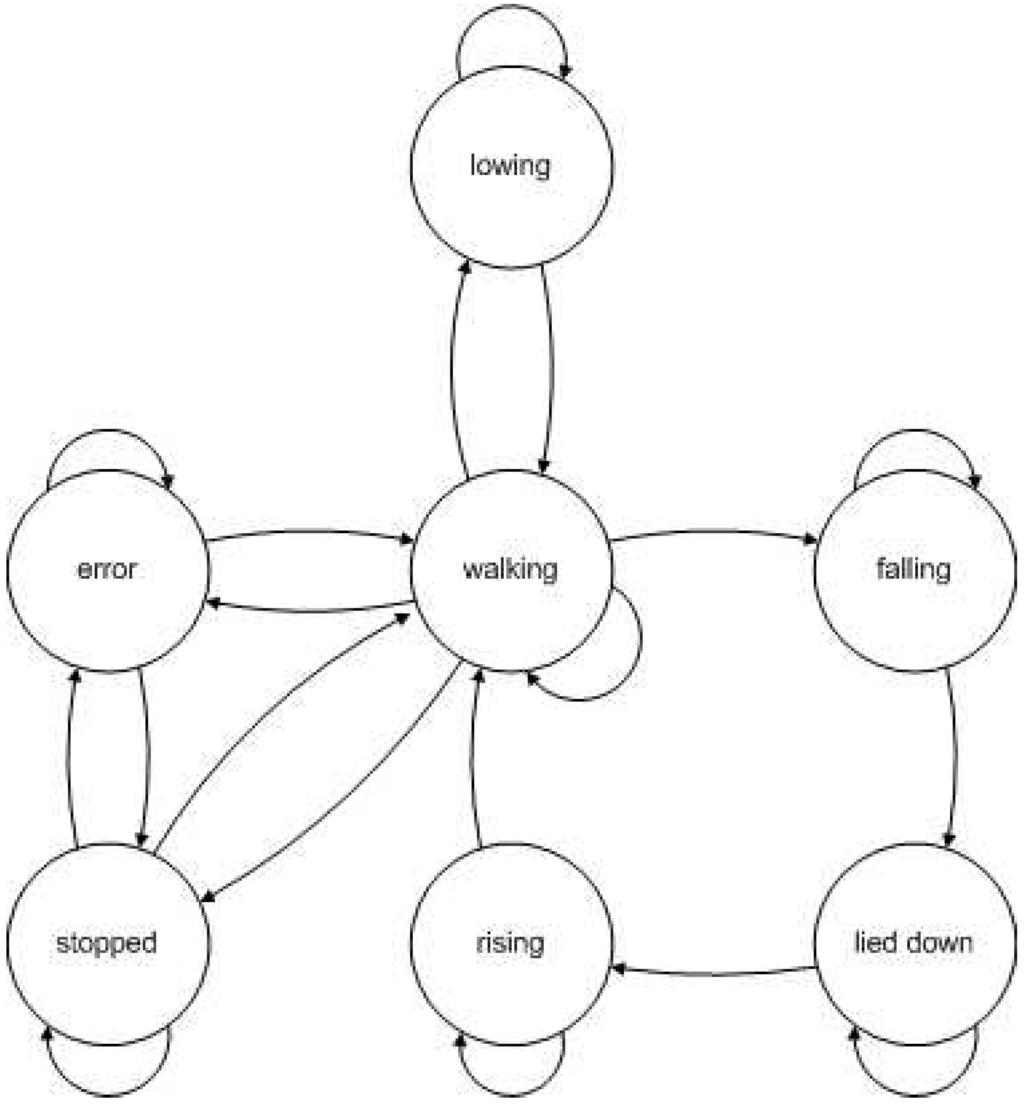
Figure 8. Structure of the HMM used in experiment 3

Taking as the quality meassure the global accuracy of the HMM induced by the result subsets, the solution found by GA is a bit better than the solution found by BFS. According to cobfusion matrices of both classifiers (Table 11 and Table 12), solution found by BFS is better for predicting falling and error while the easiest are walking and stopped, whereas the solution found by GA is better for bending, stopped, lied down and rising.

Solutions found by both BFS and GA include shape descriptors and optical flow and trajectory eccentricity meassures.

4.5. Overall Discussion

Observing confusion matrices, it can be said that the activities performed on more frames are the best classified. That is due to the feature subset evaluation function used, that tries to maximize the global accuracy of the classifier. This effect can be avoided modifying the feature subset evaluation function to reward the correct classification of activities with fewer frames.

Solutions found by GA are smaller than the solutions found by BFS, so classification using the HMM generated by GA is easier than with the obtained by BFS. Besides classification cost, considering that the time needed to extract all the features is the same, extracting five features need less time than extracting nine, so the overall system using the solution by GA will be quicker. Also, the temporal window needed to extract the features found by GA tend to be smaller than for the features found by BFS (22 vs 11 frames), so the system using that feature set will have to store less information in its memory.

5. Conclusion

In this paper a set of candidate features that may represent human activities has been presented. Searching over the possible feature subsets, Hidden Markov Models for classifying activities have been built using only features that are relevant for target classes, over the traditional application where the features employed have to be defined a prioir. The Genetic Algorithm used to explore the feature subsets space has shown to be better than the Best First Search for almost every criteria. It has been observed that the accuracy predicting activities has decreased when the number of activities to predict has grown, because the probability of assigning an observation to the wrong class increases.

When different sensors are used, the selected feature subset used for activity recognition may come from different ones, discarding that sensors that don’t provide any information for the activities to recognized.