1. Introduction
A force with a high frequency content acting at a point on a slender solid with uniform cross section (waveguide) generates mechanical waves. These waves, generally termed as Guided Waves (GWs) due to the fact that the solid serves as a waveguide, propagate with defined wavelength, phase velocity, energy velocity, attenuation and wavestructure (wave shape over the waveguide cross-section). Due to the interaction between the wave’s wavelength and the waveguide cross-section geometry, some or all of these wave features change when varying the frequency of propagation (dispersive behavior). Today, GWs are employed in several industrial applications for material characterization, impact and shock-induced wave propagation, acoustic focusing and advanced material design. Modeling these propagating waves in complex waveguides is not an easy task, especially at high frequency, where the wavelengths are small and the wavestructures have a complex shape.
Among others, Spectral Finite Element (SFE) formulations are well established algorithms to simulate guided waves propagating in waveguides. The key point of SFE formulations consists in the hybrid displacement field adopted to describe the motion of a propagative guided wave. A transient wave is described, in fact, coupling a bi-dimensional finite element mesh over the waveguide cross-section and harmonic functions along the wave propagation direction. Next, a displacement-based variational scheme and the application of Fourier transform contractions leads to the governing wave equation in the frequency-wavenumber domain as a system of algebraic equations. Non trivial solutions of the homogenous part of the wave equation, easily calculated by using standard routines for eigenvalue problems, allow tracing the dispersive spectrum of the waveguide. Compared to other methods the main advantages in this calculation are: no missing roots; capability to handle waveguides of arbitrary cross-section; possibility to model high degree anisotropic waveguides with no extra effort; fast and reliable high frequency computation. A literature review on SFE formulations, acknowledged also as semi-analytical finite element (SAFE) formulations or waveguide finite element (WFE) methods, can be found in the book by Liu and Xi [
1].
The SFE calculated waveguide spectrum, can also be exploited for the construction of the time-transient response due to the waves excited by a time-varying load. Time-transient response is essential to actuators design, quantitative non-destructive evaluation of cracks size and location as well as for structural health monitoring purposes. In brief, the time-transient response at a point can be obtained by means of the inverse Fourier transform, which turns into the time domain the waveguide frequency response calculated as a summation of the modal data contribution at that point weighted with the spectrum of the applied load. Applications of this procedure to calculate the time-transient response in undamped waveguides, such as plates [
2] and pipes [
3], have been proposed in the past.
Lately, some work has been devoted to extend SFE procedures to damped waveguides. In particular Bartoli
et al., [
4] generalized the SFE formulation to compute the modal spectrum in lossy waveguides by accounting for material damping, at the finite element level, by introducing complex constitutive viscoelastic relations.
The scheme proposed in [
4] has been next used to extract the damped dispersion curves in pipes [
5] and helical waveguides [
6], and subsequently exploited to extend SFE formulations to the calculation of the time-transient response in damped pipes [
7] and rails [
8].
In particular, in [
7] where the scheme proposed in [
4] was fully used, the SFE formulation is based on the analytical derivation of the complex stiffness matrices from the material acoustic properties. This also allows handling of frequency dependent linear viscoelastic rehological models, once the bulk properties are known. However, since the formulation in [
7] was purposely developed for damped axially symmetric waveguides it is limited to them.
The formulation proposed in [
8], can also deal with waveguides with generic cross section. However, the damping is simply introduced by adding an imaginary “stiffness” proportional to real “stiffness”, simulating thus a sort of hysteretic material for the waveguide.
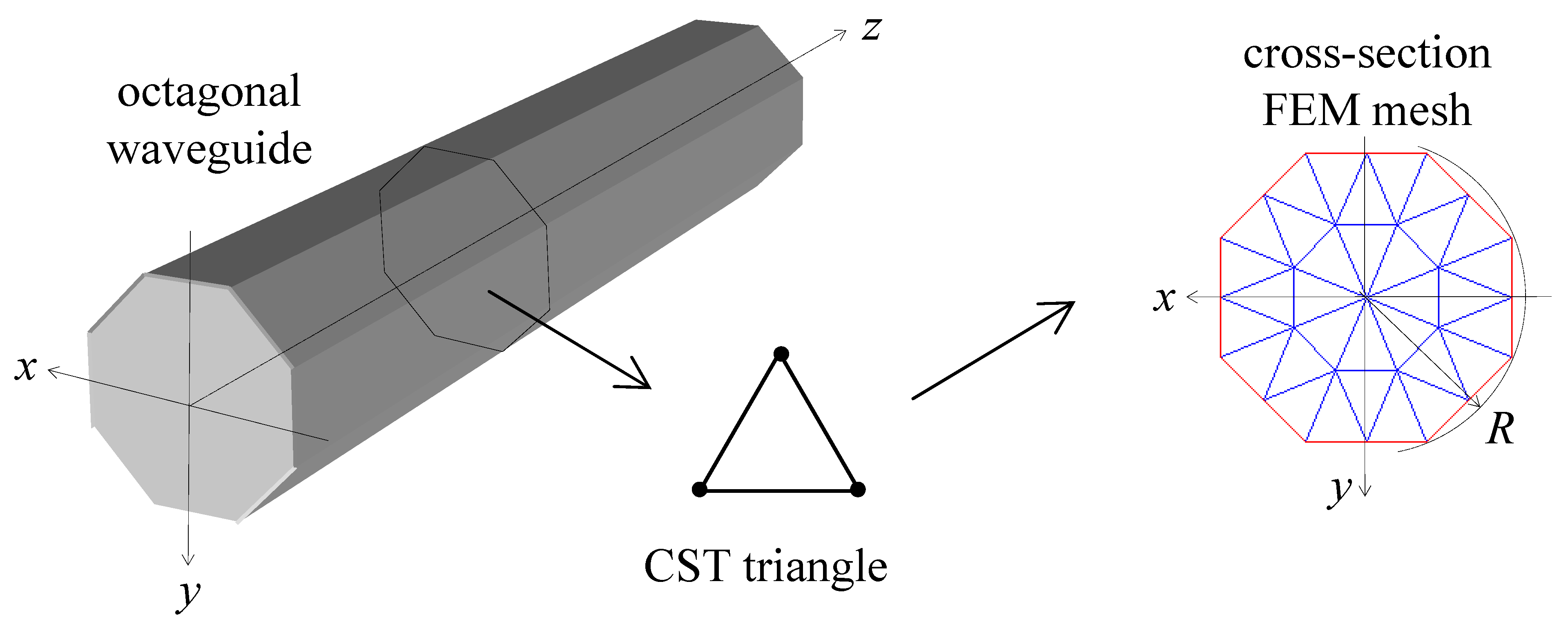
Herein, a damped spectrally formulated plane triangular finite element with constant strain description (CST) is proposed to extend the formulation in [
7] to waveguides of arbitrary cross-section. Damping is accounted analytically starting from the damped bulk properties of the material.
The proposed algorithm can thus provide the dispersion curves as well as calculate the time transient response in waveguides of arbitrary cross-section accounting for any linear viscoelastic constitutive model that can be formulated in the frequency domain.
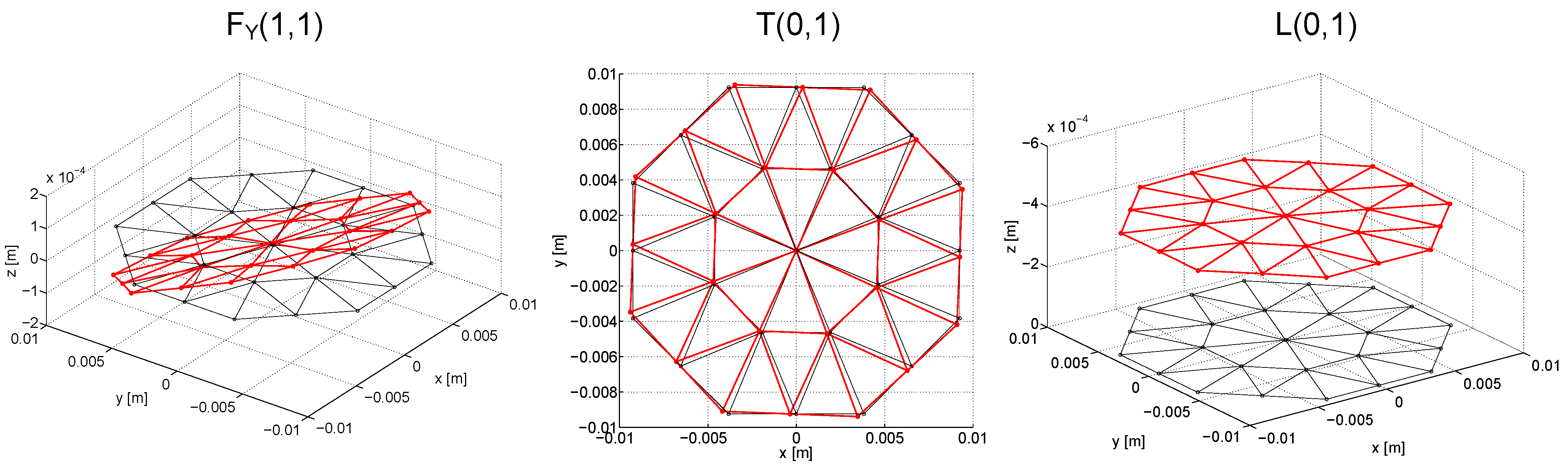
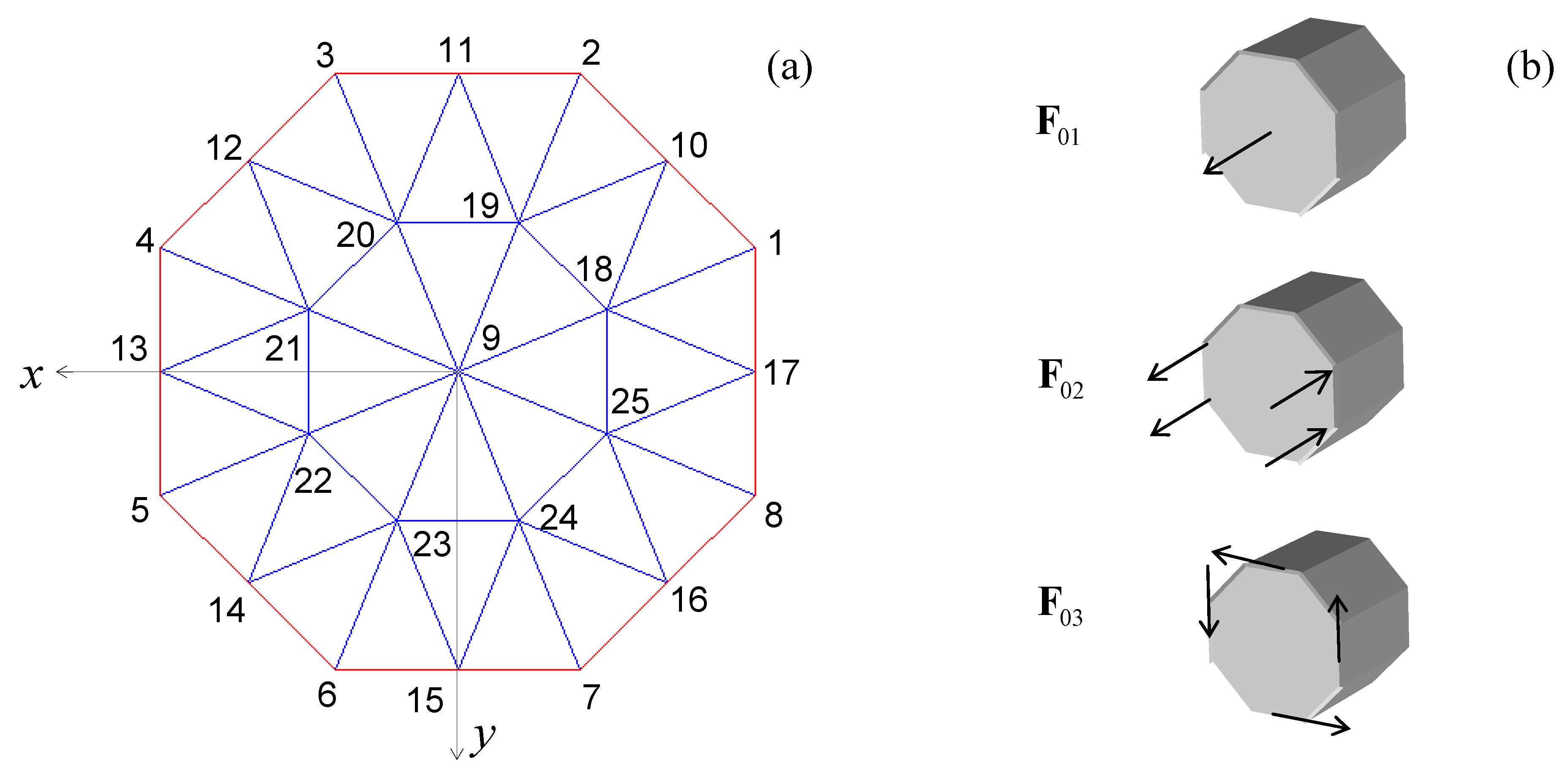
The formulation is next adopted to analyze the problem of guided waves propagating in octagonal damped bars that to the authors’ best knowledge has never been addressed. Octagonal bars, having a generic cross section, are representative of any arbitrary cross section waveguide and therefore useful to prove the reliability of the formulation. In addition since an octagonal bar has a behavior somehow similar to the one well-known of an equivalent rod with circular cross-section, the formulation and its results were controlled by means of the algorithm developed in [
5] for axially symmetric waveguides.
Finally, stress waves in octagonal bars are of interest since they can reveal some useful information on the behaviour of guided waves propagating in octagonal tubes, largely used for highway signal marks and lighting poles. These structures present two critical regions that are susceptible of corrosion because of the deposit of water: the base of the pole at the street level and the underground zone where the pole joins the concrete foundation. While the base of the pole can be rapidly inspected in several ways, the screening of the underground zone presents more difficulties.
Therefore, a guided waves based non-destructive technique that operating from the outside near surface is capable to reveal the state of corrosion in the underground zone could be really appealing. Here, the basis for the numerical simulation are set. In this study several cases have been investigated to show the performance of the proposed procedure by considering different source-receiver distances and different excitations.
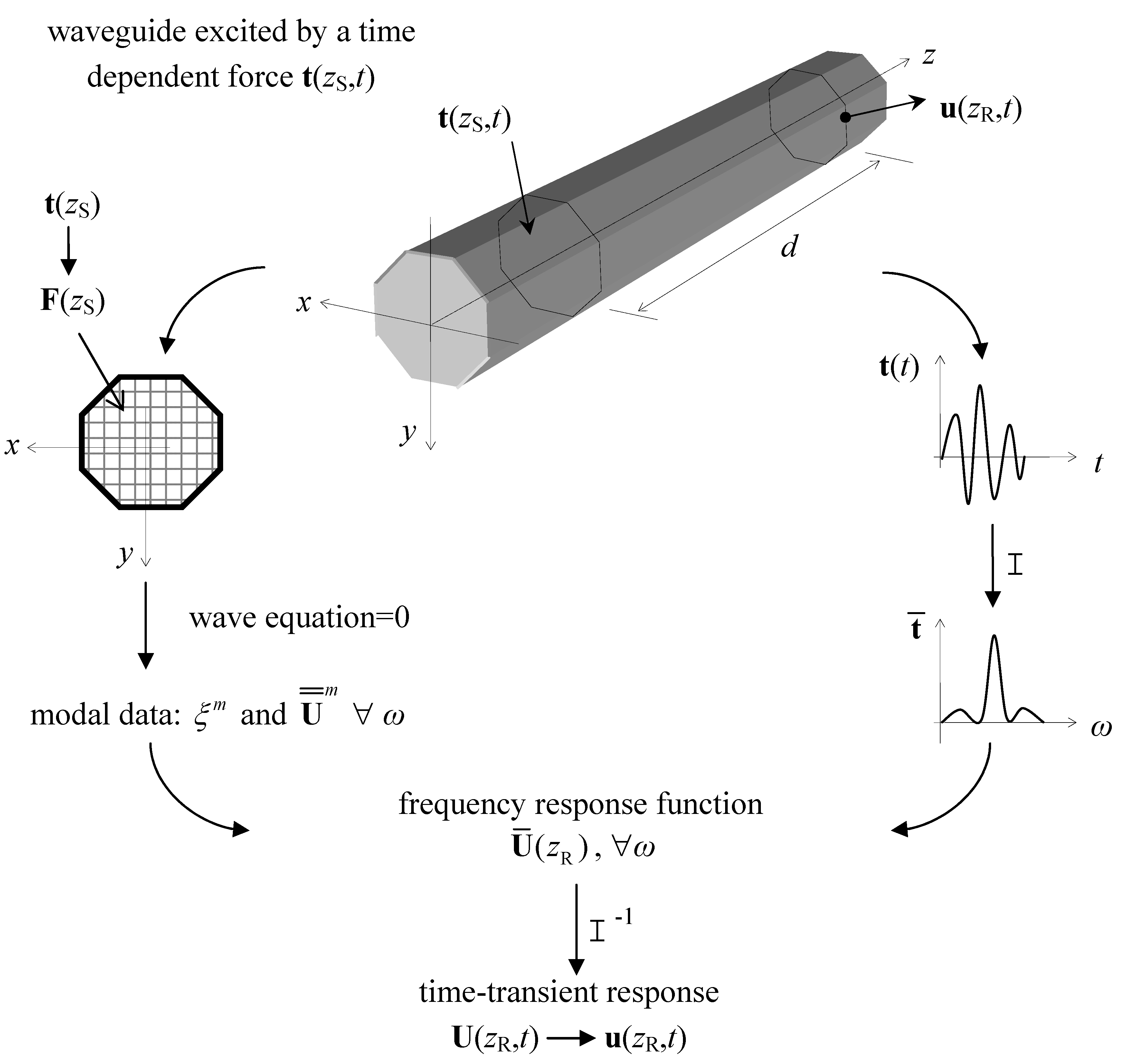
1.1. Matlab Overall Strategy
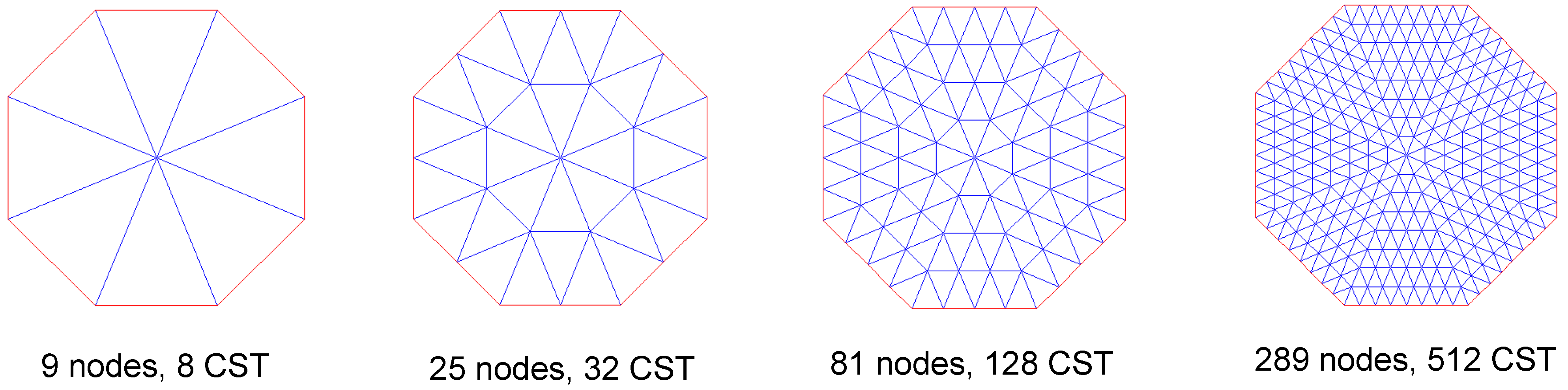
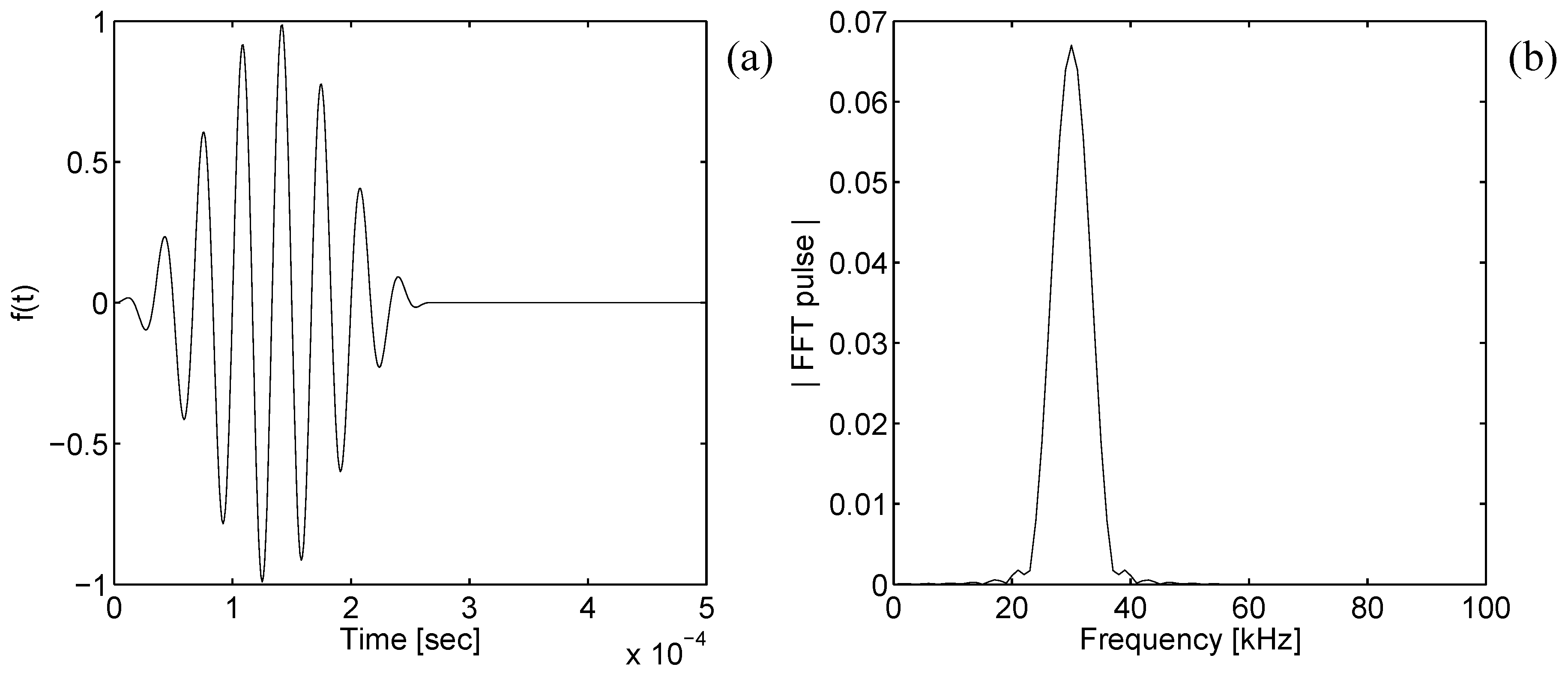
The procedure for the construction of the damped time-transient response is described in the following. First, home made routines are developed to set the spectral damped CST finite element. The “pdetool” of Matlab is next used to draw the cross-section of the waveguide and to create the plane finite element mesh data. Then, a standard finite element assembly procedure generates the frequency-wavenumber dependent homogeneous governing wave equation. In parallel, the applied forcing function at a certain z-coordinate (where the subscript S stands for source location) is discretized over the finite element mesh and its frequency spectrum is calculated by means of the “fft” function of Matlab.
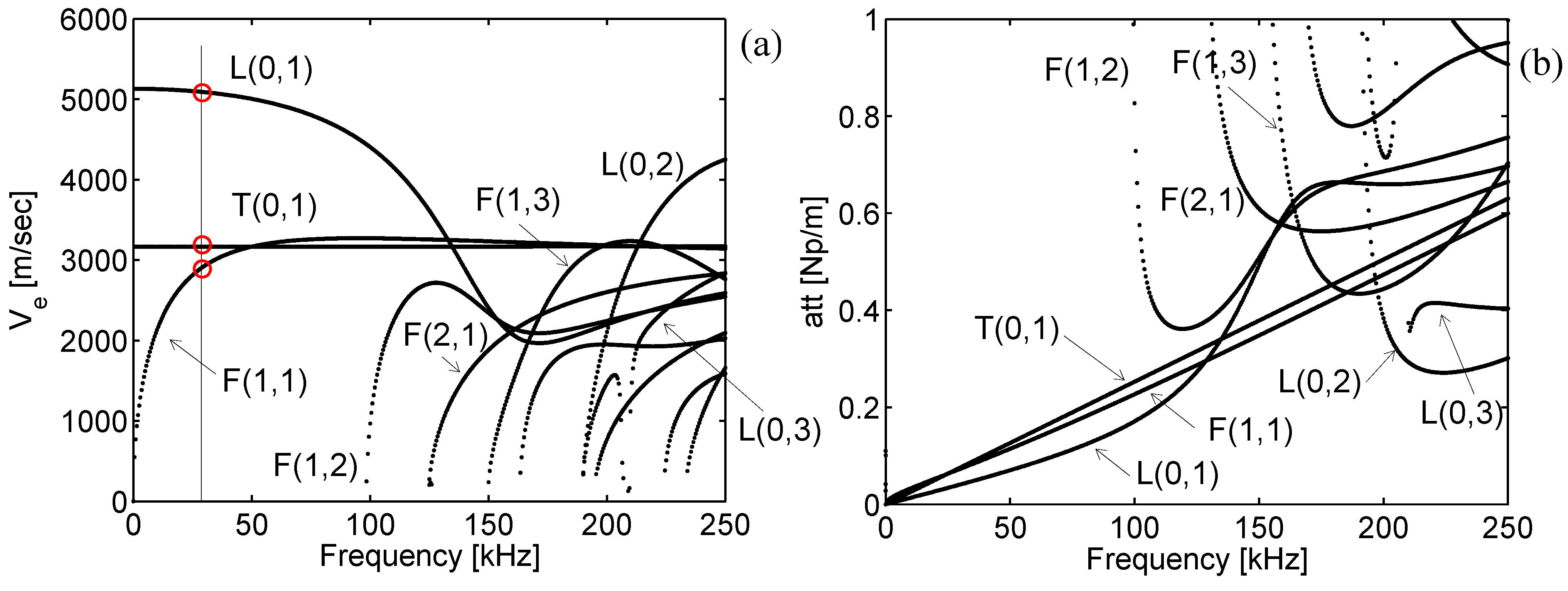
For a given frequency in input (), the solution of the homogeneous form of the wave equation using the function “eig” leads to all the complex wavenumbers () and wavestructures () of the existing waves at that frequency, where is the number of degrees of freedom (dofs) of the mesh. The waves phase/energy velocity and attenuation are calculated from these modal properties by means of simple formulae.
Figure 1.
Schematic representation of the overall strategy.
Figure 1.
Schematic representation of the overall strategy.
Also, the modal properties (ξ
m,
) weighted by the spectrum of the applied force at the given frequency
yield the waveguide frequency response
of all the mesh dofs at a distance
away from the wave source (where the subscript R stands for receiver point). Repeating this procedure for all the frequencies of interest allows both to trace the dispersion curves and to collect the frequency response
, in other words to set up the frequency response function (FRF). Finally, the FRF is transformed into the time-transient damped response
U(
zR,
t) (damped time-transient Green’s function) by means of the time inverse Fourier transform (“
ifft”), from which the response
u(
zR,
t), can be easily extracted. A schematic representation of the overall proposed strategy is shown in
Figure 1.
4. Discussion and Conclusions
In this study an ad-hoc developed constant strain triangular (CST) finite element has been presented for calculating the three-dimensional time-transient response in a viscoelastic octagonal rod. The Hamilton’s principle has been used to formulate the weak form of the wave equation that is next transformed in the frequency domain. The major benefit of the frequency transformation comes from the possibility to easily account for linear viscoelastic constitutive relations. By solving a complex eigenvalue problem for a given wave frequency, wave equation roots are obtained in terms of complex wavenumbers, describing the spatial frequency and attenuation of the guided waves. A modal summation procedure and the application of the inverse time Fourier transform lead to the time-transient response of the problem for an applied time-dependent load.
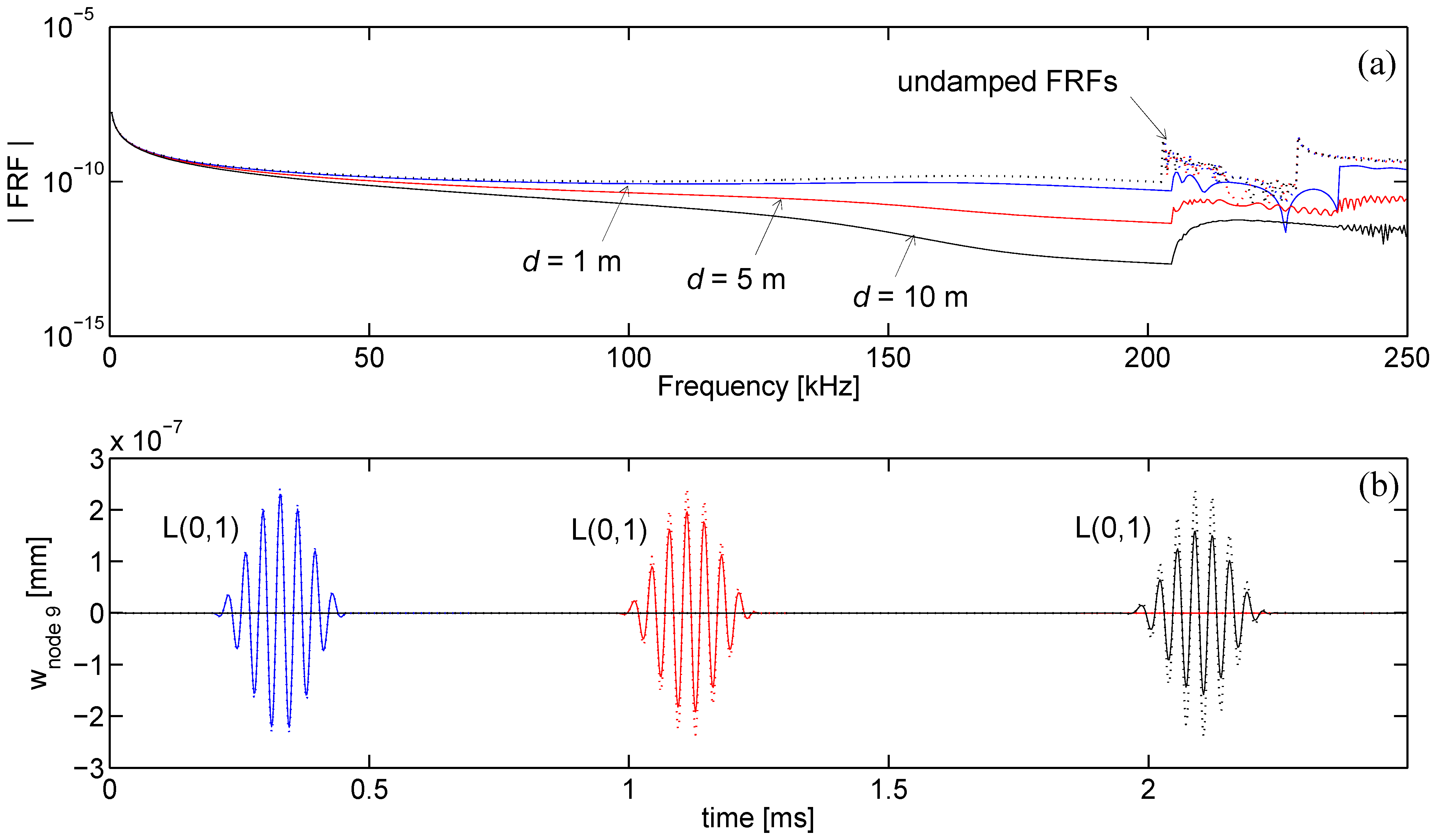
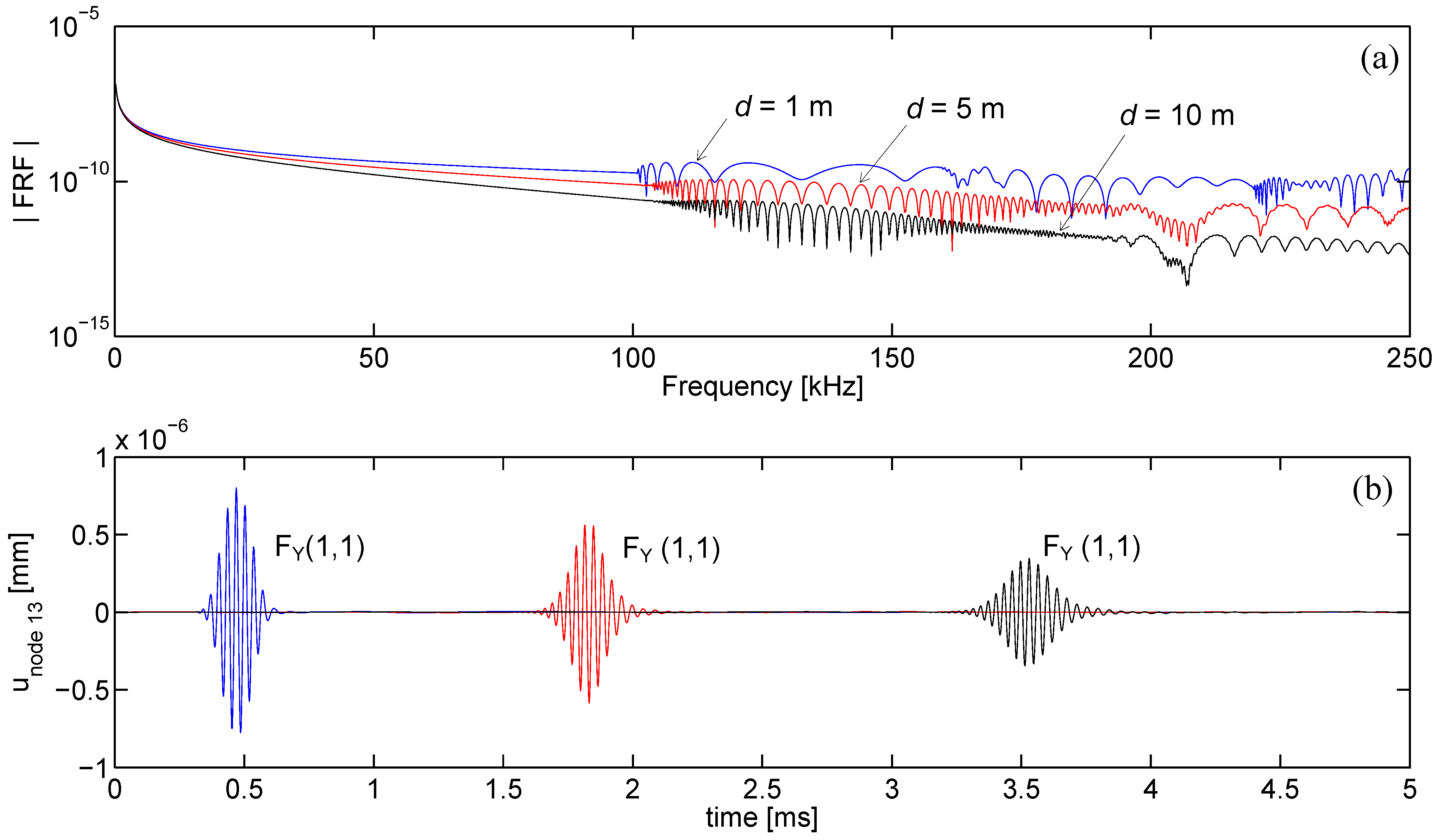
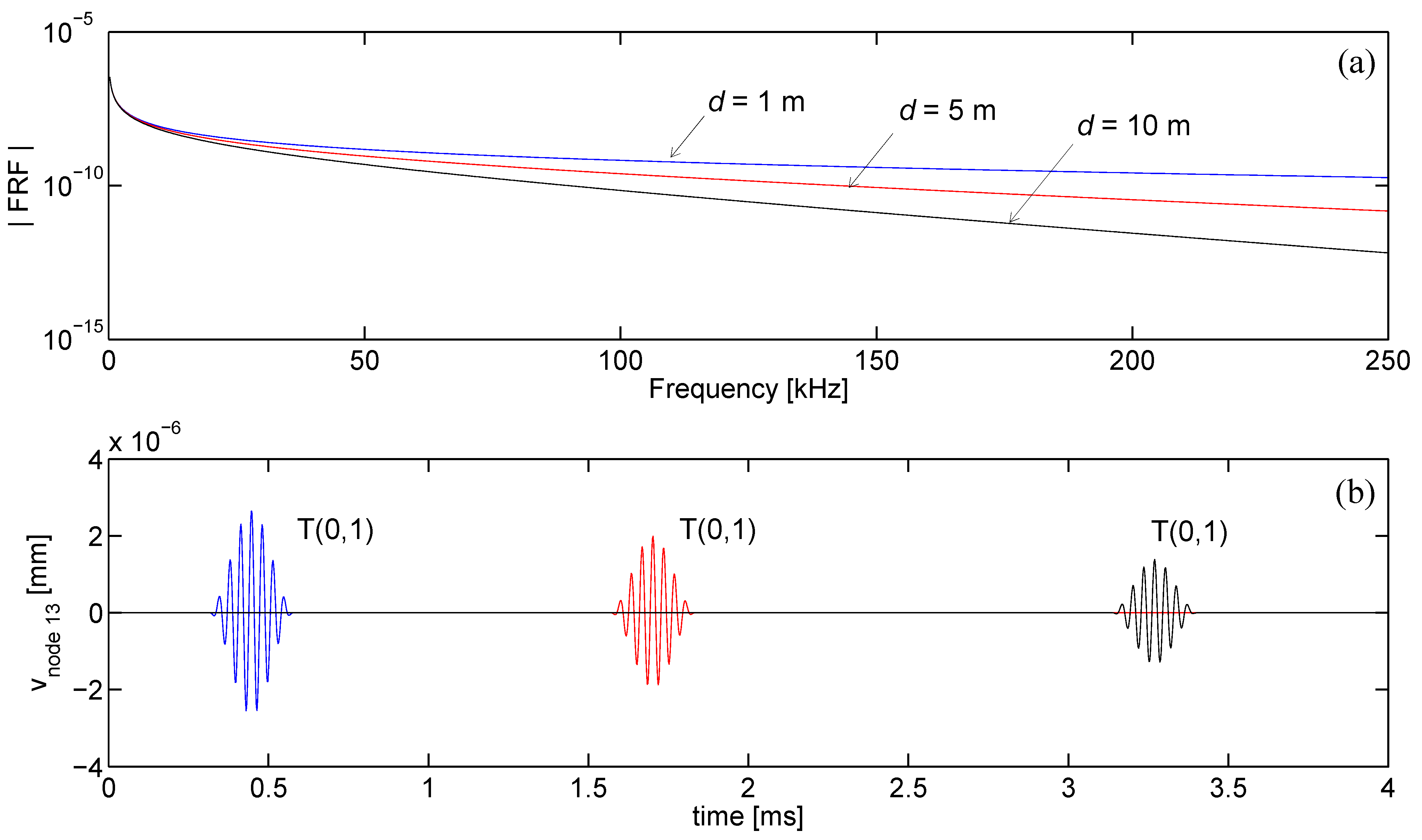
In the computation of the time-transient response, the proposed SFE formulation is reliable, capturing mode separation as well as pulse dispersion, stable, showing no or limited activity before the first arrival, and fast. The computational time mainly depends on the maximum excited frequency that sets the minimum number of finite elements in the mesh and the sampling frequency for which the waveguide frequency response [via Equation (29)] must be calculated to guarantee time-transient solution accuracy. For the proposed formulation the distance source-receiver only marginally affects the computational time and memory requirements, resulting advantageous if compared to a time transient Finite Element simulation for wave problems where an increased propagation distance involves a massive increase of dofs. This is particular true for high frequency computations, where the wavelengths are small and an accurate prediction by FE procedures involves an intensive three-dimensional discretization.
For example, the computation of each FRF and the corresponding time response required approximately 260 seconds using a Pentium 4 processor on a PC with 2 GB of RAM. This computational time is negligible if compared to the time needed by an equivalent full 3D Finite Element simulation to simulate waves at 10 meters distance.
In addition, SFE formulations allow for a very efficient multiple time-transient response calculation by means of an optimized post-processing procedure. In the time-transient response calculation, in fact, the majority of the computational CPU time is required to compute the waveguide eigenvalues and eigenvectors at several different frequencies solving the eigenvalue problem of Equation (18). The required time increases substantially for an increased number of dofs of the considered waveguide mesh. For a given waveguide, and especially for large dofs problems, wavenumbers and wavevectors can be calculated at the several different frequencies of interest only once and stored. Next, these data can be used to quickly calculate the time-transient response of the waveguide at the different dofs of the mesh, considering different distances source-receiver and also different spatial and temporal load distribution.