Poroelastic Medium with Non-Penetrating Crack Driven by Hydraulic Fracture: FEM Approximation Using HHT-α and Semi-Smooth Newton Methods
Abstract
1. Introduction
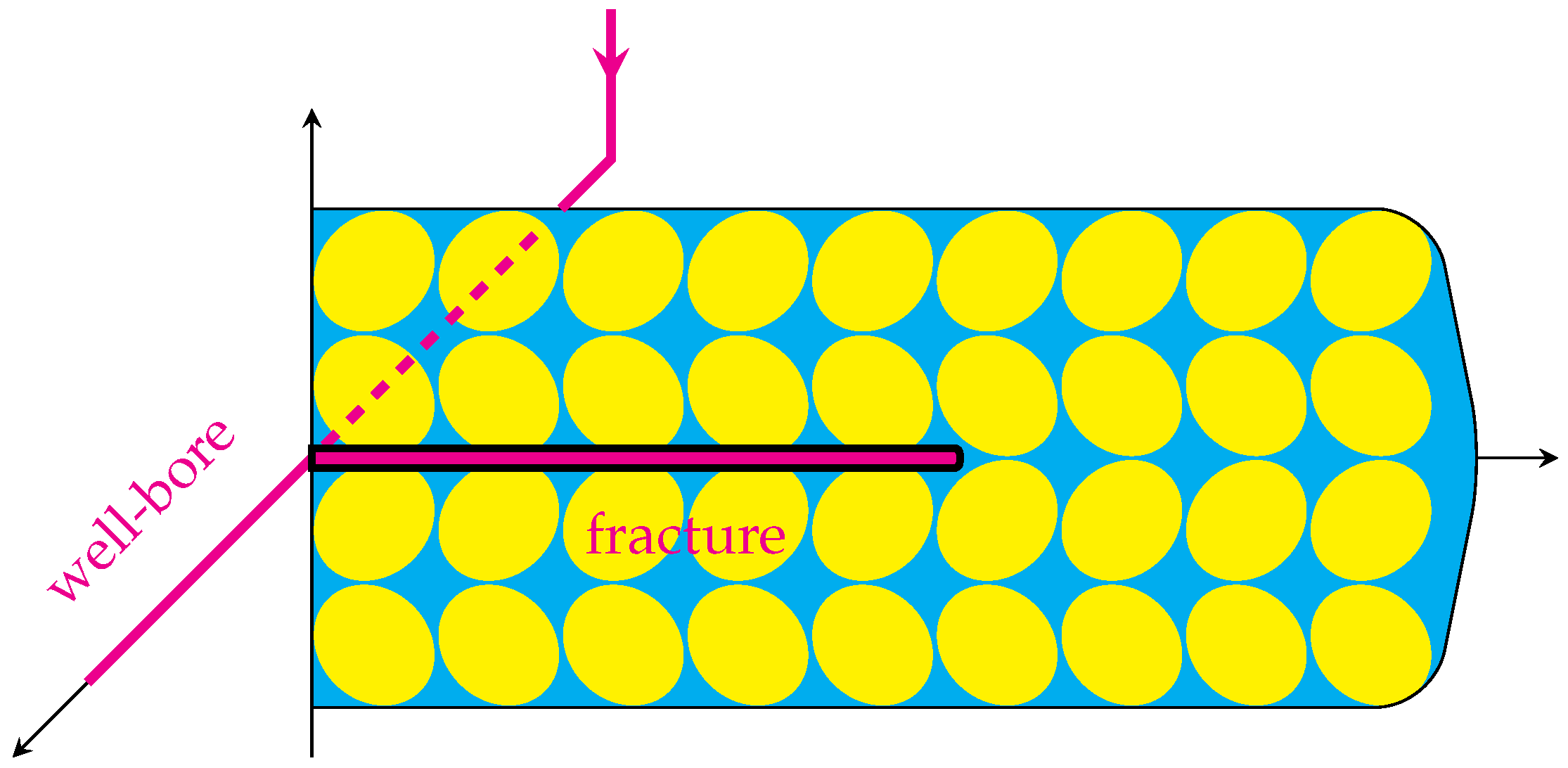
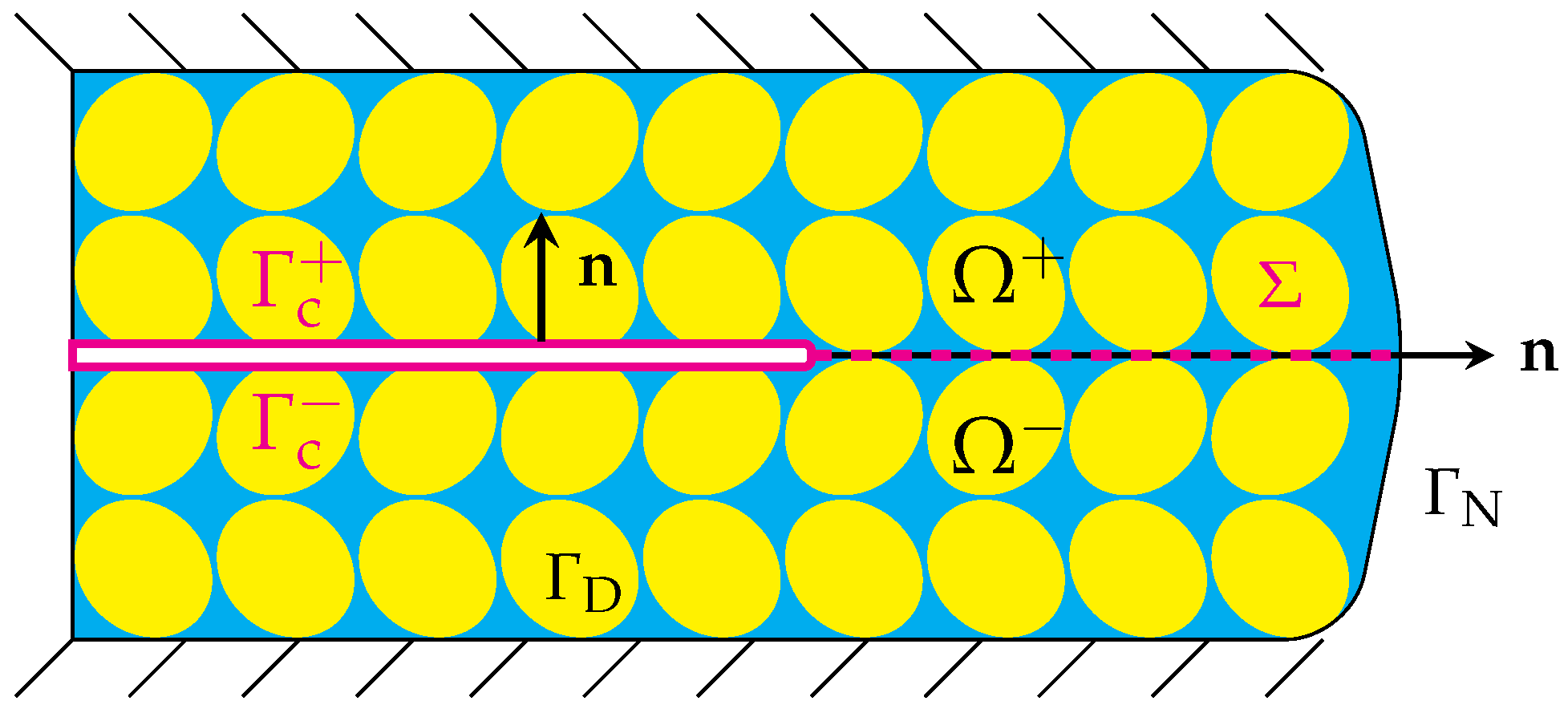
2. Setting of the Poroelastic Dynamic Contact Problem for Fluid-Driven Crack
3. Full Discretization of the Dynamic Contact Problem
4. Semi-Smooth Newton Method for the Solution of the Mixed Variational Problem
- 1.
- Initialization:
- 2.
- Iteration step:
- 3.
- Iteration step:
- 4.
- Stopping rule:
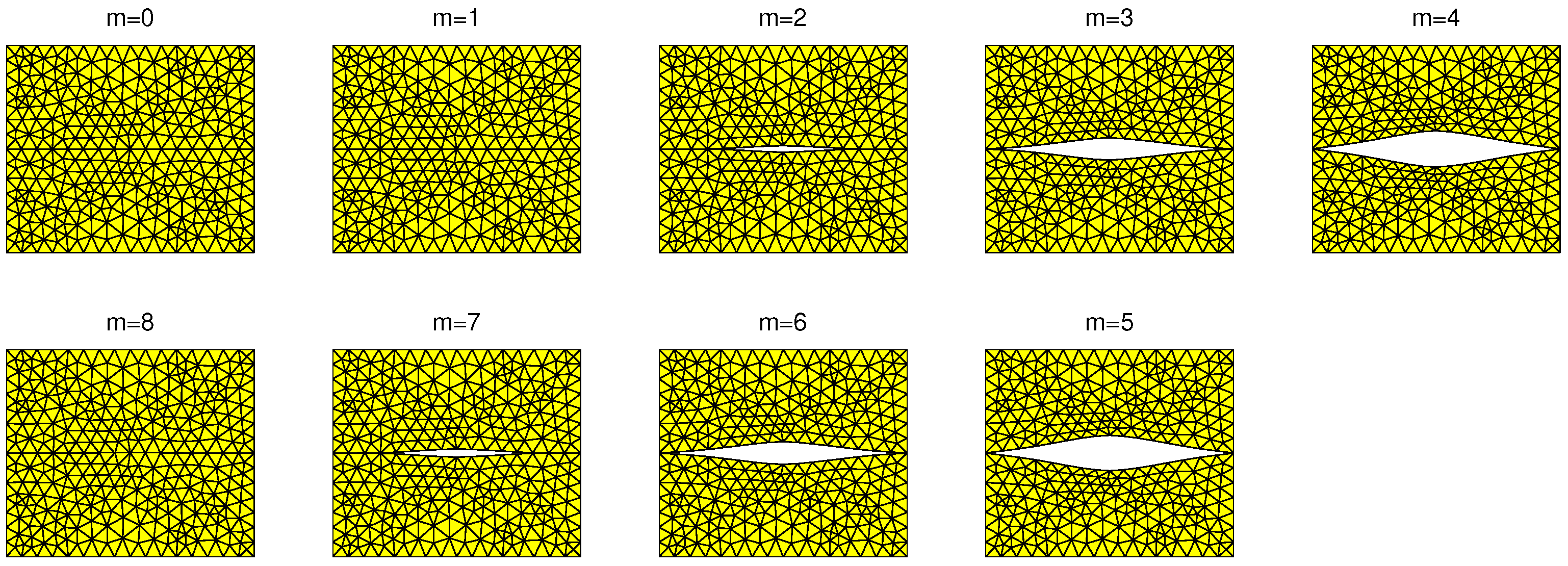
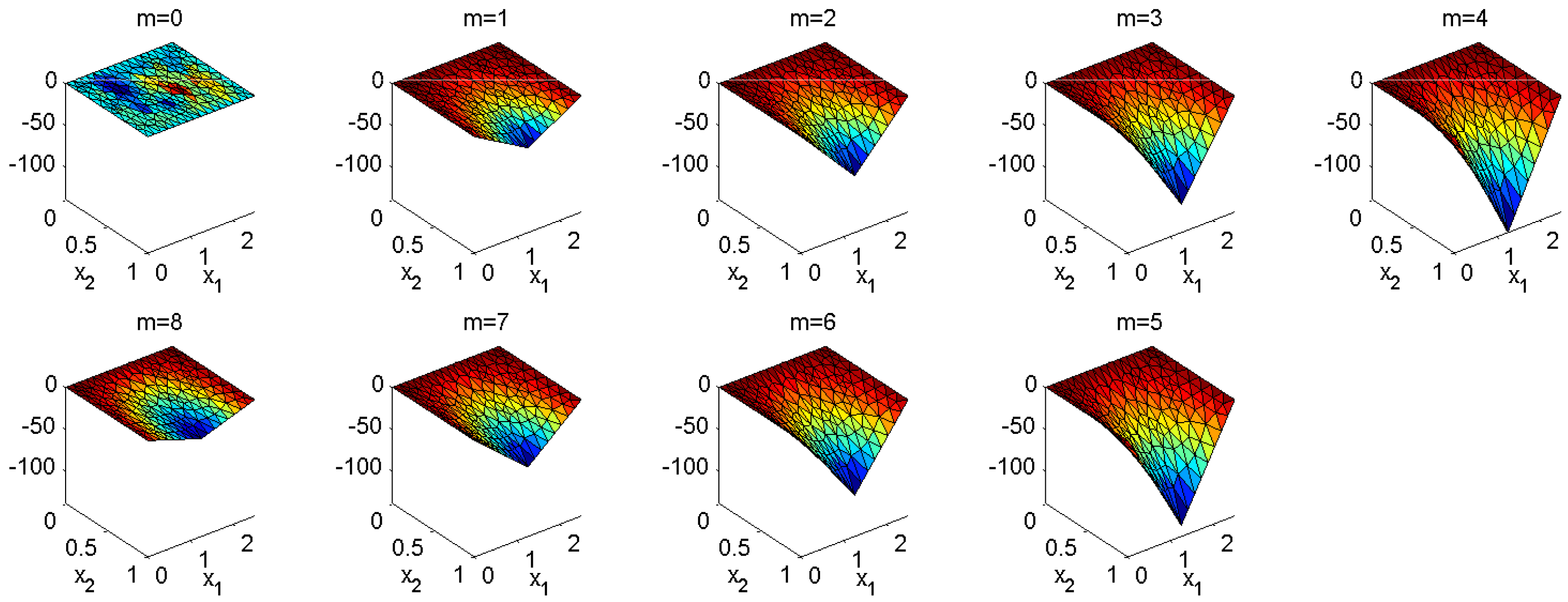
5. Numerical Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Itou, H.; Kovtunenko, V.A.; Lazarev, N.P. Poroelastic problem of a non-penetrating crack with cohesive contact for fluid-driven fracture. Appl. Eng. Sci. 2023, 15, 100136. [Google Scholar] [CrossRef]
- Kovtunenko, V. Poroelastic medium with a non-penetrating crack driven by hydraulic fracture: Variational inequality and its semidiscretization. J. Comput. Optim. Appl. 2022, 405, 113953. [Google Scholar] [CrossRef]
- Kovtunenko, V.; Lazarev, N. The energy release rate for non-penetrating crack in poroelastic body driven by hydraulic fracture. Math. Mech. Solids 2023, 28, 592–610. [Google Scholar] [CrossRef] [PubMed]
- Economides, M.; Nolte, K. (Eds.) Reservoir Stimulation; Wiley: Chichester, UK, 2000. [Google Scholar]
- Biot, M. Theory of propagation of elastic waves in a fluid saturated porous solid. I and II. J. Acoust. Soc. Am. 1956, 28, 168–191. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics; Wiley: Chichester, UK, 2004. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar] [CrossRef]
- Barenblatt, G.; Zheltov, I.; Kochina, I. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Khristianovic, S.; Zheltov, Y. Formation of vertical fractures by means of highly viscous fluids. In Proceedings of the 4th World Petroleum Congress, Rome, Italy, 6–15 June 1955; Volume II, pp. 579–586. [Google Scholar]
- Meirmanov, A. Mathematical Models for Poroelastic Flows; Atlantis Press: Paris, France, 2014. [Google Scholar] [CrossRef]
- Alekseev, G.; Spivak, Y.; Yashchenko, E. Theoretical analysis of the 2D thermal cloaking problem. J. Phys. Conf. Ser. 2017, 803, 012001. [Google Scholar] [CrossRef]
- Antontsev, S.; Kuznetsov, I.; Sazhenkov, S.; Shmarev, S. Solutions of impulsive p(x,t)-parabolic equations with an infinitesimal initial layer. Nonlinear Anal. Real World Appl. 2024, 80, 104162. [Google Scholar] [CrossRef]
- Kovtunenko, V.; Zubkova, A. Mathematical modeling of a discontinuous solution of the generalized Poisson–Nernst–Planck problem in a two-phase medium. Kinet. Relat. Mod. 2018, 11, 119–135. [Google Scholar] [CrossRef]
- Rudoy, E.M.; Sazhenkov, S.A. The homogenized dynamical model of a thermoelastic composite stitched with reinforcing filaments. Phil. Trans. R. Soc. A 2024, 382, 20230304. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Khludnev, A. On cracks of minimal opening in thermoelastic plates. Z. Angew. Math. Mech. 2000, 80, 253–258. [Google Scholar] [CrossRef]
- Showalter, R.; Stefanelli, U. Diffusion in poro-plastic media. Math. Meth. Appl. Sci. 2004, 27, 2131–2151. [Google Scholar] [CrossRef]
- Zienkiewicz, O.; Shiomi, T. Dynamic behaviour of saturated porous media; the generalized Biot formulation and its numerical solution. Int. J. Numer. Anal. Methods Geomech. 1984, 8, 71–96. [Google Scholar] [CrossRef]
- Bratov, V.; Morozov, N.; Petrov, Y. Dynamic Strength of Continuum; St. Petersburg University: Saint Petersburg, Russia, 2009. [Google Scholar]
- Bunger, A.; Detournay, E.; Garagash, D. Toughness-dominated hydraulic fracture with leak-off. Int. J. Fract. 2005, 134, 175–190. [Google Scholar] [CrossRef]
- Peirce, A.; Detournay, E. An implicit level set method for modeling hydraulically driven fractures. Comput. Methods Appl. Mech. Eng. 2008, 197, 2858–2885. [Google Scholar] [CrossRef]
- Shelukhin, V.; Baikov, V.; Golovin, S.; Davletbaev, A.; Starovoitov, V. Fractured water injection wells: Pressure transient analysis. Int. J. Solids Struct. 2014, 51, 2116–2122. [Google Scholar] [CrossRef]
- Borden, M.; Verhoosel, C.; Scott, M.; Hughes, T.; Landis, C. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 77–95. [Google Scholar] [CrossRef]
- Mikayelyan, H. Some recent results on regularity of the crack-tip/crack-front of Mumford–Shah minimizers. In Mathematical Analysis of Continuum Mechanics and Industrial Applications III: Proceedings of the International Conference CoMFoS18; Itou, H., Hirano, S., Kimura, M., Kovtunenko, V., Khludnev, A., Eds.; Springer: Singapore, 2020; pp. 23–33. [Google Scholar] [CrossRef]
- Mikelić, A.; Wheeler, M.; Wick, T. A phase-field method for propagating fluid-filled fractures coupled to a surrounding porous medium. SIAM Multiscale Model. Simul. 2015, 13, 367–398. [Google Scholar] [CrossRef]
- Mallikarjunaiah, M.; Gou, K. Crack-tip field characterization in nonlinearly constituted and geometrically linear elastoporous solid containing a star-shaped crack: A finite element study. arXiv 2025, arXiv:2507.09263. [Google Scholar] [CrossRef]
- Shylaja, G.; Naidu, V.K.; Venkatesh, B.; Mallikarjunaiah, M. Finite element modeling of V-notched thermoelastic strain-limiting solids containing inclusions. arXiv 2025, arXiv:2507.09300. [Google Scholar] [CrossRef]
- Bach, M.; Khludnev, A.; Kovtunenko, V. Derivatives of the energy functional for 2D-problems with a crack under Signorini and friction conditions. Math. Meth. Appl. Sci. 2000, 23, 515–534. [Google Scholar] [CrossRef]
- Khludnev, A.; Kovtunenko, V. Analysis of Cracks in Solids; Volume 6: Advances in Fracture Mechanics Series; WIT-Press: Southampton, UK; Boston, MA, USA, 2000. [Google Scholar]
- Khludnev, A.M.; Kovtunenko, V.A.; Tani, A. Evolution of a crack with kink and non-penetration. J. Math. Soc. Jpn. 2008, 60, 1219–1253. [Google Scholar] [CrossRef]
- Khludnev, A.; Sokołowski, J. Griffith formulae for elasticity systems with unilateral conditions in domains with cracks. Eur. J. Mech. A Solids 2000, 19, 105–119. [Google Scholar] [CrossRef]
- Popova, T. The problem on T-shape junction of thin inclusions. Sib. Electron. Math. Rep. 2024, 21, 1578–1593. [Google Scholar]
- Kovtunenko, V. Numerical simulation of the non-linear crack problem with non-penetration. Math. Meth. Appl. Sci. 2004, 27, 163–179. [Google Scholar] [CrossRef]
- Baykin, A.; Golovin, S. Modelling of hydraulic fracture propagation in inhomogeneous poroelastic medium. J. Phys. Conf. Ser. 2016, 722, 012003. [Google Scholar] [CrossRef]
- Amor, H.; Marigo, J.J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2017, 57, 1209–1229. [Google Scholar] [CrossRef]
- Hintermüller, M.; Ito, K.; Kunisch, K. The primal-dual active set strategy as a semismooth Newton method. SIAM J. Optim. 2002, 13, 865–888. [Google Scholar] [CrossRef]
- Hüeber, S.; Stadler, G.; Wohlmuth, B. A primal-dual active set algorithm for three-dimensional contact problems with Coulomb friction. SIAM J. Sci. Comput. 2008, 30, 572–596. [Google Scholar] [CrossRef]
- Kučera, R.; Motyčková, K.; Markopoulos, A.; Haslinger, J. On the inexact symmetrized globally convergent semi-smooth Newton method for 3D contact problems with Tresca friction: The R-linear convergence rate. Optim. Methods Softw. 2020, 35, 65–86. [Google Scholar] [CrossRef]
- Abide, S.; Barboteu, M.; Cherkaoui, S.; Dumont, S. Unified primal-dual active set method for dynamic frictional contact problems. Fixed Point Theory Algorithms Sci. Eng. 2022, 2022, 19. [Google Scholar] [CrossRef]
- Hintermüller, M.; Kovtunenko, V.A.; Kunisch, K. Generalized Newton methods for crack problems with non-penetration condition. Numer. Meth. Partial Differ. Equ. 2005, 21, 586–610. [Google Scholar] [CrossRef]
- Hintermüller, M.; Kovtunenko, V.; Kunisch, K. A Papkovich–Neuber-based numerical approach to cracks with contact in 3D. IMA J. Appl. Math. 2009, 74, 325–343. [Google Scholar] [CrossRef]
- Chouly, F.; Hild, P.; Renard, Y. A Nitsche finite element method for dynamic contact: 1 and 2. ESAIM Math. Model. Numer. Anal. 2015, 49, 481–528. [Google Scholar] [CrossRef]
- Bause, M.; Radu, F.; Köcher, U. Space–time finite element approximation of the Biot poroelasticity system with iterative coupling. Comput. Methods Appl. Mech. Eng. 2017, 320, 745–768. [Google Scholar] [CrossRef]
- Gwinner, J.; Stephan, E.P. Advanced Boundary Element Methods. Treatment of Boundary Value, Transmission and Contact Problems; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Linck, V.; Bayada, G.; Baillet, L.; Sassi, T.; Sabil, J. Finite element analysis of a contact with friction between an elastic body and a thin soft layer. J. Tribol. 2005, 127, 461–468. [Google Scholar] [CrossRef]
- Mikelić, A.; Wang, B.; Wheeler, M. Numerical convergence study of iterative coupling for coupled flow and geomechanics. Comput. Geosci. 2014, 18, 325–341. [Google Scholar] [CrossRef]
- Aimi, A.; Dallospedale, S.; Desiderio, L.; Guardasoni, C. A space–time energetic BIE method for 3D elastodynamics: The Dirichlet case. Comput. Mech. 2023, 72, 885–905. [Google Scholar] [CrossRef]
- Coppolino, L.; Desiderio, L. Space-time energetic Galerkin BEM for the numerical solution of 3D elastodynamic problems: Overcoming challenges of the strongly singular integral operator. Comput. Mech. 2025, 76. [Google Scholar] [CrossRef]
- Laursen, T.A. Computational Contact and Impact Mechanics; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Chouly, F.; Hild, P.; Renard, Y. Finite Element Approximation of Contact and Friction in Elasticity; Birkhäuser: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Eck, C.; Jarušek, J.; Krbec, M. Unilateral Contact Problems: Variational Methods and Existence Theorems; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar] [CrossRef]
- Kashiwabara, T.; Itou, H. Unique solvability of a crack problem with Signorini-type and Tresca friction conditions in a linearized elastodynamic body. Phil. Trans. R. Soc. A 2022, 380, 20220225. [Google Scholar] [CrossRef]
- Migórski, S.; Ochal, A.; Shillor, M.; Sofonea, M. Nonsmooth dynamic frictional contact of a thermoviscoelastic body. Appl. Anal. 2018, 97, 1228–1245. [Google Scholar] [CrossRef]
- Hilber, H.M.; Hughes, T.J.R.; Taylor, R.L. Improved numerical dissipation for time integration algorithms in structural dynamics. Earthq. Eng. Struct. Dyn. 1977, 5, 283–292. [Google Scholar] [CrossRef]
- Laursen, T.; Chawla, V. Design of energy conserving algorithms for frictionless dynamic contact problems. Int. J. Numer. Methods Eng. 1997, 40, 863–886. [Google Scholar] [CrossRef]
- Kovtunenko, V.A.; Renard, Y. Convergence analysis of semi-smooth Newton method for mixed FEM approximations of dynamic two-body contact and crack problems. J. Comput. Appl. Math. 2025, 471, 116722. [Google Scholar] [CrossRef]
- Kovtunenko, V.A.; Renard, Y. FEM approximation of dynamic contact problem for fracture under fluid volume control using HHT-α and semi-smooth Newton methods. Appl. Numer. Math. 2025, 218, 148–158. [Google Scholar] [CrossRef]
- Itou, H.; Kovtunenko, V.; Rajagopal, K. Nonlinear model of a porous body with fluid-driven fracture under cohesion contact conditions and fluid volume control. Math. Mod. Meth. Appl. Sci. 2025, 35, 2311–2328. [Google Scholar] [CrossRef]
- Kovtunenko, V.A. Space-time finite element based primal-dual active set method for the non-smooth problem of impact of rigid obstacle by elastic bar. Comput. Math. Model. 2025. [Google Scholar] [CrossRef]
- Kovtunenko, V.A. Space-time primal-dual active set method: Benchmark for collision of elastic bar with discontinuous velocity. Computation 2025, 13, 210. [Google Scholar] [CrossRef]
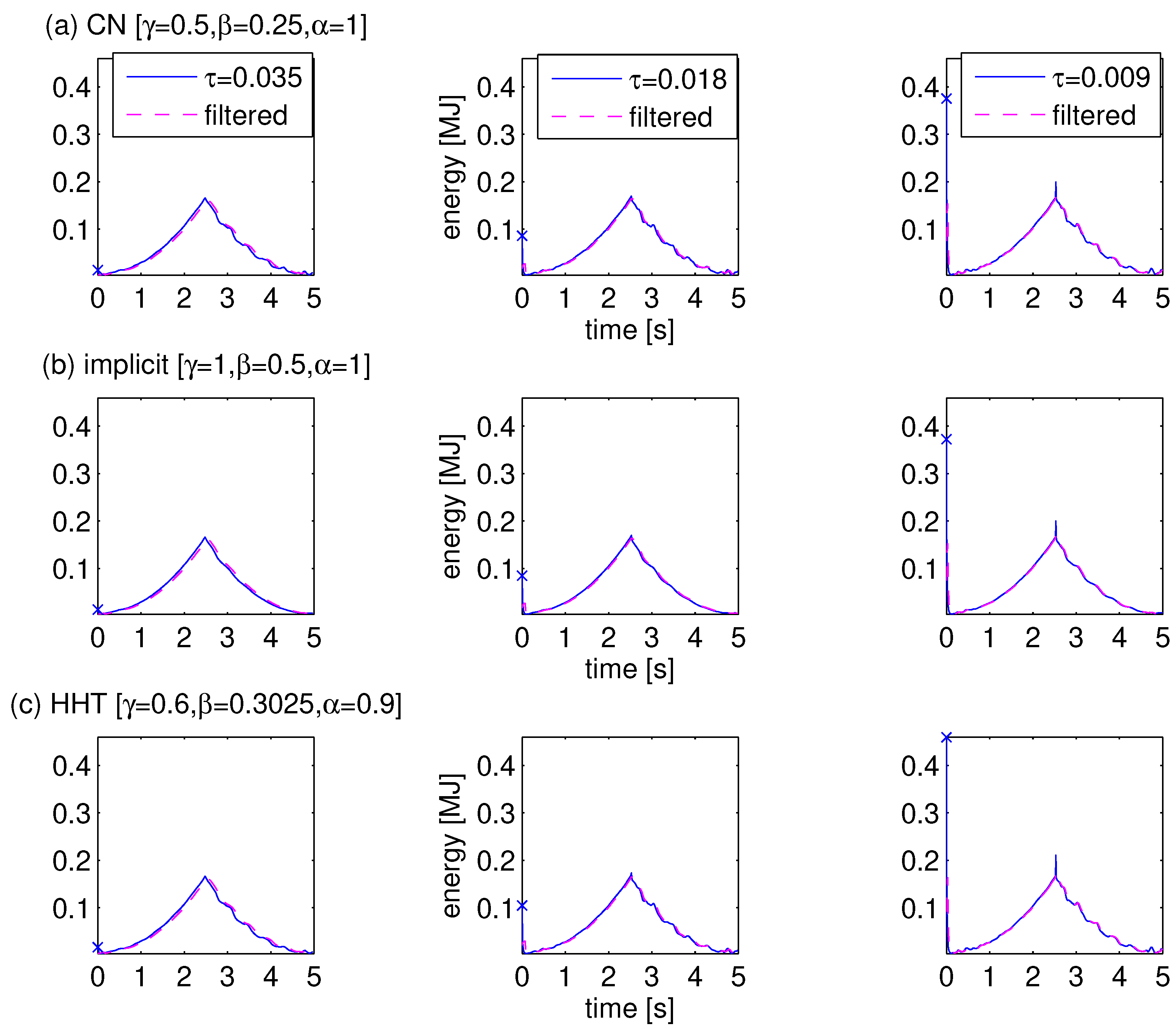
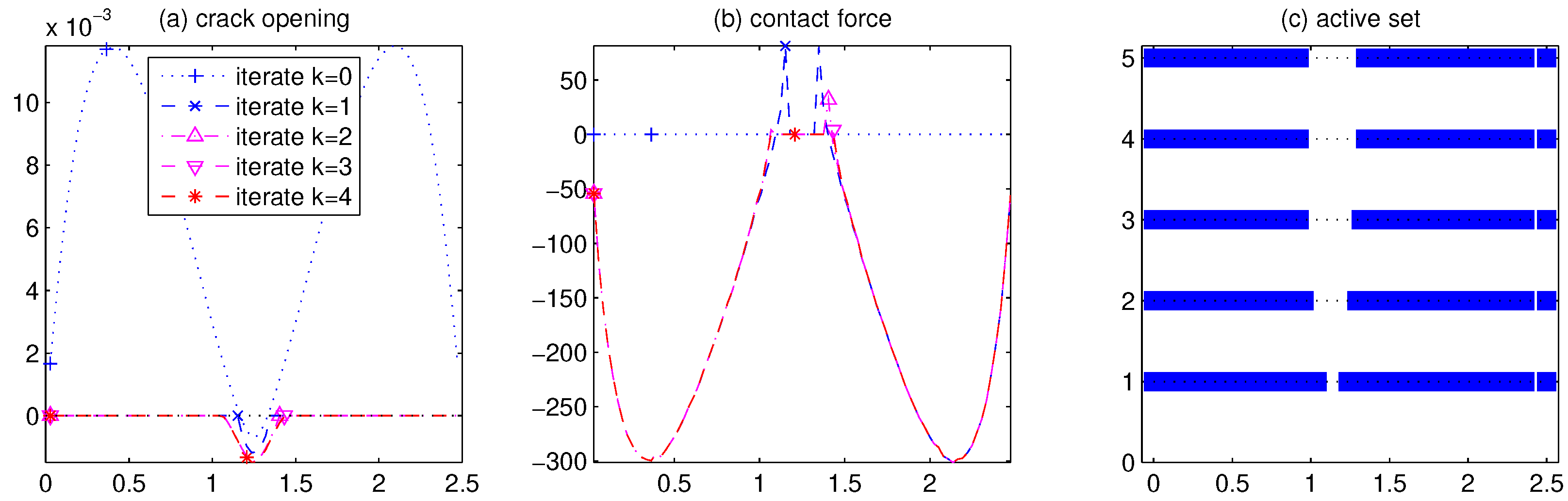
| Scheme: | |||
|---|---|---|---|
| 0.0141 | 0.0230 | 0.1196 | |
| 0.0117 | 0.0229 | 0.1181 | |
| 0.0138 | 0.0255 | 0.1318 |
| Step-Size | Constraints | Iterations | CPU Times |
|---|---|---|---|
| 0.312 | 15 | 5 | 0.0018 |
| 0.138 | 35 | 4 | 0.0199 |
| 0.092 | 53 | 4 | 0.0560 |
| 0.070 | 70 | 5 | 0.1518 |
| 0.056 | 88 | 4 | 0.1815 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovtunenko, V.A.; Atlasiuk, O.M. Poroelastic Medium with Non-Penetrating Crack Driven by Hydraulic Fracture: FEM Approximation Using HHT-α and Semi-Smooth Newton Methods. Algorithms 2025, 18, 579. https://doi.org/10.3390/a18090579
Kovtunenko VA, Atlasiuk OM. Poroelastic Medium with Non-Penetrating Crack Driven by Hydraulic Fracture: FEM Approximation Using HHT-α and Semi-Smooth Newton Methods. Algorithms. 2025; 18(9):579. https://doi.org/10.3390/a18090579
Chicago/Turabian StyleKovtunenko, Victor A., and Olena M. Atlasiuk. 2025. "Poroelastic Medium with Non-Penetrating Crack Driven by Hydraulic Fracture: FEM Approximation Using HHT-α and Semi-Smooth Newton Methods" Algorithms 18, no. 9: 579. https://doi.org/10.3390/a18090579
APA StyleKovtunenko, V. A., & Atlasiuk, O. M. (2025). Poroelastic Medium with Non-Penetrating Crack Driven by Hydraulic Fracture: FEM Approximation Using HHT-α and Semi-Smooth Newton Methods. Algorithms, 18(9), 579. https://doi.org/10.3390/a18090579








