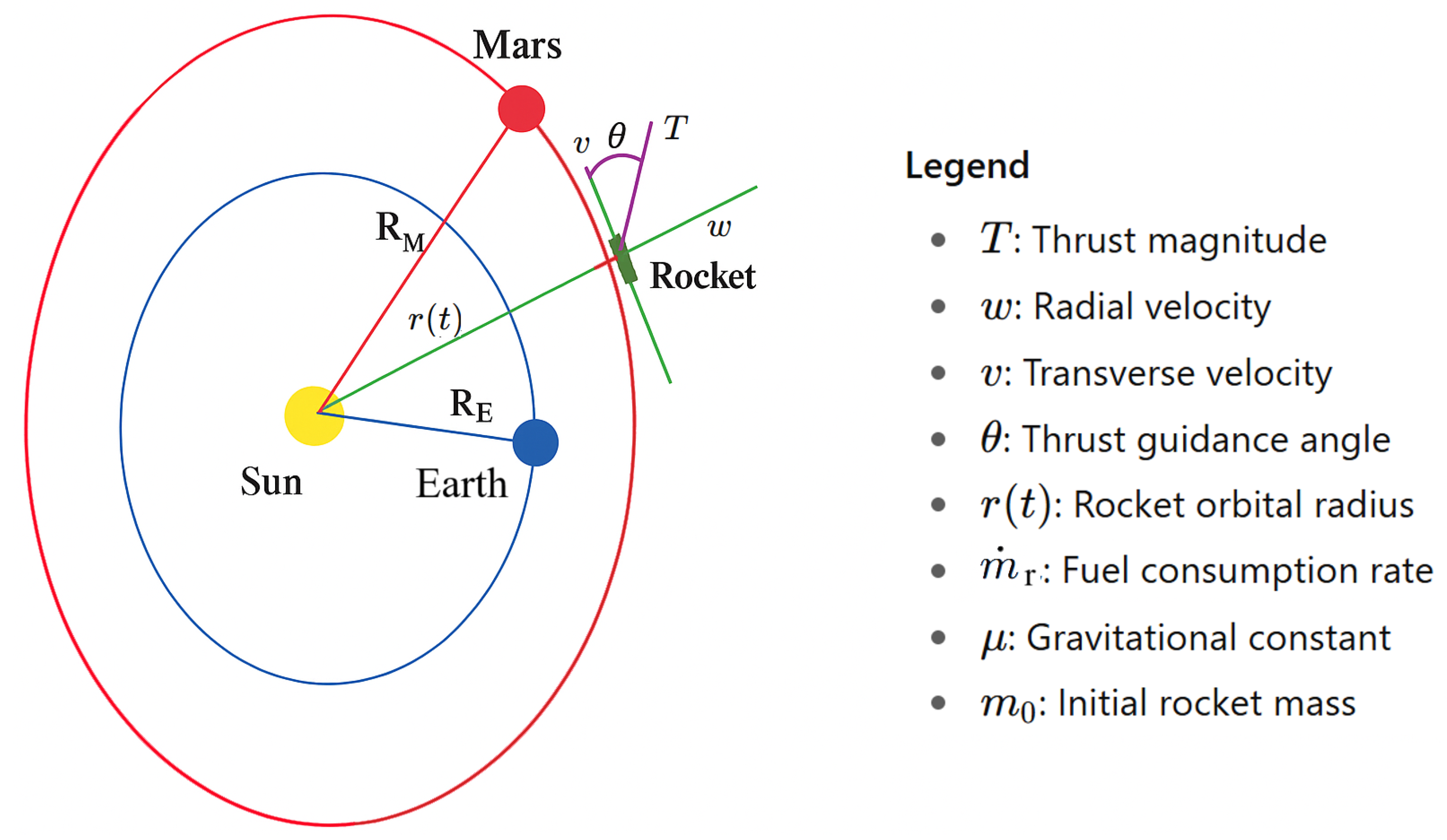
An Overview of the Euler-Type Universal Numerical Integrator (E-TUNI): Applications in Non-Linear Dynamics and Predictive Control

Abstract

A Universal Numerical Integrator (UNI) is a computational framework that combines a classical numerical integration method, such as Euler, Runge–Kutta, or Adams–Bashforth, with a universal approximator of functions, such as a feed-forward neural network (including MLP, SVM, RBF, among others) or a fuzzy inference system. The Euler-Type Universal Numerical Integrator (E–TUNI) is a particular case of UNI based on the first-order Euler integrator and is designed to model non-linear dynamic systems observed in real-world scenarios accurately. The UNI framework can be organized into three primary methodologies: the NARMAX model (Non-linear AutoRegressive Moving Average with eXogenous input), the mean derivatives approach (which characterizes E–TUNI), and the instantaneous derivatives approach. The E–TUNI methodology relies exclusively on mean derivative functions, distinguishing it from techniques that employ instantaneous derivatives. Although it is based on a first-order scheme, the E–TUNI achieves an accuracy level comparable to that of higher-order integrators. This performance is made possible by the incorporation of a neural network acting as a universal approximator, which significantly reduces the approximation error. This article provides a comprehensive overview of the E–TUNI methodology, focusing on its application to the modeling of non-linear autonomous dynamic systems and its use in predictive control. Several computational experiments are presented to illustrate and validate the effectiveness of the proposed method.

1. Introduction

The numerical integration of non-linear dynamic systems is a central problem in computational modeling and control engineering. Classical methods such as Euler, Runge–Kutta, and predictor–corrector are widely used, but they often present limitations in terms of accuracy, stability, and adaptability, especially when applied to highly non-linear systems or model-based predictive control tasks. This scenario motivates the development of methodologies that combine simplicity, robustness, and generality while maintaining computational efficiency.

In this context, the Euler-Type Universal Numerical Integrator (E–TUNI) is proposed as a methodology that preserves the structural simplicity of the Euler scheme but extends its formulation to achieve better performance and greater applicability through its coupling with an Artificial Neural Network (ANN). By coupling the concept of a universal approximator of functions to the mean-derivative formulation, E-TUNI offers a flexible and practical framework for the simulation of non-linear systems and for applications in model-based predictive control.

Therefore, the main contributions of this paper are as follows: (i) presenting a basic mathematical formulation of E–TUNI, (ii) demonstrating four representative technological applications of E-TUNI in non-linear dynamics and/or predictive control, including the non-linear pendulum and the orbital transfer problem, (iii) illustrating a procedure for obtaining approximate continuous solutions from the naturally discrete scheme of E–TUNI (see Example 3 in Section 6), (iv) critically discussing the advantages and limitations of E–TUNI in comparison with other universal numerical integrators, pointing out potential directions for future research (see Example 4 in Section 6), (v) evaluating the computational cost of E–TUNI in different scenarios, showing that the method can be competitive or even superior to traditional methods in large-scale problems (see again Example 4), and (vi) pointing out how E–TUNI can be incorporated into hybrid frameworks, bringing the method closer to current research lines in deep learning applied to differential equations.

The remainder of this article is organized as follows: Section 2 presents a literature review on E–TUNI and other types of Universal Numerical Integrators (UNIs). Section 3 briefly defines the type of neural predictive control problem that is addressed in this article. Section 4 presents the notation and variables used in this formulation. Section 5 provides a theoretical overview of E–TUNI in a predictive control structure. Section 6 describes the numerical simulations and applications. Finally, Section 7 concludes the article with a summary of the results and prospects for future work.

2. Related Work

One of the earliest works on artificial neural networks is attributed to McCulloch and Pitts in [1], dated 1943. In the eighty years of development of artificial intelligence and neural networks, many significant advances have emerged. For example, in [2], Kolmogorov (1957) demonstrated that any n-dimensional function can be represented as a linear combination of non-linear one-dimensional functions. This result was later recognized in [3], where the concept of Kolmogorov neural networks was introduced. The classical back-propagation algorithm for training MLP networks was proposed in [4], and subsequent work [5,6] demonstrated that MLPs are universal approximator of functions. A detailed summary of the advances in neural networks in the 20th century can be found in [7].

One of the most relevant applications of neural networks is the modeling of non-linear dynamical systems. In [8], the concept of a Universal Numerical Integrator (UNI) was introduced, defined as the coupling of a conventional numerical integrator (e.g., Euler, Runge–Kutta, predictor–corrector, among others) to a universal approximator of functions (e.g., MLP, SVM, RBF, wavelet networks, fuzzy inference systems, paraconsistent inference systems, among others). The classification proposed in [8] divides UNIs into three main categories: (i) the NARMAX model, (ii) the mean derivative methodology (e.g., E–TUNI), and (iii) the instantaneous derivative methodology (e.g., Runge–Kutta neural network, Adams–Bashforth neural network, predictor–corrector neural network, among others).

Classic references on numerical integrators can be found in [9,10,11]. In [12,13], the NARMAX model is discussed in detail using neural networks. Euler’s original work from 1768 is presented in [14], in which the first-order scheme based on instantaneous derivatives was proposed. Although simple, Euler’s method is relatively imprecise. However, when mean derivatives replace instantaneous derivatives, the process becomes as accurate as higher-order integrators, which motivates the structure of the Euler-Type Universal Numerical Integrator (E–TUNI).

It should be noted that in [8], the E–TUNI was called “Euler Neural Network,” while in [15] the same term appeared in another context. To avoid ambiguity, in this work we adopt the designation E-TUNI. References [16,17,18,19] discuss the mean derivative methodology in different contexts, including predictive control [16], qualitative design analysis [17], and quantitative mathematical analysis [18]. In [19], the E-TUNI is applied technologically and mathematically in backward integration processes.

The first work identified in the literature on UNIs is attributed to Wang and Lin (1998) [20], who introduced the Runge–Kutta Neural Network (RKNN). Later work explored its application in control [21,22], while others addressed neural differential equations more broadly [23]. It is also important to note that, to our knowledge, the Predictor–Corrector Neural Network (PCNN) has not yet been formally introduced in the literature.

Finally, both the NARMAX model and the mean derivative methodology (E–TUNI) are intrinsically linked to a fixed integration step $\Delta t$. Changing the integration step requires a new neural network training process. In contrast, methodologies based on instantaneous derivatives (RKNN, ABNN, PCNN, among others) allow variations of $\Delta t$, within certain stability limits, without the need for retraining [8,17,18,20]. For validation and testing purposes, simple theoretical models of non-linear differential equations can be found in [24].

3. Neural Predictive Control Problem Formulation

Neural predictive control is an advanced strategy that combines prediction of future system behavior and optimization of control actions. Unlike traditional methods, which rely on complex mathematical models, neural predictive control uses artificial neural networks to learn directly from historical data, adaptively capturing non-linearities and complex dynamics.

The process begins with the collection of relevant variables, such as past system states, previous control actions, and external disturbances. A neural network (often an MLP) is trained to act as a predictive model, estimating future states based on these inputs. An optimizer then calculates the optimal sequence of control actions that minimizes a performance criterion, such as the error between the prediction and a desired target. The first action in this sequence is applied to the system, and the cycle repeats in real time, continually readjusting itself with new data.

The advantage of this method is that the neural network eliminates the need for explicit analytical equations, adapts to operational changes, and robustly handles noise. Typical applications include temperature control in industrial environments, flow management in watersheds, and chemical process automation. To implement it, the architecture of the artificial neural network is defined, representative data is collected, and the predictive control algorithm is integrated into the system. In short, neural predictive control offers a powerful and flexible alternative for controlling dynamic systems, combining machine learning and control theory in a cohesive, future-oriented framework.

In this article, a first-order Euler integrator is coupled to a neural network with a Multi-Layer Perceptron (MLP) architecture. This structure is the representative dynamic model of our real plant, which we call E–TUNI. The E–TUNI architecture is then coupled to a predictive control structure that minimizes the Mean Squared Error (MSE) of a quadratic functional composed of two parts to be optimized: (i) a smooth control policy and (ii) the tracking of a reference trajectory. In aerospace engineering problems, as discussed at the end of this article, achieving autonomous controllability of satellites and rockets is of fundamental importance, eliminating the need for human intervention.

4. Preliminaries and Symbols Used

To facilitate a deeper understanding of the theoretical framework developed in this paper, we present a complete definition of all symbols and variables used throughout the work. The proposed methodology is named Euler Type Universal Numerical Integrator (E–TUNI), and it is based on a forward integration scheme that operates in a discrete-time setting. This approach is designed to approximate the behavior of continuous-time autonomous ordinary differential equations by means of a discrete formulation. For clarity, all notations used in this context are listed below and classified into two main categories: (i) variables defined in continuous time and (ii) variables defined in discrete time.

(i) Continuous Variables

• $\dot{y}=f\left(y\right)$⋯ System of continuous differential equations.
• $y={[y_1{y}_2\cdots y_n]}^T$⋯ State Variables.
• $f\left(y\right)={[f_1\left(y\right)f_2\left(y\right)\cdots f_n\left(y\right)]}^T$⋯ Instantaneous derivative functions.
• $y_j^i\left(t\right)=g_j^i\left(t\right)$⋯ Particular continuous and differentiable curve of a family of solution curves of the dynamical system $\dot{y}=f\left(y\right)$.
• ${\dot{y}}_j^i\left(t\right)={\dot{g}}_j^i\left(t\right)$⋯ First derivative of $y_j^i\left(t\right)$.

(ii) Discrete Variables

• ${}^{k}y^i=y^i(t_0+k·\Delta t)$⋯ Vector of state variables at time $t_k$.
• ${}^{k}y_j^i$⋯ Scalar state variable for $j=1,2,\cdots ,n$ at time $t_k$. It is a generic discretization point of the state variables generated by the integers i, j, and k.
• $n=n_y$⋯ Total number of state variables.
• ${}^{k}u=u(t_0+k·\Delta t)$⋯ Vector of control variables at time $t_k$.
• ${}^{k}u_j$⋯ Scalar control variable for $j=1,2,\cdots ,m$ at time $t_k$.
• $n_u$⋯ Total number of control variables.
• ${}^{k+1}y^i=y^i[t_0+(k+1)·\Delta t]$⋯ Exact vector of state variables at time $t_{k+1}$.
• ${}^{k+1}y_j^i$⋯ Exact scalar state variable for $j=1,2,\cdots ,n$ at time $t_{k+1}$.
• ${}^{k+1}\widehat{y}^i={\widehat{y}}^i[t_0+(k+1)·\Delta t]$⋯ Estimated Vector of state variables by UNI or E-TUNI at time $t_{k+1}$.
• ${}^{k+1}\widehat{y}_j^i$⋯ Scalar state variable estimated by UNI or E-TUNI for $j=1,2,\cdots ,n$ at time $t_{k+1}$.
• ${}^{k+1}\tilde{y}^i$⋯ Estimated Vector of state variables when using only the integrator and without using the neural network at time $t_{k+1}$.
• $ta{n}_{\Delta t}{}^k\alpha ^i=ta{n}_{\Delta t}{}^k\alpha ^i={[ta{n}_{\Delta t}{}^k\alpha _1^{i}ta{n}_{\Delta t}{}^k\alpha _2^i\cdots ta{n}_{\Delta t}{}^k\alpha _n^i]}^T$⋯ Exact vector of positive mean derivative functions at time $t_k$.
• $ta{n}_{\Delta t}{}^k\alpha _j^i=ta{n}_{\Delta t}{}^k\alpha _j^i={\displaystyle \frac{{}^{k+1}y_j^i-{}^{k}y_j^i}{\Delta t}}$⋯ Scalar positive mean derivative functions for $j=1,2,\cdots ,n$ at time $t_k$.
• $ta{n}_{\Delta t}{}^k\widehat{\alpha }^i={[ta{n}_{\Delta t}{}^k\widehat{\alpha }_1^{i}ta{n}_{\Delta t}{}^k\widehat{\alpha }_2^i\cdots ta{n}_{\Delta t}{}^k\widehat{\alpha }_n^i]}^T$⋯ Estimated vector of positive mean derivative functions by the E-TUNI at time $t_k$.
• $tan{}^k\theta ^i={[ta{n}^k{\theta }_1^{i}ta{n}^k{\theta }_2^i\cdots ta{n}^k{\theta }_n^i]}^T$⋯ Vector of positive instantaneous derivatives at time $t_k$.
• $ta{n}^k{\theta }_j^i=\underset{\Delta t\to 0}{lim}{\displaystyle \frac{{}^{k+1}y_j^i{-}^k{y}_j^i}{\Delta t}}$⋯ Scalar positive instantaneous derivative for $j=1,2,\cdots ,n$ at instant $t_k$.
• $t_k$⋯ Time instant $t_k=t_0+k·\Delta t$.
• $t_{k+1}$⋯ Time instant $t_{k+1}=t_0+(k+1)·\Delta t$.
• $\Delta t$⋯ Integration step.
• i⋯ Over-index that enumerates a particular curve from the family of curves of the dynamical system to be modeled ($i=1,2,\cdots ,q$).
• j⋯ Under-index that enumerates the state and control variables.
• k⋯ Over-index that enumerates the discrete time instants ($k=1,2,\cdots ,r$).
• r⋯ Total number of horizons of the time variable.
• q⋯ Total number of curves from the family of curves of the dynamic system to be modeled.
• $t_k^{*}$⋯ Instant of time within the interval $[t_k,t_{k+1}]$ as a result of the Differential Mean Value Theorem (see Theorem 1).
• $t_k^x$⋯ Instant of time within the interval $[t_k,t_{k+1}]$ as a result of the Integral Mean Value Theorem (see Theorem 2).
• m⋯ Total number of horizons in a predictive control structure.

To interpret the notation used in this work, it is essential to distinguish between the variables ${}^{k+1}y^i$, ${}^{k+1}\tilde{y}^i$, and ${}^{k+1}\widehat{y}^i$. The vector variable ${}^{k+1}y^i$ is the exact value of the state variables at time $t_{k+1}=t_0+(k+1)·\Delta t$. The vector variable ${}^{k+1}\tilde{y}^i$ is the estimated value of the state variables using only the numerical integrator. Finally, the vector variable ${}^{k+1}\widehat{y}^i$ is the estimated value of the state variables using the numerical integrator coupled to an artificial neural network. Figure 1 follows this convention and helps to understand better the notations adopted here. Additionally, it is important to understand the meaning of the auxiliary variables i, j, and k. This is accomplished in the next paragraph.

A key point in this notation is the interpretation of the over-indexes k and i and the under-index j in the variables ${}^{k}y_j^i$ and $ta{n}_{\Delta t}{}^k\alpha _j^i$. When the auxiliary variables i, j, and k are used simultaneously, they uniquely identify the secant ($ta{n}_{\Delta t}{}^k\alpha _j^i$) at the point ${}^{k}y_j^i$. Note that the over-index k indicates the time instant $t_k=t_0+k·\Delta t$ of the secant, the under-index j indicates the state variable in question, where $j=1,2,\cdots ,n$, and the over-index i$(i=1,2,\cdots ,q)$ indicates the particular curve where the respective secant is located, from the family of possible curves of the system of differential equations considered. The value of q can be as large as desired. The larger the value of q, the more different curves the neural network trains on, and the better its generalization. This convention is quite useful to fully understand the formal proof of the general expression of E–TUNI that is performed in Section 5.3.

5. Mathematical Development

In this section, we present a concise and complete description of the Euler-Type Universal Numerical Integrator (E–TUNI). To this end, we present a formal mathematical proof for the general expression that governs E–TUNI’s operation to generate discrete solutions for autonomous non-linear dynamical systems governed by ordinary differential equations. Additionally, we also present the correct way to use E–TUNI in a predictive control framework. We conclude this section by obtaining an approximate mathematical expression for E-TUNI to provide a continuous solution, rather than a discrete solution, for autonomous dynamical systems.

5.1. Basic Mathematical Development of E-TUNI

We provide a brief mathematical description of E–TUNI below. Then, in the following sub-section, we perform a formal mathematical demonstration of the general expression of the first-order Euler integrator designed with mean derivative functions. So, by definition, the secants or mean derivatives $ta{n}_{\Delta t}{}^k\alpha _j^i$ for $j=1,2,\cdots ,n$ between the points ${}^{k+1}y_j^i$ and ${}^{k}y_j^i$ are given by:

$$ta{n}_{\Delta t}{}^k\alpha _j^i={\displaystyle \frac{{}^{k+1}y_j^i-{}^{k}y_j^i}{\Delta t}}$$

(1)

where ${}^{k+1}y_j^i=y_j^i[t+(k+1)·\Delta t]$ is the forward state of the dynamic system, ${}^{k}y_j^i=y_j^i[t+k·\Delta t]$ is the present state of the dynamical system, the over-index k on the left indicates the instant k, the over-index i on the right suggests a discretization of the continuum, the sub-index j on the right indicates the $j-th$ state variable, n is the total number of state variables, and $\Delta t$ is the integration step. We talk more about the over-index i later in this article.

A geometric and intuitive difference between the mean and the instantaneous derivative functions is shown in Figure 1. In line with Figure 1 and Figure 2, the E-TUNI is entirely based on the concept of mean derivative functions and not on the idea of instantaneous derivative functions. As will be seen throughout this article, this change is quite significant when incorporated adequately into the Euler-type first-order integrator. Furthermore, the mean derivative functions can also be obtained from supervised training with input/output patterns using a neural network with any feed-forward architecture (MLP, RBF, SVM, among others).

It is also essential to note that it is possible to train E–TUNI in two different ways, namely, (a) through the direct approach or (b) through the indirect or empirical approach. In the direct approach, the neural network is trained decoupled from the Euler-type integrator, while in the indirect or empirical approach the neural network is trained coupled to the structure of the first-order Euler integrator. For this reason, in the indirect approach the back-propagation algorithm needs to be modified slightly. In the references [8,17,18], this is explained in more detail.

In this way, we have a non-linear dynamic system of n simultaneous first-order equations with dependent variables $y_1,y_2,\cdots ,y_n$. If each of these variables satisfies a given initial condition for the same value a of t, then we have an initial value problem for a first-order system, and we can write:

$$\left\{\begin{array}{cc}{\dot{y}}_1=f_1(y_1,y_2,\cdots y_n),& y_1\left(a\right)={\eta }_1\\ {\dot{y}}_2=f_2(y_1,y_2,\cdots y_n),& y_2\left(a\right)={\eta }_2\\ ⋮& ⋮\\ {\dot{y}}_n=f_n(y_1,y_2,\cdots y_n),& y_n\left(a\right)={\eta }_n\end{array}\right.$$

(2)

In [14], the mathematician Leonard Euler himself proposed in 1768 the first numerical integrator in the history of mathematics to approximately solve non-linear dynamical systems governed by Equation (2). This solution, which is well-known to everyone, is given by:

$$\left\{\begin{array}{c}{}^{k+1}y_1^i\cong tan{}^k\theta _1^i·\Delta t+{}^{k}y_1^i\\ {}^{k+1}y_2^i\cong tan{}^k\theta _2^i·\Delta t+{}^{k}y_2^i\\ ⋮\\ {}^{k+1}y_n^i\cong tan{}^k\theta _n^i·\Delta t+{}^{k}y_n^i\end{array}\right.$$

(3)

where $tan{}^k\theta _j^i$ for $j=1,2,\cdots ,n$ are instantaneous derivative functions, according to the graphical notation shown in Figure 1. On the other hand, there is an attempt in [19] to prove mathematically that if you exchange the instantaneous derivatives in (3) for the mean derivatives, then the solution proposed by Leonard Euler becomes accurate, i.e.,

$$\left\{\begin{array}{c}{}^{k+1}y_1^i=ta{n}_{\Delta t}{}^k\alpha _1^i·\Delta t+{}^{k}y_1^i\\ {}^{k+1}y_2^i=ta{n}_{\Delta t}{}^k\alpha _2^i·\Delta t+{}^{k}y_2^i\\ ⋮\\ {}^{k+1}y_n^i=ta{n}_{\Delta t}{}^k\alpha _n^i·\Delta t+{}^{k}y_n^i\end{array}\right.$$

(4)

Comparing Equations (3) and (4), it is observed that the instantaneous derivative functions do not depend on the integration step, but the mean derivative functions do. Additionally, the equations in (4) can also be expressed in a more compact notation, given by:

$${}^{k+1}y^i=ta{n}_{\Delta t}{}^k\alpha ^i·\Delta t+{}^{k}y^i$$

(5)

where ${}^{k+1}y^i=$[${}^{k+1}y_1^i$ ${}^{k+1}y_2^i$⋯${}^{k+1}y_n^i$${]}^T$, $ta{n}_{\Delta t}{}^k\alpha ^i=$[$ta{n}_{\Delta t}{}^k\alpha _1^i$ $ta{n}_{\Delta t}{}^k\alpha _2^i$⋯$ta{n}_{\Delta t}{}^k\alpha _n^i$${]}^T$ e ${}^{k}y^i=$[${}^{k}y_1^i$ ${}^{k}y_2^i$⋯${}^{k}y_n^i$${]}^T$. The generalization of the mean derivatives methodology to multiple backward inputs and/or multiple forward outputs is relatively easy. This expression can be obtained by the following equation:

$${}^{k+p}y_j^i=\sum _{m=0}^{p-1}ta{n}_{\Delta t}{}^{k+m}\alpha _j^i·\Delta t+{}^{k}y_j^i$$

(6)

where p is the number of backward and/or forward instants and $j=1,2,\cdots ,n$. For example, if $p=$$p_1+p_2$ then it is possible to design an E–TUNI with $p_1$ inputs in the role of backward mean derivatives and $p_2$ outputs in the role of forward mean derivatives. In this way, the reader is free to choose the values of $p_1$ and $p_2$ as long as the previous equality is satisfied. However, it should be noted that the first input of the neural network must be an absolute value, not a relative one.

On the other hand, notice that if the reader tries to compare the NARMAX model with the E–TUNI structure, one can see that the former is very similar to the latter. In the NARMAX model, for example, the output of the universal approximator of functions is the forward instant $y_j(t+\Delta t)$. However, in the E-TUNI model, the output of the universal approximator of functions is the mean derivative function $ta{n}_{\Delta t}{}^k\alpha _j^i$ at the present instant. This description is the only practical difference between these two methodologies. However, the E-TUNI may be a little more computationally efficient than the NARMAX model, as explained in the following paragraph.

Considering the direct approach to training the mean derivative functions required by the E–TUNI structure, it is then possible to perform a theoretical analysis of the local error committed by this first-order universal numerical integrator. Thus, let the exact value ${}^{k+1}\overline{y}_j^i$ and the estimated value ${}^{k+1}\widehat{y}_j^i$ be obtained, respectively, by Equations (7) and (8) of a given solution of a generic dynamical system.

$${}^{k+1}\overline{y}_j^i=ta{n}_{\Delta t}{}^k\alpha _j^i·\Delta t+{}^{k}y_j^i$$

(7)

$${}^{k+1}\widehat{y}_j^i=(ta{n}_{\Delta t}{}^k\alpha _j^i\pm e_m)·\Delta t+{}^{k}y_j^i$$

(8)

where $e_m$ is the mean absolute error of the output variables of the universal approximator of functions used to learn the mean derivative functions. Thus, if Equation (7) is subtracted from Equation (8) and the result of this subtraction is squared, we have:

$${\left(\begin{array}{c}{}^{k+1}\overline{y}_j^i-{}^{k+1}\widehat{y}_j^i\end{array}\right)}^2={\Delta t}^2·e_m^2$$

(9)

Equation (9) states that the local squared error made by E–TUNI can dampen the squared error of training the universal approximator of functions, used in neural training; if $0<\Delta t<1$. If $\Delta t>1$, the local error will be amplified. However, for a more accurate analysis of the global training error, further studies are needed.

Equation (9) is fundamental, as it partially explains why training the E–TUNI with a mean square error $e_m^2$, greater than that obtained by training the NARMAX model can also yield good results from estimation and potentially surpass those obtained in the NARMAX methodology. However, as stated earlier, this is true only if $\Delta t<1$. Finally, an E–TUNI neural integrator can be used for supervised training of a generic plant.

5.2. Predictive Control Designed with E–TUNI

In a typical neural predictive control scheme, a feed-forward neural network can be trained to learn a discrete E-TUNI model. This discrete model can then be used as an internal response model to obtain smooth control actions that are capable of tracking a reference trajectory by minimizing a quadratic functional of the following form [16,25]:

$$\begin{array}{c}J=\{{\displaystyle \sum _{j=1}^m}{[y_r\left(t_j\right)-\widehat{y}\left(t_j\right)]}^T·r_y^{-1}\left(t\right)·[y_r\left(t_j\right)-\widehat{y}\left(t_j\right)]+\\ {\displaystyle \sum _{j=0}^{m-1}}{[u\left(t_j\right)-u\left(t_{j-1}\right)]}^T·r_u^{-1}\left(t\right)·[u\left(t_j\right)-u\left(t_{j-1}\right)]\}/2\end{array}$$

(10)

where $y_r\left(t_j\right)$ is the reference trajectory at the instant $t_j$, m is the number of horizons ahead, $r_y^{-1}\left(t_j\right)$ and $r_u^{-1}\left(t_j\right)$ are positive definite weight matrices, and $\widehat{y}\left(t_j\right)$ is the output of the previously trained E–TUNI. Thus, in [25] it is shown that it is necessary to know the partial derivatives ${\displaystyle \frac{\partial {}^{k+q}y^i}{\partial {}^{k}u}}$ to solve the problem of optimization given by the equation iteratively (10) through the Kalman filter. Also, in [25] these partial derivatives can be calculated as follows:

$${\displaystyle \frac{{\partial }^{k+q}{y}^i}{{\partial }^{k}u}}=\left(\begin{array}{c}{\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }^i}{{\partial }^{k+q-1}{y}^i}}·\Delta t+I\end{array}\right)·{\displaystyle \frac{{\partial }^{k+q-1}{y}^i}{{\partial }^{k}u}}$$

(11)

$$toq=2,3,...,m$$

where

$${\left[\begin{array}{c}{\displaystyle \frac{{\partial }^{k+q-1}{y}^i}{{\partial }^{k}u}}\end{array}\right]}_{n_y\times n_u}=$$

$$\Delta t·\left[\begin{array}{cccc}{\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-2}{\alpha }_1^i}{{\partial }^k{u}_1}}& {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-2}{\alpha }_1^i}{{\partial }^k{u}_2}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-2}{\alpha }_1^i}{{\partial }^k{u}_{n_u}}}\\ {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-2}{\alpha }_2^i}{{\partial }^k{u}_1}}& {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-2}{\alpha }_2^i}{{\partial }^k{u}_2}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-2}{\alpha }_2^i}{{\partial }^k{u}_{n_u}}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-2}{\alpha }_{n_y}^i}{{\partial }^k{u}_1}}& {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-2}{\alpha }_{n_y}^i}{{\partial }^k{u}_2}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-2}{\alpha }_{n_y}^i}{{\partial }^k{u}_{n_u}}}\end{array}\right]$$

(12)

$${\left[\begin{array}{c}{\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }^i}{{\partial }^{k+q-1}{y}^i}}\end{array}\right]}_{n_y\times n_y}=$$

$$\left[\begin{array}{cccc}{\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }_1^i}{{\partial }^{k+q-1}{y}_1^i}}& {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }_1^i}{{\partial }^{k+q-1}{y}_2^i}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }_1^i}{{\partial }^{k+q-1}{y}_{n_y}^i}}\\ {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }_2^i}{{\partial }^{k+q-1}{y}_1^i}}& {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }_2^i}{{\partial }^{k+q-1}{y}_2^i}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }_2^i}{{\partial }^{k+q-1}{y}_{n_y}^i}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }_{n_y}^i}{{\partial }^{k+q-1}{y}_1^i}}& {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }_{n_y}^i}{{\partial }^{k+q-1}{y}_2^i}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^{k+q-1}{\alpha }_{n_y}^i}{{\partial }^{k+q-1}{y}_{n_y}^i}}\end{array}\right]$$

(13)

$${\left[\begin{array}{c}{\displaystyle \frac{{\partial }^{k+1}{y}^i}{{\partial }^{k}u}}\end{array}\right]}_{n_y\times n_u}=$$

$$\Delta t·\left[\begin{array}{cccc}{\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_1^i}{{\partial }^k{u}_1}}& {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_1^i}{{\partial }^k{u}_2}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_1^i}{{\partial }^k{u}_{n_u}}}\\ {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_2^i}{{\partial }^k{u}_1}}& {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_2^i}{{\partial }^k{u}_2}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_2^i}{{\partial }^k{u}_{n_u}}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_{n_y}^i}{{\partial }^k{u}_1}}& {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_{n_y}^i}{{\partial }^k{u}_2}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_{n_y}^i}{{\partial }^k{u}_{n_u}}}\end{array}\right]$$

(14)

In Equations (11)–(14), we have that $n_y=n$ is the total number of state variables and $n_u$ is the total number of control variables. Furthermore, to derive these equations, it was assumed that the neural network, which learns the mean derivative functions, was designed with only one backward input for the state and control variables, and also only one forward output for the mean derivatives.

So, for example, if a neural network with an MLP architecture is used, the calculation of the partial derivatives, necessary for the use of the gradient training algorithm, can be obtained as follows [25]:

$$\begin{array}{c}{\left[\begin{array}{cccc}ta{n}_{\Delta t}{}^k\alpha _1^i,& ta{n}_{\Delta t}{}^k\alpha _2^i,& \cdots ,& ta{n}_{\Delta t}{}^k\alpha _{n_y}^i\end{array}\right]}^T=\\ f_{NN}^{MLP}={\left[\begin{array}{ccccc}{y}_1\left(t\right),\cdots ,& y_{n_y}\left(t\right),& u_1\left(t\right),& \cdots ,& u_{n_u}\left(t\right)\end{array}\right]}^T\end{array}$$

(15)

where

$${\displaystyle \frac{\partial y^l}{\partial {\overline{y}}^k}}={\displaystyle \frac{\partial y^l}{\partial {\overline{y}}^{k+1}}}·W^{k+1}·I_{f^{\prime }\left({\overline{y}}^k\right)}tok=l-1,l-2,\cdots ,1$$

$${\displaystyle \frac{\partial y^l}{\partial {\overline{y}}^l}}=I_{f^{\prime }\left({\overline{y}}^l\right)}$$

$$I_{f^{\prime }\left({\overline{y}}^l\right)}=\left[\begin{array}{cccc}{I}_{f^{\prime }\left({\overline{y}}_1^l\right)}& 0& \cdots & 0\\ 0& I_{f^{\prime }\left({\overline{y}}_2^l\right)}& \cdots & 0\\ 0& 0& \ddots & 0\\ 0& 0& \cdots & I_{f^{\prime }\left({\overline{y}}_{n_k}^l\right)}\end{array}\right]$$

It is essential to note that l is a generic layer of the MLP network. So $y^l$ are the output values of the l layer, and when l is the last layer, then these outputs necessarily are the mean derivative functions. The $f^{\prime }(·)$ functions can be any sigmoid function. Furthermore, if another neural architecture is used, for example, RBF networks or Wavelets, it will only change Equation (15). Equations (11)–(14) remain unchanged. The reason for this is that the equations from (11)–(14) refer exclusively to the type of integrator used, which, in this case, is necessarily the E–TUNI.

On the other hand, Equation (15) refers exclusively to the type of feed-forward neural network used, which, in this case, is necessarily the MLP network. Thus, Equation (15) is nothing more than an iterative version of the back-propagation algorithm, which calculates the partial derivatives from the output of the MLP network, concerning its inputs and not concerning the synaptic weights.

It is also worth noticing that, to fully understand the equations from (11)–(14), it is convenient to consult the references [25], as it is necessary to make a temporal chain of several first-order Euler integrators, which work exclusively with mean derivative functions. This fact is because the horizon m has, in general, temporal advances in an amount greater than the total number of delayed inputs of the E–TUNI used.

Thus, the determination of predictive control actions can be treated as a stochastic parameter estimation problem, if the minimization of the functional of Equation (10) is viewed as the following stochastic problem:

$$y_r\left(t_j\right)=\widehat{y}\left(t_j\right)+v_y\left(t_j\right)$$

(16)

$$0=u\left(t_{j-1}\right)-u\left(t_{j-2}\right)+v_u\left(t_{j-1}\right)$$

(17)

$$E\left[v_y\left(t_j\right)\right]=0,E[v_y\left(t_j\right).v_y^T\left(t_j\right)]=r_y\left(t_j\right)$$

(18)

$$E\left[v_u\left(t_j\right)\right]=0,E[v_u\left(t_j\right).v_u^T\left(t_j\right)]=r_u\left(t_j\right)$$

(19)

with $j=1,2,\cdots ,m$ and $\widehat{y}\left(t_j\right)$ is the dynamics obtained through E-TUNI. To stochastically solve the equations from (16)–(19), an iterative approach is necessary, where in each iteration a perturbation is made to obtain a linear approximation of (16) and (17) through the Kalman filter. Thus, to solve the problem of Equation (16), a perturbation is performed to obtain a linear approximation of this same equation, as follows:

$$\alpha \left(i\right)·[y_r\left(t_j\right)-\overline{y}(t_j;i)]=\sum _{k=0}^{j-1}{[\partial \widehat{y}\left(t_j\right)/\partial u\left(t_k\right)]}_{\overline{u}(t_k;i)}·[u(t_k,i)-\overline{u}(t_k,i)]+v_y\left(t_j\right)$$

(20)

For a detailed knowledge of the equations of the Kalman filter, which solves this problem iteratively, see [25].

5.3. Correct Mathematical Demonstration of the E-TUNI General Expression

In this section, we formally demonstrate the general mathematical expression for E-TUNI, which is nothing more than a first-order Euler-type integrator that works with mean derivative functions. This development is done here because, as mentioned previously, there is a proof error in the general expression for E–TUNI presented in reference [16]. Furthermore, this proof will be summarized, as it has already been extensively detailed in [19]. Therefore, the starting point is Figure 3.

So, for the reader to understand this figure, we explain it, starting from the point ${}^{k}y_j^i$. The point ${}^{k}y_j^i$ is an instant of the solution of the considered autonomous dynamic system. The variable j means the $j-th$ state variable of the considered dynamic system, where $j=1,2,\cdots ,n$, that is, there are a total of n state variables. The variable i represents the $i-th$ curve of the family of curves confined in the interval $[y_j^{min}\left(t_0\right),$$y_j^{max}\left(t_0\right)]$ and which is the solution of the considered dynamic system. By the continuum hypothesis, one can have infinite curves ($i=1,2,\cdots ,\infty$). The variable k represents the k-th instant of time, that is, $t^k=t_0+k·\Delta t$. In the case of the variable k, if the dynamical system solution does not come out of the region of interest [$y_j^{min}\left(t_0\right),$$y_j^{max}\left(t_0\right)$] and the system is autonomous, then the variable k can also go to infinity ($k=1,2,\cdots ,\infty$). Also, when we write $y_j^i\left(t_k^x\right)$ or $y_j^i\left(t_k^{*}\right)$ it means that $t_k<t_k^x<t_{k+1}$ and $t_k<t_k^{*}<t_{k+1}$.

This notation for ${}^{k}y_j^i$ is sufficient to uniquely map it to its respective region of interest, where its associated secant characteristic $ta{n}_{\Delta t}{}^k\alpha _j^i$ is confined. So, in this case, for example, we can say that for the state ${}^{k}y_j^i=y_j^i(t_0+k·\Delta t)$ we have its associated characteristic secant given by $ta{n}_{\Delta t}{}^k\alpha _j^i$.

Thus, the secant $ta{n}_{\Delta t}{}^k\alpha _j^i$ is associated with the state variable $y_j$ with a curve i specific to the family of solutions, in this case, by $y_j^i\left(t\right)$ and the instant $t_k$. The fact that the secant is associated with the instant $t_k$ means that it is confined to the closed interval $[t_k,t_{k+1}]$. Thus, the secant $ta{n}_{\Delta t}{}^k\alpha _j^i$ starts at $t_k$ and ends at $t_{k+1}$.

Furthermore, the states $y_j^i\left(t_k^x\right)$ and $y_j^i\left(t_k^{*}\right)$ are special states, where both $t_k^x$ and $t_k^{*}$ are also confined to the closed interval $[t_k,t_{k+1}]$. The instants $t_k^x$ and $t_k^{*}$ are directly associated, respectively, with the integral mean value theorem and the differential mean value theorem [26]. So, having made these preliminary considerations, we begin now with this demonstration in a precise manner. Thus, let the following autonomous system of non-linear differential equations be given by:

$$\dot{y}=f\left(y\right)$$

(21)

$$y={\left[\begin{array}{cccc}{y}_1& y_2& \cdots & y_n\end{array}\right]}^T$$

(22)

$$f\left(y\right)={\left[\begin{array}{cccc}{f}_1\left(y\right)& f_2\left(y\right)& \cdots & f_n\left(y\right)\end{array}\right]}^T$$

(23)

Consider also, by definition, $y_j^i=y_j^i\left(t\right)$ for $j=1,2,$$\cdots ,n$ a particular trajectory for a family of solutions to the system of differential equations $\dot{y}=f\left(y\right)$ passing through $y_j^i\left(t_0\right)$ at instant $t_0$, i.e., initializing from a domain of interest $[y_j^{min}\left(t_0\right),$$y_j^{max}\left(t_0\right){]}^n$, where $y_j^{min}\left(t_0\right)$ and $y_j^{max}\left(t_0\right)$ are finite. It is also appropriate to introduce the following vector notation over (21):

$$y_0^i=y^i\left(t_0\right)={\left[\begin{array}{cccc}{y}_1^i\left(t_0\right)& y_2^i\left(t_0\right)& \cdots & y_n^i\left(t_0\right)\end{array}\right]}^T$$

(24)

$$y^i=y^i\left(t\right)={\left[\begin{array}{cccc}{y}_1^i\left(t\right)& y_2^i\left(t\right)& \cdots & y_n^i\left(t\right)\end{array}\right]}^T$$

(25)

In [26], by definition, the secant curve between two points ${}^{k}y_j^i$ and ${}^{k+1}y_j^i$ belonging to the curve $y_j^i\left(t\right)$ to $j=1,2,\cdots ,n$ is the line segment joining these two points. Thus, the tangents of the secants between the points ${}^{k}y_1^i$ and ${}^{k+1}y_1^i$, ${}^{k}y_2^i$ and ${}^{k+1}y_2^i$, ⋯, ${}^{k}y_n^i$ and ${}^{k+1}y_n^i$ are defined as:

$$ta{n}_{\Delta t}{\alpha }^i(t+k·\Delta t)=ta{n}_{\Delta t}{}^k\alpha ^i=$$

$${\left[\begin{array}{cccc}ta{n}_{\Delta t}{}^k\alpha _1^i& ta{n}_{\Delta t}{}^k\alpha _2^i& \cdots & ta{n}_{\Delta t}{}^k\alpha _n^i\end{array}\right]}^T$$

(26)

with,

$$ta{n}_{\Delta t}{}^k\alpha _j^i={\displaystyle \frac{{}^{k+1}y_j^i-{}^{k}y_j^i}{\Delta t}}$$

(27)

for $j=1,2,\cdots ,n$. Thus, we can now state the two fundamental theorems to consolidate our proof. These two theorems are the differential mean value theorem and the integral mean value theorem, which are presented below without proof [26].

Theorem 1

(The Differential Mean Value Theorem). If a function $g_j^i\left(t\right)$ for $j=1,2,\cdots ,n$ is a continuous function and defined over the closed interval $[t_k,t_{k+1}]$ is differentiable over the open interval $(t_k,t_{k+1})$, then there is at least one number $t_k^{*}$ with $t_k<t_k^{*}<t_k+\Delta t=t_{k+1}$, such that

$${\dot{g}}_j^i\left(t_k^{*}\right)={\displaystyle \frac{{}^{k+1}g_j^i-{}^{k}g_j^i}{\Delta t}}$$

(28)

Theorem 2

(The Integral Mean Value Theorem). If a function $g_j^i\left(t\right)$ for $j=1,2,\cdots ,n$ is a continuous function and defined over the closed interval $[t_k,t_{k+1}]$, then there is at least one inner point $t_k^x$ in $[t_k,t_{k+1}]$, such that

$$g_j^i\left(t_k^x\right)·\Delta t={\int }_{t_k}^{t_{k+1}}{g}_j^i\left(t\right)dt$$

(29)

It is important to note that, generally, $t_k^{*}$ is different from $t_k^x$. Also, the mean value theorems say nothing about how to determine the values of $t_k^{*}$ and $t_k^x$. These two theorems simply state that $t_k^{*}$ and $t_k^x$ are confined to the closed interval $[t_k,t_{k+1}]$.

Property 1.

Applying Theorem 2 on the curve ${\dot{g}}_j^i\left(t\right)$ is equivalent to applying Theorem 1 on the curve $g_j^i\left(t\right)$ both on the same interval closed $[t_k,t_{k+1}]$, that is, ${\dot{g}}_j^i\left(t_k^x\right)={\dot{g}}_j^i\left(t_k^{*}\right)$.

Proof. 

It is detailed in reference [19]. □

Principle 1.

Given the non-linear autonomous dynamic system ${\dot{y}}_j^i=$$f_j(y_1^i,y_2^i,\cdots ,y_n^i)$$=f_j\left(y^i\right)$ and their respective general solutions $y_j^i\left(t\right)=g_j^i\left(t\right)$ for $j=1,2,\cdots ,n$ and $i=1,2,\cdots ,\infty$, then the autonomous instantaneous derivative functions $f_j\left(y^i\right)$ can be replaced by the exclusively non-autonomous instantaneous derivative functions given by ${\dot{g}}_j^i\left(t\right)$, that is, $f_j(y_1^i,y_2^i,\cdots ,y_n^i)=$$f_j\left(y^i\right)=$${\dot{g}}_j^i\left(t\right)=$$h_j^i\left(t\right)$ for $j=1,2,\cdots ,n$ and $i=1,2,\cdots ,\infty$.

Proof. 

It is detailed in reference [19]. □

Theorem 3.

The discrete and exact general solution for the autonomous system of non-linear ordinary differential equations of the type ${\dot{y}}^i=f\left(y^i\right)$ can be established through the first-order Euler relation of the type ${}^{k+1}y_j^i=$$ta{n}_{\Delta t}{}^k\alpha _j^i·\Delta t$$+{}^{k}y_j^i$, for ${}^{k}y_j^i$ and $\Delta t$ fixed; since that the general solution of this dynamical system, given by, $y_j^i\left(t\right)=g_j^i\left(t\right)$ and ${\dot{y}}_j^i\left(t\right)={\dot{g}}_j^i\left(t\right)$ are, previously, known for $j=1,2,\cdots ,n$; $i=1,2,\cdots ,\infty$ and tϵ$[t_o,t_f]$. Furthermore, the solutions $g_j^i\left(t\right)$ for $j=1,2,\cdots ,n$ must all be continuous and differentiable. However, note that ${\dot{g}}_j^i\left(t\right)$ for $j=1,2,\cdots ,n$ is suffice to be continuous.

Proof. 

It is detailed quite clearly in reference [19]. This proof is consolidated using the theorems and principles described prior in this section. The initial starting point, to fully understand this demonstration, is to know the mapping described in Figure 3. □

Finally, the E–TUNI universal numerical integrator is suitable for solving only ordinary differential equations. However, it should be noted that the current use of neural networks in solving Partial Differential Equations (PDEs) is quite extensive [27,28,29,30,31,32,33,34,35]. Additionally, ref. [36] explains how to use the Runge–Kutta numerical integrator to solve partial differential equations (mainly hyperbolic ones). Therefore, using the E–TUNI to solve partial differential equations may be a good option for future work and should be investigated more carefully.

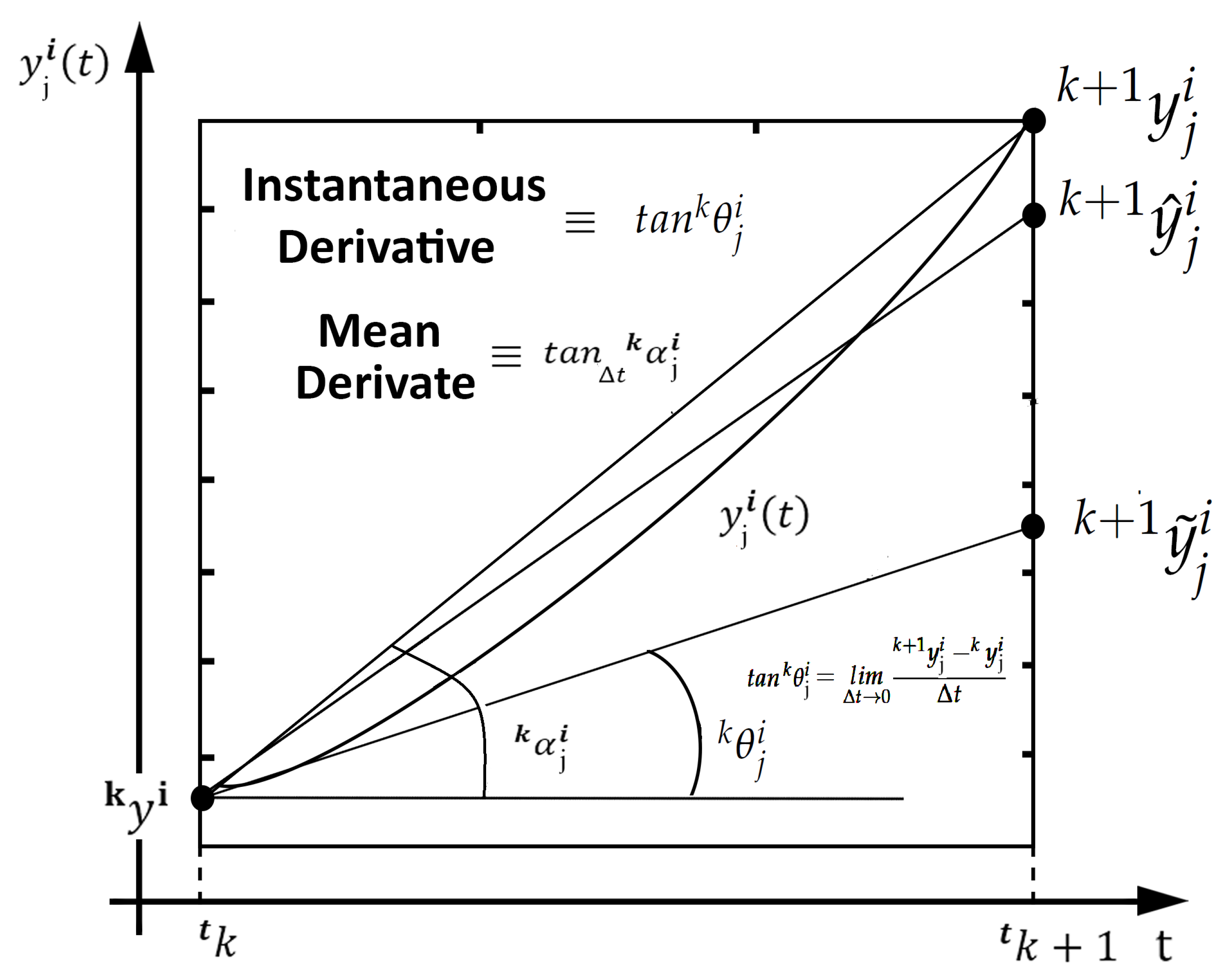
5.4. Mathematical Relationship Between Mean and Instantaneous Derivatives

A very remarkable fact is that it is possible to obtain an equation that relates the instantaneous derivative functions to the mean derivative functions. This equation can be easily obtained using the chain rule for functions on several independent variables [26]. In this way, two previously trained neural networks are known to represent the instantaneous and mean derivative functions, respectively, by:

$${\left[\begin{array}{cccc}{\dot{y}}_1\left(t\right),& {\dot{y}}_2\left(t\right),& \cdots ,& {\dot{y}}_{n_y}\left(t\right)\end{array}\right]}^T=$$

(30)

$${\left[\begin{array}{cccc}ta{n}^k{\theta }_1^i,& ta{n}^k{\theta }_2^i,& \cdots ,& ta{n}^k{\theta }_{n_y}^i\end{array}\right]}^T=$$

$$f_{NN}^{id}{\left[\begin{array}{ccccc}{y}_1\left(t\right),& y_2\left(t\right),& \cdots ,& y_{n_y}\left(t\right),& \widehat{w}\end{array}\right]}^T$$

and

$${\left[\begin{array}{cccc}ta{n}_{\Delta t}{}^k\alpha _1^i,& ta{n}_{\Delta t}{}^k\alpha _2^i,& \cdots ,& ta{n}_{\Delta t}{}^k\alpha _{n_y}^i\end{array}\right]}^T=$$

(31)

$$f_{NN}^{md}{\left[\begin{array}{ccccc}{y}_1\left(t\right),& y_2\left(t\right),& \cdots ,& y_{n_y}\left(t\right),& \widehat{w}\end{array}\right]}^T$$

For reasons of simplification, we do not consider the case using control variables in Equations (30) and (31). So, if we use the chain rule [26] in Equation (31) we get:

$${\displaystyle \frac{d}{dt}}ta{n}_{\Delta t}{}^k\alpha _j^i=$$

(32)

$${\displaystyle \frac{\partial ta{n}_{\Delta t}{}^k\alpha _j^i}{{\partial }^k{y}_1^i}}·{\displaystyle \frac{d^k{y}_1^i}{dt}}+\cdots +{\displaystyle \frac{\partial ta{n}_{\Delta t}{}^k\alpha _j^i}{{\partial }^k{y}_{n_y}^i}}·{\displaystyle \frac{d^k{y}_{n_y}^i}{dt}}=$$

$$\left[\begin{array}{ccc}{\displaystyle \frac{\partial ta{n}_{\Delta t}{}^k\alpha _j^i}{{\partial }^k{y}_1^i}},& \cdots ,& {\displaystyle \frac{\partial ta{n}_{\Delta t}{}^k\alpha _j^i}{{\partial }^k{y}_{n_y}^i}}\end{array}\right]·\left[\begin{array}{c}{\displaystyle \frac{d^k{y}_1^i}{dt}}\\ ⋮\\ {\displaystyle \frac{d^k{y}_{n_y}^i}{dt}}\end{array}\right]=$$

$$\left[\begin{array}{ccc}{\displaystyle \frac{\partial ta{n}_{\Delta t}{}^k\alpha _j^i}{{\partial }^k{y}_1^i}},& \cdots ,& {\displaystyle \frac{\partial ta{n}_{\Delta t}{}^k\alpha _j^i}{{\partial }^k{y}_{n_y}^i}}\end{array}\right]·\left[\begin{array}{c}ta{n}^k{\theta }_1^i\\ ⋮\\ ta{n}^k{\theta }_{n_y}^i\end{array}\right]=$$

$${\displaystyle \frac{\partial ta{n}_{\Delta t}{}^k\alpha _j^i}{{\partial }^k{y}^i}}\circ ta{n}^k{\theta }^{i}toj=1,2,\cdots ,n_y$$

For the sake of simplicity, we can represent the expression (32) as follows:

$$ta{n}_{\Delta t}^k{\Psi }_j^i={\displaystyle \frac{d}{dt}}ta{n}_{\Delta t}{}^k\alpha _j^i={\displaystyle \frac{\partial ta{n}_{\Delta t}{}^k\alpha _j^i}{{\partial }^k{y}^i}}\circ ta{n}^k{\theta }^i$$

(33)

$$toj=1,2,\cdots ,n_y$$

The operator ∘ is just the usual dot product applied over a Euclidean space. So, just for completeness, the vector form of Equation (33) can also be expressed by:

$${\displaystyle \frac{d}{dt}}ta{n}_{\Delta t}{}^k\alpha ^i={\displaystyle \frac{\partial ta{n}_{\Delta t}{}^k\alpha ^i}{{\partial }^k{y}^i}}·ta{n}^k{\theta }^i$$

(34)

where

$${\displaystyle \frac{d}{dt}}ta{n}_{\Delta t}^k{\alpha }^i=\left\{\begin{array}{c}{\displaystyle \frac{d}{dt}}ta{n}_{\Delta t}^k{\alpha }_1^i\\ {\displaystyle \frac{d}{dt}}ta{n}_{\Delta t}^k{\alpha }_2^i\\ ⋮\\ {\displaystyle \frac{d}{dt}}ta{n}_{\Delta t}^k{\alpha }_{ny}^i\end{array}\right\}$$

(35)

$${\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }^i}{{\partial }^k{y}^i}}=\left[\begin{array}{ccc}{\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_1^i}{{\partial }^k{y}_1^i}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_1^i}{{\partial }^k{y}_{n_y}^i}}\\ {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_2^i}{{\partial }^k{y}_1^i}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_2^i}{{\partial }^k{y}_{n_y}^i}}\\ ⋮& \ddots & ⋮\\ {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_{n_y}^i}{{\partial }^k{y}_1^i}}& \cdots & {\displaystyle \frac{\partial ta{n}_{\Delta t}^k{\alpha }_{n_y}^i}{{\partial }^k{y}_{n_y}^i}}\end{array}\right]$$

(36)

$$ta{n}^k{\theta }^i=\left\{\begin{array}{c}ta{n}^k{\theta }_1^i\\ ta{n}^k{\theta }_2^i\\ ⋮\\ ta{n}^k{\theta }_{n_y}^i\end{array}\right\}$$

(37)

There is an essential fact between instantaneous and mean derivative functions. Using these two kinds of derivative functions, that is, $ta{n}^k{\theta }^i$ and $ta{n}_{\Delta t}^k{\alpha }^i$, it is possible to interpolate a parabola between the discrete interval $[t_k,t_{k+1}]$, which passes at least at two precise points of the exact solution of the considered non-linear dynamical system, in this same interval. Thus,

Table 1. Coordinate points within the interval $[t_k,t_{k+1}]$.

n	Time	$\mathit{y}\left(\mathit{t}\right),$ $\dot{\mathit{y}}\left(\mathit{t}\right)$ and $\ddot{\mathit{y}}\left(\mathit{t}\right)$	Determining Form
1	$t_k$	${}^{k}y_j^i$	Initial Instant
2	$t_{k+1}$	${}^{k+1}y_j^i$	Given by E-TUNI
3	$t_k^x$	${\dot{y}}_j^i\left(t_k^x\right)=ta{n}_{\Delta t}{}^k\alpha _j^i$	Output of net
4	$t_k^x$	${\ddot{y}}_j^i\left(t_k^x\right)=ta{n}_{\Delta t}{}^k\Psi _j^i$	From Equations (33) or (34)

considers the points used to perform this parabolic interpolation, and Equations (39)–(41) are the coefficients of the parabola (38).

$${}^{k}y_j^i\left(t\right)={\alpha }_k·t^2+{\beta }_k·t+{\gamma }_k$$

(38)

$${\alpha }_k={\displaystyle \frac{1}{2}}·ta{n}_{\Delta t}{}^k\Psi _j^i$$

(39)

$${\beta }_k=ta{n}_{\Delta t}{}^k\alpha _j^i-{\displaystyle \frac{1}{2}}·(t_{k+1}+t_k)·ta{n}_{\Delta t}{}^k\Psi _j^i$$

(40)

$${\gamma }_k={\displaystyle \frac{1}{2}}·(t_k·t_{k+1}·ta{n}_{\Delta t}{}^k\Psi _j^i-2·t_k·ta{n}_{\Delta t}{}^k\alpha _j^i+2{·}^k{y}_j^i)$$

(41)

where $tϵ[t_k,t_{k+1}].$

6. Results and Analysis

In this article, we perform a complete computational numerical analysis, studying the training of the neural integration structures discussed in the previous sections, i.e., the E–TUNI. Thus, for all the experiments that are presented below, it was standardized to use MLP neural networks with the traditional back-propagation [4] and Kalman filter [37,38,39] training algorithms in Example 2 and the Levenberg–Marquardt [40] training algorithm in Examples 3 and 4. All experiments were trained using only one inner layer in the MLP network.

Example 1.

Check the validity of Principle 1 for the dynamical system $\dot{y}=f\left(y\right)=y^2$.

Proof. 

From $\dot{y}={\displaystyle \frac{dy}{dt}}=y^2$, then, ${\int }_{y\left(t_0\right)}^{y\left(t\right)}{y}^{-2}dy={\int }_{t_o}^{t}dt$, as a result of the fundamental theorem of calculus. Solving this integral analytically results in $y\left(t\right)={\displaystyle \frac{y\left(t_0\right)}{-y\left(t_0\right)t+y\left(t_0\right)t_0+1}}$. Differentiating the function $y\left(t\right)$, with respect to time t, we have that $\dot{y}=\dot{g}\left(t\right)$ = $y\left(t_0\right){\displaystyle \frac{d}{dt}}{[-y\left(t_0\right)t+y\left(t_0\right)t_0+1]}^{-1}$ = ${\displaystyle \frac{y^2\left(t_0\right)}{{[-y\left(t_0\right)t+y\left(t_0\right)t_0+1]}^2}}$. Thus, replacing $y\left(t\right)$ in $\dot{y}=y^2$ results in $\dot{y}=f\left(y\right)=y^2=$${\left[\begin{array}{c}{\displaystyle \frac{y\left(t_0\right)}{-y\left(t_0\right)t+y\left(t_0\right)t_0+1}}\end{array}\right]}^2$$=\dot{g}\left(t\right)$. □

The graph in Figure 4 illustrates the drawing of the function $y\left(t\right)$ (upper part) and the drawing of the function $\dot{y}\left(t\right)$ (lower part). For a proper understanding of the graphs in Figure 4, it should be noted that $t_0=0$, and there are seven curves in the graphs of Figure 4 representing the solution family of Example 1. For example, in $y\left(t_0\right)=y\left(0\right)=1$ a particular solution of the dynamical system $\dot{y}=y^2$ that have a vertical asymptote at $t=1$ (upper part of Figure 4). Note that, to the left of this asymptote, the solution of the dynamical system has been plotted in blue. On the other hand, to the right of this asymptote, the solution has been plotted in red. This convention is followed to plot the remaining solutions that appear in Figure 4. It is also important to note that the blue curves have distinct vertical asymptotes for each of the initial conditions. On the other hand, all red curves have horizontal asymptotes at $y=0$, when t tends to infinity.

Note that Principle 1 is valid for discontinuous solutions in $y\left(t\right)$. However, the use of the general expression of E–TUNI to learn this discontinuous solution is not possible according to the theory presented in this article. The reasons for this impossibility are as follows: (i) the integral and differential mean value theorems require that the E–TUNI solution be continuous and differentiable, and (ii) E–TUNI would have to learn a numerical value equal to infinity, at the points of the vertical asymptotes shown in Figure 4 (upper part), and this is impossible, as conventional computers have finite memory. For the use of E–TUNI, in examples like this further studies are required.

Example 2.

Solve the predictive control problem, necessarily using E–TUNI as a model of the non-linear plant, for the system of non-linear ordinary differential equations, which describes the Earth/Mars orbit transfer dynamics for a rocket of mass $m_r$, as shown in Figure 5. Solve this problem for two different horizons, that is, $m=1$ and $m=20$, according to Equations (10)–(20). The set of ordinary differential equations describing this problem is given below [24,25]:

$$\begin{array}{c}\dot{m_r}=-0.0749\\ \dot{r}=w\\ \dot{w}={\displaystyle \frac{v^2}{r}}-{\displaystyle \frac{\mu }{r^2}}+{\displaystyle \frac{T·sin\theta }{m}}\\ \dot{v}={\displaystyle \frac{-w·v}{r}}+{\displaystyle \frac{T·cos\theta }{m}}\end{array}$$

(42)

An illustrative scheme of this dynamic system can be seen in Figure 5. So, the state variables for this predictive control problem are $m_r$ (rocket mass), r (orbit radius), w (radial velocity), and v (transverse velocity). The only controlling variable is the thrust angle $\theta$ of the rocket. The normalized constants of this problem are $\mu =1.0$ (gravitational constant), $T=0.1405$ (rocket thrust), $t_o=0$ (initial instant), and $t_f=3.3$ (final instant). In this problem, the unit of the time variable t adopted is equal to 58.2 days; that is, for example, in Figure 6 each unit of time (time variable is normalized) is equal to 58.2 days.

We trained the E–TUNI using an MLP network with only one inner layer. This inner layer contained 41 neurons and one bias neuron. We applied the hyperbolic tangent activation function in the inner layer, while we used a purely linear activation function at the network output. The training and testing yielded Mean Square Errors (MSEs) of $9.021\times {10}^{-6}$ and $1.067\times {10}^{-5}$, respectively.

In the neural training of the E–TUNI structure, two standard training algorithms were used: the classic back-propagation [4] and the Kalman filter with recursive and parallel processing [39]. They have been casually changed. In addition, this training took a considerable amount of time, as a shallow architecture network was used instead of a deep architecture network.

Figure 6 presents the trajectory traced by the Kalman filter for a predictive control structure whose plant model was obtained through E–TUNI. The solid line is the reference trajectory, and the dotted line is the trajectory tracked by the Kalman filter. Figure 7 presents the control estimated by the Kalman filter in a predictive control structure designed according to Equations (10)–(20) and associated with the trajectory traced in Figure 6. However, the Kalman filter equations employed were taken from [25]. The integration step used was $\Delta t=0.1$ and the horizon equal to $m=1$. As can be seen, the estimated control was not very good for just using one horizon in Equation (10).

On the other hand, Figure 8 and Figure 9 present the same E–TUNI structure as in the previous case, but now in a new control estimating with the horizon used equally to $m=20$ (see Equation (10)). Note that this small change significantly improved the result obtained. However, while the training time for a horizon of $m=1$ may only take between an hour or two, the training time for a horizon of $m=20$ can be as long as ten days, if the integration step is changed from $\Delta t=0.1$ to $\Delta t=0.01$. For a better understanding of E–TUNI coupled to a predictive control structure, see reference [25].

Figure 6, Figure 7, Figure 8 and Figure 9 are an original extension of what can be found in [25]. In [25], the predictive control structure with E–TUNI for reference trajectories displaced from the initial condition was not explored, as presented here. Similar behavior for the other state variables m, w, and v was observed. Therefore, we have omitted the other graphics due to space constraints.

Figure 10 and Figure 11 were taken from [16] (see page 149 and Figure 6.11). They represent the application of a predictive control structure on the E–TUNI, for the case where a deviation between the reference trajectories and the initial condition of the dynamic system in question was not imposed. However, note that an integration step of $\Delta t=0.01$ and a horizon of $m=10$ was used. Note also that the 10-fold reduction in the integration step, although it makes the algorithm much slower, manages to considerably refine the control policy obtained in Figure 11, compared to Figure 7 and Figure 9.

Example 3.

The non-linear simple pendulum is a second-order autonomous system given by $l·\ddot{\theta }+g·sin\theta =0$. Note that l and g are, respectively, the length of the pendulum and the local acceleration due to gravity. Here, we solve this problem by using E–TUNI for several different integration steps. Furthermore, for each of these integration steps we obtain the interpolating parabolas governed by the equations from (38)–(41).

To precisely understand the resolution of Example 3, we follow the following basic algorithm:

• Step 1. Generate the E-TUNI input/output training patterns through the Runge–Kutta 4-5 integrator, applied to the non-linear simple pendulum equation. Note that, as this dynamical system is a non-linear equation, its solution in the phase plane is not a perfect circle.
• Step 2. Use the Levenberg–Marquardt algorithm in the direct approach to training two distinct neural networks, namely: (i) a neural network to learn the instantaneous derivative functions and (ii) another neural network to learn the mean derivative functions.
• Step 3. Determine the vector ${\displaystyle \frac{d}{dt}}ta{n}_{\Delta t}{}^k\Psi ^i$ using the equations from (34)–(37). Just pay attention to the fact that the partial derivatives ${\displaystyle \frac{\partial }{{\partial }^k{y}^i}}ta{n}_{\Delta t}{}^k\alpha ^i$ were obtained numerically and not analytically. For this, a ${\Delta }^k{y}^i={10}^{-6}$ was used.
• Step 4. Determine the interpolating parabolas within a horizon of interest $[t_0,t_f]$ and with a step of $\Delta t$. For this, the equations from (38)–(41) were used recursively.
• Step 5. Compare the results obtained for different $\Delta t$ integration steps. Also, compare the solution of the interpolating parabolas with the mean derivative equations.
• Step 6. A summary of this algorithm is presented in Figure 12 and Figure 13.

To solve this problem effectively, all graphical simulation results will be displayed using an MLP neural network with only one inner layer (a shallow network). In the inner layer, the hyperbolic tangent sigmoid activation function was employed, while a purely linear function was used in the output of the neural network. The training algorithm used was the traditional Levenberg–Marquardt [40], which always employed the direct approach of E–TUNI, rather than the indirect approach. For that, MATLAB R2024b Update 1 (24.2.0.2740171) and its Neural Network Toolbox were used.

The dynamical system in question was trained within the finite domains $Do{m}^{\theta }=[-\pi /2,+\pi /2]$$rad$ and $Do{m}^{\dot{\theta }}=[-2,+2]$${\displaystyle \frac{rad}{s}}$. For all neural networks trained, 400 training patterns were used; $75\%$ of them were used for training, $15\%$ for validation, and $15\%$ for testing. All training has been standardized to be trained with exactly $10,000$ epochs.

Table 2. Summary of training performed for Example 3.

$\mathbf{\Delta }\mathit{t}$	MSE of Validation Patterns	Direct Approach
-	$2.5624\times {10}^{-11}$	Instantaneous Derivatives
$0.01$	$2.4351\times {10}^{-10}$	Mean Derivatives
$0.25$	$3.5268\times {10}^{-8}$	Mean Derivatives
$1.00$	$2.1592\times {10}^{-6}$	Mean Derivatives
$10.0$	$1.7520\times {10}^{-3}$	Mean Derivatives

summarizes the main results achieved in these training sessions.

Analyzing Table 2, it is observed that the greater the integration step $\Delta t$ used in the E-TUNI training, the greater the training error for the validation patterns. This fact experimentally confirms (9), which states that the integration step $\Delta t$ amplifies the Mean Squared Error (MSE) of E–TUNI training when it is greater than $1.00$.

However, the most interesting numerical results, concerning Example 3, are shown in Figure 12 and Figure 13. In Figure 12, the integration steps are decreased from top to bottom. Notice that when the integration step $\Delta t$ is equal to $10.0$, E–TUNI could not accurately learn the angular position prediction $\theta$ (see all blue points in Figure 12). With the integration steps $\Delta t$ equal to or less than $1.00$, E–TUNI was able to learn them perfectly. The reason for this is that multiple instances of E–TUNI training were carried out for the integration step $\Delta t$ equal to $10.0$, but the best result achieved was the one presented in Table 2, that is, $MSE=1.7520\times {10}^{-3}$, confirming, again, the validity of Equation (9) as a limiting factor for this method. The E–TUNI training, which involved integration steps $\Delta t$ equal to or less than $1.00$, was easily learned by the MLP neural networks in the first attempts.

Figure 13 also presents several simulation graphs with the integration steps $\Delta t$, used in the E–TUNI training, also decreasing from top to bottom. The dotted pink lines represent the true values of the dynamical system in question. The solid lines in blue represent the mean derivatives between two consecutive points. Continuous lines in red interpolate parabolas between two successive points. Note that, for tiny $\Delta t$ integration steps, the parabolic interpolation using mean and instantaneous derivatives functions, simultaneously, is quite accurate and relatively better than using E–TUNI alone.

Analyzing Figure 13 more closely, observe that the E–TUNI equation is equivalent to consecutive uniform rectilinear movements and with constant velocities equal to the mean derivatives (constant from interval to interval). On the other hand, the equations of the interpolating parabolas are consecutive equations of uniformly varied motions and with consecutive accelerations $ta{n}_{\Delta t}{}^k\Psi _j^i$ (also constant interval to interval).

Note also that uniformly varied motions (interpolating parabolas) allow at most one change of direction in their motion. However, uniform rectilinear motion (E–TUNI) does not. For this reason, it appears that interpolating parabolas are more accurate than mean derivative curves for tiny integration steps. Because neural networks are universal approximators of functions [2,5,6], the physical variables that can be used as input to E–TUNI can be any.

Additionally, the Euler integrator, designed exclusively with instantaneous derivative functions, is never able to achieve the equivalent precision of the Euler integrator, designed with mean derivative functions. This fact happens mainly if substantial integration steps are used.

Finally, it is only possible to use control variables (in the inputs of E–TUNI) to obtain the parabolic interpolations if the control variable remains with its constant value throughout the entire interval $[t_k,t_{k+1}]$. This property is only practical for control if the E–TUNI integration step is tiny and close to zero.

Example 4.

Solve the dynamical Lorenz equation involving deterministic chaos using three algorithms that use Universal Numerical Integrators (UNIs). These three algorithms are the NARMAX model, E–TUNI, and RKNN. Perform a comparative study of these three basic methodologies on UNIs. Equation (43) represents the dynamical system in question. In this simulation, use the default parameters $\sigma =10$, $\rho =28$, and $\beta =8/3$.

$$\begin{array}{c}{\dot{y}}_1=\sigma ·(y_2-y_1)\\ {\dot{y}}_2=y_1·(\rho -y_3)-y_2\\ {\dot{y}}_3=y_1·y_2-\beta ·y_3\end{array}$$

(43)

The Lorenz system, composed of three non-linear ordinary differential equations, was originally derived by Edward Lorenz in 1963 as a simplified model for studying atmospheric convection. This system exhibits the fundamental properties that define deterministic chaos.

Table 3. Learning performance comparison between NARMAX, E–TUNI, and RKNN neural training methods (Example 4).

	NARMAX	E–TUNI	RKNN
$e_m^2$ (Training)	$2.25\times {10}^{-8}$	$8.67\times {10}^{-6}$	$1.80\times {10}^{-6}$
$e_m^2$ (Validation)	$2.59\times {10}^{-8}$	$1.04\times {10}^{-5}$	$1.71\times {10}^{-6}$
$e_m^2$ (Testing)	$2.96\times {10}^{-8}$	$1.13\times {10}^{-5}$	$3.77\times {10}^{-6}$
$\Delta t$ (Training) [s]	0.01	0.01	Not applicable
$\Delta t$ (Simulation) [s]	0.01	0.01	0.01
Propagation Interval [s]	[0, 25]	[0, 25]	[0, 25]
Training Patterns	1600	1600	1600
Testing Patterns	400	400	400
Training Algorithm	LM	LM	LM
Hidden Layers (HLs)	1	1	1
Neurons	30	30	30
Activation Function	tansig	tansig	tansig
Learning Rate	0.2	0.2	0.2
Training Domain	$\underset{y_1}{[-20,20]}$, $\underset{y_2}{[-20,20]}$, $\underset{y_3}{[0,51]}$	same	same

presents the main training parameters for the experiment related to Example 4. As can be seen, the first three rows of Table 3 present the mean squared errors for training, validation, and testing, respectively. This table also has three columns of training data. The first column presents the training data for the NARMAX model, the second column presents the training data for E–TUNI, and the third column presents the training data for RKNN. All four experiment tables follow this same pattern.

Figure 14 presents the numerical solution of the Lorenz equation using the Runge–Kutta 4-5 algorithm with the instantaneous derivative functions given by Equation (43). This solution in red is used as a benchmark. Figure 15 compares the benchmark solution with the results obtained by the NARMAX, E–TUNI, and RKNN models. Note that all the hybrid models used had difficulty learning this dynamic. However, these models showed great versatility for future improvement using deep learning neural networks. The reason why models utilizing some UNI had trouble learning this dynamic equation is explained in the following paragraphs.

For an Artificial Neural Network (ANN) to learn the inherent dynamics of the Lorenz system and maximize its short-term prediction window, the Mean Squared Error (MSE) of training must be minimized. However, due to the property of extreme sensitivity to initial conditions—a phenomenon popularly known as the “Butterfly Effect”—no MSE value, no matter how small, will guarantee prediction accuracy over an infinite time horizon. Thus, the neural network becomes susceptible to the exact error amplification mechanism identified by Lorenz, which exemplifies the intrinsic limits to the predictability of chaotic systems. The necessity of a low MSE for this dynamic model is crucial, and its reasons and limitations can be elucidated in two main points:

(i) Exponential Error Amplification: In inherently chaotic systems, such as the Lorenz system, any modeling or estimation error, no matter how minute, is amplified exponentially over time. Consequently, to maximize the prediction horizon—defined as the time interval during which the prediction remains useful—it is essential to minimize the initial error to the maximum technically feasible extent. To illustrate, a training MSE on the order of ${10}^{-1}$ would result in an almost instantaneous divergence of predictions. An MSE of ${10}^{-3}$ would allow for a small number of predictive steps before divergence, while values on the order of ${10}^{-6}$ or ${10}^{-8}$, as achieved in the present study, provide a significantly longer prediction horizon.

(ii) Fundamental Limit of Predictability: Even achieving an exceptionally low training MSE, approaching machine precision, does not overcome the fundamental barrier imposed by the chaotic nature of the system. The inevitable failure of long-term prediction is not a deficiency of the Artificial Neural Network (ANN) architecture, but rather an intrinsic property of the system under study. Therefore, the objective of minimizing the MSE is not to enable perpetual prediction—a theoretical impossibility—but rather to extend the limit of the useful prediction horizon to its maximum.

7. Conclusions

This work presented the formulation of the Euler-Type Universal Numerical Integrator (E–TUNI), highlighting its structural simplicity and applicability to non-linear dynamics and predictive control problems. In addition to demonstrating its feasibility, the results obtained allow us to discuss some relevant implications. In particular, E–TUNI proves to be a competitive integrator in terms of accuracy, even while maintaining a first-order formulation, and can be naturally incorporated into model-based control schemes. This property suggests that the methodology can serve as a practical alternative to classical integrators in scenarios where algorithmic simplicity and low computational cost are decisive factors.

However, the analysis also reveals limitations. The main limitation is its dependence on the fixed integration step $\Delta t$, which necessitates retraining the neural network whenever it is altered. This characteristic reduces the flexibility of E–TUNI compared to instantaneous derivative methodologies (such as RKNN and PCNN). Furthermore, although experiments have indicated good performance on low- to medium-dimensional problems, the method’s scalability to higher-order dynamical systems has not yet been comprehensively evaluated, which remains an open question.

These limitations point to possible future extensions. First, adapting E–TUNI to variable-step schemes could broaden its applicability to systems with multiple dynamical regimes. Second, its integration with modern learning techniques, such as Physics-Informed Neural Networks (PINNs) or hybrid networks based on differential programming, could expand the method’s scope to more complex multidisciplinary problems, including bioengineering, astrodynamics, and quantitative finance. Finally, a formal stability and error analysis, accompanied by comparative studies with benchmark methods, represents an essential step toward consolidating E-TUNI as a tool for widespread use in the scientific community.

In summary, the results presented here demonstrate the potential of E–TUNI, but also make it clear that its consolidation as a methodological alternative will depend on further studies on stability, scalability, and integration with emerging machine learning techniques. The method should be understood not simply as a variation of the Euler scheme but also as a promising and extensible framework capable of inspiring new lines of research in universal numerical integration.