Abstract
CRISPR-Cas9 has emerged as a remarkably powerful gene editing tool and has advanced both research and gene therapy applications. Machine learning models have been developed to predict off-target cleavages. Despite progress, accuracy, stability, and interpretability remain open challenges. Combining predictive modeling with interpretability can provide valuable insights into model behavior and increase its trustworthiness. This study proposes a group-wise L1 regularization method guided by SHAP values. For the implementation of this method, the CRISPR-M model was used, and SHAP-informed regularization strengths were calculated and applied to features grouped by relevance. Models were trained on HEK293T and evaluated on K562. In addition to the CRISPR-M baseline, three variants were developed: L1-Grouped-Epigenetics, L1-Grouped-Complete, and L1-Uniform-Epigenetics (control). L1-Grouped-Epigenetics, using penalties split by on- and off-target epigenetic factors, moderately improved mean precision, AUPRC, and AUROC relative to the baseline, as well as showing reduced variability in precision and AUPRC across seeds, although its mean recall and F-metrics were slightly lower than those of CRISPR-M. L1-Grouped-Complete achieved the highest mean AUROC and Spearman correlation and presented lower variability than CRISPR-M for recall, F1, and F-beta, despite reduced recall and F-metrics relative to CRISPR-M. Overall, this approach required only minor architectural adjustments, making it adaptable to other models and domains. While results demonstrate potential for enhancing interpretability and robustness without sacrificing predictive performance, further validation across additional datasets is required.
1. Introduction
CRISPR-Cas9’s effectiveness and simplicity have established it in gene editing and therapeutic research. Off-target cleavages remain a major concern due to their potential to compromise genomic integrity and pose risks to patient safety [1,2,3]. This challenge is further complicated by several factors, including the noisy nature of biological mechanisms and the influence of epigenetic factors [4]. Deep learning models have been developed to help address this issue and make the application of CRISPR-Cas9 safer and more accurate, including CRISPR-M, which predicts off-target effects, with an epigenetically informed version achieving better performance than the versions without epigenetic data [5].
CRISPR-Cas9 datasets are often imbalanced, as the HEK293T and K562 datasets are [6,7], with far fewer positive samples (on-targets) than negative ones (off-targets) [8], making it challenging to maintain high performance and generalizability.
Despite its importance, interpretability is often overlooked, leading to the loss of critical insights in sensitive domains like gene editing [9,10,11,12,13]. Even though there are studies attempting to integrate interpretability into the training process of models, through validation loss, gradients, or attention mechanisms, these approaches often lack simplicity and flexibility, limiting their broader applications. Examples include loss-guided constraints on explanations [14,15], gradient or attention-based alignment [16], and SHAP-informed regularization of learning dynamics [17,18]. Several recent studies have explored attribution-based regularization strategies, utilizing feature importance (either directly or at the modality level) informed by interpretability considerations or domain knowledge and regulating the model through the loss function, aiming to align model representations or behaviors with attribution patterns [19,20,21,22].
Moreover, training fluctuations caused by randomness and certain regularization techniques can make model behavior inconsistent across runs, limiting reproducibility and interpretability [23,24,25]. The lack of reproducibility in biomedical AI can have direct and significant consequences for patient health, the validity of scientific findings, and the ethical advancement of the field [26].
Despite advances in deep learning, processing features without prioritization during training can limit model performance and overlook valuable signals, causing less control over the models’ behavior, inefficient debugging, and reduced trust. This highlights the need for models that combine interpretability, adaptability, and stability with strong performance, clear explanations, and more consistent training.
In this paper, we present an interpretability-informed group regularization method addressing the previously mentioned challenges, designed to integrate model interpretability into the training process. The method applied regularization by penalizing feature groups inversely to their importance, with groupings derived from structural and relational aspects of the data. Each group’s importance was used to assign a corresponding regularization strength, allowing stronger regularization in the less important groups and weaker in the more important ones. To test the proposed method, the CRISPR-M model was trained, and three models were developed, one as a control model with uniform regularization strength and two variants using the proposed regularization approach. The first applied group regularization across all feature sets (L1-Grouped-Complete), while the second incorporated grouped epigenetic features (L1-Grouped-Epigenetics) to explore the model’s behavior and performance, alongside their impact on stability.
2. Materials and Methods
The models were trained on the HEK293T dataset and evaluated on the K562 dataset [6,7]. The HEK293T dataset contains 132,914 samples, with 536 positives and 132,378 negatives, and 11 input features, while the K562 dataset contains 13,496 samples, with 74 positives and 13,422 negatives, and the same feature format. Both datasets include sequence-based features as well as epigenetic factors (CTCF, DNase, H3K4me3, RRBS), with approximate negative-to-positive ratios of 250:1 (HEK293T) and 180:1 (K562).
CRISPR-M is a multi-view deep learning model designed to predict the sgRNA off-target effects for target sites containing indels and mismatches. It encodes sequence data using word embedding and positional encoding. It contains a three-branch neural network with two of the branches processing the target and off-target sequences, and the third branch captures the target and off-target sequence interactions. For feature extraction, it also uses convolutional neural network layers to capture spatial dependencies and bidirectional long short-term memory recurrent neural network layers to handle sequential dependencies [5].
SHAP values were obtained by applying a CRISPR-M model, trained exclusively on the HEK293T dataset, to the independent K562 dataset, ensuring that the model had no prior exposure to K562 during training. A separate CRISPR-M model was trained on HEK293T and evaluated on K562, to provide a fair baseline for comparing against the regularized models.
The L1-Grouped-Epigenetics model was developed to evaluate the effect of applying SHAP-informed regularization strengths to groups of epigenetic factors. This model extends the CRISPR-M architecture by applying SHAP-informed L1 regularization to dense layers corresponding to grouped epigenetic on- and off-target factors. Each epigenetic branch also includes Dropout and Batch Normalization layers to control overfitting and stabilize training, aligning its processing path with the rest of the model architecture.
More precisely, we used eight on- and off-target groups of epigenetic factors (CTCF, DNase, H3K4me3, and RRBS), which have previously been associated with CRISPR-Cas9 off-target activity [4] and were defined based on the data structure of the datasets that were used (HEK293T, K562). SHAP method was selected for its strong theoretical foundation and ability to provide consistent, additive explanations for the global contribution of features, enabling the quantification of individual feature importance [10]. Each group’s data were processed separately and had L1 Regularization [27] applied with the regularization strengths computed from the K562-derived SHAP values. Dropout and Batch Normalization [28,29] were added to the epigenetic factor branches to process them similarly to the rest of the data. The regularization strengths were calculated as follows:
- Step 1:
- The SHAP values were extracted for the epigenetic data and were split into the on- and off-target epigenetic groups.
- Step 2:
- The mean absolute contribution for each feature group was calculated.
- Step 3:
- Normalize the mean contributions across groups using
- Step 4:
- The normalized values were reversed to reflect the importance-to-penalty relationship, where less important groups receive stronger regularization.
The L1-Uniform-Epigenetics model was developed as a control model, with the same epigenetic data process as the L1-Grouped-Epigenetics. Like the other models, L1-Uniform-Epigenetics was trained on the HEK293T dataset and evaluated on the K562 dataset. However, in this model the regularization factor strength is uniform regularization (0.01), rather than SHAP-informed values, a commonly used value for L1 regularization. The L1-Uniform-Epigenetics was used for the comparison with the L1-Grouped-Epigenetics, evaluating the effects of the SHAP-informed regularization strengths on the prediction performance of the model.
The L1-Grouped-Complete model was developed to isolate and evaluate the effect of the proposed method by removing all other regularization techniques the model had (Dropout and Batch Normalization). This model also was trained on HEK293T and evaluated on K562 datasets. The epigenetic data was grouped according to each epigenetic factor and separated further to target and off-target groups; the three other groups of data inputs were kept as they were. L1 Regularization was the only technique used in this model and the regularization strength in each group was calculated as follows:
- Step 1:
- SHAP values were extracted and grouped accordingly.
- Step 2:
- The mean absolute contribution for each feature group.
- Step 3:
- The calculated values were normalized, using the same normalization formula described above.
- Step 4:
- The normalized values were reversed to reflect the importance-to-penalty relationship.
- Step 5:
- The values were scaled to the range [0.001, 1] (with min = 0.001 and max = 1) to ensure a small but non-zero penalty for even the most important group.
After the calculation, the regularization strengths were applied to a dense layer for each group, without any other regularization technique.
For model training, TensorFlow 2.9.0, Keras 2.9.0, SHAP 0.44.1, NumPy 1.22.0, and pandas 1.4.0, together with scikit-learn 1.1.0 for data splitting and evaluation metrics. For the subsequent analysis and penalty calculations, NumPy 2.2.3 and pandas 2.2.3 were used. The remaining dependencies follow the environment and configuration specified in the original CRISPR-M implementation [5].
To provide additional insight into practical feasibility, we estimated the computational cost of the SHAP value computation step that precedes the final training phase. Training the model required ~58 min on our setup. SHAP value computation took ~105 min, primarily due to the relatively large number of validation and background samples used (50 and 200, respectively, selected from a pool of 500 random samples). This additional runtime reflects the overhead introduced by SHAP-based interpretability methods. The runtime for retraining the model with the SHAP-informed regularization strengths is not included in the total runtime reported above. Experiments were conducted on an Azure D8s_v3 virtual machine (8 vCPUs, 32 GB RAM, 128 GB SSD).
The primary aim of this experiment was to evaluate whether SHAP-guided group-level regularization improves the prediction performance in highly imbalanced CRISPR-Cas9 datasets, by comparing models with and without SHAP-informed regularization.
3. Results
To evaluate the effectiveness and stability of the SHAP-informed group-specific regularization method, the models CRISPR-M, L1-Uniform-Epigenetics, L1-Grouped-Epigenetics and L1-Grouped-Complete were trained, evaluated and compared across multiple metrics including Accuracy, Precision, Recall, F1-score, F-beta Score, AUROC, AUPRC, Spearman Correlation.
3.1. Regularization Strengths
The group regularization strengths were calculated for L1-Grouped-Epigenetics and L1-Grouped-Complete using SHAP values. Specifically, CRISPR-M was first trained on the HEK293T dataset, and the trained model was then used to compute SHAP values on the K562 dataset.
For L1-Grouped-Epigenetics, the regularization strengths were applied to the eight target and off-target epigenetic groups. The process involved calculating the absolute mean contribution, normalized and reversed. Table 1 summarizes the regularization strengths for the epigenetic groups. Nonetheless, we acknowledge that systematic tuning of penalty scaling choices (e.g., normalization scheme, scaling range) could further refine performance and may be explored in future studies.

Table 1.
Regularization strengths for L1-Grouped-Epigenetics.
On-target epigenetic groups, having zero contribution to predictions based on SHAP analysis, received the strongest penalties. The other epigenetic groups were penalized less, having non-zero contribution to the predictions. The calculated strengths were as follows:
The L1-Grouped-Complete regularization strengths were calculated and applied to all data groups (sequence and epigenetic data, target and off-target). The SHAP-informed penalties for all sequence and epigenetic input groups are shown in Table 2.

Table 2.
Regularization strengths for L1-Grouped-Complete.
The results were scaled using the scaling formula described in Section 2, with values ranging from 0.001 to 1, ensuring that even the most important group received a small penalty. Thus, the most-important data group received the weakest penalty, and the least-important received the strongest within this range. The calculated strengths were as follows.
3.2. Performance Comparison
3.2.1. Quantitative Results
To provide an initial comparison, Table 3 reports the results from the first training run of each model. All models achieved high Accuracy. CRISPR-M obtained the highest Recall, AUPRC, and F1/F-beta, while L1-Uniform-Epigenetics also maintained relatively high Recall. L1-Grouped-Complete achieved the strongest AUROC and highest Precision, whereas L1-Grouped-Epigenetics performed moderately in AUROC and Precision but showed lower Recall. These results indicate that SHAP-informed grouping can improve certain metrics such as AUROC and Precision, though trade-offs remain, particularly in Recall and F1. The subsequent Section 3.3 evaluates mean performance and stability across three training runs.

Table 3.
Performance comparison across models.
3.2.2. Visual Analysis
Precision and Recall curves, and the TPR and FPR curves output by the CRISPR-M evaluation framework, are shown in Figure 1. While Recall and TPR are mathematically equivalent in binary classification, both plots are included here to reflect the native output structure of the CRISPR-M evaluation framework. For clarity, they are interpreted identically in the context of this analysis. The Precision plot suggests that CRISPR-M achieved high Precision at lower thresholds compared to the other models, followed by L1-Grouped-Complete, while L1-Grouped-Epigenetics and L1-Uniform-Epigenetics reached their peaks later. In contrast, the Recall plot shows that L1-Grouped- Epigenetics and L1-Uniform-Epigenetics maintained higher Recall for longer, whereas CRISPR-M dropped off earliest. The FPR plot indicates that CRISPR-M exhibited a higher false positive rate overall, while L1-Uniform-Epigenetics and L1-Grouped-Complete maintained lower FPR values. Finally, in the TPR plot, CRISPR-M slightly outperformed the others, suggesting it identified true positives earlier.
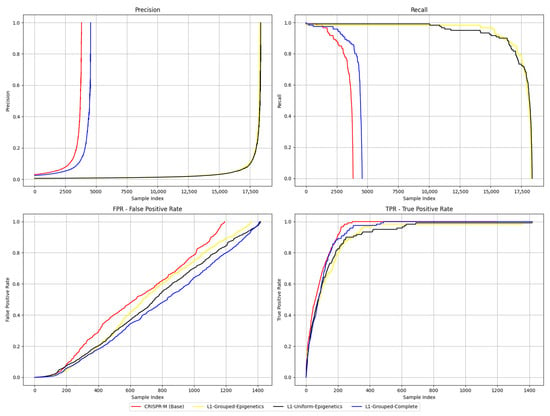
Figure 1.
Precision, Recall, TPR, and FPR curves. (Recall and TPR are mathematically equivalent in binary classification, both are shown to match the CRISPR-M output.).
3.3. Models Predictive Performance Across Training Cycles
CRISPR-M, L1-Grouped-Epigenetics, and L1-Grouped-Complete were each trained in three cycles to assess stability. The results indicated that L1-Grouped-Complete achieved higher mean performance metrics than CRISPR-M, while also showing generally low variability across metrics. In particular, it achieved the lowest CV in AUROC and Recall, though variability in Precision and AUPRC was higher than that of L1-Grouped-Epigenetics. The L1-Grouped-Epigenetics variant displayed balanced performance overall, having the highest Recall, F1, and F-beta scores, though with low precision. It showed more consistent performance than CRISPR-M and L1-Grouped-Complete in most of the metrics. CRISPR-M had the lowest mean values in most metrics (AUROC, AUPRC, Recall, F1, F-beta, and Spearman correlation) and also showed the greatest variability across cycles, particularly in Recall, AUPRC, F-beta, and Spearman correlation, highlighting its sensitivity to training fluctuations.
In this study, the outcomes of the three training cycles were used to calculate the mean, standard deviation, and coefficient of variation for each model and each metric. While both SHAP-guided variants improved over CRISPR-M, their trade-offs were clear, L1-Grouped-Complete excelled in metrics such as AUROC, AUPRC and Precision, while L1-Grouped-Epigenetics in Recall, F1 and F-beta with more consistent stability. Although the reported metrics suggest improved stability and performance, no statistical significance tests were performed due to the small sample size (three training cycles per model). Power analysis indicates that at least 10 cycles per model would be required to achieve reliable statistical power (≥80%) for pairwise tests such as the paired t-test or Wilcoxon signed-rank test. We acknowledge this as a limitation and plan to incorporate statistical validation in future studies with more extensive training repetitions. Numerical results (mean, standard deviation, and coefficient of variation) are given in Table 4 and Table 5, and a graphical comparison is shown in Figure 2.

Table 4.
Mean performance comparison: CRISPR-M vs. L1-Grouped-Epigenetics vs. L1-Grouped-Complete.

Table 5.
Stability comparison: CRISPR-M vs. L1-Grouped-Epigenetics vs. L1-Grouped-Complete.
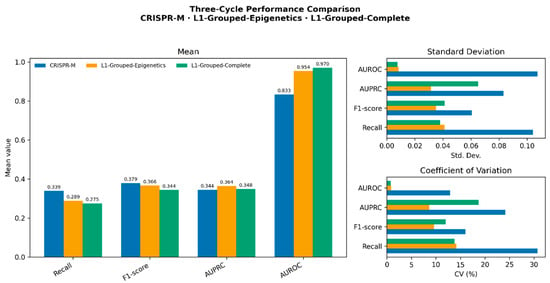
Figure 2.
Graphical comparison of mean, std. dev., and CV.
3.4. Summary of Results
The results suggest that SHAP-informed group regularization can provide modest improvements in predictive performance and stability compared to the CRISPR-M baseline. The findings reported here are based on the mean performance across three training cycles, which better reflects model stability than single-run outcomes.
The L1-Grouped-Epigenetics model achieved higher Recall, F1, and F-beta scores and showed relatively consistent behavior across metrics, while the L1-Grouped-Complete model performed best in AUROC, AUPRC, and Precision. In contrast, CRISPR-M, despite showing high performance in its first run, performed much worse in the other two cycles, resulting in the lowest mean values and the highest variability overall. For comparison, the L1-Uniform-Epigenetics model was trained only once, but its weaker performance relative to L1-Grouped-Epigenetics suggests that applying uniform penalties is less effective than incorporating interpretability guidance.
Overall, the SHAP-guided approaches offered complementary strengths (more sensitivity for L1-Grouped-Epigenetics and more ranking accuracy for L1-Grouped-Complete), while both performed more reliably than the baseline. These findings highlight the potential of interpretability-informed regularization, though the gains observed here remain modest and will require further validation across datasets and settings.
4. Discussion
We proposed a group-level regularization method that integrates interpretability into training by assigning penalties based on SHAP-derived feature importance. SHAP was selected for its strong theoretical foundation and its ability to provide consistent, model-agnostic estimates of global feature contributions [10]. This integration aimed to address key challenges in deep learning models, including unstable training dynamics [23,25], limited transparency, and fairness concerns [14,15]. Given the diverse effects of epigenetic factors on CRISPR-Cas9 cleavage and their variable contributions to predictive models [4], the method prioritizes high-importance features while still incorporating less informative ones, mimicking a prioritization strategy often used in manual feature selection. We scaled each group’s mean contribution and adjusted the regularization strengths accordingly, so that more important groups received weaker penalties, while less important ones received stronger penalties.
To assess the effectiveness of SHAP-informed regularization, two CRISPR-M variants were implemented using the proposed method. L1-Grouped-Epigenetics applied SHAP-guided penalties to epigenetic groups, while L1-Grouped-Complete extended the grouping to both epigenetic (on- and off-target) and sequence features. A control model, L1-Uniform-Epigenetics, used uniform penalties across epigenetic groups and shared the same architecture as L1-Grouped-Epigenetics. It was trained once for comparison. To avoid circular dependencies, SHAP values were not computed on the train, validation, or test splits used for model evaluation. Instead, CRISPR-M was trained only on the HEK293T dataset, and the trained model was then applied to compute SHAP values on the separate K562 dataset. This ensured that the SHAP-informed regularization strengths were calculated independently of the data later used for predictive evaluation.
Both SHAP-informed models showed modest improvements over CRISPR-M, though the gains varied by metric. L1-Grouped-Epigenetics achieved higher scores on most metrics and the best overall mean performance, while L1-Grouped-Complete performed best in AUROC and Spearman Correlation. The L1-Uniform-Epigenetics control, trained once for comparison, underperformed relative to L1-Grouped-Epigenetics, supporting the value of SHAP-informed penalties over uniform assignments.
Across three training cycles, CRISPR-M achieved the highest Recall and F-scores, but its mean performance was lowest on most other metrics, showing the greatest variability and confirming its sensitivity to training fluctuations. In contrast, the SHAP-guided models demonstrated more reliable outcomes overall, which is important for monitoring and deploying predictive models in sensitive domains [23,24,25,26].
This method could be implemented using different grouping strategies. Although a relationship-based grouping was used in this study, other strategies, such as importance-based grouping, could also be applied. While this work focused on CRISPR-M with HEK293T and K562 datasets, the simplicity and flexibility of the method make it adaptable to other domains, models and datasets [21,22]. It does not alter the core model architecture and can be integrated into any setting that supports group-wise regularization. Because it relies on interpretable outputs, it also provides a natural avenue to incorporate fairness and transparency considerations into training [12,13].
The results here indicate potential for modest performance and stability gains. However, further validation is needed to evaluate the approach in other biological contexts, data types, or architectures. Future studies could also explore whether alternative grouping strategies or interpretability methods enhance its generalizability and impact.
A variety of recent studies have explored ways to integrate interpretability signals directly into model training using regularization-based strategies. These approaches can be grouped by how they incorporate interpretability, the level at which they operate, and the complexity they introduce. A commonly explored approach uses loss-based regularization, where interpretability outputs are converted into auxiliary loss terms to guide model training [14,15,30]. These approaches typically operate at the feature level, require access to integrated gradients or other internal signals, and are often model-specific, which can raise training complexity. Other methods adopt input masking or dropout mechanisms to embed interpretability signals into training dynamics [31,32,33]. While these can improve robustness, they often require repeated interpretability computation during training, which introduces considerable computational overhead. Finally, some approaches integrate interpretability into training dynamics via feature weighting or gradient scaling [18], including SHAP-informed adjustments to learning rates or gradients, which enhances model performance but at the cost of repeated SHAP evaluation.
In contrast to existing interpretability-guided regularization approaches, which often act at the feature level and require architectural changes, the proposed method applies a post hoc SHAP-informed group-wise L1 penalty, offering a modular, model-agnostic alternative. By aggregating importance across meaningful feature groups, it avoids the repeated interpretability computations required by some other strategies and remains relatively simple to integrate. While the gains observed here were modest, the approach offers a practical tradeoff between scalability, interpretability, and training stability, and introduces a novel perspective on group-level regularization. Further testing and refinements are needed to validate its reproducibility [26] and generalizability, including more systematic tuning of regularization strengths to better capture each model’s optimal configuration. Since different interpretability methods can produce different results [34], exploring alternative approaches alongside SHAP may also help assess the robustness of this strategy.
While SHAP was chosen here for its ability to produce global, model-agnostic feature importance values, assessing whether similar group-level regularization strategies can be derived from methods such as LIME or Integrated Gradients remains a relevant topic for examination. As LIME provides instance-level explanations, while gradient-based methods often require model-specific access, and these differences in scope made SHAP a more appropriate choice for this initial approach. However, broader experimentation is needed to assess whether this regularization strategy generalizes across interpretability methods.
It should be noted that the grouping of features introduces a degree of subjectivity, as different grouping strategies (e.g., domain-driven, data-driven or importance-driven) may affect the outcomes and generalizability of this method [20,22]. Implementing this method may increase computational cost due to the use of interpretability and the additional training cycle that is needed [12,13]. Future work may explore ways to reduce this overhead, such as optimizing SHAP sample sizes or adopting faster approximations for feature importance.
5. Conclusions
This study proposed an interpretability-informed regularization method for CRISPR-Cas9 off-target prediction, aimed at enhancing model performance, interpretability and training stability. SHAP-informed Group L1 Regularization was applied, with strengths determined by the predictive contribution of each feature group. Stronger penalties were assigned to less important groups and weaker penalties to more important ones, reflecting an inverse importance-penalty relationship.
Two models were developed using distinct grouping strategies and regularization strength calculations. The results showed that the method offered improvements in several key metrics compared to CRISPR-M, though trade-offs remained across others. The SHAP-guided models also demonstrated more consistent behavior across training runs. A control model was developed to compare the effects of uniform and SHAP-informed regularization strengths. This comparison revealed the effectiveness of the interpretability-informed regularization method. The two variants exhibited different trade-offs: L1-Grouped-Epigenetics achieved balanced performance and the most consistent results across training cycles, while L1-Grouped-Complete reached the highest AUROC but with greater variability. Unlike methods that constrain explanations via loss functions or attention mechanisms, this approach directly adjusts regularization strengths at the group level, offering targeted control and simplicity.
This prioritization of information based on importance, or grouping by functional context, suggests an alignment with mechanisms observed in human learning or biological systems. The method holds potential for cross-domain implementation, as it does not require major architectural changes and only depends on feature grouping and prioritization. However, further applications and testing are required to assess its robustness and generalizability.
Each step of this method can be modified. Alternative interpretable methods, grouping strategies, regularization strength calculations, and regularization techniques could also be used in its implementation. The extra training cycle required to compute SHAP values adds computational cost, which should be taken into account in practical implementations [13]. Future work could focus on optimizing the interpretability step to reduce runtime, making the approach more scalable for large datasets. The integration of interpretability into model training is especially important in domains such as bioinformatics, where understanding and trusting predictions can directly impact research and clinical decisions [26].
In more advanced implementations of this method, models could dynamically adjust their regularization strengths or feature groupings during training based on each group’s importance. Interpretability-guided regularization has the potential to offer more intuitive transparency and greater control over model behavior, though further testing is needed to ensure predictive performance is not compromised. To validate these findings, further testing across diverse models and datasets is necessary, along with refinements at each stage of the method.
Author Contributions
Conceptualization, E.T. and H.K.; methodology, E.T.; software, E.T.; validation, E.T. and H.K.; data curation, E.T.; writing—original draft preparation, E.T.; writing—review and editing, H.K.; visualization, E.T.; supervision, H.K.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Datasets can be provided at request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ansori, A.N.m.; Antonius, Y.; Susilo, R.J.k.; Hayaza, S.; Kharisma, V.D.; Parikesit, A.A.; Zainul, R.; Jakhmola, V.; Saklani, T.; Rebezov, M.; et al. Application of CRISPR-Cas9 Genome Editing Technology in Various Fields: A Review. Narra J. 2023, 3, e184. [Google Scholar] [CrossRef]
- Hsu, P.D.; Lander, E.S.; Zhang, F. Development and Applications of CRISPR-Cas9 for Genome Engineering. Cell 2014, 157, 1262–1278. [Google Scholar] [CrossRef]
- Gostimskaya, I. CRISPR–Cas9: A History of Its Discovery and Ethical Considerations of Its Use in Genome Editing. Biochem. Mosc. 2022, 87, 777–788. [Google Scholar] [CrossRef] [PubMed]
- Mak, J.K.; Störtz, F.; Minary, P. Comprehensive Computational Analysis of Epigenetic Descriptors Affecting CRISPR-Cas9 off-Target Activity. BMC Genom. 2022, 23, 805. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Guo, J.; Liu, J. CRISPR-M: Predicting sgRNA off-Target Effect Using a Multi-View Deep Learning Network. PLoS Comput. Biol. 2024, 20, e1011972. [Google Scholar] [CrossRef] [PubMed]
- Chuai, G.; Ma, H.; Yan, J.; Chen, M.; Hong, N.; Xue, D.; Zhou, C.; Zhu, C.; Chen, K.; Duan, B.; et al. DeepCRISPR: Optimized CRISPR Guide RNA Design by Deep Learning. Genome Biol. 2018, 19, 80. [Google Scholar] [CrossRef]
- The ENCODE Project Consortium. The ENCODE (ENCyclopedia of DNA Elements) Project. Science 2004, 306, 636–640. [Google Scholar] [CrossRef]
- Guan, Z.; Jiang, Z. A Systematic Method for Solving Data Imbalance in CRISPR Off-Target Prediction Tasks. Comput. Biol. Med. 2024, 178, 108781. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- Azodi, C.B.; Tang, J.; Shiu, S.-H. Opening the Black Box: Interpretable Machine Learning for Geneticists. Trends Genet. 2020, 36, 442–455. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards A Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608. [Google Scholar] [CrossRef]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Interpretable Machine Learning: Definitions, Methods, and Applications. arXiv 2019, arXiv:1901.04592. [Google Scholar] [CrossRef] [PubMed]
- Ross, A.S.; Hughes, M.C.; Doshi-Velez, F. Right for the Right Reasons: Training Differentiable Models by Constraining Their Explanations. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; International Joint Conferences on Artificial Intelligence Organization: Melbourne, Australia, 2017; pp. 2662–2670. [Google Scholar]
- Rieger, L.; Singh, C.; Murdoch, W.; Yu, B. Interpretations Are Useful: Penalizing Explanations to Align Neural Networks with Prior Knowledge. In Proceedings of the 37th International Conference on Machine Learning, PMLR 119, Online, 21 November 2020; pp. 8116–8126. [Google Scholar]
- Wang, M.; Wang, J.; He, H.; Wang, Z.; Huang, G.; Xiong, F.; Li, Z.; E, W.; Wu, L. Improving Generalization and Convergence by Enhancing Implicit Regularization. Adv. Neural Inf. Process. Syst. 2024, 37, 118701–118744. [Google Scholar]
- Cheng, Q.; Qu, S.; Lee, J. SHAPNN: Shapley Value Regularized Tabular Neural Network. arXiv 2023, arXiv:2309.08799. [Google Scholar] [CrossRef]
- Graham, J.; Sheng, V.S. SHAP Informed Neural Network. Mathematics 2025, 13, 849. [Google Scholar] [CrossRef]
- Yerramilli, S.; Tamarapalli, J.S.; Francis, J.; Nyberg, E. Attribution Regularization for Multimodal Paradigms. arXiv 2024, arXiv:2404.02359. [Google Scholar] [CrossRef]
- Erion, G.; Janizek, J.D.; Sturmfels, P.; Lundberg, S.; Lee, S.-I. Improving Performance of Deep Learning Models with Axiomatic Attribution Priors and Expected Gradients. Nat. Mach. Intell. 2021, 3, 620–631. [Google Scholar] [CrossRef]
- Vukadin, D.; Šilić, M.; Delač, G. Large Language Models as Attribution Regularizers for Efficient Model Training. arXiv 2025, arXiv:2502.20268. [Google Scholar]
- Inecik, K.; Theis, F. scARE: Attribution Regularization for Single Cell Representation Learning. Biorxiv 2023, 2023, 547784. [Google Scholar]
- Garbin, C.; Zhu, X.; Marques, O. Dropout vs. Batch Normalization: An Empirical Study of Their Impact to Deep Learning. Multimed. Tools Appl. 2020, 79, 12777–12815. [Google Scholar] [CrossRef]
- Jordan, K. On the Variance of Neural Network Training with Respect to Test Sets and Distributions. arXiv 2023, arXiv:2304.01910. [Google Scholar]
- Altarabichi, M.G.; Nowaczyk, S.; Pashami, S.; Mashhadi, P.S.; Handl, J. Rolling the Dice for Better Deep Learning Performance: A Study of Randomness Techniques in Deep Neural Networks. Inf. Sci. 2024, 667, 120500. [Google Scholar] [CrossRef]
- Han, H. Challenges of Reproducible AI in Biomedical Data Science. BMC Med. Genom. 2025, 18, 8. [Google Scholar] [CrossRef] [PubMed]
- Ng, A.Y. Feature Selection, L1 vs. L2 Regularization, and Rotational Invariance. In Proceedings of the Twenty-First International Conference on Machine Learning—ICML ’04, Banff, AB, Canada, 4–8 July 2004; ACM Press: New York, NY, USA, 2004; p. 78. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015. [Google Scholar]
- Ferreira, P.; Titov, I.; Aziz, W. Explanation Regularisation through the Lens of Attributions. arXiv 2025, arXiv:2407.16693. [Google Scholar]
- Nayyem, N.; Rakin, A.; Wang, L. Bridging Interpretability and Robustness Using LIME-Guided Model Refinement. arXiv 2024, arXiv:2412.18952. [Google Scholar] [CrossRef]
- Ismail, A.A.; Bravo, H.C.; Feizi, S. Improving Deep Learning Interpretability by Saliency Guided Training. arXiv 2021, arXiv:2111.14338. [Google Scholar] [CrossRef]
- Gururaj, S.; Grüne, L.; Samek, W.; Lapuschkin, S.; Weber, L. Relevance-driven Input Dropout: An Explanation-guided Regularization Technique. arXiv 2025, arXiv:2505.21595. [Google Scholar]
- Lipton, Z.C. The Mythos of Model Interpretability. arXiv 2017, arXiv:1606.03490. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).