Data-Driven Prior Construction in Hilbert Spaces for Bayesian Optimization

Abstract

We propose a variant of Bayesian optimization in which probability distributions are constructed using uncertainty quantification (UQ) techniques. In this context, UQ techniques rely on a Hilbert basis expansion to infer probability distributions from limited experimental data. These distributions act as prior knowledge of the search space and are incorporated into the acquisition function to guide the selection of enrichment points more effectively. Several variants of the method are examined, depending on the distribution type (normal, log-normal, etc.), and benchmarked against traditional Bayesian optimization on test functions. The results show competitive performance, with selective improvements depending on the problem structure, and faster convergence in specific cases. As a practical application, we address a structural shape optimization problem. The initial geometry is an L-shaped plate, where the goal is to minimize the volume under a horizontal displacement constraint expressed as a penalty. Our approach first identifies a promising region while efficiently training the surrogate model. A subsequent gradient-based optimization step then refines the design using the trained surrogate, achieving a volume reduction of more than $30\%$ while satisfying the displacement constraint, without requiring any additional evaluations of the objective function.

1. Introduction

Optimization of expensive-to-evaluate black-box functions is a problem found in a wide range of technological and engineering applications [1,2,3]. Two broad application fields include the tuning of Machine Learning (ML) and general Artificial Intelligence (AI) models [4,5,6], as well as multiple forms of engineering design optimization, such as shape, topology, and material optimization, spanning from structural to electronic engineering [7,8,9]. In both fields, complex computational models are required to evaluate the objective or performance function, resulting in elevated computation time for each evaluation. Additionally, these models behave as black-boxes, meaning that general properties of the underlying model (such as its derivative or gradient) are not available.

Bayesian Optimization (BO) is an optimization framework particularly well-suited to address the aforementioned black-box, expensive-to-evaluate optimization problem [10,11,12,13,14,15].

This article presents an algorithm that combines the advantages of classical Bayesian optimization with prior distributions constructed from an initial design of experiment (DoE), based on uncertainty quantification (UQ) techniques. While both the metamodel and prior distributions utilize the same DoE, they encode complementary information about the problem. The metamodel seeks to approximate the objective function across the entire domain, leveraging spatial correlations between samples. In contrast, the prior distributions quantify the search space in a Bayesian sense by identifying regions where the objective is likely to attain good or bad performance contingent on the observations.

In engineering contexts, expert priors are often unavailable or difficult to justify, particularly in early design phases. In such cases, investing in a small exploratory DoE enables data-driven prior construction that can guide the optimization process efficiently from the outset, as demonstrated in this work.

The organization of this article is the following: Section 2 reviews the fundamentals of Bayesian optimization and the original BOPrO scheme. Section 3 details the construction of the UQ-based performance prior and its integration into the complete algorithm. Section 4 presents numerical results from six academic test functions and a case study from an engineering application, highlighting the applicability of the proposed method. Finally, Section 5 summarizes the conclusions and outlines future research directions.

2. Background

We are interested in solving the following global optimization problem:

$${\displaystyle {\mathbf{x}}^{\ast }=argmin\left\{f\left(\mathbf{x}\right)\mid \mathbf{x}\in \mathcal{X}\subset {\mathbb{R}}^d\right\},}$$

(1)

where $f:\mathcal{X}\subset {\mathbb{R}}^d\to \mathbb{R}$ is the function to be minimized.

Sequential Bayesian estimation gives rise to a global optimization framework, commonly referred to as BO, which is particularly suited for problems such as the one described above. BO relies on the fundamental principle of Bayesian updating. A typical iteration of a Bayesian Optimization Algorithm (BOA) proceeds as follows [16]:

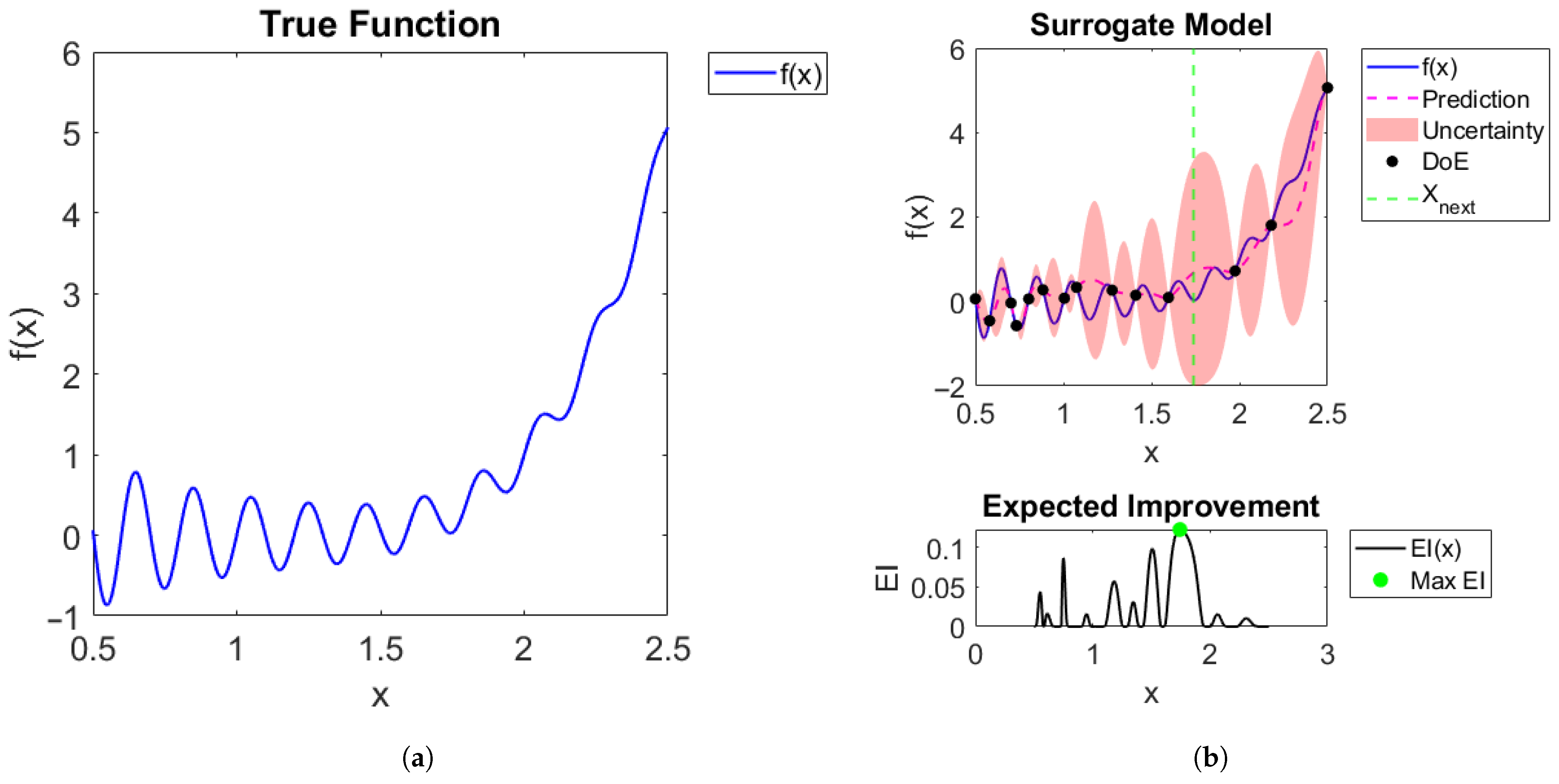
• Generate a surrogate model of the objective function f, usually under the form of a stochastic process.
• Select a new point to evaluate the true objective function.
• Update the surrogate model using the Bayesian update, the pair of the new point and the value of the objective function in it.

2.1. Standard Bayesian Optimization (SBO)

The most commonly used surrogate model in BOA is the $\mathcal{GP}$ [15,17,18,19,20,21]. A $\mathcal{GP}$ generalizes the multivariate Gaussian distribution to an infinite-dimensional stochastic process, where any finite collection of function evaluations follows a joint multivariate normal distribution. Just as a standard Gaussian distribution describes a random variable by its mean and covariance, a $\mathcal{GP}$ defines a distribution over functions, fully specified by a mean function $m\left(\mathbf{x}\right)$ and a covariance (or kernel) function $k(\mathbf{x},{\mathbf{x}}^{\prime })$ [19]:

$${\displaystyle f\sim \mathcal{G}\mathcal{P}\left(m,k\right).}$$

(2)

In practice, when the $\mathcal{GP}$ is evaluated at a finite set of input locations $\{{\mathbf{x}}_1,\dots ,{\mathbf{x}}_n\}$, the corresponding function values follow a joint multivariate normal distribution: $\mathbf{f}\sim \mathcal{N}(\mathbf{m},\mathbf{K})$, where $\mathbf{m}={(m\left({\mathbf{x}}_1\right),\dots ,m\left({\mathbf{x}}_n\right))}^{\top }$ is often set to zero and the covariance matrix $\mathbf{K}$ has elements $K_{i,j}:=k({\mathbf{x}}_i,{\mathbf{x}}_j)$. Equation (2) thus represents the prior distribution $p\left(f\right)$ induced by the $\mathcal{GP}$, encoding assumptions about the smoothness and structure of the underlying objective function.

The choice of a $\mathcal{GP}$ greatly simplifies the Bayesian update procedure, as the $\mathcal{GP}$ is conjugate to itself. This property ensures that the posterior distribution remains a $\mathcal{GP}$, and that the update merely involves a straightforward modification of the mean and covariance functions [16]. More precisely, we assume that a set of observations, ${\mathcal{D}}_t={\left\{\left({\mathbf{x}}_i,y_i\right)\right\}}_{i=1}^t$, has already been collected from previous iterations, where the outputs are noise-free evaluations of a deterministic function, i.e., $y_i=f\left({\mathbf{x}}_i\right)$. Let $\mathbf{y}={\left[y_1,\dots ,y_t\right]}^T$ denote the vector of corresponding observations. Then, Bayes’ theorem yields the posterior distribution [19]:

$${\displaystyle p\left(f\mid {\mathcal{D}}_t\right)\propto p\left({\mathcal{D}}_t\mid f\right)·p\left(f\right),}$$

(3)

where the posterior distribution, $f\mid {\mathcal{D}}_t\sim \mathcal{GP}\left({\mu }_t,k_t\right)$, remains a $\mathcal{GP}$ due to the aforementioned conjugacy. This updated distribution leads to the following expression for the predictive distribution at any next evaluation point $\mathbf{x}$ [19]:

$${\displaystyle f\left(\mathbf{x}\right)\mid {\mathcal{D}}_t\sim \mathcal{N}\left(\mu \left(\mathbf{x}\right),{\sigma }^2\left(\mathbf{x}\right)\right),}$$

(4)

with the predictive mean and variance given by

$$\begin{array}{cc}\hfill \mu \left(\mathbf{x}\right)& ={\mathbf{k}}^T{\mathbf{K}}^{-1}\mathbf{y},\hfill \\ \hfill {\sigma }^2\left(\mathbf{x}\right)& =k(\mathbf{x},\mathbf{x})-{\mathbf{k}}^T{\mathbf{K}}^{-1}\mathbf{k},\hfill \end{array}$$

(5)

where $\mathbf{k}=\left[k(\mathbf{x},{\mathbf{x}}_1),\dots ,k(\mathbf{x},{\mathbf{x}}_t)\right]$.

To select the next point $\mathbf{x}$, in BOA, one must solve an auxiliary optimization problem involving the maximization of an acquisition function $\alpha$. One of the most widely used acquisition functions is the expected improvement (EI). Let $f_{★}$ denote the best (i.e., lowest) function value observed up to iteration t, and assume that the predictive distribution at $\mathbf{x}$ follows Equations (4) and (5). Then, the EI at a candidate point $\mathbf{x}$ is defined as follows [16]:

$${\alpha }_{EI}\left(\mathbf{x}\right)=\mathbb{E}\left[u_{EI}\left(\mathbf{x}\right)\mid {\mathcal{D}}_t\right],\mathrm{with}{u}_{EI}\left(\mathbf{x}\right)=max\left\{0,f_{★}-f\left(\mathbf{x}\right)\right\}.$$

(6)

Another popular acquisition function is the probability of improvement (PI):

$${\alpha }_{PI}\left(\mathbf{x}\right)=\mathbb{P}\left(f\left(\mathbf{x}\right)<f_{★}\mid {\mathcal{D}}_t\right),$$

(7)

which can also be written as

$${\alpha }_{PI}\left(\mathbf{x}\right)=\mathbb{E}\left[u_{PI}\left(\mathbf{x}\right)\mid {\mathcal{D}}_t\right],\mathrm{with}{u}_{PI}\left(\mathbf{x}\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}f\left(\mathbf{x}\right)<f_{★},\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(8)

Thanks to the properties of the $\mathcal{GP}$ predictive posterior, closed-form expressions can be obtained for both EI and PI. Let $\mathsf{\Phi }$ and $\phi$ denote, respectively, the standard normal cumulative distribution function and the standard normal probability density function $\mathcal{N}(0,1)$. Since the predictive distribution at a candidate point $\mathbf{x}$ is Gaussian with mean $\mu \left(\mathbf{x}\right)$ and standard deviation $\sigma \left(\mathbf{x}\right)$, the EI can be expressed as [16]:

$${\displaystyle {\alpha }_{EI}\left(\mathbf{x}\right)=\sigma \left(\mathbf{x}\right)·\left[z\left(\mathbf{x}\right)·\mathsf{\Phi }\left(z\left(\mathbf{x}\right)\right)+\phi \left(z\left(\mathbf{x}\right)\right)\right],}$$

(9)

with

$$z\left(\mathbf{x}\right)={\displaystyle \frac{f_{★}-\mu \left(\mathbf{x}\right)}{\sigma \left(\mathbf{x}\right)}}.$$

(10)

Similarly, the PI is given by

$${\alpha }_{PI}\left(\mathbf{x}\right)=\mathsf{\Phi }\left(z\left(\mathbf{x}\right)\right).$$

(11)

To illustrate how the SBO works in practice, we will consider a one-dimensional synthetic test function proposed by Gramacy and Lee [22], presented in Figure 1. Figure 1a shows the objective function, and Figure 1b shows the optimization process at iteration 1, which includes the predictive mean of $\mathcal{GP}$, the associated uncertainty, and the next point to be evaluated, which represents the maximum of the acquisition function.

2.2. BOPrO

Bayesian optimization with a prior for the optimum (BOPrO), proposed by Souza et al. [23], is a recently developed version of BO inspired by the Tree-structured Parzen Estimator (TPE) algorithm [24]. It allows users to introduce intuitive domain knowledge into the optimization process through priors. These priors do not modify the surrogate model (e.g., a $\mathcal{GP}$). Instead, they are combined with the probability of improvement (PI) to form a pseudo-posterior or posterior pseudo-density. In this context, a pseudo-posterior is a non-normalized posterior, or also a density that does not integrate to 1 over the prescribed domain. The pseudo-posteriors act as weighting functions in the Bayesian updating. They are integrated into the acquisition function, particularly in the calculation of a modified expected improvement, which implies that the priors directly adjust the importance assigned to different regions of the search space in the EI evaluation. Consequently, regions favored by a prior are more likely to be explored at the beginning of the iteration process. As the iterations progress, the effect of the prior decreases, and the predictive model’s influence dominates the search.

The mathematical expression corresponding to the modified version of the expected improvement criterion, adopted by BOPrO to effectively integrate the pseudo-posterior into the process of selecting new points, is formally derived from the TPE framework. It reads as follows:

$$E{I}_{f_{\gamma }}\left(\mathbf{x}\right)\propto {\left(\gamma +{\displaystyle \frac{b\left(\mathbf{x}\right)}{g\left(\mathbf{x}\right)}}(1-\gamma )\right)}^{-1},$$

(12)

where g and b are non-normalized density functions describing, respectively, the promising and less promising areas of the search space. The $\gamma$ value acts as a quantile threshold that determines at which point a function value can be considered good.

The main contribution of BOPrO is the practical implementation of this pseudo-posterior to quantify performance.In the case of $g\left(\mathbf{x}\right)$, a prior distribution $p_g\left(\mathbf{x}\right)$ is integrated, reflecting the user’s belief about promising regions, together with a probability derived from the model ${\mathcal{M}}_g\left(\mathbf{x}\right)$, which represents the possibility, under the surrogate $\mathcal{GP}$, that the value of the function $\mathbf{x}$ falls below a threshold $f_{\gamma }$. We can express this pseudo-posterior as follows:

$$g\left(\mathbf{x}\right)\propto p_g\left(\mathbf{x}\right)·{\mathcal{M}}_g{\left(\mathbf{x}\right)}^{{\displaystyle \frac{t}{\beta }}}.$$

(13)

The density for the unpromising regions is given by

$$b\left(\mathbf{x}\right)\propto p_b\left(\mathbf{x}\right)·{\mathcal{M}}_b{\left(\mathbf{x}\right)}^{{\displaystyle \frac{t}{\beta }}},$$

(14)

where $p_b\left(\mathbf{x}\right)=1-p_g\left(\mathbf{x}\right)$ represents the prior for bad regions, t is the current iteration, and $\beta$ is a hyperparameter that affects the balance between prior and model importance, with higher $\beta$ values prioritizing the prior and requiring more data to overrule it [23].

The probability ${\mathcal{M}}_g$ is defined as follows:

$${\mathcal{M}}_g\left(\mathbf{x}\right)=\mathsf{\Phi }\left({\displaystyle \frac{f_{\gamma }-\mu \left(x\right)}{\sigma \left(x\right)}}\right),$$

(15)

and the probability for unpromising regions is given by

$${\mathcal{M}}_b\left(\mathbf{x}\right)=1-{\mathcal{M}}_g\left(\mathbf{x}\right).$$

(16)

Algorithm 1 describes the optimization process carried out by BOPrO in detail.

Algorithm 1: BOPrO Algorithm. ${\mathcal{D}}_t$ keeps track of all function evaluations so far: ${(x_i,y_i)}_{i=1}^t$ [23].

3. Data-Driven Prior Construction in Hilbert Spaces for Bayesian Optimization

3.1. Preliminaries

The BOPrO framework is a technical development adapted for machine learning applications, with the properties of the algorithm explicitly crafted for this type of problem. The specification of the performance priors is designed to facilitate its use by an ML expert with domain knowledge in hyperparameter tuning. The goal is to provide a practical tool to codify this expert knowledge into a prior that performs the following:

• Describes the belief that some areas of the search space are more (or less) promising.
• Can be combined with the information available, both from model evaluations and from surrogate model predictions. This formulation poses significant limitations when the domain of application is different, such as in structural design or general engineering design optimization. Notably, in such applications, expert knowledge may not be available, or it may not be sufficiently reliable, or the expert may provide input at a different stage of the process.

Our proposed method, Data-Driven Prior Construction in Hilbert Spaces for Bayesian Optimization (HSBO), takes some of the central ideas in BOPrO (and the TPE algorithm). In particular, we retain the adapted version of the EI acquisition function and the structure of the priors over the search space, informing the early stages of the optimization iteration process. However, unlike the previous work, we replace the expert knowledge codified in the performance priors by systematic and reproducible distributions, learned directly from initial observations. To achieve this, we follow the methodology introduced by Souza et al. [25], who proposed two approaches based on Hilbertian representations to construct distributions: the first relying on De Finetti’s Representation Theorem, and the second directly providing UQ-based priors suitable for Bayesian procedures. In our framework, we specifically adopt the latter approach, which is detailed in Section 5.3 of the book [16].

3.2. Construction of Priors

The Hilbert Approach (HA), which can be viewed as an extension of Polynomial Chaos Approximations (PCA), can be applied under the following basic conditions:

• The uncertainties can be modeled by a random vector U and the variable of interest is $X=X\left(U\right)$;
• The random variable U takes its values on an interval $\mathsf{\Omega }$ of real numbers (or, more generally, on a bounded subset $\mathsf{\Omega }$ of ${\mathbb{R}}^n$);
• X belongs to the space of square summable random variables: $E\left(X^2\right)<\infty$, id est, X has finite moment of order 2;
• Some statistical information about the couple $(U,X)$ is available.

These assumptions ensure that X can be represented by an infinite expansion involving a convenient orthonormal Hilbert basis ${\left\{{\phi }_i\right\}}_{i\in \mathbb{N}}\subset L^2\left(\mathsf{\Omega }\right)$, allowing one to represent X as [25,26]

$$X=\sum _{i\in \mathbb{N}}{x}_i{\phi }_i\left(U\right).$$

(17)

As previously observed, U is a suitable random variable used to construct a stochastic representation of X. Nevertheless, in practical situations, U can be an artificial variable, conveniently chosen [16,27]. Artificial variables are used, namely, when no information is available about the source of randomness: then, U is chosen by the user, and it is mandatory to create an artificial correlation between samples of the artificial variable and samples of X. For instance, we can arrange both in an increasing order: $X_1\le X_2\le \dots \le X_n$, and $U_1\le$$U_2\le \dots \le U_n$—this generates a non-negative covariance between X and the artificial U.

In practice, the expansion is truncated at order k, yielding the following approximation:

$${\displaystyle X=\sum _{i\in \mathbb{N}}{x}_i{\phi }_i\left(U\right)\approx P_{k}X=\sum _{i=0}^k{x}_i{\phi }_i\left(U\right).}$$

(18)

The finite representation $P_{k}X$ is determined by finding the coefficients $\mathbf{x}={\left(x_0,x_1,\dots ,x_k\right)}^t$. A popular method for the determination of $\mathbf{x}$ is collocation, which considers a sample $\mathcal{U}=\left(U_1,\dots ,U_n\right)$ and solves the linear system [27]:

$$\mathit{M}\mathit{x}=\mathit{N},{\mathit{M}}_{ij}={\phi }_j\left(U_i\right),N_i=X_i,1\le i\le n,0\le j\le k$$

(19)

The reader can find in the literature works using such an approach [27,28]. In general, $k+1<n$ (the system is overdetermined) and Equation (19) must be solved by a least squares approach. Once $P_{k}X$ is determined, the representation can be used to generate the distribution of X. For instance, we can generate a large sample of variates from U (eventually, a deterministic one):

$${\mathcal{U}}_g=\left(U_1,\dots ,U_{ng}\right)$$

(20)

and use it to generate a large sample ${\mathcal{X}}_g$ from X as $X_i=P_{k}X\left(U_i\right)$, $i=1,\dots ,ng$. Then, ${\chi }_g$ is used to estimate the cumulative distribution function (CDF) and probability density function (PDF) of X, by using the empirical CDF of the large sample.

From the Bayesian standpoint, estimates can be obtained by minimizing a loss function defined over the estimated PDF. This approach can be used to define a univariate parametric prior distribution $p_{\widehat{\theta }}\left(x\right)$, where the parametric family (e.g., Gaussian, log-normal) is selected by the user.

In the case of a multidimensional input, we assume independence between dimensions, so that the prior multivariate distribution is constructed as the product of the univariate marginals:

$$p\left(x\right)=\prod _{j=1}^d{p}_{{\widehat{\theta }}_j}\left(x_j\right).$$

(21)

This independence hypothesis, although simplistic and not necessarily valid in all cases, is adopted here as a reasonable working assumption to facilitate model construction and advance the validation of the proposed ideas. If independence among variables is not assumed, the prior definition and estimation become more complex and computationally expensive, as the joint distributions can no longer be expressed as a product of univariate marginals. This approach requires the explicit modeling of the dependence structure among variables, a task that can be achieved by introducing copula models or parametric multivariate distributions. The use of copulas requires careful consideration of the selected parametric family. In the case of multivariate distributions, the number of parameters that need to be estimated drastically increases with the dimension of the problem (e.g., calculating a full covariance matrix and potentially joint higher-order moments), and the estimation of these parameters from limited data is in itself a difficult task.

The full optimization procedure is detailed in Algorithm 2.

Note that two quantile thresholds are used in our method:$f_{{\gamma }_{gb}}$ is fixed at the initialization stage to split the DoE into good and bad subsets, while $f_{\gamma }$ is recomputed at each iteration for the probability of improvement in the acquisition function.

Algorithm 2: Data-driven prior construction in Hilbert spaces for Bayesian optimization

Let us return to the case study introduced in Section 2, this time applying the method we propose. The objective is to visualize the interaction between the different elements of the framework: the surrogate model, the acquisition function, the prior distributions, and the update points. Figure 2a shows the true function $f\left(x\right)$ along with the DoE, which is the same one used for the SBO example (see Figure 1b). Figure 2b shows the priors $p_g\left(x\right)$ and $p_b\left(x\right)$, constructed with the Hilbertian approach. Figure 2c illustrates the prediction and uncertainty band associated with the $\mathcal{GP}$ model. Figure 2d shows the probability models ${\mathcal{M}}_g\left(x\right)$ and ${\mathcal{M}}_b\left(x\right)$, which use the information provided by the $\mathcal{GP}$ to quantify the probability that a given input belongs to the good or bad region. Figure 2e shows the weighted scores $g\left(x\right)$ and $b\left(x\right)$ obtained by combining the priors with the probability model. We observe that some regions considered promising by the PI are penalized because they belong to the bad prior. In contrast, other regions gain importance as they are reinforced by the good prior. Finally, Figure 2f shows the EI, where the maximum no longer coincides with that of SBO. This change is a direct consequence of the integration of performance priors, which guide the algorithm to select a different update point than SBO.

4. Results and Discussion

In this section, we test our proposed method on six test functions and one engineering application. Our results are contrasted with SBO as a baseline. The test functions have been chosen to explore the general behavior of the method, even though they are not expensive black-box functions. The application is a good representative of the kind of problem where BO is expected to excel.

Our focus here is exploratory, as we seek to identify an interesting behavior of the proposed method against SBO, and with varied objective functions. We have thus selected performance metrics that reflect a mix of robustness (success rate), reliability (proximity to the optimum), and convergence speed (simple regret plots); moreover, particular attention is given to the variability of the method given different instances of the DoE, leading us to report extremes, averages, and variances of each instance of our method for several runs.

4.1. Test Design and Technical Aspects

HSBO is evaluated by identifying the global minima of a set of test functions from the Virtual Library of Simulation Experiments [22].

Table A1. Test cases.

Function	Dimension	Design Space	Minimun	Target
(F1) Gramacy and Lee
$f\left(x\right)={\displaystyle \frac{sin\left(10\pi x\right)}{2x}}+{(x-1)}^4$	1	$\left[0.52.5\right]$	−0.86901	−0.8256
(F2) Cross-in-Tray
$f\left(\mathbf{x}\right)=-0.0001{\left(\left|sin\left(x_1\right)sin\left(x_2\right)exp\left(\left|100-{\displaystyle \frac{\sqrt{x_1^2+x_2^2}}{\pi }}\right|\right)\right|+1\right)}^{0.1}$	2	${[-1010]}^2$	−2.06261	−1.9595
(F3) Branin
$\begin{array}{c}f\left(\mathbf{x}\right)=a{\left(x_2-b{x}_1^2+c{x}_1-r\right)}^2+s(1-t)cos\left(x_1\right)+s,\mathrm{where}\\ a=1,b={\displaystyle \frac{5.1}{4{\pi }^2}},c={\displaystyle \frac{5}{\pi }},r=6,s=10,t={\displaystyle \frac{1}{8\pi }}\end{array}$	2	$[-510]\times \left[015\right]$	0.397887	0.4178
(F4) Hartmann 3-Dimensional
$\begin{array}{c}f\left(\mathbf{x}\right)=-{\displaystyle \sum _{i=1}^4}{\alpha }_{i}exp\left(-{\displaystyle \sum _{j=1}^3}{A}_{ij}{\left(x_j-P_{ij}\right)}^2\right),\mathrm{where}\\ \alpha ={(1.0,1.2,3.0,3.2)}^T\\ \mathbf{A}=\left(\begin{array}{ccc}3.0\hfill & 10\hfill & 30\hfill \\ 0.1\hfill & 10\hfill & 35\hfill \\ 3.0\hfill & 10\hfill & 30\hfill \\ 0.1\hfill & 10\hfill & 35\hfill \end{array}\right)\\ \mathbf{P}={10}^{-4}\left(\begin{array}{ccc}3689& 1170& 2673\\ 4699& 4387& 7470\\ 1091& 8732& 5547\\ 381& 5743& 8828\end{array}\right)\end{array}$	3	${\left[01\right]}^2$	−3.86278	−3.6696
(F5) Sum of Different Powers Function
$f\left(\mathbf{x}\right)={\sum }_{i=1}^d{\left|x_i\right|}^{i+1}$	4	${[-11]}^4$	0	0.001
(F6) Hartmann 6-Dimensional
$\begin{array}{c}f\left(\mathbf{x}\right)=-{\displaystyle \sum _{i=1}^4}{\alpha }_{i}exp\left(-{\displaystyle \sum _{j=1}^6}{A}_{ij}{\left(x_j-P_{ij}\right)}^2\right),\mathrm{where}\\ \alpha ={(1.0,1.2,3.0,3.2)}^T\\ \mathbf{A}=\left(\begin{array}{cccccc}10& 3& 17& 3.50& 1.7& 8\\ 0.05& 10& 17& 0.1& 8& 14\\ 3& 3.5& 1.7& 10& 17& 8\\ 17& 8& 0.05& 10& 0.1& 14\end{array}\right)\\ \mathbf{P}={10}^{-4}\left(\begin{array}{cccccc}1312& 1696& 5569& 124& 8283& 5886\\ 2329& 4135& 8307& 3736& 1004& 9991\\ 2348& 1451& 3522& 2883& 3047& 6650\\ 4047& 8828& 8732& 5743& 1091& 381\end{array}\right)\end{array}$	6	${\left[01\right]}^6$	−3.32237	−3.1563

in Appendix A shows the mathematical expression, the problem size, the search space, the known global minimum, and the threshold considered as the success criterion. This threshold is defined by applying a relative error criterion of $5\%$, using the following formula:

$$\mathrm{target}=\mathrm{global}\mathrm{minimum}+0.05\times \mid \mathrm{global}\mathrm{minimum}\mid .$$

(22)

In the particular case of the Sum of Different Powers function, whose global minimum is zero, a target equal to ${10}^{-3}$ is arbitrarily set to avoid zero values.

Different families of parametric distributions (e.g., Gaussian, log-normal, etc.) are fitted to the parameters estimated using the Hilbert approximation implemented in the proposed method and compared with SBO. Ten runs of the code are performed, each with a randomly generated DoE. An optimization budget equal to 15× dimension is set. The size of the DoE is set to 10× problem dimension. The hyperparameter $\beta$ was assigned values between 10 and 100. The first type of threshold $\gamma$ takes values between 0.01 and 0.05, while the second type of threshold ${\gamma }_{gb}=0.5$.

4.2. Benchmark Problems

Figure 3 provides an overall view of the performance of the proposed method under different prior distributions across six benchmark functions. Figure 3a shows the results obtained for the Gramacy and Lee function. Both SBO and HSBO with the Pearson distribution perform well. Figure 3b shows the results obtained for the Cross-in-Tray function. The normal and log-normal prior distributions offer better performance compared to the SBO reference. Although SBO shares a low median, it has an outlier, indicating that in at least one run it deviated significantly from the optimum. Figure 3c shows the results obtained for the Branin function. Although the prior-based configurations show competitive performance, in this particular case they fail to exceed the baseline (SBO). Figure 3d shows the results for the Hartmann 3D function. Here, the baseline and the HSBO configurations with different prior distributions perform very similarly. The medians and dispersion of the relative errors are practically equivalent, suggesting that, in this case, none of the approaches offers a significant advantage over the others. Figure 3e illustrates the distribution of final function values across runs. The box plots clearly show the stability of SBO, together with HSBO using normal and Pearson priors, which remain concentrated near zero. In contrast, log-normal, exponential, and Rayleigh priors exhibit wider spreads and higher median values, reflecting reduced robustness. As illustrated in Figure 3f, none of the methods is able to reach the global minimum of the Hartmann 6D function within 60 iterations. All priors display similar performance, with only slight variations in dispersion.

In addition to the box plot presented in Figure 3a–f, we provide complementary numerical results in

Table 1. Performance at final iteration ($f_{15}$) over 10 runs: Gramacy and Lee 1D function.

Method	Min (${\mathit{f}}_{15}$)	Max (${\mathit{f}}_{15}$)	Mean (${\mathit{f}}_{15}$)	Std (${\mathit{f}}_{15}$)	Success Rate
					(f(x) < Target)
SBO (baseline)	−0.8690	−0.8492	−0.8648	$7.6\times {10}^{-3}$	10/10
HSBO with normal prior	−0.8690	−0.6622	−0.8407	$6.5\times {10}^{-2}$	9/10
HSBO with log-normal prior	−0.8690	−0.6619	−0.8271	$8.7\times {10}^{-2}$	8/10
HSBO with exponential prior	−0.8690	−0.5185	−0.8099	$1.3\times {10}^{-1}$	8/10
HSBO with Rayleigh prior	−0.8690	−0.5185	−0.7922	$1.3\times {10}^{-1}$	7/10
HSBO with Pearson prior	−0.8690	−0.8492	−0.8648	$7.6\times {10}^{-3}$	10/10

,

Table 2. Performance at final iteration ($f_{30}$) over 10 runs: Cross-in-Tray 2D function.

Method	Min (${\mathit{f}}_{30}$)	Max (${\mathit{f}}_{30}$)	Mean (${\mathit{f}}_{30}$)	Std (${\mathit{f}}_{30}$)	Success Rate
					(f(x) < Target)
SBO (baseline)	−2.0626	−1.8894	−2.0447	$5.5\times {10}^{-2}$	9/10
HSBO with normal prior	−2.0626	−2.0620	−2.0625	$1.96\times {10}^{-4}$	10/10
HSBO with log-normal prior	−2.0626	−2.0426	−2.0564	$7.0\times {10}^{-3}$	10/10
HSBO with exponential prior	−2.0456	−1.8891	−1.9740	$4.7\times {10}^{-2}$	7/10
HSBO with Rayleigh prior	−2.0456	−1.8327	−1.9601	$6.6\times {10}^{-2}$	6/10
HSBO with Pearson prior	−2.0626	−1.8833	−2.0270	$7.4\times {10}^{-2}$	8/10

,

Table 3. Performance at final iteration ($f_{30}$) over 10 runs: Branin 2D function.

Method	Min (${\mathit{f}}_{30}$)	Max (${\mathit{f}}_{30}$)	Mean (${\mathit{f}}_{30}$)	Std (${\mathit{f}}_{30}$)	Success Rate
					(f(x) < Target)
SBO (baseline)	0.3980	0.4303	0.4114	$1.3\times {10}^{-2}$	6/10
HSBO with normal prior	0.3980	0.5495	0.4322	$4.4\times {10}^{-2}$	3/10
HSBO with log-normal prior	0.3980	0.5495	0.4322	$4.4\times {10}^{-2}$	3/10
HSBO with exponential prior	0.3980	0.4449	0.4171	$1.6\times {10}^{-2}$	4/10
HSBO with Rayleigh prior	0.3980	0.5495	0.4322	$4.4\times {10}^{-2}$	3/10
HSBO with Pearson prior	0.3980	0.4801	0.4252	$2.4\times {10}^{-2}$	3/10

,

Table 4. Performance at final iteration ($f_{45}$) over 10 runs: hartmann 3D function.

Method	Min (${\mathit{f}}_{45}$)	Max (${\mathit{f}}_{45}$)	Mean (${\mathit{f}}_{45}$)	Std (${\mathit{f}}_{45}$)	Success Rate
					(f(x) < Target)
SBO (baseline)	−3.8609	−3.8428	−3.8539	$6.5\times {10}^{-3}$	10/10
HSBO with normal prior	−3.8609	−3.8428	−3.8539	$6.5\times {10}^{-3}$	10/10
HSBO with log-normal prior	−3.8609	−3.8428	−3.8539	$6.5\times {10}^{-3}$	10/10
HSBO with exponential prior	−3.8609	−3.8428	−3.8539	$6.5\times {10}^{-3}$	10/10
HSBO with Rayleigh prior	−3.8609	−3.8428	−3.8539	$6.5\times {10}^{-3}$	10/10
HSBO with Pearson prior	−3.8609	−3.8428	−3.8539	$6.5\times {10}^{-3}$	10/10

,

Table 5. Performance at final iteration ($f_{60}$) over 10 runs: Sum of Different Powers function.

Method	Min (${\mathit{f}}_{60}$)	Max (${\mathit{f}}_{60}$)	Mean (${\mathit{f}}_{60}$)	Std (${\mathit{f}}_{60}$)	Success Rate
					(f(x) < Target)
SBO (baseline)	$2.3\times {10}^{-5}$	$2.2\times {10}^{-4}$	$1.3\times {10}^{-4}$	$6.5\times {10}^{-5}$	10/10
HSBO with normal prior	$2.3\times {10}^{-5}$	$2.2\times {10}^{-4}$	$1.3\times {10}^{-4}$	$6.5\times {10}^{-5}$	10/10
HSBO with log-normal prior	$4.0\times {10}^{-4}$	$3.3\times {10}^{-3}$	$1.3\times {10}^{-3}$	$9.9\times {10}^{-4}$	5/10
HSBO with exponential prior	$2.7\times {10}^{-3}$	$9.3\times {10}^{-2}$	$4.3\times {10}^{-2}$	$3.1\times {10}^{-2}$	-
HSBO with Rayleigh prior	$2.7\times {10}^{-3}$	$9.3\times {10}^{-2}$	$4.4\times {10}^{-2}$	$3.2\times {10}^{-2}$	-
HSBO with Pearson prior	$2.3\times {10}^{-5}$	$5.0\times {10}^{-4}$	$1.5\times {10}^{-4}$	$1.4\times {10}^{-4}$	10/10

and

Table 6. Performance at final iteration ($f_{90}$) over 10 runs: hartmann 6D function.

Method	Min (${\mathit{f}}_{90}$)	Max (${\mathit{f}}_{90}$)	Mean (${\mathit{f}}_{90}$)	Std (${\mathit{f}}_{90}$)	Success Rate
					(f(x) < Target)
SBO (baseline)	−3.0166	−2.9428	−2.9742	$2.0\times {10}^{-2}$	-
HSBO with normal prior	−3.0166	−2.9428	−2.9740	$2.0\times {10}^{-2}$	-
HSBO with log-normal prior	−3.0166	−2.9583	−2.9864	$1.6\times {10}^{-2}$	-
HSBO with exponential prior	−3.0166	−2.9428	−2.9742	$2.0\times {10}^{-2}$	-
HSBO with Rayleigh prior	−3.0166	−2.9428	−2.9742	$2.0\times {10}^{-2}$	-
HSBO with Pearson prior	−2.9871	−2.9184	−2.9632	$2.3\times {10}^{-2}$	-

. For each test function and each prior distribution used in the HSBO framework, we indicate the following:

• Maximum and minimum values reached by the function (corresponding to the 10 runs) obtained in the last iteration. This allows us to capture the worst and best performance of the algorithm.
• Mean of the function values at the last iteration (corresponding to the 10 runs) and the standard deviation of these values.
• Success rate, defined as the number of executions in which the function reached a value below the target.

These statistics provide additional information about the stability and robustness of our proposal, allowing us to evaluate how often a method successfully identifies a near-optimal solution.

While the numerical results presented in the tables and box plots report the quantitative results of each test case,

Table 7. Summary of observed patterns and associated key findings across benchmark functions.

Patterns	Key Points
Normal and log-normal priors	Across most test cases, they achieve high success rates, generally comparable to SBO. On the Cross-in-Tray function, characterized by sharp curvature and several localized minima, both priors outperform SBO by improving stability and robustness.
Pearson prior	Across most benchmark functions, it maintains high success rates, generally comparable to the SBO baseline. On unimodal problems, Pearson stands out as the most stable prior: for irregular shapes with steep changes (Gramacy and Lee) it performs best overall, while for smooth convex functions (Sum of Different Powers) it outperforms the other priors but remains slightly below SBO.
Exponential and Rayleigh priors	Generally less reliable, with high variance and lower success rates across test cases.
Dimensionality effect	Performance decreases with dimensionality, as illustrated by Hartmann 6D.
Problem structure dependency	Some problems, such as Branin, resist improvement from priors (SBO remains superior).

summarizes the general patterns observed across all test cases, highlighting which priors tend to perform best depending on the characteristics of the different problems. This general description can serve as a practical guide when selecting prior distributions in new applications.

In addition to the main performance indicators presented through box plots and summary tables for the benchmark functions, we also reported the evolution of the simple regret metric. Following the definition in [29,30], the simple regret at iteration t is expressed as

$${\widehat{r}}_t^{+}=f\left({\mathbf{x}}^{\ast }\right)-\underset{{\mathbf{x}}_t\in {\mathcal{D}}_{1:t}}{min}f\left({\mathbf{x}}_t\right),$$

(23)

where ${\mathbf{x}}^{\ast }$ denotes the global optimum of the objective function and ${\mathcal{D}}_{1:t}$ is the set of evaluated points up to iteration t. The mean simple regret over 10 independent runs is plotted on a logarithmic scale in Appendix B, providing an additional perspective on the convergence behavior of the algorithms across the sequence of iterations.

4.3. Application: Shape Optimization of a Solid in Linear Elasticity Under Uniaxial Loading

A structural optimization problem is addressed in which the initial geometry, which is L-shaped, is parameterized using isogeometric analysis (IGA) on a finite element mesh constructed from non-uniform rational B-spline (NURBS) surfaces [31]. The mechanical solver used is based on a MATLAB R2024b implementation of IGA in 2D linear elasticity, originally developed by Vinh Phu Nguyen (Johns Hopkins University) for educational and academic purposes.

The numerical model is based on the open-source code MIGFEM by Vinh Phu Nguyen (Johns Hopkins University/Monash University), available on the author’s GitHub online repository (See reference [31] for details).

This MATLAB code implements linear isogeometric analysis (IGA) for 1D, 2D, and 3D elasticity problems, including $h/p/k$ refinement and Bézier extraction. This implementation includes the construction of stiffness matrices from NURBS, adaptive h refinement, and the treatment of natural and essential boundary conditions.

This code has been adapted to incorporate a shape optimization problem, in which the geometry of the L-shaped plate is perturbed by three design parameters that vertically modify certain NURBS control points. The design vector is denoted as follows:

$$\mathbf{x}=\left[\begin{array}{c}{\epsilon }_{y1}\hfill \\ {\epsilon }_{y2}\hfill \\ {\epsilon }_{y3}\hfill \end{array}\right]\in \mathcal{X}\subset {\mathbb{R}}^3$$

where each variable ${\epsilon }_{yi}$ represents a vertical disturbance applied to a NURBS control point.

Figure 4 summarizes the reference mechanical problem and its numerical setup. Figure 4a illustrates the L-shaped domain and boundary conditions, where uniaxial tension is applied on the right edge while the left and bottom sides are clamped. The control points in Figure 4b parameterize the geometry and serve as design variables in the optimization process. The initial mesh shown in Figure 4c guarantees element quality before deformation, and the displacement field in Figure 4d reveals the expected stress concentration at the re-entrant corner.

The goal is to minimize the total volume while ensuring that the average horizontal displacement matches a prescribed target. The optimization problem is therefore formulated as follows:

$$\underset{\mathbf{x}\in \mathcal{X}}{min}f\left(\mathbf{x}\right):=V\left(\mathbf{x}\right)+\lambda ·\left|{\overline{u}}_x\left(\mathbf{x}\right)-u_{\mathrm{target}}\right|$$

where

• $V\left(\mathbf{x}\right)$ is the total volume of the generated structure;
• ${\overline{u}}_x\left(\mathbf{x}\right)={\displaystyle \frac{1}{|{\Gamma }_D|}}{\sum }_{i\in {\Gamma }_D}{u}_x^{\left(i\right)}$ is the average horizontal displacement on the right boundary ${\Gamma }_D$;
• $u_{\mathrm{target}}$ =0.0013 is the target displacement;
• $\lambda =100$ is a regularization coefficient.

Each evaluation of $f\left(\mathbf{x}\right)$ requires solving an isogeometric elasticity FE problem:

$$\mathbf{K}\left(\mathbf{x}\right)\mathbf{u}\left(\mathbf{x}\right)=\mathbf{F},$$

where $\mathbf{K}\left(\mathbf{x}\right)$ is the stiffness matrix depending on the geometry modified by $\mathbf{x}$, and $\mathbf{u}\left(\mathbf{x}\right)$ is the associated displacement field. This formulation guarantees mechanical consistency via the imposed equilibrium, while the volume term, although approximate, plays a regularizing role, guiding the solution toward more compact forms without explicitly restricting the space of admissible designs.

To initiate the optimization process, a DoE comprising 12 samples was generated using Latin hypercube sampling (LHS). The admissible set $\mathcal{X}$ is defined by the lower and upper bounds ${[-0.50.5]}^3$. To evaluate the acquisition function at each iteration, a Monte Carlo sampling of ${10}^6$ points was extracted from the design space. The hyperparameters of the proposed optimization algorithm were established as follows: the quantile threshold $\gamma =0.01$ was used in the definition of the probability of improvement, and the scale coefficient $\beta =100$. Furthermore, to divide the DoE into good and bad subsets, ${\gamma }_{gb}=0.5$ response values were taken to construct prior distributions representing the promising and unpromising regions of the design space.

Figure 5 shows the volume evolution during the optimization. Starting from the original L-shaped design, the first 20 iterations with the proposed HSBO method progressively reduced the volume, particularly in the early steps. After this phase, the best HSBO solution and the trained Gaussian surrogate were used as the starting point for a local gradient-based optimization with Matlab’s fmincon (interior-point algorithm, default settings). This second stage successfully converged to the optimum, yielding a total volume reduction of about 30% compared to the initial design.

In terms of computational cost, HSBO required 12 functional evaluations to build the DoE, and 20 additional evaluations during the iterative process, for a total of 32. Since fmincon was applied to the Gaussian process surrogate, no additional functional evaluations were required during this refinement step. This hybrid approach illustrates HSBO’s versatility and efficiency in training the Gaussian surrogate with scarce data, achieving high accuracy in the region surrounding the optimum.

Figure 6 shows the results of the optimized L. Figure 6a shows the final positions of the three control points that act as design variables. Their vertical displacements generate the diagonal notch responsible for the volume reduction. Figure 6b shows the resulting refined NURBS mesh, which has uniform quality elements and a deformation field without local concentrations, confirming the mechanical consistency of the optimized shape. Figure 6c shows the contour of the horizontal displacement $u_x$, which exhibits a nearly linear gradient between the embedded edge and the right edge; the uniform color band on ${\Gamma }_D$ confirms that the average displacement reaches the target $u_{\mathrm{target}}=1.3\times {10}^{-3}\mathrm{m}$ with minimal dispersion.

5. Conclusions and Future Work

In this article, we have presented HSBO, a method that combines Bayesian–Hilbertian UQ modeling techniques within the framework of Bayesian optimization. The function of HA is to construct structured performance priors over the search space, identifying promising performance regions to guide the Bayesian enrichment process.

Numerical tests, carried out on various benchmark functions with varying characteristics and dimensions, reveal that the proposed method provides a systematic framework for constructing priors that can improve the classical performance of BO when the problem structure aligns with the selected parametric family. The performance improvement can manifest itself in the form of increased success rate, faster convergence, or greater proximity to the optimum with a fixed budget, which means that even in situations where the global minimum is not identified, the method converges to regions very close to the optimum, providing an excellent starting point for gradient-based refinement methods.

Future research can advance in several directions. First, explicit modeling of dependencies between data could be investigated to improve the construction of priors, as the current approach assumes independence. Second, sensitivity analyses of key hyperparameters, particularly $\gamma$ and $\beta$, would be useful not only to confirm their influence but also to determine appropriate value ranges depending on the type of problem. Third, the adoption of alternative surrogate models could be explored to evaluate possible advantages over the current option. Finally, another promising avenue would be to extend the method to constrained optimization, configuring the prior distributions in such a way that they naturally respect the feasibility conditions.