A Strongly Robust Secret Image Sharing Algorithm Based on QR Codes
Abstract
1. Introduction
- (1)
- Improved noise resistance of the secret sharing scheme: Compared with existing algorithms, the proposed algorithm demonstrates higher noise resistance.
- (2)
- Enhanced lossless reconstruction capability of secret images: The proposed algorithm achieves the lossless reconstruction of secret images under certain noise densities, and its lossless reconstruction capability surpasses that of existing algorithms.
- (3)
- Meaningful sharing strategy: For the first time, this paper realizes a secret sharing strategy that simultaneously possesses noise resistance and the meaningful sharing of shares, without pixel expansion.
- (4)
- Improved sharing efficiency: While achieving noise resistance based on the P-SIS framework, the additional computational overhead introduced by the proposed algorithm is minimal, and thus the impact on sharing efficiency remains within an acceptable range.
2. Related Works
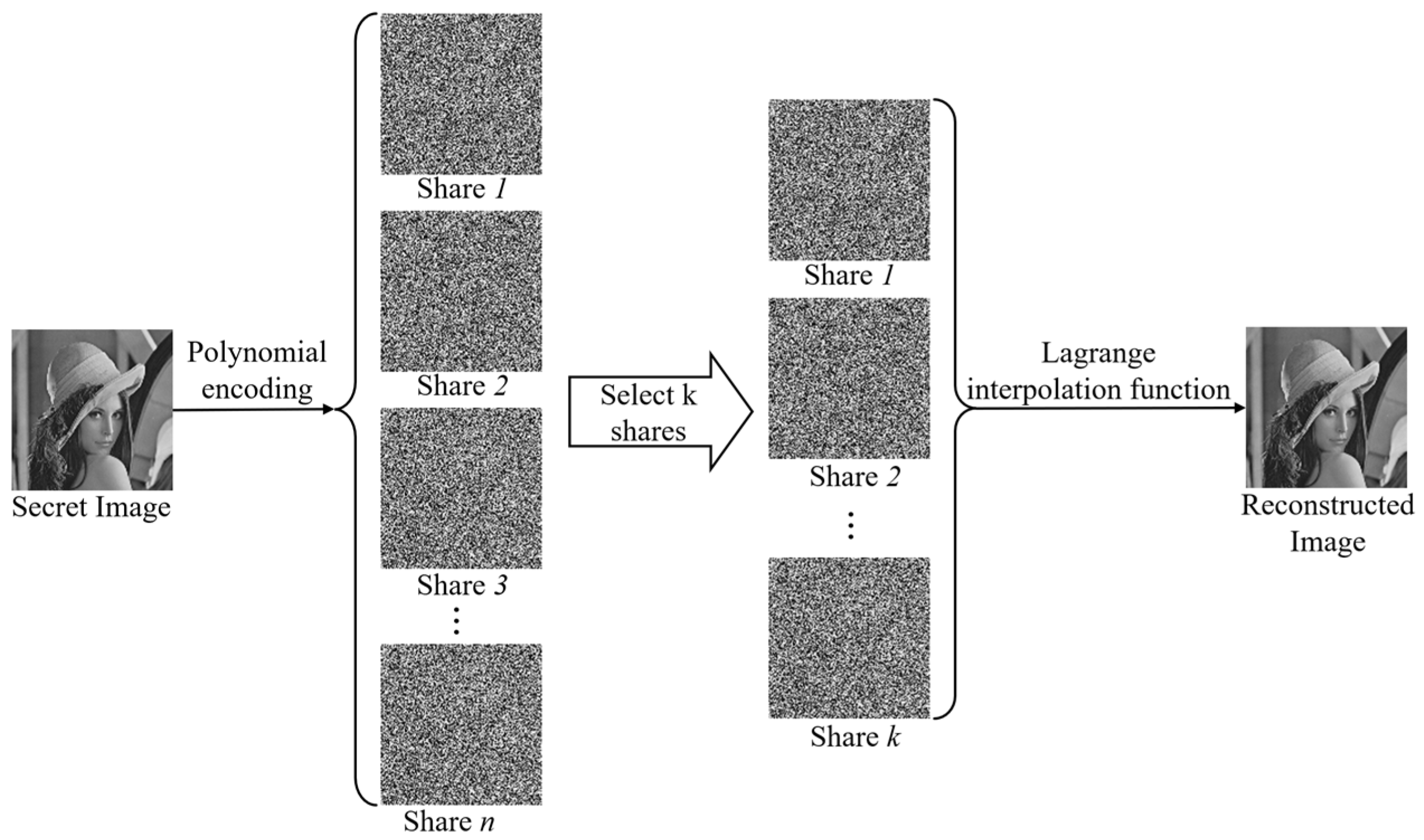
2.1. Polynomial-Based Secret Sharing
2.2. RS Code
3. The Proposed Scheme
3.1. Design Concept
3.2. Proposed Scheme
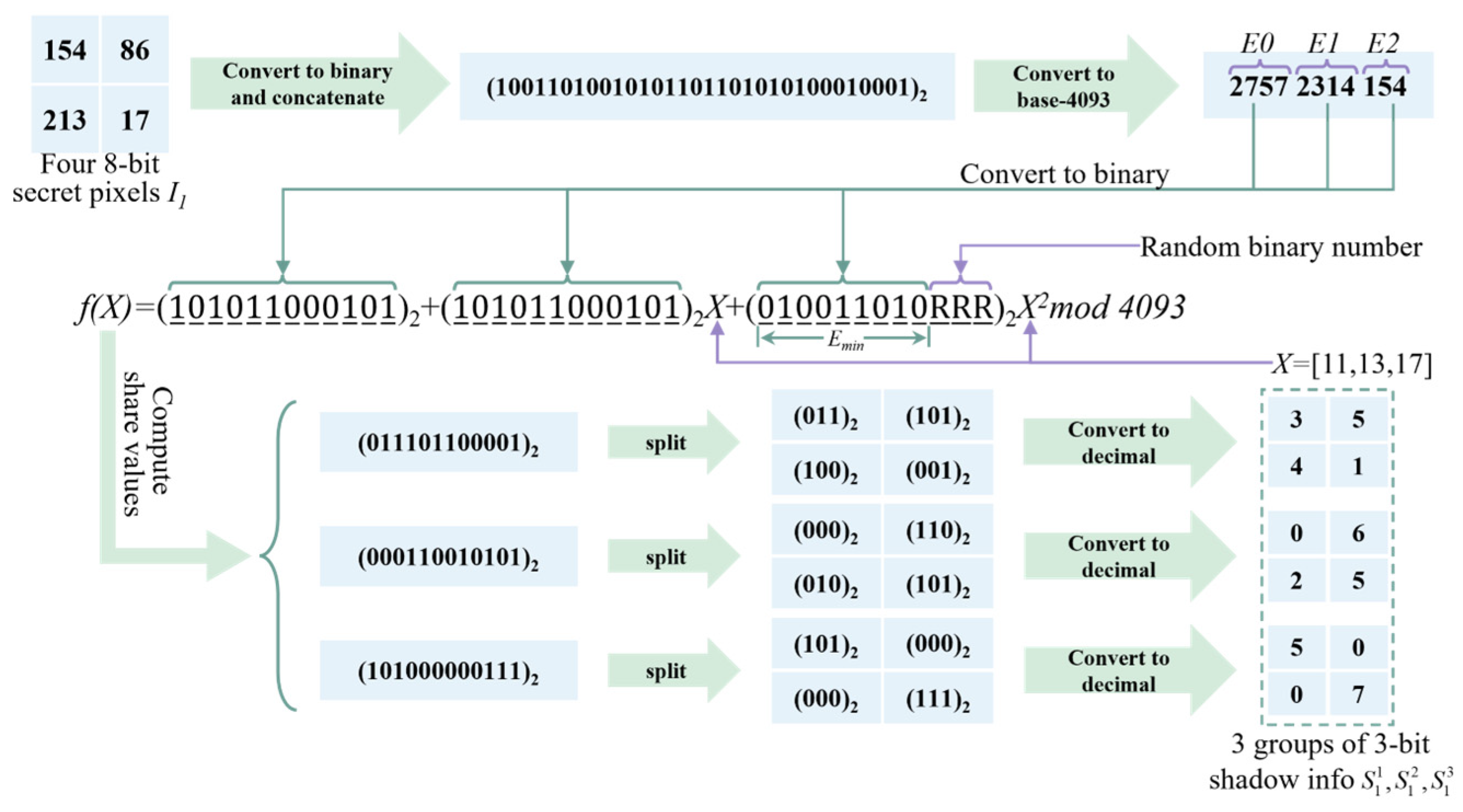
3.2.1. G4/G16 Secret Image Sharing Strategies
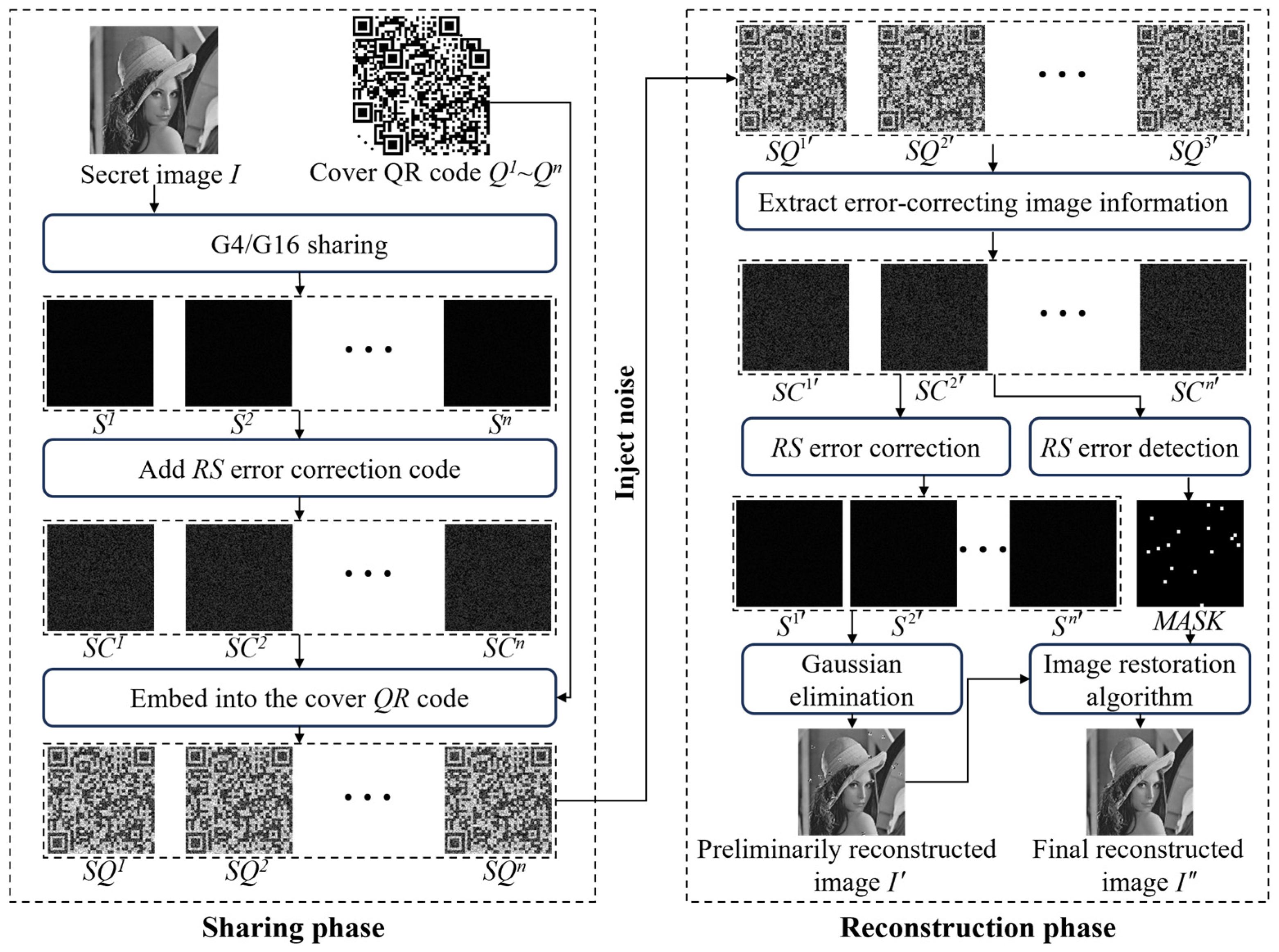
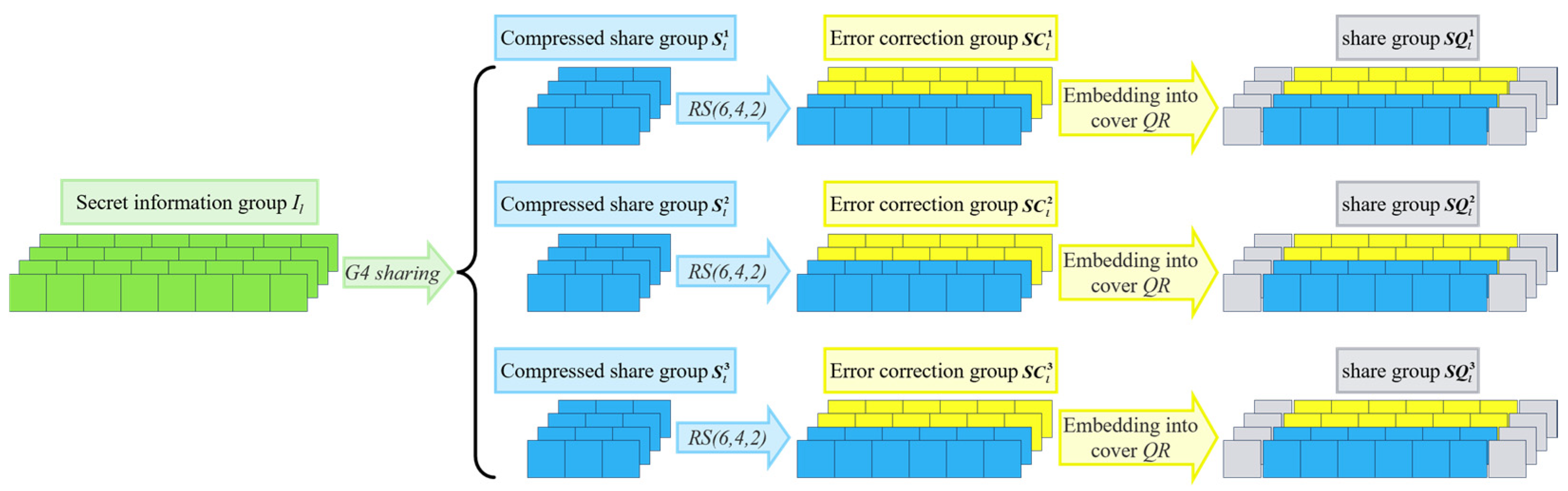
3.2.2. Sharing Procedure Based on QR Code
| Algorithm 1: Sharing Algorithm ( Sharing) |
| Input: Secret image size of ; carrier QR codes size of ; threshold ; number of participants ; identity authentication information . Output: share images . |
| Step 1: The secret image is divided into multiple secret information groups of size , with the total number of groups denoted as , i.e., . Similarly, each of the carrier QR codes is partitioned into groups of the same size , resulting in a total number of carrier groups also equal to . Step 2: Set . Step 3: Data Preprocessing. Let denote the bitwise concatenation of and . Define the modulus as . Convert the secret information group into its binary representation, denoted as , where . Subsequently, convert into a 3-digit base- representation, with each digit denoted as , , , where , , and . Let the minimum bit length that can be embedded into the embeddable coefficient in E2 be denoted as , where . Step 4: Generation of Compressed Share Groups , where , . First, generate a set of random coefficients , and set , , and . Let denote a random number with a bit length of . Then, substitute into the following polynomial function: Step 5: Generate the error-correction groups from the compressed share groups. For the -th compressed share group, pairwise concatenate its four pieces of information to obtain two 6-bit-length data segments, denoted as and , where and . Subsequently, input and into the to produce two 6-bit-length error-correction codes and . Finally, , , , and constitute the -th error-correction group, denoted as , , , and , respectively. In this step, . Step 6: Embed the error-correction group information into the carrier QR codes. Let denote the -th piece of information in the -th share group of the -th share image. Define , , , and , where . Step 7: Increment by 1 and repeat Step 3 to Step 6 until all secret information groups have been processed. Step 8: Output the share images . |
3.2.3. Reconstruction Procedure Based on QR Code
| Algorithm 2: Reconstruction Algorithm (G4 Sharing) |
| Input: share images , each of size , and authentication information . Output: Secret image . |
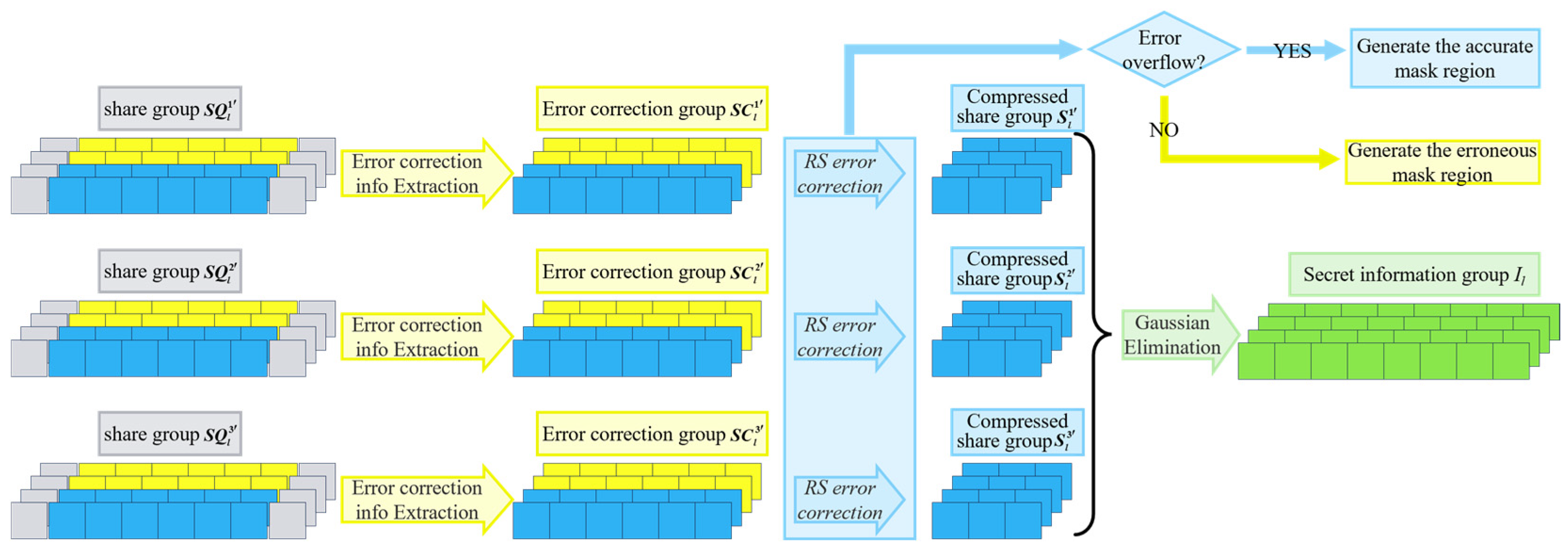
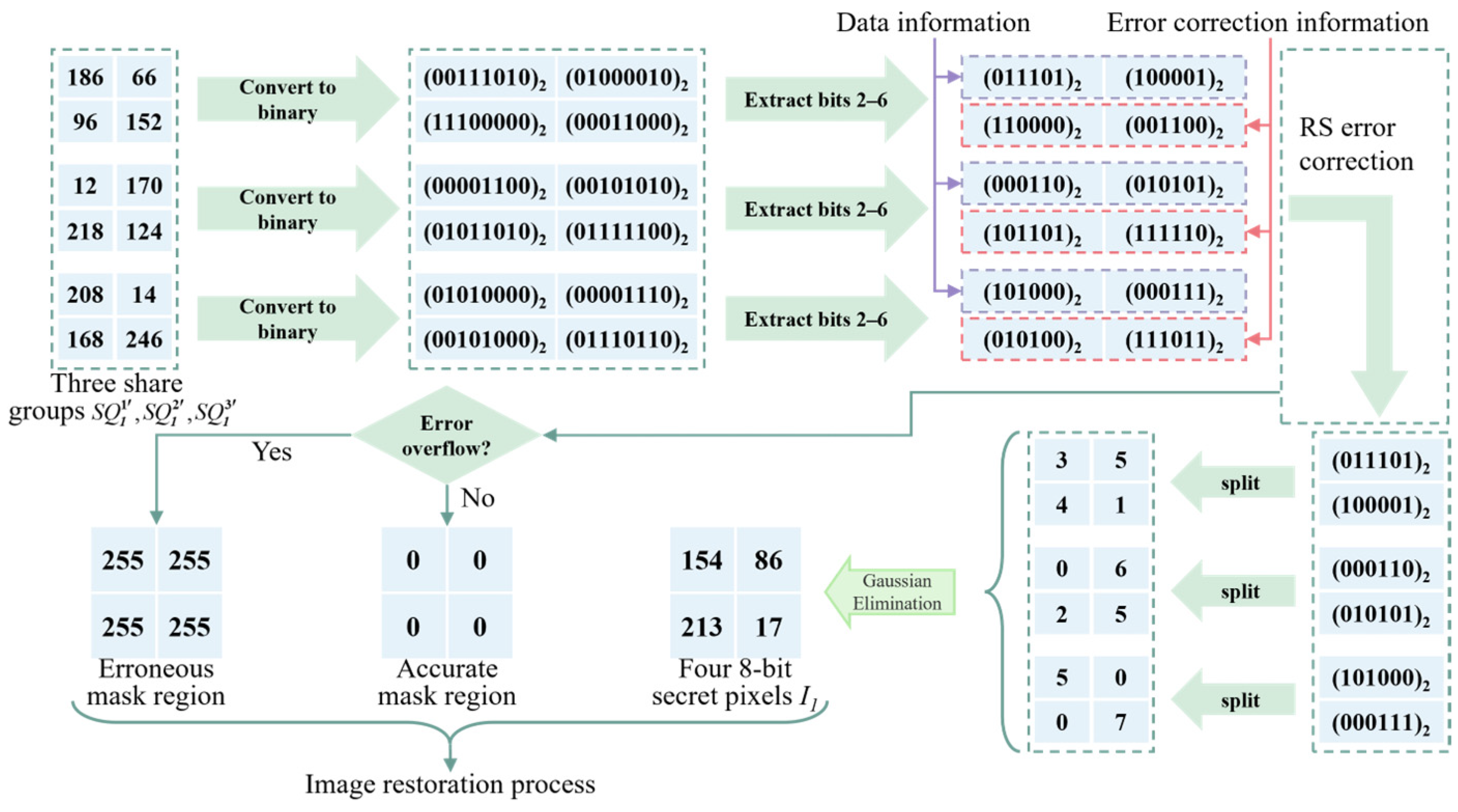
| Step 1: Partition each of the t share images into multiple share groups of size . The total number of share groups is denoted as , where . Define as the error mask of size , initialized with all zeros. Similarly, divide into groups of size , where denotes the -th group of mask information. Step 2: Set . Step 3: Extracting Error-Correction Groups from t Share Groups. Let denote the -th element of the -th share group in the -th share image, and denote the -th element of the -th error-correction group in the -th error-correction image. Define: , , , , where . Accordingly, the t error-correction groups can be obtained. Step 4: Decode the error-correction groups using RS coding. For the -th error-correction group, directly input the four 6-bit elements into the RS decoder. Denote the decoded data as and , both of which have a bit length of 6. Simultaneously, use RS decoding to record whether an overflow error has occurred in the i-th group. Subsequently, split and into four compressed share elements of 3 bits each. Let denote the -th element in the -th compressed share group of the -th compressed share image, i.e., define: , , , , where . After decoding all groups, determine whether any error-correction group has encountered an overflow. If none has, proceed to Step 6. Step 5: Set all values in to 255 to indicate that an error has occurred in the corresponding region. Step 6: All compressed share groups are input into the Gaussian elimination algorithm to obtain a 32-bit binary sequence, denoted as . This sequence is then equally divided into four 8-bit segments, yielding four secret pixels denoted as . Here, represents the -th group of secret information, i.e., . Step 7: Repeat Steps 3 through 6 until , incrementing by 1 in each iteration. Step 8: Input the error mask and the reconstructed secret image into the image inpainting algorithm to obtain the final reconstructed secret image , in which the erroneous regions have been corrected. Step 9: Output the final secret image . |
4. Experimentational Results and Analysis
4.1. Simulation Experiment
4.2. Security Analysis
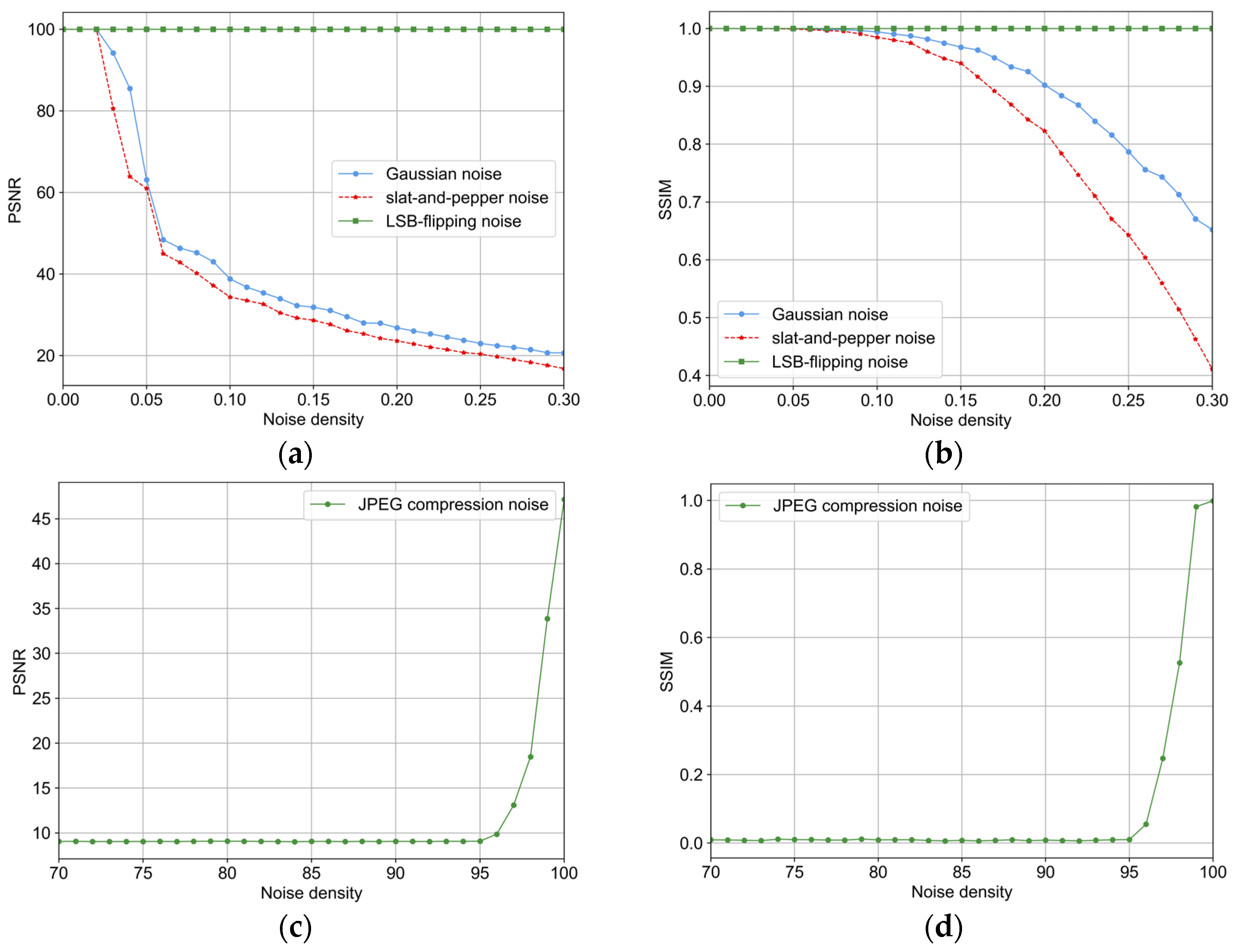
4.3. Anti-Noise Experiment
4.3.1. Resistance to Different Types of Noises
4.3.2. Resistance to Combined Noise
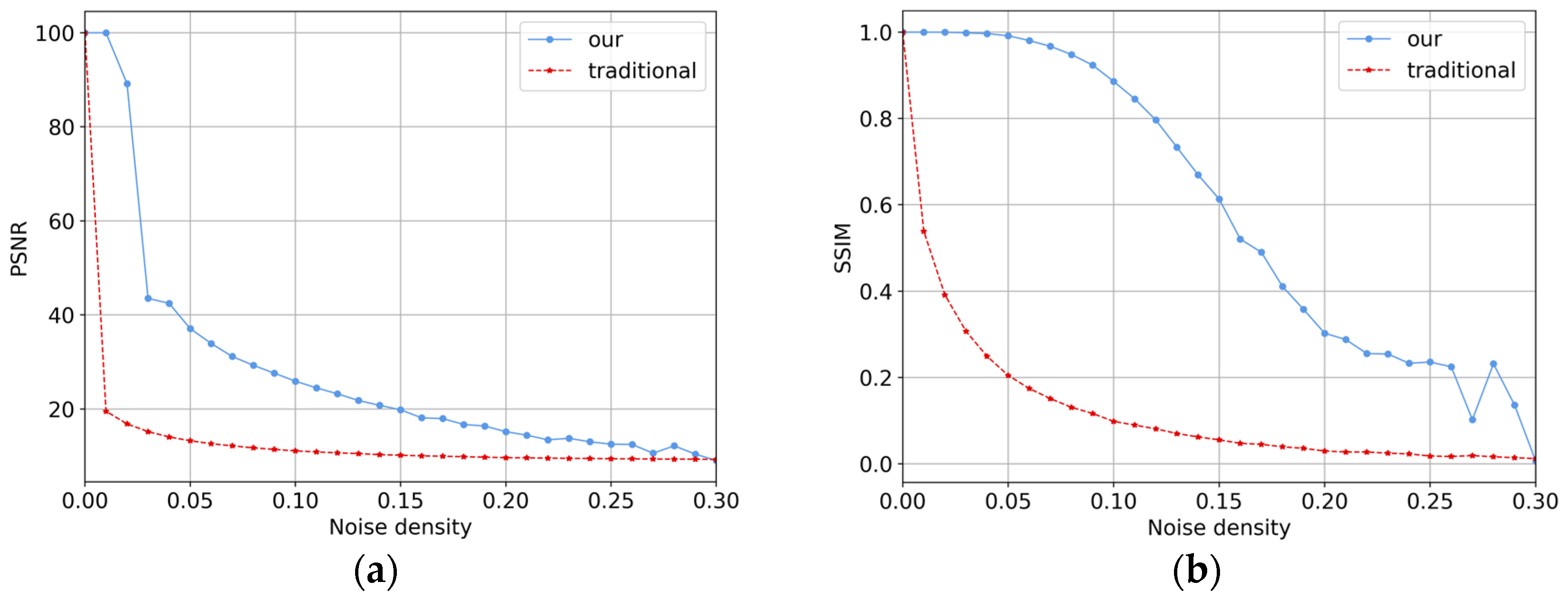
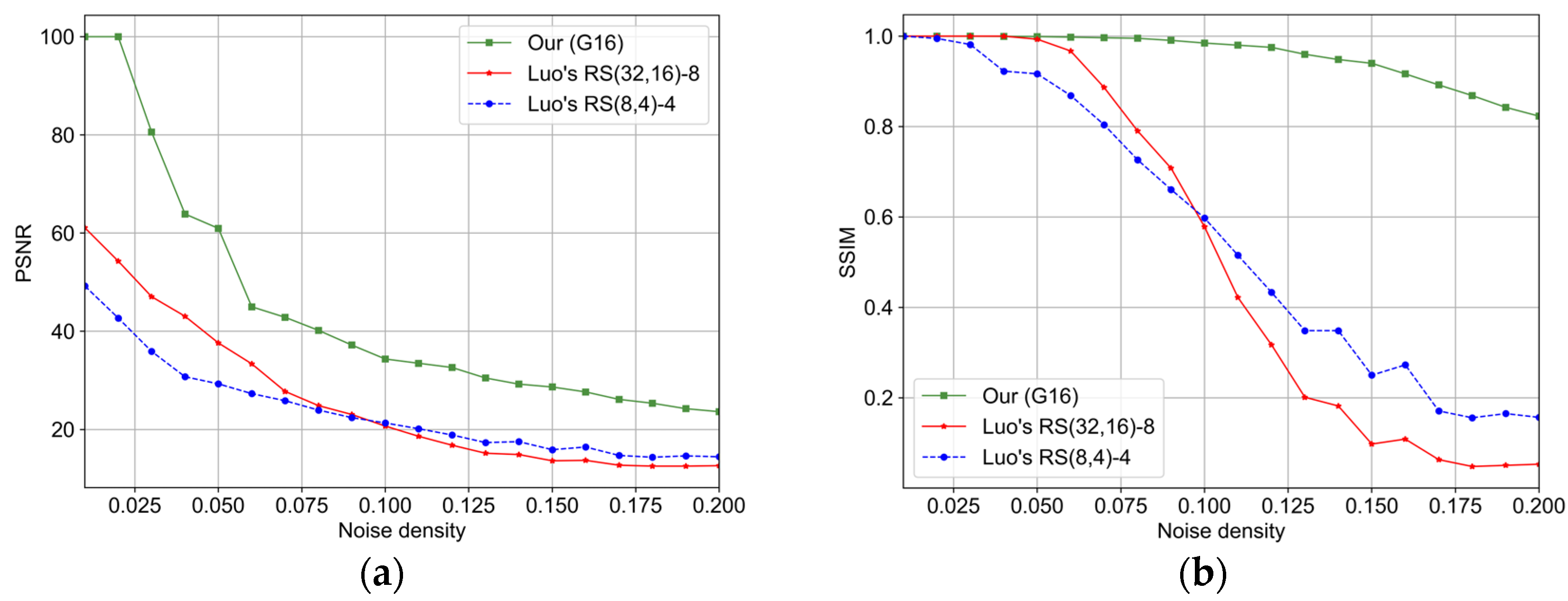
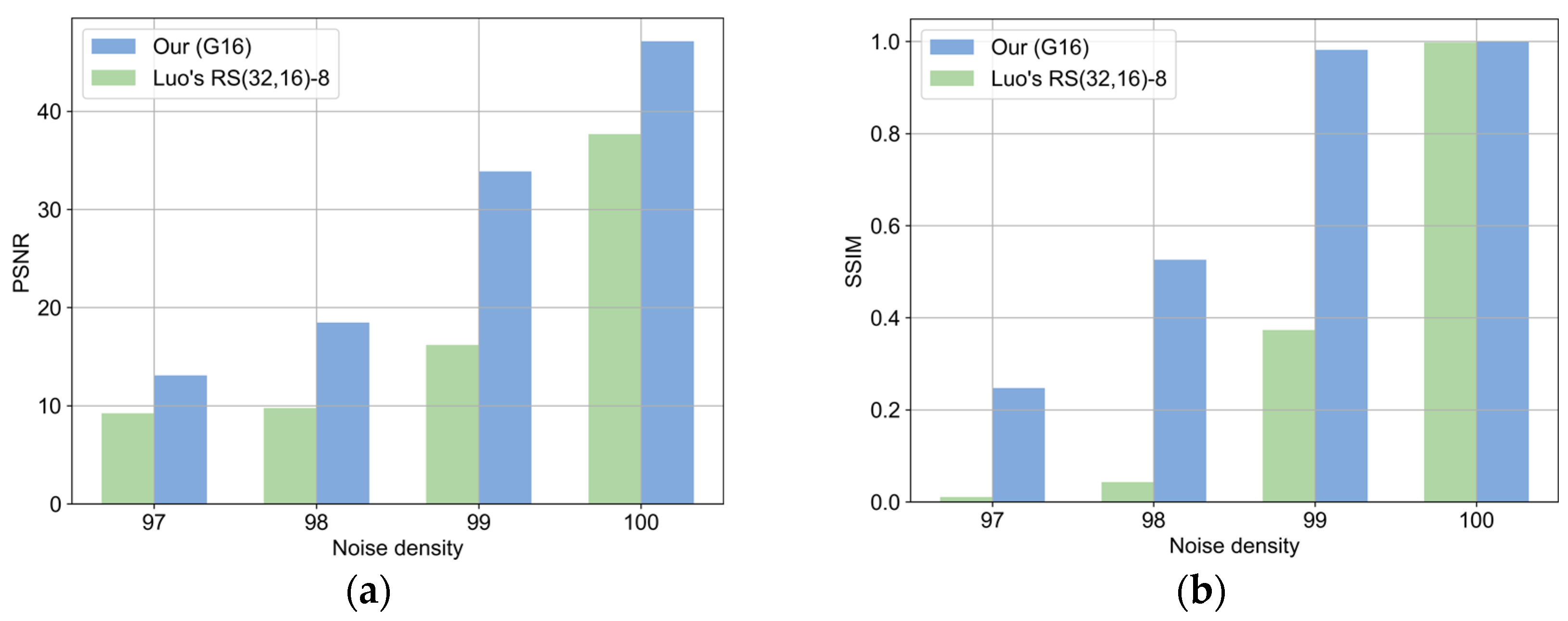
4.4. Comparison
4.4.1. Comparison with Luo et al.
4.4.2. Comparison with Other Works
4.5. Execution Time Analysis
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Parihar, B.; Rawat, A.S.; Deshmukh, M. A survey on counting-based secret sharing schemes for resource-constrained environments: Techniques, security, challenges, and future directions. J. Supercomput. 2024, 80, 17633–17687. [Google Scholar] [CrossRef]
- Salman, L.A.; Hashim, A.T.; Hasan, A.M. Selective medical image encryption using polynomial-based secret image sharing and chaotic map. Int. J. Saf. Secur. Eng. 2022, 12, 357–369. [Google Scholar] [CrossRef]
- Xiong, L.; Han, X.; Yang, C.N. CP-PSIS: CRT and polynomial-based progressive secret image sharing. Signal Process. 2021, 185, 108064. [Google Scholar] [CrossRef]
- Prashanti, G.; Bhat, M.N. Cheating identifiable polynomial based secret sharing scheme for audio and image. Multimed. Tools Appl. 2024, 83, 403–423. [Google Scholar] [CrossRef]
- Gao, K.; Horng, J.H.; Chang, C.C.; Chang, C.C. Linguistic secret sharing via ambiguous token selection for IOT security. Electronics 2024, 13, 4216. [Google Scholar] [CrossRef]
- Huang, J.; Cui, Q.; Zhou, Z.; Yu, K.; Yang, C.N.; Choo, K.K.R. Encrypted domain secret medical-image sharing with secure outsourcing computation in IoT environment. IEEE Internet Things J. 2023, 11, 2382–2393. [Google Scholar] [CrossRef]
- Alwan, A.H.; Hashim, A.T.; Ali, S.A. Partial encryption scheme of medical images based on DWT, secret image sharing and hyperchaotic system. Trait. Signal 2024, 41, 1807. [Google Scholar] [CrossRef]
- Zhou, Z.; Wan, Y.; Cui, Q.; Yu, K.; Mumtaz, S.; Yang, C.N.; Guizani, M. Blockchain-based secure and efficient secret image sharing with outsourcing computation in wireless networks. IEEE Trans. Wirel. Commun. 2023, 23, 423–435. [Google Scholar] [CrossRef]
- Sarkar, P.; Nag, A.; Singh, J.P. Blockchain-based authenticable (k, n) multi-secret image sharing scheme. J. Electron. Imaging 2023, 32, 053019. [Google Scholar] [CrossRef]
- Yan, X.; Li, L.; Chen, J.; Sun, L. Public key based bidirectional shadow image authentication without pixel expansion in image secret sharing. Front. Inf. Technol. Electron. Eng. 2023, 24, 88–103. [Google Scholar] [CrossRef]
- Attasena, V.; Darmont, J.; Harbi, N. Secret sharing for cloud data security: A survey. VLDB J. 2017, 26, 657–681. [Google Scholar] [CrossRef]
- Sun, Y.; Lu, Y.; Yan, X.; Liu, L.; Li, L. Robust secret image sharing scheme against noise in shadow images. IEEE Access 2021, 9, 23284–23300. [Google Scholar] [CrossRef]
- Zhou, Z.; Su, Y.; Li, J.; Yu, K.; Wu, Q.M.J.; Fu, Z.; Shi, Y. Secret-to-image reversible transformation for generative steganography. IEEE Trans. Dependable Secur. Comput. 2022, 20, 4118–4134. [Google Scholar] [CrossRef]
- Cheraghchi, M. Nearly optimal robust secret sharing. Des. Codes Cryptogr. 2019, 87, 1777–1796. [Google Scholar] [CrossRef]
- Luo, S.; Liu, Y.; Yan, X.; Yu, Y. Secret image sharing scheme with lossless recovery and high efficiency. Signal Process. 2023, 206, 108931. [Google Scholar] [CrossRef]
- Yan, X.; Liu, L.; Li, L.; Lu, Y. Robust secret image sharing resistant to noise in shares. ACM Trans. Multimed. Comput. Commun. Appl. 2021, 17, 1–22. [Google Scholar] [CrossRef]
- Liu, X.B.; Koh, S.N.; Wu, X.W.; Chui, C.C. Reconstructing a linear scrambler with improved detection capability and in the presence of noise. IEEE Trans. Inf. Forensics Secur. 2011, 7, 208–218. [Google Scholar] [CrossRef]
- Luo, S.; Liu, Y.; Yan, X.; Sun, Y. Robust secret image sharing scheme with improved anti-noise capability. Signal Process. 2024, 219, 109423. [Google Scholar] [CrossRef]
- Sklar, B. Reed-Solomon Codes. 2001, pp. 1–33. Available online: http://hscc.cs.nthu.edu.tw/~sheujp/lecture_note/rs.pdf (accessed on 15 August 2025).
- Cox, R. Qart Codes. Available online: http://research.swtch.com/qart (accessed on 15 August 2025).
- Maduskar, D.; Dube, N. Navier–stokes-based image inpainting for restoration of missing data due to clouds. In Innovations in Computational Intelligence and Computer Vision, Proceedings of the ICICV 2020, Jaipur, India, 17–19 January 2020; Springer: Singapore, 2021; pp. 497–505. [Google Scholar]



| Symbol | Description |
|---|---|
| Original secret image. | |
| QR code carrier. | |
| , | Length and width of the original secret image and QR code carrier image. |
| n represents the number of pixels in each pixel group, and n is a perfect square. For example, G4 represents a pixel group containing 4 pixels, with a group size of 2 × 2; G16 represents a pixel group containing 16 pixels, with a group size of 4 × 4. | |
| The l-th pixel group in the original secret image. | |
| The pixel value corresponding to indices i, j in the l-th pixel group of the original secret image. , , | |
| The l-th pixel group in the p-th QR code carrier. , | |
| The pixel value at indices i, j in the l-th pixel group of the p-th QR code carrier. | |
| , , | The l-th compressed share group in the p-th compressed share image, the l-th error-correction share group in the p-th error-correction share image, and the l-th share group in the p-th share image. , |
| , , | The i-th pixel in the l-th compressed share group of the p-th compressed share image, the i-th pixel in the l-th error-correction share group of the p-th error-correction share image, and the i-th pixel in the l-th share group of the p-th share image. |
| Represents a segment of RS encoding, where the bit length of each codeword is m, the total length is r, and the length of the data codewords is d. |
| Features | Luo’s [15] | Yan’s [10] | Sun’s [12] | Luo’s [18] | Ours |
|---|---|---|---|---|---|
| Resistance to noise | No | Weak | Weak | Strong | Very strong |
| Resistible noise types | 0 | ≥3 | ≥3 | ≥4 | ≥4 |
| Lossless reconstruction capability | Weak | Weak | Weak | Strong | Very Strong |
| No pixel expansion | Yes | Yes | Yes | Yes | Yes |
| Meaningful share | No | No | No | No | Yes |
| Size: 128 × 128 | Size: 256 × 256 | |||
|---|---|---|---|---|
| Sharing Time | Reconstruction Time | Sharing Time | Reconstruction Time | |
| (3, 3) | 1.07 s | 1.45 s | 4.51 s | 6.56 s |
| (4, 5) | 1.71 s | 1.95 s | 7.69 s | 9.81 s |
| (7, 10) | 3.63 s | 3.37 s | 16.80 s | 26.71 s |
| Size: 128 × 128 | Size: 256 × 256 | |||
|---|---|---|---|---|
| Sharing Time | Reconstruction Time | Sharing Time | Reconstruction Time | |
| (3, 3) | 0.39 s | 0.89 s | 1.60 s | 4.09 s |
| (4, 5) | 0.64 s | 1.17 s | 2.84 s | 9.46 s |
| (7, 10) | 1.27 s | 2.02 s | 5.78 s | 18.80 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, P.; Chen, C.; Wan, X. A Strongly Robust Secret Image Sharing Algorithm Based on QR Codes. Algorithms 2025, 18, 535. https://doi.org/10.3390/a18090535
Huang P, Chen C, Wan X. A Strongly Robust Secret Image Sharing Algorithm Based on QR Codes. Algorithms. 2025; 18(9):535. https://doi.org/10.3390/a18090535
Chicago/Turabian StyleHuang, Pengcheng, Canyu Chen, and Xinmeng Wan. 2025. "A Strongly Robust Secret Image Sharing Algorithm Based on QR Codes" Algorithms 18, no. 9: 535. https://doi.org/10.3390/a18090535
APA StyleHuang, P., Chen, C., & Wan, X. (2025). A Strongly Robust Secret Image Sharing Algorithm Based on QR Codes. Algorithms, 18(9), 535. https://doi.org/10.3390/a18090535







