Intelligent Method for Generating Criminal Community Influence Risk Parameters Using Neural Networks and Regional Economic Analysis
Abstract
1. Introduction and Related Works
1.1. Relevance of the Research
1.2. State of the Art
1.3. Main Attributes of the Research
2. Materials and Methods
2.1. The Economic Activity, the Criminal Communities’ Influence Intensity, and the Risk Parameter Method Development
- E(t) is the economic activity index or the economic development aggregate parameter (e.g., the investment, income, and employment level);
- C(t) is the criminal community’s influence intensity (the criminal structures, their activity, and influence on economic activity);
- I(t) is a risk parameter characterising the threat level to economic stability caused by criminal structures.
- The basic logic of economic activity growth is determined by taking into account its naturally limited development, the negative impact of crime, and controlled external influence.
- The reasons for the change in the criminal activity level are formulated, taking into account its dependence on the economic base, accumulated risk, and natural attenuation.
- The integral risk accumulation mechanism is described by taking into account both current changes in the economy and crime, as well as the accumulated “memory” effect.
- An equations vector system is formed, combining three variables and allowing us to analyse their joint dynamics and the influence of the control signals.
- All possible stationary combinations of economic, crime, and risk levels are identified;
- The model is linearised around each such state, minor deviations are introduced, and only linear terms are selected.
- The Jacobian matrix is constructed to describe the system’s sensitivity to minor disturbances.
- The characteristic equation is derived from the Jacobian matrix, which specifies the conditions under which disturbances decay or grow.
- The stability criterion is applied, determining the parameters under which the system remains in equilibrium, and the Hopf bifurcation condition is formulated.
- The research geographic area is designated, and the economic, criminal, and risk parameter dependence on coordinates and time is specified.
- The spatial distribution of processes is taken into account through the diffusion operator, as well as distributed control actions.
- A complete space–time equation system is written for all three variables, taking into account diffusion and control.
- The initial and boundary conditions are determined for the correct formulation of the problem in a given territory.
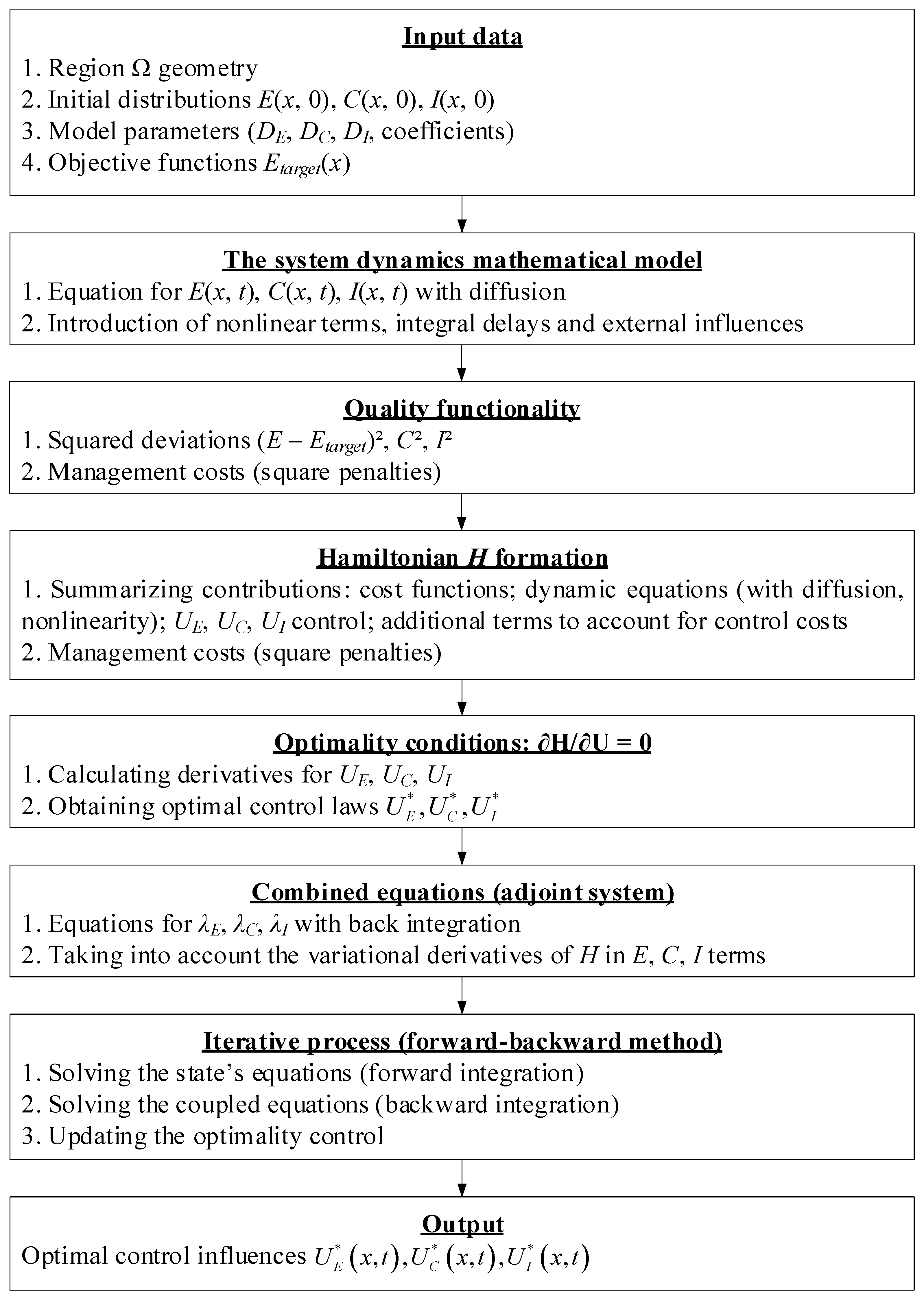
- The control quality target functional and the corresponding Hamiltonian with adjoint variables are formed.
- The optimality conditions are derived, and the iterative algorithm “forward–backward” is described for finding optimal control strategies.
- Changes in economic activity E(t) depend on its growth rates, criminal activity C(t), and feedback through the risk parameter I(t).
- The criminal structures’ C(t) dynamics are defined as their exponential growth with a limitation depending on the economic base E(t), as well as external and internal factors.
- The risk parameter I(t) accumulates information on the E(t) and C(t) current and past dynamics, reflecting both the direct impact of changes and the lagged effects.
2.2. Determining the Stability Boundaries
2.3. Development of a Spatial Optimisation Method
2.4. Development of a Neural Network for the Optimal Control Problem’s Numerical Solution
3. Case Study
3.1. Problem Statement
3.2. Selecting a Neural Network Architecture
| Algorithm 1: The pseudocode of the NARX neural network training (author’s research). |
| Initialisation: set network architecture and initial weights W, b set combined loss function L = Lsup + α · Lres Training cycle: for epoch = 1 to Epochs do for each batch X = {E(x), C(x), I(x)} from dataset do // Forward pass ŨE, ŨC, ŨI ← Network.forward(X) // Calculate losses Lsup ← ∥ŨE–UE_target∥^2 + ∥ŨC–UC_target∥^2 + ∥ŨI–UI_target∥^2; Lres ← PDE_residuals(E, C, I, ŨE, ŨC, ŨI); L ← Lsup + α · Lres; // Backpropagation gradients ← backprop(L) W, b ← optimizer.update(W, b, gradients) end for // (if needed) change learning rate end for |
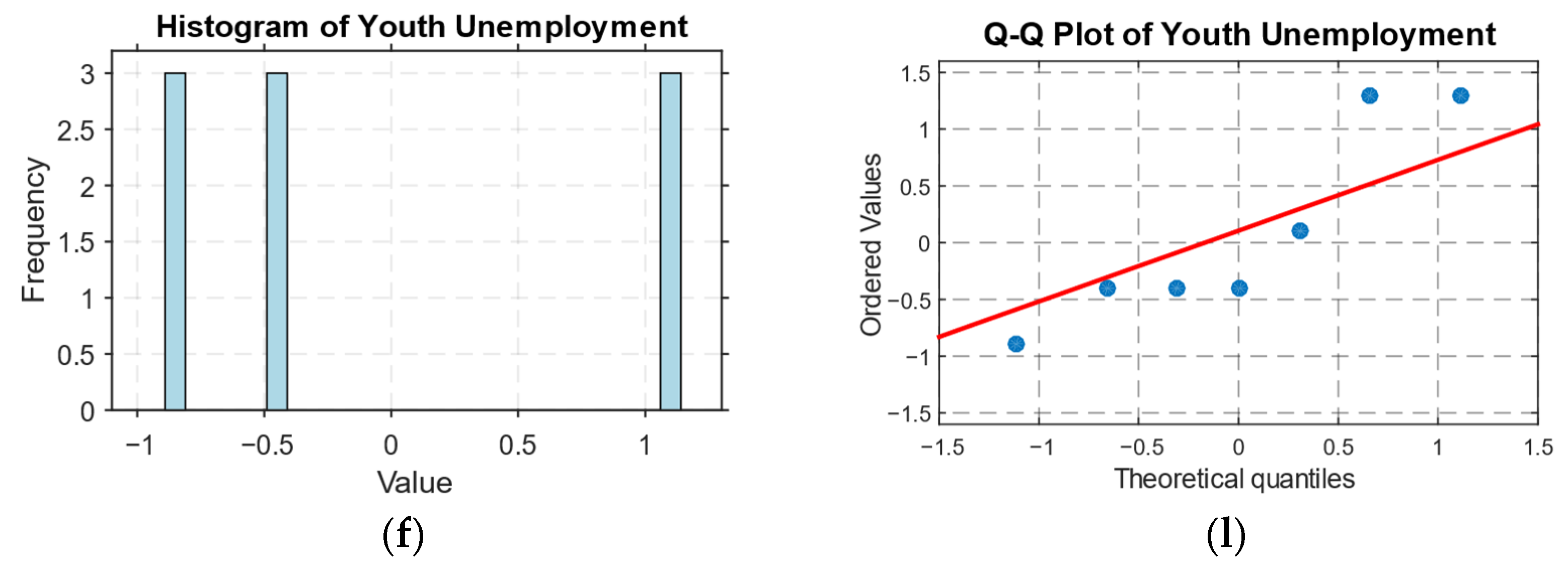
3.3. Data Collection and Preparation
3.4. Simulation Results
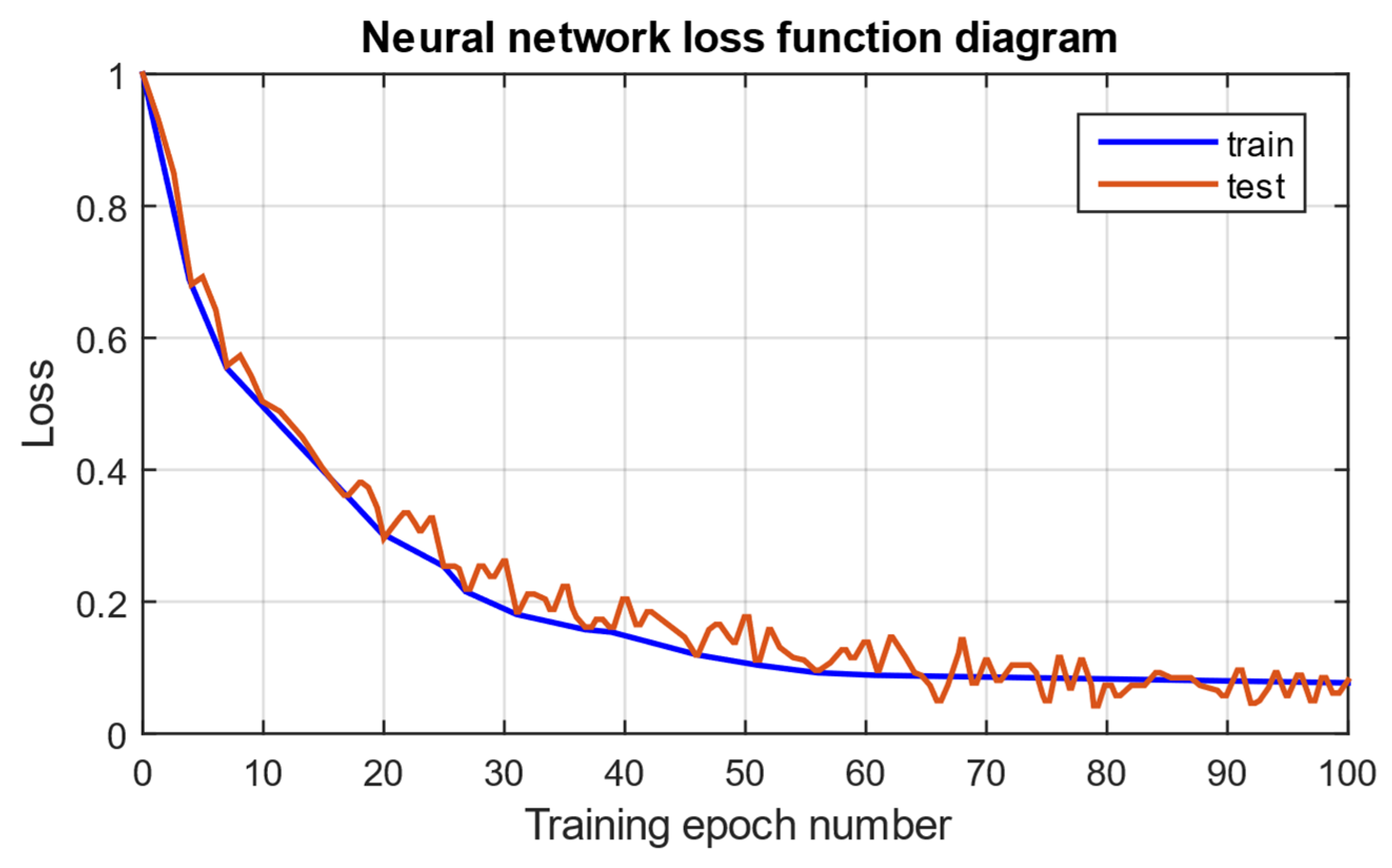
3.5. The Neural Network Performance Evaluation
4. Discussion
4.1. Obtained Results’ Evaluation
4.2. Estimating Computational Complexity
4.3. The Obtained Results in Practical Implementation
4.4. The Obtained Results for Limitations and Prospects for Further Research
- The reaction–diffusion equation model (19) takes into account only the economic and criminal activity deterministic dynamics without random fluctuations or external noise, which limits its applicability in unpredictable crises and abrupt social change conditions.
- The system’s linearisation around the stationary points (7) and (8) provides only local stability criteria and does not reflect possible behaviour under significant disturbances or bifurcations far from equilibrium.
- The neural network preprocessing and training are based on data from only three months (September–November 2024), which reduces the prediction reliability for other seasons and long-term trends.
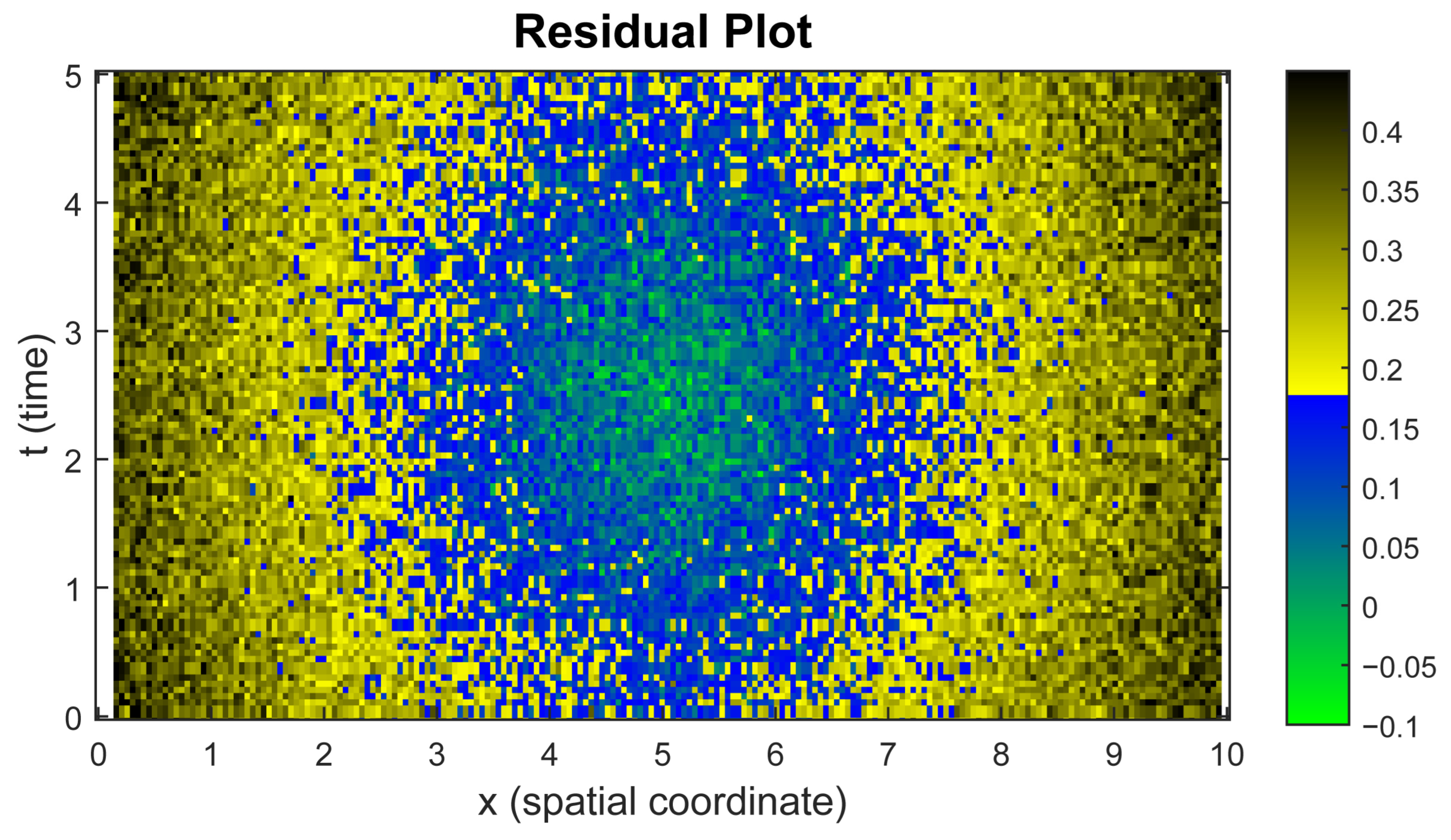
- The residual errors distribution shows significant errors in the boundary conditions of the model (see Figure 12), which can lead to inaccuracies in areas with sharp gradients in economic or criminal parameters.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cretu-Adatte, C.; Azi, J.W.; Beaudet-Labrecque, O.; Bunning, H.; Brunoni, L.; Zbinden, R. Unravelling the Organisation of Ivorian Cyberfraudsters: Criminal Networks or Organised Crime? J. Econ. Criminol. 2024, 3, 100056. [Google Scholar] [CrossRef]
- Béchervaise, N.E.; Benjamin, C.G. Visionary or Criminal: From Profit through Morality to Socially Sustainable Entrepreneurship. Procedia-Soc. Behav. Sci. 2013, 99, 339–350. [Google Scholar] [CrossRef]
- Street, B. The Impact of Economic Opportunity on Criminal Behavior: Evidence from the Fracking Boom. J. Public Econ. 2025, 248, 105402. [Google Scholar] [CrossRef]
- Croci, G.; Gomez, J. Breaking the Cycle: The Role of the Criminal Justice System in Understanding Homicide Rates. J. Crim. Justice 2025, 99, 102450. [Google Scholar] [CrossRef]
- Han, H.; Zhang, P.; Liu, C.; Zheng, Y. Financial Technology Development, Regional Marketization, and the Effectiveness of Criminal Investigation Cases. Financ. Res. Lett. 2025, 81, 107459. [Google Scholar] [CrossRef]
- Ibrahim, O.M.; Okuonghae, D.; Ikhile, M.N.O. A Mathematical Model of Criminal Gang Rivalry: Understanding the Dynamics and Implications. Results Control Optim. 2024, 14, 100398. [Google Scholar] [CrossRef]
- Yin, L.; Liu, R. A Normalized Deep Neural Network with Self-Attention Mechanisms Based Multi-Objective Multi-Verse Optimization Algorithm for Economic Dispatch. Appl. Energy 2025, 383, 125414. [Google Scholar] [CrossRef]
- Vladov, S. Cognitive Method for Synthesising a Fuzzy Controller Mathematical Model Using a Genetic Algorithm for Tuning. Big Data Cogn. Comput. 2025, 9, 17. [Google Scholar] [CrossRef]
- Vladov, S.; Vysotska, V.; Sokurenko, V.; Muzychuk, O.; Nazarkevych, M.; Lytvyn, V. Neural Network System for Predicting Anomalous Data in Applied Sensor Systems. Appl. Syst. Innov. 2024, 7, 88. [Google Scholar] [CrossRef]
- La Rocca, M.; Fasano, F.; Staglianò, R.; La Rocca, E.T.; Deloof, M. The Financial Life Cycle of European SMEs before, during and after Crisis Periods. What Is the Role of a Country’s Financial System? Int. Rev. Financ. Anal. 2025, 104, 104342. [Google Scholar] [CrossRef]
- Prievozník, P.; Strelcová, S. The Impact of Crisis Phenomena on Economic Security in the Automotive Industry and the Quality of Life of Employees. Transp. Res. Procedia 2023, 74, 1412–1418. [Google Scholar] [CrossRef]
- Luan, C.; Liu, R. Integrated Ecological and Environmental Spatial Soft Constraint Mechanism: Urban Multi-Objective Land Use Optimization under Multiple Scenarios. J. Environ. Manag. 2025, 385, 125661. [Google Scholar] [CrossRef]
- Oh, S.; Choi, A. How Does Divergence of Control and Cash-Flow Rights Influence Cost Stickiness? Br. Account. Rev. 2025, 57, 101495. [Google Scholar] [CrossRef]
- Moloudpourfard, B.; Zarandi, M.T.; Pouyakian, M. Updating the “Cost Factor” in the William Fine Risk Assessment Method Following Economic Power: A Case Study of Selected Production Industries in Iran. Heliyon 2025, 11, e42405. [Google Scholar] [CrossRef]
- Calabrò, F.; Minniti, G.E.; Fotia, A.; Pucinotti, R. Recovery of Historic Real Estate: Life Cycle Costing and Economic Feasibility. Procedia Struct. Integr. 2024, 64, 1759–1766. [Google Scholar] [CrossRef]
- Drydakis, N. Business Disruptions Due to Social Vulnerability and Criminal Activities in Urban Areas. J. Crim. Justice 2024, 95, 102293. [Google Scholar] [CrossRef]
- Huang, H.; Xu, X.; Du, S. Can Financial Innovation and Industrial Structure Upgrading Reduce Regional Criminal Activity Levels? Financ. Res. Lett. 2025, 75, 106862. [Google Scholar] [CrossRef]
- Tonkonoff, S. Crime as Social Excess. Hist. Hum. Sci. 2014, 27, 60–74. [Google Scholar] [CrossRef]
- Stephan, A. The Cartel Trial: Issues of Dishonesty and Jury Nullification. J. Compet. Law Econ. 2023, 19, 312–332. [Google Scholar] [CrossRef]
- Telep, C.W.; Weisburd, D.; Gill, C.E.; Vitter, Z.; Teichman, D. Displacement of Crime and Diffusion of Crime Control Benefits in Large-Scale Geographic Areas: A Systematic Review. J. Exp. Criminol. 2014, 10, 515–548. [Google Scholar] [CrossRef]
- Zakaria, A.; Osman, S.; Etwire, C.J.; Makinde, O.D. Modeling the Dynamics of Some Common Reported Offenses by the Ghana Police Service. Partial Differ. Equ. Appl. Math. 2025, 14, 101171. [Google Scholar] [CrossRef]
- Mamo, D.K.; Kinyanjui, M.N.; Teklu, S.W.; Hailu, G.K. Mathematical Modeling and Analysis of the Co-Dynamics of Crime and Drug Abuse. Sci. Rep. 2024, 14, 26461. [Google Scholar] [CrossRef]
- Rehman, A.; Wu, R. Hopf–Hopf Bifurcation of the Memory-Based Diffusive Bacterial Infection Model. Phys. D Nonlinear Phenom. 2025, 476, 134653. [Google Scholar] [CrossRef]
- Provatidis, C.; Eisenträger, S. Macroelement Analysis in T-Patches Using Lagrange Polynomials. Mathematics 2025, 13, 1498. [Google Scholar] [CrossRef]
- Vladov, S.; Scislo, L.; Sokurenko, V.; Muzychuk, O.; Vysotska, V.; Osadchy, S.; Sachenko, A. Neural Network Signal Integration from Thermogas-Dynamic Parameter Sensors for Helicopters Turboshaft Engines at Flight Operation Conditions. Sensors 2024, 24, 4246. [Google Scholar] [CrossRef]
- Vladov, S.; Sachenko, A.; Sokurenko, V.; Muzychuk, O.; Vysotska, V. Helicopters Turboshaft Engines Neural Network Modeling under Sensor Failure. J. Sens. Actuators 2024, 13, 66. [Google Scholar] [CrossRef]
- Hu, F.; Lin, J. Temporal Enhancement of Top-N Recommendation on Heterogeneous Graphs. Appl. Sci. 2025, 15, 3929. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, G.; Jia, C.; Wu, Y. Attention-Based Batch Normalization for Binary Neural Networks. Entropy 2025, 27, 645. [Google Scholar] [CrossRef]
- Yan, D.; Guan, Q.; Ou, B.; Yan, B.; Zhu, Z.; Cao, H. A Deep Reinforcement Learning-Based Decision-Making Approach for Routing Problems. Appl. Sci. 2025, 15, 4951. [Google Scholar] [CrossRef]
- Raj, N.; Murali, J.; Singh-Peterson, L.; Downs, N. Prediction of Sea Level Using Double Data Decomposition and Hybrid Deep Learning Model for Northern Territory, Australia. Mathematics 2024, 12, 2376. [Google Scholar] [CrossRef]
- Fiedler, C.; Jacobs, P.-P.; Müller, M.; Kolbig, S.; Grunert, R.; Meixensberger, J.; Winkler, D. A Comparative Study of Automatic Localization Algorithms for Spherical Markers within 3D MRI Data. Brain Sci. 2021, 11, 876. [Google Scholar] [CrossRef] [PubMed]
- Pau, D.P.; Aymone, F.M. Mathematical Formulation of Learning and Its Computational Complexity for Transformers’ Layers. Eng 2023, 5, 34–50. [Google Scholar] [CrossRef]
- Rusyn, B.; Kosarevych, R.; Lutsyk, O.; Korniy, V. Segmentation of atmospheric clouds images obtained by remote sensing. In Proceedings of the 14th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 20–24 February 2018; pp. 213–216. [Google Scholar] [CrossRef]
- Rusyn, B.; Prudyus, I.; Ostap, V. Fingerprint image enhancement algorithm. In Proceedings of the Experience of Designing and Applications of CAD Systems in Microelectronics. Proceedings of the VI-th International Conference. (IEEE Cat. No.01 EX473), Lviv-Slavsko, Ukraine, 12–17 February 2001; pp. 193–194. [Google Scholar] [CrossRef]
- Morozov, V.V.; Kalnichenko, O.V.; Mezentseva, O.O. The method of interaction modeling on basis of deep learning the neural networks in complex IT-projects. Int. J. Comput. 2020, 19, 88–96. [Google Scholar] [CrossRef]
- Shakhovska, N.; Yakovyna, V.; Kryvinska, N. An improved software defect prediction algorithm using self-organizing maps combined with hierarchical clustering and data preprocessing. Lect. Notes Comput. Sci. 2020, 12391, 414–424. [Google Scholar] [CrossRef]
- Chumachenko, D.; Sokolov, O.; Yakovlev, S. Fuzzy Recurrent Mappings in Multiagent Simulation of Population Dynamics Systems. Int. J. Comput. 2020, 19, 290–297. [Google Scholar] [CrossRef]
- Turchenko, V.; Chalmers, E.; Luczak, A. A deep convolutional auto-encoder with pooling—Unpooling layers in caffe. Int. J. Comput. 2019, 18, 8–31. [Google Scholar] [CrossRef]
- Marakhimov, A.R.; Khudaybergenov, K.K. Approach to the synthesis of neural network structure during classification. Int. J. Comput. 2020, 19, 20–26. [Google Scholar] [CrossRef]
- Sachenko, A.; Kochan, V.; Kochan, R.; Turchenko, V.; Tsahouridis, K.; Laopoulos, T. Error compensation in an intelligent sensing instrumentation system. In Proceedings of the 18th IEEE Instrumentation and Measurement Technology Conference. Rediscovering Measurement in the Age of Informatics (Cat. No.01CH 37188), IMTC 2001, Budapest, Hungary, 21–23 May 2001; Volume 2, pp. 869–874. [Google Scholar] [CrossRef]
- Mekni, A.; Narayan, J.; Gritli, H. Quinary Classification of Human Gait Phases Using Machine Learning: Investigating the Potential of Different Training Methods and Scaling Techniques. Big Data Cogn. Comput. 2025, 9, 89. [Google Scholar] [CrossRef]
- Elhady, G.F.; Elwahsh, H.; Alsabaan, M.; Ibrahem, M.I.; Shemis, E. A Formal Fuzzy Concept-Based Approach for Association Rule Discovery with Optimized Time and Storage. Mathematics 2024, 12, 3590. [Google Scholar] [CrossRef]
- Yu, Z.; Deng, H.; Tang, S. A Judging Scheme for Large-Scale Innovative Class Competitions Based on Z-Score Pro Computational Model and BP Neural Network Model. Entropy 2025, 27, 591. [Google Scholar] [CrossRef]
- Komar, M.; Golovko, V.; Sachenko, A.; Bezobrazov, S. Development of neural network immune detectors for computer attacks recognition and classification. In Proceedings of the 2013 IEEE 7th International Conference on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS), Berlin, Germany, 12–14 September 2013; pp. 665–668. [Google Scholar] [CrossRef]
- Dai, Y.; Jin, T.; Song, Y.; Sun, S.; Wu, C. Convolutional Neural Network with Spatial-Variant Convolution Kernel. Remote Sens. 2020, 12, 2811. [Google Scholar] [CrossRef]
- Ge, X.; Khazaei, J. Physics-Informed Convolutional Neural Network for Microgrid Economic Dispatch. Sustain. Energy Grids Netw. 2024, 40, 101525. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Y. Enhancement Economic System Based-Graph Neural Network in Stock Classification. IEEE Access 2023, 11, 17956–17967. [Google Scholar] [CrossRef]









| Research Approach | Advantages | Disadvantages | References |
|---|---|---|---|
| Mathematical modelling with optimal control methods and neural networks | The comprehensive analysis of socio-economic processes allows for the identification of patterns and the development of recommendations. | Full integration with classical dynamic models is not always provided; problems with adapting methods to the social environment and constantly changing conditions are possible. | [6,7,8,9] |
| Advisory solutions for rapid response | They ensure prompt response from government agencies and help to minimise the negative consequences. | There may be insufficient detailing of local features, which leads to the risk of oversimplifying the situation and limiting the accuracy of the proposed measures. | [10,11] |
| The integration of artificial intelligence methods with classical dynamics models | Opens up new perspectives in solving spatial optimisation problems, taking into account the complex interaction. | Requires significant computational resources and adaptation to the area under research specifics, which can complicate the model’s practical application. | [12] |
| Neural network application for numerical problem solving, improving prediction accuracy and cost optimisation | Allows for increasing the predictions and optimising management costs accuracy, improving the quality of numerical solutions. | Dependence on large amounts of data, the risk of overfitting models, and the difficulty of interpreting the results obtained can reduce the model’s validity without sufficient control. | [13,14,15] |
| Classical logistic growth models and statistical methods | Ease of implementation; proven methodological approaches for analysing individual aspects. | Lack of comprehensiveness: the relationship between economic development and criminal activity is not taken into account, resulting in a fragmented analysis of problems and limited applicability for crisis management. | [16,17] |
| Reaction–diffusion systems | Taking into account spatial effects, the risks of geographical distribution modelling are possible. | Classical models often ignore lagging effects and nonlinear feedback, which can reduce predictive accuracy and limit the ability to adequately respond to rapidly changing processes. | [18,19,20] |
| Logistic equations for the economic and criminological dynamics of simultaneous modelling | An attempt to integrate the two spheres’ dynamics allows for the assessment of the mutual influence of economic growth and criminal activity. | The simplified approach often fails to capture the honest feedback between the economy and criminal structures, as the criminal communities’ influence is either taken into account as an external disturbance or ignored altogether, which reduces the model’s reliability in predicting mutual influence. | [21,22] |
| Equation | Partial Derivative | ||
|---|---|---|---|
| Name | Formula | Variable | Formula |
| Economic activity equation | By E: | ||
| By C: | |||
| By I: | |||
| Criminal activity equation | Let us write the internal function so as to highlight the dependence on E and C: | By E: | |
| By C: | By adding the term—δ · C, we obtain | ||
| By I: | J23 = σ. | ||
| Stage Number | Stage Name | Stage Description |
|---|---|---|
| 1 | Initialisation | They set the system state initial distributions (economy, crime, risk) and the control actions’ initial approximation. |
| 2 | Straight pass (“forward”) | With current controls, the evolution in time and space is modelled, obtaining predictive trajectories of key indicators. |
| 3 | Return pass (“back”) | Based on the conjugate variables’ final conditions, the corresponding equations are integrated in the opposite direction, forming the deviations’ “value” fields. |
| 4 | Controls adjustment | Using the forward and backward pass results, the control actions are updated in order to reduce the target functional, again setting new control laws. |
| 5 | Convergence check | The change in the corrections’ control quality or the magnitude is evaluated; when a given criterion is reached, the iterations are terminated, otherwise they return to the forward pass. |
| Stage Number | Stage Name | Description |
|---|---|---|
| 1 | Data collection | The neural network’s input is spatial data X(x) = {E(x, t), C(x, t), I(x, t)} at a selected point in time (or a time sequence if a recurrent component or 3D convolutions are used [30,31]). |
| 2 | Forward pass | In the first step, the data is passed through convolutional layers to extract spatial features. Then, fully connected (1 × 1 convolution) layers transform the extracted features into control actions UE(x, t), UC(x, t), and UI(x, t). |
| 3 | Calculate the loss function | The loss function L is calculated. |
| 4 | Error backpropagation | By the backpropagation procedure [32], the filter weights K(l), biases b(l), and matrices W(FC1) and W(FC2) are updated. |
| 5 | Gradually decrease the loss function | The model is trained iteratively until convergence, which ensures the optimal control strategy approximation for each point x in the territory. |
| Region ID | Time | Economic Activity E | Criminal Activity C | Risk Index I | Population Density | Police Resources | Youth Unemployment |
|---|---|---|---|---|---|---|---|
| A01 | 0 | 1.55 | 0.12 | 0.89 | 1200 | 0.4 | 0.22 |
| A01 | 1 | 1.51 | 0.18 | 1.04 | 1200 | 0.4 | 0.22 |
| A01 | 2 | 1.47 | 0.29 | 1.21 | 1200 | 0.4 | 0.22 |
| A02 | 0 | 1.20 | 0.40 | 1.40 | 950 | 0.5 | 0.35 |
| A02 | 1 | 1.18 | 0.55 | 1.62 | 950 | 0.5 | 0.35 |
| A02 | 2 | 1.15 | 0.65 | 1.73 | 950 | 0.5 | 0.35 |
| A03 | 0 | 1.70 | 0.05 | 0.78 | 1400 | 0.2 | 0.18 |
| A03 | 1 | 1.65 | 0.07 | 0.85 | 1400 | 0.2 | 0.18 |
| A03 | 2 | 1.60 | 0.10 | 0.93 | 1400 | 0.2 | 0.18 |
| … | … | … | … | … | … | … | … |
| Region ID | Analytical Expression | Resulting Value |
|---|---|---|
| Accuracy | 0.9907 | |
| Precision | 0.9842 | |
| Recall | 0.9983 | |
| F1-score | 0.9912 | |
| Average time, minutes | – | 64 |
| Average accuracy | 0.9902 | |
| Dispersion accuracy | 0.00000103 |
| The Compared Neural Network Architecture | Comparison Aims | Comparison Metric | Results Obtained | ||
|---|---|---|---|---|---|
| Metric Name | Description | Using the Compared Neural Network | Using the Developed Neural Network | ||
| LSTM Recurrent Network [7] | Better modelling of the time dependencies (e.g., risk dynamics over time) | MSE | The dynamics prediction error estimation | 0.0187 | 0.0124 |
| Temporal correlation coefficient | How accurately the model captures the temporal structure | 0.79 | 0.91 | ||
| Convolutional Neural Network for Working with Spatial Distributions [45] | The accuracy of identifying geographic risk patterns accuracy | Intersection over Union (IoU) | Overlap between predicted and actual hotspots | 0.63 | 0.74 |
| Dice coefficient | Used when data is unbalanced | 0.71 | 0.83 | ||
| Physics-Informed Neural Networks (PINNs) [46] | To what extent does the model satisfy the physical–semantic equation (PSE) | Residual loss | Average residual between the partial differential equations’ left and right parts | 0.0151 | 0.0093 |
| Conservation score | How well the conservation laws are observed in the model | 0.87 | 0.96 | ||
| GNN (Graph Neural Networks) [47] | Using the connections topology between regions (e.g., migration, criminal routes) | Node classification accuracy | The city/region node classification accuracy | 0.9735 | 0.9907 |
| F1-score | Robustness to link noise | 0.9726 | 0.9912 | ||
| No. | Research Direction | Objective | Methods/Instruments | Planned Result |
|---|---|---|---|---|
| 1 | Introduction of stochastic components into the model | Accounting for random fluctuations and unpredictable social events | Stochastic differential equations (SDEs), Itô-type models | Increasing the model’s realism under uncertainty |
| 2 | Expanding the training data time interval | Seasonal and short-term distortion elimination | Long-term data collection, aggregation methods | Increasing the neural network’s generalising ability |
| 3 | Modelling interregional interactions | Accounting for the migration, cross-border crime, and information exchange impact | Graph Neural Networks (GNNs), spatial graphs | Spatial-network prediction of risk distribution |
| 4 | The integration of econometric models and expert assessments integration | Increasing interpretability and linking to real political decisions | Bayesian networks, expert systems | Hybrid risk management model |
| 5 | The effectiveness and adaptation to real-life applications evaluation | The model’s validation in pilot regions, and adaptation to the municipal level | Real-world testing | Recommendations for implementation in regional management systems |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vladov, S.; Chyrun, L.; Muzychuk, E.; Vysotska, V.; Lytvyn, V.; Rekunenko, T.; Basko, A. Intelligent Method for Generating Criminal Community Influence Risk Parameters Using Neural Networks and Regional Economic Analysis. Algorithms 2025, 18, 523. https://doi.org/10.3390/a18080523
Vladov S, Chyrun L, Muzychuk E, Vysotska V, Lytvyn V, Rekunenko T, Basko A. Intelligent Method for Generating Criminal Community Influence Risk Parameters Using Neural Networks and Regional Economic Analysis. Algorithms. 2025; 18(8):523. https://doi.org/10.3390/a18080523
Chicago/Turabian StyleVladov, Serhii, Lyubomyr Chyrun, Eduard Muzychuk, Victoria Vysotska, Vasyl Lytvyn, Tetiana Rekunenko, and Andriy Basko. 2025. "Intelligent Method for Generating Criminal Community Influence Risk Parameters Using Neural Networks and Regional Economic Analysis" Algorithms 18, no. 8: 523. https://doi.org/10.3390/a18080523
APA StyleVladov, S., Chyrun, L., Muzychuk, E., Vysotska, V., Lytvyn, V., Rekunenko, T., & Basko, A. (2025). Intelligent Method for Generating Criminal Community Influence Risk Parameters Using Neural Networks and Regional Economic Analysis. Algorithms, 18(8), 523. https://doi.org/10.3390/a18080523






