Concrete is one of the most important building materials in the construction industry and is widely used in construction projects in different climatic environments [
1]. Owing to the special geographical and climatic conditions, the freeze–thaw cycle caused by the long, dry, and cold climate and the large temperature difference between day and night will markedly shorten the life of concrete in cold plateau areas. In severe cases, it can cause damage or functional failure of concrete structures and even lead to serious casualties, economic losses, and extensive social impacts [
2]. Thus, the frost resistance of concrete has become an important factor to ensure the safety and durability of buildings in these types of areas [
3]. In cold environments, the relative dynamic elastic modulus and mass loss rate can effectively characterise the frost resistance of concrete [
4]. These two evaluation indicators reflect the changes in physical and mechanical properties of concrete during freeze–thaw cycles, which are crucial for understanding and improving the frost resistance of concrete.
In recent years, many studies have examined the frost resistance of concrete. From the aspect of additives in concrete, Craeye et al. [
5] used superabsorbent polymer instead of an air entrainer in concrete, which improved the freeze–thaw resistance of concrete road infrastructure. Bian et al. [
6] found that adding basalt fibre can substantially improve the freeze–thaw resistance and sulphate attack resistance of concrete. Wang et al. [
7] found that concrete with 2% nano-silica added can improve its frost resistance under the freeze–thaw cycle condition of −40 °C to + 5 °C. Liu et al. [
8] used organic and inorganic crystalline materials to study the frost resistance of concrete by surface coating and soaking and found that organic crystalliser can increase the frost resistance by 2.5 times. He et al. [
9] found that 15% microbead content can highly improve the strength and frost resistance of expanded polystyrene concrete. In addition, from the aspect of concrete structural characteristics, Liu et al. [
10] found that the porosity, aggregate particle size, and water/binder ratio of porous concrete had significant effects on its frost resistance. Zhou et al. [
11] found that the larger the particle size of aggregate, the greater the heterogeneity of the internal structure of concrete, which will lead to further defects and weaknesses and serious damage during freeze–thaw cycles. Du et al. [
12] found that the pores of 3D-printed concrete primarily gathered near the interface; additionally, the porosity of the interlayer interface was lower than that of the interwire interface, thus showing excellent frost resistance. The traditional experimental methods used in the above research often require a long time and cost. Thus, with the rapid development of computer technology, ensemble learning algorithms have shown remarkable potential in solving complex problems in many engineering and scientific fields [
13]. Some scholars have also used ensemble learning algorithms to study concrete performance prediction, especially frost resistance. Li et al. [
14] established a prediction model of concrete freeze–thaw mass loss rate with high accuracy and strong generalisation ability based on support vector machine regression and random forest regression. Tang et al. [
15] combined random forest and wavelet neural network technology, selected the influencing factors from the proportion of concrete materials, and established a high-precision prediction model of concrete frost resistance. Wang et al. [
16] proposed an effective method for predicting the frost resistance of concrete by optimising the concrete ratio index by using a random forest algorithm. Gao et al. [
17] established six ML models, and the performance statistics show that the XGBoost ensemble learning algorithm based on boosting has the best prediction performance for the frost resistance of rubber concrete. However, the existing study based on ensemble learning models such as RF and SVM still has some drawbacks. These models are prone to errors when dealing with imbalanced sample distributions and strong nonlinear correlations among variables. Moreover, the performance of these models is highly sensitive to the setting of hyperparameters, which requires manual adjustment based on experience and thus cannot guarantee optimal performance in multi-feature complex datasets. Meanwhile, such methods often lack a global search mechanism, making them prone to getting stuck in local optima, resulting in poor stability of the prediction results and limited generalization ability. The application of an intelligent optimisation algorithm can somewhat overcome these problems. Zhang et al. [
18] adopted the Bayesian optimisation random forest ensemble learning method to establish a three-stage frost resistance prediction model for an accurate and quick prediction of the frost resistance of concrete. Chen et al. [
19] proposed the use of NSGA-II in optimising the random forest model to improve the frost resistance of concrete in severe cold areas, realise the economic and environmentally friendly production of concrete, and improve the safety performance and service life of the project.
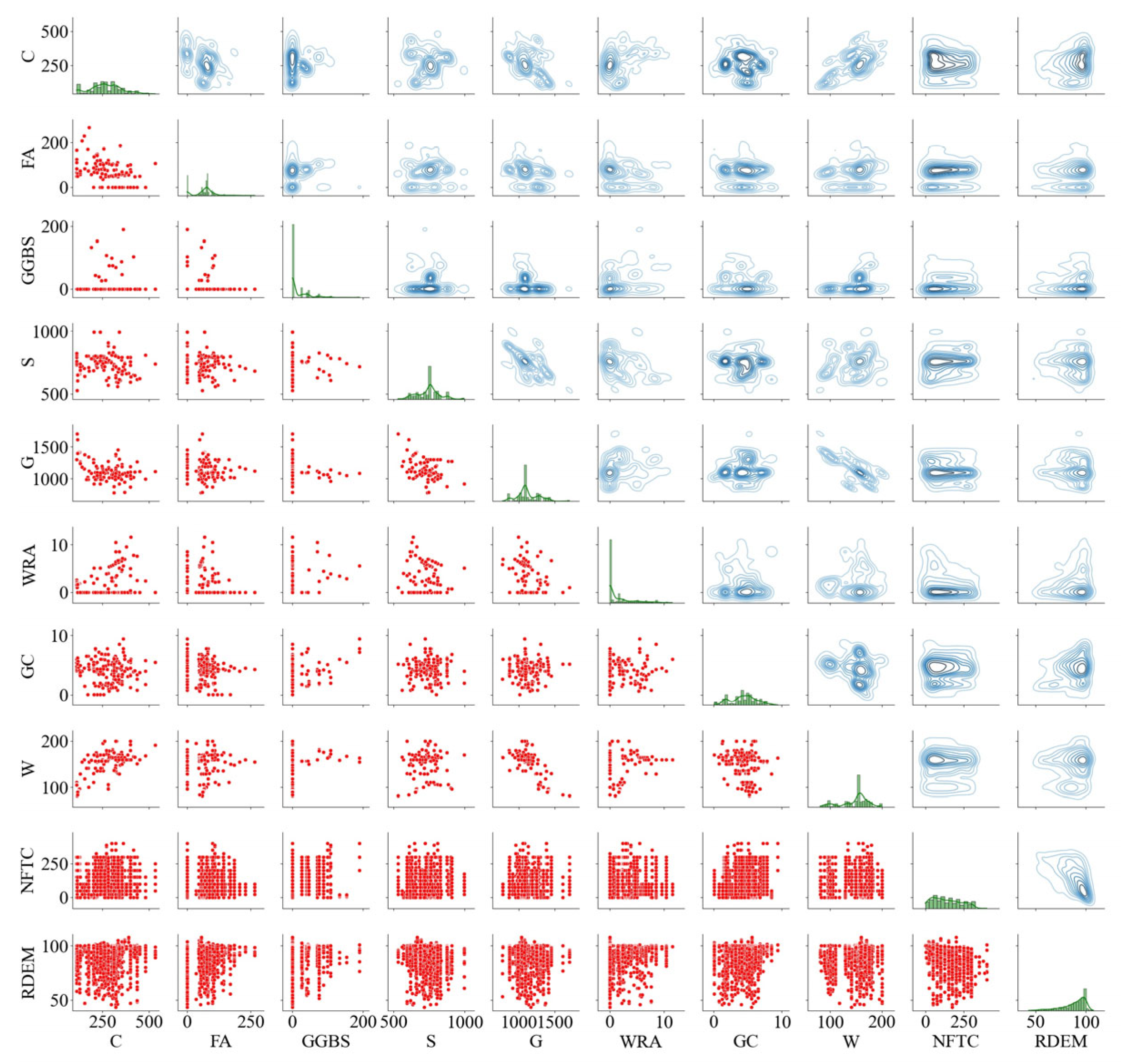
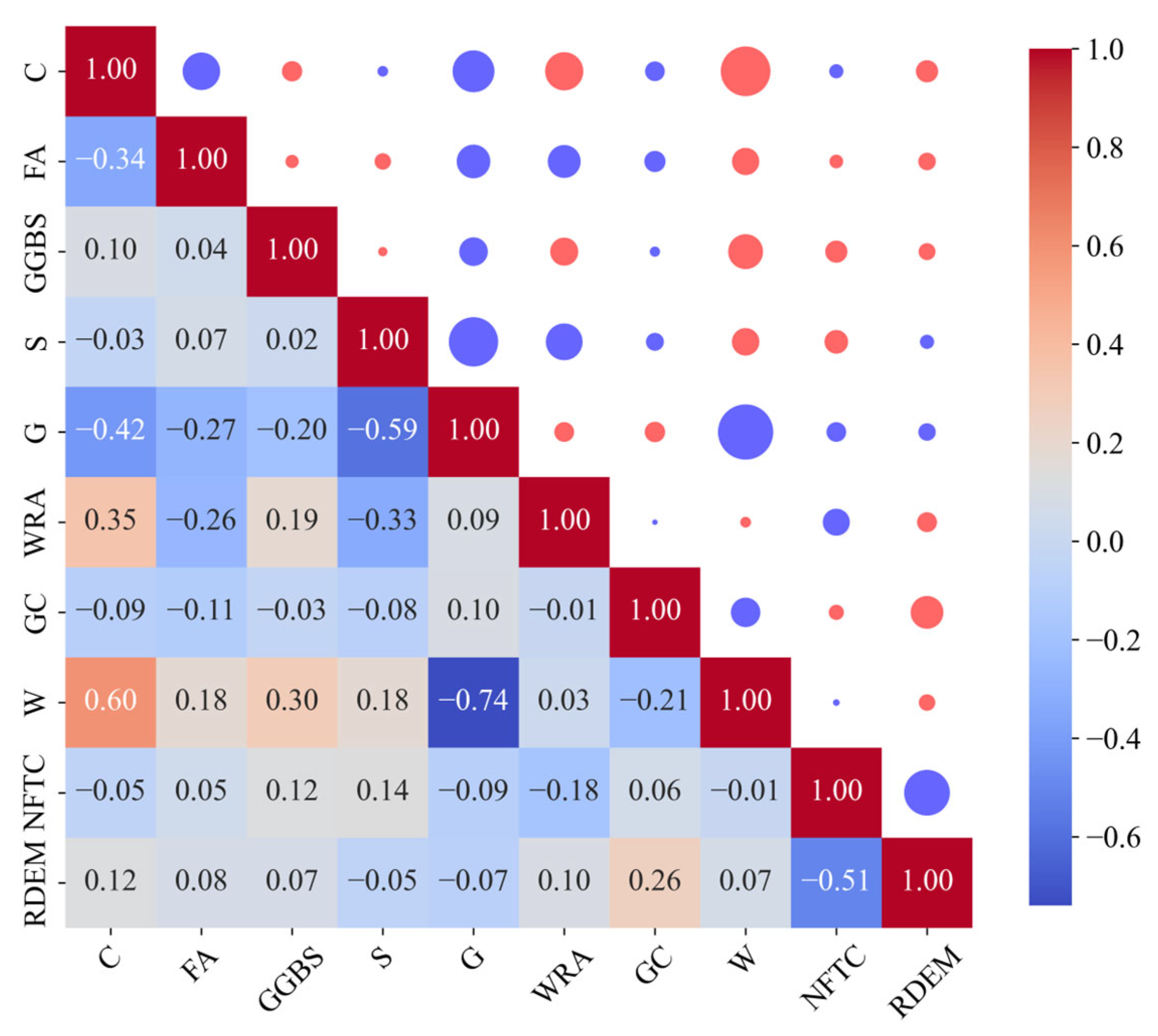
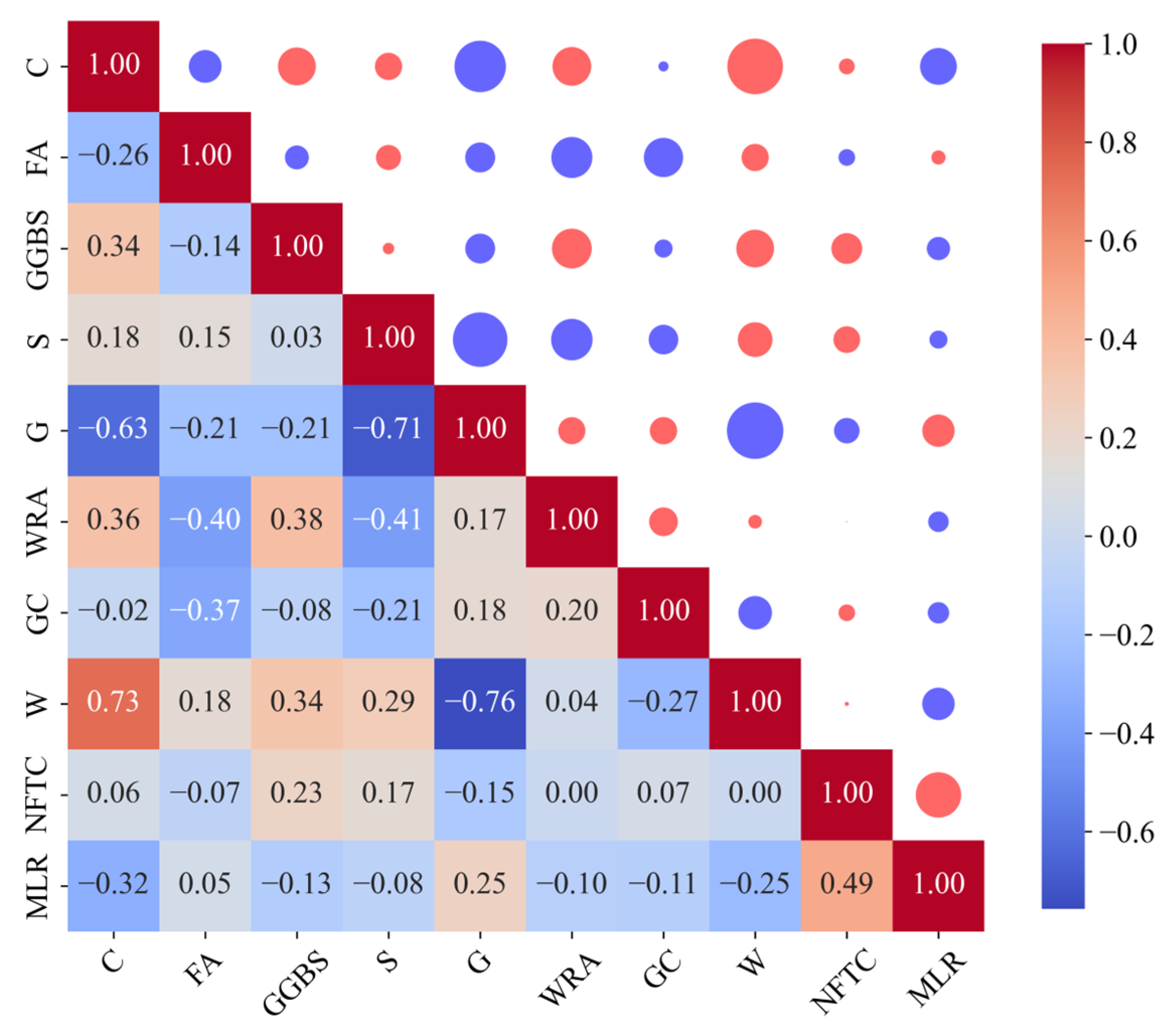
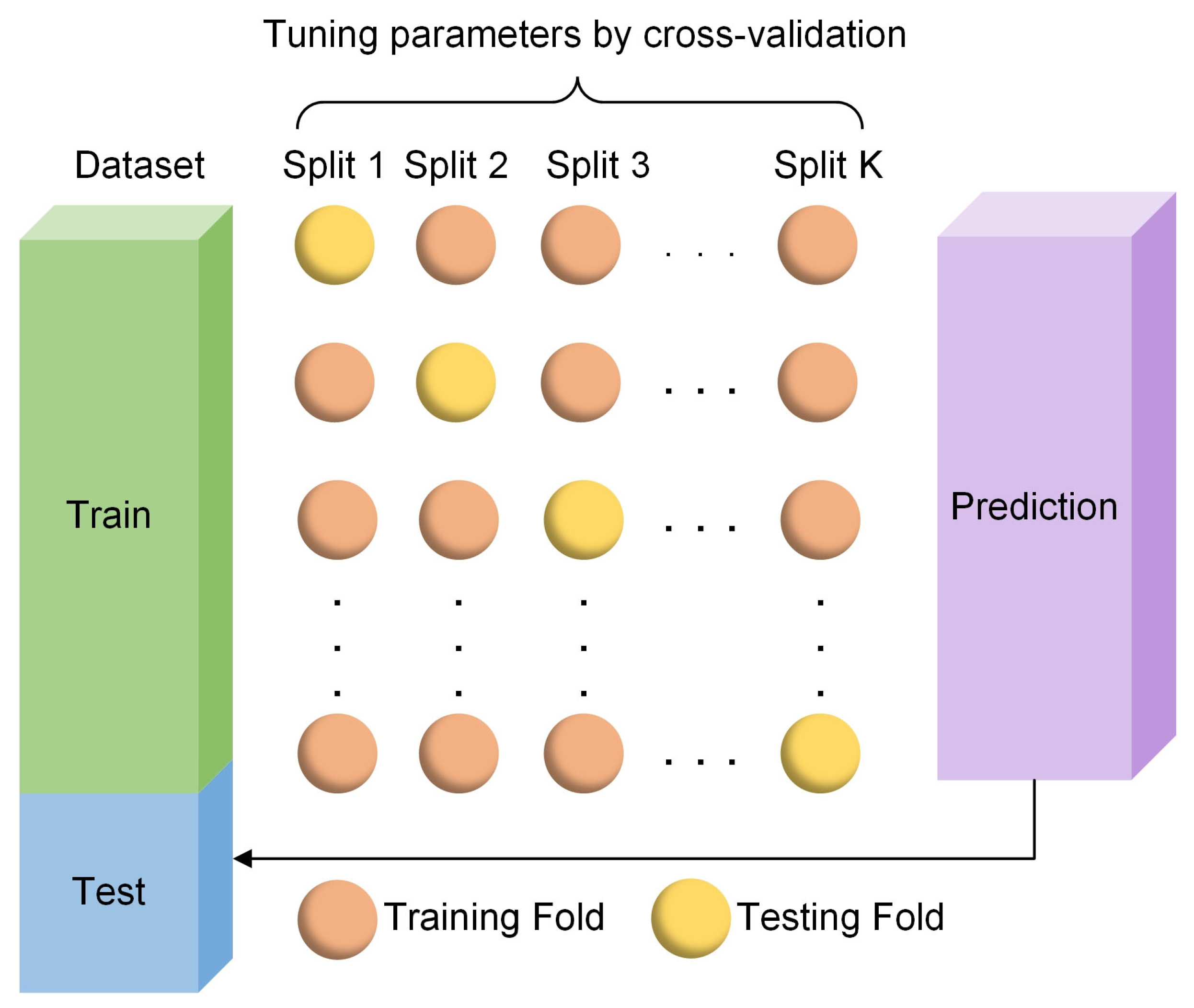
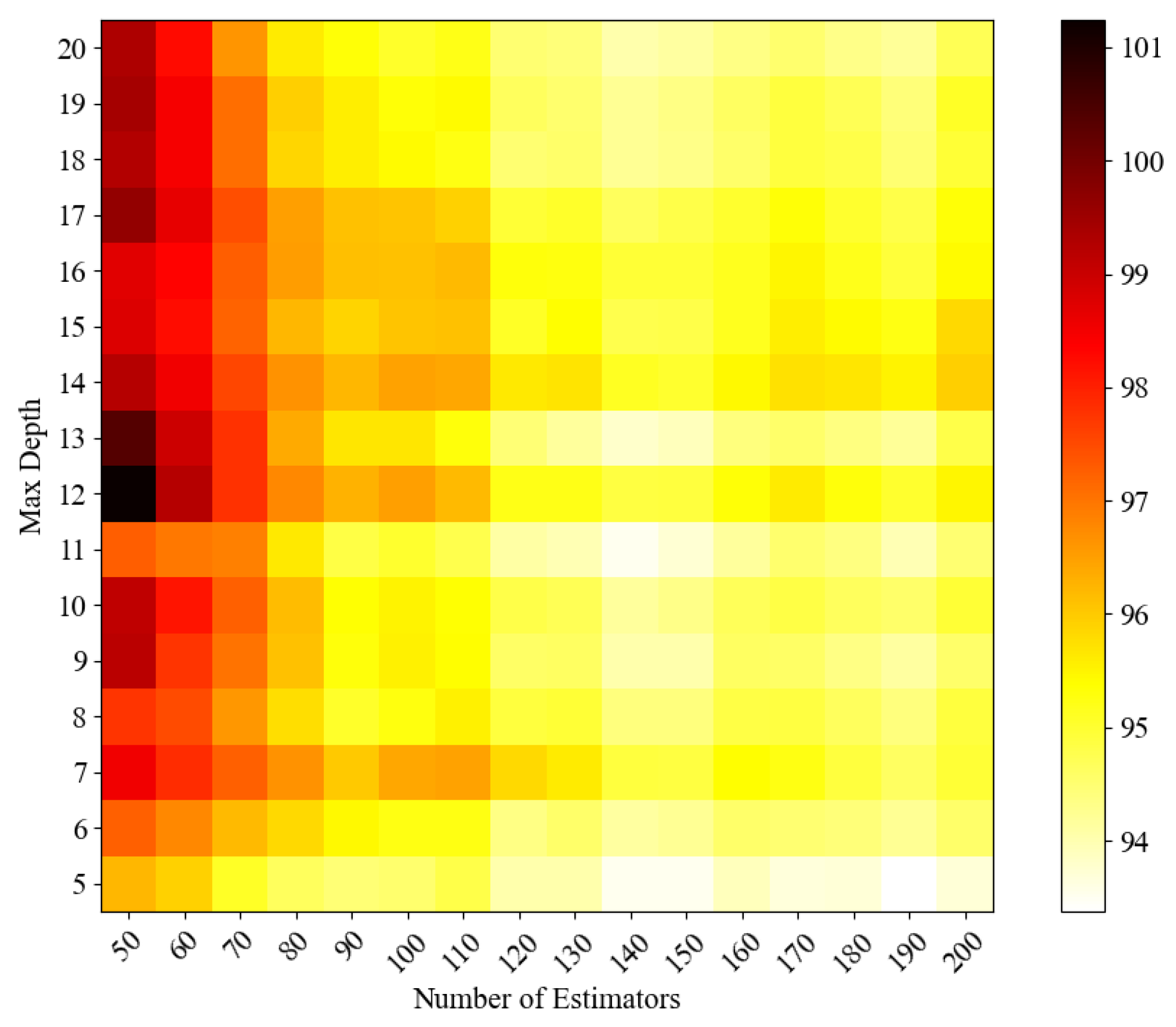
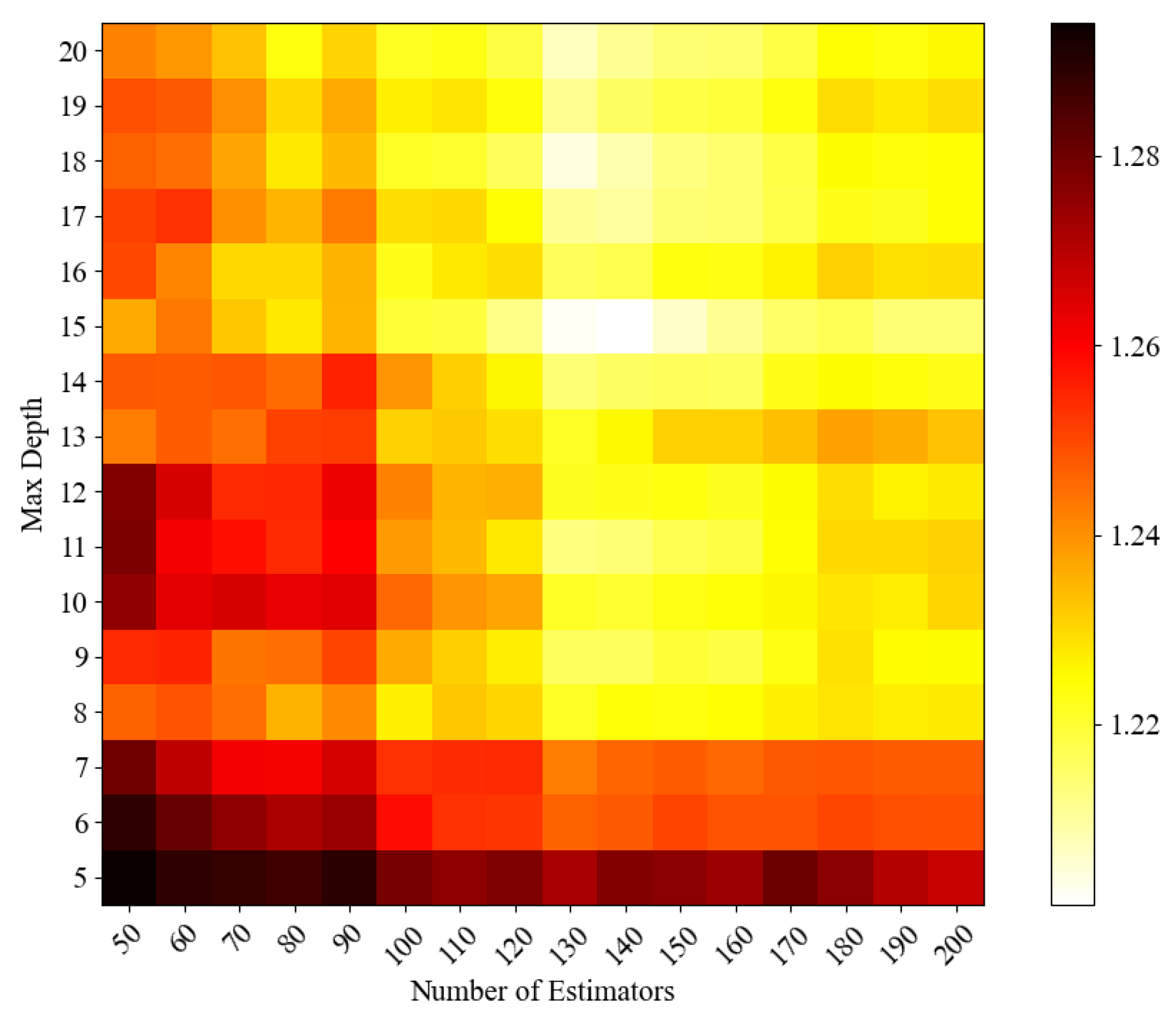
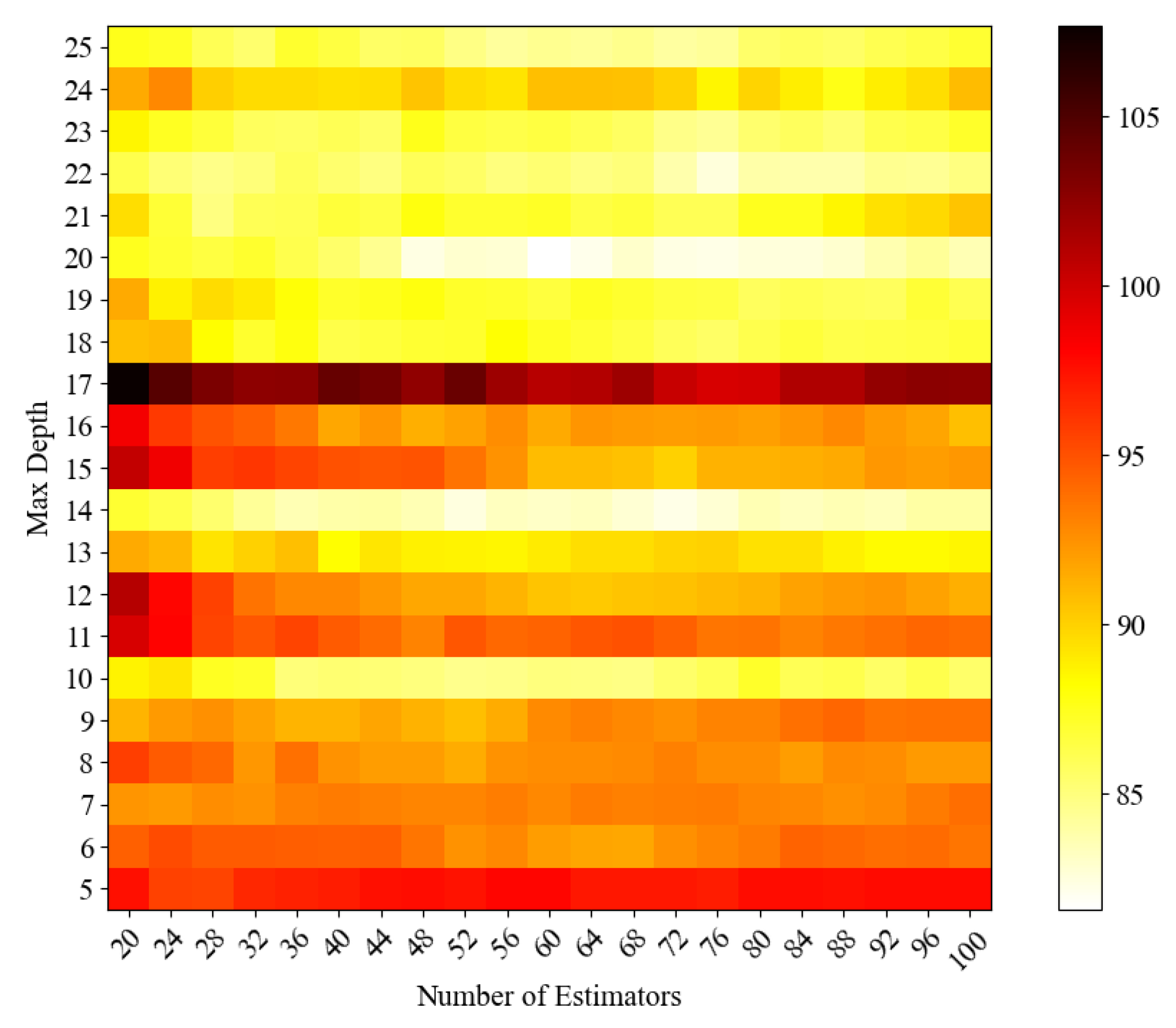
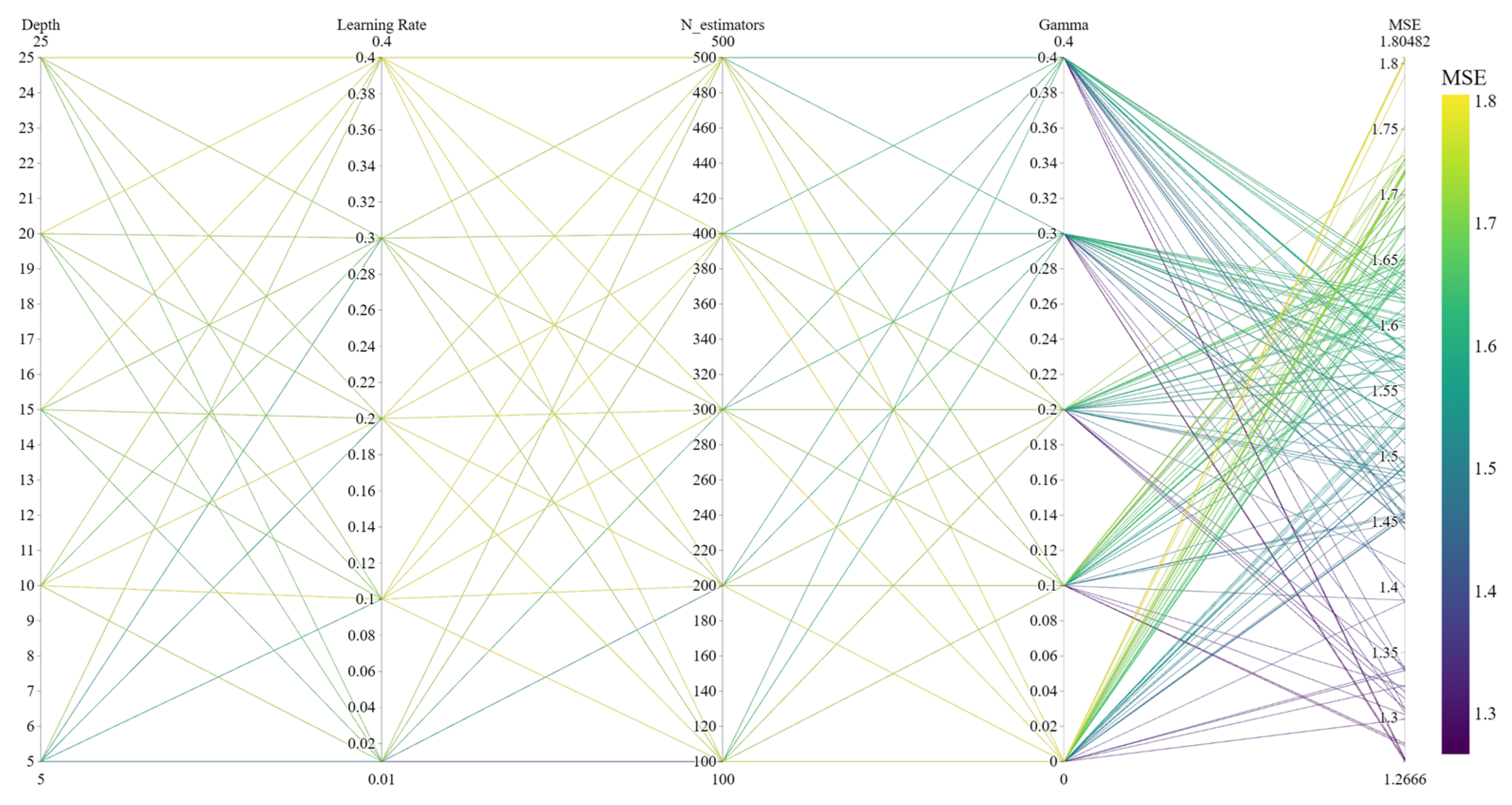
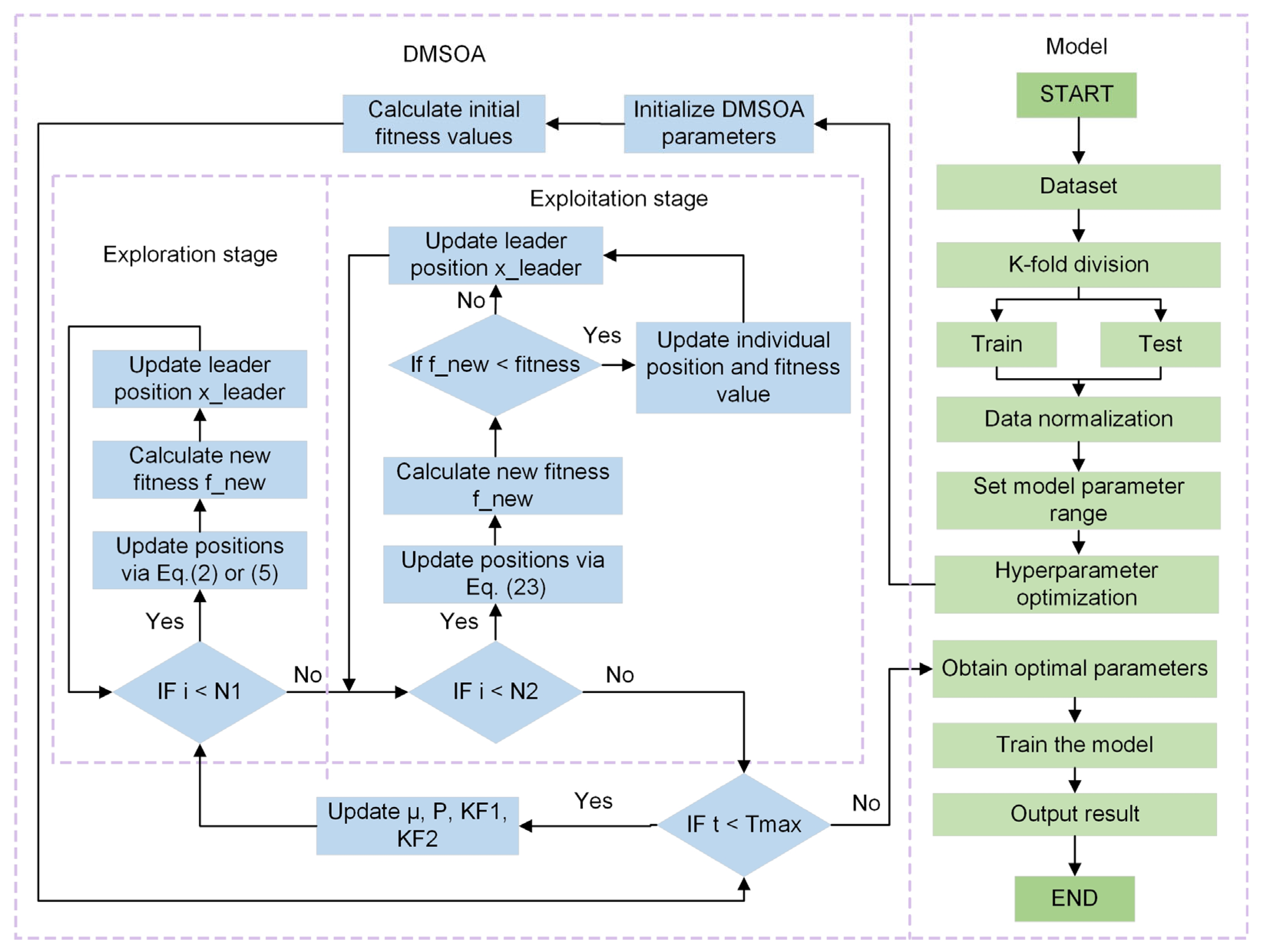
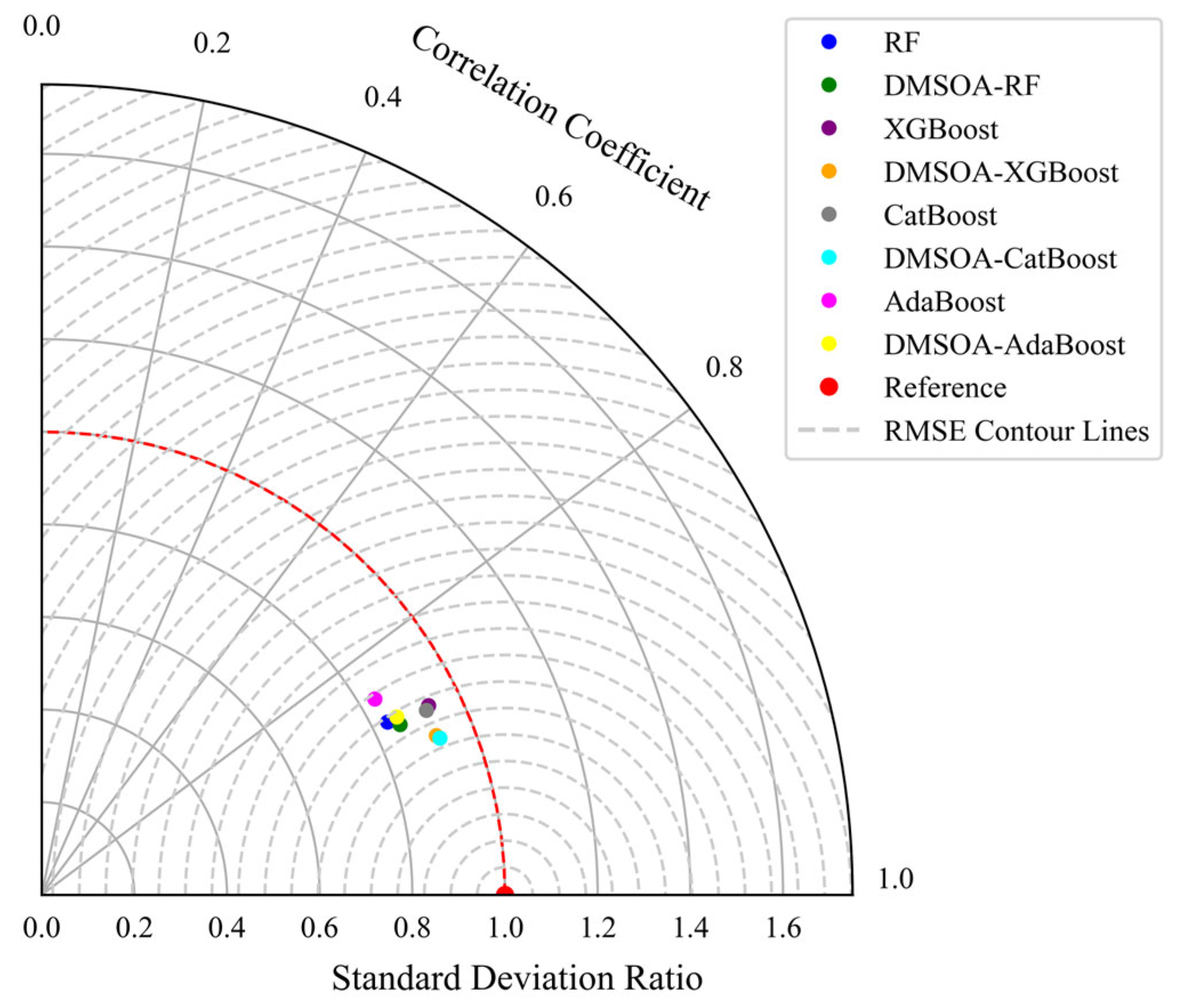
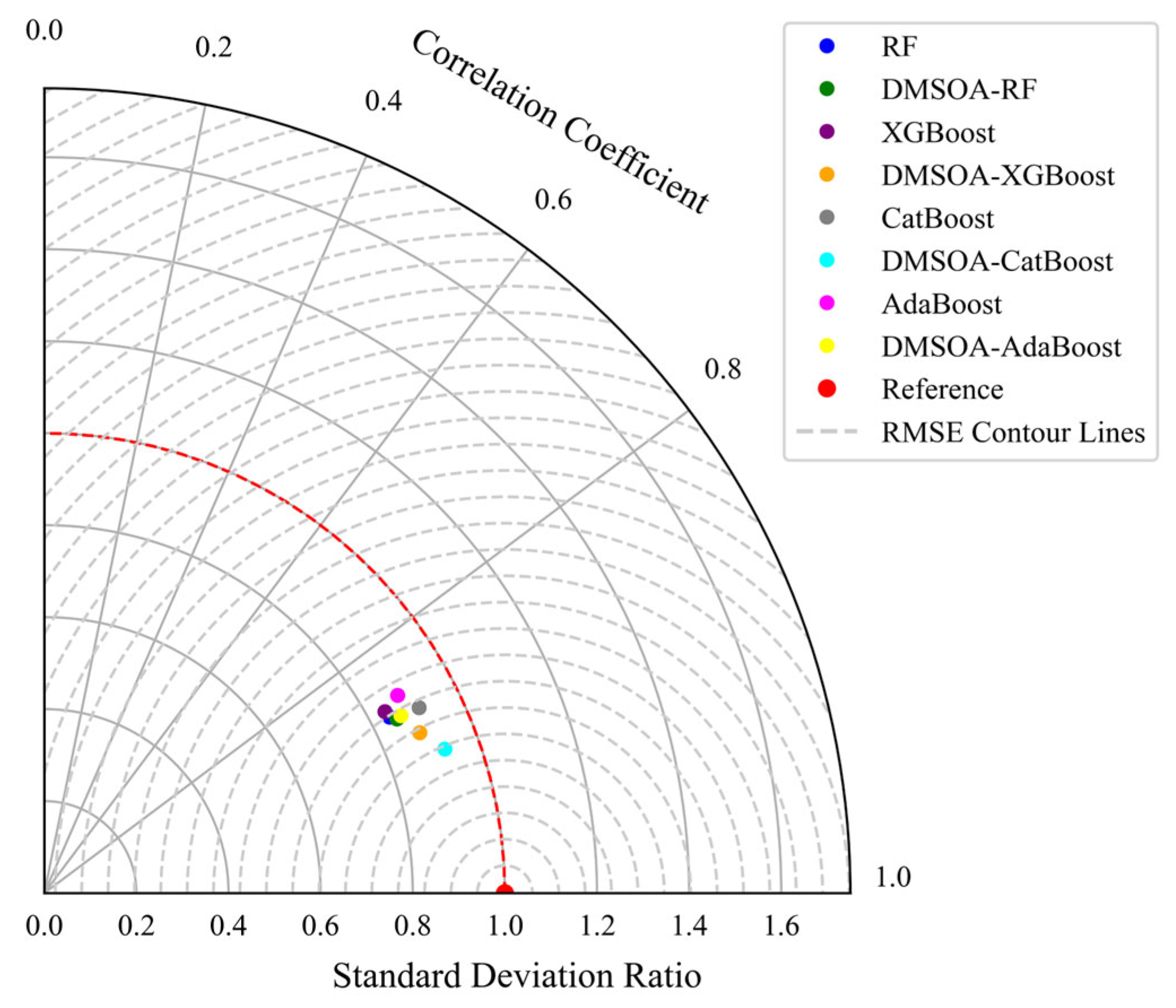
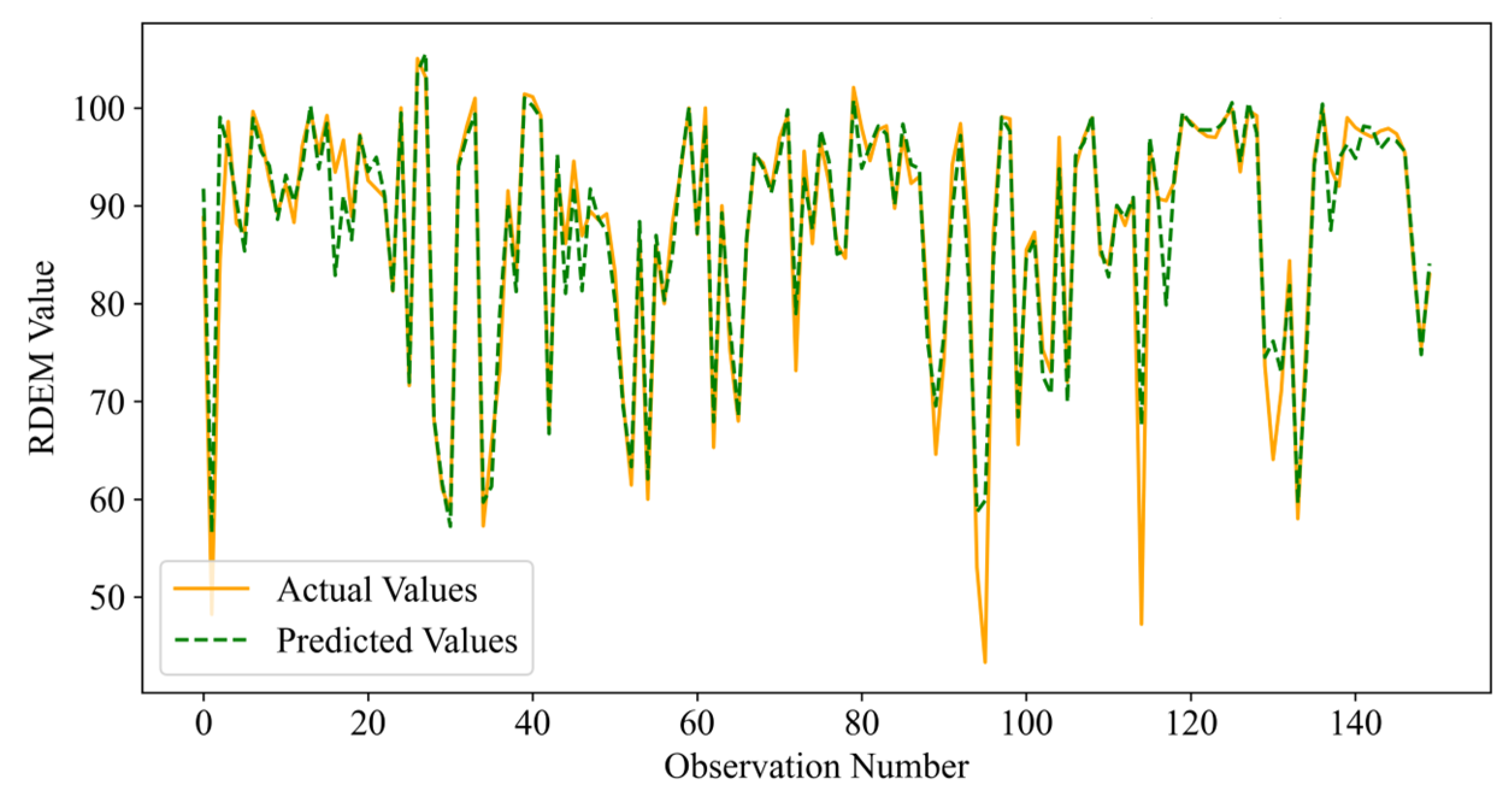
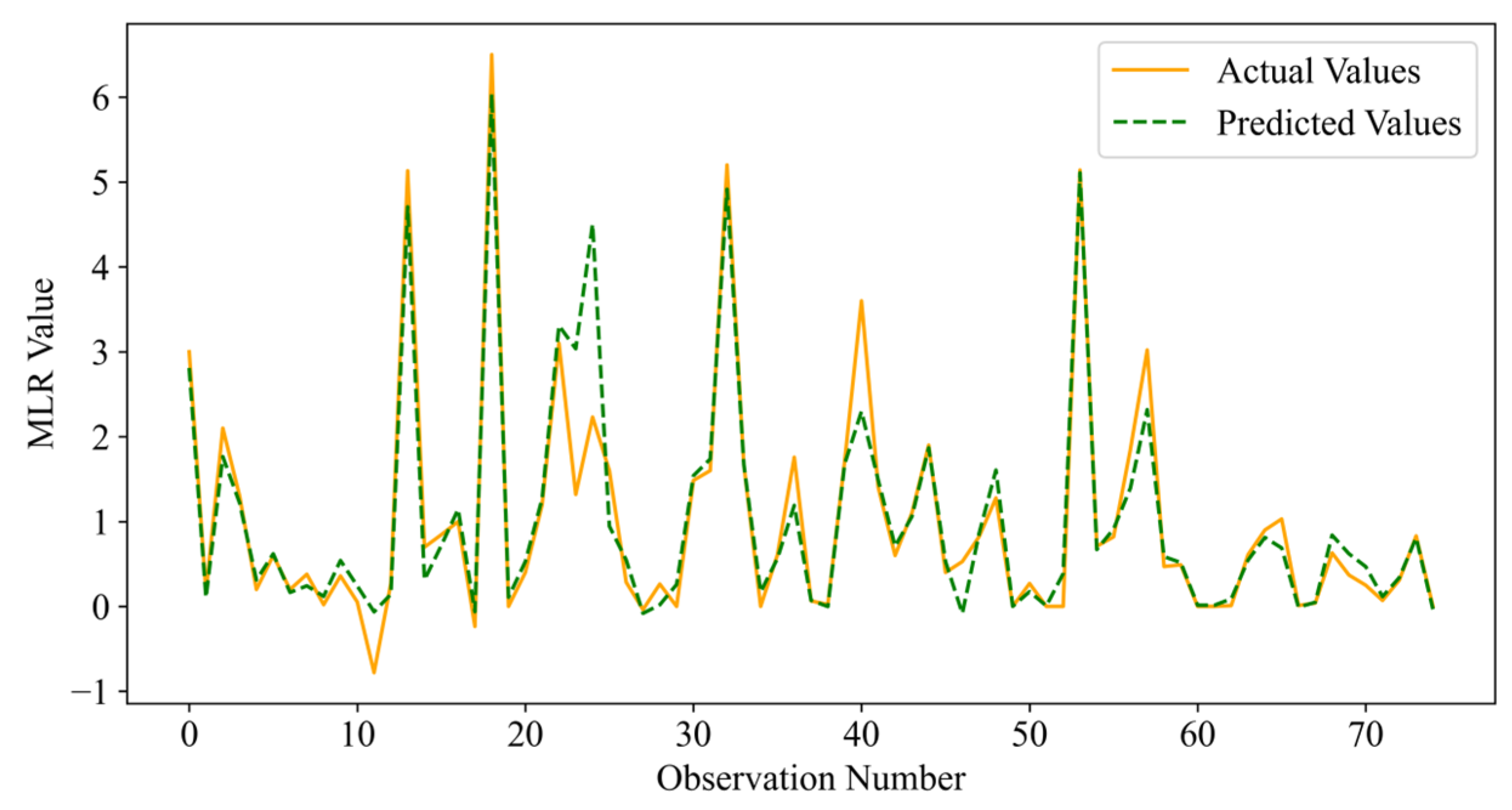
Although intelligent optimisation algorithms have begun to be applied in the prediction of concrete frost resistance, relatively few related studies focus on their utilisation; thus, further exploration is needed. In this paper, a dynamic multi-stage optimisation algorithm (DMSOA) is used to optimise the ensemble learning algorithm to predict the frost resistance of concrete. More than 7090 sets of experimental data are collected, and nine attributes of cement, water, fly ash, coarse aggregate, fine aggregate, mineral powder, water-reducing agent, initial air content of concrete and freeze–thaw cycle times are utilised as input variables. Considering that RF, AdaBoost, CatBoost, and XGBoost are widely used and perform well in relevant studies, this study chooses them to construct benchmark models for comparison. DMSOA and other optimisation algorithms are also used to optimise and establish optimisation models. In addition, all models are evaluated to provide the most accurate prediction model for the frost resistance of concrete. This process not only can greatly save on engineering cost but also has an important guiding significance for engineering design.