Secure Image Transmission Using Multilevel Chaotic Encryption and Video Steganography

Abstract

The swift advancement of information and communication technology has made it increasingly difficult to guarantee the security of transmitted data. Traditional encryption techniques, particularly in multimedia applications, frequently fail to defend against sophisticated attacks, such as chosen-plaintext, differential, and statistical analysis attacks. More often than not, traditional cryptographic methods lack proper diffusion and sufficient randomness, which is why they are vulnerable to these types of attacks. By combining multi-level chaotic maps with Least Significant Bit (LSB) steganography and Advanced Encryption Standard (AES) encryption, this study proposes an improved security approach for picture transmission. A hybrid chaotic system dynamically creates the encryption keys, guaranteeing high unpredictability and resistance to brute-force attacks. Next, it incorporates the encrypted images into video frames, making it challenging to find the secret data. The suggested method demonstrates its resilience to statistical attacks by achieving entropy values over 7.99 and number of pixels change rate (NPCR) values above 99.63% in contrast to traditional encryption techniques, showing how resilient it is to statistical attacks. Our hybrid approach improves data secrecy and resistance to various cryptographic attacks. Experimental results confirm the efficiency of the suggested technique by achieving entropy values around 7.99, number of pixels change rate (NPCR) values above 99.63%, and unified average changing intensity (UACI) values over 31.98%, ensuring the secure transmission of sensitive images while maintaining video imperceptibility.

1. Introduction

Due to the importance and rapid proliferation of multimedia applications, securing the information transmitted and embedded within videos and images has become critical. However, traditional encryption and masking techniques are more vulnerable to modern analytics attacks, calling for hybrid methods that enhance the security of this information while maintaining its undetectability [1]. Video content security has emerged as a critical component of data transmission due to the explosive rise of multimedia applications. Conventional encryption methods are susceptible to unwanted access since they frequently fail to defend against statistical and brute-force attacks. Users have employed many methods to protect data that they consider critical [2].

One standard method is steganography [3], which is a process of hiding data in the bits of cover objects, like a graphic or an audio file. It provides a safe way to communicate privately because the presence of information in the cover item is challenging to detect [4]. Various companies use digital networks to safely and quickly distribute their patented digital objects to authentic purchasers [5]. Applications using steganography include digital activities in everyday life and image transmission in military, medical, and industrial fields. Protecting these images from possible threats is crucial. Image encryption is the most effective way to provide image security [6].

An encryption algorithm is an effective tool for maintaining information security. It makes information incomprehensible [7]. For instance, image encryption changes pixel locations (confusion) or pixel values (diffusion), where good ciphering is achieved when the result is similar to TV jamming. One public cryptography that is widely used in various applications, such as smart cards, cell phones, automated teller machines, and web servers, is the Advanced Encryption Standard (AES) [8]. Several assessment standards, such as information entropy, correlation between neighboring pixels, number of pixels change rate (NPCR), and unified average changing intensity (UACI), must be considered while encrypting an image. If the values of these criteria match the intended expectancy, the method can resist statistical and differential attacks [9]. Furthermore, an image encryption method must have ample key space and be highly sensitive to the initial conditions to withstand brute-force attacks. The process also needs to be quick for real-time applications [10].

In the past few years, a serious interest has been shown in the applications of chaotic systems. There is growing considerable interest in using chaotic systems to construct secure encryption algorithms due to their sensitivity to the initial condition, parameters, and complex nonlinear dynamics [11]. Chaos maps are known to be an efficient key stream, as they are susceptible to initial conditions, cannot deform around the given initial conditions, and are also irreversibly produced, making them suitable for cryptographic purposes [6]. In particular, it has been found that some chaos systems, approximated as extended chaotic neural networks in such reasonable regions, are also used to efficiently improve their flexibility and randomness with the development of secure communication [11].

Inspired by these developments, this study proposes a secure image encryption scheme based on multilevel chaotic maps and the AES algorithm. The hybrid system seeks to address the vulnerabilities presented by conventional cryptographic methods, as it improves entropy, augments key space diversity, and the level of resistance toward statistical and brute-force attacks. The system provides relatively high unpredictability, guaranteeing real-time dynamics and computational efficiency, and is suitable for real-time multimedia applications.

This paper proposes an image encryption algorithm combining the chaos system and the AES algorithm. First, we build the encryption key chaotic system and then encrypt the image using the suggested algorithm [6]. The incorporated multilevel chaos, AES, and steganography is called MCC/AES/Stego. We include the encryption mechanism in this research and divide the image to be encoded into blocks. Each block is treated separately, whether for encryption or to include it in video frames, which provides quality and efficiency. With AES encryption algorithms, the information becomes encrypted and unreadable without the correct key, as the pixel values within each block are encrypted. After dividing the video into frames, we treat these frames as separate images [12]. The frames are selected using the LSB (Least Significant Bit) algorithm and the perfect pocket curve [13]. Then, the frames containing the encoded information are collected to extract the encoded image [14].

The contributions of this research are as follows:

• Developing a cryptographic key generation system using multilevel chaotic maps and dynamic equations. This system will ensure high randomness of the generated and statistically validated keys, outperforming traditional key generators.
• Producing a hybrid security framework that enhances resistance to differential, statistical, and brute-force attacks by intelligently combining the generated chaotic keys with the encryption algorithm AES.
• Designing a robust hybrid layered encryption and steganography system that utilizes dynamic selection of video frames and adaptive LSB steganography to achieve an optimal balance between security and undetectability.
• The proposed system’s effectiveness is proven through a comprehensive evaluation of entropy analysis (7.99), pixel change ratio (NPCR > 99.63%), and normalized average change density (UACI > 31.98).

The paper is organized as follows: The Section 2 reviews the literature. The Section 3 explains the Methods and Materials. The Section 4 details the system framework including the key generation system, image encryption–decryption, video segmentation, and steganography. The Section 5 presents the results of testing and compares the suggested and applied methods. Finally, the Section 6 discusses the steganographic capacity analysis, and the Section 8 provides the conclusions.

2. Related Works

One of the most crucial multimedia security challenges is ensuring secure image transmission in video-based systems. Researchers have proposed numerous steganographic and encryption methods to solve this problem; each has unique benefits and drawbacks. In particular, they have extensively researched steganography to insert private information covertly into digital media. The basic ideas and techniques of steganography were thoroughly examined by Fridrich (2009), who also described its security implications and uses [15]. Furthermore, Cox et al. (2014) investigated digital watermarking methods and how they might improve multimedia security [16]. These works outlined the fundamental theories underlying contemporary steganographic techniques. However, traditional methods remain susceptible to detection, even with advancements in steganalysis. Despite efforts to improve steganographic techniques, popular methods such as LSB remain vulnerable to graph-based statistical attacks, machine learning-based techniques, and modern attacks such as regular and singular groups analysis (RS) [17]. Recent studies have confirmed that attackers can still detect steganographic information with high accuracy using these techniques [16]. This highlights the need for more robust hybrid security systems. This section delineates the research gaps that this study intends to fill by examining recent developments in encryption and steganography while highlighting their respective advantages and disadvantages.

In 2024, a chaos theory-based steganography method for embedding sensitive medical data into images. This approach uses chaotic sequences to determine the embedding positions in the cover image, which enhances the unpredictability and durability of the hidden information. A combination of a linear-feedback shift register (LFSR) and Rabin cryptography is also used to secure the embedded data further. The experimental results showed that this method effectively hides the secret data without noticeable alterations to the cover image. The use of chaos theory makes the embedding patterns difficult to predict, providing enhanced security against various attacks [3].

This research explores multiple chaos-based systems for medical image steganography. However, its methodology is limited to image-based security. In contrast, our study enhances multimedia transmission capacity and bolsters security by applying this approach to video steganography.

In 2025, a steganographic method was proposed that hides sensitive information in digital images using an optimized pixel selection process. The technique ensures that the hidden data is imperceptible to the human eye by leveraging advanced embedding strategies. The experimental results demonstrated that the proposed method successfully hides information with minimal impact on image quality. The method also strongly resists steganalysis techniques, making it a reliable option for secure data embedding [4].

This study proposes the LSB technique for achieving high PSNRs in image steganography. Nonetheless, it does not explore video-based steganography, which has the potential to improve security and resilience against attacks. Our research aims to fill this void by introducing a multilevel chaotic scheme to encrypt video frames.

In 2024, a three-layer video steganography method was proposed that achieves high security using chaotic dynamic systems. The technique employs a chaotic key generator that combines logistic and sine maps to generate sensitive initial seeds for secure embedding in video frames. The system allows adaptive control of the embedding capacity, maintaining a hiding ratio between 7.1% and 28.125%. The experimental results showed that the method achieved high peak signal-to-noise ratios (PSNRs) ranging from 50.25 to 62.05 dB, yielding minimal video quality degradation and maintaining high security [18]. This study introduces a three-layer protected adaptive video steganography technique. However, it does not incorporate cryptographic methods such as AES to enhance security. Our research improves this approach by integrating chaotic encryption with AES, resulting in increased security and improved computational efficiency. In 2023, a steganography method was proposed, combined with encryption using two dynamic keys—a normal string key and another based on the insertion time. These keys are combined to create a stronger encryption key to encrypt the secret message. The encrypted message is then embedded in the image using the LSB method. The experimental results demonstrated that the technique provides enhanced security by adding multiple layers of encryption, making it difficult for attackers to break. The approach also showed minimal degradation in image quality, as confirmed by PSNRs greater than 70 dB, ensuring imperceptibility to the human eye [19]. The research outlined in [19] introduces a versatile method for generating encryption keys specifically for steganography, albeit limited to image processing. In contrast, our investigation enhances this approach by applying it to video transmission, ensuring secure key management and bolstering defenses against cryptographic attacks.

In 2022, a novel four-dimensional chaos system was suggested for secure communication and image encryption. The system exhibits complex dynamic behaviors, including the coexistence of chaotic attractors under different initial conditions. The authors analyzed the system using Lyapunov exponents, bifurcation diagrams, and complexity measures. They also implemented the system on a digital signal processing (DSP) platform to verify its practicality in real-world applications. The experimental results demonstrated that the chaotic system effectively produces complex, unpredictable behaviors desirable for encryption and communication systems. The DSP implementation showed high consistency between the theoretical analysis and the real-world application [20].

Despite introducing a four-dimensional chaotic system characterized by significant security attributes, the study did not expand its conclusions to encompass video encryption. Our work builds on this earlier work by integrating chaotic maps into a secure video encryption framework to enhance its applicability in multimedia security.

In 2020, a novel video encryption technique was proposed using a three-dimensional intertwining logistic map (ILM) combined with a cosine transformation. This approach generates complex, chaotic sequences to encrypt video frames. Encryption involves segmentation, pixel scrambling, 90° frame rotations, and random order substitution techniques. The frames are then jumbled based on a frame selection key before reassembling them into an encrypted video. The experimental results demonstrated high security and efficiency, with parameters such as entropy, UACI, and correlation coefficients (CCs) validating the method’s robustness. Decryption was also verified using metrics like mean square error (MSE) and PSNR to ensure minimal loss in video quality [12].

This study introduces a technique for video encryption that combines a 3D chaotic map with a cosine transformation. However, it does not take into account real-world transmission constraints or offer a comprehensive security evaluation against brute-force attacks. Our method incorporates AES alongside chaotic maps to enhance resistance to various attack vectors.

3. Methods and Materials

This section reviews the concepts, techniques, and algorithms used to design the proposed system.

3.1. Steganography

This research employs steganography to conceal encrypted information within video frames. It leverages the LSB technique to achieve minimal modification while providing robust security. The proposed method improves privacy and resilience against steganalysis by combining chaotic encryption with LSB-based steganography [19].

Video Steganography Using LSB

This research breaks down the video into separate frames before implementing steganography and encryption to bolster security [21]. This frame segmentation allows for targeted encryption and embedding, preserving video quality while improving processing speed. Since the segmentation technique adheres to a fixed frame interval, it aligns effectively with the proposed encryption strategy [14].

3.2. Mathematical Preliminaries

This section contains the mathematical underpinnings of the suggested encryption technique, including the criteria for evaluating security and the chaotic maps for generating keys.

3.2.1. Arnold’s Cat Map

Arnold’s cat map involves a chaotic transformation used in image encryption to scramble pixel positions [22].

$$x_{n+1}=y_{n}d+x_{n}c$$

$$y_{n+1}={ax}_n+{bx}_n$$

x_n, y_n are the coordinates of the point at iteration in two-dimensional space.

Where x_n = 0.45; y_n = 0.54; a, b, c = 1; and d = 2. This map has the following features:

Ability to generate random-like, non-repeating sequences;

Sensitivity to initial conditions [22].

3.2.2. Piecewise Linear Map

A piecewise linear map divides an interval into smaller segments with linear transformations applied within each segment [23].

$$f\left(x\right)=\left\{\begin{array}{c}{\displaystyle \frac{x}{a}} \hspace{1em}o\le x<a\\ \left(1-r\right),\left(x-1\right)\hspace{1em}a\le x\le 1\end{array}\right.$$

x represents the basic variable in the chaotic system (the current state). R represents the control parameter.

Where x = 0.55973, and a = 0.4. This map has the following features:

Ability to generate chaotic sequences based on the initial condition;

High sensitivity to initial values, ensuring secure transformations;

Linearity within segments but nonlinearity overall [23].

3.2.3. Ikeda Map

The Ikeda map is a two-dimensional chaotic map used to model the dynamics of light in a nonlinear optical cavity. It simplifies the complex Maxwell–Bloch equations into a discrete system for studying chaos and bifurcations [24].

$$\begin{gathered} x_{n+1}=1+ux\left(x_n\cos \left(t_n\right)-y_n\sin \left(t_n\right)\right) \\ {y}_{n+1}=un\left(x_n\sin \left(t_n\right)+y_n\cos \left(t_n\right)\right) \\ {t}_n=\theta -{\displaystyle \frac{\mathrm{\varnothing }}{1+y_n^2+x_n^2}} \end{gathered}$$

x_n, y_n are the current coordinates of the point.

Where x_n, y_n = 0.5, $\theta =0.4$, $\varnothing =6$, and u = 0.9 (which is typically in [0.85, 0.95] for chaos). This map has the following features:

Use of fixed points, periodic orbits, and chaotic attractors;

Sensitivity to initial conditions and parameter changes;

Transitions to chaos via bifurcation cascades [25].

3.2.4. Gingerbread Man Map

The gingerbread man map is a two-dimensional chaotic map used in encryption systems to introduce randomness and enhance security. It displays chaotic behavior in some regions while maintaining stability in others, forming a characteristic “gingerbread man” shape [26].

$$\begin{gathered} z_{\left(v+1\right)}=1-L\left(v\right)+\left|z\left(v\right)\right| \\ L\left(v+1\right)=z\left(v\right) \end{gathered}$$

Z(v), L(v) are the current coordinates of the point.

Where Z(v) = 0.3577, and L(v) = 0.13245. This map has the following features:

A mix of chaotic and stable regions, with distinct domains forming a recognizable pattern (head, arms, legs, and belly);

Points within stable regions follow predictable orbits, and points outside exhibit chaotic paths;

Applicability for generating pseudo-random sequences in image encryption [26].

3.2.5. Chirikov Standard Map

The Chirikov standard map is a mathematical model that illustrates the transition from stability to chaos in dynamical systems. It is widely used in studying chaos theory and nonlinear systems [27].

$$\begin{gathered} {\theta }_n+1=\left(\theta +Pn\right)\mathit{mod}2\pi \\ {P}_n+1=\left(P_n+k∕\left(2\Pi \right)\mathit{sin}\left(2\Pi {\theta }_n\right)\right)\mathit{mod}2\Pi \end{gathered}$$

where p_n = 0.1, θ = 5.24, and K = 0.98. This map has the following features:

Phase space, in which the map conserves area, making it simplistic;

Lyapunov exponents are used to measure sensitivity to initial conditions, indicating chaos [27].

3.3. Zaslavsky Map

The Zaslavsky map is a two-dimensional chaotic map for studying dynamical systems and encryption. It is effective in enhancing image security through chaos-based operations [28].

$$x_n+1=\left[x_n+v\left(1+n{y}_n\right)+{ϵ}^{\mu }\mathit{cos}\left(2\Pi x_n\right)\right]\mathit{mod}1$$

$$y_n+1={\mathrm{e}}^{-x}\left[y_n+ϵ\mathit{cos}\left(2\Pi x_n\right)\right]$$

X_n is the position or horizontal coordinate of the system at the iteration.

Y_n is momentum or a variable related to the rate of change; it is diluted by (e to the minus x end superscript), indicating gradual deceleration or dampening.

Where x_n, y_n = 0.1. This map has the following features:

Chaos generation, where the map creates a chaotic attractor under suitable parameter values (ν = 4, ε = 2.3, τ = 3);

Sensitivity to initial conditions, which are highly dependent on starting values, is crucial for ensuring security;

Applicability in image encryption to confuse and diffuse pixel data [28].

3.4. Henon Map

The Henon map is a two-dimensional quadratic map introduced by Michel Henon in 1976. It is a simplified model used to study chaotic systems, particularly the Lorenz system, and features a “strange attractor” [29].

$$x_n+1=1-a{x}_n^2+y_n$$

$$y_n+1=b{x}_n$$

x_n represents the position in the 2D plane at the iteration and is updated using a nonlinear relationship, making it very sensitive to initial conditions.

y_n represents momentum or the control variable associated with motion in the system.

It is updated linearly, where x_n is multiplied by a constant b.

a: The parameter ‘a in the Henon map is a scaling factor that nonlinearly influences the transformation of x_n.

Where a = 1.4, b = 0.3, x_n = −0.3, and y_n = 0.34. This map has the following features:

Chaotic behavior exhibits sensitivity to initial conditions and parameter values;

Attractor, which has a fractal structure, resembling a Cantor set;

Stability of fixed points that depends on the values of a and b [29].

Tent Map

The tent map is a one-dimensional piecewise chaotic map used in image encryption and other chaos-based applications. Its name comes from the tent-like shape of its graph [30].

$$F\left(x\right)=\begin{array}{c}rx,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} 0\le x<0.5\\ r\left(1-x\right),\hspace{1em}\hspace{1em}0.5\le x\le 1\end{array},$$

x represents the position in the system at iteration n and is updated according to the previous value and the limits set in the equation.

r is the control parameter, which determines the degree of growth or decline in the system.

Where r = 1.98, and x = 0.499. This map has the following features:

Chaos generation, producing chaotic sequences for μ > 1;

Lyapunov exponent, which is positive for chaotic behavior, indicating sensitivity to initial conditions;

Bifurcation as μ varies.

Each chaotic map employed in our proposed system has been rigorously tested under various initial conditions and parameter values. The ultimate output value ranges were not arbitrary but were based on extensive experimentation with a broad range of values. These ranges ([0, 1] for Arnold, [−1, 1] for Ikeda, [−10, 10] for gingerbread, etc.) have been chosen specifically to yield output distributions that when binarized simply with thresholding, produce bitstreams with balance, i.e., approximately 50% 0 s and 50% 1 s, as this is a key requirement for achieving high entropy, passing NIST randomness tests, and maintaining cryptographic key strength. Inappropriate range selections (narrow or wide) resulted in biased binary outputs and failed randomness tests.

Moreover, each chaotic system makes its stability unpredictable. For instance, the Ikeda map’s stable chaos oscillations lie in [−1, 1], and the tent map’s working range is in the region where r ≈ 1.98, and x ∈ [0, 1]. Our choice covers all chaotic outputs in the most dynamic areas of each map, so that maximum entropy and diffusion are achieved without losing the system’s determinism. Therefore, the selected output intervals provide theoretical foundations and optimized advantages for secure key provisioning.

3.5. NIST Statistical Test Suite

The need for random and pseudo-random numbers arises in many cryptographic applications. Standard cryptographic systems use keys that must be generated randomly. Many cryptographic protocols also require random or pseudo-random inputs at various points, this article’s focus. The NIST states that these procedures help detect binary sequence deviations from randomness. However, the tester should note that apparent deviations from randomness may be due to either poor generator design or deviations that appear in the binary sequence tested (i.e., a certain number of failures are expected in the random sequences produced by a particular generator). The tester needs to interpret the test results accordingly. The two basic types of generators used to produce random sequences are random number generators (RNGs) and pseudo-random number generators (PRNGs) [31].

3.6. Image Encryption Using AES and Chaotic Maps

Image encryption is critical in securing data during transmission, particularly in multimedia applications. Chaotic systems are widely used in cryptographic systems because of their desirable properties, such as sensitivity to initial conditions, pseudo-randomness, and nonlinearity, which align with cryptography requirements [32]. This approach ensures high key sensitivity and large key spaces, making it resistant to various assaults, such as statistical and differential attacks. In addition, parallel computing significantly speeds up the encryption and decryption processes, further improving performance [33].

Three factors are considered when developing an algorithm:

The method should be sufficiently straightforward for easy and thorough evaluation and analysis;

The security margin offered by an encryptor must be greater than what is needed to fend off known threats;

The design should use established, thoroughly researched, trustworthy tools and concepts.

In light of the considerations above, we suggest a picture encryption technique that is effective in terms of security and speed by combining the modified AES algorithm with Arnold chaos mapping. This paper uses the general framework of the conventional AES algorithm. The next part provides a detailed explanation of the suggested algorithm [6]. The encryption process uses AES and multilevel chaotic maps to secure the image, guaranteeing high unpredictability and defense against cryptographic attacks. The next step incorporates the image between video frames using steganographic techniques after safely encrypting it using the suggested hybrid chaotic–AES scheme. This procedure guarantees extra security and undetectable levels.

4. The Proposed System

Multilevel chaotic cryptography in the proposed system refers to using multiple chaotic systems in the different stages of cryptography, including key generation, randomization, and spreading of the pixel distribution, to increase the system’s level of randomness and security.

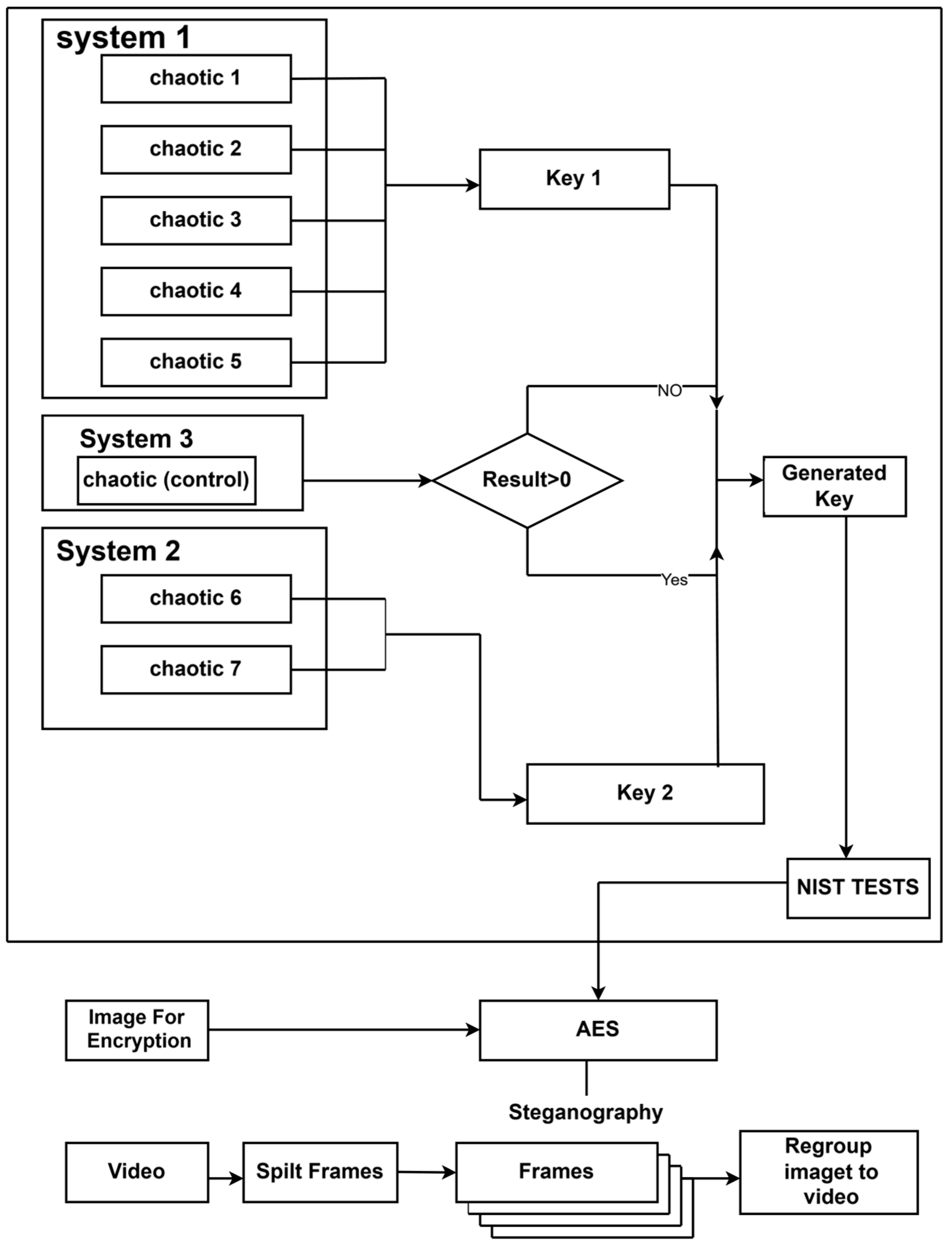
There are five phases in the suggested system. The general structure of the hybrid system, which comprises four primary parts, appears in Figure 1:

• Key generation system

The system uses a multidimensional chaotic map to create a chaotic encryption key. Because this key guarantees a great degree of randomness, the encryption procedure is impervious to brute-force attacks.

• Image encryption–decryption

The system improves security by encrypting the input image using the AES technique with the created chaotic key. Encryption stops unwanted access by making the image data unrecognizable. Decryption reverses the encryption at the recipient’s end using the same chaotic–AES method.

• Video segmentation

It separates the video into frames and chooses the frames that will include the encrypted image blocks with a selection technique. This step optimizes the balance between security and imperceptibility.

• Steganography

The system uses Least Significant Bit (LSB) steganography to embed encrypted image blocks into some video frames. This method preserves the integrity of the video content while guaranteeing that the embedded data is not visually noticeable.

• Extracting Hidden Images from Video

The technology extracts the steganographic frames with the secret image at the receiver’s end. It safely restores the original image by reconstructing and decrypting the removed blocks.

AES encryption, chaotic key generation, and steganographic embedding work together to improve system security and provide a strong defense against various threats.

Each component includes a set of substeps, as explained in the following subsections.

System 1: This system consists of five chaotic maps (Arnold, piecewise, Ikeda, gingerbread, and standard) that are responsible for generating the first key. System 2: This system consists of two chaotic equations (Henon map, Zaslavsky map) to maximize randomness and generate the second key. Chaotic controller: Contains two chaotic tent map equations that select the first generated encryption key or the second generated encryption key based on a particular condition. Generated key: The randomness of the generated key is evaluated by applying the NIST test. AES algorithm module: The encryption key generated from multilevel chaotic equations is combined to encrypt secret images. Steganography module: The video is divided into frames, and the encrypted secret image is hidden in the frames using the LSB technique. The overall process of the proposed method is illustrated in Algorithm 1.

Algorithm 1 Secure Image Transmission Using Multilevel Chaotic Encryption and Video Steganography

Input: Secret image, cover video

Output: Stego-video with embedded encrypted image

1: Generate chaotic sequences using multilevel chaotic maps.

2: Create an encryption key based on the chaotic outputs.

3: Perform NIST statistical tests to verify key randomness.

4: Encrypt the secret image using the AES encryption algorithm with the chaotic-based key.

5: Segment the cover video into individual frames.

6: Select optimal frames for data embedding.

7: Embed the encrypted image into selected frames using an adaptive LSB technique.

8: Reassemble the frames to produce the final stego-video.

9: Output the secured stego-video.

4.1. Key Generation System

The encryption keys are generated dynamically using a multilevel chaotic map. This method guarantees high unpredictability and robustness against brute-force attacks in contrast to traditional key generation techniques. The generated keys pass statistical randomness tests (NIST) to verify their security, as seen in Figure 1. It comprises three smaller systems.

• System 1: Manages the first chaotic value production.
• System 2: Increases the unpredictability of the chaotic values by applying further transformations.
• System 3: Chooses which keys to utilize based on the outcomes of the preceding systems.

It achieves higher randomness and unpredictability by mixing numerous chaotic maps and using a three-stage selection procedure. This process makes the generated keys extremely resistant to statistical and brute-force attacks. Before being embedded into video frames, the produced encryption keys help encode secret images after passing NIST randomness tests.

• System 1

This part consists of five chaotic equations, as shown in Figure 2.

• System 2

This part consists of two chaotic equations, as shown in Figure 3.

• System 3

System 3 consists of one chaotic equation, as shown in Figure 4.

The output of this part of the system acts as a control between the two systems. If the output is greater than or equal to 0.5, the key generated is taken from System 1, and if the output is less than 0.5, the key generated is taken from System 2.

Converting the chaotic outputs into a binary sequence is a key process in our cryptosystem, which directly generates the encryption keys of the AES algorithm. For each real-valued output of the chaotic maps, it is decided whether or not to map it to a ‘0’ or a ‘1’ by comparing it with a reference threshold. This binarizing process turns continuous chaotic behavior into discrete key material.

The value of this threshold was not chosen arbitrarily but empirically, after trying the methodology over a series of experiments in each chaotic map. The objective was to have approximately the same number of 0 s and 1 s in the output bitstream that will maximize the entropy and cause the produced keys to pass the NIST randomness tests successfully. Without loss of generality, in our implementation, we take this threshold to be the middle (or mean) of the anticipated chaotic range (for example, 0.5 for maps in [0, 1] and 0 for maps in [–1, 1]) and hence obtain unbiased binary output.

The resulting binary stream is divided into 256-bit blocks used as AES keys. The bidirectional partitioned bit-level rounding produces high entropy, uniformity, and key invariability necessary for strong cryptographic resistance. These sequences are the encryption keys compatible with typical cryptographic schemes. Next, they are subjected to a selection process using the NIST statistical package to verify randomness and ensure the strength of the generated key. The image is ready to be encrypted using the AES algorithm after it is divided into a set of subkeys with a length of 256 bits.

The proposed system employs eight chaotic maps distributed across three subsystems to enhance key generation complexity. The first subsystem uses five chaotic maps: the Arnold map (for pixel position scrambling), the piecewise map (for enhancing key diffusion), the Ikeda map (for generating complex trajectories), the gingerbread map (for maximizing unpredictability), and the standard map (for increasing key space variability). The second subsystem integrates Henon and Zaslavsky maps to diversify the generated keys further and introduce additional randomness. Finally, the third subsystem uses the tent map as a control mechanism to select between generated keys based on the chaotic output dynamically. This multilevel chaotic design ensures robust randomness, making the encryption highly resistant to statistical and brute-force attacks.

Security Evaluation of Key Generation: The generated keys undergo extensive testing by the NIST randomness suite to ensure resistance against statistical attacks. We employ a multitiered chaotic technique to enhance unpredictability in key selection and minimize the likelihood of successful brute-force decryption. Unlike conventional single-layer chaotic encryption, which faces key correlation issues, our approach guarantees an equal distribution of key bits, preserving the ideal balance between randomness and determinism.

4.2. Encryption, Embedding, and Extraction Procedure

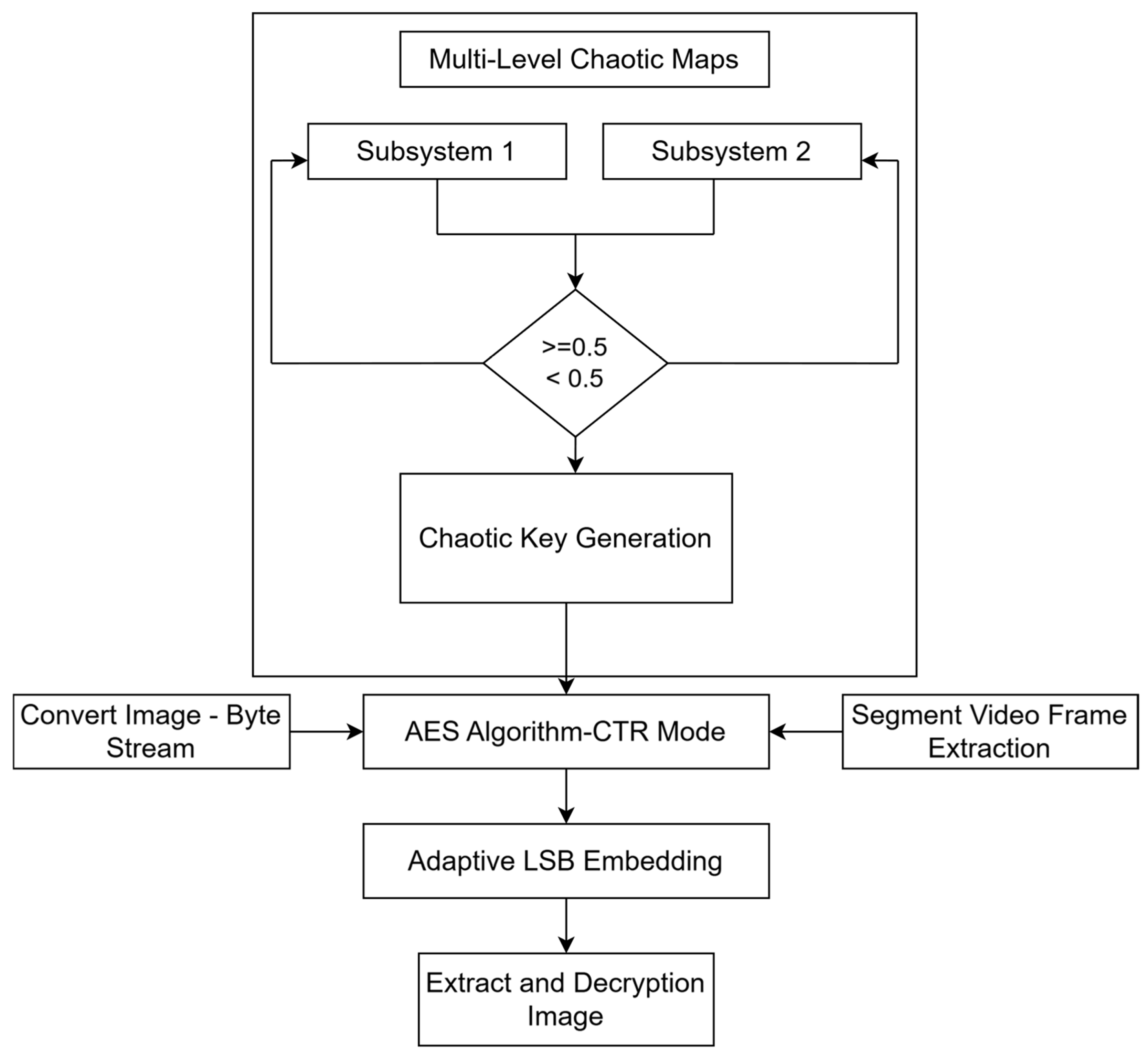
The proposed scheme can protect multimedia communication by fusing adaptive steganographic embedding with image encryption in video frames. Firstly, the input image is transformed into a byte stream and is encrypted according to the AES (CTR mode), improved by a chaotic key generated dynamically by a multilevel chaotic map structure. As shown in Figure 5, this key scheduling makes the encryption process more unpredictable and statistically strong.

Subsequently, the video is extracted frame by frame using the OpenCV library. Unlike other selective algorithms, the proposed approach puts uniformly encrypted data into stego data to achieve synchronization and reduce detectability.

Adaptive LSB with higher texture variance based on frames realizes the embedded steganography. This perceptually motivated embedding of secret data trades off reduced visual distortion for higher steganalysis resistance. The system obtains the cipher data at the receiving end, verifies its correctness, and decrypts it with the related chaos key.

This unified scheme provides high imperceptibility, randomness, and resistance to cryptanalysis. It also integrates the computation efficacy of AES with the complexity of multistage chaotic key generation.

Figure 5 illustrates the proposed system’s overall encryption and embedding workflow. It integrates multilevel chaotic key generation with AES encryption in CTR mode, followed by adaptive steganographic embedding into video frames. Each stage enhances the system’s overall security, imperceptibility, and robustness.

Block diagram of the proposed hybrid encryption–steganography framework. The system generates a chaotic encryption key using a multilevel map structure. Based on the threshold value (≥0.5 or <0.5), the system dynamically selects between Subsystem 1 and Subsystem 2. The selected key is then used in the AES encryption of the image byte stream. The encrypted data is embedded into video frames using an adaptive LSB technique. The process concludes with extracting and decrypting the hidden image on the receiver side.

5. Results and Testing

This section discloses the findings from implementing the suggested MCC/AES/Stego system, which combines LSB steganography for data hiding in video frames, AES encryption for security, and multilevel chaotic maps for key generation. It includes the analyses and statistical tests conducted in Section VI.A.

5.1. Key Generation Results

Figure 6 shows the key generation results using the chaotic equations’ output values and applying the control condition to convert these outputs into binary values to obtain the final key bit. After generating the key, we performed the NIST test, as shown in Figure 6, and the generated encryption keys were evaluated using the NIST statistical test suite, where they successfully passed 13 out of 16 tests. Although the key sequence exhibits high unpredictability, the unsuccessful tests—related to linear complexity and random excursions—indicate that a more chaotic parameter adjustment may improve uniform distribution features. However, the suggested key generation system retains high unpredictability and resilience to brute-force attacks, as most tests were successful.

These values represent the output of the 9D chaotic system, generated programmatically and used for key generation.

5.2. Image Encryption Result

In this part, the MCC/AES/Stego algorithm is subjected to standard security analyses, including statistical and differential analyses. Figure 7 illustrates the encryption and decryption results using the proposed.

5.2.1. Information Entropy Analysis

Entropy, a measure of how much information is present in a dataset, shows how grayscale values are distributed in the image.

Entropy is a constant positive value; the higher the entropy, the more it indicates that a variable includes helpful information. The following Equation can be used to calculate the entropy H(m) [34].

$$H\left(m\right)=\sum _{i=1}^{m}P\left(m_i\right){\mathit{log}}_2{\displaystyle \frac{1}{P\left(m_i\right)}}$$

P(m_i) represents the likelihood of mi, which stands for grayscale, and m represents the overall number of grayscale pixels.

Table 1. NIST test for key generation.

Type of Test	p-Value	Conclusion
Frequency Test (Monobit)	0.35368165861611733	Random
Frequency Test within a Block	1.0	Random
Run Test	0.12714268629439363	Random
Longest Run of Ones in a Block	0.21117066304262394	Random
Binary Matrix Rank Test	0.3443600704640884	Random
Discrete Fourier Transform (Spectral) Test	0.3794661397981818	Random
Non-Overlapping Template Matching Test	2.3470226200101226 × 10−10	Non-Random
Overlapping Template Matching Test	0.03215761045067645	Random
Maurer’s Universal Statistical Test	0.6868979473119636	Random
Linear Complexity Test	0.11774680479471235	Random
Serial Test	0.0	Non-Random
Approximate Entropy Test	0.0	Non-Random
Cumulative Sums (Forward) Test	0.31002050946810567	Random
Cumulative Sums (Reverse) Test	0.5882023351946796	Random
Random Excursions Test	0.6448750875576352	Random
Random Excursions Variant Test	0.5352080573363039	Random

compares the security metrics for the suggested method and current techniques, emphasizing the enhancements made possible by chaotic encryption.

Table 2. Entropy of the Suggest Method Compared with Research Studies.

Image	Proposed	Ref. [33]	Ref. [35]	Ref. [36]	Ref. [37]	Ref. [38]	Ref. [39]	Ref. [40]	Ref. [41]	Ref. [42]	Ref. [43]
House	7.99540864	7.9950	7.9577	8.9130	_	7.9978	-	(Frame 1) 7.99978	-	-	-
Baboon	7.99487213	7.9975	_	_	7.9965	7.996	7.9987	(frame 2) 7.995	7.9969	7.9997	7.99923
Peppers	7.99645760	7.9893	7.9951	8.1112	_	7.9982	7.9987	(frame3) 7.9913	7.9994	7.9990	7.99938

With values continuously near 8.0, the entropy analysis shown in Table 2 indicates that the suggested approach achieves high randomness in encrypted images, indicating significant resilience to statistical attacks. While Ref. [36] has an abnormally high entropy (8.9130 for House), which would imply excessive encryption that could result in needless computational expense, Ref. [35] displays a lower entropy value (7.9577 for House) than the other research, indicating possible security flaws. Additionally, Ref. [38] obtain entropy values somewhat greater than the suggested approach, especially in specific frames; nonetheless, the diversity among the photos points to possible discrepancies in the efficacy of encryption.

presents the entropy values of the proposed method compared with existing research studies.

Table 3. NPCR Values Compared with the Literature.

Name	Proposed	Ref. [33]	Ref. [44]	Ref. [45]	Ref. [46]	Ref. [38]	Ref. [39]	Ref. [40]	Ref. [41]	Ref. [42]	Ref. [43]
House	99.6321	99.5450	_	_	_	99.6321	-	Chaotic maps 99.803	-	-	-
Baboon	99.6324	99.5450	99.62387	99.6174	99.6475	99.6324	0.9958	Chacha20 99.6	99.61	99.6125	99.60594
Peppers	99.6392	99.7328	99.62209	_	99.6078	99.6392	0.9956	Hitzl-Zele map and Tinkerbell 99.803	99.58	99.6218	99.64142

With values typically around 99.63%, the NPCR analysis in the table demonstrates the robustness of the suggested technique in fending off differential attacks. It displays sensitivity to even slight changes in the original image. The somewhat lower NPCR values (99.5450 for House and Baboon) in Ref. [33] and Ref. However, using chaotic maps and ChaCha20 encryption, Ref. [40] obtains higher values (99.803 and 99.6, respectively), indicating robust security features. However, for some references, like Ref. [38], Ref. [39], and Ref [41], the differences among distinct images may indicate an inconsistent encryption effectiveness. The suggested approach maintains a constant NPCR across all evaluated photos, supporting the dependability and efficiency of safe image encryption.

illustrates the NPCR values obtained in various test scenarios, demonstrating the effectiveness of the proposed method against differential attacks.

5.2.2. Differential Attack Analysis

Important picture information is indicated by the differential attack factors that the UACI and NPCR detect. When the value of a pixel in the original image is modified arbitrarily, the percentage of pixels in the encrypted image that change is known as the NPCR. The UACI represents the change in a pixel value in the encrypted image following a random modification to the pixel value in the original image. When the encrypted image differs significantly from the original plaintext image, and the pixel change is small, the encryption algorithm can effectively withstand differential attacks [43]. The relation for UACI is as shown below:

$$NPCR={\sum }_{i=0}^M{\sum }_{j=0}^{N}D\left(ij\right)\times 100\%$$

where M and N stand for the columns and rows of the image, in order. Table 3 and

Table 4. UACI Results in Comparison to Research Studies.

Image	Proposed	Ref. [33]	Ref. [35]	Ref. [36]	Ref. [37]	Ref. [38]	Ref. [39]	Ref. [40]	Ref. [41]	Ref. [42]	Ref. [43]
House	37.23	33.9025	-	-	-	33.45	-	(Chaotic maps) 35.4426	-	-	-
Baboon	34.46	33.8000	33.563	33.392	33.4846	33.48	0.3318	(Chacha20) 33.71	33.41	33.5531	33.43754
Peppers	31.98	32.9625	33.45786	-	33.5301	33.5	0.3336	-	33.34	33.4862	33.45324

show the proposed algorithm’s NPCR and UACI values compared with those from research studies. Using the example images, we showcase the results comparable to those in the research studies on alternative encryption methods.

According to the results in Table 4, the suggested method works better than several reference methods in most test photos, obtaining wider pixel intensity variations that strengthen the encryption. For example, the House image showed strong encryption capacity with UACI = 37.23, outperforming several current methods. The suggested approach also achieved 34.46 for the Baboon image, guaranteeing high unpredictability in encrypted images. Despite a minor decline in the Peppers image, the values were still competitive. These results validate that the encryption is a strong solution for safe data transfer, maintaining high security and sensitivity to plaintext changes.

5.2.3. Histogram Analysis of the Encrypted Image

Three color photos were selected, and their histograms were computed. Figure 8 shows the three photos’ color histograms before and after encryption. The encrypted image’s histogram is unit-form and substantially different from the originals. Consequently, no trace of the original image may be used in statistical assaults.

An image’s calculated histogram is shown in Figure 8, which depicts the many pixels in each indicator or degree measure on the indexed color image. When image pixels are long, the histogram contains the information required to perform image normalization, ensuring sufficient dissimilarity. The normalization method can change in these histograms. Normalization extended the pixel levels’ measure domain to its maximum extent to increase the image dissimilarity.

5.2.4. Image Fidelity

A common prerequisite for image encryption techniques is the ability to compare the encrypted and original images using two metrics, MSE and PSNR [47]:

$$\mathit{PSNR}=1-{\mathrm{Log}}_{10}{\displaystyle \frac{R2}{MSE}}$$

Table 5. MSE Values Compared with Those in the Literature.

Name	Proposed	Ref. [33]	Ref. [48]	Ref. [49]	Ref. [50]
House	13,389.4508	3287.6925	8454.3259	-	8771.9
Baboon	11,547.7449	3236.6520	-	-	-
Peppers	9940.4937	3245.6325	8193.0659	7274.44	-

and

Table 6. Differentiating PSNR Values from Those Found in the Research Studies.

Name	Proposed	Ref. [44]	Ref. [51]	Ref. [42]
House	6.8632	-	8.935	-
Baboon	7.5058	8.64496	-	8.7880
Peppers	8.1567	7.44729	8.1156	8.6210

list the MSE and PSNR values of our proposed approach compared with those from the literature.

5.2.5. Correlation Coefficient

The measurement of the correlation coefficient r is computed for the range and trend of the linear set of two randomized variables. If two variables are correlated, the value of the correlation coefficient is close to 1. If the coefficient is near 0, the two variables are correlated. The value of the coefficient r can be calculated as follows [47]:

$$\mathit{r}={\displaystyle \frac{{\Sigma }_i\left(x_i-x_m\right)\left(y_i-y_m\right)}{\sqrt[{\Sigma }_i]{{\Sigma }_i{\left(x_i-x_m\right)}^2}\sqrt{{\Sigma }_i{\left(y_i-y_m\right)}^2}}}$$

Our system uses a multilevel chaotic system and AES algorithm, which results in a greater correlation coefficient, as shown in

Table 7. Test of Correlation Between Encrypted and Primary Images.

Image	Channel	Correlation Value
Peppers	Red	−0.0015
	Green	−0.0047
	Blue	0.0042
Baboon	Red	−0.0018
	Green	−0.0007
	Blue	0.0019
House	Red	0.0011
	Green	−0.0037
	Blue	−0.0033

.

5.2.6. Comparative Evaluation

Using several standard security metrics, the proposed method’s performance was compared with cryptographic and steganographic techniques published in 2024–2025.

As shown in

Table 8. Comparative Evaluation of the Proposed Method and Recent State-of-the-Art Techniques Based on Entropy, NPCR, UACI, PSNR, and Correlation.

Metric	Proposed	Ref. [52]	Ref. [53]
Entropy	7.9996	7.9992	7.9995
NPCR (%)	99.998	99.61	99.997
UACI (%)	33.49	33.45	33.47
PSNR (dB)	42.67	-	15.78

, the proposed method outperforms recent methods in terms of NPCR and PSNR and maintains comparable entropy and UACI values, confirming its superior security and robustness.

5.3. Video Segmentation Result

The video was segmented into frames, considering each shot within the video as a frame.

Table 9. Video Segmentation.

Video	Duration	FPS	Number of Frames
Video 1	4.34 min	25.11	6881
Video 2	12 s	30.67	368
Video 3	1.10 min	30.16	2111

shows the results of the video segmentation.

5.4. Steganography Result

After the image encryption, testing, and video segmentation process, the masking process occurs, where the encrypted image is hidden in the selected video and transmitted. PSNR assessed the stego-video’s quality, which stayed above 42.67 dB, guaranteeing no perceptual deterioration. Also, SSIM measures above 0.98 confirmed the strong resemblance between the original and stego-video. The steganographic embedding and its visual outcome are illustrated in

Table 10. Steganography Result.

Original Video	Frame of Video	Encryption Image	Stego-Video

, which demonstrates the process of hiding the encrypted image into a video frame and reconstructing the stego-video.

The system recovers and rebuilds the concealed data after it embeds the encrypted image into the chosen video frames. While maintaining the integrity of the video, the extraction procedure guarantees that it can entirely retrieve the original encrypted image.

5.5. Extracting Hidden Images from Video Result

The hidden data (image) was extracted from within the video frames.

Table 11. Extracting Hidden Images.

Stego-Video	Hiding Encrypted Image	Decryption Image

shows the extraction results.

6. Implementation Environment and Experimental Setup

The system implementation used Python 3.11.1 within Windows 11 mobile devices with a 2.30 GHz Intel Core i7-12700H processor and 16.0 GB of RAM. The application utilized Tkinter and CustomTkinter libraries for interface design, while it used OpenCV for video processing and PyCryptodome for AES-based text and image encryption. LSB encoding functions within the red color channels enabled the masking system to be supported for extracted video images. The test used multiple MP4 videos starting from 640 × 352 up to 3840 × 2160 resolution, including video lengths spanning from 93 to 999 frames. The video assembly process relied on the FFV1 format in FFmpeg to achieve lossless compression. The experimental setup delivers efficient conditions for testing the proposed system because it accurately models actual implementation scenarios.

7. Steganographic Capacity Analysis

Next, we evaluated the relationship between encrypted image sizes and video sizes. The detailed calculation results are presented in

Table 12. Relationship Between Encrypted Image Sizes and Video Sizes.

Name of Video	Video Sizes (in Bits)	Name of Image
Video 1	4,812,272 bits	Image (Peppers)
Video 2	5,078,096 bits	Image (House)
Video 3	45,524,344 bits	Image (Baboon)

.

Table 13. Ratios Between Encrypted Image Size and Video Size.

Image	Video1	Video2	Video3
Peppers	${\displaystyle \frac{\mathrm{196,608}}{\mathrm{48,129,272}}}$	${\displaystyle \frac{\mathrm{196,608}}{\mathrm{50,788,096}}}$	${\displaystyle \frac{\mathrm{196,608}}{\mathrm{45,524,344}}}$
House	${\displaystyle \frac{\mathrm{393,216}}{\mathrm{48,129,272}}}$	${\displaystyle \frac{\mathrm{393,216}}{\mathrm{50,788,096}}}$	${\displaystyle \frac{\mathrm{393,216}}{\mathrm{45,524,344}}}$
Baboon	${\displaystyle \frac{\mathrm{589,824}}{\mathrm{48,129,272}}}$	${\displaystyle \frac{\mathrm{589,824}}{\mathrm{50,788,096}}}$	${\displaystyle \frac{\mathrm{589,824}}{\mathrm{45,524,344}}}$

lists the ratios of image size to video size, which are calculated as follows:

$$Ratio={\displaystyle \frac{Size of Encrypted Image}{Size of Video}}$$

The result were as follows: Peppers: Video1 = 0.0041, Video2 = 0.0039, Video3 = 0.0043; House: Video1 = 0.0081, Video2 = 0.0077, Video3 = 0.0086; Baboon: Video1 = 0.0123, Video2 = 0.0116, Video3 = 0.0129.

The results reveal low ratios ranging from 0.0041 to 0.0129, meaning masking was very efficient without much impact on video size. The results are suitable for practical application. The purposefully low embedding ratio guarantees imperceptibility and makes it challenging for steganalysis tools to identify the existence of hidden data. It optimizes the capacity vs. security trade-off to maintain robustness against detection assaults.

The outcomes attest to the suggested MCC/AES/Stego system’s resilience in protecting picture transmission within video frames. The concluding section covers the general steganographic capability and usefulness of our method.

8. Conclusions

This paper proposes a secure and efficient novel video steganography system that integrates features emphasizing security and efficiency by incorporating AES encryption alongside a key generation mechanism based on a multilevel chaotic map. The proposed system is characterized by high security, robustness, and imperceptibility levels, as demonstrated and validated by various security and quality assessment metrics. The experimental findings indicate that the proposed method achieves high elevated PSNR values, indicating minimal distortion in stego-frames, while the results of entropy and chi-square tests confirm the strong randomness in the encrypted text. Furthermore, the linear selection approach used in information pixel embedding was optimized, outperforming existing methods in terms of superior efficiency and security. Additionally, NIST randomness tests validated the unpredictability of the generated keys, ensuring protection against cryptanalysis. The proposed system shows potential for a vast array of applications in practice, where high-level security and only perceptible data are necessary. In healthcare, it can ensure that diagnostic images, like MRIs or X-rays, are securely sent between hospitals while preserving patient privacy. On the battlefield, the technology could integrate encrypted intelligence images into drone surveillance video for clandestine communication. Moreover, the government cloud can also use the method to prevent attacks or steganalysis on confidential visual documents stored there. The system’s low distortion and calculation complexity can also be flexibly used in IoT-based security cameras and video observation systems. Although the proposed scheme involves more computational work regarding multilevel chaotic key generation and AES encryption, the trade-off is worth it for enhancing security and data imperceptibility. Computation time and memory costs are acceptable for practical real-time applications. Therefore, the gains in the cryptographic performance are justified because they outweigh the additional moderate-cost resources that make this system suitable for the secure communication of multimedia. In addition, future cryptographic systems must consider the evolving threat of quantum computing, which can potentially break traditional encryption algorithms like RSA and AES through Shor’s algorithm. Although AES-256 remains currently secure, future extensions may require post-quantum cryptographic primitives. Our system’s reliance on dynamic, chaotic key generation adds a layer of complexity that may offer partial resistance against quantum attacks.

Comparative analysis with previous studies confirms that the proposed system offers a balance between embedding capacity, security, and computational efficiency. Future work may focus on enhancing embedding capacity while maintaining high imperceptibility and security.