Bottlenose Dolphins’ Clicks Comply with Three Laws of Efficient Communication
Abstract
1. Introduction
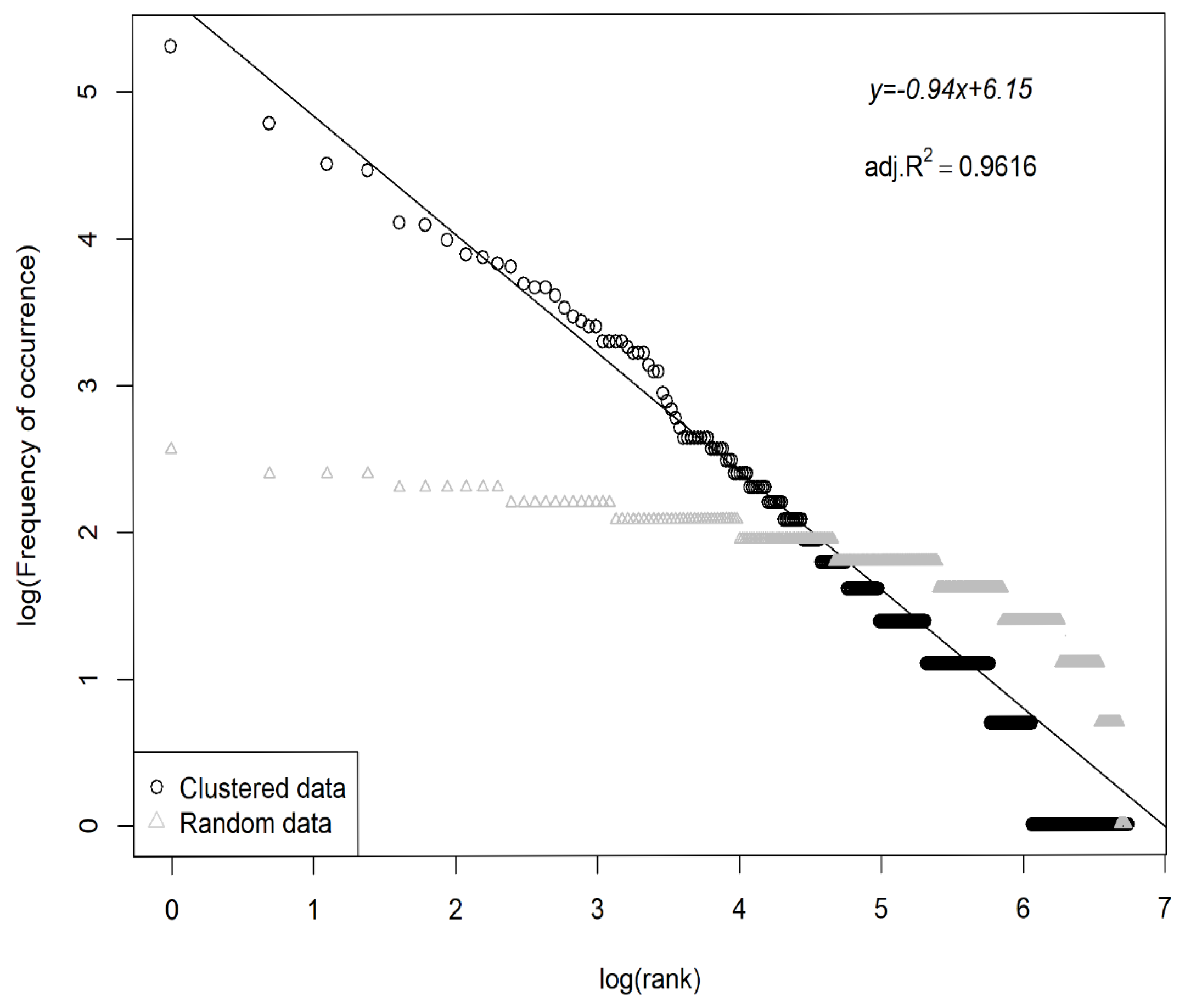
- Zipf–Mandelbrot’s rank–frequency law—also known as Zipf’s law [1], formulated as
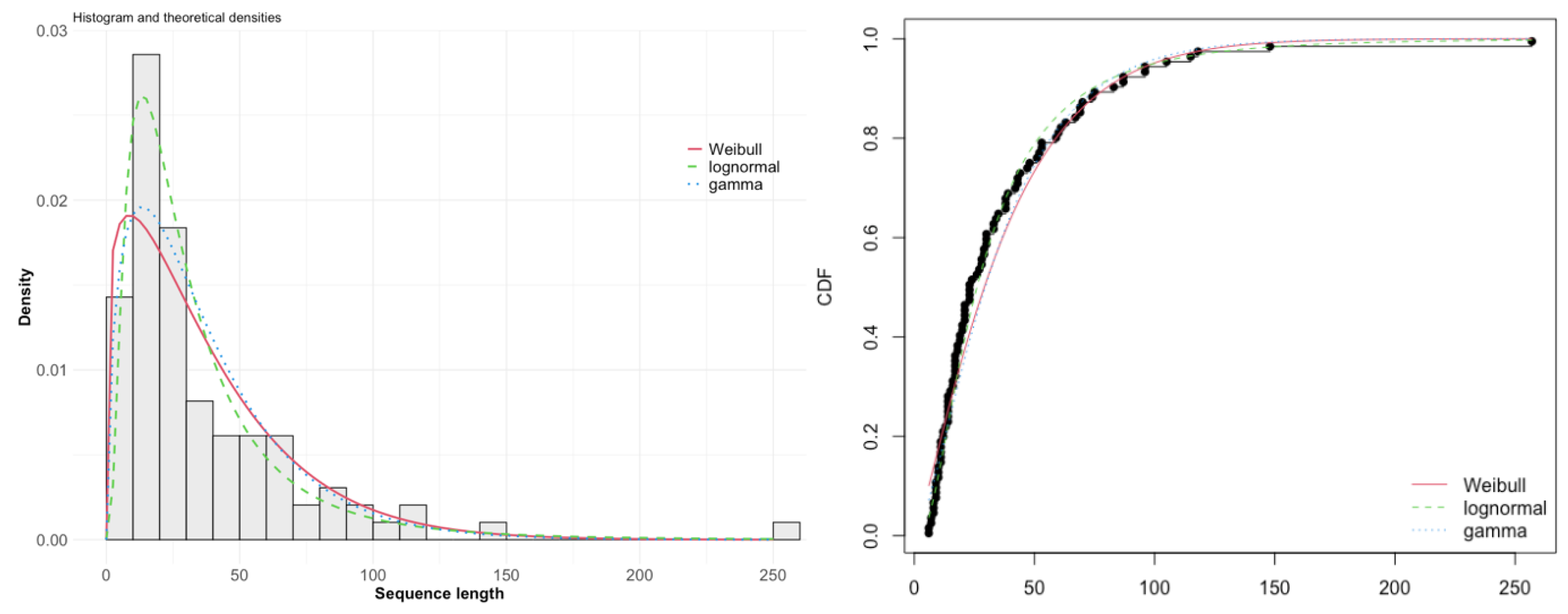
- Zipf’s law of abbreviation—broadly states that the length of a linguistic unit reversely correlates with its frequency of use; viz., more frequent sequences tend to be shorter [1]. Language studies on the relation between word length in terms of letters in English and Swedish and their frequencies [6] and the length of sentences in terms of the number of words for American English [7] found that it follows the gamma distribution for probability density:
- Menzerath–Altmann’s law—indicates a reverse correlation between a sequence’s size and its constituent parts. In other words, the longer a sequence, the shorter its constituents, and vice versa. In natural language, the law applies at different levels of linguistic description, e.g., sentences (size measured in terms of number of clauses), words (measured in terms of number of syllables), and other linguistic units. Altmann [8] proposed the following formulation of this law:
- (i)
- Evolutionary Pressures: Species that rely heavily on vocal communication for survival, such as primates, cetaceans, and certain birds, have evolved complex vocal systems optimised for efficiency and structure to enhance communication effectiveness.
- (ii)
- Social Structure: Animals with complex social structures, like dolphins and primates, benefit from efficient communication to maintain social bonds, coordinate group activities, and navigate social hierarchies.
- (iii)
- Cognitive Abilities: Species with higher cognitive abilities are more likely to develop sophisticated communication systems that follow linguistic laws. This includes the ability to learn, remember, and produce a wide range of sound vocalisations.
- (iv)
- Environmental Factors: The habitat and environmental conditions can influence the development of communication systems. For example, animals in dense forests may develop shorter, more frequent calls to avoid sound attenuation, while those in open environments may use longer calls.
- (v)
- Phylogenetic Constraints: Some species may have inherent biological limitations that prevent the development of complex vocal systems. These constraints can be anatomical, neurological, or related to the species’ evolutionary history.
- (vi)
- Functional Needs: The specific needs of a species, such as hunting, mating, or territory defence, can shape their communication systems. Species that rely on vocalisations for these critical functions are more likely to develop efficient and structured communication.
2. Materials and Methods
2.1. Recordings
2.2. Ethics
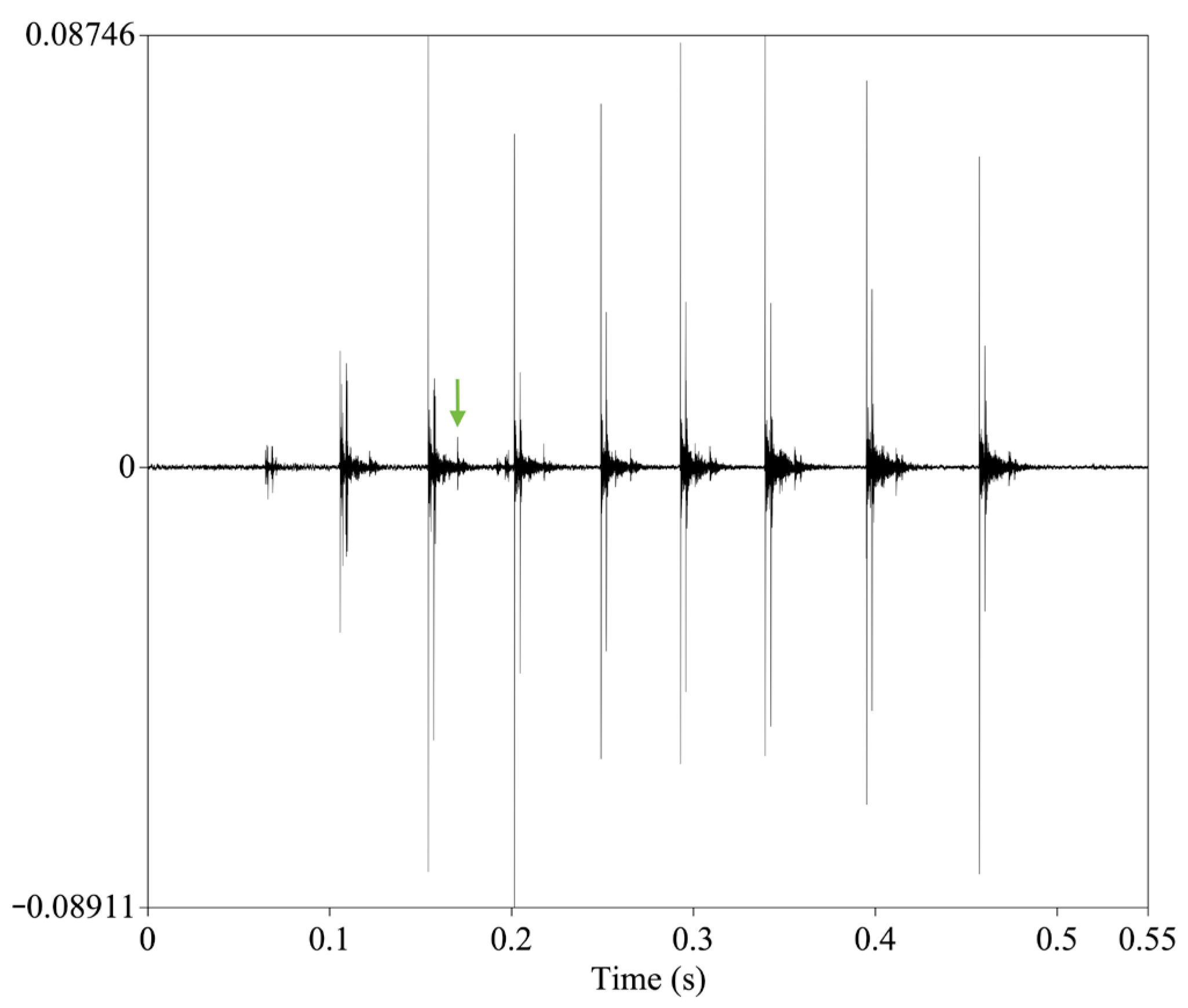
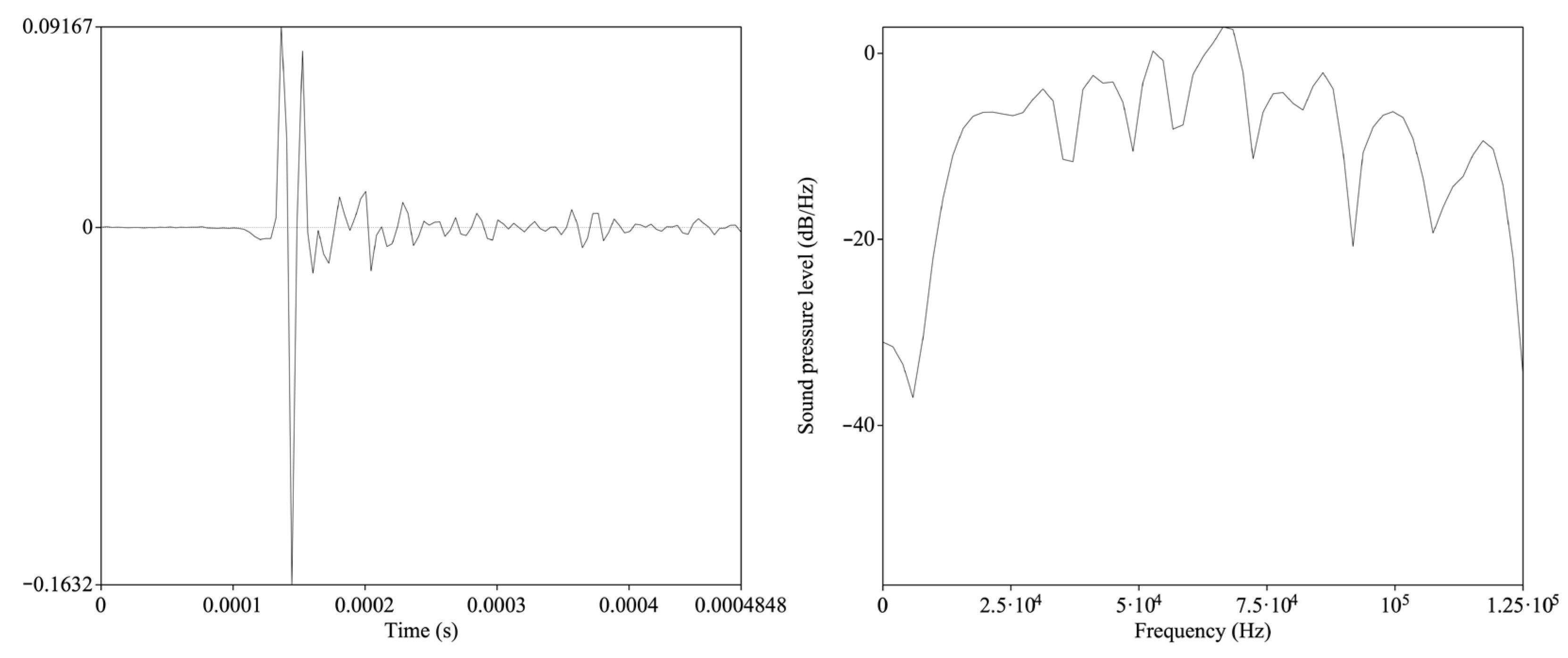
2.3. Signal Analysis
2.4. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data Acquisition and Signal Detection Parameters
| Hydrophone | Brüel & Kjær Type 8104-W-001 |
| Hydrophone sensitivity | −205dB re 1V/μPa |
| Hydrophone bandwidth | 0 Hz to 120 kHz |
| Hydrophone depth | 0.5 m |
| Amplifier | Brüel & Kjær NEXUS 2692-A-0S4 |
| Amplifier sensitivity | 10 mV/Pa |
| Amplifier bandwidth | 0 Hz to 120 kHz |
| DAQ system | National Instruments NI USB-6211 |
| DAQ-system input range | −10 V to 10 V |
| DAQ-system sensitivity | 91.6 μV |
| DAQ-system bandwidth | 0 Hz to 450 kHz |
| DAQ-system sample rate | 250 kHz |
| DAQ-system ADC resolution | 16 Bits |
| DAQ software | Signal Notes |
| Note: All recordings were made using a battery power supply, with the equipment disconnected from the AC power source to minimise 50 Hz power line interference. | |
| File type | wav (uncompressed linear PCM format) |
| File sample rate | 250 kHz |
| File resolution | 16 bits |
| Duration | 5 min |
| Normalisation level | ± 1 V |
| Filtration I | Filter type: | Butterworth HPF |
| Order: | 4th | |
| Cut-off frequency: | 100 Hz | |
| Segmentation I | Frame length: | 100 msec |
| Detection condition: | Median frequency above 5 kHz and | |
| maximum level above 0.05 V of | ||
| normalised level | ||
| Filtration II | Filter type: | Butterworth HPF |
| Order: | 2nd | |
| Cut-off frequency: | 5 kHz | |
| Segmentation II | Frame length: | 2.5 msec |
| Detection condition: | Kurtosis above 30 |
References
- Zipf, G.K. Human Behavior and the Principle of Least Effort. Available online: https://archive.org/details/in.ernet.dli.2015.90211/page/n7/mode/2up (accessed on 1 June 2025).
- Piantadosi, S.T. Zipf’s word frequency law in natural language: A critical review and future directions. Psychon. Bull. Rev. 2014, 21, 1112–1130. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. An Informational Theory of the Statistical Structure of Languages. In Communication Theory; Jackson, W., Ed.; Academic Press: Princeton, NJ, USA, 1953; Available online: https://pdodds.w3.uvm.edu/research/papers/others/1953/mandelbrot1953a.pdf (accessed on 1 June 2025).
- Suzuki, R.; Buck, J.R.; Tyack, P.L. The use of Zipf’s law in animal communication analysis. Anim. Behav. 2005, 69, 9–17. [Google Scholar] [CrossRef]
- Semple, S.; Ferrer-i-Cancho, R.; Gustison, M.L. Linguistic laws in biology. Trends Ecol. Evol. 2022, 37, 53–66. [Google Scholar] [CrossRef]
- Sigurd, B.; Eeg-Olofsson, M.; van Weijer, J. Word length, sentence length, and frequency-Zipf revisited. Stud. Linguist. 2004, 58, 37–52. [Google Scholar] [CrossRef]
- Kučera, H.; Francis, W.N. Computational Analysis of Present-Day American English. Available online: https://archive.org/details/computationalana00kuce/page/n5/mode/2up (accessed on 1 June 2025).
- Altmann, J. Baboon Mothers and Infants. The University of Chicago Press: Chicago, IL, USA; London, UK, 1980. [Google Scholar]
- Ferrer-i-Cancho, R.; Hernández-Fernández, A.; Lusseau, D.; Agoramoorthy, G.; Hsu, M.J.; Semple, S. Compression as a Universal Principle of Animal Behavior. Cogn. Sci. 2013, 37, 1565–1578. [Google Scholar] [CrossRef]
- Gustison, M.L.; Semple, S.; Ferrer-i-Cancho, R.; Bergman, T.J. Gelada vocal sequences follow Menzerath’s linguistic law. Proc. Natl. Acad. Sci. USA 2016, 113, E2750–E2758. [Google Scholar] [CrossRef]
- Fedurek, P.; Zuberbühler, K.; Semple, S. Trade-offs in the production of animal vocal sequences: Insights from the structure of wild chimpanzee pant hoots. Front. Zool. 2017, 14, 50. [Google Scholar] [CrossRef]
- Bezerra, B.M.; Souto, A.S.; Radford, A.N.; Jones, G. Brevity is not always a virtue in primate communication. Biol. Lett. 2011, 7, 23–25. [Google Scholar] [CrossRef]
- Clink, D.J.; Ahmad, A.H.; Klinck, H. Brevity is not a universal in animal communication: Evidence for compression depends on the unit of analysis in small ape vocalizations. R. Soc. Open Sci. 2020, 7, 200151. [Google Scholar] [CrossRef]
- Zhang Ch Zheng, Z.; Lucas, J.R.; Wang, Y.C.; Fan, X.; Zhao, X.; Feng, J.; Sun, C.; Jiang, T. Do bats’ social vocalizations conform to Zipf’s law and the Menzerath-Altmann law? iScience 2024, 27, 110401. [Google Scholar] [CrossRef]
- Youngblood, M. Language-like efficiency in whale communication. Sci. Adv. 2025, 11, eads6014. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Ma, H.; Ma, C.; Garber, P.A.; Fan, P. Male gibbon loud morning calls conform to Zipf’s law of brevity and Menzerath’s law: Insights into the origin of human language. Anim. Behav. 2020, 160, 145–155. [Google Scholar] [CrossRef]
- Youngblood, M. Language-like efficiency and structure in house finch song. Proc. R. Soc. 2024, 291, 291–20240250. [Google Scholar] [CrossRef]
- Gilman, R.T.; Durrant, C.; Malpas, L.; Lewis, R.N. Does Zipf’s law of abbreviation shape bird song? bioRxiv 2023. [Google Scholar] [CrossRef]
- Frasier, K.E.; Roch, M.A.; Soldevilla, M.S.; Wiggins, S.M.; Garrison, L.P.; Hildebrand, J.A.; Glotin, H. Automated classification of dolphin echolocation click types from the Gulf of Mexico. PLOS Comput. Biol. 2017, 13, e1005823. [Google Scholar] [CrossRef]
- Herzing, D.L. Clicks, whistles and pulses: Passive and active signal use in dolphin communication. Acta Astronaut. 2014, 105, 534–537. [Google Scholar] [CrossRef]
- Houser, D.S.; Helweg, D.A.; Moore, P.W. Classification of dolphin echolocation clicks by energy and frequency distributions. J. Acoust. Soc. Am. 1999, 106, 1579–1585. [Google Scholar] [CrossRef]
- Meyer, J.; Magnasco, M.O.; Reiss, D. The Relevance of Human Whistled Languages for the Analysis and Decoding of Dolphin Communication. Front. Psychol. 2021, 12, 689501. [Google Scholar] [CrossRef]
- Ferrer-i-Cancho, R.; McCowan, B.A. Law of Word Meaning in Dolphin Whistle Types. Entropy 2009, 11, 688–701. [Google Scholar] [CrossRef]
- Kriesell, H.J.; Elwen, S.H.; Nastasi, A.; Gridley, T. Identification and Characteristics of Signature Whistles in Wild Bottlenose Dolphins (Tursiops truncatus) from Namibia. PLoS ONE 2014, 9, e106317. [Google Scholar] [CrossRef]
- Janik, V.M.; Sayigh, L.S.; Wells, R.S. Signature whistle shape conveys identity information to bottlenose dolphins. Proc. Natl. Acad. Sci. USA 2006, 103, 8293–8297. [Google Scholar] [CrossRef] [PubMed]
- Popper, A.N. Sound emission and detection by delphinids. In Cetacean Behavior: Mechanisms and Functions; Herman, L.M., Ed.; John Wiley: New York, NY, USA, 1980. [Google Scholar]
- Whitlow, W.L.A. Sonar of Dolphins; Springer-Verlag: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Spence, H.R. The Importance of Bioacoustics for Dolphin Welfare: Soundscape Characterization with Implications for Management. Ph.D. Dissertation, The City University of New York, New York, NY, USA, 2015. [Google Scholar]
- Blomqvist, C.; Amundin, M. An acoustic tag for recording directional pulsed ultrasounds aimed at free-swimming bottlenose dolphins (Tursiops truncatus) by conspecifics. Aquat. Mamm. 2004, 30, 345–356. [Google Scholar] [CrossRef]
- Branstetter, B.; Finneran, J.; Fletcher, E.; Weisman, B.; Ridgway, S. Dolphins can maintain vigilant behavior through echolocation for 15 days without interruption or cognitive impairment. PLoS ONE 2012, 7, e47478. [Google Scholar] [CrossRef] [PubMed]
- Atem, A.C.G.; Rasmussen, M.H.; Wahlberg, M.; Petersen, H.C.; Miller, L.A. Changes in click source levels with distance to targets: Studies of free-ranging white-beaked dolphins Lagenorhynchus albirostris and captive harbour Porpoises Phocoena Phocoena. Bioacoustics 2009, 19, 49–65. [Google Scholar] [CrossRef]
- Finneran, A.E.; Mulsow, J.; Finneran, J.J. Detection of simulated patterned echo packets by bottlenose dolphins (Tursiops truncatus). J. Acoust. Soc. Am. 2020, 148, 1007–1013. [Google Scholar] [CrossRef]
- Finneran, J.J. Dolphin "packet" use during long-range echolocation tasks. J. Acoust. Soc. Am. 2013, 133, 1796–1810. [Google Scholar] [CrossRef]
- Dupeng, L.; Zhangzhaohui. Bottlenose dolphin echolocation clicks characteristics acquisition and analysis. In Proceedings of the International Conference on Signal Processing, Communications and Computing, ICSPCC 2019, Dalian, China, 20–22 September 2019; pp. 1–4. [Google Scholar]
- McCowan, B.; Reiss, D. Quantitative Comparison of Whistle Repertoires from Captive Adult Bottlenose Dolphins (Delphinidae, Tursiops truncatus): A Re-evaluation of the Signature Whistle Hypothesis. Ethology 1995, 100, 194–209. [Google Scholar] [CrossRef]
- McCowan, B.A. New Quantitative Technique for Categorizing Whistles Using Simulated Signals and Whistles from Captive Bottlenose Dolphins (Delphinidae, Tursiops truncatus). Ethology 2010, 100, 177–193. [Google Scholar] [CrossRef]
- McCowan, B.; Hanser, S.F.; Doyle, L.R. Quantitative tools for comparing animal communication systems: Information theory applied to bottlenose dolphin whistle repertoires. Anim. Behav. 1999, 57, 409–419. [Google Scholar] [CrossRef]
- Arnon, I.; Kirby, S.; Allen, J.; Garrigue, C.; Carroll, E.L.; Garland, E.C. Whale song shows language-like statistical structure. Science 2025, 387, 649–653. [Google Scholar] [CrossRef]
- Kershenbaum, A.; Sayigh, L.S.; Janik, V.M. The encoding of individual identity in dolphin signature whistles: How much information is needed? PLoS ONE 2013, 8, e77671. [Google Scholar] [CrossRef] [PubMed]
- Oswald, J.N.; Walmsley, S.F.; Casey, C.; Fregosi, S.; Southall, B.; Janik, V.M. Species information in whistle frequency modulation patterns of common dolphins. Phil. Trans. R. Soc. 2021, 376, 20210046. [Google Scholar] [CrossRef] [PubMed]
- Kohlsdorf, D.; Herzing, D.; Starner, T. In Proceedings of the An Auto Encoder for Audio Dolphin Communication. In Proceedings of the International Joint Conference on Neural Networks (IJCNN-2020), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Frey, B.J.; Dueck, D. Clustering by Passing Messages Between Data Points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef]
- Bodenhofer, U.; Kothmeier, A.; Hochreiter, S. APCluster: An R package for affinity propagation clustering. Bioinformatics 2011, 27, 2463–2464. [Google Scholar] [CrossRef]
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. lme4: Linear Mixed-Effects Models Using Eigen and S4. Available online: http://CRAN.R-project.org/package=lme4 (accessed on 1 June 2025).
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 1 June 2025).
- Cranford, T.W.; Amundin, M.; Norris, K.S. Functional morphology and homology in the odontocete nasal complex: Implications for sound generation. J. Morphol. 1996, 228, 223–285. [Google Scholar] [CrossRef]
- Cranford, T.W. Hearing by Whales and Dolphins. In Search of Impulse Sound Sources in Odontocetes; Springer: New York, NY, USA, 2000. [Google Scholar]
- Henderson, E.E.; Hildebrand, J.A.; Smith, M.H.; Falcone, E.A. The behavioral context of common dolphin (Delphinus sp.) vocalizations. Mar. Mammal Sci. 2012, 28, 439–460. [Google Scholar] [CrossRef]
- Chomsky, N. Aspects of The Theory of Syntax; The MIT Press: Boston, MA, USA, 1965. [Google Scholar]
- Hockett, C. The origin of speech. W.H. Freeman and Co. 1960. Available online: https://chd.ucsd.edu/_files/winter2009/Hockett.1960.pdf (accessed on 1 June 2025).
- Ouattara, K.; Lemasson, A.; Zuberbuhler, K. Campbell’s monkeys concatenate vocalizations into context-specific call sequences. Proc. Natl. Acad. Sci. USA 2009, 106, 22026–22031. [Google Scholar] [CrossRef]
- Suzuki, T.N.; Wheatcroft, D.; Griesser, M. Call combinations in birds and the evolution of compositional syntax. PLoS Biol. 2018, 16, e2006532. [Google Scholar] [CrossRef]
- Ryabov, V.A. The study of acoustic signals and the supposed spoken language of the dolphins. St. Petersburg Polytech. Univ. J. Phys. Math. 2016, 2, 231–239. [Google Scholar] [CrossRef]
- Jones, B.; Zapetis, M.; Samuelson, M.M.; Ridgway, S. Sounds produced by bottlenose dolphins (Tursiops): A review of the defining characteristics and acoustic criteria of the dolphin vocal repertoire. Bioacoustics 2020, 29, 399–440. [Google Scholar] [CrossRef]
- Janik, V.M. Chapter 4 Acoustic Communication in Delphinids. Adv. Study Behav. 2009, 40, 123–157. [Google Scholar] [CrossRef]
- Williams, C.B. A Note on the Statistical Analysis of Sentence-Length as a Criterion of Literary Style. Biometrika 1940, 31, 356. [Google Scholar] [CrossRef]
- Siswadi; Quesenberry, C.P. Selecting among Weibull, lognormal and gamma distributions using complete and censored smaples. Nav. Res. Logist. Q. 1982, 29, 557–569. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stepanov, A.; Zhivomirov, H.; Nedelchev, I.; Ganchev, T.; Stateva, P. Bottlenose Dolphins’ Clicks Comply with Three Laws of Efficient Communication. Algorithms 2025, 18, 392. https://doi.org/10.3390/a18070392
Stepanov A, Zhivomirov H, Nedelchev I, Ganchev T, Stateva P. Bottlenose Dolphins’ Clicks Comply with Three Laws of Efficient Communication. Algorithms. 2025; 18(7):392. https://doi.org/10.3390/a18070392
Chicago/Turabian StyleStepanov, Arthur, Hristo Zhivomirov, Ivaylo Nedelchev, Todor Ganchev, and Penka Stateva. 2025. "Bottlenose Dolphins’ Clicks Comply with Three Laws of Efficient Communication" Algorithms 18, no. 7: 392. https://doi.org/10.3390/a18070392
APA StyleStepanov, A., Zhivomirov, H., Nedelchev, I., Ganchev, T., & Stateva, P. (2025). Bottlenose Dolphins’ Clicks Comply with Three Laws of Efficient Communication. Algorithms, 18(7), 392. https://doi.org/10.3390/a18070392






