Numerical and Theoretical Treatments of the Optimal Control Model for the Interaction Between Diabetes and Tuberculosis
Abstract
1. Introduction
2. Non-Autonomous Mathematical Model System Formulation
- (a)
- represents a TB prevention effort that screens for LTBIs among key groups of people in the population (i.e., people living with HIV or NIDDM, TB patients, family members, coworkers, and roommates) and promptly provides saturated treatment to those who have TB infections in the latent form. The cost of implementing this control includes identifying and screening key individuals who are at risk of being latently infected with tuberculosis, providing medications or directly observed treatment (DOT) to patients, and also non-death productivity losses by the patients.
- (b)
- is the tuberculosis and diabetes intervention to prevent people from developing either or both diseases. This is carried out through health and wellness promotions in the community, i.e., community awareness campaigns that encourage those diagnosed with pre-diabetes or gestational diabetes to go for routine screening with a diagnostic test for diabetes mellitus. Healthy diets and lifestyles advocacy. Prevention efforts towards developing complications are aimed at diabetic patients who are free of complications. Mass sensitization in the community on tuberculosis prevention. The cost of implementing this intervention strategy includes providing health education at home, hospitals, schools, and through mass and social media.
- (c)
- denotes TB control strategy that provides treatment to non-diabetic individuals suffering from active tuberculosis disease. The cost of implementing this control involves the amount spent on receiving treatment for tuberculosis by the patients, health care, allocation of resources for the treatment and management of people suffering from active tuberculosis infections and so on.
- (d)
- represents the TB treatment effort that caters to people living with tuberculosis and diabetes. The cost of implementing the control includes the expenses when receiving simultaneous treatment for tuberculosis and noninsulin-dependent diabetes mellitus, management of diabetic complications, health care workers, funding TB-NIDDM clinics, and so on.
- The homogeneous mixing of individuals in the population and people in different classes interact.
- It is assumed that no individual in the population has permanent immunity to tuberculosis.
- The tuberculosis infection progression is from latency to the active disease stage, i.e., people first harbor tuberculosis infections in latent form and later become infectious either through exogenous reinfection or endogenous reactivation.
- We also assume the bidirectional link between tuberculosis and diabetes, i.e., diabetic patients can develop tuberculosis and tuberculosis patients can also become diabetic.
3. Analysis of the Mathematical Model with Constant Control Parameters
3.1. Equilibrium Points
3.2. Sensitivity Analysis
4. Theoretical Study of the Optimal Control Model Problem
4.1. Existence of an Optimal Control
4.2. Characterization of the Optimal Control
5. Numerical Simulations
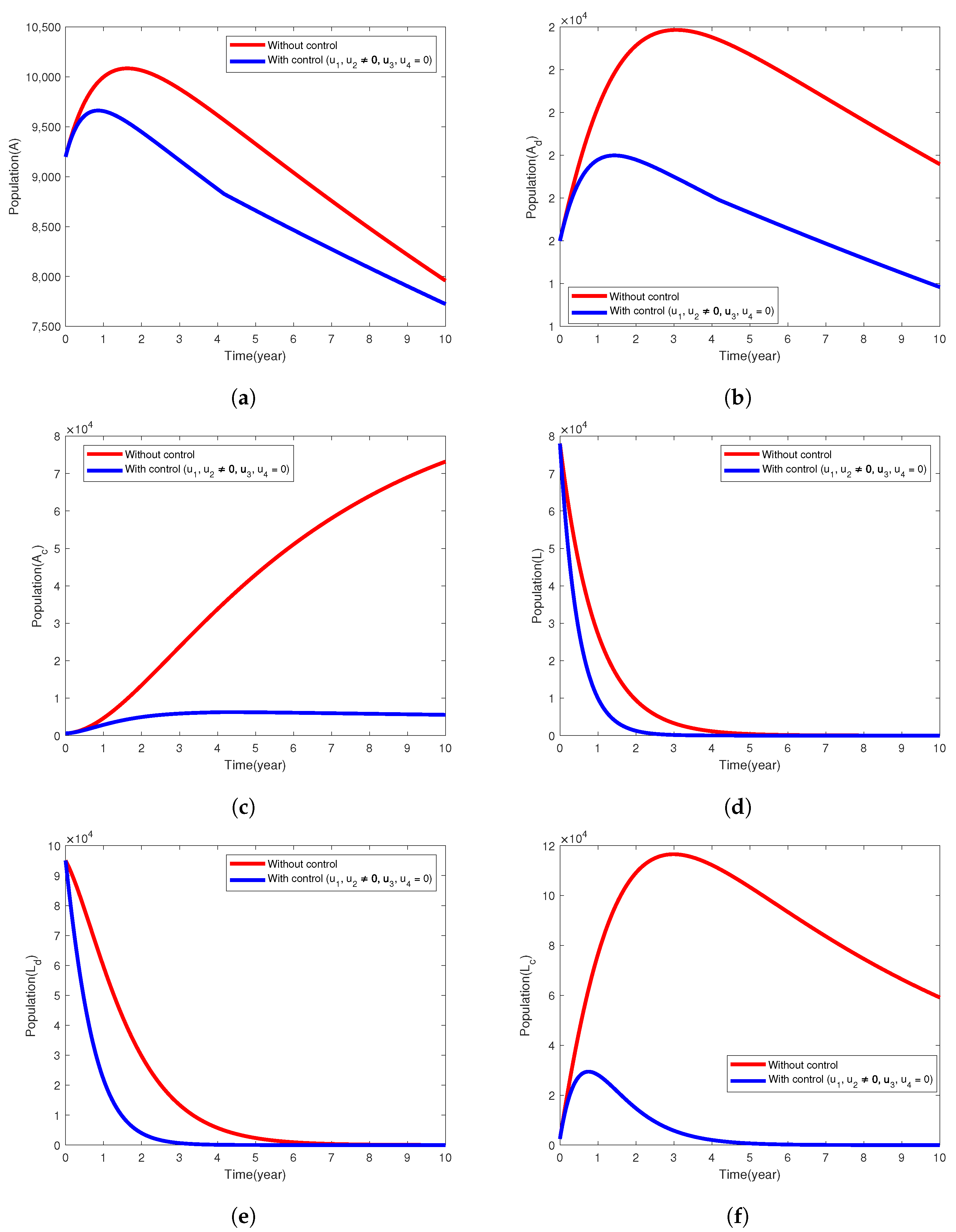
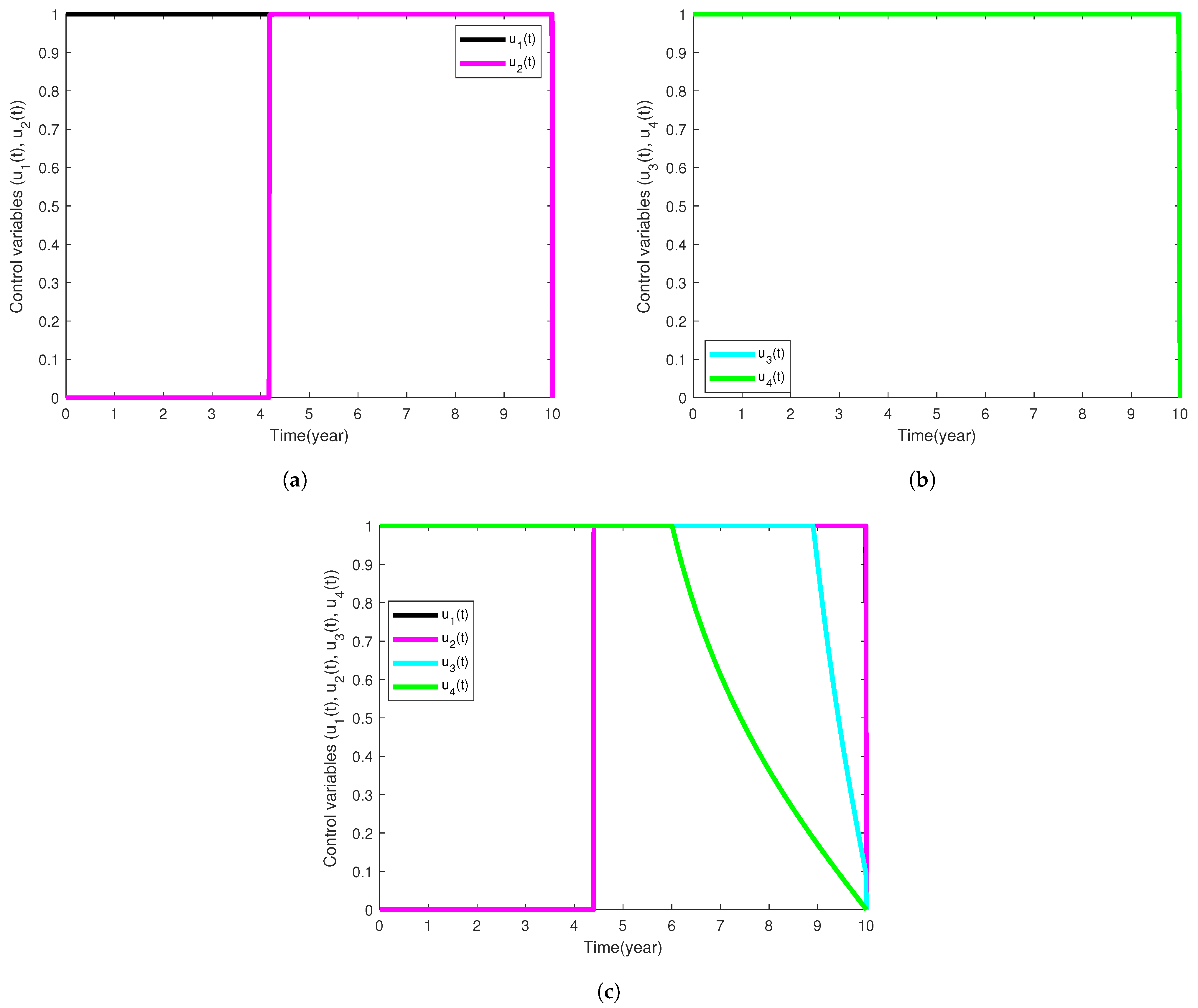
5.1. Intervention Strategy with Prevention of TB and Diabetes
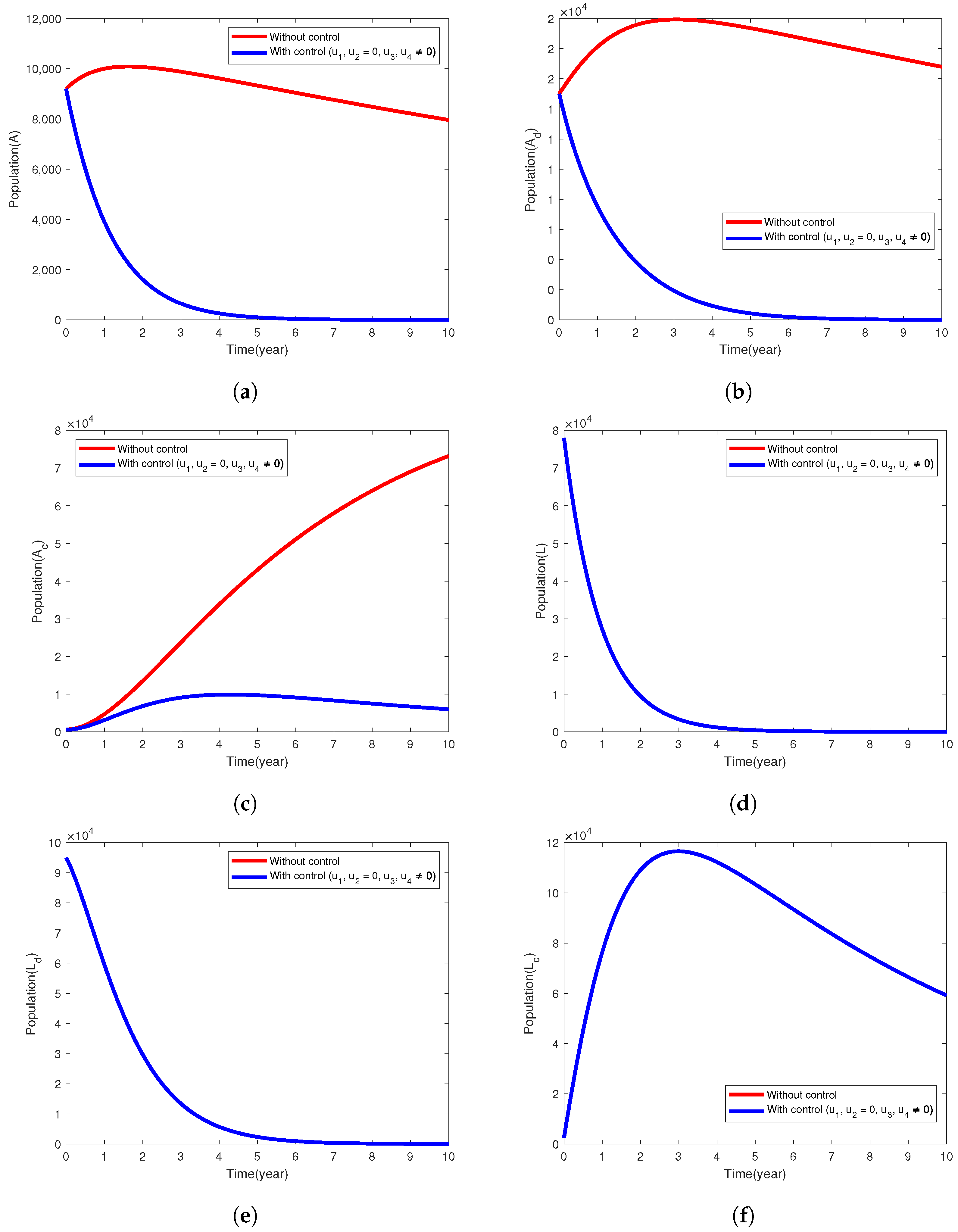
5.2. Intervention Strategy with Only Treatment of Active Cases of TB
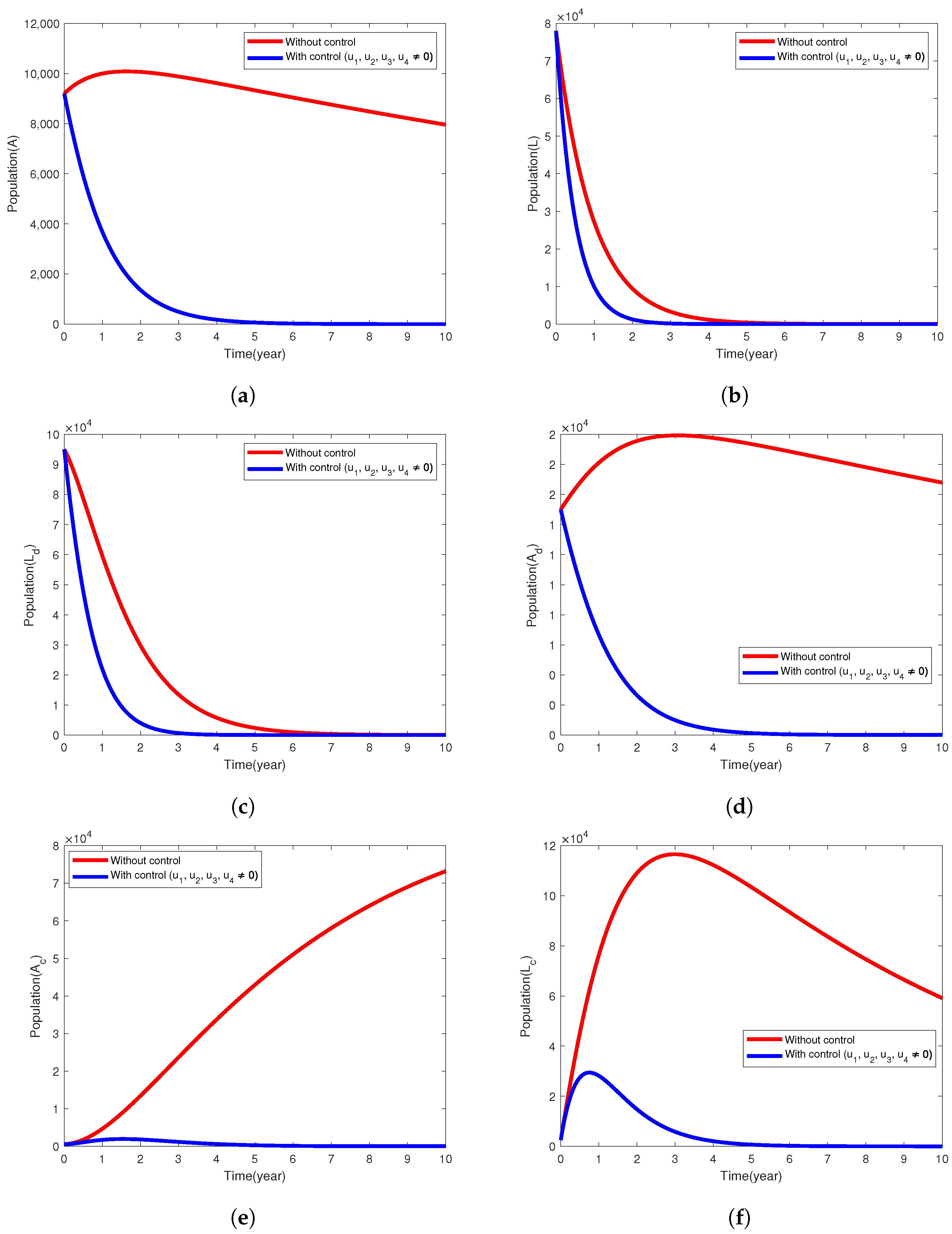
5.3. Intervention Strategy with Prevention and Treatment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 2
Appendix B. Proof of Theorem 3
References
- abcNEWS, Kansas Faces One of the Largest Tuberculosis Outbreaks in Us History. Available online: https://abcnews.go.com/Health/kansas-faces-largest-tuberculosis-outbreak-us-history-health/story?id=118174420 (accessed on 30 January 2025).
- Orcau, À.; Caylà, J.A.; Martínez, J.A. Present epidemiology of tuberculosis. prevention and control programs. Enfermedades Infecc. Microbiol. Clin. 2011, 29, 2–7. [Google Scholar] [CrossRef] [PubMed]
- CDC. 2024 Tuberculosis (TB) Surveillance Report. Available online: https://www.cdc.gov/tb/risk-factors/diabetes.html (accessed on 21 May 2025).
- WHO. Global Tuberculosis Report 2024. Available online: https://www.who.int/teams/global-programme-on-tuberculosis-and-lung-health/tb-reports/global-tuberculosis-report-2024 (accessed on 21 May 2025).
- CDC, Provisional 2024 Tuberculosis Data, United States. Available online: https://www.cdc.gov/tb-data/2024-provisional/index.html (accessed on 21 May 2025).
- Cao, H.; Song, B.; Zhou, Y. Treatment strategies for the latent tuberculosis infections. J. Math. Biol. 2023, 86, 93. [Google Scholar] [CrossRef] [PubMed]
- Agwu, C.O.; Omame, A.; Inyama, S.C. Analysis of mathematical model of diabetes and tuberculosis co-infection. Int. J. Appl. Comput. Math. 2023, 9, 36. [Google Scholar] [CrossRef]
- Suárez, I.; Fünger, S.M.; Kröger, S.; Rademacher, J.; Fätkenheuer, G.; Rybniker, J. The diagnosis and treatment of tuberculosis. Dtsch. Aerzteblatt Int. 2019, 116, 729–735. [Google Scholar] [CrossRef]
- World Health Organization. Communicable Diseases Cluster. What is Dots?: A Guide to Understanding the Who-Recommended tb Control Strategy Known as Dots; Technical Report; World Health Organization: Geneva, Switzerland, 1999. [Google Scholar]
- Jeon, C.Y.; Murray, M.B. Diabetes mellitus increases the risk of active tuberculosis: A systematic review of 13 observational studies. PLoS Med. 2008, 5, e152. [Google Scholar]
- Krishna, S.; Jacob, J.J. Diabetes Mellitus and Tuberculosis, Endotext; MDText. com, Inc.: South Dartmouth, MA, USA, 2021. [Google Scholar]
- Moualeu, D.; Bowong, S.; Tewa, J.; Emvudu, Y. Analysis of the impact of diabetes on the dynamical transmission of tuberculosis. Math. Model. Nat. Phenom. 2012, 7, 117–146. [Google Scholar] [CrossRef]
- Tan, G.H.; Nelson, R.L. Pharmacologic treatment options for non-insulin-dependent diabetes mellitus. Mayo Clin. Proc. 1996, 71, 763–768. [Google Scholar] [CrossRef]
- Yorke, E.; Atiase, Y.; Akpalu, J.; Sarfo-Kantanka, O.; Boima, V.; Dey, I.D. The bidirectional relationship between tuberculosis and diabetes. Tuberc. Res. Treat. 2017, 2017, 1702578. [Google Scholar] [CrossRef]
- Bates, M.; Marais, B.J.; Zumla, A. Tuberculosis comorbidity with communicable and noncommunicable diseases. Cold Spring Harb. Perspect. Med. 2015, 5, a017889. [Google Scholar] [CrossRef]
- Vento, S.; Lanzafame, M. Tuberculosis and cancer: A complex and dangerous liaison. Lancet Oncol. 2011, 12, 520–522. [Google Scholar] [CrossRef]
- van Crevel, R.; Critchley, J.A. The interaction of diabetes and tuberculosis: Translating research to policy and practice. Trop. Med. Infect. Dis. 2021, 6, 8. [Google Scholar] [CrossRef]
- Nichols, G.P. Diabetes among young tuberculous patients, a review of the association of the two diseases. Am. Rev. Tuberc. Pulm. Dis. 1957, 76, 1016–1030. [Google Scholar]
- Garg, M.; Baliga, K. Management of type 2 diabetes (niddm). Med. J. 2002, 58, 53. [Google Scholar] [CrossRef][Green Version]
- Lefèbvre, P.J.; Scheen, A.J. Management of non-insulin-dependent diabetes mellitus. Drugs 1992, 44, 29–38. [Google Scholar] [CrossRef]
- Restrepo, B.I. Diabetes and Tuberculosis, Understanding the Host Immune Response Against Mycobacterium Tuberculosis Infection; Springer: Cham, Switzerland, 2018; pp. 1–21. [Google Scholar]
- Root, H.F. The association of diabetes and tuberculosis. New Engl. J. Med. 1934, 210, 127–147. [Google Scholar] [CrossRef]
- Alavi, S.M.; Khoshkhoy, M.M. Pulmonary tuberculosis and diabetes mellitus: Co-existence of both diseases in patients admitted in a teaching hospital in the southwest of iran. Casp. J. Intern. Med. 2012, 3, 421. [Google Scholar]
- Pan, S.-C.; Ku, C.-C.; Kao, D.; Ezzati, M.; Fang, C.-T.; Lin, H.-H. Effect of diabetes on tuberculosis control in 13 countries with high tuberculosis: A modelling study. Lancet Diabetes Endocrinol. 2015, 3, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, A.R.; Pinto, C.M. Non-integer order analysis of the impact of diabetes and resistant strains in a model for tb infection. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 104–126. [Google Scholar] [CrossRef]
- Jajarmi, A.; Ghanbari, B.; Baleanu, D. A new and efficient numerical method for the fractional modeling and optimal control of diabetes and tuberculosis co-existence. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 093111. [Google Scholar] [CrossRef]
- Moya, E.D.; Pietrus, A.; Oliva, S.M. A mathematical model for the study of effectiveness in therapy in tuberculosis taking into account associated diseases. Contemp. Math. 2021, 2, 77–102. [Google Scholar]
- Awad, S.F.; Critchley, J.A.; Abu-Raddad, L.J. Impact of diabetes mellitus on tuberculosis epidemiology in indonesia: A mathematical modeling analysis. Tuberculosis 2022, 134, 102164. [Google Scholar] [CrossRef] [PubMed]
- Rasheed, S.; Iyiola, O.S.; Oke, S.I.; Wade, B.A. Exploring a mathematical model with saturated treatment for the co-dynamics of tuberculosis and diabetes. Mathematics 2024, 12, 3765. [Google Scholar] [CrossRef]
- Afolabi, S.; Ajadi, N.; Jimoh, A.; Adenekan, I. Predicting diabetes using supervised machine learning algorithms on e-health records. Inform. Health 2025, 2, 9–16. [Google Scholar] [CrossRef]
- Afolabi, Y.; Wade, B. Dynamics of transmission of a monkeypox epidemic in the presence of an imperfect vaccination. Results Appl. Math. 2023, 19, 100391. [Google Scholar] [CrossRef]
- Iyiola, O.; Oduro, B.; Akinyemi, L. Analysis and solutions of generalized chagas vectors re-infestation model of fractional order type. Chaos Solitons Fractals 2021, 145, 110797. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2012. [Google Scholar]
- Blackwood, J.C.; Childs, L.M. An introduction to compartmental modeling for the budding infectious disease modeler. Lett. Biomath. 2018, 5, 195–221. [Google Scholar] [CrossRef]
- Iyiola, O.; Oduro, B.; Zabilowicz, T.; Iyiola, B.; Kenes, D. System of time fractional models for COVID-19: Modeling, analysis and solutions. Symmetry 2021, 13, 787. [Google Scholar] [CrossRef]
- Biala, T.A.; Afolabi, Y.O.; Khaliq, A. How efficient is contact tracing in mitigating the spread of COVID-19? A mathematical modeling approach. Appl. Math. Model. 2022, 103, 714–730. [Google Scholar] [CrossRef]
- Dere, Z.O.; Cogan, N.G.; Karamched, B.R. Optimal control strategies for mitigating antibiotic resistance: Integrating virus dynamics for enhanced intervention design. Math. Biosci. 2025, 386, 109464. [Google Scholar] [CrossRef]
- Oke, S.I.; Ekum, M.I.; Akintande, O.J.; Adeniyi, M.O.; Adekiya, T.A.; Achadu, O.J.; Matadi, M.B.; Iyiola, O.S.; Salawu, S.O. Optimal control of the coronavirus pandemic with both pharmaceutical and non-pharmaceutical interventions. Int. J. Dyn. Control 2023, 11, 2295–2319. [Google Scholar] [CrossRef]
- Omede, B.I.; Odionyenma, U.B.; Ibrahim, A.A.; Bolaji, B. Third wave of covid-19: Mathematical model with optimal control strategy for reducing the disease burden in nigeria. Int. J. Dyn. Control 2023, 11, 411–427. [Google Scholar] [CrossRef] [PubMed]
- Olaniyi, S.; Okosun, K.; Adesanya, S.; Lebelo, R. Modelling malaria dynamics with partial immunity and protected travellers: Optimal control and cost-effectiveness analysis. J. Biol. Dyn. 2020, 14, 90–115. [Google Scholar] [CrossRef] [PubMed]
- Capasso, V.; Serio, G. A generalization of the kermack-mckendrick deterministic epidemic model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Mengistu, A.K.; Witbooi, P.J. Mathematical Analysis of tb Model with Vaccination and Saturated Incidence Rate; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Egonmwan, A.O.; Okuonghae, D. Analysis of a mathematical model for tuberculosis with diagnosis. J. Appl. Math. Comput. 2019, 59, 129–162. [Google Scholar] [CrossRef]
- den Driessche, P.V.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Baba, I.A.; Abdulkadir, R.A.; Esmaili, P. Analysis of tuberculosis model with saturated incidence rate and optimal control. Phys. A Stat. Mech. Its Appl. 2020, 540, 123237. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; Routledge: New York, NY, USA, 2018. [Google Scholar]
| Model Parameter | Description | Baseline Values Per Year | Range | Reference |
|---|---|---|---|---|
| Constant per-capita recruitment rate | 667,685 | [600,000, 700,000] | [12] | |
| Rate of acquiring diabetes mellitus without developing complications | 0.009 | [0.00466, 0.0133] | [12] | |
| Rate of acquiring complicated form of diabetes mellitus | 0.01 | [0.00413, 0.0159] | [7] | |
| Death rate as a result of severe complications associated with diabetes in the compartment | 0.005 | [0.00376, 0.00624] | [7] | |
| Death rate as a result of severe complications associated with diabetes in the compartment | 0.1 | [0.000398, 0.000602] | [7] | |
| Exogenous reinfection rate | 0.05 | [0.0221, 0.0779] | [6] | |
| Exogenous reinfection rate | [0.00897, 0.0920] | [7] | ||
| Exogenous reinfection rate | [0.0349, 0.0671] | [7] | ||
| Death rate as a result of complications linked directly to diabetes in the compartment | 0.1 | [0.000398, 0.000602] | [7] | |
| Mortality rate owing to active tuberculosis in the A compartment | 0.0025 | [0.00219, 0.00281] | [6] | |
| Mortality rate owing to active tuberculosis in the compartment | [0.00158, 0.00467] | [7] | ||
| Mortality rate owing to active tuberculosis in the compartment | [0.000807, 0.00701] | [7] | ||
| Modification parameter that adjusts the accelerated rate of contracting the Mycobaterium TB in the latent form among diabetic individuals that experienced no complication | 1.01 | [0.459, 1.543] | [7] | |
| Modification parameter that adjusts the accelerated rate of developing LTBIs among those having diabetes with complications | 2.851 | [2.247, 3.455] | Assumed | |
| Modification parameter that adjusts the accelerated rate at which individuals in the class acquire noncomplicated form of diabetes | 1.01 | [1, 1.5] | [7] | |
| Modification parameter that adjusts the accelerated rate at which those in the class acquire complicated form of diabetes | 1.05 | [1, 1.5] | [7] | |
| Rate of acquiring diabetes mellitus without developing complications in the L compartment | 1.01 | [1, 2] | [7] | |
| Rate of acquiring diabetes mellitus without developing complications in the compartment | 1.01 | [1, 2] | [7] | |
| Transmission probability per contact with infectious diabetic and non-diabetic individuals | [42] | |||
| Saturating factor | [6] | |||
| Modification parameter | 5.597 | [5.168, 6.026] | Assumed | |
| Modification parameter | 5.14 | [4.723, 5.557] | Assumed | |
| Per-capita rate at which latent TB infections progress to infectious TB disease among individuals without diabetes | 0.023 | [0.00565, 0.0404] | [42] | |
| Per-capita rate at which latent TB infections progress to infectious TB disease among individuals with noncomplicated form of diabetes | [0.0169, 0.0751] | [7] | ||
| Per-capita rate at which latent TB infections progress to infectious TB disease among individuals with complicated form of diabetes | [0.0827, 0.101] | [7] | ||
| b | Saturation | 0.7 | [0, 1] | Assumed |
| Natural mortality rate per-capita | 0.02041 | [0.0202, 0.02189] | [43] |
| Parameter | Index | Parameter | Index |
|---|---|---|---|
| 0.0247 | 0.2561 | ||
| 0.5733 | 0.6768 | ||
| 0.2891 | 0.2228 | ||
| 0.3219 | 0.0591 | ||
| 1 | 1 | ||
| 0.3438 | 0.1575 | ||
| −0.3958 | |||
| −1.1599 | |||
| −0.0038 | −0.9211 | ||
| −0.00016905 | −0.0017 | ||
| −0.0050 | −1.4621 | ||
| −0.0055 | −0.00064477 | ||
| 0.1358 | −0.0338 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasheed, S.; Iyiola, O.S.; Oke, S.I.; Wade, B.A. Numerical and Theoretical Treatments of the Optimal Control Model for the Interaction Between Diabetes and Tuberculosis. Algorithms 2025, 18, 348. https://doi.org/10.3390/a18060348
Rasheed S, Iyiola OS, Oke SI, Wade BA. Numerical and Theoretical Treatments of the Optimal Control Model for the Interaction Between Diabetes and Tuberculosis. Algorithms. 2025; 18(6):348. https://doi.org/10.3390/a18060348
Chicago/Turabian StyleRasheed, Saburi, Olaniyi S. Iyiola, Segun I. Oke, and Bruce A. Wade. 2025. "Numerical and Theoretical Treatments of the Optimal Control Model for the Interaction Between Diabetes and Tuberculosis" Algorithms 18, no. 6: 348. https://doi.org/10.3390/a18060348
APA StyleRasheed, S., Iyiola, O. S., Oke, S. I., & Wade, B. A. (2025). Numerical and Theoretical Treatments of the Optimal Control Model for the Interaction Between Diabetes and Tuberculosis. Algorithms, 18(6), 348. https://doi.org/10.3390/a18060348







