Abstract
Heart attack is a leading cause of mortality, necessitating timely and precise diagnosis to improve patient outcomes. However, timely diagnosis remains a challenge due to the complex and nonlinear relationships between clinical indicators. Machine learning (ML) and deep learning (DL) models have the potential to predict cardiac conditions by identifying complex patterns within data, but their “black-box” nature restricts interpretability, making it challenging for healthcare professionals to comprehend the reasoning behind predictions. This lack of interpretability limits their clinical trust and adoption. The proposed approach addresses this limitation by integrating predictive modeling with Explainable AI (XAI) to ensure both accuracy and transparency in clinical decision-making. The proposed study enhances heart attack prediction using the University of California, Irvine (UCI) dataset, which includes various heart analysis parameters collected through electrocardiogram (ECG) sensors, blood pressure monitors, and biochemical analyzers. Due to class imbalance, the Synthetic Minority Over-sampling Technique (SMOTE) was applied to enhance the representation of the minority class. After preprocessing, various ML algorithms were employed, among which Artificial Neural Networks (ANN) achieved the highest performance with 96.1% accuracy, 95.7% recall, and 95.7% F1-score. To enhance the interpretability of ANN, two XAI techniques, specifically SHapley Additive Explanations (SHAP) and Local Interpretable Model-Agnostic Explanations (LIME), were utilized. This study incrementally benchmarks SMOTE, ANN, and XAI techniques such as SHAP and LIME on standardized cardiac datasets, emphasizing clinical interpretability and providing a reproducible framework for practical healthcare implementation. These techniques enable healthcare practitioners to understand the model’s decisions, identify key predictive features, and enhance clinical judgment. By bridging the gap between AI-driven performance and practical medical implementation, this work contributes to making heart attack prediction both highly accurate and interpretable, facilitating its adoption in real-world clinical settings.
1. Introduction
Cardiovascular diseases (CVDs), including heart attacks, continue to be one of the major causes of death and disability globally, putting a heavy strain on healthcare systems and communities for effective diagnosis and treatment [1]. Nearly one-third of all fatalities that occur around the world result from cardiovascular illnesses and disorders, including heart attacks, which claim over 17 million lives annually [2]. There is an immediate need for efficient measures aimed at prevention, early diagnosis, and effective management. The first and foremost step in this regard will be identifying those who are at high risk for heart attacks and intervening with them promptly via lifestyle changes, targeted therapy, and medical interventions, which may significantly lower death rates [3,4,5].
However, the detection of a heart attack may prove to be a difficult task due to its dependence on multiple diverse factors. The genesis of these conditions lies in the interplay of genetic predispositions, underlying physiological abnormalities, and changeable lifestyle factors, including poor diet, smoking, lack of physical activity, and stress [6,7]. Moreover, the advancement of heart disease is commonly hindered by comorbidities like diabetes, hypertension, and obesity, which can make risk evaluation and prediction models more intricate [8]. Although traditional clinical diagnostic tools are helpful to some extent, they cannot integrate and analyze such a large amount of available diverse data involving these risk factors. Therefore, there is an increasing demand for more advanced and data-driven approaches to improve risk prediction and stratification.
In recent times, artificial intelligence (AI), especially within the scope of ML and DL, has opened doors for new possibilities in predictive analytics for the healthcare domain [9]. The state-of-the-art methodologies allow for the analysis of large-scale datasets to detect patterns and correlations that evade ordinary statistical methods [10]. However, there are limitations that may occur with the use of diverse forms of data. The class imbalance issue is one of the most important problems that ML models face when used on healthcare datasets. In many existing datasets, the samples of patients at risk of heart attack are far less than the other patients or healthy subjects [11]. This imbalanced nature of the dataset results in biased predictions in terms of sensitivity and generalizability on unseen data due to the model’s preference toward the majority class. This is a challenge that is addressed by generating synthetic data samples to successfully build robust and reliable predictive systems [12].
The other crucial problem with using AI for heart attack prediction is the interpretability of predictive models. Although many of the ML algorithms, for example, Random Forest (RF), Support Vector Machine (SVM), K-Nearest Neighbors (KNN), and neural networks can reach high prediction accuracy [13,14], they usually function as a “black-box” system. The lack of transparency imposes several limitations, especially in healthcare, which require high levels of trust, accountability, and ethical considerations. Clear and understandable explanations of model predictions need to be made by healthcare practitioners and patients alike to make informed decisions in diagnosis and treatment [15,16].
Feature engineering (FE) has become a necessary tool for improving the explainability of ML models [17]. It involves analyzing and interpreting raw data and extracting meaningful variables that are strongly associated with cardiovascular risks. FE can be effectively used to extract features related to cardiac disease, such as cholesterol levels, age, blood pressure, etc. Besides enhancing the predictive accuracy, it enables the model prediction to become more transparent for healthcare professionals to understand and more confident with its prediction [18,19]. Moreover, key predictors can be found by using more advanced feature selection methods, such as wrapper and embedded, in order to further increase ML model interpretability and robustness [20,21]. However, the main weakness of manual FE is that it is prone to designer’s assumptions bias, which can result in overlooking important information in the data. Furthermore, manual methods heavily rely on domain expertise, which may not always be capable of identifying complex, nonlinear relationships that automated feature learning approaches can uncover [22,23]. This motivates the need for systematic, data-driven approaches that are complementary or, in some cases, replace FE.
To address the above issues, a groundbreaking method called XAI has emerged recently. By offering a more objective assessment of feature relevance than human techniques, XAI provides automated and transparent explanations of feature contributions to the model’s predictions [24]. Furthermore, XAI approaches differ from conventional FE as they reveal latent data linkages, addressing interpretability challenges in complex ML models—an issue particularly critical in industries like healthcare, where patient safety is paramount. One of the most popular XAI approaches, SHAP, utilizes Shapley values, which are based on cooperative game theory, to quantify each feature’s contribution to the model predictions. For the purpose of heart attack prediction, SHAP details the ways in which hypertension and cholesterol influence model behavior on a global scale as well as patient-specific results. Modern black-box models can benefit from SHAP, a state-of-the-art technique for enhancing transparency [25,26], as it provides reliable and consistent explanations.
Another XAI technique that is worth noting is LIME, which develops interpretable diverse models to approximate the behavior of complex models locally for specific predictions [27]. For the purpose of heart attack prediction, LIME provides clinicians with a means to understand why a particular patient was flagged as high risk by the model by highlighting the most important features contributing to that prediction. Due to this interpretability, healthcare professionals can make better decisions on diagnosis and treatment [28,29]. Although the study does not rely on traditional manual FE techniques, domain knowledge remains integral to interpreting the results. XAI tools are utilized to identify the most influential features, but their clinical validation and interpretation require healthcare expertise. This approach aims to reduce the manual overhead of FE while preserving the critical role of domain-informed analysis in high-stakes applications like heart attack prediction.
Previous research has examined pipelines that integrate SMOTE, grid search, and shallow ANN architectures; however, many have concentrated predominantly on attaining high predictive metrics, neglecting the essential requirements for clinical interpretability and simplicity, particularly in small medical datasets. This study seeks to address this gap by concentrating on low-complexity, interpretable ANN models that can be meaningfully explained using SHAP and LIME, so ensuring the models are both precise and clinically applicable. Unlike black-box deep learning approaches, which often lack transparency, our approach prioritizes models that balance performance with explainability, a combination that is essential for adoption in real-world cardiology settings where model decisions must align with domain knowledge and be trusted by clinicians.
The study uses a publicly available UCI cardiac dataset [30] and applied SMOTE to fix class imbalance. The dataset gathers various heart analysis parameters of patients using a variety of medical sensors, including ECG sensors, blood pressure monitors, and biochemical analyzers. Essential physiological data from these sensors allows for precise analysis and the prediction of cardiac disease. The data collected from these diverse sensors provide a comprehensive overview of patient’s cardiac health conditions. The obtained data can be used to acquire significant hidden patterns that reside within the dataset, which may be used to understand the relation of various attributes with heart attacks. For this purpose, several ML algorithms, including Logistic Regression (LR), SVM, AdaBoost, RF, Bagging, KNN, Naive Bayes (NB), Voting Classifier, and ANN, were applied to the dataset for prediction. To further guarantee interpretability and provide feature-level insights into the model’s judgments, XAI approaches such as SHAP and LIME are used. The proposed work aims to tackle the two problems of accurate predictions and transparency regarding predictions generated by ML models. The key contributions of this study are as follows:
- SMOTE is applied to deal with the class imbalance problem in the cardiac dataset to improve its predictive performance and generalization;
- Implementation of multiple ML algorithms and neural networks to compare predictive accuracy and robustness;
- Application of XAI techniques such as SHAP and LIME to enhance interpretability and facilitate key insights into key risk factors for heart attacks;
- The identification and ranking of the important features contributing to heart attacks, aiding in the development of effective preventive and personalized medical strategies;
- The research framework is made reproducible and accessible to further studies using a publicly available UCI cardiac dataset.
The rest of the manuscript is organized as follows: Section 2 highlights the existing literature for the given research problem. Section 3 underlines the adopted methodology for the proposed work. Section 4 discusses results that were obtained after experimentations. Section 5 concludes our findings and provides future directions for the given research problem.
2. Literature Review
Cardiovascular diseases (CVDs), including heart attacks, account for 17 million fatalities per year, making them the major cause of mortality globally [2]. The need for efficient methods of detecting and preventing heart attacks in their early stages has grown in recent years. Data-driven approaches have recently gained popularity, with ML and XAI assisting in the understanding of CVD risk factors and improving prediction accuracy [31].
2.1. Machine Learning in Heart Attack Prediction
One major area where ML algorithms have seen extensive application is the prediction of heart attack after acute myocardial infarction (MI), which involves analyzing clinical information for patterns and correlations [32]. Decision Tree (DT) and Logistic Regression (LR) are two examples of popular, easy-to-understand algorithms. Many new models, including neural networks, SVM, and RF, have entered the field of heart failure (HF) prognosis and prediction; these models enhance predictive performance by capitalizing on intricate nonlinear interactions between features [2,32].
A.A. Stonier et al. [33] applied ML algorithms, including RF, Regression, KNN, and NB, on electronic health records and clinical reports to forecast heart attacks. The findings indicate that the most suitable ML algorithm for early cardiovascular disease detection is RF, achieving an accuracy of 88.52%. M. Oliveira et al. [32] investigated the potential of ML algorithms to enhance clinical decision-making and personalize patient treatment. ML algorithms were used to analyze patient data from Portuguese hospitals to forecast acute MI (AMI) mortality. Stochastic Gradient Descent achieved an area under the curve (AUC) value of 79%, which was increased to 81% for SVM, after adding laboratory variables. Moreover, the model was improved using FE and SMOTE with an AUC of 88% and a recall of 80%. M. B. Shahnawaz and H. Dawood [34] presented a DL approach to automated MI detection utilizing ultrashort-term heart rate variability (HRV) analysis of single-lead ECGs. The proposed system extracted time and frequency domain, and nonlinear HRV features to predict the occurrence of MI using an ANN model. The model achieved a sensitivity level of 100% and an accuracy of 99.1%.
R. Khera et al. [35] assessed ML models with the goal of forecasting in-hospital mortality after AMI. The observation was that for the risk classifications of high-risk people, a marginal increase in performance when compared to LR was seen while using the XGBoost classifier model (C statistic 0.90 vs. 0.89). It indicates that while ML models did not significantly enhance overall discrimination, XGBoost surpassed other models in calibration and risk resolution, indicating that XGBoost has the potential to enhance AMI risk assessment. Furthermore, X. Li et al. [36] similarly examined the efficacy of several ML models in predicting HF occurrences after AMI and proposed the HF-Lab9 model. Among the seven ML algorithms evaluated, XGBoost outperformed the remaining with key features, including glucose levels, lipids, and troponin I. An AUC of 0.966 was achieved by the XGBoost-based HF-Lab model, demonstrating both predictive accuracy and clinical value in the early evaluation of HF risk for patients with AMI.
P. O. de Capretz [37] used ML to forecast the likelihood of AMI or mortality in patients presenting with acute chest pain by analyzing their ECG and blood tests performed at the time of presentation. Input characteristics such as age, sex, ECG, and first blood tests were used to create two ML models based on LR and ANN, utilizing data from 9,519 individuals. A convolutional neural network (CNN) performed better than traditional approaches by ruling out 55% of instances and ruling in 5.3% of instances without requiring further tests.
2.2. Challenges with Class Imbalance in Medical Datasets
A major problem with CVD predictive modeling is imbalanced class distributions. For instance, in many existing cardiac databases, compared to individuals at low or no risk, there are far fewer samples of patients at high risk of heart attacks. This imbalance skews predictions, favoring the majority class and reducing sensitivity for underrepresented groups [38,39].
Addressing this problem has led to the widespread usage of the SMOTE for dataset balancing. In order to improve the model’s performance on unbalanced datasets, SMOTE creates synthetic samples for the minority class by interpolating the current data points. M. Waqar et al. [11] examined ML-based heart attack prediction using the UCI dataset without manual FE. SMOTE was used to fix the issue of class imbalance and boost classification accuracy. In order to guarantee high reliability in heart attack prediction, they discovered that a fine-tuned SMOTE-based ANN outperforms existing models. P. Iacobescu et al. [40] used the Synthetic Minority Over-sampling Technique – Edited Nearest Neighbors (SMOTE-ENN) for class imbalance correction and optimized hyperparameters to assess seven different classification algorithms. The algorithms included RF, LR, KNN, and neural networks. When compared to more conventional models, KNN performed best to achieve an accuracy of 99% and AUC (0.99). The study’s findings stress the significance of tackling class imbalance and optimizing feature selection to enhance prediction accuracy and showcase KNN as a promising contender for early CVD diagnosis.
H. Karamti et al. [41] presented an automated cervical cancer prediction system that used KNN imputation and SMOTE to handle missing values and class imbalance. An exceptional accuracy of 99.99% was attained by a stacked ensemble Voting Classifier, combining three ML models. By comparing several scenarios, the study showed that KNN-imputed SMOTE features greatly improved prediction performance. K. Welvaars et al. [42] improved the accuracy, precision, and recall of many classifiers by their evaluation of several resampling approaches, including Adaptive Synthetic Sampling (ADASYN) and SMOTE. Although resampling sometimes overestimated positive instances due to calibration challenges, enhanced discrimination ability, particularly for predicting high- and low-risk instances, increases clinical utility.
Y.C. Wang and C.H. Cheng [43] suggested a hybrid strategy that combines SMOTE, undersampling, particle swarm optimization (PSO), and MetaCost to address this problem. It was observed that Ensemble Learning enhanced AUC, recall, and F1-score, whereas MetaCost enhanced sensitivity in experiments conducted on nine medical datasets. SMOTE significantly enhanced AUC, and undersampling improved sensitivity and decreased misclassification costs for very imbalanced data. In order to maximize predictive performance in medical diagnosis, the overall findings suggest that resampling approaches should be used depending on the imbalance ratio within the dataset.
2.3. Importance of Feature Selection and Insights
Feature selection plays a crucial role in constructing reliable and understandable prediction models. In the healthcare domain, features like age, cholesterol levels, blood pressure, diabetes, hypertension, and smoking status are common impactful risk factors for CVDs [44,45]. However, modern studies have highlighted that factors like body mass index (BMI), stress levels, and aberrant resting ECG are known to be significant predictors of CVD mortality [46,47,48].
In order to increase ML models’ forecast accuracy, feature selection is critical. Y. Lee and J. Seo [49] emphasized the significance of statistically validating features in medical ML models, especially for HF prediction. Although biomarkers are ranked using conventional feature importance approaches, they often lack statistical significance assessment. To address this, a novel approach was put out to maximize biomarker selection and assess the relevance of feature importance values. This method improved diagnosis, therapy, and disease management by guaranteeing statistically significant traits, which increased the dependability of clinical decision-making. A. S. Mohd Faizal et al. [50] demonstrated that the performance of the reduced models was enhanced by the selected features when compared to full models that utilized all available data and had 62 features. RF, combined with recursive feature elimination (RFE) and RF importance (RFI), achieved a higher area under the precision-recall curve (AUPRC) scores (0.8048–0.8505). AUPRC of 0.8462 for a five-feature model (troponin I, High-Density Lipoprotein (HDL) cholesterol, HbA1c, anion gap, and albumin) indicated the importance of these characteristics in AMI prediction.
T. N. Anthony et al. [51] used feature selection to improve the model’s performance by refining relevant text-based features through Term Frequency—Inverse Document Frequency (TF-IDF) and handcrafted techniques. The model attained up to 100% accuracy in cross-validation and 95% on unseen data by combining feature selection with data augmentation and hyperparameter tuning, highlighting its crucial role in maximizing accuracy. In another study, R. Ghafari et al. [52] reduced the feature set to 50 by using the RFE method to filter out the most pertinent predictors for MI complications. By using this RFE, XGBoost proved to be the best model, achieving a high accuracy of 91.47% and an F1-score of 95.14% in identifying fatal complications. L. Wang et al. [53] used clinical data from 3061 cases to develop a stacking ensemble model to predict in-hospital mortality in patients with non-ST-segment elevation myocardial infarction (NSTEMI). The technique used over-sampling to address class imbalance, RFE for feature selection, and a two-layer stacking model that integrated seven base classifiers with XGBoost as the meta-model. With an AUC of 0.987, the model outperformed standalone classifiers such as RF, SVM, DT, and LR.
M. Senan et al. [54] used the SelectKBest function in conjunction with chi-squared statistical analysis for FE in order to improve predictive accuracy. Two datasets were used to train optimized classifiers, with the RF model achieving accuracy scores of 100% and 97.68% across datasets, as well as precision, recall, and F1 scores occasionally reaching 100%. S.B. Akter et al. [55] emphasized the importance of unbiased feature selection in improving MI risk prediction. Despite dataset imbalances, the Triple Criteria Selection (TCS) approach was developed to refine the most pertinent self-reported features and ensure model reliability. The Dual-Path Artificial Neural Network (DP-ANN) and Minority Weighted Sampling (MWS) were integrated with TCS to reduce bias and produce balanced performance with Area Under the Curve—Receiver Operating Characteristic evaluation metric (AUC-ROC: 89.5%). Key predictors were further validated by SHAP analysis, emphasizing the vital role feature selection plays in improving MI risk assessment and early identification.
2.4. XAI in Healthcare
The “black box” nature of ML models often limits their adoption in clinical settings. The accuracy of these models may be high; however, their lack of transparency makes it challenging to understand the decision-making process for specific scenarios. The goal of XAI is to overcome this difficulty by providing a rationale for the model’s predictions [56,57,58]. SHAP and LIME emerge as two popular methods for explaining individual predictions and feature contribution [59,60].
X. Zhu et al. [61] used the SHAP technique to analyze deep ML models developed for predicting in-hospital mortality in patients with initial AMI. SHAP helps increase model transparency, which is directly related to improving patient outcomes by helping doctors understand the most important risk variables. Through the use of SHAP analysis, it was revealed that key predictors of mortality risk include D-dimer, brain natriuretic peptide, and cardiogenic shock. X. Qi et al. [62] used ML models to determine the effect of dietary antioxidants on disease prediction, showing the importance of feature selection for clinical decision-making and its ability to understand the results. The integration of key antioxidant, demographic, and health-related information improved model performance. SHAP analysis of feature significance shows that naringenin, magnesium, and vitamin C are the most important contributors. Peng et al. [63] used SHAP analysis to identify important clinical features that contribute to the mortality prediction of HF patients, thereby increasing model transparency and interpretability. This study was a retrospective cohort study that used Medical Information Mart for Intensive Care Database-IV (MIMIC-IV) and eICU Database. The goal was to employ interpretable ML to predict 28-day all-in-hospital mortality causes in patients with HF and highlighted age, mechanical ventilation, and anion gap as the key factors.
R. O. Alabi et al. [60] used LIME and SHAP techniques to enhance ML model interpretability and identify key prognostic factors for Nasopharyngeal Carcinoma (NPC) survival, such as age, T-stage, and M-stage. SHAP measured the influence of each feature on predictions, while LIME offered case-specific explanations that allowed for individualized risk assessment and well-informed clinical decision-making. Similarly, P.C. Bizimana et al. [64] used LIME and SHAP to increase the interpretability of the ML model. SHAP quantified the influence of each feature on predictions and identified key risk factors, whereas LIME provided case-specific justifications.
Existing heart attack prediction models often overlook the imbalance in the UCI dataset, where negative instances are significantly fewer than positive ones. This imbalance leads to biased predictions and misleading evaluations, especially when accuracy is the primary metric. Unlike prior studies that focus mainly on accuracy, our research incorporates precision, recall, and F1-score for a more balanced assessment. However, a more critical limitation in the previous literature is the lack of interpretability in AI-driven predictions, as most ML models function as black boxes, making it challenging for healthcare professionals to trust their outputs. To address this, XAI techniques, specifically SHAP and LIME, are integrated to enhance transparency and feature identification. Unlike conventional approaches that rely on manual FE, which is resource-intensive and domain-dependent, our study eliminates the need for such manual efforts by using XAI to automatically highlight the most relevant features contributing to predictions. This ensures that medical practitioners can make informed decisions based on interpretable model insights rather than relying solely on opaque algorithmic outputs. Furthermore, our research uniquely combines XAI with a high-performing ANN model, achieving both accuracy and interpretability. By bridging the gap between automated AI decision-making and clinical expertise, the proposed approach provides a reliable and cost-effective solution that improves trust in AI-driven healthcare applications while enhancing the transparency and effectiveness of heart attack prediction systems.
3. Materials and Methods
In the proposed study, the publicly available UCI cardiac attack dataset is used and preprocessed for missing values, followed by normalization using the standard scalar technique. SMOTE was then applied to address the class imbalance, ensuring a more representative dataset for training ML models. The balanced dataset was subsequently used to train various models, including AdaBoost, RF, KNN, Bagging, SVM, and ANN. Following extensive testing, the ANN model is found to be the most accurate model for classification.
To enhance the interpretability of the ANN model, XAI techniques like LIME and SHAP were applied. LIME explains individual predictions locally, while SHAP provides global insights into feature influence. Both techniques helped identify significant features in the heart attack prediction, enhancing clinical interpretability. This improved transparency aids in more accurate diagnoses and treatment planning, making AI-driven decisions more actionable for healthcare professionals. Figure 1 depicts the flow of the study.
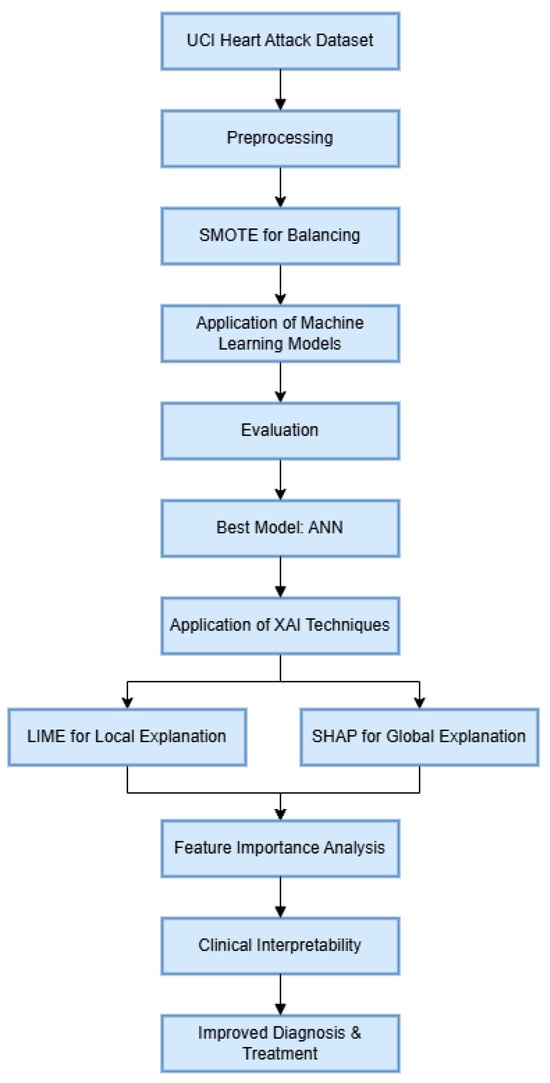
Figure 1.
Proposed workflow of the experiment.
3.1. Dataset
This study utilizes the UCI heart attack dataset, which contains 303 records and 76 attributes. The original UCI Heart Disease dataset comprises 76 raw variables; however, the official UCI repository indicates that practically all previous research utilizes a standardized selection of 14 clinically validated features [22,30]. This study adheres to the established practice by utilizing the generally accepted 14-attribute subset without engaging in further manual feature engineering or selective reduction. This guarantees alignment with previous benchmarks and applicability to clinical practice. Table 1 provides a detailed explanation of these attributes. Thirteen of these characteristics are used to predict cardiac disease. The “Target” variable serves as the output feature, indicating the presence or absence of a heart attack.

Table 1.
Dataset description.
3.2. Sensors’ Detail
The UCI Heart Disease dataset acquires patient health vitals using a variety of medical sensors and diagnostic instruments. Standard patient records are utilized to measure gender and age. A sphygmomanometer is used to measure Testbps and biochemical analyzers are used to measure Fbs and Chol. ECG devices record ST depression (Old Peak) and Restecg readings in order to identify irregularities in cardiac activity. During physical activity, heart rate (Thalach) is recorded using heart rate monitors. Stress test devices that monitor the heart’s reaction to exertion are used to evaluate Exang. Nuclear imaging scanners are used in thal to examine heart blood flow. Arterial blockages are revealed by the number of main vessels colored (Ca), which is determined by coronary angiography and fluoroscopy imaging. These cutting-edge medical sensors and diagnostic instruments guarantee precise data gathering for the study and prediction of cardiac disease.
3.3. Preprocessing of Dataset
After acquiring data, the dataset underwent preprocessing, which included handling missing values, normalization, and outlier treatment. Missing values were addressed using mean imputation, while outlier analysis revealed no significant deviation. The data were normalized using min-max scaling to transform values between 0 and 1, ensuring uniform input for the models. Finally, the output variable was converted from multiclass to binary, where 1 indicates the existence of heart attack, whereas 0 denotes no heart attack.
3.4. Dataset Imbalance Issue
Out of the total of 303 records in the dataset, 164 fall into the positive class (1) and 139 into the negative class (0). This uneven distribution of the data is a key factor contributing to the declining accuracy of classification models. Unbalance data is one of the most important factors that may adversely affect most ML models’ performance. In the current dataset, the negative class has fewer instances, which may lead to less reliable predictions due to insufficient data to capture its underlying patterns. To address this, data balancing techniques can be applied to ensure equal representation of both classes, leading to more accurate and reliable outcomes.
3.5. SMOTE for Data Balancing
SMOTE [65] is a widely used technique for handling class imbalance when building a classifier. An imbalanced dataset is one in which the underlying output classes are not evenly distributed. When dealing with the classification challenge of an imbalanced dataset, SMOTE is often employed [66]. SMOTE generates synthetic samples for the underrepresented class through interpolation, enhancing data diversity and improving model generalization. Therefore, SMOTE was applied to address the class imbalance issue by increasing the minority class instances. While SMOTE introduces synthetic examples during training, this can sometimes lead to less interpretable decision boundaries as these synthetic data points do not represent real observations. Moreover, SMOTE may increase model variance if the generated samples are overly simplistic or do not capture true underlying data patterns. Therefore, the model’s interpretability via SHAP and LIME was conducted on original test samples to preserve real-world interpretability. Furthermore, model performance was evaluated using 10-fold cross-validation.
3.6. ML Models
After preprocessing the data, multiple ML models were employed to evaluate their effectiveness in classification. KNN classified data points based on their closest neighbors, with k set to 3 for optimal performance. SVM constructed a decision boundary for classification using a linear kernel. LR models the relationship between dependent and independent variables to predict outcomes. RF, an ensemble of decision trees, was implemented with tuned hyperparameters to improve accuracy. NB, a probabilistic classifier based on Bayes’ theorem, assumes feature independence and is useful for sparse datasets. Additionally, Ensemble Learning techniques were explored, including Boosting, which iteratively improves weak models; Bagging, which enhances accuracy through resampling; and Majority Voting, where multiple classifiers’ predictions are aggregated to determine the final output. Furthermore, an ANN model was applied, outperforming all other ML algorithms in accuracy and robustness. For this study, a single-hidden-layer ANN was chosen to balance model complexity and interpretability and align with our focus on explainable models. In the following section, the proposed ANN model is elaborated.
3.7. Proposed ANN Model
The proposed ANN model consists of three layers: an input layer with 12 neurons using the ReLU activation function (AF), a hidden layer with 8 neurons also using ReLU, and an output layer with a sigmoid AF for binary classification (1 for yes, 0 for no). ReLU ensures that negative values are converted to zero, while sigmoid differentiates outputs into two classes. The architecture is designed to prevent overfitting, with hyperparameters optimized to a batch size of 10, 150 epochs, and a single hidden layer. The model minimizes the error between training and testing data by adjusting weights and biases during learning. Each neuron processes multiple inputs, applies weighted calculations with bias, and passes the result through an AF to generate an outcome, refining weights iteratively to improve accuracy.
AF will be given as follows:
where g is the AF applied to the outcomes of Equation (1).
Z = g(S)
The proposed ANN architecture is fully connected, meaning that every neuron in one layer is connected to every other layer’s neurons. Moreover, it also underlines that more focus should be placed on how a given network’s layer generates an output from a given input. Equation (3) summarizes the general equation for the generation of output for a given layer.
The equation applies to a single layer; however, the proposed architecture consists of an input layer, one hidden layer, and an output layer. The hidden layer processes the input layer’s output using similar calculations. Binary cross-entropy is employed as the loss function, making it suitable for binary classification tasks where two output classes are predicted.
In the binary cross-entropy function, represents the actual label (1 for a positive heart attack case and 0 for a negative one), and denotes the predicted probability of a positive case. The Adam optimizer [67] is employed to update the model’s weights, offering an adaptive estimation of the first- and second-order moments. Adam is computationally efficient, resource-friendly, and particularly effective for large-scale datasets with numerous parameters. Figure 2 shows the proposed neural network architecture used in the study.
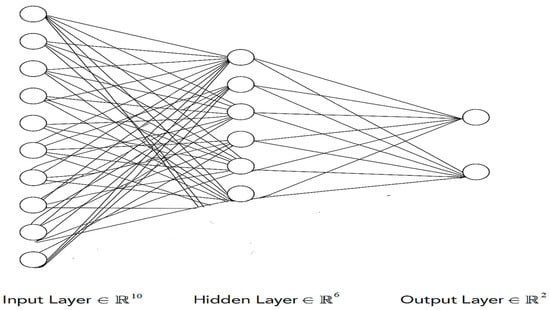
Figure 2.
Proposed ANN model architecture.
Hyperparameter tuning plays a critical role in improving classification accuracy [68,69]. While several techniques exist [70], no state-of-the-art method guarantees optimal tuning. In this research, the grid search technique [71] was employed to optimize hyperparameters for various ML models. Grid search involves testing multiple hyperparameter values to identify the best combination that yields the highest classification accuracy. The proposed ANN model utilizes the ReLU AF for input layers and a sigmoid AF for the output layer. It is trained with a batch size of 10 for 150 epochs, incorporating one hidden layer. To prevent overfitting, a dropout rate of 0.1 is applied. The model optimizes using the Adam optimizer and employs binary cross-entropy as the loss function for effective binary classification. The hyperparameters for all of the models are reported in Table 2.

Table 2.
Hyperparameters tuned for all models using grid search.
3.8. XAI Techniques
After applying various ML models for prediction, XAI techniques like LIME and SHAP were employed to improve the interpretability of the top-performing ANN model. LIME was used to produce local explanations for specific predictions by constructing simple, interpretable surrogate models that approximate the behavior of complex classifiers in a local neighborhood of individual data points. This enabled the critical features that influenced the predictions of the model for a particular patient, i.e., cholesterol levels, blood pressure, and age, to be identified. Healthcare professionals gained insight into why individual predictions were made, thus enhancing trust and transparency through the use of LIME. Global feature importance and dependency analysis between features were analyzed using SHAP. Feature interactions and nonlinear relationships were discovered using the SHAP dependency plots and provided deeper insights into the model’s decision-making process. For both classes, SHAP summary plots were generated to illustrate overall feature importance, while force and waterfall plots explained individual predictions by showing each feature’s contribution. Moreover, to gain insight into subgroup-specific trends, SHAP value analysis was carried out for both classes.
This study combined LIME and SHAP to obtain an overall and interpretable analysis of ML classifiers’ behavior. These techniques uncovered essential information on the key contributors to heart attack risk, like cholesterol, systolic blood pressure, and lifestyle habits, to help healthcare professionals with actionable information for diagnosis and treatment. In addition to improving the reliability and accuracy of the heart attack prediction system, XAI methods enabled increased trust and confidence in the predictions of the models, fulfilling the pressing need for transparency in healthcare AI applications.
3.9. Tools and Techniques
This proposed work makes use of the Anaconda platform, Tensor Flow (TF), and Keras to execute its intended task. The TF library is used as the backend for the implementation of neural networks. In order to create neural networks, the TF can process and analyze massive datasets using a graphical processing unit (GPU) and central processing unit (CPU). It is also supported by a variety of ML algorithms. Moreover, the Keras library is used for the implementation of ANN due to its simplicity. Due to the small size of the given dataset, a machine powered with a third-generation Intel Core i5-3320M processor (Santa Clara, CA, USA) is used for experimentations. It contains 500 GB of hard disk drive (HDD) storage and 4 GB of random access memory (RAM). Along with a local computer, Google Colab is also utilized for quick execution, especially for neural networks, followed by the application of XAI techniques to increase the classification models’ interpretability.
3.10. Statistical Evaluation
To rigorously compare classifier performance, we applied the paired t-test, a statistical method used to evaluate whether the mean difference between two paired sets of observations is significantly different from zero.
Formally, given two sets of paired measurements (e.g., ANN accuracies) and (e.g., Random Forest accuracies), we define the differences .
We calculate the following:
The mean difference is calculated as in Equation (5):
The standard deviation of the differences as highlighted in Equation (6):
The t-statistic is given by Equation (7):
The t-statistic is compared to the t-distribution with degrees of freedom to obtain the p-value. If , the difference is considered statistically significant. This test is well suited to model comparisons because we evaluate performance on the same data splits, making the pairs naturally dependent.
4. Results and Discussion
An imbalance dataset was used in the experimentation where SMOTE was applied to create a balance of classes within the dataset. Furthermore, various ML models were applied with the intention of finding the model that can best classify the given dataset. After experimentation, it was observed that SMOTE-based ANN has outperformed all other models with an accuracy of 96%. It is worth mentioning that in order to prevent data leakage and ensure valid performance estimation, SMOTE was applied only within the training folds during cross-validation rather than on the entire dataset before splitting. This prevents synthetic samples from appearing simultaneously in both training and test sets. Additionally, we included an external 20% holdout validation set to assess model generalization beyond cross-validation. In order to comprehensively assess the performance of ML algorithms, additional metrics such as precision, recall, and F1-score were utilized alongside accuracy. Table 3 depicts the evaluation results obtained after applying various ML algorithms on a balanced dataset before and after applying SMOTE. The results obtained for both classes show how SMOTE has effectively assisted in enhancing the evaluation results for the minor class, ultimately enhancing values for evaluation parameters. Moreover, to further analyze the impact of information leakage and the performance of ANN, we conducted a comprehensive comparative analysis of nine classifiers: ANN, Random Forest, SVM, KNN, Naive Bayes, Logistic Regression, AdaBoost, Bagging, and a Voting Ensemble using pairwise t-test. Using 30 repeated runs for each model, we calculated the average accuracy and applied paired t-tests comparing ANN’s performance against each alternative. ANN achieved a mean accuracy of 96.1%, outperforming all other models, with the next-best Random Forest averaging 85%. Paired t-tests revealed statistically significant differences in performance (all p-values < 0.0001), confirming that ANN’s superiority was not due to random variation but represents a robust, statistically validated improvement. The 95% confidence intervals for ANN’s accuracy (95.2–97.0%) showed no overlap with the confidence ranges of competing models, reinforcing its leading position. Figure 3 presents boxplots illustrating the accuracy distributions across all models, clearly demonstrating ANN’s dominance in both central tendency and spread. These results establish ANN as the most effective and reliable classifier for heart disease prediction within our study framework.

Table 3.
Average accuracy, precision, recall, and F1-measure of different ML algorithms applied on dataset before and after applying SMOTE.
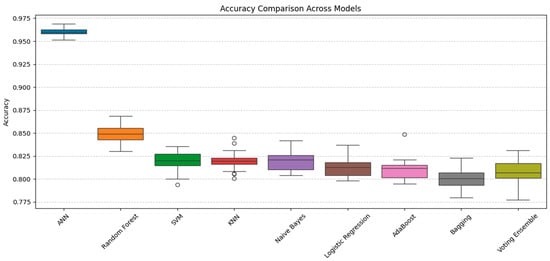
Figure 3.
The paired t-tests comparison of ANN’s performance against other models.
Furthermore, to ensure the reliability of results external holdout of 20% was also set for testing purposes. The holdout method, which involves consistently reserving a segment of the dataset for testing while utilizing the remainder for training, guarantees that model assessment accurately represents generalizability instead of overfitting to particular data divisions, hence enhancing the reliability of the provided metrics. Table 4 displays the average performance metrics—precision, recall, F1-measure, accuracy, and ROC-AUC—of various machine learning algorithms applied to the UCI Heart Disease dataset utilizing a cross-validation holdout of 20. The Artificial Neural Network (ANN) exhibits exceptional performance, achieving 95% accuracy, 95.3% precision, 94.9% recall, 94.8% F1-measure, and 98% ROC-AUC a, significantly surpassing traditional machine learning algorithms. Random Forest emerges as the most effective classical model, with 84% accuracy along with robust precision. Ensemble approaches, including Bagging, AdaBoost, and Voting Ensemble, attain moderate accuracies of approximately 80–81%, although individual models such as SVM, KNN, Logistic Regression, and Naive Bayes fall within the 80–82% accuracy range. Using the above results of the holdout, we further analyze the performance of ANN using ROC curve analysis, as shown in Figure 4. It evaluates the classification efficacy of several machine learning models, with each line illustrating the balance between true positive and false positive rates across different thresholds. The Artificial Neural Network (ANN) exhibits the greatest AUC of 0.98, signifying near-perfect class discrimination and markedly higher performance compared to the other models. The elevated AUC indicates that the ANN continuously attains an optimal balance between sensitivity and specificity, hence reducing both false positives and false negatives. Conversely, models such as Logistic Regression, Naive Bayes, and the Voting Ensemble exhibit lower AUCs of 0.72, indicating diminished overall classification efficacy. The diagonal dashed line (AUC = 0.5) signifies random chance, and the greater the distance of a model’s curve below this line, the superior its predictive capability—with ANN markedly surpassing all other models in this aspect. Further, to ensure the complete efficiency of obtained results, 10-fold cross-validation is also applied, as shown in Table 5. It can be observed from the above results that the ANN model demonstrated superior performance compared to traditional classifiers, as has also been shown in other disease prediction studies [72,73]. Despite ensemble methods typically performing well, ANN achieved the best balance between sensitivity and specificity after SMOTE was applied, highlighting its capacity to capture nonlinear relationships in the limited dataset. Moreover, Table 6 summarizes the training and testing times of all employed models. Bagging and RF demonstrated the fastest execution with only 2 s for training and 0.3 s for testing; however, the performance was notably low. In contrast, AdaBoost showed high computation time (61 s training, 6.1 s testing) but with comparatively lower performance. In contrast, ANN requires more time, like AdaBoost, i.e., 69 s for training and 5 s for testing, but the performance of ANN justifies its higher computational cost.

Table 4.
Average accuracy, precision, recall, and F1-measure of different ML algorithms applied on dataset with CV Holdout of 20.
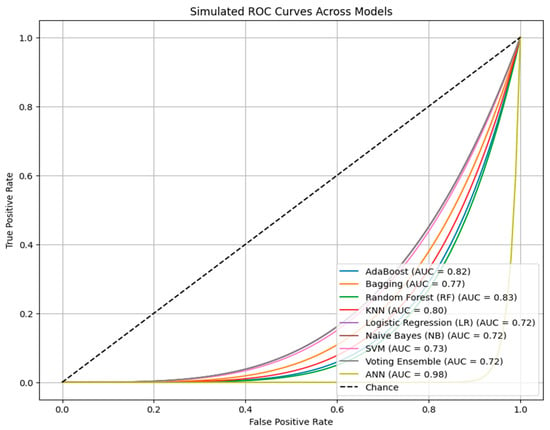
Figure 4.
The ROC curves for various ML algorithms applied in the study depicting the relationship between true positive and false positive rates.

Table 5.
Ten-fold cross-validation results for ANN.

Table 6.
Training and testing time of different ML algorithms applied on dataset after applying SMOTE.
XAI-Based Feature Importance Analysis
The main focus of this study is to integrate high-performing AI models with real-world applicability, ensuring that AI-driven heart attack prediction is both accurate and interpretable. To achieve this, (XAI) techniques, specifically LIME and SHAP, are applied to the optimal classification model, ANN.
This study focuses on enhancing model interpretability using the UCI Heart Disease dataset. LIME provides localized explanations by analyzing individual predictions, while SHAP offers global insights into feature importance, interactions, and subgroup trends. By integrating both methods, this research ensures greater transparency, reliability, and interpretability, enabling healthcare professionals to make informed, data-driven decisions for improved patient outcomes. In the rest of the section, we will examine the dataset across various XAI models in order to identify important features that are most important in regard to heart attack prediction.
Figure 5 shows the LIME analysis of the ANN model for heart attack risk assessment. The graph shows that one of the most useful features among all the features is “oldpeak”, which reveals its strong impact on the prediction. Moreover, “cp” and “thalach’ also contribute to model decisions, thus illustrating their clinical significance. Notably, the most important features are slope (weight = 0.08) and thal (weight ≈ 0.07), both showing negative correlations and having the greatest influence on the prediction of heart disease. The demographic factors “age” and “sex” are moderately important, as already shown to be the case with cardiovascular health. Finally, the importance of traditional metrics such as “trestbps”, “chol”, and “restecg” is lower in the model, which implies that these metrics do not have a prominent impact on the predictive outputs of the proposed model.
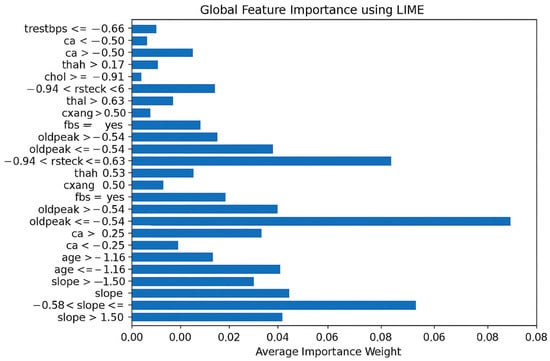
Figure 5.
Global feature importance using LIME.
Figure 6 showcases the LIME-based local explanation of the ANN model’s prediction. It indicates an 85% probability for the “Normal” class and 15% for “Abnormal”. Features supporting “Abnormal” include age (0.07 < age ≤ 0.73) and fasting blood sugar (fbs ≤ −0.39), suggesting slight heart condition risks. Conversely, slope (≤1.02), thal (≤−0.50), and maximum heart rate (thalach > 0.72) strongly oppose the “Abnormal” prediction, associating them with better cardiac health. Resting ECG (restecg ≤ 0.96) and cholesterol (chol ≤ −0.68) provide minor negative influences. The explanation highlights slope, thal, and thalach as key in reducing heart attack risk. This transparency enhances trust in the ANN’s decision-making for medical professionals.
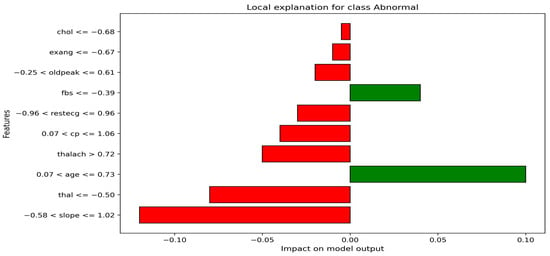

Figure 6.
LIME-based local explanation of the ANN.
Figure 7 visualizes local model explanations by displaying feature weights for a specific prediction. “Age” (0.07 < age ≤ 0.73) is the top positive contributor to the “Abnormal” class, indicating a higher heart attack risk. The strongest negative contributors favoring the “Normal” class are “slope” (−0.58 < slope ≤ 1.02) and “thal” (thal ≤ −0.50), suggesting a lower risk. “Maximum heart rate achieved” (thalach > 0.72) and “fasting blood sugar” (fbs ≤ −0.39) slightly support the “Abnormal” class, while “cholesterol” (chol ≤ −0.68) and “exercise-induced angina” (exang ≤ −0.67) mildly favor the “Normal” class. Features like “resting ECG” (restecg) and “chest pain type” (cp) have minimal impact on this prediction. The model’s decision is primarily influenced by “slope”, “thal”, and “age”, with “age” being the strongest abnormality indicator. However, opposing factors suggest the model leans toward predicting “Normal”. This visualization clarifies feature contributions, enhancing trust in the model’s healthcare applications.
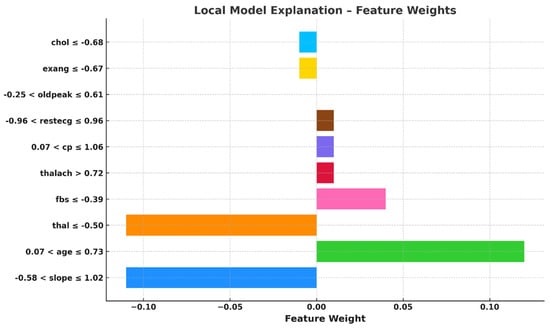
Figure 7.
Feature weights-based local explanation using LIME.
Figure 8 shows the SHAP summary plot for Class 1 (Abnormal), which corresponds to the patients who had heart attacks. It emphasizes the most important features affecting the models’ predictions. The graph concludes that “ca”, “cp”, and “thal” features are the most important features in determining whether a patient has a heart attack or not. The high values of “ca” have a high contribution to heart attack predictions, i.e., the higher the number of affected vessels, the higher the risk. Likewise, “cp” and abnormal “thal” values are also strong pointers.
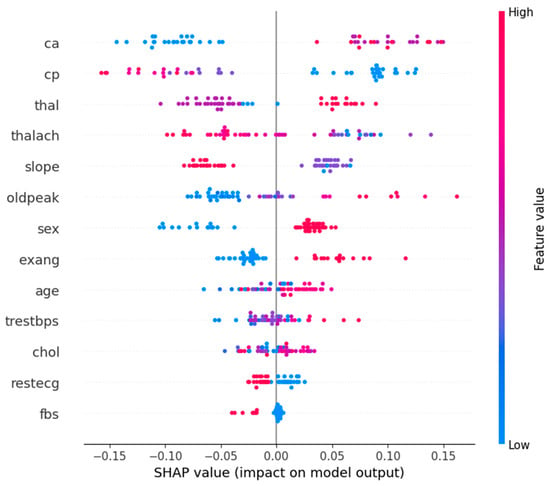
Figure 8.
Feature summary plot for Class 1.
On the contrary, small SHAP values for low “oldpeak” (ST depression) and “thalach” (maximum heart rate) correspond to low heart attack probability. In fact, the need for a holistic diagnostic approach is reinforced by the way complex interactions between features such as “slope”, “sex”, and “age” are captured by the model. The understanding of these feature contributions is clinically useful in helping healthcare professionals to prioritize key risk factors.
Figure 9 shows the SHAP summary plot for Class 0 (normal or not heart attack) patients with key features explained. Variables that contribute to normal classification are “cp”, “ca”, and “thal”, with comparatively low values within the graph. On the contrary, higher values of “oldpeak” and “thalach” tend to decrease the probability of being in a normal class, as these are indicative of heart problems. It shows how features like “slope” and “thalach” interact with each other to distinguish risk patients from normal patients. Clinically, “ca” and “thal” serve as strong indicators of normalcy, while “oldpeak” and “thalach” signal potential risks.
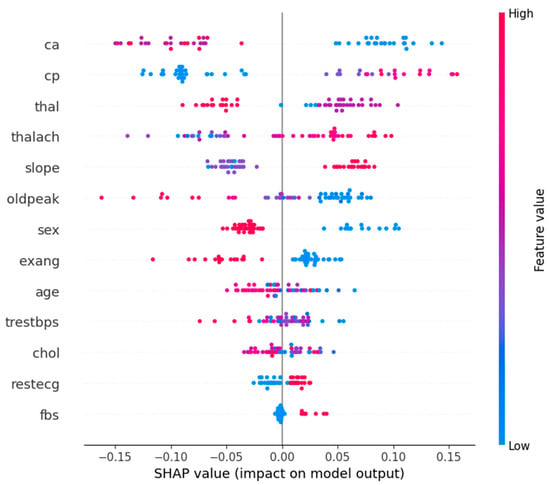
Figure 9.
Feature summary plot for Class 0.
Figure 10 shows the SHAP value analysis of Class 0 (normal) and Class 1 (heart attack). After analyzing the graph, key features that contribute to Class 0 are “cp”, “ca”, and “thal”. In Class 1, oldpeak (ST depression) and slope (heart’s stress response) have the highest influence, followed by cp and ca in the heart attack prediction. Sex and thalach (max heart rate) have moderate features, while fbs (fasting blood sugar) has minimal features. It can be observed for both classes that cp and ca are dominant predictors, but oldpeak and slope have a much higher influence in heart attack cases, further proving that they are clinically relevant.
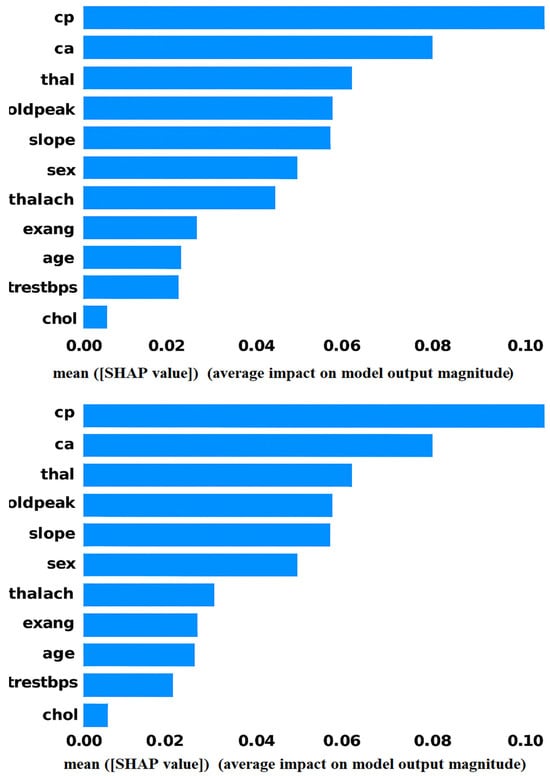
Figure 10.
Shape value analysis for both classes (a) Class 0 (Normal) and (b) Class 1 (heart attack).
Figure 11 illustrates the SHAP force plot, showing how individual features influence a specific heart attack (Class 1) prediction. Red arrows push the model toward higher risk, while blue arrows reduce it. Key risk factors include age (57), high resting blood pressure (150), and male sex, while protective factors like no major vessel narrowing (ca = 0), atypical angina (cp = 2), and high maximum heart rate (thalach = 174) lower the probability. The base value (0.5284) represents the model’s expected output, with a final prediction of f(x) = 0.101, indicating a low heart attack likelihood. Overall, normality-driving features dominate, leading to a classification closer to normal (Class 0).

Figure 11.
Feature shape force plot.
Figure 12 depicts the waterfall plot, which clearly shows how individual features influence the prediction of a heart attack. The strongest contributors to a higher likelihood of a heart attack are the absence of major vessel narrowing (ca = 0, +0.11), atypical angina (cp = 2, +0.10), and a high maximum heart rate (thalach = 174, +0.08). Additionally, a flat ST-segment slope (slope = 2, +0.07) and a fixed heart defect (thal = 2, +0.06) further push the model toward predicting a heart attack. Meanwhile, features like gender (sex = 1, −0.03) and other minor factors slightly reduce the risk, but their impact is relatively small compared to the risk-driving features. The final prediction (f(x) = 0.956) indicates a high likelihood of a heart attack, with the sum of all feature contributions leading to this outcome.
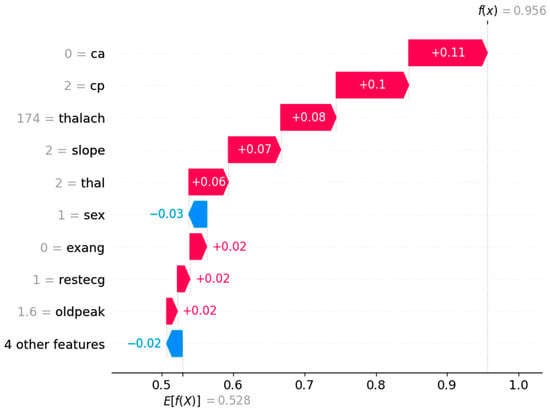
Figure 12.
Shape waterfall plot.
Figure 13 shows the SHAP dependence plots depicting how age and chest pain type (cp) influence heart attack predictions, showing their interactions with other features. The first plot shows that younger age reduces heart attack risk, while older age increases it, with a sharp rise in risk above 60. The second plot highlights that typical or no chest pain (low cp) has little impact, while atypical or non-anginal pain (high cp) significantly raises the risk, especially when combined with a higher number of blocked vessels (ca). Age and chest pain type are thus crucial predictors, with age steadily increasing risk and high cp values amplifying it further.
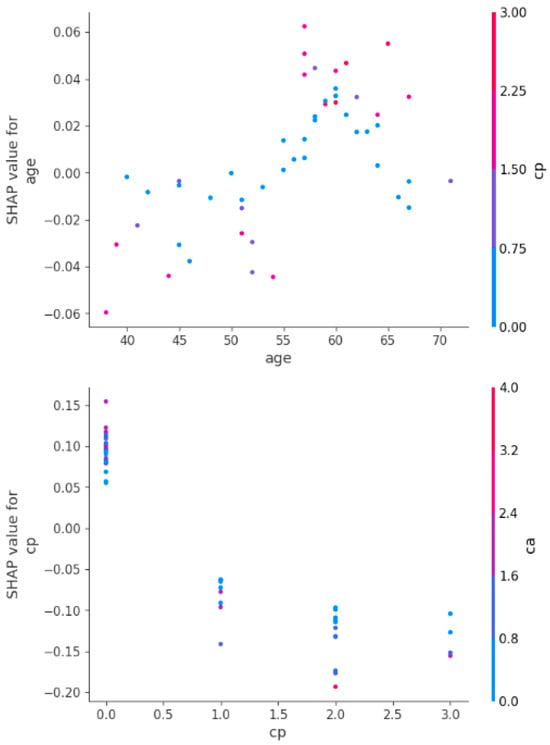
Figure 13.
Shape dependency plots for age and chest pain features.
It is important to note that LIME and SHAP provide complementary perspectives on feature importance. LIME explains local predictions by approximating the model’s behavior for individual instances, while SHAP offers global feature attributions across the entire dataset. We have ensured that the combined insights from both methods align with clinically validated risk factors and provide a holistic understanding for practitioners.
Based on the analysis of the results from various XAI techniques, such as SHAP and LIME, several key features emerged as significant predictors of heart attack risk. Age consistently played a crucial role, with its increasing values contributing to a higher risk, particularly for individuals over 60 years old. Chest pain type (cp) was another dominant feature, with atypical or non-anginal pain (high cp) significantly amplifying the risk of a heart attack, especially when combined with other factors like the number of blocked vessels (ca). Other critical features identified included oldpeak (ST depression), which strongly influenced heart attack predictions, and maximum heart rate (thalach), which helped differentiate between normal and abnormal heart conditions. These features consistently appeared as high-impact contributors in the model’s decision-making process.
Further examination of the feature interactions revealed that cholesterol levels (chol) and resting blood pressure (trestbps) also had important roles, though their influence was more moderate compared to the primary predictors. Slope, thalassemia test results (thal), and sex were identified as contributors that, when combined with other factors, could shift the prediction toward higher or lower heart attack risk. The combination of age, cp, and ca were especially influential, demonstrating a complex interaction between demographic factors, clinical indicators, and physiological measurements in predicting heart attack likelihood. These insights underscore the importance of incorporating these critical features for more accurate and explainable heart disease risk assessments.
5. Conclusions and Future Work
The main objective of this study is to predict heart disease occurrence using ML and DL models, emphasizing both predictive accuracy and model interpretability. Heart attack prediction was performed using the UCI dataset, which includes key cardiac health attributes such as heart rate, blood pressure, cholesterol levels, and stress test results. These parameters were collected through various medical sensors, including ECG sensors, blood pressure monitors, and biochemical analyzers. After tackling the class imbalance nature of the dataset, it was fed into various ML models, among which ANN demonstrated the highest classification performance, achieving 96% accuracy, 96.1% recall, and a 95.7% F1-score. By utilizing minimal data preprocessing, this method significantly reduces execution time compared to prior approaches. However, optimizing hyperparameters remains an area for further refinement to enhance predictive accuracy. Additionally, exploring advanced neural network architectures, such as adversarial networks or attention-based models, could potentially improve performance further.
The key contribution and novelty of this study is the integration of XAI techniques, specifically SHAP and LIME, to improve the interpretability of the outperforming ANN model. This focus on XAI distinguishes our work, enabling healthcare practitioners to comprehend the model’s decision-making process. These techniques provide transparency into the most influential sensor-derived features in heart disease prediction, fostering trust in AI-driven outcomes and supporting clinicians in making informed decisions. Improved interpretability ensures that the model’s predictions can be effectively adopted in real-world clinical settings, where understanding the rationale behind each decision is critical for patient care.
A key limitation of this study is the relatively small sample size of the dataset. Since the data are derived from an ICU cohort, caution is required when generalizing the findings to broader populations. Additionally, the limited dataset comprising 303 samples may contribute to model variance, even with the application of SMOTE and cross-validation. Additionally, given the small size of the UCI dataset and the synthetic nature of SMOTE-generated samples, future work should include larger, multicenter datasets and real-world clinical validation to ensure the robustness and generalizability of our findings.
Beyond heart disease prediction, the methodologies presented in this research can be extended to other critical conditions, including diabetes and cancer. Furthermore, incorporating Internet of Things (IoT) technology into the proposed framework would facilitate real-time monitoring of patients’ health metrics through wearable and non-invasive sensors, enabling proactive medical interventions. By combining accurate AI-driven predictions, enhanced interpretability through XAI techniques, and IoT-based healthcare solutions, this work may be adopted to develop a more transparent, efficient, and patient-centric healthcare system, bridging the gap between cutting-edge AI advancements and practical clinical applications. Furthermore, other interpretability techniques like Integrated Gradients, DeepLIFT, or Counterfactual Explanations could offer additional perspectives, and there are plans to explore them in future work. Similarly, the performance of LoRAS and ProWRAS can be assessed along with SMOTE.
Author Contributions
Conceptualization, M.W. and M.B.S.; methodology, M.W. and M.B.S.; software, M.W. and U.M.; validation, M.W., M.B.S. and H.D. (Hussain Dawood); formal analysis, M.W., M.B.S., H.D. (Hassan Dawood) and S.S.; investigation, M.B.S. and H.D. (Hussain Dawood); resources, M.W. and U.M.; data curation, M.W.; writing—original draft preparation, M.W. and M.B.S.; writing—review and editing, M.W., M.B.S., S.S., H.D. (Hassan Dawood), U.M. and H.D. (Hussain Dawood). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
This study utilizes a publicly available standard dataset, which can be accessed through the UCI Machine Learning Repository at https://archive.ics.uci.edu/ml/datasets/heart+disease [Accessed on 15 November 2024].
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ML | Machine learning |
| DL | Deep learning |
| XAI | Explainable AI |
| SMOTE | Synthetic Minority Over-sampling Technique |
| SHAP | SHapley Additive Explanations |
| LIME | Local Interpretable Model-Agnostic Explanations |
| FE | Feature engineering |
| AF | Activation function |
| ANN | Artificial Neural Networks |
| CVDs | Cardiovascular diseases |
| UCI | University of California, Irvine |
| DT | Decision Tree |
| LR | Logistic Regression |
| AUC | area under the curve |
| SMOTE-ENN | Synthetic Minority Over-sampling Technique—Edited Nearest Neighbors |
| ADASYN | Adaptive Synthetic Sampling |
| HDL | High-Density Lipoprotein |
| TF-IDF | Term Frequency – Inverse Document Frequency |
| NPC | Nasopharyngeal Carcinoma |
References
- Birger, M.; Kaldjian, A.S.; Roth, G.A.; Moran, A.E.; Dieleman, J.L.; Bellows, B.K. Spending on cardiovascular disease and cardiovascular risk factors in the United States: 1996 to 2016. Circulation 2021, 144, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Saqib, M.; Perswani, P.; Muneem, A.; Mumtaz, H.; Neha, F.; Ali, S.; Tabassum, S. Machine learning in heart failure diagnosis, prediction, and prognosis. Ann. Med. Surg. 2024, 86, 3615–3623. [Google Scholar] [CrossRef] [PubMed]
- Padda, I.; Fabian, D.; Farid, M.; Mahtani, A.; Sethi, Y.; Ralhan, T.; Das, M.; Chandi, S.; Johal, G. Social Determinants of Health and its Impacts on Cardiovascular Disease in Underserved Populations: A Critical Review. Curr. Probl. Cardiol. 2024, 49, 102373. [Google Scholar] [CrossRef]
- Sliwa, K.; Viljoen, C.A.; Stewart, S.; Miller, M.R.; Prabhakaran, D.; Kumar, R.K.; Thienemann, F.; Piniero, D.; Prabhakaran, P.; Narula, J.; et al. Cardiovascular disease in low-and middle-income countries associated with environmental factors. Eur. J. Prev. Cardiol. 2024, 31, 688–697. [Google Scholar] [CrossRef]
- Ezzati, M.; Obermeyer, Z.; Tzoulaki, I.; Mayosi, B.M.; Elliott, P.; Leon, D.A. Contributions of risk factors and medical care to cardiovascular mortality trends. Nat. Rev. Cardiol. 2015, 12, 508–530. [Google Scholar] [CrossRef]
- Ahmed, A.A.A.; Al-Shami, A.M.; Jamshed, S.; Zawiah, M.; Elnaem, M.H.; Mohamed Ibrahim, M.I. Awareness of the risk factors for heart attack among the general public in Pahang, Malaysia: A cross-sectional study. Risk Manag. Healthc. Policy 2020, 13, 3089–3102. [Google Scholar] [CrossRef]
- Consortium, G.C.R. Global effect of modifiable risk factors on cardiovascular disease and mortality. N. Engl. J. Med. 2023, 389, 1273–1285. [Google Scholar]
- Lopez, E.O.; Ballard, B.D.; Jan, A. Cardiovascular disease. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2023. [Google Scholar]
- Badawy, M.; Ramadan, N.; Hefny, H.A. Healthcare predictive analytics using machine learning and deep learning techniques: A survey. J. Electr. Syst. Inf. Technol. 2023, 10, 40. [Google Scholar] [CrossRef]
- Amiri, Z.; Heidari, A.; Navimipour, N.J.; Unal, M.; Mousavi, A. Adventures in data analysis: A systematic review of Deep Learning techniques for pattern recognition in cyber-physical-social systems. Multimed. Tools Appl. 2024, 83, 22909–22973. [Google Scholar] [CrossRef]
- Waqar, M.; Dawood, H.; Dawood, H.; Majeed, N.; Banjar, A.; Alharbey, R. An Efficient SMOTE-Based Deep Learning Model for Heart Attack Prediction. Sci. Program. 2021, 2021, 6621622. [Google Scholar] [CrossRef]
- Onakpojeruo, E.P.; Mustapha, M.T.; Ozsahin, D.U.; Ozsahin, I. A comparative analysis of the novel conditional deep convolutional neural network model, using conditional deep convolutional generative adversarial network-generated synthetic and augmented brain tumor datasets for image classification. Brain Sci. 2024, 14, 559. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, C.M.; Patel, P.; Ghetia, T.; Mazzeo, P.L. Effective heart disease prediction using machine learning techniques. Algorithms 2023, 16, 88. [Google Scholar] [CrossRef]
- Jindal, H.; Agrawal, S.; Khera, R.; Jain, R.; Nagrath, P. Heart disease prediction using machine learning algorithms. Mater. Sci. Eng. 2024, 392, 012072. [Google Scholar] [CrossRef]
- Stiglic, G.; Kocbek, P.; Fijacko, N.; Zitnik, M.; Verbert, K.; Cilar, L. Interpretability of machine learning-based prediction models in healthcare. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2020, 10, e1379. [Google Scholar] [CrossRef]
- Abdullah, T.A.; Zahid, M.S.M.; Ali, W. A review of interpretable ML in healthcare: Taxonomy, applications, challenges, and future directions. Symmetry 2021, 13, 2439. [Google Scholar] [CrossRef]
- Zacharias, J.; von Zahn, M.; Chen, J.; Hinz, O. Designing a feature selection method based on explainable artificial intelligence. Electron. Mark. 2022, 32, 2159–2184. [Google Scholar] [CrossRef]
- Kamsali, S.; Swathi, B.; Rudrakumar, M. Predictive Analytics in Healthcare by Leveraging Feature Engineering and Machine Learning. Afr. J. Bio. Sci. 2024, 6, 1437–1444. [Google Scholar]
- Qadri, A.M.; Raza, A.; Munir, K.; Almutairi, M.S. Effective feature engineering technique for heart disease prediction with machine learning. IEEE Access 2023, 11, 56214–56224. [Google Scholar] [CrossRef]
- Navin, K.; Nehemiah, H.K.; Nancy Jane, Y.; Veena Saroji, H. A classification framework using filter–wrapper based feature selection approach for the diagnosis of congenital heart failure. J. Intell. Fuzzy Syst. 2023, 44, 6183–6218. [Google Scholar] [CrossRef]
- Noroozi, Z.; Orooji, A.; Erfannia, L. Analyzing the impact of feature selection methods on machine learning algorithms for heart disease prediction. Sci. Rep. 2023, 13, 22588. [Google Scholar] [CrossRef]
- Abbasi, M.S.; Al-Sahaf, H.; Mansoori, M.; Welch, I. Behavior-based ransomware classification: A particle swarm optimization wrapper-based approach for feature selection. Appl. Soft Comput. 2022, 121, 108744. [Google Scholar] [CrossRef]
- Remeseiro, B.; Bolon-Canedo, V. A review of feature selection methods in medical applications. Comput. Biol. Med. 2019, 112, 103375. [Google Scholar] [CrossRef] [PubMed]
- Hassija, V.; Chamola, V.; Mahapatra, A.; Singal, A.; Goel, D.; Huang, K.; Scardapane, S.; Spinelli, I.; Mahmud, M.; Hussain, A. Interpreting black-box models: A review on explainable artificial intelligence. Cogn. Comput. 2024, 16, 45–74. [Google Scholar] [CrossRef]
- Ekanayake, I.; Meddage, D.; Rathnayake, U. A novel approach to explain the black-box nature of machine learning in compressive strength predictions of concrete using Shapley additive explanations (SHAP). Case Stud. Constr. Mater. 2022, 16, e01059. [Google Scholar] [CrossRef]
- Makumbura, R.K.; Mampitiya, L.; Rathnayake, N.; Meddage, D.; Henna, S.; Dang, T.L.; Hoshino, Y.; Rathnayake, U. Advancing water quality assessment and prediction using machine learning models, coupled with explainable artificial intelligence (XAI) techniques like shapley additive explanations (SHAP) for interpreting the black-box nature. Results Eng. 2024, 23, 102831. [Google Scholar] [CrossRef]
- Garreau, D.; Luxburg, U. Explaining the explainer: A first theoretical analysis of LIME. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 2–4 May 2024; pp. 1287–1296. [Google Scholar]
- Srinivasu, P.N.; Sirisha, U.; Sandeep, K.; Praveen, S.P.; Maguluri, L.P.; Bikku, T. An Interpretable Approach with Explainable AI for Heart Stroke Prediction. Diagnostics 2024, 14, 128. [Google Scholar] [CrossRef]
- Rezk, N.G.; Alshathri, S.; Sayed, A.; El-Din Hemdan, E.; El-Behery, H. XAI-Augmented Voting Ensemble Models for Heart Disease Prediction: A SHAP and LIME-Based Approach. Bioengineering 2024, 11, 1016. [Google Scholar] [CrossRef]
- Asuncion, A.; Newman, D. Uci Machine Learning Repository; Irvine, CA, USA, 2007. Available online: https://archive.ics.uci.edu/ml/datasets/heart+disease (accessed on 8 October 2024).
- Dritsas, E.; Trigka, M. Efficient data-driven machine learning models for cardiovascular diseases risk prediction. Sensors 2023, 23, 1161. [Google Scholar] [CrossRef]
- Oliveira, M.; Seringa, J.; Pinto, F.J.; Henriques, R.; Magalhães, T. Machine learning prediction of mortality in acute myocardial infarction. BMC Med. Inform. Decis. Mak. 2023, 23, 70. [Google Scholar] [CrossRef]
- Stonier, A.A.; Gorantla, R.K.; Manoj, K. Cardiac disease risk prediction using machine learning algorithms. Healthc. Technol. Lett. 2024, 11, 213–217. [Google Scholar] [CrossRef]
- Shahnawaz, M.B.; Dawood, H. An Effective Deep Learning Model for Automated Detection of Myocardial Infarction Based on Ultrashort-Term Heart Rate Variability Analysis. Math. Probl. Eng. 2021, 2021, 6455053. [Google Scholar] [CrossRef]
- Khera, R.; Haimovich, J.; Hurley, N.C.; McNamara, R.; Spertus, J.A.; Desai, N.; Rumsfeld, J.S.; Masoudi, F.A.; Huang, C.; Normand, S.-L. Use of machine learning models to predict death after acute myocardial infarction. JAMA Cardiol. 2021, 6, 633–641. [Google Scholar] [CrossRef]
- Li, X.; Shang, C.; Xu, C.; Wang, Y.; Xu, J.; Zhou, Q. Development and comparison of machine learning-based models for predicting heart failure after acute myocardial infarction. BMC Med. Inform. Decis. Mak. 2023, 23, 165. [Google Scholar] [CrossRef] [PubMed]
- de Capretz, P.O.; Björkelund, A.; Björk, J.; Ohlsson, M.; Mokhtari, A.; Nyström, A.; Ekelund, U. Machine learning for early prediction of acute myocardial infarction or death in acute chest pain patients using electrocardiogram and blood tests at presentation. BMC Med. Inform. Decis. Mak. 2023, 23, 25. [Google Scholar] [CrossRef] [PubMed]
- Alkhawaldeh, I.M.; Albalkhi, I.; Naswhan, A.J. Challenges and limitations of synthetic minority oversampling techniques in machine learning. World J. Methodol. 2023, 13, 373. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Khorshidi, H.A.; Aickelin, U. A review on over-sampling techniques in classification of multi-class imbalanced datasets: Insights for medical problems. Front. Digit. Health 2024, 6, 1430245. [Google Scholar] [CrossRef]
- Iacobescu, P.; Marina, V.; Anghel, C.; Anghele, A.-D. Evaluating Binary Classifiers for Cardiovascular Disease Prediction: Enhancing Early Diagnostic Capabilities. J. Cardiovasc. Dev. Dis. 2024, 11, 396. [Google Scholar] [CrossRef]
- Karamti, H.; Alharthi, R.; Anizi, A.A.; Alhebshi, R.M.; Eshmawi, A.A.; Alsubai, S.; Umer, M. Improving prediction of cervical cancer using knn imputed smote features and multi-model ensemble learning approach. Cancers 2023, 15, 4412. [Google Scholar] [CrossRef]
- Welvaars, K.; Oosterhoff, J.H.; van den Bekerom, M.P.; Doornberg, J.N.; van Haarst, E.P.; OLVG Urology Consortium; Machine Learning Consortium; van der Zee, J.A.; van Andel, G.A.; Lagerveld, B.W. Implications of resampling data to address the class imbalance problem (IRCIP): An evaluation of impact on performance between classification algorithms in medical data. JAMIA Open 2023, 6, ooad033. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Cheng, C.-H. A multiple combined method for rebalancing medical data with class imbalances. Comput. Biol. Med. 2021, 134, 104527. [Google Scholar] [CrossRef]
- Shaima, C.; Moorthi, P.V.; Shaheen, N.K. Cardiovascular diseases: Traditional and non-traditional risk factors. J. Med. Allied Sci. 2016, 6, 46. [Google Scholar] [CrossRef]
- Van Bussel, E.; Hoevenaar-Blom, M.; Poortvliet, R.; Gussekloo, J.; Van Dalen, J.; Van Gool, W.; Richard, E.; van Charante, E.M. Predictive value of traditional risk factors for cardiovascular disease in older people: A systematic review. Prev. Med. 2020, 132, 105986. [Google Scholar] [CrossRef]
- Kee, C.C.; Sumarni, M.G.; Lim, K.H.; Selvarajah, S.; Haniff, J.; Tee, G.H.H.; Gurpreet, K.; Faudzi, Y.A.; Amal, N.M. Association of BMI with risk of CVD mortality and all-cause mortality. Public Health Nutr. 2017, 20, 1226–1234. [Google Scholar] [CrossRef]
- Lee, H.; Shin, H.; Oh, J.; Lim, T.-H.; Kang, B.-S.; Kang, H.; Choi, H.-J.; Kim, C.; Park, J.-H. Association between body mass index and outcomes in patients with return of spontaneous circulation after out-of-hospital cardiac arrest: A systematic review and meta-analysis. Int. J. Environ. Res. Public Health 2021, 18, 8389. [Google Scholar] [CrossRef] [PubMed]
- Braun, J.; Patel, M.; Kameneva, T.; Keatch, C.; Lambert, G.; Lambert, E. Central stress pathways in the development of cardiovascular disease. Clin. Auton. Res. 2024, 34, 99–116. [Google Scholar] [CrossRef]
- Lee, Y.; Seo, J. Suggestion of statistical validation on feature importance of machine learning. In Proceedings of the 2023 45th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Sydney, Australiam, 24–27 July 2023; pp. 1–4. [Google Scholar]
- Mohd Faizal, A.S.; Hon, W.Y.; Thevarajah, T.M.; Khor, S.M.; Chang, S.-W. A biomarker discovery of acute myocardial infarction using feature selection and machine learning. Med. Biol. Eng. Comput. 2023, 61, 2527–2541. [Google Scholar] [CrossRef] [PubMed]
- Anthony, T.; Mishra, A.K.; Stassen, W.; Son, J. The feasibility of using machine learning to classify calls to South African emergency dispatch centres according to prehospital diagnosis, by utilising caller descriptions of the incident. Healthcare 2021, 9, 1107. [Google Scholar] [CrossRef]
- Ghafari, R.; Azar, A.S.; Ghafari, A.; Aghdam, F.M.; Valizadeh, M.; Khalili, N.; Hatamkhani, S. Prediction of the fatal acute complications of myocardial infarction via machine learning algorithms. J. Tehran Univ. Heart Cent. 2023, 18, 278. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Li, F.; Li, C.; Xu, H. Mortality prediction of inpatients with NSTEMI in a premier hospital in China based on stacking model. PLoS ONE 2024, 19, e0312448. [Google Scholar] [CrossRef]
- Senan, E.M.; Abunadi, I.; Jadhav, M.E.; Fati, S.M. Score and Correlation Coefficient-Based Feature Selection for Predicting Heart Failure Diagnosis by Using Machine Learning Algorithms. Comput. Math. Methods Med. 2021, 2021, 8500314. [Google Scholar] [CrossRef]
- Akter, S.B.; Akter, S.; Tuli, M.D.; Eisenberg, D.; Lotvola, A.; Islam, H.; Fernandez, J.F.; Hüttemann, M.; Pias, T.S. Fair and explainable Myocardial Infarction (MI) prediction: Novel strategies for feature selection and class imbalance correction. Comput. Biol. Med. 2025, 184, 109413. [Google Scholar] [CrossRef] [PubMed]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on explainable artificial intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Van der Velden, B.H.; Kuijf, H.J.; Gilhuijs, K.G.; Viergever, M.A. Explainable artificial intelligence (XAI) in deep learning-based medical image analysis. Med. Image Anal. 2022, 79, 102470. [Google Scholar] [CrossRef]
- Das, A.; Rad, P. Opportunities and challenges in explainable artificial intelligence (xai): A survey. arXiv 2020, arXiv:2006.11371. [Google Scholar]
- Aldughayfiq, B.; Ashfaq, F.; Jhanjhi, N.; Humayun, M. Explainable AI for retinoblastoma diagnosis: Interpreting deep learning models with LIME and SHAP. Diagnostics 2023, 13, 1932. [Google Scholar] [CrossRef]
- Alabi, R.O.; Elmusrati, M.; Leivo, I.; Almangush, A.; Mäkitie, A.A. Machine learning explainability in nasopharyngeal cancer survival using LIME and SHAP. Sci. Rep. 2023, 13, 8984. [Google Scholar] [CrossRef]
- Zhu, X.; Xie, B.; Chen, Y.; Zeng, H.; Hu, J. Machine learning in the prediction of in-hospital mortality in patients with first acute myocardial infarction. Clin. Chim. Acta 2024, 554, 117776. [Google Scholar] [CrossRef]
- Qi, X.; Wang, S.; Fang, C.; Jia, J.; Lin, L.; Yuan, T. Machine learning and SHAP value interpretation for predicting comorbidity of cardiovascular disease and cancer with dietary antioxidants. Redox Biol. 2025, 79, 103470. [Google Scholar] [CrossRef]
- Peng, S.; Huang, J.; Liu, X.; Deng, J.; Sun, C.; Tang, J.; Chen, H.; Cao, W.; Wang, W.; Duan, X. Interpretable machine learning for 28-day all-cause in-hospital mortality prediction in critically ill patients with heart failure combined with hypertension: A retrospective cohort study based on medical information mart for intensive care database-IV and eICU databases. Front. Cardiovasc. Med. 2022, 9, 994359. [Google Scholar]
- Bizimana, P.C.; Zhang, Z.; Hounye, A.H.; Asim, M.; Hammad, M.; El-Latif, A.A.A. Automated heart disease prediction using improved explainable learning-based technique. Neural Comput. Appl. 2024, 36, 16289–16318. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Blagus, R.; Lusa, L. SMOTE for high-dimensional class-imbalanced data. BMC Bioinform. 2013, 14, 1–16. [Google Scholar] [CrossRef]
- Ogundokun, R.O.; Maskeliunas, R.; Misra, S.; Damaševičius, R. Improved CNN based on batch normalization and adam optimizer. In Proceedings of the International Conference on Computational Science and Its Applications, Istanbul, Türkiye, 3 July 2025; pp. 593–604. [Google Scholar]
- Du, X.; Xu, H.; Zhu, F. Understanding the effect of hyperparameter optimization on machine learning models for structure design problems. Comput.-Aided Des. 2021, 135, 103013. [Google Scholar] [CrossRef]
- Onakpojeruo, E.P.; Mustapha, M.T.; Ozsahin, D.U.; Ozsahin, I. Enhanced MRI-based brain tumour classification with a novel Pix2pix generative adversarial network augmentation framework. Brain Commun. 2024, 6, fcae372. [Google Scholar] [CrossRef] [PubMed]
- Feurer, M.; Hutter, F. Hyperparameter Optimization; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Liashchynskyi, P.; Liashchynskyi, P. Grid search, random search, genetic algorithm: A big comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Uzun Ozsahin, D.; Precious Onakpojeruo, E.; Bartholomew Duwa, B.; Usman, A.G.; Isah Abba, S.; Uzun, B. COVID-19 prediction using black-box based Pearson correlation approach. Diagnostics 2023, 13, 1264. [Google Scholar] [CrossRef]
- Hsu, C.-T.; Huang, C.-Y.; Chen, C.-H.; Deng, Y.-L.; Lin, S.-Y.; Wu, M.-J. Machine learning models to predict osteoporosis in patients with chronic kidney disease stage 3–5 and end-stage kidney disease. Sci. Rep. 2025, 15, 11391. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).